Запись числа в двоичной системе счисления – Двоичная система счисления

Содержание

Что такое двоичная система счисления? Как перевести десятичное число в двоичное? :: SYL.ru

С двоичной системой счисления мы сталкиваемся при изучении компьютерных дисциплин. Ведь именно на базе этой системы построена работа процессора и некоторые виды шифрования. Существуют специальные алгоритмы для записи десятичного числа в двоичной системе и наоборот. Если знать принцип построения системы, оперировать в ней будет несложно.

Принцип построения системы из нулей и единиц

Двоичная система счисления построена с использованием двух цифр: ноль и один. Почему именно эти цифры? Это связано с принципом построения сигналов, которые используются в работе процессора. На самом низком уровне сигнал принимает только два значения: «ложь» и «истина». Поэтому было принято отсутствие сигнала, «ложь», обозначать нулем, а наличие его, «истину», единицей. Такое сочетание легко реализовать технически. Числа в двоичной системе формируются так же, как и в десятичной. Когда разряд достигает своей верхней границы, он обнуляется, и добавляется новый разряд. По такому принципу осуществляется переход через десяток в десятичной системе. Таким образом, числа состоят из сочетаний нулей и единиц, и это сочетание называется «двоичная система счисления».

Запись числа в системе
В десятичной	В двоичной	В десятичной	В двоичной
0	0	5	101
1	1	6	110
2	10	7	111
3	11	8	1000
4	100	9	1001

Как двоичное число записать в виде десятичного?

Существуют онлайн-сервисы, которые осуществляют перевод числа в двоичную систему и наоборот, но лучше уметь делать это самостоятельно. Двоичная система при переводе обозначается нижним индексом 2, например, 101₂. Каждое число в любой системе можно представить в виде суммы чисел, например: 1428 = 1000 + 400 + 20 + 8 – в десятичной системе. Так же представляется число в двоичной. Возьмем произвольное число 101 и рассмотрим его. В нем 3 разряда, поэтому раскладываем число по порядку таким способом: 101₂=1×2²+0×2¹+1×2⁰=4+1=5_10,где индекс 10 обозначает десятичную систему.

Как записать простое число в двоичной системе?

Очень легко осуществить перевод в двоичную систему счисления с помощью деления числа на два. Делить необходимо до тех пор, пока это будет возможно выполнить нацело. Например, возьмем число 871. Начинаем делить, обязательно записывая остаток:

871:2=435 (остаток 1)

435:2=217 (остаток 1)

217:2=108 (остаток 1)

108:2=54 (остаток 0) и так далее до конца.

Ответ записывается по полученным остаткам по направлению от конца к началу: 871₁₀=101100111₂. Проверить правильность вычислений можно с помощью обратного перевода, описанного ранее.

Для чего нужно знать правила перевода?

Двоичная система счисления применяется в большинстве дисциплин, связанных с микропроцессорной электроникой, кодированием, передачей и шифрованием данных, в различных направлениях программирования. Знания основ перевода из любой системы в двоичную помогут программисту разрабатывать различные микросхемы и осуществлять управление работой процессора и других подобных систем программным способом. Двоичная система счисления также необходима для реализации способов передачи пакетов данных по зашифрованным каналам и создания на их основе программных проектов типа «Клиент-сервер». В школьном курсе информатики основы перевода в двоичную систему и наоборот являются базовым материалом для изучения программирования в будущем и создания простейших программ.

www.syl.ru

Двоичная система счисления, 0 и 1, двоичные числа

Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:

Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.

Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.

Общая форма записи двоичных чисел

Для целых двоичных чисел можно записать:

a_n−1a_n−2…a₁a₀=a_n−1⋅2ⁿ⁻¹+a_n−2⋅2ⁿ⁻²+…+a₀⋅2⁰

Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Правила сложения двоичных чисел

Основные правила сложения однобитовых чисел

0+0=0
0+1=1
1+0=1
1+1=10

Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.

Пример сложения двоичных чисел

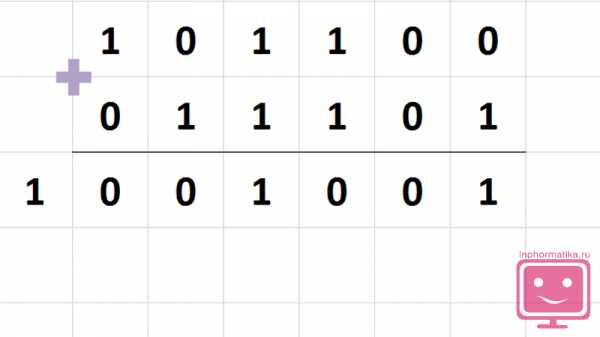
Правила вычитания двоичных чисел

0-0=0
1-0=0
10-1=1

Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.

Вычитание методом заимствования

Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.

Вот несколько простых примеров:

1 — 0 = 1
11 — 10 = 1
1011 — 10 = 1001

Рассмотрим более сложную задачу. Вы должны запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 — 1).

110 — 101 = ?

В первом столбце справа вы получаете разность 0 — 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).

Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 1010 — 101 = ?
Вы вычли («позаимствовали») 10 из первого числа, поэтому вы можете написать это число вместо цифры, стоящей справа (в разряд единиц). 101100 — 101 = ?
Вычтите цифры в правом столбце. В нашем примере:
101100 — 101 = ?
Правый столбец: 10 — 1 = 1.
102 = (1 x 2) + (0 x 1) = 210 (цифры нижнего регистра обозначают систему счисления, в которой записаны числа).
12 = (1×1) = 110.

Таким образом, в десятичной системе эта разность записывается в виде: 2 — 1 = 1.

Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):

101100 — 101 = __1 = _01 = 001 = 1.

Вычитание методом дополнения

Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.

Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).

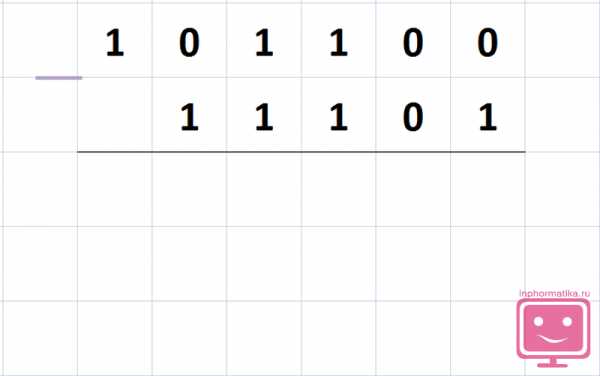
Рассмотрим пример: 101100₂— 11101₂= ?

Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.

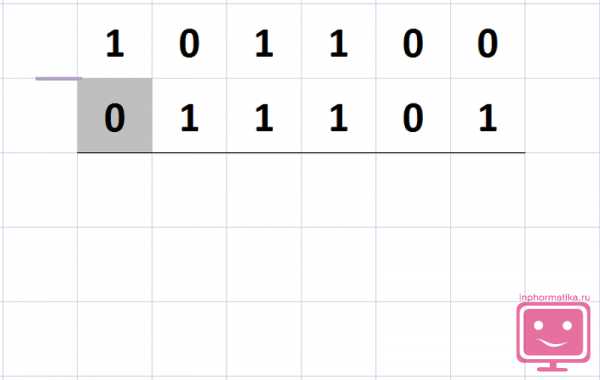
101100₂ — 011101₂= ?

В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.

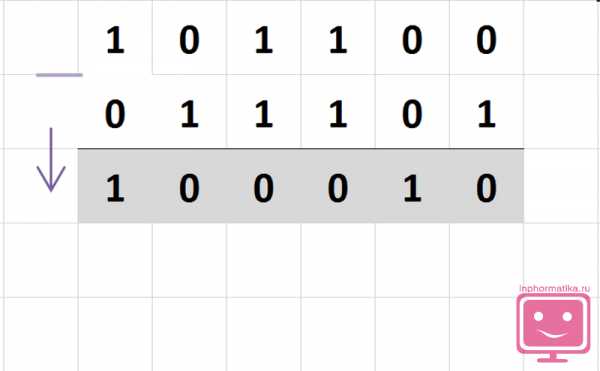
011101₂ → 100010₂.

На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 — 0 = 1 и 1 — 1 = 0.

К полученному вычитаемому прибавьте единицу.

100010₂+ 1₂ = 100011₂

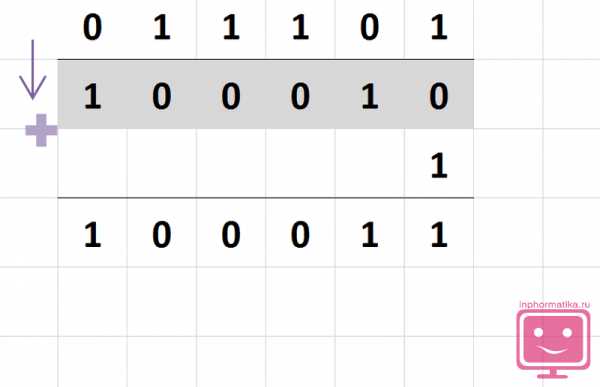
Теперь вместо вычитания сложите два двоичных числа.

101100₂ +100011₂= ?

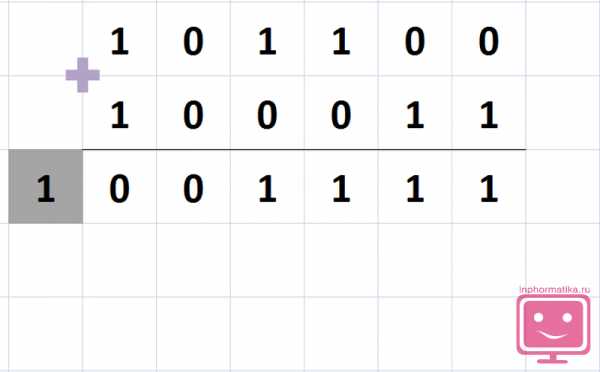
Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.

1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 101101₂ нужно вычесть 11011₂

2) Обозначим как A число 101101₂ и как B число 11011₂.

3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).

Разр.	6	5	4	3	2	1	0
A		1	0	1	1	0	1
B			1	1	0	1	1

4) Вычтем разряд за разрядом из числа A число B записывая результат в C начиная с младших разрядов. Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.

Заем из текущего разряда O_i-1	A_i	B_i	C_i	Заем из следующего разряда O_i+1
	0	0	0
	0	1	1	1
	1	0	1
	1	1	0
1	0	0	1	1
1	0	1	0	1
1	1	0	0
1	1	1	1	1

Весь процесс сложения наших чисел выглядит следующим образом:

(красным шрифтом показаны заёмы из соответствующего разряда)

Получилось 101101₂ — 11011₂ = 10010₂
или в десятичной системе счисления: 45₁₀ — 27₁₀ = 18₁₀

Правила умножения двоичных чисел.

В целом эти правила очень просты и понятны.

0*0=0
0*1=0
1*0=0
1*1=1

Умножение многоразрядных двоичных чисел происходит точно также как и обычных. Каждое значащий разряд умножаем на верхнее число по приведенным правилам, соблюдая позиции. Умножать просто — так как умножение на единицу даёт одно и тоже число.

×				1	1	1	0
×					1	0	1

+				1	1	1	0
+		1	1	1	0

	1	0	0	0	1	1	0

Система счисления Методы перевода десятичного числа в двоичное

inphormatika.ru

Урок №32 Двоичная система счисления

Основные темы параграфа:

♦ десятичная и двоичная системы счисления;
♦ развернутая форма записи числа;
♦ перевод двоичных чисел в десятичную систему;
♦ перевод десятичных чисел в двоичную систему;
♦ арифметика двоичных чисел.

В данной главе речь пойдет об организации вычислений на компьютере. Вычисления связаны с хранением и обработкой чисел.

Компьютер работает с числами в двоичной системе счисления.

Эта идея принадлежит Джону фон Нейману, сформулировавшему в 1946 году принципы устройства и работы ЭВМ. Выясним, что такое система счисления.

Десятичная и двоичная системы счисления

Системой счисления называют определенные правила записи чисел и связанные с ними способы выполнения вычислений.

нас будут интересовать двоичная и десятичная системы счисления.

Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число цифр определяет основание системы счисления. Если число цифр — десять, то основание системы счисления равно десяти. В двоичной же системе существует всего две цифры: 0 и 1. Основание равно двум. Возникает вопрос, можно ли с помощью всего двух цифр представить любую величину. Оказывается, можно!

Развернутая форма записи числа

Вспомним принцип записи чисел в десятичной системе счисления. Значение цифры в записи числа зависит не только от самой цифры, но и от места расположения этой цифры в числе (говорят: от позиции цифры). Например, в числе 333 первая справа цифра обозначает: три единицы, следующая — три десятка, следующая — три сотни. Этот факт можно выразить равенством:

333₁₀ = 3 · 10² + 3 · 10¹ + 3 · 10⁰ = 300 + 30 + 3.

В данном равенстве выражение, стоящее справа от знака «равно», называется развернутой формой записи многозначного числа. Вот еще пример развернутой формы записи многозначного десятичного числа:

8257₁₀ = 8 · 10³ + 2 · 10² + 5 · 10¹ + 7 · 10⁰= 8000 + 200 + 50 + 7.

Таким образом, с продвижением от цифры к цифре справа налево «вес» каждой цифры увеличивается в 10 раз. Это связано с тем, что основание системы счисления равно десяти.

Перевод двоичных чисел в десятичную систему

А вот пример многозначного двоичного числа:

110101₂.

Двойка внизу справа указывает на основание системы счисления. Это нужно для того, чтобы не перепутать двоичное число с десятичным. Ведь существует же десятичное число 110101! Вес каждой следующей цифры в двоичном числе при продвижении справа налево возрастает в 2 раза. Развернутая форма записи данного двоичного числа выглядит так:

110101₂ = 1 · 2⁵+ 1 · 2⁴ + 0 · 2³ + 1 · 2² + 0 · 2¹ + 1 · 2⁰ = 53₁₀.

Таким способом мы перевели двоичное число в десятичную систему.

Переведем в десятичную систему еще несколько двоичных чисел.

10₂ = 2¹ = 2; 100₂= 2² = 4; 1000₂ = 2³ = 8;
10000₂ = 2⁴ = 16; 100000₂ = 2⁵ = 32 и т. д.

Таким образом, получилось, что двузначному десятичному числу соответствует шестизначное двоичное! И это характерно для двоичной системы: быстрый рост количества цифр с увеличением значения числа.

Вот как выглядит начало натурального ряда чисел в десятичной (А₁₀) и двоичной (А₂) системах счисления:

A₁₀	1	2	3	4	5	6	7	8	9	10
A₂	1	10	11	100	101	110	111	1000	1001	1010

A₁₀	11	12	13	14	15	16	17	18	19	20
A₂	1011	1100	1101	1110	1111	10000	10001	10010	10011	10100

Перевод десятичных чисел в двоичную систему

Как перевести двоичное число в равное ему десятичное, вам должно быть понятно из рассмотренных выше примеров. А как осуществить обратный перевод: из десятичной системы в двоичную? Для этого нужно суметь разложить десятичное число на слагаемые, представляющие собой степени двойки. Например:

15₁₀ = 8 + 4 + 2 + 1 = 1 · 2³ + 1 · 2² + 1 · 2¹ + 1 · 2⁰ = 1111₂.

Это сложно. Есть другой способ, с которым мы сейчас и познакомимся.

Существует процедура, позволяющая легко выполнить перевод десятичного числа в двоичную систему. Она состоит в том, что данное десятичное число делится на 2. Полученный остаток — это младший разряд искомого числа. Полученное частное снова делится на 2, полученный при этом остаток — это следующий разряд искомого числа. Так продолжается до тех пор, пока частное не станет меньше двойки (основания системы). Это частное — старшая цифра искомого числа.

Существуют два способа записи деления на 2. Продемонстрируем это на примере перевода числа 37 в двоичную систему.

Здесь а₅, а₄, а₃, а₂, а₁, а₀ — обозначения цифр в записи двоичного числа по порядку слева направо. В результате перевода получим: 37₁₀ = 100101₂.

Арифметика двоичных чисел

Правила двоичной арифметики гораздо проще правил десятичной арифметики. Вот все возможные варианты сложения и умножения однозначных двоичных чисел.

0 + 0 = 0                      0 x 0 = 0
0 + 1 = 1                      0 x 1 = 0
1 + 0 = 1                      1 x 0 = 0
1 + 1 = 10                    1 x 1 = 1

Своей простотой и согласованностью с битовой структурой компьютерной памяти двоичная система счисления и привлекла изобретателей компьютера. Ее гораздо проще реализовать техническими средствами, чем десятичную систему.

Вот пример сложения столбиком двух многозначных двоичных чисел:

1011011101
+111010110
10010110011

А теперь посмотрите внимательно на следующий пример умножения многозначных двоичных чисел:

1101101
x 101
1101101
1101101
1000100001

После небольшой тренировки любой из вас такие вычисления будет выполнять автоматически.

Коротко о главном

Система счисления — определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений.

Основание системы счисления равно количеству используемых в ней цифр.

Двоичные числа — числа в двоичной системе счисления. В их записи используются две цифры: 0 и 1.

Развернутая форма записи двоичного числа — это его представление в виде суммы степеней двойки, умноженных на 0 или на 1.

Использование двоичных чисел в компьютере связано с битовой структурой компьютерной памяти и простотой двоичной арифметики.

Вопросы и задания

1. Назовите преимущества и недостатки двоичной системы счисления по сравнению с десятичной.
2. Какие двоичные числа соответствуют следующим десятичным числам:
128; 256; 512; 1024?
3. Чему в десятичной системе равны следующие двоичные числа:
1000001; 10000001; 100000001; 1000000001?
4. Переведите в десятичную систему следующие двоичные числа:
101; 11101; 101010; 100011; 10110111011.
5. Переведите в двоичную систему счисления следующие десятичные числа:
2; 7; 17; 68; 315; 765; 2047.
6. Выполните сложение в двоичной системе счисления:
11 + 1; 111 + 1; 1111 + 1; 11111 + 1.
7. Выполните умножение в двоичной системе счисления:
111 · 10; 111 · 11; 1101 · 101; 1101 · 1000.

Домашнее задание N 12

Редактировалось Дата: Воскресенье, 03 Февраль 2019

www.fordus.org.ua

Двоичная система счисления

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.

Сложение, вычитание и умножение двоичных чисел.

Таблица сложения

Пример: 1001 + 10 = 1011

Таблица вычитания

Пример: 1111101 — 10001 = 1101100

Таблица умножения

Пример: 1111 · 1001 = 10000111

Перевод чисел.

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

Пример: 73₁₀ = 1001001₂

Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.

Пример: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). Представим его в виде суммы степеней с основанием 2: 10110110₂ = (1·2⁷)+(0·2⁶)+(1·2⁵)+(1·2⁴)+(0·2³)+(1·2²)+(1·2¹)+(0·2⁰) = 128+32+16+4+2 = 182₁₀

Другие заметки по информатике

edu.glavsprav.ru

Бинарные числа: двоичная система счисления

Бинарные числа — это числа из двоичной системы счисления, имеющей основание 2. Она непосредственно реализована в цифровой электронике, используется в большинстве современных вычислительных устройств, включая компьютеры, мобильные телефоны и разного рода датчики. Можно сказать, что все технологии нашего времени построены на бинарных числах.

Запись чисел

Любое число, сколь бы большим оно ни было, в двоичной системе записывается посредством двух символов: 0 и 1. Например цифра 5 из всем знакомой десятичной системы в двоичной будет представлено как 101. Бинарные числа могут быть обозначены префиксом 0b или амперсандом (&), например: &101.
Во всех системах счисления, исключая десятичную, символы читаются по одиночке, то есть взятое в пример 101 читается как «один ноль один».

Перевод из одной системы в другую

Программисты, постоянно работающие с двоичной системой счисления, на ходу могут перевести бинарное число в десятичное. Это действительно можно сделать и без всяких формул, особенно если человек имеет представление о том, как работает самая малая часть компьютерного «мозга» — бит.

Цифра ноль так же обозначает 0, а цифра один в двоичной системе тоже будет единицей, но что делать дальше, когда цифры закончились? Десятичная система «предложила» бы в таком случае ввести термин «десяток», а в бинарной системе это будет называться «двойка».

Если 0 это &0 (амперсанд — обозначение двоичной системы), 1 = &1, то 2 будет обозначаться как &10. Тройку тоже можно записать в двух разрядах, она будет иметь вид &11, то есть одна двойка и одна единица. Возможные комбинации исчерпаны, и в десятичной системе на этом этапе вводятся сотни, а в двоичной — «четверки». Четыре — это &100, пять — &101, шесть — &110, семь — &111. Следующая, более крупная единица счета — это восьмерка.

Можно заметить особенность: если в десятичной системе разряды умножаются на десять (1, 10, 100, 1000 и так далее), то в двоичной, соответственно, на два: 2, 4, 8, 16, 32. Это соответствует размеру флеш-карт и прочих накопителей, использующихся в компьютерах и других устройствах.

Что такое бинарный код

Числа, представленные в двоичной системе счисления, называются бинарными, однако в таком виде можно представить и не числовые значения (буквы и символы). Таким образом, в цифрах можно закодировать слова и тексты, правда вид они будут иметь не столь лаконичный, ведь для записи всего одной буквы потребуется несколько нолей и единиц.

Но каким образом компьютерам удается считывать такое количество информации? На самом деле все проще, чем кажется. Люди, привыкшие к десятичной системе счисления, сначала переводят двоичные числа в более привычные, и только потом производят с ними какие-либо манипуляции, а в основе компьютерной логики изначально лежит бинарная система чисел. Единице в технике соответствует высокое напряжение, а нулю — низкое, либо для единицы напряжение есть, а для ноля вообще отсутствует.

Бинарные числа в культуре

Ошибкой будет считать, что двоичная система счисления — это заслуга современных математиков. Хотя бинарные числа и являются основополагающими в технологиях нашего времени, использовались они уже очень давно, причем в разных уголках планеты. Используются длинная линия (единица) и прерывистая (ноль), кодирующие восемь символов, означающих восемь стихий: небо, землю, гром, воду, горы, ветер, огонь и водоем (массу воды). Этот аналог 3-битных цифр описывался в классическом тексте книги Перемен. Триграммы составляли 64 гексаграммы (6-битные цифры), порядок которых в книге Перемен был расположен в соответствии с двоичными цифрами от 0 до 63.

Этот порядок был составлен в одиннадцатом веке китайским ученым Шао Юном, хотя нет доказательств того, что он действительно понимал двоичную систему счисления в целом.

В Индии еще до нашей эры тоже применялись бинарные числа в математической основе для описания поэзии, составленные математиком Пингалой.

Узелковая письменность инков (кипу) считается прообразом современных баз данных. Именно они впервые применили не только бинарный код числа, но и не числовые записи в двоичной системе. Узелковое письмо кипу характерно не только первичными и дополнительными ключами, но и использованием позиционных чисел, кодированием с помощью цвета и сериями повторений данных (циклами). Инки впервые применили способ ведения бухгалтерского учета, называемый двойной записью.

Первый из программистов

Двоичную систему счисления, основанную на цифрах 0 и 1, описал и знаменитый ученый, физик и математик, Готфрид Вильгельм Лейбниц. Он увлекался древней китайской культурой и, изучая традиционные тексты книги Перемен, заметил соответствие гексаграмм бинарным числам от 0 до 111111. Он восхитился свидетельствам подобных достижений в философии и математике для того времени. Лейбница можно назвать первым из программистов и информационных теоретиков. Именно он обнаружил, что если записать группы двоичных чисел вертикально (одно под другим), то в получившихся вертикальных столбцах чисел будут регулярно повторяться ноли и единицы. Это позвонило ему предположить, что возможно существование совершенно новых математических законов.

Лейбниц понял и то, что бинарные числа оптимальны для применения в механике, основой которой должна быть смена пассивных и активных циклов. На дворе был 17 век, а этот великий ученый изобрел на бумаге вычислительную машину, работавшую на основе его новых открытий, однако быстро понял, что цивилизация еще не достигла такого технологического развития, и в его время создание такой машины будет невозможным.

fb.ru

таблица, примеры десятичной, восьмеричной и других систем

Самой короткой системой счисления является двоичная. Она полностью основана на позиционной форме записи числа. Основной характеристикой считается принцип удвоения цифры при выполнении перехода от определённой позиции к последующей. Из одной системы счисления в другую можно осуществить перевод как при помощи специальной программы, так и вручную.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Историческое признание

Появление двоичной СС в истории связано с учёным математиком В.Г. Лейбницем. Именно он впервые заговорил о правилах выполнения операций с числовыми значениями данного рода. Но первоначально этот принцип остался невостребованным. Мировое признание и применение алгоритм получил на заре возникновения вычислительных машин.

Удобство и несложность выполнения операций привели к необходимости более детального изучения данного подраздела арифметики, который стал незаменимым при развитии компьютерной технологии с программным обеспечением. Впервые такие механизмы появились на немецком и французском рынках.

Внимание! Конкретную точку над превосходством двоичной системы по отношению десятичной, именно в данной отрасли, было поставлено в 1946 году и обосновано в статье А. Бекса, Х. Гольдстайна и Дж.Фон Неймана.

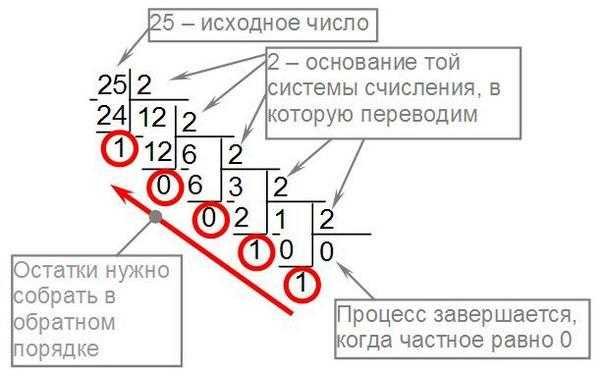
Перевод числа из десятичной системы счисления в двоичную.

Особенности двоичной арифметики

Вся двоичная СС основана на применении только двух символов, которые очень точно совпадают с особенностями цифровой схемы. Каждый из символов отвечает за определённое действие, которое зачастую подразумевает два состояния:

наличие отверстия или его отсутствие, к примеру, перфокарты или перфоленты;
на магнитных носителях отвечает за состояние намагничивания или размагничивания;
по уровню сигнала, высокий или низкий.

В науке, в которой применяется СС, введена определённая терминология, суть ее состоит в следующем:

Бит – двоичный разряд, который состоит из двух составляющих, несущих в себе определённый смысл. Размещённый слева, определяется как старший и является приоритетным, а справа – младшим, являющийся менее весомым.
Байт – это единица, которая состоит из восьми битов.

Многие модули воспринимают и обрабатывают информацию порциями или словами. Каждое слово имеет разный вес и может состоять из 8-ми, 16-ти или 32-х битов.

Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения

Правила переводов из одной системы в другую

Одним из важнейших факторов арифметики машин является перевод из одной СС в другую. Поэтому обратим внимание на основные алгоритмы выполнения процесса, который покажет, как перевести число в двоичную систему.

Переводим десятичную систему в двоичную

Первоначально обратимся к вопросу, как осуществить перевод системы из десятичной в двоичную систему счисления. Для этого существует правило перевода из десятичных чисел в двоичный код, которое подразумевает математические действия.

Необходимо число, записанное в десятичном виде разделить на 2. Деление выполнять до тех пор, пока в частном не останется единица. Если необходима двоичная система счисления перевод осуществляется так:

186:2=93 (ост. 0)

93:2=46 (ост. 1)

46:2=23 (ост. 0)

23:2=11 (ост. 1)

11:2=5 (ост. 1)

5:2=2 (ост.1)

2:2=1

После того, как процесс деления закончен, то единицу в частном и все остатки записываем последовательно в обратном делению порядке. То есть, 18610=1111010. Правило перевода десятичных чисел в СС надо соблюдать всегда.

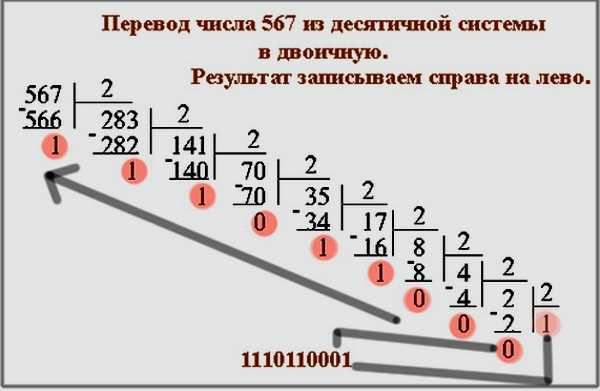
Перевод числа из десятичной системы в двоичную.

Это интересно! Изучение основных правил умножения: как из неправильной дроби сделать правильную

Перевод из десятичной СС в восьмеричную

Аналогичный процесс проводится при переводе из десятичной СС в восьмеричную. Его ещё называют «правилом замещения». Если в предыдущем примере деление данных осуществлялось на 2, то здесь необходимо делить на 8. Алгоритм перевода числа X10 в восьмеричную состоит из следующих шагов:

Число X10 начинают делить на 8. Полученное частное берём для следующего деления, а остаток записывается, как бит младшего порядка.
Продолжаем деление до тех пор, пока не получим в результат частного равного нулю или остаток, который по своему значению меньше восьми. При этом все остатки записываем, как младшие порядки бита.

К примеру, необходимо перевести число 160110 в восьмеричное.

1601:8=200 (ост. 1)

200:8=25 (ост. 0)

25:8=3 (ост.1)

Итак, получим: 161010=31018.

Перевод из десятичной системы в восьмеричную.

Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством

Записываем десятичное число шестнадцатеричным

Перевод из десятичной в шестнадцатиричную СС осуществляется аналогично с использованием системы замещения. Но кроме цифр применяют ещё и буквы латинского алфавита A, B, C, D, E, F. Где A обозначает остаток 10, а F остаток 15. Десятичное число делят на 16. К примеру, переводим 10710 в шестнадцатеричную:

107:16=6 (ост. 11 – заменяем В)

6 – меньше, чем шестнадцать. Деление прекращаем и записываем 10710=6В16.

Переходим из другой системы в двоичную

Следующий вопрос, как преобразовать из восьмеричной в двоичную запись числа. Перевод чисел из любой системы в двоичную выполняется достаточно просто. Помощником в этом деле выступает таблица для систем счисления.

Важно! Сам принцип основывается на замене набора цифр одной системы на числа другой. Пример перевода 247388=1010011101122

Аналогичный ответ имеет вопрос, как перевести из шестнадцатиричной в двоичную. Необходимо преобразовать каждый символ числа А16 в набор символов двоичного числа. Выполнить это можно посредством представленной таблицы.

Шестнадцатеричная	Двоичная
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

К примеру, число А2316=1010000100112.

Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства

Перевод чисел в восьмеричную и шестнадцатеричную систему счисления и обратно

Перевод между двоичной, восьмеричной, и шестнадцатеричной системой счисления

Итог

Кроме всех перечисленных систем, существует и четвертичная система, основанием которой является цифра 4. Записывается она посредством четырёх символов 0, 1, 2, 3. К примеру 1010=224, а 1510=334.

Это интересно! Что такое экстремумы функции: критические точки максимума и минимума

uchim.guru

Двоичная система счисления. Запись чисел в двоичной системе счисления

Двоичная система счисления. Запись чисел в двоичной системе счисления.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью цифр — символов некоторого алфавита. Например, в десятичной системе для записи числа существует десять всем хорошо известных цифр: О, 1, 2 и т. д.

Все системы счисления делятся на позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в записи числа, а в непозиционных — не зависит. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Каждая позиционная система использует определенный алфавит цифр и основание. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа.

Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная и двоичная (табл. 1).

Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.

Число 555 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10.

В развернутой форме запись числа 555 в десятичной системе выглядит следующим образом:

Как видно из примера, число в позиционных системах счисления записывается в виде суммы степеней основания (в данном случае 10), коэффициентами при этом являются цифры данного числа.

В двоичной системе основание равно 2, а алфавит состоит из двух цифр (0 и 1). В развернутой форме двоичные числа записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.

Например, развернутая запись двоичного числа 1012 будет иметь вид:

studfiles.net

Запись числа в двоичной системе счисления – Двоичная система счисления — Википедия