Вычертить цапфу в прямоугольной диметрии – Разузнай! — Диметрия и изометрия — Что такое диметрия — Прямоугольная диметрия — Как построить диметрию — Что такое изометрия — Прямоугольная изометрия

2,3,4.Прямоугольная изометрия, Прямоугольная диметрия.

Пр

Прямоугольная изометрия характеризуется тем, что коэффициенты искажения составляют 0,82. Их получают из соотношения (1).

Для прямоугольной изометрии из соотношения (1) получаем:

Зu² = 2, или и = v — w = (2/3)^1/2 = 0,82, т. е. отрезок координатной оси

длиной 100 мм в прямоугольной изометрии изобразится отрезком аксонометрической оси длиной 82 мм. При практических построениях пользоваться такими коэффициентами искажения не совсем удобно, поэтому ГОСТ 2.317—69 рекомендует пользоваться приведенными коэффициентами искажения:

и = v = w — 1.

Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т. е. масштаб изображения в прямоугольной изометрии будет М^А 1,22: 1.

Аксонометрические оси в прямоугольной изометрии располагаются под углом 120° друг к другу (рис. 157). Изображение окружности в аксонометрии представляет интерес, особен-

Рис. 157

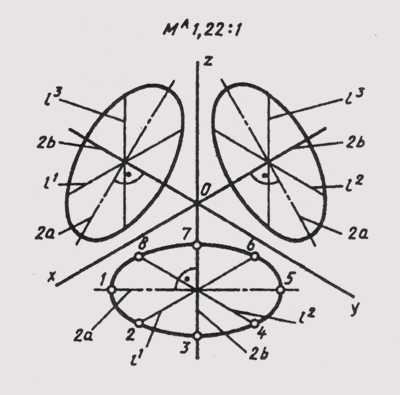
Рис. 158

Рис. 159

но окружностей, принадлежащих координатным или им параллельным плоскостям.

В общем случае окружность проецируется в эллипс, если плоскость окружности расположена под углом к плоскости проекции (см. § 43). Следовательно, аксонометрией окружности будет эллипс. Для построения прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.

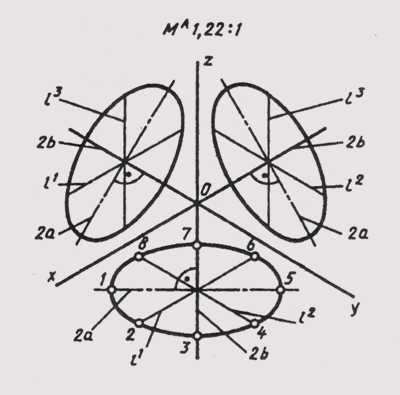
В прямоугольной изометрии равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы (рис. 158).

Размеры осей эллипсов при использовании приведенных коэффициентов искажения равны: большая ось 2а= 1,22d, малая ось 2b = 0,71d, где d — диаметр изображаемой окружности.

Диаметры окружностей, параллельных координатным осям, проецируются отрезками, параллельными изометрическим осям, и изображаются равными диаметру окружности: l¹=l² =l³ = d, при этом

l¹||x; l²||y; l³||z.

Эллипс, как изометрию окружности, можно построить по восьми точкам, ограничивающим его большую и малую оси и проекции диаметров, параллельных координатным осям.

В практике инженерной графики эллипс, являющийся изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим такие же

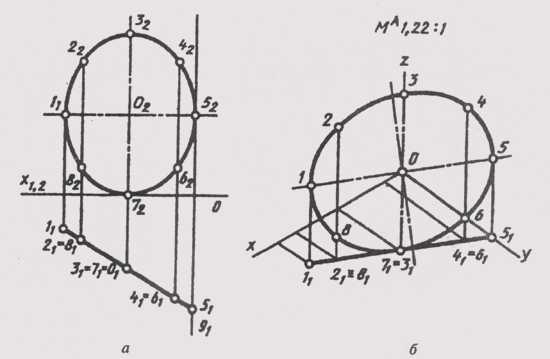
Рис. 160

оси: 2a = 1,22d и 2b = 0,71 d. На рис. 159 показано построение осей такого овала для изометрии окружности диаметра d.

Для построения аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения, нужно выделить на окружности некоторое число точек, построить аксонометрию этих точек и соединить их плавной кривой; получим искомый эллипс— аксонометрию окружности (рис. 160).

На окружности, расположенной в горизонтально проецирующей плоскости, взято 8 точек (1,2,… 8). Сама окружность отнесена к натуральной системе координат (рис. 160, а).Проводим оси эллипса прямоугольной изометрии и, используя приведенные коэффициенты искажения, строим вторичную проекцию окружности 1¹ ₁,…, 5¹₁ по координатам х и у (рис. 160, б). Достраивая аксонометрические координатные ломаные для каждой из восьми точек, получаем их изометрию (1

1, 2¹, … 8¹). Соединяем плавной кривой изометрические проекции всех точек и получаем изометрию заданной окружности.

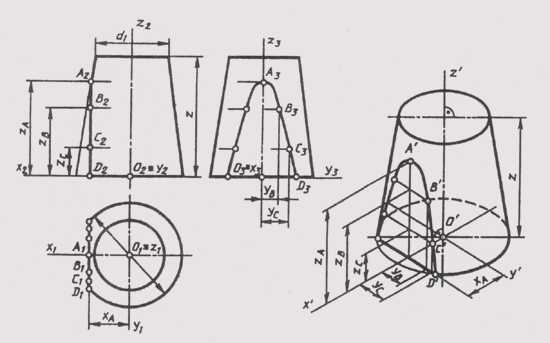
Изображение геометрических поверхностей в прямоугольной изометрии рассмотрим на примере построения стандартной прямоугольной изометрии усеченного прямого кругового конуса (рис. 161).

На комплексном чертеже изображен конус вращения, усеченный горизонтальной плоскостью уровня, расположенной на высоте z от нижнего основания, и профильной плоскостью уровня, дающей в се-

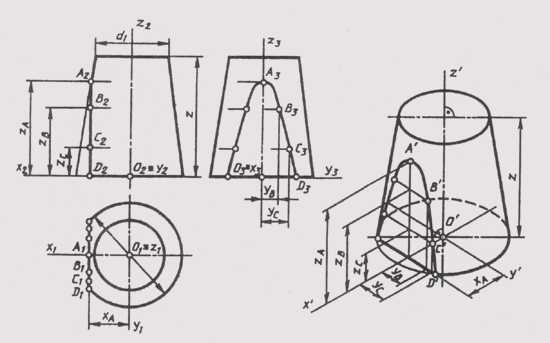
Рис. 161

чении на поверхности конуса гиперболу с вершиной в точке А. Проекции гиперболы построены по отдельным ее точкам.

Отнесем конус к натуральной системе координат Oxyz. Построим проекции натуральных осей на комплексном чертеже и отдельно их изометрическую проекцию. Построение изометрии начинаем с построения эллипсов верхнего и нижнего оснований, которые являются изометрическими проекциями окружностей оснований. Малые оси эллипсов совпадают с направлением изометрической оси 

О_Z (см. рис. 158). Большие оси эллипсов перпендикулярны малым. Величины эллипсов осей определяются в зависимости от величины диаметра окружности (d — нижнего основания и d₁ — верхнего основания). Затем строят изометрию сечения конической поверхности профильной плоскости уровня, которая пересекает основание по прямой, отстоящей от начала координат на величину X_A и параллельной оси О_у.

Изометрия точек гиперболы строится по координатам, замеряемым на комплексном чертеже, и откладываем без изменения вдоль соответствующих изометрических осей, так как приведенные коэффициенты искажения и = v = w = 1. Изометрические проекции точек гиперболы соединяем плавной кривой. Построение изображения конуса заканчивается проведением очерковых образующих касательной к эллипсам оснований. Невидимая часть эллипса нижнего основания проводится штриховой линией.

 

157.gif 158.gif

159.gif

160.gif

161.gif

Прямоугольная диметрия

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:

u²

+(u/2)²+u²=2;

u² =8/9; u = w = (8/9)^1/2=0,94; v = 0,47.

В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1 и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рис. 162. Аксонометрический масштаб для прямоугольной диметрии будет М^A 1,06 : 1.

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а¹ = 1,066d, малая ось — 2b

1 = 0,95d (рис. 163). Диаметры.окруж-

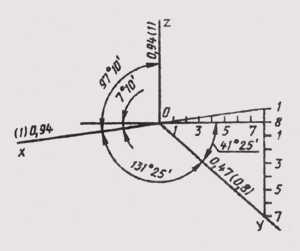
Рис. 162

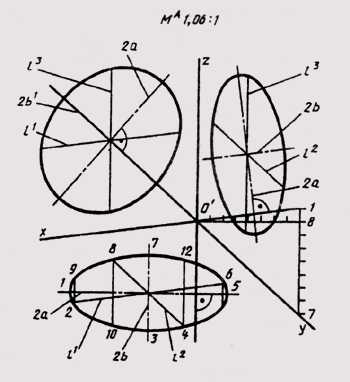
Рис. 163

Рис. 164

ности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l¹ = l² = d; l = 0,5d, при этом || Ох; l² ||Оу; l³ || Oz.

Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.

Изображение геометрических поверхностей в прямоугольной диметрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 164 приведен пример комплексного чертежа полого цилиндра высотой 

Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.

Для наглядности построим вырез четверти цилиндра, построение которого видно из рис. 164. Направление штриховки выреза выберем, как показано на рис. 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.

 

162.gif

163.gif

164.gif

Начертательная геометрия.

studfiles.net

2.1. Построение плоских фигур в прямоугольной диметрии

На рис. 10 изображены некоторые плоские фигуры в прямоугольных диметрических проекциях. Построение их аналогично изометрическим проекциям, лишь по направлению оси Y требуется уменьшение размеров в 2 раза.

На рис. 11 изображён в горизонтальной плоскости правильный пятиугольник АВСDЕ. Координатные оси проходят через центр описанной окружности. Через вершины А и С проведена горизонтальная прямая, параллельная оси Х, пересекающая ось Y в точке М.

Пример построения прямоугольной диметрии пятиугольника в плоскости XОY:

Проводим аксонометрические оси Х и Y. На оси Y в обе стороны от точки О откладываем отрезки, равные половине величины отрезков ОМ, ОВ и ОN. Через полученные точки М и N проводят прямые, параллельные оси Х, и откладывают на них соответственно натуральные величины стороны пятиугольника ЕD и вспомогательной прямой АС. Полученные пять вершин пятиугольника соединяют между собой.

На рис. 10 изображены диметрические проекции плоских фигур, расположенных параллельно горизонтальной, фронтальной и профильной плоскостям проекций.

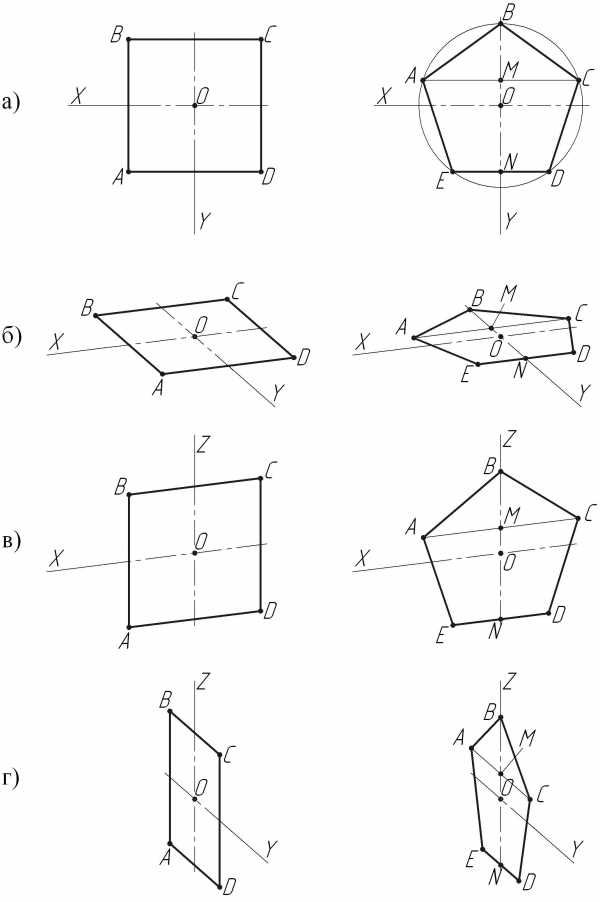
Рис. 10. Диметрическое изображение плоских фигур

а) на чертеже; б) на плоскости H; в) на плоскости V; г) на плоскости W.

На рис. 11 изображено проецирование в диметрии окружностей, расположенных в плоскостях, параллельных плоскостям проекций. Согласно ранее сформулированного положения для эллипса, расположенного в горизонтальной плоскости, большая ось направлена перпендикулярно к оси Z, а малая совпадает с осьюZ. Для эллипса, расположенного во фронтальной плоскости, большая ось направлена перпендикулярно к оси Y, а малая совпадает с осью Y и т.д. В отличие от изометрического изображения эллипсов в различных плоскостях, в диметрии размеры эллипсов одинаковы лишь в горизонтальной (Н) и профильной (W) плоскостях. Во фронтальной плоскости проекции малая ось эллипса выполняется большей, чем в двух других (0,95dпротив 0,35d).

Правило определения главных осей эллипса: большая ось эллипса располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая ось совпадает с направлением этой оси.

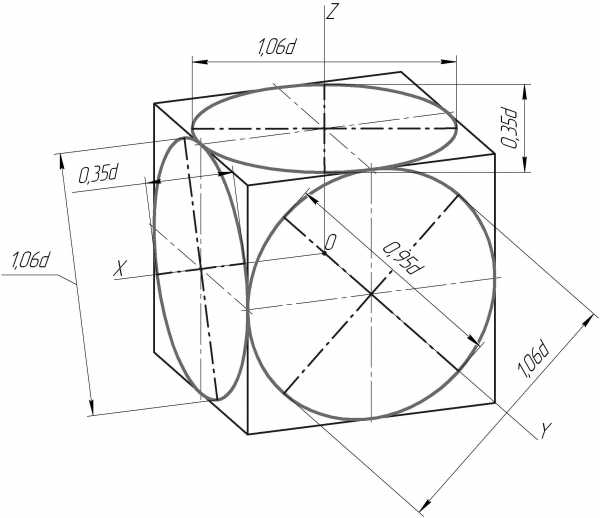
Рис. 11 Проецирование окружностей в диметрии на гранях куба

2.2. Способ построения овалов в диметрии

а. Порядок выполнения овала на плоскости, параллельной горизонтальной и профильной плоскостям проекций (рис. 12, а).

1. Проводим из точки О большие полуоси овала ОА= ОВ (АВ = 1,06d), где d – заданный диаметр окружности.

2. Из точки О проводим малые полуоси овала ОС = ОD. Малая ось овала СD = 0,35d.

3. Из точки О на малых полуосях овала откладываем отрезок ОЕ = ОЕ₁=АВ (на рис. 12,а отрезок ОЕ₁ не показан) равный 1,06d.

4. Проводим дуги окружностей радиусом R= ЕС= Е₁D из точек Е и Е₁.

5. Из точек А и В на больших полуосях овала откладываем отрезки АК= ВК₁= 1/2 ОС.

6. Из точек К и К₁ проводим дуги окружностей радиусом r = АК= ВК_1.

б. Порядок построения овала на плоскости, параллельной фронтальной плоскости проекций (рис. 12, б).

1. Из точки О проводим окружность радиусом r = ОК₁= 0,1d, (где d — заданный диаметр окружности) и оси овала АВ и СD. АВ  Y, СD  АВ, АВ = 1,06d, СD = 0,95d.

2. Из точки Е проводим дугу окружности радиусом R= ЕС. Аналогичное построение из точки Е₁.

3. Из точки К₁ проводим дугу окружности радиусом R₁= АК₁= КВ, полученное изображение является на плоскости V овалом.

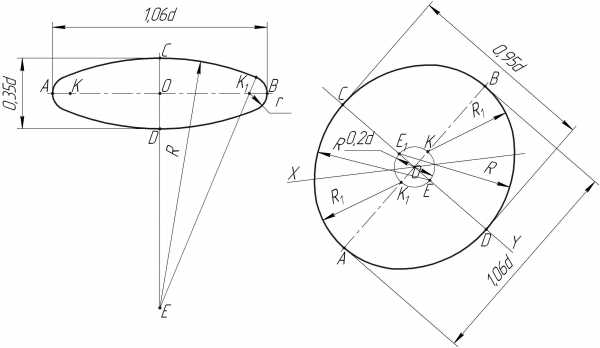
а) б)

Рис. 12. Построение овалов в диметрической проекции:

а) в плоскости Н и W; б) в плоскости V

studfiles.net

Прямоугольная диметрия

В прямоугольной диметрической проекции натуральные коэффициенты искажения следующие имеют значение:

Приведенные коэффициенты:.

В прямоугольной диметрии ось z располагается вертикально. Угол между линией горизонта (рис. 2.2) и осью x составляет 710, а между линией горизонта и осью y — 4125.

Для построения угла, приблизительно равного 710, строят прямоугольный треугольник, катеты которого составляют одну и восемь единиц; для построения угла, приблизительно равного 4125, строят прямоугольный треугольник с катетами семь и восемь единиц.

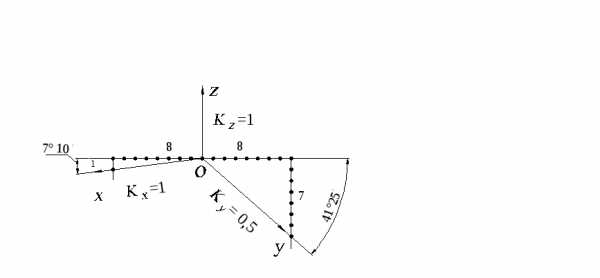
Рис. 2.2

Косоугольная фронтальная изометрия

В косоугольной фронтальной изометрии приведенные коэффициенты искажения равны по всем осям.

В косоугольной фронтальной изометрии ось z располагается вертикально (рис. 2.3), угол между осями z и x составляет 90, а между линией горизонта и осью y — 45(допускается проводить ось y под углом 30 или 60).

Рис. 2.3

Косоугольная фронтальная диметрия

В косоугольной фронтальной диметрии приведенные коэффициенты равны:

.

Расположение осей следующее (рис. 2.4): ось z располагается вертикально, угол между осями z и x составляет 90, а между линией горизонта и осью y — 45 (допускается проводить ось y под углом 30 или 60).

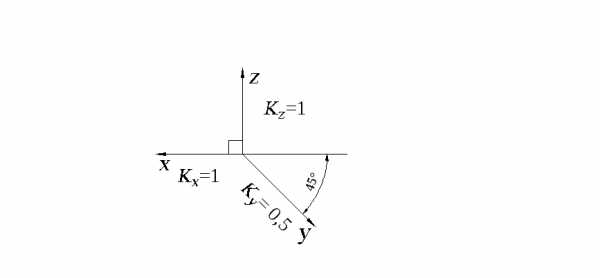
Рис. 2.4.

Косоугольная горизонтальная изометрия

В косоугольной горизонтальной изометрии приведенные коэффициенты искажения равны по всем осям:

.

Расположение осей следующее (рис. 2.5): ось z располагается вертикально, угол между осями x и y составляет 90º, а угол между линией горизонта и осью y составляет 30º (допускается проводить ось y под углом 45º или 60º).

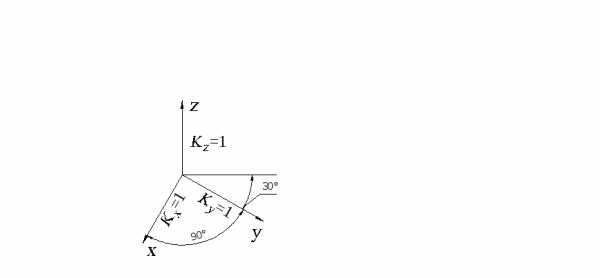
Рис. 2.5.

Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов (рис. 2.6), лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.

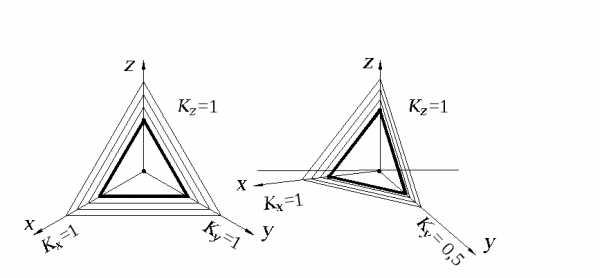
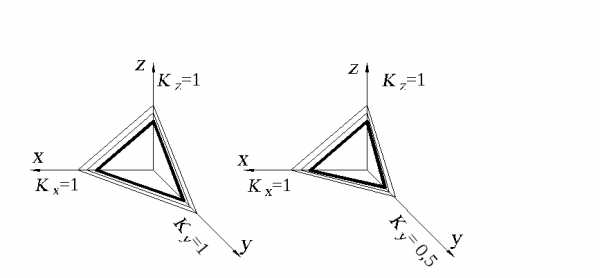
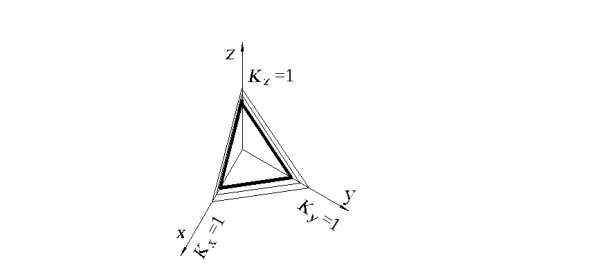
Рис. 2.6.

При нанесении размеров в аксонометрических проекциях выносные линии проводят параллельно аксонометрическим осям, размерные – параллельно измеряемому отрезку.

Порядок выполнения наглядного изображения призмы

1. Выбрать соответствующую аксонометрическую проекцию. Призму, в основании которой лежит правильный треугольник, пятиугольник или шестиугольник следует выполнить в прямоугольной изометрии или диметрии. Призму, в основании которой лежит четырехугольник следует выполнить в прямоугольной диметрии.

2. Построить аксонометрические оси и изображение плоской фигуры основания в аксонометрии (рис. 2.8, а).

3. Выполнить основные контуры призмы (рис. 2.8, б).

4. Нанести линии уступов и углублений горизонтальных вырезов призмы (рис.2.8, в).

5. Построить вертикальное цилиндрическое отверстие. В прямоугольной аксонометрии окружности вычерчиваются в виде эллипсов (рис. 2.8, г). При вычерчивании эллипсов следует предварительно построить их главные оси (большую и малую). Затем построить окружность исходного диаметра. Следующим этапом в построении является нахождение центров большого и малого радиусов. Пересечение вспомогательной окружности исходного диаметра с малой осью эллипса дает центры О₁ и О_2. Точки А, B, С, D – точки пересечения исходной окружности с осями проекций. Соединяем центры O₁и O₂ c точками B и D. Полученными радиусами проводим дуги BC и AD. На пересечении радиусов с большой осью эллипса получим центры О₃ и О₄ малого радиуса. Проводим еще две дуги AB и CD радиусом O₃B = O₄C (рис. 2.9).

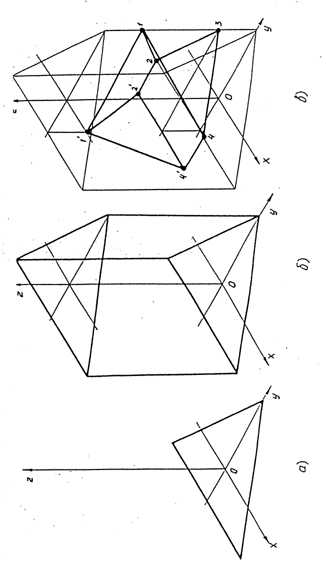
Рис. 2.8

Рис. 2.9

Рис. 2.10

При вычерчивании эллипсов в диметрической прямоугольной проекции следует начинать с вычерчивания осей. Затем необходимо построить окружность исходного диаметра и из центра О в обе стороны по вертикали отложить расстояние, равное диаметру заданной окружности, получаем новые центры О₁ и О₂. Точки А, B, С, D – точки пересечения исходной окружности с осями проекций. Соединяем центр О₁ с точкой D, а центр О₂ с точкой В, на пересечении этих линий с большой осью эллипса находим еще два новых центра — О₃ и О₄. Из этих центров проводим: дуги ВС и AD радиусом R = O₂B = O₁D; дуги AB и CD радиусом r = О₃С = О₄B (рис. 2.10).

6. Выполнить разрезы и сечения. При построении разрезов секущие плоскости следует проводить параллельно плоскостям, определяемым аксонометрическими осями, т.е. xОy, xОz, yОz. Нанести направление линии штриховки с учетом коэффициентов искажения по аксонометрическим осям (рис. 2.8, д)

7. Обвести чертеж соответствующими линиями (рис. 2.8, е).

8. В правый верхний угол чертежа поместить образец соответствующей аксонометрической проекции. Показать углы наклона аксонометрических осей. Указать коэффициенты искажения и направление штриховки в разрезах и сечениях.

9. Заполнить основную надпись и дополнительную графу.

Пример аксонометрического чертежа призмы показан на (рис. 2.11).

Рис. 2.11

Т е м а 3

studfiles.net

5.2. ПРЯМОУГОЛЬНАЯ ДИМЕТРИЯ

330	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ

Вто время как прямоугольная изометрия существует только одна, прямоугольных диметрий можно построить бесчисленное множество. Наиболее простую и распространенную диметрию получают, если

u = wи v= u2 .

Вычислим показатели искажений по осям. Из уравнения u2 +v2 +w2 = 2 имеем:

u2 +u2 +u2 =2 , 4

откуда

u = 2 32 ≈ 0,94 ,

тогда

u = w = 0, 94;v = u2 = ≈ 0,942 ≈ 0, 47 .

Итак, диметрический масштаб измерения по двум осям x′ иz′ равен≈ 0,94, а по осиy′ равен≈ 0,47, т. е. по аксонометрическим осям происходит

сокращение размеров на эти величины.

На практике пользуются приведенными показателями искажения: вместо 0,94 принимают 1, а вместо 0,47 – 0,5. Тогда изображение становится увеличенным в 1,06 раза по сравнению с диметрией, построенной с помощью точ-

	ных показателей искажения	1	=	0,5	=1, 06 .
		0,94		0, 47

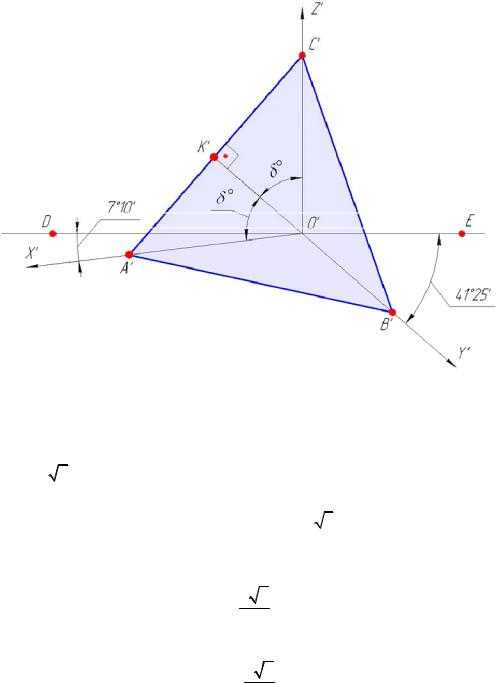
Определим углы между осями прямоугольной диметрии, для чего воспользуемся треугольником следов A′ B′ C′ (рис. 12). Так какиз-заравенства показателей искажения по осямx′иz′ он – равнобедренный, то его высота является в то же время и медианой, т. е.A′K′=K′ C′. Из прямоугольного треугольникаO′ K′ C′ имеем:

sin δ = OK′′CC′′ = 2AO′C′C′′ , так какK′C′ = 12 A′C′.

Г л а в а 14. Аксонометрические проекции

331

Рис. 12

Чтобы определить это соотношение, выразим оба его члена через отрезок

OC

′

натуральной координатной оси z. Равнобедренный треугольник

′ ′ ′

A O C

является проекцией прямоугольного треугольника

′

′

(см. рис. 5), поэтому

A OC

′ ′

= OC

′

2 .

A C

Далее имеем

′ ′

′

, но ω=

2

2

.

3

O C

= ω OC

Поэтому

O′C′ =2 32 OC′,

откуда

2O′C′ =4 32 OC′.

332		ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ
Следовательно,
		4		2			3
sin δ = (OC′	2)	:			OC′	=	4	= 0,75.
				3
что соответствует равенству угла δ°					′	. Тогда угол			′ ′	′	равняется
				= 48°35					A O C

двум углам δ°, т. е. 97°10′.

Обычно ось z′ при построении диметрических проекций располагают вертикально, тогда треугольник следов и его высоты (аксонометрические оси)

займут положение,		показанное		на			рис. 12. В этом		случае угол	′ ′	=
										DO A
′		′	′		′		′	′	′	′
= (97°10	−90°)= 7°10 , угол		DO K			= (δ−7°10 )= (48°35			−7°10 )= 41°25 .

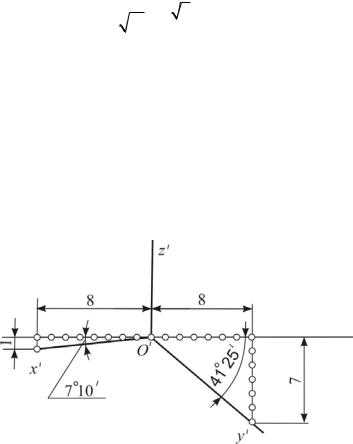
Расположение аксонометрических осей показано на рис. 13: ось z′ – вертикально, осьx′ составляет с горизонтальной линией угол 7°10′ , а осьy′ –

41°25′.

Рис. 13

Углы между осями можно брать из соотношения катетов прямоугольных треугольников, гипотенузы которых указывают направление осей. Так,

′	=	1	;	′	=	7
tg 7°10		8		tg 41°25		8 .

При построении точной прямоугольной диметрии значения координат по направлению осей x′ иz′ умножают на величину 0,94, а по осиy′ – на величи-

ну 0,47.

На практике пользуются ПРИВЕДЕННЫМИ показателями искажений, равными 1 и 0,5, при этом все элементы изображения увеличиваются в 1/0,94 = = 1,06 раза.

Г л а в а 14. Аксонометрические проекции

333

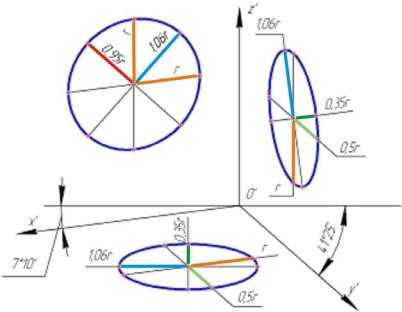
На рис. 14 показаны три эллипса, изображающие окружности, расположенные в плоскостях, параллельных координатным плоскостям в прямоугольной диметрии.

Рис. 14

В диметрии, так же как в изометрии, большие оси эллипсов перпендикулярны осям, отсутствующим в плоскости изображаемой окружности, а малые имеют направления аксонометрических осей. В натуральной диметрии большие оси эллипсов равны диаметру d окружности, а в приведенной они равны 1,06d. На рис. 14 указаны размеры осей эллипсов с учетом приведенных показателей искажения.

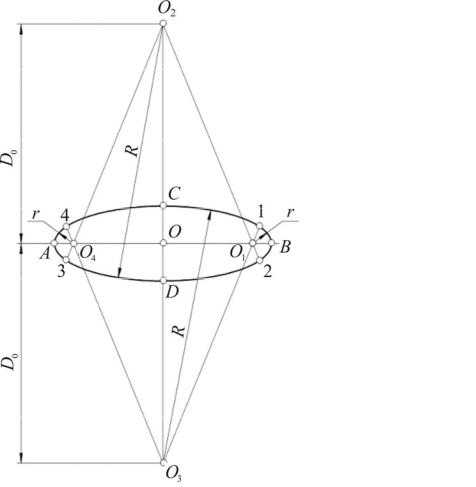
На практике часто эллипсы заменяют овалами. Для их построения в плоскостях xOy иyOz (и им параллельных) проводят большие и малые оси

D = AB=1, 06dи d			= СD =	1	D		, затем на продолжении малой оси от точ-
		0
	0		3		0

ки О в ту и другую стороны откладывают размерD0, получая центрыО2 иО3 (рис. 15). Из этих центров через точкиС иD проводят дуги радиусом

R = D0 + 12 d0 .

334	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ

Из центров О1 иО4, отстоящих от концовА иВ большой оси на расстоянии

14 d0, проводят дуги радиусомr. Эти дуги доводят до точек сопряжения 1 и 2, 3 и 4, полученных на продолжении линии центров сопрягаемых дуг.

АВ z или AB x AB= D0 = 1,06d

1

СD = d0 =3 D0 = 0,35d

1

R = D0 +2 d0

1

r = 4 d0

d – диаметр окружности

Рис. 15

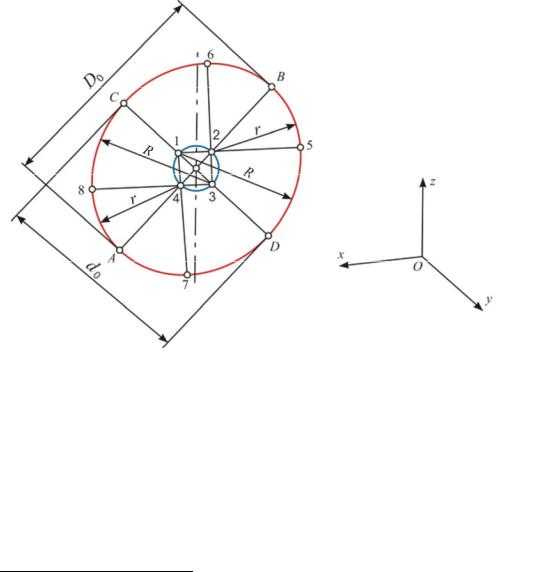
Для построения овала, расположенного в плоскости xOz (или в плоскости, параллельной ей), проводят прямую, перпендикулярную осиy, отсутствующей в данной плоскости (рис. 16). На этой прямой откладывают величину большой

оси D0 =АВ. Малую осьd0 =СD откладывают на прямой, совпадающей

Г л а в а 14. Аксонометрические проекции

335

снаправлением оси y, перпендикулярнойАВ. Из точки пересечения большой

ималой осей проводят окружность диаметра d1 = 0,2d, получая центры 1, 2, 3 и 4. Из центров 1 и 3 проводят дуги радиусомR, а из центров 2 и 4 – дуги радиусомr. Дуги радиусамиR иr доводят до точек сопряжения 5 и 6, полученных на продолжении линии центров сопрягаемых дуг.

АВ y

AB =D0 = 1,06d

СD = d0 =0,94d

d – диаметр окружности

Рис. 16

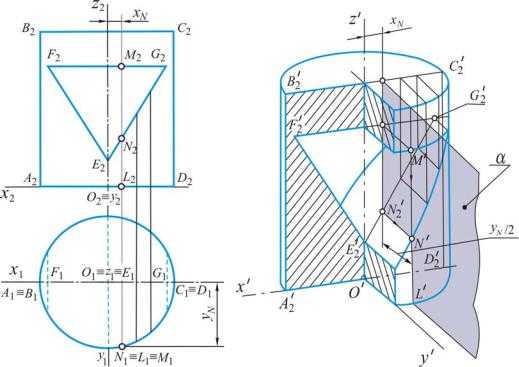
Пример. Построить прямоугольную диметрию цилиндра со сквозным отверстием треугольной формы (рис. 17)*.

Начало координат совместим с центром нижнего основания, а ось z c осью цилиндра. В данном случае вторичную проекцию целесообразно построить на координатной плоскостиx′O′z′ , поскольку для этого потребуется провести только прямые линии. Такой проекцией служит параллелограммA2′B2′C2′D2′ и

треугольник E2′F2′G2′ . Для того чтобы придать чертежу большую наглядность, цилиндр изобразим с вырезом одной четверти.

* Пример приведен из работы [19].

336	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ

Рис. 17

Не останавливаясь на вычерчивании эллипсов – контуров верхнего и нижнего оснований цилиндра, рассмотрим построение одной из точек N′ эллиптической дуги, по которой наклонная плоскость треугольного отверстия пересекает цилиндрическую поверхность.

Аксонометрическую проекцию N′ точкиN можно найти как с помощью ортогонального чертежа, так и независимо от него. В первом случае на ортогональных проекциях определяем две прямоугольные координатыxN иyN

этой точки. Затем с помощью координаты xN на прямойE2′G2′ показываем вторичную проекциюN2′ . Наконец, черезN2′ проводим прямую, параллельную осиy′, и откладываем на ней от точкиN2′ отрезок, равный 0,5yN . Дру-

гими словами, N′ строим способом координат.

Та же точка может быть определена пересечением образующей L′M ′ цилиндра и горизонталиN2′N′ наклонной плоскости отверстия, причем и обра-

зующая, и горизонталь должны принадлежать одной плоскости α, параллельной координатной плоскостиy′O′z′. На рис. 17 аналогично найдены и осталь-

ные точки кривой наклонного сечения.

studfiles.net

Как чертить в диметрии

Основная задача любого чертежа — дать максимально точное представление об изображенных на нем объектах. С помощью одних только ортогональных проекций этой цели не добиться, поэтому государственными стандартами предусмотрены варианты объемного изображения. Диметрическая проекция — один из них. Диметрия может быть фронтальной или прямоугольной.

Вам понадобится

• — чертежные принадлежности:
• — бумага;

Инструкция

• Определите положение осей натуральной системы координат. Поставьте точку пересечения осей и обозначьте ее как О. Проведите от нее вверх вертикальный луч. Это будет ось Z. Через эту же точку начертите горизонтальную линию, но никак ее не обозначайте, она нужна как вспомогательная.
• В отличие от изометрической проекции, в диметрии углы между осями не равны. Точка О является вершиной всех трех углов. Отложите в этой точке от горизонтального отрезка, идущего влево, 7°11′. Проведите через точку О и эту новую точку луч и обозначьте его как Х. От горизонтального отрезка, идущего вправо, отложите 41°25′. Это будет ось Y. Такое расположение осей применяется в прямоугольной диметрической проекции.
• В диметрической проекции применяются реальные и приведенные коэффициенты искажения. В отличие от изометрической проекции, где такие коэффициенты одинаковы по всем осям, в диметрии они разные. В прямоугольной диметрической проекции реальный коэффициент по оси У равен 0,47, а по Х и Z – 0. 94. Однако на практике реальными коэффициентами почти никогда не пользуются, поскольку государственные стандарты рекомендуют применение приведенных коэффициентов. Они равны 0,5 и 1 соответственно.
• Для создания фронтальной диметрии точно так же определите положение исходной точки О, начертите вертикальную ось ОZ и проведите в обе стороны от нее горизонтальные линии. Положение осей Х и У будет иным. Для оси У отложите угол в 45° или 30°. Ось Х расположена горизонтально. Учтите коэффициенты искажения. В данном случае приведенные коэффициенты по осям Х и Z будут равны 1, а по оси У — 0, 5.
• Вычислите размеры объекта, которые необходимо отложить по всем осям. Учитывайте коэффициенты искажения. Для вычислений лучше сделать набросок на черновике, чтобы была возможность выполнить дополнительные построения и сделать нужные расчеты с помощью тригонометрических функций. Отложите по всем трем осям полученные размеры.
• Начертите проекции окружностей. В диметрии, как и в изометрии, они выглядят как эллипсы. У эллипса есть большой и малый диаметры. Между ними и реальным диаметром окружности существует определенная связь. Для того чтобы вычислить большую ось эллипса, нужно диаметр окружности умножить на 1,06. Для расчета малой оси умножьте ту же величину на 0,35.

completerepair.ru

Прямоугольная диметрия

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:

u²+(u/2)²+u²=2;

u² =8/9; u = w = (8/9)^1/2=0,94; v = 0,47.

В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рисунке 162. Аксонометрический масштаб для прямоугольной диметрии будет М^A1,06 : 1.

 

Рисунок 162 — Расположение осей стандартной прямоугольной диметрии

 

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а¹ = 1,066d, малая ось — 2b¹= 0,95d (рисунок 163). Диаметры. окружности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l¹ = l² = d; l = 0,5d, при этом || Ох; l²|| Оу; l³|| Oz.

Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.

 

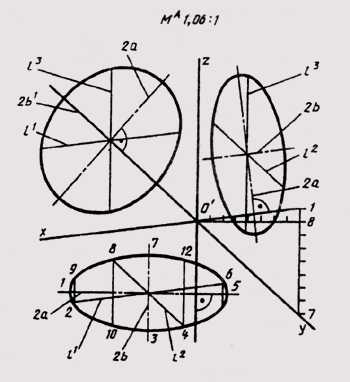
Рисунок 163 – Большая и малая оси в диметрии

Изображение геометрических поверхностей в прямоугольной диметрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рисунке 164 приведен пример комплексного чертежа полого цилиндра высотой Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.

Для наглядности построим вырез четверти цилиндра, построение которого видно из рисунке 164. Направление штриховки выреза выберем, как показано на рисунок 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.

 

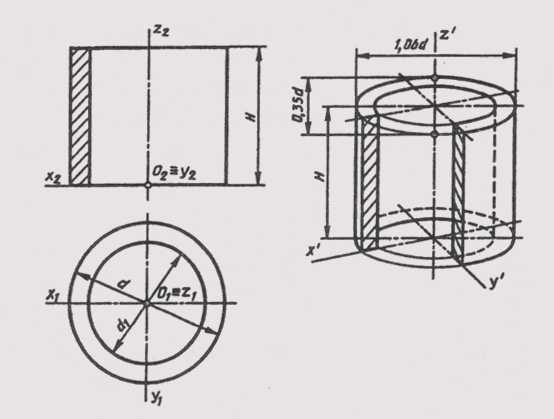
Рисунок 164 — Комплексный чертеж полого цилиндра

 

Вопросы для самопроверки

1 Как образуется аксонометрический чертеж?

2 Каково деление аксонометрических проекций в зависимости от направления проецирования?

3 Как располагаются оси в прямоугольной диметрии?

4 Чему раны большая и малая оси в изометрии и диметрии?

 

 

---

Дата добавления: 2017-12-05; просмотров: 142;

---

znatock.org

78. Прямоугольная диметрия | Техническая библиотека lib.qrz.ru

 

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:

u²+(u/2)²+u²=2;

u² =8/9; u = w = (8/9)^1/2=0,94; v = 0,47.

В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1 и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рис. 162. Аксонометрический масштаб для прямоугольной диметрии будет М^A1,06 : 1.

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а¹ = 1,066d, малая ось — 2b¹= 0,95d (рис. 163). Диаметры.окруж-

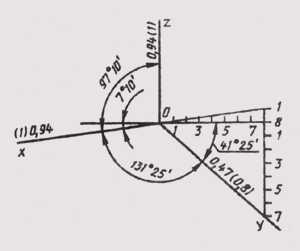
Рис. 162

Рис. 163

Рис. 164

ности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l¹ = l² = d; l = 0,5d, при этом || Ох; l²|| Оу; l³|| Oz.

Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.

Изображение геометрических поверхностей в прямоугольной ди-метрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 164 приведен пример комплексного чертежа полого цилиндра высотой Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.

Для наглядности построим вырез четверти цилиндра, построение которого видно из рис. 164. Направление штриховки выреза выберем, как показано на рис. 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.

 

lib.qrz.ru