1.5 Алгоритм построения комплексного чертежа точки
1. На оси абсцисс отложите координату Х и обозначьте АХ.
2. Через АХ проведите вертикальную линию связи, перпендикулярно оси Х. На этой линии связи отложите координату YA от оси Х (с учетом знака). Полученную горизонтальную проекцию точки обозначьте А1.
3. На вертикальной линии связи отложите координату ZA от оси Х (с учетом знака). Полученную фронтальную проекцию точки обозначьте А2.
4. Из фронтальной проекции точки А2 проведите горизонтальную линию связи, перпендикулярно оси Z. Пересечение линии связи с осью Z обозначьте АZ.
5. Замерьте расстояние от оси X до горизонтальной проекции точки А1 (координату YA).
6.Отложите измеренное расстояние (координату YA) на горизонтальной линии связи от оси Z (с учетом знака YA). Полученную профильную проекцию точки обозначьте А3.
Если все координаты точки имеют числовые значения, то точка расположена в пространстве. Если точка имеет одну нулевую координату, то точка принадлежит плоскости проекций. Если точка имеет две нулевые координаты, то точка принадлежит оси проекций
1.6 Построение комплексного чертежа точки, принадлежащей пространству
Наглядное изображение
Комплексный чертеж
Пояснения
Дано: А(20,10,15) 1
Построить: комплексный чертеж
Y
1.По оси абсцисс от начала координат влево отложите Х =20.
2. Из Аx проведите вертикальную линию связи .
3. По линии связи, от оси Х вниз, отложите координату Y= 10 (вверх, если Y отриц.)
Обозначьте проекцию точки А1.
4. От оси Х, по линии связи отложите вверх Z =15 (вниз, если Z отриц.). Обозначьте проекцию точки А2.
Наглядное изображение
Комплексный чертеж
Пояснения
5.Из А2 проведите горизонтальную линию связи.
6.Замерьте
расстояние от оси Х до А
7. Отложите это расстояние от оси Z по горизонтальной линии связи, вправо (если Y отриц., то влево).
8.Обозначьте проекцию точки А3
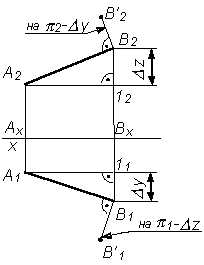
1.7 Построение комплексного чертежа точки, принадлежащей плоскости проекций
Наглядное изображение
Комплексный чертеж
Пояснения
Дано: В(20,0,15)
Построить: комплексный чертеж
Так как координата Y=0, то точка В принадлежит фронтальной плоскости проекций.
0
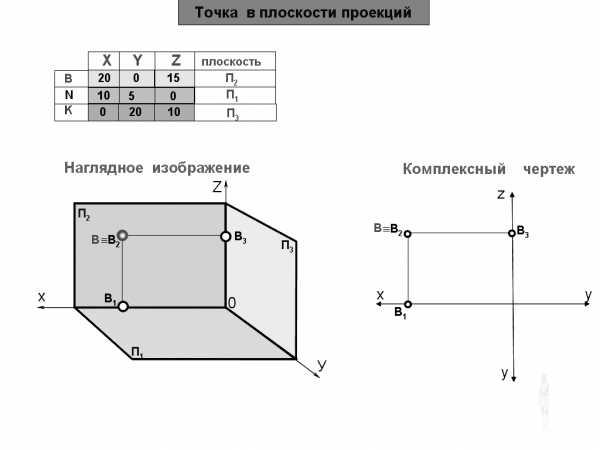
Наглядное изображениеКомплексный чертеж
Пояснения
Дано: N (20,10,0)
Построить: комплексный чертеж
Так как координата Z=0, то точка N принадлежит горизонтальной плоскости проекций.
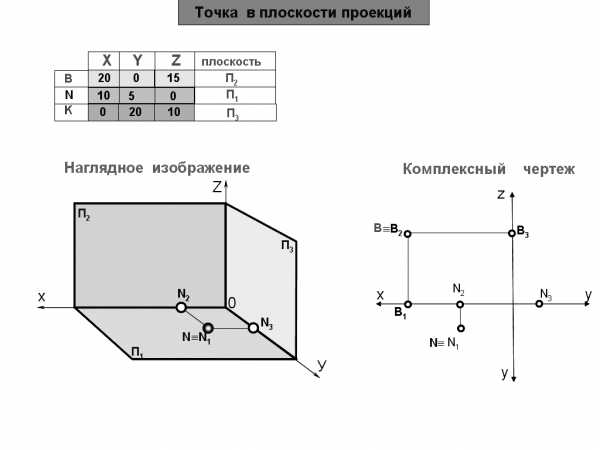
1.8 Построение комплексного чертежа точки, принадлежащей оси
Наглядное изображение
Комплексный чертеж
Пояснения
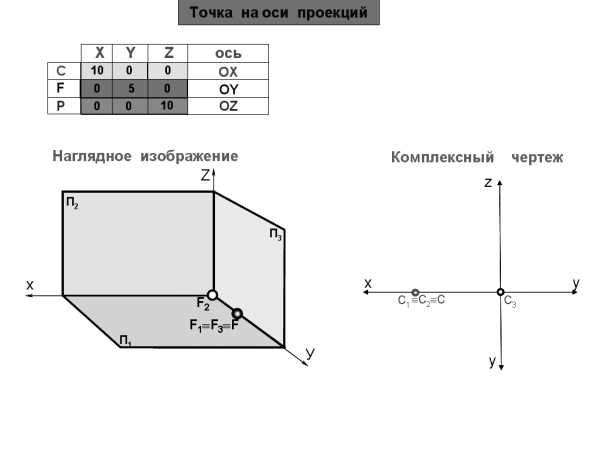
Дано: С (20,0,0)
Построить: комплексный чертеж.
Точка С принадлежит оси Х, т.к. две координаты имеют нулевые значения:
Y=0, Z=0.
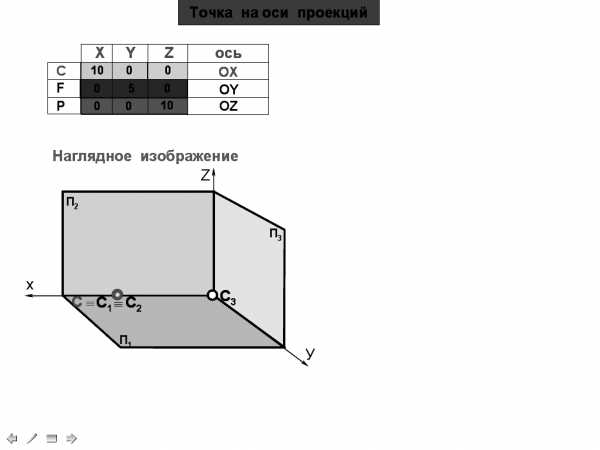
0
Наглядное изображение
Комплексный чертеж
Пояснения
Дано: С (0,0,15)
Построить: комплексный чертеж.
Точка P принадлежит оси Z, т.к. две координаты имеют нулевые значения:
X=0, Y=0.
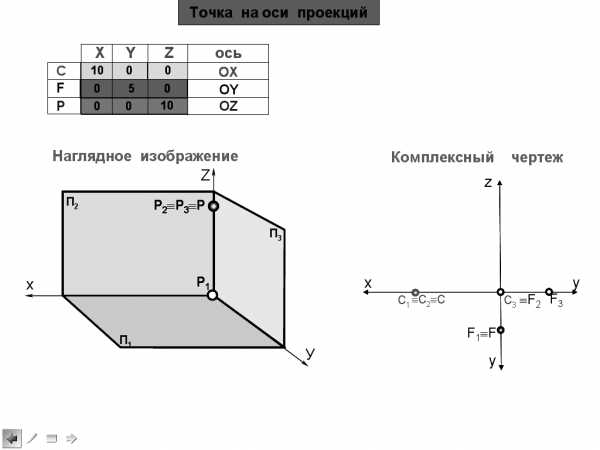
Дано: F (0,10,0)
Построить: комплексный чертеж.
Точка F принадлежит оси Y, т.к. две координаты имеют нулевые значения:
X=0, Z=0.
studfiles.net
Проецирование точки — Всё для чайников
- Главная
- Видеотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Обществознание
- Обществознание — как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение
- Материаловедение
- Сварка
- Электротехника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
- Естествознание
- Библиотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Астрономия
- Обществознание
- Иностранные языки
- Технические науки
- Теоретическая механика и сопромат
- Сварка
- Железная дорога
- Паспорта и техническая документация
- Металлообра-батывающие станки
- Деревообра-батывающие станки
- Сварочное оборудование
- Естествознание
- Правила
- Контакты
- Вы здесь:
- Главная
- Видеотека
forkettle.ru
Комплексный чертёж точки.
Наибольшее применение на практике получил чертёж, составленный из двух или более связанных между собой ортогональных проекций изображаемой фигуры. Такой чертёж называется комплексным чертежом в ортогональных проекциях или комплексным чертежом.
Принцип образования чертежа состоит в том, что данная фигура проецируется ортогонально на 2 взаимно ^-е плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа.
Одна из плоскостей проекций располагается горизонтально, обозначается П1 и называется горизонтальной плоскостью проекций.
2-я плоскость располагается вертикально перед наблюдателем, обозначается П2 – фронтальная плоскость проекций. Прямая пересечения плоскостей – ось проекций.
А1 – горизонтальная проекция А2 – фронтальная проекция
hА – высота точки А
fА – глубина т.А
Спроецируем ортогонально на плоскости проекций П1 и П2 какую-нибудь
точку А, тогда получим две её проекции: горизонтальную проекцию А1 на плоскости П1 и фронтальную проекцию А2 на плоскости П2. Проецирующие прямые AA1 и АА2, при помощи которых точка А проецируется на плоскости проекций, определяют проецирующую плоскость A1AA2, перпендикулярную к обеим плоскостям проекций и к оси проекций X. Прямые AхA1 и АхА2, являющиеся проекциями проецирующей плоскости на плоскостях проекций П1 и П2, будут перпендикулярны к оси проекций X.
Обратно, каждая пара точек А1 и А2, соответственно принадлежащих плоскостям П1 и П2 и расположенных на перпендикулярах к оси X, восставленных из одной и той же точки Ах, определяют в пространстве единственную точку А. В самом деле, если провести через точку A1 и А2 перпендикуляры А1А и А2А соответственно к плоскостям П1 и П2, то они, находясь в одной плоскости А1АхА2, пересекутся в некоторой точке А. Расстояние A1А точки А от горизонтальной плоскости проекций называется высотой h точки А, ее расстояние А2А от фронтальной плоскости проекций – глубиной f точки А.
Чтобы получить плоский чертеж, совместим плоскость проекций П1 с плоскостью П2, вращая переднюю полуплоскость П1 вокруг оси Х вниз. В результате получим комплексный чертеж точки А (рис. 4), состоящий из двух проекций А1 и А2 точки А, лежащих на одной прямой, перпендикулярной к оси X. Прямая А1А2, соединяющая две проекции точки, называется вертикальной линией связи.
Полученный комплексный чертеж будет обратимым, т.е. по нему можно восстановить оригинал. В самом деле, рассматривая, например, фронтальную проекцию А2 точки А и имея на чертеже ее глубину f=АхА1, можно построить точку А. Для этого надо восстановить перпендикуляр к плоскости чертежа в его точке А2 и от плоскости чертежа отложить глубину искомой точки, тогда конец перпендикуляра определит положение точки А.
На практике часто бывает безразличным положение изображаемой фигуры относительно неподвижной системы плоскостей проекций, поэтому при образовании комплексного чертежа можно отказаться от фиксации плоскостей проекций и оси проекций не изображать. Основанием этому может служить отмеченное шестое свойство параллельной проекции не изменять проекции фигуры при параллельном переносе плоскости проекций.
Плоскости проекций П1 и П2 разбивают все пространство на четыре части, называемые квадрантами или четвертями. При этом условимся нумеровать квадранты в порядке, указанном на рис., и называть их I, II, III и IV квадрантами.
Рис. 5 Двухкартинный комплексный чертёж
|
Если точка А лежит в I квадранте, то ее горизонтальная проекция A1 будет принадлежать передней полуплоскости П1, а фронтальная проекция А2 — верхней полуплоскости П2. При совмещении плоскостей проекций горизонтальная проекция A1 точки А окажется расположенной ниже оси Х12, а фронтальная проекция А2 — выше оси Х12 (рис. 5). В зависимости от положения точек в различных квадрантах пространства будем иметь соответствующее расположение их проекций на комплексном чертеже (рис. 5), так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит точка.
Итак, комплексный чертеж, состоящий из двух ортогональных проекций (называемый еще двухкартинным чертежом), является обратимым чертежом. Однако реконструкция оригинала часто становится проще, когда помимо двух основных проекций имеется еще одна проекция на третью плоскость. В качестве такой плоскости проекций применяется плоскость, перпендикулярная к обеим основным плоскостям П1 и П2, которая называется профильной плоскостью проекций. Ее обозначают П3. Три плоскости проекций П1, П2 и П3 образуют систему трех взаимно перпендикулярных плоскостей (рис. 6). Ребра полученного трехгранника будем обозначать через X, У, Z.
Рис. 6
| П3 – профильная плоскость проекций А3 – профильная проекция т.А рА – широта т.А | трёхкартинный комплексный чертёж т.А |
Рассмотрим построение трехкартинного комплексного чертежа. Пусть А — некоторая точка пространства. Опустим из точки А перпендикуляры на плоскости проекций П1, П2 и П3: ААi^Пi (i = 1, 2, 3). Основания этих перпендикуляров (точки А1, А2, А3) и являются соответственно горизонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций П1, П2 и П3. Заметим при этом, что проецирующие плоскости AA1A2, AA1A3 и АА2А3 перпендикулярны соответственно осям X, У, Z. Обозначив точки пересечения этих плоскостей с осями через А12, А13, А23, заметим, что как прямые A1A12 и А12А2 перпендикулярны к оси X, так и две другие пары прямых A1A13, А13А3 и А2А23, А23А3 должны быть перпендикулярны соответственно осям Y и Z. Расстояние точки А от горизонтальной плоскости проекций П1 мы назвали ранее высотой точки А, а расстояние точки А от фронтальной плоскости проекций П2 — ее глубиной; расстояние точки А от профильной плоскости проекций П3 будем называть широтой точки А.
При построении плоского чертежа плоскость П2 считается неподвижной, а остальные плоскости П1 и П3 совмещаются с ней путем вращения соответственно вокруг осей Х и Z в направлении, указанном на рис. стрелками. После совмещения плоскости П1 с фронтальной плоскостью П2 отрезки А1А12^Х12 и A12A2^X12 окажутся расположенными на одной прямой. Аналогично после совмещения плоскости П3 с плоскостью П2 отрезки A2A23^Z23 и А23А3^Z23 расположатся на линии связи А2А3^Z23.
В результате указанного совмещения плоскостей проекций получаем комплексный чертеж точки А, состоящий из трех ортогональных проекций (трехкартинный). При этом линии связи должны быть перпендикулярны к осям: А1А2^Х12, А2А3^Z23, а отрезки А1А12 и А23А3 равны, ибо А1А12 = А23А3 =А2А есть глубина точки А.
Рассмотрим, какой линией связи можно соединять горизонтальную и профильную проекции точки А. Для этого обратим внимание на квадрат А13ОА3А*. Диагональ этого квадрата является биссектрисой угла Х12ОZ23. Следовательно, линия связи, соединяющая проекции А1 и А3, представляет собой ломаную линию с вершиной на биссектрисе угла Х12ОZ23, состоящую из двух звеньев (горизонтального и вертикального). В дальнейшем эту линию будем называть горизонтально-вертикальной линией связи. Часть этой ломаной заменяют иногда дугой окружности.
Введенная система трех плоскостей проекций П1, П2 и П3 разбивает все пространство на восемь частей, называемых октантами. Их нумеруют следующим образом: слева от профильной плоскости октанты сохраняют нумерацию квадрантов, а справа от плоскости П3 идут номера 5, 6, 7 и 8. При совмещении плоскостей проекций передняя часть горизонтальной плоскости опускается вниз, а задняя поднимается вверх; передняя часть профильной плоскости удаляется от нас направо, а задняя приближается слева.
Множество горизонтальных проекций всех точек пространства назовем полем горизонтальных проекций П1 (соответствующая проекция фигуры называется видом сверху), а множество фронтальных проекций всех точек пространства — полем фронтальных проекций П2 (соответствующая проекция фигуры называется видом спереди или главным видом). Аналогично множество профильных проекций всех точек пространства назовем полем профильных проекций П3 (соответствующая проекция фигуры называется видом слева).
Чтобы иметь возможность точного построения комплексных чертежей каких-либо фигур, необходимо уметь задавать положения проекций точек, определяющих данные фигуры, при помощи чисел. Для этого, как известно, следует пользоваться координатным методом. Рассмотрим трехгранник, образованный системой плоскостей проекций П1, П2 и П3. На осях X, У, Z установим единицу измерения е. За начало отсчета примем точку О пересечения трех плоскостей проекций (вершину трехгранника). Положительное направление на каждой оси установим, как показано на рис. Тогда трехгранник OXYZ можем рассматривать как прямоугольную декартову систему координат с координатными осями: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат.
Ломаная ОА12А1А, определяющая положение точки А относительно координатной системы OXYZ, называется, как, уже было сказано ранее, координатной ломаной линией. Звенья этой ломаной называются отрезками координат: ОА — отрезок абсциссы, А12А1 — отрезок ординаты, А1А — отрезок аппликаты точки А. Длины отрезков координат точки А, измеренные установленной единицей длины е, называются координатами точки А:
Координаты точки А можно рассматривать, как ее расстояния до плоскостей проекций, поэтому координаты будут иметь следующие значения: ZА — высота, YA — глубина, ХA — широта точки А. Координаты точки называются определителем точки.
По заданным координатам точку А(ХА,YA,ZA) можно построить следующим образом. Сначала с помощью единицы длины е строится отрезок OA12, затем отрезок A12A1, параллельный оси Y, и, наконец, отрезок А1А, параллельный оси Z. В результате получаем точку А.
5. Комплексный чертёж прямой линии
Пусть в I четверти расположен отрезок прямой l не параллельный и не перпендикулярный ни к одной из плоскостей проекций. Для построения его ортогональных проекций возьмём на прямой 2 точки и спроецируем их на П1 и П2. Полученные проекции точек и определяют искомые проекции отрезка прямой.
Прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения.
К прямым частного положения относятся параллельные или ^-ые какой-либо плоскости проекций.
Прямая, //-ая какой-либо плоскости проекций, называется прямой уровня.
//-ая П1 – горизонталь,
//-ая П2 – фронталь,
//-ая П3 – профильная прямая уровня.
Прямая уровня на плоскость проекций, которой она параллельна, проецируется без искажений в натуральную величину. При этом её проекция на этой плоскости с осями координат образует углы, равные углам наклона этой прямой к соответствующим плоскостям проекций.
Для задания профильной прямой уровня необходимо задавать на ней проекции двух точек.
Прямая, ^-я какой-либо плоскости проекций, называется проецирующей прямой.
^-я к П1 – горизонтально проецирующая,
^-я к П2 – фронтально проецирующая,
^-я к П3 – профильно проецирующая.
2 точки, проекции которых на какую-либо плоскость проекций совпадают, называются конкурирующие точки.
Если совпадают горизонтальные проекции – горизонтально конкурирующие.
Из двух горизонтально конкурирующих точек на П1 будет видна та, фронтальная проекция которой находится выше от оси х12.
Из двух фронтально конкурирующих точек на П2 будет видна та, горизонтальная проекция которой находится дальше от оси х12.
6. Определение натуральной величины отрезка прямой
Натуральная величина отрезка прямой является гипотенузой прямоугольного треугольника одним катетом которого служит проекция отрезка на какую-либо плоскость проекций, а другим катетом разность расстояний концов этого отрезка до этой плоскости проекций.
Похожие статьи:
poznayka.org
7. Глава 6. Проекции точки. Комплексный чертеж
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов
Рис. 60
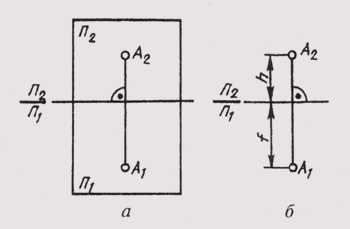
Рис. 61
пространства на ней будем обозначать с индексом 1 : А1, а1, S1 … и называть горизонтальными проекциями (точки, прямой, плоскости).
Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П2. Проекции элементов пространства на ней будем обозначать с индексом 2: А2, <a2, S2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.
Спроецируем точку А ортогонально на обе плоскости проекций:
АА1_|_ П1;AА1 ^П1=A1;
АА2_|_ П2;AА2 ^П2=A2;
Проецирующие лучи АА1 и АА2взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1и фронтальную А2проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.
lib.qrz.ru
4. Точка на комплексном чертеже.
Метод проекций.
Проекция (лат. projectio — выбрасывание вперёд) — изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости.
Термин проекция также означает метод построения такого изображения и технические приёмы, в основе которых лежит этот метод.
Принцип
Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S(центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Соединив эти точки прямыми линиями в том же порядке, как они соединены в предмете, получим на плоскостиперспективное изображение предмета или центральную проекцию.
Если центр проекции бесконечно удалён от картинной плоскости, то говорят о параллельной проекции, а если при этом проекционные лучи падают перпендикулярно к плоскости — то обортогональной проекции.
Проекция широко применяется в инженерной графике, архитектуре, живописи и картографии.
Изучением проекций и методов проектирования занимается начертательная геометрия.
Проекционный чертеж– чертеж, построенный методом проецирования пространственных объектов на плоскость. Является основным средством для анализа свойств пространственных фигур.
Аппарат проецирования:
Центр проецирования (S)
Проекционные лучи
Объект проецирования
Проекция
Комплексный чертеж– эпюр Монжа. Декартова система координат, ось (x,y,z)
Плоскости:
Фронтальная – вид спереди;
Горизонтальная – вид сверху;
Профильная – вид сбоку.
Состав комплексного чертежа:
1) Плоскости проекций
2) Оси проекций (пересечение плоскостей проекций)
3) Проекции
Линии связи.
Основные свойства ортогонального проецирования.
2 связанные между собой ортогональные проекции однозначно определяют положение точки относительно плоскостей проекции. 3-яя проекция не может быть задана произвольно.
Ортогональные проекции.
Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка (рис. 58). Это объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А’В’ = ABcosa.
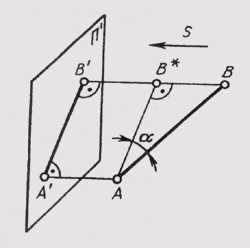
Рис. 58
При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.
Теорема о проецировании прямого угла. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой же угол.
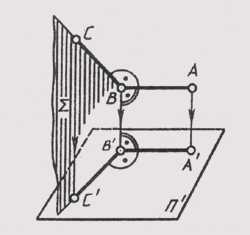
Рис. 59
Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости п’ (рис. 59). Проецирующая плоскость перпендикулярна плоскости п’. Значит, АВ _|_S, так как АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В’С’. Но так какАВ || А’В’ _|_ В’С’, т. е. на плоскости п’ угол между А’В’ и В’С равен 90°.
Обратимость чертежа. Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А (см. рис. 53) не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций п’. Любая точка проецирующего луча, проходящего через точку А, будет иметь своей проекцией точку А’. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа. В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрические чертежи).
Комплексный чертеж.
Прямая на комплексном чертеже:
Прямая общего положения– не параллельна и не перпендикулярна к плоскостям проекции.
Линии уровня– линии, параллельные плоскостям проекции:
Горизонталь
Фронталь
Профильная
Общее свойство: у линий уровня одна проекция равна натуральной величине, другие проекции параллельны осям проекций.
Проецирующие прямые– дважды линии уровня (если перпендикулярны одной из плоскостей, то параллельны 2 другим):
Горизонтально-проецирующая
Фронтально-проецирующая
Профильно-проецирующая
Конкурирующие точки– точки, лежащие на одной линии связи.
Взаимное расположение 2 прямых:
Пересекающееся – имеют 1 общую точку и общие проекции этой точки
Параллельные – проекции всегда параллельны у 2 параллельных прямых
Скрещивающиеся – не имеют общих точек, пересекаются только проекции, а не сами прямые
Конкурирующие – прямые лежат в плоскости перпендикулярной к одной из плоскостей проекций (н-р, горизонтально-конкурирующие)
Элементы трехпроекционного комплексного чертежа точки.
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-
Рис. 62
ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубинуfточки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-
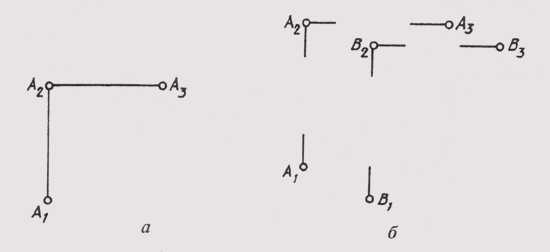
Рис. 63
ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
5. Прямая на комплексном чертеже. Основные положения.
Комплексный чертеж прямой линии.
Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.
На рис. 69, а показаны прямая l и принадлежащие ей точки А и В. Для построения фронтальной проекции прямой l2 достаточно построить фронтальные проекции точек А2 и В2 и соединить их прямой. Аналогично строится горизонтальная проекция, проходящая через горизонтальные проекции точек А1 и В1. После совмещения плоскости П1 с плоскостью П2 получим двухпроекционный комплексный чертеж прямой l (рис. 69, б).
Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.
6. Определение натуральной величины отрезка прямой общего положения.
Определение натуральной величины отрезка прямой линии.
При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.
Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).
Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.
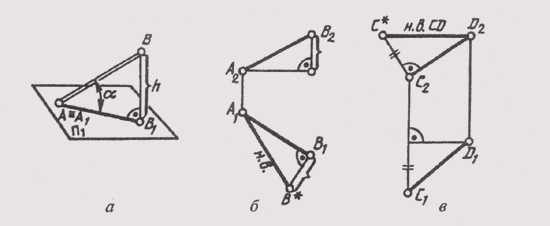
Рис. 78
Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них (см. § 36) или вводом новой плоскости проекций (заменой одной из плоскостей проекций) так, чтобы она была параллельна одной из проекций отрезка (см. §§58, 59).
треугольника.
Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника.
Вербальная форма | Графическая форма |
1. Определить на комплексном чертеже Аz, Bz, Ay, By: D z – разность расстояний от точек А и В до плоскости p1; D y – разность расстояний от точек А и В до плоскости p2 | |
2. Взять любую точку проекции прямой АВ, провести через нее перпендикуляр к отрезку: а) либо перпендикуляр к А2В2 через точку В2 или А2; б) либо перпендикуляр к А1В1 через точку В1 или А1 | |
3. На этом перпендикуляре от точки В2 отложить D y или от точки B1 отложить D z |
|
4. Соединить A2 и В’2; A1 и В’1 | |
5. Обозначить натуральную величину отрезка АВ (гипотенузу треугольника): |АВ| = А1В’1 = А2В’2 | |
6. Отметить углы наклона к плоскости проекции p1 и p2: a – угол наклона отрезка АВ к плоскости p1; б – угол наклона отрезка АВ к плоскости p2 |
При решении подобной задачи находить натуральную величину отрезка можно только один раз (либо на p 1, либо на p 2). Если требуется определить углы наклона прямой к плоскостям проекций, то данное построение выполняется дважды – на фронтальной и горизонтальной проекциях отрезка.
studfiles.net
Эпюр (комплексный чертеж) точки
Ортогональное проецирование точек
Любой геометрический образ можно представить как совокупность множества точек. Поэтому очень важно уметь строить их проекции. Суть ортогонального проецирования точки показана на рисунке 1. Дана некоторая плоскость П1– плоскость проекций и точка А, расположенная в пространстве. Для получения ортогональной проекции точки А на плоскости П1 необходимо через эту точку провести прямую l (проецирующий луч) перпендикулярно плоскости П1. Точка пересечения А1 прямой l с плоскостью П1 называется ортогональной проекцией точки А.
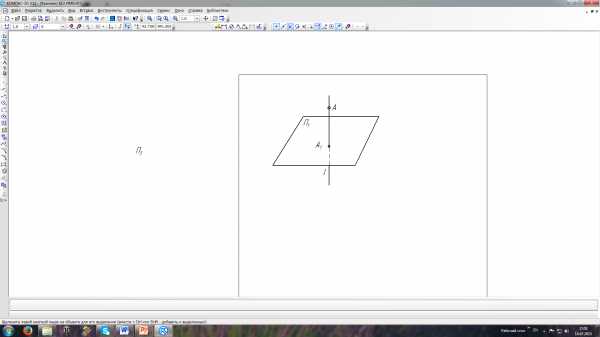
Рисунок 1
Как видно из чертежа, имея точку в пространстве, можно однозначно получить ее проекцию на некоторой плоскости.
В технических чертежах принято проецировать геометрические образы на три взаимно перпендикулярные плоскости – П1 , П2 и П3 (рисунок 2).
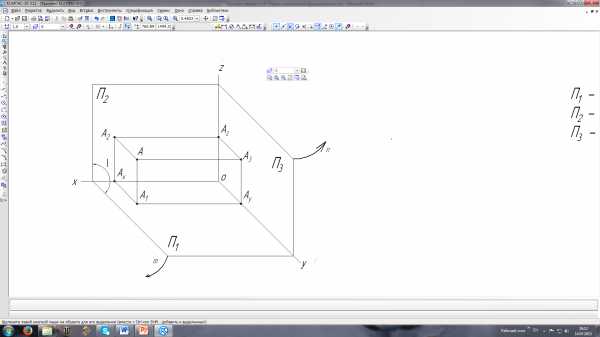
Рисунок 2
П1 – горизонтальная, П2 – фронтальная, П3 – профильная плоскости проекций. Это очень удобно для решения различных задач. Третья плоскость проекций П3 позволяет решить ряд задач, которые трудно осуществить на двух плоскостях. Как видно из рисунка 2, чтобы получить проекции точки А на плоскостях П1 , П2 и П3, необходимо из точки А провести перпендикуляры к этим плоскостям до их пересечения с плоскостями проекций в точках А1 , А2 , А3 .
Эпюр (комплексный чертеж) точки
На практике объемную систему, показанную на рисунке 2, применять сложно. Используют ее трансформацию (рисунок 3), которая называется «эпюр» или «комплексный чертеж». Фронтальную плоскость проекций П2 вместе с фронтальной проекцией точки А2 оставляют неподвижной. Горизонтальную плоскость проекций П1 вместе с горизонтальной проекцией точки А1 поворачивают вокруг оси ох по направлению стрелки m до совмещения с плоскостью П2. Профильную плоскость проекций П3 вместе с проекцией точки А3 поворачивают вокруг оси oz по направлению стрелки n также до совмещения с плоскостью П2. Полученный плоский чертеж, где все три плоскости проекций совмещены с одной, и называется эпюром. Здесь нет самой точки, есть только ее проекции. По их расположению и судят о положении точки в пространстве, а если это какой-то объект, то и о его форме и размерах. Как правило, на эпюре границ плоскостей П1 , П2 и П3 не дают, а показывают только оси системы.
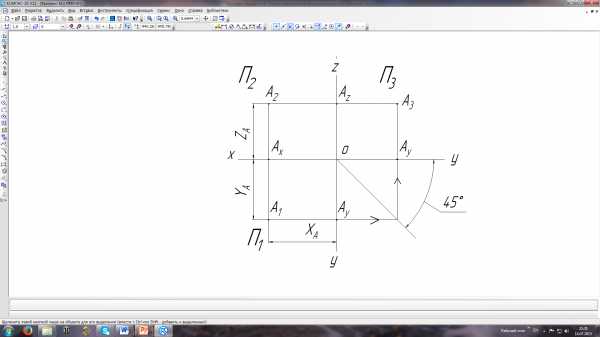
Рисунок 3
Анализируя эпюр, отметим его основные свойства:
– две проекции точки всегда лежат на одном перпендикуляре к оси их разделяющей;
– точку в пространстве определяют две её проекции или три координаты.
Горизонтальная и фронтальная проекции А1 и А2 точки А всегда находятся на одном перпендикуляре к оси ox. Фронтальная А2 и профильная А3 проекции точки лежат на одном перпендикуляре к оси oz.
Сформулируем также правила построения проекций точки на эпюре по заданным координатам. Если задана точка тремя координатами – A (x, y, z), то для построения ее проекций необходимо:
1) Отложить координату x точки А (отрезок ОАx).
2) Через полученную точку Аx провести перпендикуляр к оси ox.
3) Вверх по перпендикуляру от точки Аx откладываем координату z точки А. Получаем фронтальную проекцию точки – А2.
4) Вниз по перпендикуляру от точки Аx откладываем координату y точки А. Получаем горизонтальную проекцию точки – А1.
5) Профильную проекцию точки А3 строим, как показано на рисунке 3 (через биссектрису угла yOy), или иным другим способом (см. рекомендованную литературу).
Сформулированные правила построения проекций точки справедливы для первой четверти эпюра.
Похожие статьи:
poznayka.org
Проекции точки
Лекция 2
Проекции точки.
2.1. Метод проецирования.
Для построения изображения предметов на плоскости пользуются методом проецирования. Слово «проекция» — латинское, от глагола projecere, что в переводе означает «бросать вперед».
Следовательно, проекция это изображение предмета, «отброшенное» на плоскость при помощи лучей. Спроецировать предмет на плоскость это значит построить его изображение на плоскости.
Проекции разделяются на центральные и параллельные.
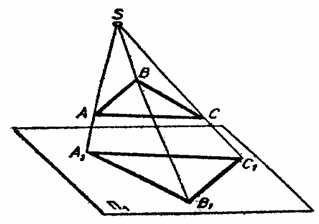
Рис. 2.1.
2.1.1. Идея центрального проецирования видна из рис. 2.1. Пусть заданы в пространстве точка S центр проекции и плоскость П1 плоскость проекции. Плоскость П1 и точка S составляют аппарат центральной проекции. Проецируемый треугольник АВС называется оригиналом, или натурой. Чтобы спроецировать заданный оригинал, нужно из центра проекции S через вершины треугольника провести проецирующие лучи до пересечения с плоскостью проекции П1. Точки пересечения А1, В1, С1, называются центральными проекциями вершин А, В, С, на плоскость П1, а треугольник А1В1С1 центральной проекции треугольника АВС. Центральные проекции (перспективу) применяют в архитектурных чертежах, в аэрофотосъемке, рисовании и др. Вследствие трудностей при построении изображений и их измерении, а также при чтении чертежей, в машиностроительном черчении центральными проекциями не используются.
2.1.2. В начертательной геометрии используют метод параллельного проецирования (рис. 2.2.). Как и в предыдущем случае, выбирают плоскость проецирования П1, но вместо центра проекции S задают направление проецирования s, т. е. считают, что точка S центр проекции расположена в бесконечности и поэтому проецирующие лучи параллельны между собой. Плоскость П1 и направление s составляют аппарат параллельной проекции. Чтобы спроецировать треугольник АВС на плоскость П1, через вершины А, В, С проводят проецирующие лучи параллельно направлению проецирования s. Треугольник А1В1С1, образованный пересечением лучей АА1, ВВ1, СС1 с плоскостью П1, и будет параллельной проекцией треугольника АВС.
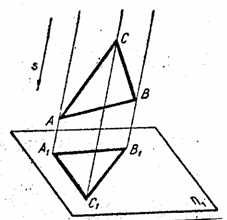
Рис. 2.2.
Параллельные проекции разделяются на прямоугольные и косоугольные. Если проецирующие углы перпендикулярны к плоскости проекций (рис. 2.3.), то способ проецирования называется прямоугольным, а полученные при этом проекции прямоугольными, или ортогональными. Если же угол наклона лучей не равен 90º, то подобная параллельная проекция называется косоугольной. В черчении используют, главным образом, прямоугольные проекции.
Рис. 2.3.
2.2. Задание точки на комплексном чертеже Монжа (эпюр Монжа)
2.2.1. Пространственная (или декартовая) система координат. Плоскости проекций
2.2.2 Проецирование точки на две плоскости проекций. Четверти пространства
2.2.3 Проекции точки на три плоскости проекций. Октанты пространства
2.2.4 Точки проекций общего и частного положения
2.2.1 Пространственная (или декартовая) система координат. Плоскости проекций
Вверх
В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексный чертеж) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрический чертеж).
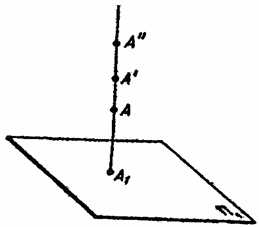
Рис. 2. 4.
Из рис. 2. 4. видно, что проекции А1 отвечает бесчисленное множество точек (А, A, A»), лежащих на проецирующем луче, идущем из А1 перпендикулярно к плоскости проекции П1.
Совокупность двух прямоугольных проекций на две взаимно перпендикулярные плоскости позволяет однозначно определить форму и положение предмета в пространстве. Однако в черчении при построении изображений чаще используют три плоскости проекции и потому рассмотрим законы проецирования на три плоскости проекции.
Пусть заданы три взаимно перпендикулярные плоскости проекций, образующих прямой трехгранный угол (рис.2.5.): П1 горизонтальная, П2 фронтальная и П3 профильная плоскости проекций; линии Оx, Оy, Оz взаимного пересечения плоскостей проекций называются осями проекций, а точка О началом осей проецирования.
Рис. 2.5.
В пространстве трехгранного угла задана точка А и требуется построить ее проекции на плоскости П1, П2, П3 (точку можно рассматривать как вершину некоторого предмета, например параллелепипеда, изображенного на рис.2.6.). Для этого из точки А проводят проецирующие лучи АА1, АА2, АА3, перпендикулярные к плоскостям проекций, до пересечения с ними. В результате пересечения получают А1 горизонтальную, А2 фронтальную, А3 профильную проекции точки А. Прямая АА1 называется горизонтально проецирующим, АА2 фронтально проецирующим, АА3 профильно проецирующим лучами. Проецирующие лучи АА1 и АА2 определяют плоскость перпендикулярную к оси Ох и ∩ плоскостям П1, П2 пересекает плоскости проекций по прямым А1Ах и А2АХ, перпендикулярно к оси Ох. Точку пересечения этой плоскости с осью Ох обозначают Ах. рассуждая аналогично, получают прямые А1Ау и А3Ау, перпендикулярные к оси Оу, и прямые А2Az и А3Az, перпендикулярные к оси Оz.
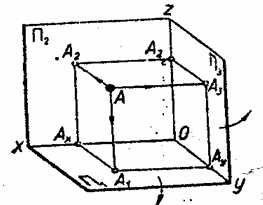
Рис. 2.6.
2.2.2 Проецирование точки на две плоскости проекций. Четверти пространства
Вверх
Две взаимно перпендикулярные плоскости проекций П1 горизонтальная плоскость проекций, П2 фронтальная плоскость проекций делят пространство на четыре квадранта (четверти):
I октант передний верхний,
II октант задний верхний,
III октант задний нижний,
IV октант — передний нижний.
Плоскости П1 и П2 пересекаются по прямой, называемой осью проекций (осью абсцисс).
Пусть дана точка А в I октанте и требуется спроецировать её (ортогонально) на плоскости П1 и П2 (рис. 2.7).
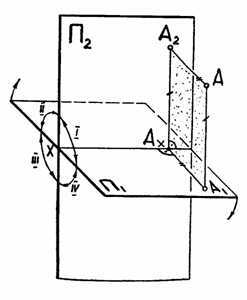Рис. 2.7
Спроецировать ортогонально точку А значит геометрически опустить из точки А на плоскости проекций П1 и П2 перпендикуляры.
АА2^П2
АА1^П1
Построим комплексный чертеж (эпюр) точки А, т.е. плоский чертеж точка А, состоящий из двух проекций точки А. Для этого мысленно удаляют точку А и проецирующие прямые АА1 и АА2, а затем вращают плоскости П1 вокруг оси Х до совмещения с плоскостью П2, вращая плоскость П1 так, чтобы передняя полуплоскость П1 оказалась под осью Х в совмещенном положении (см. стрелки рис. 2.1).
Прямая линия А2А1, соединяющая две проекции точки на чертеже, называется линией связи.
Проще начинать строить эпюр точки А с фронтальной проекции А2, т.к фронтальная плоскость совпадает с плоскостью эпюра, и поэтому расположение точки А2 относительно оси Х12 на эпюре будет таким же, как и на оригинале (рис. 2.8).
Рис. 2.8.
Отрезок А1Ах равен расстоянию точки А до фронтальной плоскости проекций П2, называемому ординатой точки А или глубиной точки А. А1Ах=АА2=УА.
Отрезок А1Ах равен расстоянию точки А до горизонтальной плоскости проекций П, называемому аппликатой точки А или высотой точки А.
А2Ах=АА1=ZА
Прочитать чертеж точки А, значит перегнуть его мысленно по оси Хх (ось абсцисс), восстановить перпендикуляры из проекций точки А, и тогда точка пересечения их будет точкой А, заданной комплексным чертежом. Таким же образом доказывается и то, что две проекции точки вполне определяют положение точки в пространстве.
Построение чертежей точек по координатам упрощается, если нанести координатные оси аппликат Z и ординат Y на наглядном рисунке плоскостей проекций П1 и П2 и на комплексном чертеже точки (рис. 2.9)
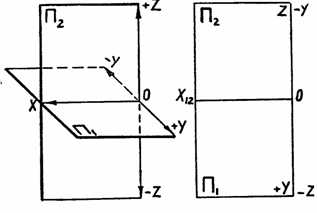
Рис. 2.9.
Таблица 1
В начертательной геометрии принята левая система координат, когда влево направлена положительная полуось абсцисс Х. Обе проекции точки могут располагаться как над осью Х-ов в зависимости от того, в каком квадранте будет расположена точка.
Построение эпюра (чертежа) точки по наглядному рисунку точки в пространстве, расположенной в той или иной четверти, проще начинать с построения фронтальной проекции точки, откладывая на эпюре по направлению линии связи размер высоты точки, а после этого надо представить себе и решить, куда вниз или вверх будет перемещаться горизонтальная проекция точки с той горизонтальной полуплоскостью, на которой она расположена, и только тогда можно решить, где над осью Х-ов, или под осью Х-ов будет расположена горизонтальная проекция точки на эпюре.
Построение наглядного рисунка точки в пространстве, расположенной в том или ином квадранте по заданному эпюру точки, лучше также начинать с фронтальной проекции, откладывая размер А2Ах высоты точки А. После этого надо решить вопрос, на какой горизонтальной полуплоскости проекции, передней или задней, должна лежать горизонтальная проекция точки. Если на эпюре горизонтальная проекция точки лежит под осью абсцисс, то она на наглядном рисунке будет расположена на передней горизонтальной полуплоскости. Если над осью абсцисс, то на задней горизонтальной полуплоскости.
2.2.3 Проекции точки на три плоскости проекций. Октанты пространства
Вверх
В начертательной геометрии принято от пространственного изображения точки и ее проекций переходить к плоскому, или комплексному, чертежу, образованному вращением плоскости проекций вокруг осей проекций (рис., 2.10.).
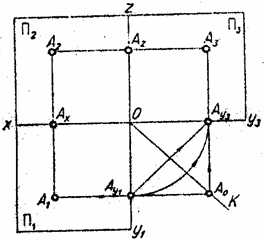
Рис. 2.10.
Сохраняя неподвижной фронтальную плоскость проекций П2, горизонтальную плоскость П1 поворачивают вокруг оси Ох вниз на 90о, а профильную вокруг оси Оz вправо на 90о до их совмещения с фронтальной плоскостью проекций. Направление изображения показано на рис. 1.6.. стрелками. Полученное изображение трех плоскостей проекций вместе с изображенными на них проекциями А1, А2, А3 точки А называют комплексным чертежом точки А. на комплексном чертеже ось Оу раздваивается и кроме вертикального положения Оу1 (вниз от точки О) занимает и второе горизонтальное положение Оу3 (вправо от точки О).
Прямую, соединяющую две проекции точки на комплексном чертеже, называют линией связи.
Из анализа рис. 1.7.. вытекают следующие основные положения:
а) горизонтальная А1 и фронтальная А2 проекции точки всегда расположены на вертикальной линии связи, перпендикулярной к оси проекций Ох;
б) Фронтальная А2 и профильная А3 проекции точки всегда расположены на горизонтальной линии связи, перпендикулярной к оси проекций ОZ;
в) горизонтальная А1 и профильная А3 проекции точки всегда расположены на линиях связи, пересекающихся на биссектрисе угла у1Оу3. Эта биссектриса получила наименование постоянной прямой чертежа (линия К), а линия связи А1А0А3 ломаной или горизонтально- вертикальной линии связи.
В начертательной геометрии часто приходится решать задачи на построение третьей проекции фигуры по двум данным. Для этого прежде нужно научиться строить третью проекцию точки, если известны две ее проекции. Выполнить это можно тремя способами.
Проекционный способ (рис 1.7.). Из фронтальной проекции А2 проводят горизонтальную линию связи. Из горизонтальной проекции А1 опускают перпендикуляр на ось Оу1, получают точку Ау1, и при помощи циркуля или прямоугольного равнобедренного треугольника находят на оси Оу3 положение точки Ау3. из этой точки проводят вертикальную линию связи до пересечения с линией связи, проведенной из А2. Точка А3 профильная проекция точки А.
Координатный способ. Из фронтальной проекции А2 проводят горизонтальную линию связи. Измеряют циркулем расстояние от проекции А1 до оси Ох (глубину точки, или координату уА) и откладывают этот отрезок на линии связи вправо от точки АZ. Получают профильную проекцию А3.
Способ с использованием постоянной прямой чертежа. Из фронтальной проекции А2 проводят горизонтальную линию связи. Из горизонтальной проекции А1 проводят линию связи до пересечения в точке А0 с постоянной прямой К, т.е. биссектрисой угла у1Оу3. из точки А0 проводят вертикальную линию связи до пересечения с линией, проведенной из фронтальной проекции А2.
Предпочтительней второй и третий способы, требующие меньшего числа построений и позволяющие использовать чертежные приборы.
В пространстве может быть взято множество точек, занимающих по отношению к плоскостям проекции различное положение. Например, пирамида и срезанный параллелепипед имеют 13 вершин- точек, различно расположенных относительно плоскостям П1, П2, П3. Чтобы определить положение каждой из этих точек в отдельности, нужно знать три ее измерения- широту, высоту, глубину.
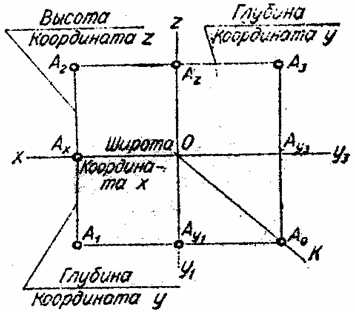
Рис.2.11.
Z высота точки (рис. 2.11.) определяется ее расположением от горизонтальной плоскости проекций или удалением ее фронтальной проекции А2 от точки Ох (АА1 = А2Ах).
У глубину точки измеряют ее расстоянием от фронтальной плоскости проекций или удалением ее горизонтальной проекции А1 от оси Ох (АА2 = А1Ах).
Х широтой точки является ее удаление от профильной плоскости проекций или расстояние от точки АХ до начала осей проекции О (АА3 = АХО). Все эти утверждения вытекают из рассмотрения треугольников АА1АХА2 и АА1АУА3.
Если принять плоскость и оси проекции за координатные плоскости и оси координат х у, z, то положение любой точки пространства может быть задано тремя ее координатами. В этом случае отрезок АА3 = АХО выражает координату х, т.е. расстояние от точки до плоскости П3, отрезок АА2 = А1АХ координату у, т.е. расстояние от точки до плоскости П2, и отрезок АА1 = А2АХ координату z, т.е. расстояние от точки до плоскости П1. Запись типа А (10, 16, 8) означает, что координата х точки А равна 10мм, координата у=16 мм, координата z= 8 мм.
Рассмотрим на примере построение проекций точки по ее координатам (измерениям). Задана точки А (25, 15, 20), т.е. х = 25мм, у = 15мм, z = 20мм. Нужно построить комплексный чертеж точки в системе трех плоскостей проекции.
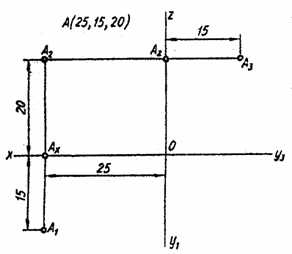
Рис. 2.12.
Проводят оси Ох, Оу, Оz (рис. 2.12.). По оси Ох влево от точки О откладывают координату х = 25мм и через полученную точку Ах проводят вертикальную линию связи. На этой линии вниз от Ах откладывают значение координаты у = 15мм и получают горизонтальную проекцию А1 точки А. на этой же линии вверх от Ах откладывают значение координаты z = 20мм и получают фронтальную проекцию А2 точки А. Найденные проекции А1 и А2 определяют положение точки. Если нужно построить третью, профильную, проекцию, из проекции А2 проводят горизонтальную линию связи и откладывают вправо от точки Аz отрезок, равный значению координаты у (АяА3 = 15мм). А3 профильная проекция точки А.
На рисунке 2.13. построены комплексные чертежи точек В (20,0,5) и С (15,0,0).
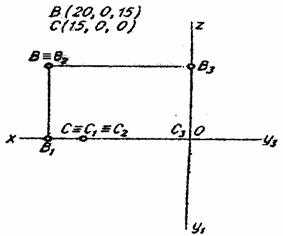
Рис. 2.13.
2.2.4 Точки проекций общего и частного положения.
Вверх
Наиболее удобной для фиксирования положения геометрической фигуры в пространстве является декартова система координат, состоящая из трех взаимно перпендикулярных плоскостей:
П1 горизонтальная плоскость проекций;
П2 фронтальная плоскость проекций;
П3 профильная плоскость проекций;
Ось х ось абсцисс;
Ось у ось ординат;
Ось z ось аппликат;
О начало координат.
Положительными направлениями оси считают: для оси х влево от начала координат, для оси у в стороны зрителя от плоскости П2, для оси z вверх от плоскости П1, противоположные направления осей считаются отрицательными (рис. 2.14.).
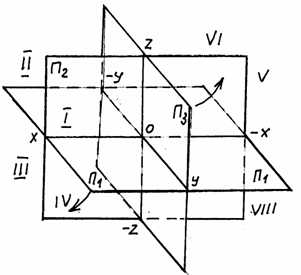
Рис. 2.14.
Плоскости проекции делят пространство на 8 частей октантов, каждый из которых представляет собой прямоугольный треугольник, где гранями являются части плоскостей проекций, а ребрами оси координат.
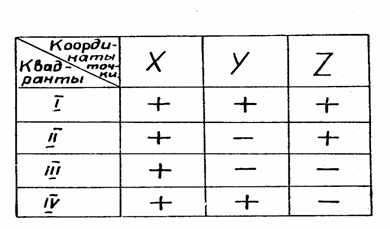
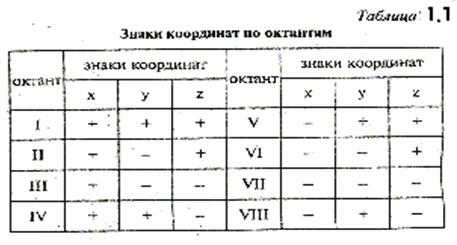
Учитывая при отсчете координат направления осей х, у, z, получим знаки координат для каждого октанта (табл. 2).
Возможны следующие случаи.
Точка расположена в пространстве. В этом случае ее зададут тремя координатами (измерениями). Все три проекции точки удалены от осей проекций (рис. 2.9.).
Точка находится на одной из плоскостей проекций П1, П2 или П3. В этом случае ее задают двумя действующими координатами, не равными нулю. Одна проекция совпадает с самой точкой, а две другие лежат на осях. На рисунке 1.10. изображены проекции точки В (20, 0, 15), лежащей в плоскости проекций П2. В этом случае фронтальная проекция В2 совпадает с самой точкой В, горизонтальная проекция В1 лежит на оси Ох, а профильная В3 на оси Оz.
Точка находится на одной из осей проекций Ох, Оу, Оz. В этом случае ее задают одной действительной координатой, не равной нулю. Две проекции совпадают с самой точкой, а третья находится в точке О начале осей проекций. На рисунке 2.10 изображены проекции точки С (15, 0, 0), лежащей на оси Ох. В этом случае горизонтальная С1 и фронтальная С2 проекции совпадают с самой точкой С, а профильная проекция С3 находится в точке О.
К чтению чертежа следует отнести решение таких вопросов:
а) определение третьей проекции точки по двум данным;
б) определение координат точки и ее положения относительно плоскостей проекции;
в) построение аксонометрического изображения точки по ее комплексному чертежу;
г) анализ взаимного расположения нескольких точек относительно плоскостей проекции и др.
На рисунке 2.15. заданы проекции точки А и В. Эти точки расположены в пространстве, так как ни одна из их координат не равна нулю. Широта точки А больше широты точки В, так как отрезок ОАх больше отрезка ОВх. Следовательно, точка А дальше отстоит от плоскости П3, чем точка В. Глубины этих точек равны вследствие равенства координат у (А1Ах = В1Вх). Из этого следует, что точки одинаково удалены от плоскости проекции П2. Высоты у точек различны. Точка В дальше от плоскости П1 на величину, равную отрезку В2В0.
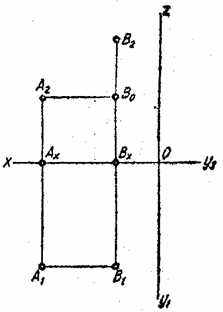
Рис. 2.15.
2.3. Обратимость чертежа
Обратимость чертежа. Проецированием на одну плоскость проекций получается изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А1 (см. рис. 2.4.) не определяет положение самой точки в пространстве, так как неизвестно, на какое расстояние она удалена от плоскости проекций П1. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображения дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа.
refleader.ru