Специальный фотоаппарат зафиксировал два положения – Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика: в начале падения и через τ = 0,31 с.

Содержание

Движение в поле силы тяжести СВОБОДНОЕ ПАДЕНИЕ

Движение в поле силы тяжести

СВОБОДНОЕ ПАДЕНИЕ

Свободное падение фотоаппарат • Специальный зафиксировал два положения падающего в воздухе из состояния покоя шарика: в начале падения и через 0, 31 с (см. рисунок). • Ускорение свободного падения по результатам такого опыта приблизительно равно

Свободное падение • С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало

• 55. Тело свободно падает из состояния покоя. На сколько увеличивается скорость тела за пятую секунду? • 56. От высокой скалы откололся и стал свободно падать камень. Какую скорость он будет иметь через 2 с после начала падения? • 57. Тело упало с некоторой высоты с нулевой начальной скоростью и при ударе о землю имело скорость 40 м/с. Чему равно время падения? Сопротивлением воздуха пренебречь. • 58. Тело брошено вертикально вверх со скоростью 20 м/с. Сопротивление воздуха пренебрежимо мало. Каково время полета тела до точки максимальной высоты? • 59. Тело брошено вертикально вверх. Через 0, 5 с после броска его скорость равна 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. • 60. Сосулька, упав с края крыши, долетела до земли за 3 с. Чему равен путь сосульки? • 61. Стрела, пущенная вертикально вниз с обрыва высотой 30 м со скоростью 5 м/с, достигает воды. Чему равно время полета стрелы?

БАЛЛИСТИЧЕСКОЕ ДВИЖЕНИЕ

• 1. С башни высотой 45 м горизонтально брошен камень. Через какое время он упадет на землю? • 2. Глыбу льда сбрасывают с крыши с высоты 25 м горизонтально со скоростью 3 м/с. На каком расстоянии от дома упадет глыба? • 3. Из окна, расположенного на высоте 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью брошен камень? • 4. Пуля вылетает из ствола в горизонтальном направлении со скоростью 800 м/с. На сколько снизится пуля во время полета, если щи г с мишенью находится на расстоянии 400 м? • 5. Тело бросили горизонтально со скоростью 40 м/с с некоторой высоты. Определите его скорость через 3 с. • 6. Камень, брошенный горизонтально со скоростью 15 м/с, упал на землю со скоростью 25 м/с. Сколько времени длился полет камня? • 7. На горе с углом наклона к горизонту 30° бросаю! горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?

Ответы

• 1. С башни высотой 45 м горизонтально брошен камень. Через какое время он упадет на землю? (3 с) • 2. Глыбу льда сбрасывают с крыши с высоты 25 м горизонтально со скоростью 3 м/с. На каком расстоянии от дома упадет глыба? (6, 7 м) • 3. Из окна, расположенного на высоте 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью брошен камень? (8 м/с) • 4. Пуля вылетает из ствола в горизонтальном направлении со скоростью 800 м/с. На сколько снизится пуля во время полета, если щи г с мишенью находится на расстоянии 400 м? (1, 25 м) • 5. Тело бросили горизонтально со скоростью 40 м/с с некоторой высоты. Определите его скорость через 3 с. (50 м/с) • 6. Камень, брошенный горизонтально со скоростью 15 м/с, упал на землю со скоростью 25 м/с. Сколько времени длился полет камня? (2 с) • 7. На горе с углом наклона к горизонту 30° бросаю! горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет? (30 м)

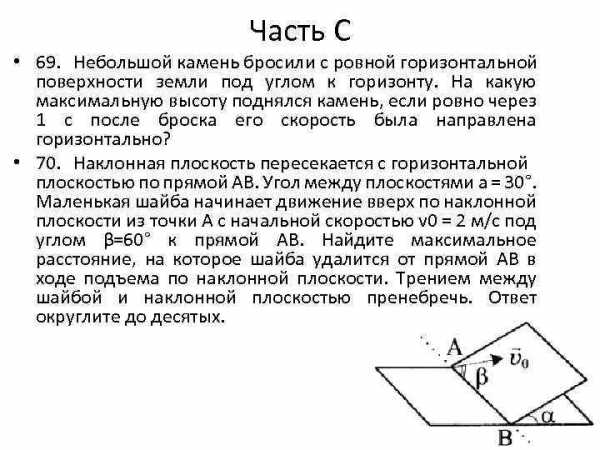Часть С • 69. Небольшой камень бросили с ровной горизонтальной поверхности земли под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально? • 70. Наклонная плоскость пересекается с горизонтальной плоскостью по прямой АВ. Угол между плоскостями а = 30°. Маленькая шайба начинает движение вверх по наклонной плоскости из точки А с начальной скоростью v 0 = 2 м/с под углом β=60° к прямой АВ. Найдите максимальное расстояние, на которое шайба удалится от прямой АВ в ходе подъема по наклонной плоскости. Трением между шайбой и наклонной плоскостью пренебречь. Ответ округлите до десятых.

Часть С • 71. С высоты Н = 30 м над землей свободно падает стальной шарик. При падении он сталкивается с неподвижной плитой, плоскость которой наклонена под углом 30° к горизонту, и взлетает на высоту h = 15 м над поверхностью земли. Каково время падения шарика до удара о плиту? Удар шарика о плиту считать абсолютно упругим. • 72. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от нее. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна 1 м/с. Ответ округлите до сотых.

present5.com

Кинематика

1. Лодка должна попасть на противоположный берег по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки и, а скорость лодки относительно воды υ. Moдуль скорости лодки относительно берега должен быть равен 1)υ+ и 2)υ— u 3)√ υ²+ и² 4)√ υ²— и²

2. Решаются две задачи: а) рассчитывается маневр стыковки двух космических кораблей; б) рассчитывается период обращения космических кораблей вокруг Земли. В каком случае космические корабли можно рассматривать как материальные точки? 1)только в первом случае 2)только во втором случае 3)в обоих случаях 4) ни в первом, ни во втором случае

3. Чему равно перемещение материальной точки за 5с, движение которой вдоль оси ОХ описывается уравнением: х = 6-4t +t²? 1)5м 2)11м 3)13м 4)18м

4. По графику зависимости модуля скорости от времени (см. рис1) определите путь, пройденный телом за 2 с. 1)6м 2)8м 3)5м 4)4м

5. На рисунке 2 представлен график зависимости координаты тела, движущегося вдоль оси ОХ, от времени. Сравните скорости υ_l, υ₂ и υ₃ тела в моменты времени t₁, t₂, t₃. 1) υ₁ > υ₂ = υ₃2) υ₁> υ₂> υ₃3) υ_l = υ

2< υ₃4) υ₁ = v₂>v₃

6. Лестница, приставленная к вертикальной стене, падает в результате скольжения ее основания по полу. Каково отношение модулей скоростей

υ_А и υ_B (см. рис3) в тот момент, когда угол между лестницей и стеной равен α l) sin α 2) cos α 3) tg α 4) ctg α

7. По графику зависимости модуля скорости от времени, представленному на рис4, определите ускорение прямолинейно движущегося тела в момент времени t=2с. 1)2м/с²2)3м/с²3)9м/с² 4)27м/с²

8. Уравнение зависимости проекции скорости движущегося тела от времени: v_x = 2 + 3t (м/с). Каково соответствующее уравнение проекции перемещения тела? 1)S_x=2t+3t² 3)S_x=2t+l,5t² 2)S

x=1,5t² 4)S_x=3t+t²

9. При свободном падении тел разной массы в трубке, из которой откачан воздух, тела движутся с одинаковым ускорением. Это объясняется тем, что сила тяжести: 1) на тела в вакууме не действует 2) пропорциональна массе тел

3) не зависит от массы тела 4) уравновешивается весом тел

10. Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика: в начале падения и через 0,31 с (см. рис5). Ускорение свободного падения по результатам такого опыта приблизительно равно…

1)10,0м/с²2)10,5м/с² 3)9,2м/с²4)11,0м/с²

11. Материальная точка, двигаясь равномерно по окружности против часовой стрелки, через 3 секунды первый раз попала из точки А в точку В (рис6). Частота обращения точки равна… 1)1/12c^-1 2) 1/4c

-1 3) 1/3c^-1 4)1/2c^-1

12. Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рис7. В каши из указанных точек траектории центростремительное ускорение максимально?

1)1 2)2 3)3 4)Во всех точках одинаково

13.На кольцевой гонке два автомобиля движутся так, что все время были расположены на одной прямой, соединяющей их положение с центром окружности (рис8) Отношение скоростей υ₁/υ₂равно1)1/2 2)2 3)√2 4)4

studfiles.net

Тест Вариант 7

А1. На рисунке представлены графики зависимости модулей скоростей четырех тел от времени. Какое из этих тел прошло наибольший путь за первые 2с?

1234

А2. Поезд движется со скоростью 15 м/с. Пассажир этого поезда видит в окне встречный поезд длиной 150 м в течение 6 с. Скорость встречного поезда равна

1) 10 м/с
2) 15 м/с
3) 20 м/с
4) 25 м/с
1234

A3.К перекрестку приближается грузовая машина со скоростью v1 и легковая машина со скоростью v2 (рис.1).

Какое направление имеет вектор скорости v21 легковой машины в системе отсчета грузовой машины (рис.2)?

1234

А4. Вертолет равномерно поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета
в системе отсчета, связанной с Землей?
1) точка. 2) окружность. 3) прямая. 4) винтовая линия.
1234

А5. Плот равномерно плывет по реке со скоростью 3 км/ч. Человек движется поперек плота со скоростью 4 км/ч относительно плота. Чему равна скорость человека в системе отсчета, связанной с берегом?
1)3 км/ч. 2)4 км/ч. 3)5 км/ч. 4)7 км/ч.
1234

А6.Двигаясь прямолинейно, одно тело за каждую секунду проходит путь 5 м. Другое тело, двигаясь по прямой в одном направлении, за каждую секунду проходит путь 10 м. Движения этих тел
1) равномерные
2) неравномерные
3) первого — неравномерное, второго — равномерное
4) нельзя сказать о характере движения тел
1234

А7. Две моторные лодки движутся вдоль реки навстречу друг другу. Скорости лодок относительно воды равны 3 и 4 м/с соответственно. Скорость течения реки равна 2 м/с. Через какое время после их встречи расстояние между лодками станет равным 84 м?
1)12 с. 2)21 с. 3)28 с. 4)42 с.
1234

А8. Спидометр автомобиля показывает
1) модуль ускорения
2) модуль мгновенной скорости
3) среднюю скорость от начала движения
4) направление скорости
1234

А9. Модуль скорости тела за некоторое время увеличился в 2 раза. Какое утверждение будет верным?
1) ускорение тела возросло в 2 раза
2) ускорение уменьшилось в 2 раза
3) ускорение не изменилось
4) тело движется ускорением
1234

А10. По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени t = 2 с.
1)1,5 м/с². 2)0,5 м/с². 3)6 м/с². 4)1 м/с²

1234

А11. Поезд отходит от станции с ускорением 0,5 м/с². Какой путь проходит поезд при движении с таким ускорением за 10 с после начала движения?
1)2,5 м. 2)5 м. 3)25 м. 4)50 м.
1234

A12.Зависимость координаты Х от времени при равноускоренном движении по оси ОХ, дается выражением:
(Х измеряется в метрах, время — в секундах). Величина начальной скорости равна
А. 0 м/с. Б. 5 м/с. В. 7,5 м/с. Г.15 м/с.
1234

А13.При свободном падении тел разной массы в трубке, из которой откачан воздух, тела движутся с одинаковым ускорением. Это объясняется тем, что сила тяжести:
1) на тела в вакууме не действует
2) не зависит от массы тела
3) пропорциональна массе тел
4) уравновешивается весом тела
1234

А14. Какой путь пройдет тело за первые 3 секунды свободного падения с V0=0. (принять g = 10 м/с²).
1)15м 2)30м 3)45м 4)90м
1234

A15. При фотографировании специальным фотоаппаратом было зафиксировано два положения свободно падающего из состояния покоя шарика: в начале падения и через 0,31 с (рис.). По результатам опыта определите ускорение свободного падения. Оно приблизительно равно
1)…10,0 м/с. 2)…10,5 м/с2. 3)… 9,2 м/с2. 4)… 11,0 м/с.

1234

Введите свою фамилию:

musoch50.narod.ru

Тесты

	Тесты по физике взяты из сборника экзаменационных заданий физика ЕГЭ 2008 г. МЕХАНИКА А. Простые задания с вариантами ответов
	Задание 1.1-А1. Поставлены две задачи: 1) рассчитать маневр стыковки двух космических кораблей; 2) рассчитать период обращения космических кораблей вокруг Земли. В каком случае космические корабли можно рассматривать как материальные точки? 1. Только в первом случае. 2. Только во втором случае. 3. В обоих случаях. 4. Ни в первом, ни во втором случае. Рекомендация по решению Задание 1.1-А2. Камень брошен из окна второго этажа с высоты 4 м и падает на землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня? 1. 3 м. 2. 4 м. 3. 5 м. 4. 7 м. Рекомендации по решению
	Задание 1.1-АЗ. На рисунке представлен график зависимости координаты движущегося тела от времени. Сравните скорости v1, v2 и v3 тела в моменты времени t1, t2, t3. 1. v1>v2=v3 2. v1>v2>v3 3. v1<v2<v3 4. v1=v2>v3 Рекомендации по решению
	Задание 1.1-А4. По графику зависимости модуля скорости от времени, представленному на рисунке, определите ускорение прямолинейного движения в момент времени t = 2 с. 1. 2 м/с2. 2. 3м/с2. 3. 9 м/с2. 4. 27 м/с2. Рекомендации по решению
	Задание 1.1-А5. На рисунке показаны три равные по модулю силы, действующие на тело, и его мгновенная скорость. Куда направлено ускорение тела? 1. Вверх. 2. Влево. 3. Вправо. 4. Направление ускорения по условию задачи определить нельзя. Рекомендации по решению
	Задание 1.1-А6. Шарик, брошенный из точки А под углом к горизонту, проходит верхнюю точку полета. Какая стрелка правильно указывает направление ускорения тела, если сопротивлением воздуха можно пренебречь? 1. 1 2. 2 3. 3 4. 4 Рекомендации по решению
	Задание 1.1-А7. Книга лежит на столе. На каком рисунке верно представлены силы взаимодействия книги и крышки стола? Рекомендации по решению
	Задание 1.1-А8. Ученик провел опыты с двумя разными пружинами, измеряя силы упругости при разных деформациях пружин. Результаты экспериментов приведены в таблице. Закон Гука в условиях проведенных опытов… 1. …подтверждается только для первой пружины. 2. …подтверждается только для второй пружины. 3. …подтверждается для обеих пружин. 4. … не подтверждается ни для одной из пружин. Рекомендации по решению
	Задание 1.1-А9. На рисунке представлен график зависимости силы трения FTp от модуля силы нормального давления N. Определить коэффициент трения скольжения. 1. 0,1. 2. 0,2. 3. 0,25. 4. 0,5. Рекомендации по решению
	Задание 1.1-А10. В 1798 г. Генри Кавендиш провел измерение G-гравитационной постоянной. Этот научный факт позволяет определить… 1. …массу Земли. 2. …период вращения Земли вокруг Солнца. 3. …период вращения Земли вокруг своей оси. 4. …расстояние от Земли до Солнца. Рекомендации по решению Задание 1.1-А11. Какое из приведенных ниже утверждений является определением, а какое — законом? 1. Импульс р равен произведению массы тела m на его скорость v . 2. Изменение импульса пропорционально силе F и времени t ее действия. 1. 1 — определение, 2 — закон. 2. 1 — закон, 2 — определение. 3. 1 и 2 — определения. Среди утверждений 1 и 2 нет ни определения, ни закона. Задание 1.1-А12. Тележка массой т, движущаяся со скоростью v, сталкивается с неподвижной тележкой такой же массы и сцепляется с ней. Скорость тележек после взаимодействия равна… 1. …v/√2 2. …v/2 3. …v 4. …2v Рекомендации по решению Задание 1.1-А13. Кинетическая энергия тела измеряется в тех же единицах, что и… 1. …работа силы. 2. …импульс силы. 3. …мощность силы. 4. …давление. Задание 1.1-А14. Кинетическая энергия тела равна 8 Дж, а величина импульса 4 Нс. Масса тела равна… 1. …0,5 кг. 2. …1 кг. 3. …2 кг. 4. …32 кг. Рекомендации по решению Задание 1.1-А15.* Подъемный кран поднимает вертикально вверх равномерно груз весом 1000 Н на высоту 5 м за 5 с. Какую механическую мощность развивает подъемный кран за время этого подъема? 1. 0 Вт. 2. 5000 Вт 3. 25 000 Вт. 4. 1000 Вт. Рекомендации по решению Задание 1.1-А16. Какое из значений для КПД наклонной плоскости, полученных учащимися при выполнении лабораторной работы, является заведомо неверным? 1. 1,5. 2. 0,75. 3. 0,60. 4. 0,33 Рекомендации по решению Задание 1.1-А17. Какие величины сохраняются для системы тел при упругом и неупругом ударах? 1. Суммарная механическая энергия и импульс шаров. 2. Только суммарная механическая энергия шаров. 3. Только суммарный импульс шаров. 4. Только суммарная скорость шаров. Рекомендации по решению Задание1.1-А18. Тормозной путь увеличивается при уменьшении… 1. …угла наклона дороги к горизонту во время движения под гору. 2. …коэффициента трения шин о дорогу. 3. …скорости перед торможением. 4. …массы автомобиля. Рекомендации по решению Задание 1.1-А19. Парашютист движется вертикально вниз с постоянной скоростью. При этом его… 1. …потенциальная энергия превращается в кинетическую. 2. …потенциальная энергия превращается во внутреннюю энергию системы «парашютист — воздух». 3. …кинетическая энергия превращается в потенциальную. 4. …кинетическая энергия превращается во внутреннюю энергию системы «парашютист — воздух». Рекомендации по решению Задание 1.1-А20. На рычаг действуют две перпендикулярные рычагу силы, плечи которых равны 0,1 м и 0,3 м. Сила, действующая на короткое плечо, равна 3 Н. Чему должна быть равна сила, действующая на длинное плечо, чтобы рычаг был в равновесии? 1. 1 Н. 2. 6 Н. 3. 9 Н. 4. 12 Н. Рекомендации по решению Задание 1.1-А21. Чему примерно равна архимедова сила, действующая на тело объемом 2 м3, наполовину погруженное в жидкость плотностью 1000 кг/м3? 1. 2000 Н. 2. 5000 Н. 3. 10 000 Н. 4. 20 000 Н. Рекомендации по решению
	Задание 1.1-А22. Груз на нитке (см. рис.) начинает двигаться из точки А и далее совершает колебания, проходя последовательно точки А-Б-В-Б-А и т. д. Период колебания — это время его движения… 1. …от точки А до точки Б. 2. …от точки Б до точки В. 3. …от точки А до точки В. 4. …от точки А до точки В и обратно до точки А.
	Задание 1.1-А23. Тело колеблется вдоль оси х так, что его координата меняется во времени по закону х = 5cos(πt) м. Период колебаний тела равен… 1. …0,5 с. 2. …2 с. 3. …л с. 4. …5 с. Рекомендации по решению Задание 1.1-А24. Если массу груза уменьшить в 4 раза, то период колебаний груза на пружине… 1. …увеличится в 4 раза. 2. …увеличится в 2 раза. 3. …уменьшится в 2 раза. 4. …уменьшится в 4 раза. Рекомендации по решению Задание 1.1-А25. Вы услышали звуковой сигнал от источника, скрытого за препятствием. Этот факт можно объяснить, рассматривая звук как… 1. …механическую волну. 2. …поток частиц, вылетающих из источника звука. 3. …поток молекул, составляющих воздух и движущихся от источника поступательно. 4. …вихревой поток воздуха, идущий из источника звука. Задание 1.1-А26. Уравнение зависимости проекции скорости движущегося тела от времени: vx=2+3t(м/с). Каково соответствующее уравнение проекции перемещения тела? 1. rx = 2t + 3t2 (м). 2. rх = 1,5t2 (м). 3. rx = 2t + 1,5t2(м). 4. rx = 3t + t2 (м). Рекомендации по решению
	Задание 1.1-А27. Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика: в начале движения и через 0,31с (см. рис.). Ускорение свободного падения по результатам такого опыта приблизительно равно… 1. …10,0 м/с2. 2. …10,5 м/с2. 3. …9,2 м/с2. 4. …11,0 м/с2. Рекомендации по решению
	Задание 1.1-А28. Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально? 1. 1. 2. 2. 3. 3. 4. Во всех точках одинаково. Рекомендации по решению
	Задание 1.1-А29. Два школьника тянут динамометр в противоположные стороны, прикладывая силы по 2 Н каждый. Чему равно показание неподвижного динамометра? 1. 0 Н. 2. 4 Н. 3. 2 Н. 4. Ответ неоднозначен. Рекомендации по решению
	Задание 1.1-АЗО. Модуль скорости автомобиля массой 500 кг изменяется в соответствии с графиком, приведенным на рисунке. Определите модуль равнодействующей силы в момент времени t = 3 с. 1. 0 Н. 2. 500 Н. 3. 1000 Н. 4. 2000 Н. Рекомендации по решению
	РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТЕСТОВЫХ ЗАДАНИЙ
	Задание 1.1-А1. Воспользоваться определением материальной точки — тело, размерами которого можно пренебречь по сравнению с другими размерами в данной задаче. К задаче
	Задание 1.1-А2. Сделать рисунок. Использовать определение вектора перемещения -это вектор, соединяющий начальное и конечное положение тела. Воспользоваться теоремой Пифагора для сторон прямоугольного треугольника: r2 = h3 + S2. К задаче
	Задание 1.1-A3. На графике зависимости координаты тела от времени проекция вектора скорости в данный момент времени численно равна тангенсу угла наклона графика (чем «круче» к оси абсцисс расположен график, тем проекция скорости больше; проекция скорости равна нулю, если график расположен параллельно оси времени, координата при этом не меняется — тело покоится). К задаче Задание 1.1-А4. При прямолинейном равноускоренном движении (из графика видно, что скорость тела увеличивается) модуль ускорения равен отношению изменения скорости к промежутку времени, за которое это изменение произошло:a=Δv/Δt. По графику определяют, что, например, за промежуток времени 3 с (от 0 до 3 с) модуль скорости увеличился с 3 до 9 м/с, т. е. на 6 м/с. К задаче Задание 1.1-А5. Воспользоваться вторым законом Ньютона: ускорение тела прямо пропорционально действующей на него равнодействующей силе и обратно пропорционально массе тела. Равнодействующая сила — векторная сумма всех сил, действующих на тело. К задаче Задание 1.1-А6. При отсутствии сопротивления воздуха на шарик действует только сила тяжести, направленная вниз. Далее надо применить второй закон Ньютона. К задаче Задание 1.1-А7. Применить третий закон Ньютона: силы взаимодействия двух тел равны по модулю, противоположны по направлению, приложены к взаимодействующим телам и направлены вдоль одной прямой. К задаче Задание 1.1-А8. Воспользоваться законом Гука: модуль силы упругости Fynp прямо пропорционален деформации х пружины Fynp = kx, где k — коэффициент пропорциональности. К задаче Задание 1.1-А9. Применить закон для модуля силы трения скольжения FTp: FTp = μN, где μ — коэффициент трения; N — модуль силы нормальной реакции опоры. По приведенному графику определить, что, например, при N = 40 Н и FTP = 10 Н. К задаче Задание 1.1-А10. Использовать закон всемирного тяготения для модуля силы F взаимодействия Земли массой М3 с телом массой т, расположенным на ее поверхности: F =GMзm/R2з , где R3 — радиус Земли. К задаче Задание 1.1-А12.* Применить закон сохранения импульса системы тел в проекции на координатную ось, направленную вдоль направления движения тележки: m1v1 + m2v2 = (т1 + т2)и, где т1 = т — масса движущейся тележки; v1=v — ее скорость; т2 = т — масса неподвижной тележки; v2 = 0 — ее скорость; и — скорость тележек после их взаимодействия (абсолютно неупругого удара). К задаче Задание 1.1-А14. Воспользоваться формулами кинетической энергии тела Ek=mv2/2 и модулем (величиной) импульса р = mv, и решить полученную систему уравнений относительно искомой величины m. К задаче Задание 1.1-А15. При равномерном подъеме груза поднимающая сила равна по модулю силе тяжести, которая равна по модулю весу груза: F = Р = 1000 Н. Работа поднимающей силы равна А = FScosa = Ph, где S = h = 5 м — высота подъема груза; а = 0 — угол между направлением поднимающей силы и направлением перемещения груза. Мощность крана равна N=A/t, где t = 5 с — время подъема груза. К задаче Задание 1.1-А16. КПД не может быть больше 100% = 1. К задаче Задание 1.1-А17. При любом ударе (как упругом, так и не упругом) сохраняется импульс системы. К задаче
	Задание 1.1-А18. При движении по наклонной поверхности под гору модуль силы трения равен FTP =μN = μmgcosa, где N — модуль силы нормальной реакции опоры; тg — модуль силы тяжести; g — величина ускорения свободного падения; a — угол, который составляет наклонная плоскость с горизонтом. Модуль ускорения а автомобиля при равнозамедленном движении можно найти из второго закона Ньютона в проекции на ось, направленную вдоль наклонной плоскости вверх: а =(Fтр-mgsina)/m = g(μcosa-sina), где т —масса автомобиля. С другой стороны, при равнозамедленном движении модуль ускорения а, пройденный до остановки путь S и модуль v0 вектора начальной скорости связаны соотношением: 2aS = v20 . Решая полученную систему уравнений, можно получить: S =v20/(2g(μcosa-sina) . Из последней формулы видно, что тормозной путь не зависит от массы тела, уменьшается при уменьшении скорости перед торможением и увеличивается при уменьшении коэффициента трения шин о дорогу. К задаче
	Задание 1.1-А19. При движении парашютиста вертикально вниз с постоянной скоростью его кинетическая энергия не изменяется, а потенциальная энергия уменьшается. При этом она превращается во внутреннюю энергию системы «парашютист — воздух». К задаче Задание 1.1-А20. Воспользоваться уравнением равновесия рычага: М1 = М2, где М1 — момент первой силы, а М2 — момент второй силы. Воспользоваться определением момента силы: М = Fl, где F — модуль силы; l — плечо силы. К задаче Задание 1.1-А21. Применить формулу для расчета архимедовой (выталкивающей) силы: Fa = pgVпогр, где ρ=1000 кг/м2 — плотность жидкости; g = 10 м/с2 — модуль ускорения свободного падения; Vпогр =0,5V= — объем тела, погруженного в жидкость К задаче Задание 1.1-А23. Воспользоваться формулой координаты при гармонических колебаний: X = Acos(ωt + φ0), где А — амплитуда колебаний; ω — циклическая частота колебаний; φ0 — начальная фаза. Путем сравнения с законом, заданным в условии задачи, определить величину ω =π рад/с. Применить формулу, связывающую циклическую частоту и период колебаний: Т=2π/ω К задаче Задание 1.1-А24. Применить формулу для периода колебаний пружинного маятника: Т = 2π√(m/k)—, где m — масса груза; k — жесткость пружины. К задаче Задание 1.1-А26. Написать уравнение проекции скорости при равнопеременном движении vx = vох + axt, где vох — проекция начальной скорости; ах — проекция ускорения. Путем сравнения с формулой проекции скорости, заданной в условии задания, получаем vox = 2 м/с, ах = 3 м/с2. Написать общее уравнение проекции перемещения и подставить полученные числовые значения: r=voxt+axt²/2=2t+1,5t²(м). К задаче Задание 1.1-А27. Из рисунка определить, что шарик пролетает расстояние h = 44 см = 0,44 м. Применить формулу пройденного пути при свободном падении тела: h =gt²/2, где t = 0,31 с — время свободного падения тела. К задаче Задание 1.1-А28. Применить формулу для модуля центростремительного ускорения при движении тела по криволинейной траектории: ацс =v2/2, где v — модуль вектора скорости; R — радиус кривизны траектории в данной точке. Так как модуль скорости точки постоянен, то центростремительное ускорение максимально в точке, в которой радиус кривизны траектории минимален. К задаче Задание 1.1-А29. Если к пружине динамометра и к его корпусу приложить равные по модулю и противоположные по направлению силы, то он останется в положении равновесия, и показание динамометра будет равно модулю приложенных сил. К задаче Задание 1.1-А30. По графику определить, что для участка графика, содержащего момент времени t = 3 с, за промежуток времени Δt = 4-2 = 2с изменение скорости равно Δv = 4 — 2 = 2 м/с. Рассчитать величину ускорения по формуле а = Δv/Δt. Определить модуль равнодействующей силы по второму закону Ньютона: F = та, где т = 500 кг — масса тела. К задаче

	В начало
	2009 год

stanislav-zevalev.narod.ru

Программа элективного курса по физике «Технология решения задач» 11 класс – УчМет

1. ТЕМАТИЧЕСКИЙ БЛОК «КИНЕМАТИКА» (Элементы кодификатора 1.1 — 1.9.)

1.1 (Б, ВО). Паром (см. рис. 6) движется по озеру со скоростью v₀= 10 м/с, автомобиль по парому так, как представлено на рисунке. Спидометр автомобиля показывает скорость v = 4 м/с. Чему равна скорость автомобиля относительно Земли?

1)4 м/с 2) 6 м/с 3)7 м/с 4) 14 м/с

Ответ: 2

1.2 (Б, ВО). Решаются две задачи:

а) рассчитывается маневр стыковки двух космических кораблей;

б) рассчитывается период обращения космических кораблей вокруг Земли.

В каком случае космические корабли можно рассматривать как материальные точки?

1) Только в первом случае.

2) Только во втором случае.

3) В обоих случаях.

4) Ни в первом, ни во втором случае.

Ответ: 2

1.3 (Б, ВО). Камень брошен из окна второго этажа с высоты 4м и падает на землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня?

1)3м 2) 4 м 3)5м 4) 7 м

Ответ: 3

1.4 (Б, ВО). На рис. 7 представлен график зависимости координаты тела, движущегося вдоль оси ОХ, от времени. Сравните скорости v_1,v₂ и v₃ тела в моменты времени t,, t₂, t₃.

l)v₁>v₂ = v₃

2) v₁ > v₂ > v₃

3) v₁ > v₂ > v₃

4) v₁= v₂ > v₃

Ответ: 4

1.4 (П, ВО). Лестница, приставленная к вертикальной стене, падает в результате скольжения ее основания по полу. Каково отношение модулей скоростей V_A и V_B (рис. 8) в тот момент, когда угол между лестницей и стеной равен а?

l) sin α

2) cos a

3) tg α

4) ctg a

Ответ: 4

1.5 (Б, ВО). По графику зависимости модуля скорости от времени, представленному на рис. 9, определите ускорение прямолинейно движущегося тела в момент времени t = 2 с.

1) 2 м/с²

2) 3 м/с²

3) 9 м/ с²

4) 27 м/с²

Ответ: 1

1.6 (П, ВО). Уравнение зависимости проекции скорости движущегося тела от времени:

v_x = 2 + 3t (м/с). Каково соответствующе уравнение проекции перемещения тела?

1) S_x = 2t + 3t² (м) 3) S_x = 2t + l,5t² (м)

2) S_x = l,5t²(m) 4) S_x = 3t +1²(m)

Ответ: 3

1.7 (Б, ВО). При свободном падении тел разной массы в трубке из которой откачан воздух, тела движутся с одинаковым ускорением. Это объясняется тем, что сила тяжести:

1) на тела в вакууме не действует

2) пропорциональна массе тел

3) не зависит от массы тела

4) уравновешивается весом тел

Ответ: 2

1.7 (П, К). Какой путь пройдет свободно падающее тело за шестую секунду? v₀ = 0 м/с, ускорение свободного падения принять равным 10 м/с².

Ответ: 55 м

1.7 (П, ВО). Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика: в начале падения и через 0,31 с (рис. 10). Ускорение свободного падения по результатам такого опыта приблизительно равно…

1) 10,0 м/с²

2) 10,5 м/с²

3) 9,2 м/с²

4) 11,0 м/с²

рис 10.

Ответ: 3

1.8 (Б, ВО). Тело движется равномерно по окружности в направлении против часовой стрелки (рис. 11). Как направлен вектор ускорения при таком движении?

1)1

2)2

3)3

4)4 Ответ: 3

1.9 (П, ВО). Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рис. 12. В какой из указанных точек траектории центростремительное ускорение максимально?

1)1

2)2

3)3

4) Во всех точках одинаково

Ответ: 3

Задача 1. Скорость катера относительно воды 5 м/с, скорость течения 2 м/с, ширина реки 100 м. Под каким углом к берегу рулевой должен направлять катер, чтобы пересечь реку по наикратчайшему пути? Сколько времени займет переправа?

Задача 2. Половину времени своего движения автомобиль ехал со скоростью 100 км/ч, оставшуюся половину времени — со скоростью 20 км/ч. Найти среднюю скорость движения.

Задача 3. Точка прошла половину пути со скоростью υ₁= 6м/с. Оставшуюся часть пути она половину времени двигалась со скоростью υ₂= 4м/с, а последний участок со скоростью υ₃= 8м/с. Определить среднюю скорость точки за все время движения. ( 5 м/с)

Задача 4. Тело без трения скатывается по наклонной плоскости ( α = 30°) длиной 5 м. Определить скорость тела у основания и время движения.

1. ТЕМАТИЧЕСКИЙ БЛОК «КИНЕМАТИКА» (Элементы кодификатора 1.1 — 1.9.)

1)4 м/с 2) 6 м/с 3)7 м/с 4) 14 м/с

1.2 (Б, ВО). Решаются две задачи:

а) рассчитывается маневр стыковки двух космических кораблей;

б) рассчитывается период обращения космических кораблей вокруг Земли.

В каком случае космические корабли можно рассматривать как материальные точки?

1) Только в первом случае.

2) Только во втором случае.

3) В обоих случаях.

4) Ни в первом, ни во втором случае.

1)3м 2) 4 м 3)5м 4) 7 м

1.4 (Б, ВО). На рис. 7 представлен график зависимости координаты тела, движущегося вдоль оси ОХ, от времени. Сравните скорости v_1,v₂ и v₃ тела в моменты времени t₁, t₂, t₃.

l)v₁>v₂ = v₃

2) v₁> v₂ > v₃

3) v₁ > v₂ > v₃

4) v₁= v₂ > v₃

l) sin α

2) cos a

3) tg α

4) ctg a

1) 2 м/с²

2) 3 м/.с²

3) 9 м/ с²

4) 27 м/ с²

1.6 (П, ВО). Уравнение зависимости проекции скорости движущегося тела от времени:

v_x = 2 + 3t (м/с). Каково соответствующе уравнение проекции перемещения тела?

1) S_x = 2t + 3t² (м) 3) S_x = 2t + l,5t² (м)

2) S_x = l,5t²(m) 4) S_x = 3t +1²(m)

1) на тела в вакууме не действует

2) пропорциональна массе тел

3) не зависит от массы тела

4) уравновешивается весом тел

1) 10,0 м/с²

2) 10,5 м/с²

3) 9,2 м/с²

4) 11,0 м/с²

рис 10.

1)1

2)2

3)3

4)4

1)1

2)2

3)3

4) Во всех точках одинаково

Задача 4. Тело без трения скатывается по наклонной плоскости ( α = 30°) длиной 5 м. Определить скорость тела

www.uchmet.ru

стр.20. 3. 2. Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика Другой смолчал и стал пред ним ходить. Сильнее бы не смог он возразить

КАРТОЧКА № 5
ВОПРОСЫ:
1 Что такое ускорение движения?
В каких единицах оно измеряется? стр.21
2 Какое движение называется равноускоренным? стр.20
3 Запишите уравнение зависимости проекции мгновенной скорости от времени для равноускоренного
движения стр.25
ЗАДАНИЯ:
1
По заданному уравнению зависимости проекции
скорости от времени определите:
характер движения материальной точки
модуль и направление начальной скорости
модуль и направление ускорения
каким будет модуль мгновенной скорости через 3с?

V = -10 + 3t
2
По графику зависимости проекции скорости от времени определите для данного тела
начальную скорость
ускорение
проекцию скорости через 4 сек после начала наблюдения
Запишите уравнение скорости
КАРТОЧКА № 6
ВОПРОСЫ:
1
Какое движение называется свободным падением тела?
К какому виду движения оно относится?
стр 52
2
Какова главная особенность свободного падения тел?

стр.54
3 Сравните свободное падение тел с движением тела, брошенного
вертикально вверх
(укажите 3 сходства и 3 отличия)
Стр.57
ЗАДАНИЯ:
1
Тело, выпущенное из рук без начальной скорости,
свободно падает.
Какова его скорость через 3 сек после
начала движения?
2
Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика:
в начале движения и через 0,31с (см. рис).
Определите ускорение свободного падения по данным результатам.
КАРТОЧКА № 7
ВОПРОСЫ:
1
Как направлена мгновенная скорость движения тела в любой точке криволинейной траектории? стр. 67,
тетрадь

2
Как направлено ускорение при равномерном движении тела по окружности? стр. 70
3 Как связан модуль центростремительного ускорения с другими величинами? стр 70
ЗАДАНИЯ:
1
Автомобиль движется с постоянной по модулю
скоростью по траектории, представленной на рисунке.
В какой из указанных точек траектории центростремительное ускорение максимально?
2
Отличаются ли центростремительные ускорения точек колеса, лежащих на ободе и точек, удаленных от центра
на расстояние, равное ½ радиуса колеса?
Во сколько раз?
КАРТОЧКА № 8
ВОПРОСЫ:
1 Сформулируйте, в чем заключается относительность движения
стр.36
2 Покажите на примере, что скорость, траектория и перемещение являются относи

filesdatabase.net

Закон Ньютона

Подготовка РайДр Тема «Кинематика. Динамика»

1.2.7 Второй закон Ньютона

А1-1. Какие из величин (скорость, сила, ускорение, перемещение) при механическом движении всегда совпадают по направлению?

1) cила и ускорение 2) cила и скорость

3) cила и перемещение 4) ускорение и перемещение

А1-2. Равнодействующая всех сил, действующих на тело, равна нулю. Какова траектория движения этого тела?

1) парабола 2) окружность

3) прямая 4) эллипс

А1-3. С использованием специального фотоаппарата зафиксировали положение движущегося тела через равные промежутки времени (см. рис.). В начальный момент времени тело покоилось. Сила, действующая на тело,

1) увеличивалась со временем 2) была равна нулю

3) была постоянна и не равна нулю 4) уменьшалась со временем

A1-4. Тело движется равноускоренно и прямолинейно. Какое утверждение о равнодействующей всех

приложенных к нему сил правильно?

1) не равна нулю, постоянна по модулю и направлению

2) не равна нулю, постоянна по направлению, но не по модулю

3) не равна нулю, постоянна по модулю, но не по направлению

4) равна нулю

A1-5. Парашютист массой 65 кг спускается с раскрытым парашютом. Чему равна сила сопротивления воздуха F_c в случае установившейся скорости парашютиста? Какова при этом равнодействующая F сил, действующих на парашютиста?

1) F_c = 0, F = 0 2) F_c = 650 Н, F = 650 Н

3) F_c = 0, F = 650 Н 4) F_c = 650 Н, F = 0

А1-6. Ускорение движения железнодорожного вагона В (см. рис.) определяется его взаимодействием с

1) рельсами 2) рельсами и вагонами А и С 3) Землей 4) тепловозом

A1-7. В процессе движения автомашины по шоссе сила сопротивления движению стала равна силе тяги двигателя. При этом автомобиль

1) стал двигаться с ускорением 2) стал двигаться равномерно

3) стал двигаться с замедлением 4) остановился

А1-8. Выберите верное утверждение.

1) перемещение определяется только действующей на тело силой

2) ускорение определяется только действующей на тело силой и его массой

3) скорость тела определяется только действующей на него силой

4) направление движения тела определяется только действующей на него силой

А1-9. Магнит прилип к вертикальной стенке вагона, движущегося с постоянной скоростью 50 км/ч по прямолинейному участку пути. Можно утверждать, что сумма сил, действующих на магнит

1) равна нулю в системе отсчета, связанной с вагоном, и не равна нулю в системе отсчета, связанной с Землей

2) не равна нулю в системе отсчета, связанной с вагоном, и равна нулю в системе отсчета, связанной с Землей

3) не равна нулю в обеих системах отсчета

4) равна нулю в системах отсчета, связанных с Землей и с вагоном

А1-10. Совпадает ли направление вектора силы, действующей на тело, и вектора ускорения, сообщаемого телу этой силой?

1) никогда не совпадает 2) совпадает для прямолинейного движения

3) совпадает для движения по окружности 4) всегда совпадает

А1-11. Космический корабль улетает от Земли. Как направлен вектор ускорения корабля в тот момент, когда вектор силы гравитационного притяжения Земли направлен под углом 120° к вектору скорости корабля? Действие остальных тел на корабль пренебрежимо мало.

1) по направлению вектора скорости 2) по направлению вектора силы

3) противоположно вектору скорости 4) по направлению суммы векторов силы и скорости

А2-1. Тело массы m движется под действием силы F. Если массу тела увеличить в два раза, а силу уменьшить в два раза, то модуль ускорения тела

1) увеличится в 4 раза 2) не изменится

3) уменьшится в 2 раза 4) уменьшится в 4 раз

А2-2. В инерциальной системе отсчета сила F, действуя на тело массой m, сообщает ему ускорение a. Как надо изменить силу, чтобы, уменьшив массу тела вдвое, уменьшить его ускорение в 4 раза?

1) увеличить в 2 раза 2) уменьшить в 2 раза

3) уменьшить в 4 раза 4) уменьшить в 8 раз

А2-3. В инерциальной системе отсчета движутся два тела. Первому телу массой m сила F сообщает ускорение а. Чему равна масса второго тела, если вдвое меньшая сила сообщила ему в 4 раза бóльшее ускорение?

1) 2 m 2) m / 8

3) m / 2 4) m

А2-4. В инерциальной системе отсчета сила F сообщает телу массой m ускорение а. Как изменится ускорение тела, если массу тела и действующую на него силу уменьшить в 2 раза?

1) увеличится в 4 раза 2) не изменится

3) уменьшится в 8 раз 4) уменьшится в 4 раза

А3-1. На левом рисунке показаны направления скорости и ускорения тела в данный момент времени. Какая из стрелок (1 — 4) на правом рисунке соответствует направлению результирующей всех сил, действующих на тело?

1) 4 2) 3

3) 2 4) 1

А3-2. На левом рисунке представлены вектор скорости и вектор равнодействующей всех сил, действующих на тело. Какой из четырех векторов на правом рисунке указывает направление вектора ускорения этого тела в инерциальных системах отсчета?

1) 1 2) 2

3) 3 4) 4

А3-3. На левом рисунке представлены векторы скорости и ускорения тела. Какой из четырех векторов на правом рисунке указывает направление вектора равнодействующей всех сил, действующих на это тело?

1) 1 2) 2

3) 3 4) 4

A4-1. На рисунке изображен график изменения модуля скорости вагона с течением времени в инерциальной системе отсчета. В какие промежутки времени суммарная сила, действующая на вагон со стороны других тел, равнялась нулю?

1) от 0 до t₁, и от t₃ до t₄

2) во все промежутки времени

3) от t₁ до t₂ и от t₂ до t₃

4) ни в один из указанных промежутков времени

A4-2. Тело движется прямолинейно вдоль оси X. Зависимость v_x(t) приведена на рисунке. Равнодействующая всех сил, действующих на тело, равна нулю:

1) в течение 2-й секунды

2) в течение 1-й и 2-й секунд

3) в течение первых трех секунд

4) в течение 2-й и 3-й секунд

A4-3. На каком участке графика (см. рис.) равнодействующая всех сил, действующих на движущийся прямолинейно автомобиль, равна нулю?

1) только 0-1 2) только 1-2

3) только 2-3 4) 0-2 и 2-3

A4-4. На рисунке изображен график изменения модуля скорости прямолинейного движения вагона с течением времени в инерциальной системе отсчета. В какие промежутки времени суммарная сила, действующая на вагон со стороны других тел, НЕ равна нулю?

1) 0-t₁; t₃ –t₄

2) Во все промежутки времени

3) t₁-t₂; t₂-t₃

4) ни в один из указанных промежутков времени

A4-5. На рисунке изображен график координаты. Равнодействующая всех приложенных к телу сил будет равна нулю на промежутке времени

1) 0 — t₁ 2) t₁— t₂

3) t₂ — t₃ 4) t₃ — t₄

A5-1. Из графика (см. рис.) зависимости скорости тела массой 5 кг от времени следует, что результирующая сила достигала максимального значения в интервале времени…

1) 5-6 с 2) 2-5 с

3) 7-10 с 4) 0-2 с

А5-2. Модуль скорости автомобиля массой 500 кг изменяется в соответствии с графиком, приведенным на рисунке. Определите модуль равнодействующей силы в момент времени t = 3 с.

1) 0 Н 2) 500 Н

3) 1000Н 4) 2000 Н

А5-3. На рисунке изображен график скорости равноускоренного движения тела

массой 100 г. На тело действует сила

1) 0,05 Н 2) 0,1 Н

3) 0,15 Н 4) 0,2 Н

А6-1. Самолет выполняет фигуру высшего пилотажа ‘мертвая петля’. Как направлен вектор ускорения самолета в тот момент времени, когда вектор равнодействующей всех сил направлен вертикально вверх к центру окружности, а вектор скорости самолета направлен горизонтально?

1) вертикально вверх 2) по направлению вектора скорости

3) противоположно вектору скорости 4) вертикально вниз

А6-2. Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью. Вектор ускорения самолета направлен

1) вертикально вверх 2) к центру окружности

3) от центра окружности 4) вертикально вниз

А6-3. Шар, подвешенный на нити, движется по круговой траектории в горизонтальной плоскости с постоянной по модулю скоростью, между нитью и вертикалью угол 25°. Вектор ускорения движения шара направлен

1) перпендикулярно прямой, вдоль которой расположена нить

2) к центру окружности

3) от центра окружности

4) вертикально вниз

А6-4. Тело, брошенное под углом к горизонту, движется по криволинейной траектории. Если сопротивление воздуха пренебрежимо мало, и в точке А этой траектории вектор скорости тела имеет направление по стрелке 1 на рисунке, то вектор его ускорения имеет направление, указанное стрелкой

1) 1 2) 2

3) 3 4) 4

А6-5. В центрифуге стиральной машины белье при отжиме движется по окружности с постоянной по модулю скоростью в горизонтальной плоскости. При этом вектор его ускорения направлен

1) по радиусу от центра окружности 2) по радиусу к центру окружности

3) вертикально вниз 4) по направлению вектора скорости

А6-6. Мотоциклист ездит по кругу на арене цирка с постоянной по модулю скоростью. Равнодействующая всех сил, действующих на мотоциклиста,

1) равна нулю 2) направлена к центру арены

3) направлена по касательной к окружности 4) направлена вертикально вниз

А6-7. Небольшое тело массой m движется по окружности радиусом R с постоянной по модулю скоростью v. Какова равнодействующая сил, действующих на тело?

1) mv²/(2R) 2) m(g + v²/R)

3) mv²/R 4) 0

А7-1. Какой из графиков зависимости координаты от времени качественно описывает движение тела, движущегося под действием равнодействующей (см. рис.), если х₀ = 0?

1) 2) 3) 4)

А7-2. На рисунке справа приведен график зависимости скорости тела от времени при прямолинейном движении. Какой из графиков выражает зависимость модуля равнодействующей всех сил, действующих на тело, от времени движения? Систему отсчета считать инерциальной.

1) 2) 3) 4)

А7-3. На рисунке представлен график зависимости силы, действующей на тело от времени. График зависимости ускорения от времени для этого же движения представлен на одном из следующих рисунков (1, 2, 3, 4). На каком именно?

1) 2) 3) 4)

А7-4. После толчка брусок скользит вверх по наклонной плоскости. В системе отсчета, связанной с плоскостью, направление оси Ох показано на левом рисунке. Направления векторов скорости v бруска, его ускорения а и равнодействующей силы F правильно показаны на рисунке

1) 2) 3) 4)

А8-1. На тело массой 200 г действует постоянная сила, сообщающая ему в течение 5 с скорость 1 м/сек. Определите величину действующей силы.

1) 0,04 Н 2) 0,4 Н

3) 4 Н 4) 40 Н

А8-2. Автомобиль массой 500 кг, разгоняясь с места равноускоренно, достиг скорости 20 м/с за 10 с. Равнодействующая всех сил, действующих на автомобиль, равна

1) 0,5 кН 2) 1 кН

3) 2 кН 4) 4 кН

А8-3. Легкоподвижную тележку массой 3 кг толкают силой 6 Н. Ускорение тележки в инерциальной системе отсчета равно:

1) 18 м/с² 2) 2 м/с²

3) 1,67 м/с² 4) 0,5 м/с²

А8-4. Равнодействующая всех сил, приложенных к телу массой 2 кг, равна 2 Н. Каковы скорость и ускорение движения тела?

1) скорость 0, ускорение 1 м/с²

2) скорость 2 м/с, ускорение 4 м/с²

3) скорость 2 м/с, ускорение 1 м/с²

4) скорость может быть любой, ускорение 1 м/с²

А8-5. Скорость лыжника при равноускоренном спуске с горы за 4 с увеличилась на 6 м/с. Масса лыжника 60 кг. Равнодействующая всех сил, действующих на лыжника, равна

1) 20 Н 2) 30 Н

3) 60 Н 4) 90 Н

А8-6. Какую силу надо приложить к телу массой 200 г, чтобы оно двигалось с ускорением 1,5 м/с²?

1) 0,1 Н 2) 0,2 Н

3) 0,3 Н 4) 0,4 Н

А8-7. Какова масса тела, которое под действием силы 0,05 Н получает ускорение 10 см/с²?

1) 1кг 2) 2 кг

3) 0,7 кг 4) 0,5 кг

tvov.ru

Движение в поле силы тяжести СВОБОДНОЕ ПАДЕНИЕ

Кинематика

Тест Вариант 7

Тесты

Программа элективного курса по физике «Технология решения задач» 11 класс – УчМет

Закон Ньютона

Добавить комментарий Отменить ответ