Построение графика параметрически заданной функции – , . —

Построение графика функции с условием

Функция может быть задана разными формулами на разных участках изменения аргумента. При задании функции можно использовать условную функцию.

Пример 3.2

Пример 3.2

Построить график функции Y(x), заданной следующим образом:

Y=ln(x), x>0

Y=1/x, x<=0

Используем условную функцию if(cond, x, y)

Условная функция возвращает x , если условие cond есть true, возвращает y, если условие есть false. Условий может быть несколько.

На графике (Рис.3.8) нанесена риска x=0

,

,

Рис. 3.8. Листинг построения графика примера 3.2

Условную функцию удобно использовать при построении области определения функции. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. С помощью условной функции можно показать график области допустимых значений .

Пример 3.3

Пример 3.3

Построить область определения функции

Ведем функцию

тогда

Область допустимых значений

Строим функцию S(x), используя условную функцию

Строим график функции S(x) (Рис.3.9)

Рис. 3.9. Листинг построения графика примера 3.3

Построение графика функции для табулированных значений

Часто бывает необходимо построить график по точкам. Для этого аргумент и функция вводятся как индексные переменные от номера точки, номер точки – ранжированная переменная.

Пример 3.4

Пример 3.4

Построить график функции по 15 точкам, x меняется от 0 до 1,5 с шагом = 0,1:

, ,

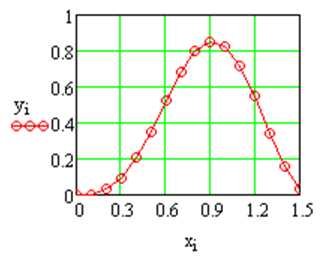
Рис. 3.10. Листинг построения графика примера 3.4

• Ввести номер точки i как ранжированную переменную.

• Ввести xi как с индексную переменную. Ввести функцию с индексом . Построить таблицы значений аргумента и функции в виде вектор-столбцов.:

• Построить график, подставляя индексные переменные (Рис.3.10).

Можно ввести x и y, как векторы. В этом случае на графике в соответствующих ячейках указываются только имена переменных (Рис.3.11).

, ,

Рис. 3.11. Листинг построения графика примера 3.4. На графике введены точки как значения векторов

Графики функции, заданной параметрически

В ряде случаев для задания функций используются параметрически заданные уравнения. Например, пусть функции x=x(t), y=y(t), непрерывны при t из (a, b) и устанавливают зависимость (x,y) точки плоскости от значения параметра t. Таким образом, задается на плоскости кривая в параметрической форме. Х=f1(t) и у=f2(t).

Пример 3.5

Пример 3.5

Построить график функции, заданной в виде:

при

В случае построения графика параметрически заданной кривой в шаблоне функции необходимо указать y(h), вместо независимой переменной x под осью абсцисс необходимо соответственно задать x(h) (Рис.3.12).

, ,

Рис. 3.12. Листинг построения графика примера 3.5

Графики в полярных координатах

В MathCAD полярные графики рисуются с использованием стандартных преобразований и. Предполагается, что r имогут принимать и положительные, и отрицательные значения. Типичный полярный график показывает зависимость выражения для радиуса от угла.

Построение графика

Полярный график строится с использованием шаблона полярного графика на панели

Графика. Выражение для функции и угла вводятся в соответствующие шаблоны графика. Можно построить несколько графиков на одном и том же чертеже. Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).

• Определить как функцию,

• заполнить шаблоны,

• отобразить график в полярных координатах (Рис.3.13).

Рис. 3.13. График в полярных координатах. В шаблонах для радиуса: r: (0;2)

studfiles.net

§4. Построение кривых, заданных параметрически

Рассмотрим способы построения кривых, заданных системой уравнений вида ,.

В ряде случаев эту систему можно решить, получив уравнение, связывающее переменные и. Например, система

,

, дает уравнение . Учитывая, что множеством значений,, является отрезок, получаем, что исходная система уравнений задаёт функцию, определенную на отрезке. Из курса аналитической геометрии также известно, что уравнения,задают окружность радиуса, а также уравнения,, задают эллипс с полуосямии.

Если явно выразить черезне удается, то используется схема, которую мы дадим на примере построения кривой, заданной системой уравнений,.

Начнем с построения графика функции . Эта функция непрерывна на всей числовой прямой,,. Первое из этих утверждений очевидное, второе следует из того, что. Далее, прифункциястремится к 0 (применяется правило Лопиталя), а функциястремится кпри.

Производная . Привыполнено неравенствои, поэтомуубывает. При, поэтомуи функция возрастает. Наименьшего значения функциядостигает при,. При этом и.

График имеет вид:

Каждому значению соответствуют два значения, обозначим ихи, причем,.

Так как функция непрерывна и убывает при, функциятакже непрерывна и возрастает при, а так какнепрерывна и возрастает при,также непрерывна и возрастает (мы использовали теорему об обратной функции).

Следовательно, по теореме о непрерывности сложной функции и- также непрерывные.

Исследуем асимптотическое поведение функций ипри. Прифункцияи, так как,, а. Так как

,

функция не имеет наклонной асимптоты.

При функцияи функция, при этом. Наконец,

.

Поэтому прямая является наклонной асимптотой для.

Вычислим производные функций и. Обе они получаются по формуле. Приполучаем, что, поэтому, как, так и- возрастающие функции.

В точке обе функциииимеют первую производную, равную.

Наконец, вторая производная равна .

Поэтому при получаем, криваявыгнута вверх, а при, криваявыгнута вниз.

Комментарий к графику: идают «клюв» — имеют особую правую касательную с тангенсом угла наклона вравным 4.

§5. Построение кривых, заданных уравнением в полярных координатах.

Рассмотрим задачу построения на плоскости , введенной прямоугольной декартовой системой координат, кривой, уравнение которой имеет вид. При этом мы считаем, что начало координат совпадает с полюсом полярной системы координат и что ось абсцисс совпадает с полярной осью. В этом случае для декартовых координат точки, имеющей полярные координаты, выполняются равенства,и уравнениеравносильно системе.

Поэтому задание кривой полярным уравнением можно рассматривать, как частный случай задания кривой системой параметрических уравнений.

Рассмотрим несколько примеров.

Уравнение или, т.е. задает прямую линию на плоскости.

Построим кардиоиду, заданную уравнением ,.

Так как функция периодическая, с периодом , рассматриваем. Так как функция чётная, достаточно построить кривую, а затем отразить ее симметрично полярной оси, т.е. оси абсцисс. При, меняющейся отдо, величинаубывает от значениядо. Поэтому эскиз части кривой приимеет примерный вид:

Эскиз всей кривой получаем отражением относительно полярной оси.

Осталось ответить на два естественных вопроса. Первый из них: чему равна абсцисса точки ? Второй вопрос – о выпуклости кривой. Для получения ответов на эти вопросы рассмотрим параметрические уравнения части кардиоиды:,.

,

.

Из уравнения при, находим,, откуда,. Этим значениям соответствуют(при),(при), абсцисс 0.

(при ) — абсцисса точки.

Таким образом, на вопрос об абсциссе точки получим ответ.

Производная .

Отметим, что в точках ,кривая имеет вертикальную касательную.

Вторая производная равна .

На промежутке эта величина меньше 0, на промежутке- больше 0.

Поэтому верхняя половина кардиоиды состоит из выгнутой вверх кривой, соединяющей точки ии выгнутой вниз кривой, соединяющей точкии.

studfiles.net

10. Построение графиков

Mathematica предоставляет набор функций для построения графиков функций, зависящих от одой и двух переменных, при этом аргументы функции могут быть заданы параметрически. Кроме того графики можно строить в различных системах координат (линейных, логарифмических, полярных и т.д.).

10.1. Двухмерные графики

Построение графика функции от одной переменной

Plot[f[x], {x, xmin, xmax}],

где f[x] – функция одной переменной, x – аргумент функции, xmin – начальное значение x, xmax – конечное значение x.

In[1]:=Plot[Sin[x], {x, 0, 2*Pi}]

Out[1] = Graphics

При построении графика можно задавать опции, позволяющие нарисовать рамку Frame, наложить сетку GridLines, дать наименования осям GridLines.

In[2]:= Plot[Sin[x^2], {x, 0, 3}, Frame -> True, GridLines -> Automatic,

AxesLabel -> {«x», «Sin[x]»}]

Out[2] = Graphics

Опция PlotRange позволяет задать границы по вертикальной оси при отображении графика.

In[3]:= Plot[Sin[x^2], {x, 0, 3}, PlotRange -> {0, 1.2}]

Out[3] = Graphics

Функция Show позволяет вывести вместе несколько графиков, построенных ранее.

In[4] := Show[Out[2], Out[3]]

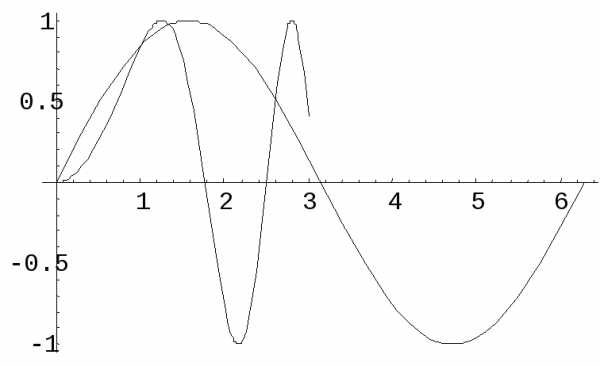
Out[4] = Graphics

10.2. Графики функций, зависящей от двух переменных

Построение графика функции от двух переменных

Plot3D[f[x, y], {x, xmin, xmax}, {y, ymin, ymax}],

где f[x, y] – функция двух переменных, x, y – аргументы функции, xmin, ymin – начальные значения x и y, xmax, ymax – конечные значения x и y.

In[5]:= Plot3D[Sin[x]*Sin[y], {x, -2, 2}, {y, -2, 2}]

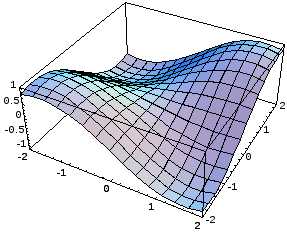
Out[5]= —SurfaceGraphics-

График линий равного уровня для функции двух переменных. Темные контуры являются низкими значениями функции, светлые контуры – высокие значения функции.

In[6]:= ContourPlot[Sin[x]*Sin[y], {x, -2, 2}, {y, -2, 2}]

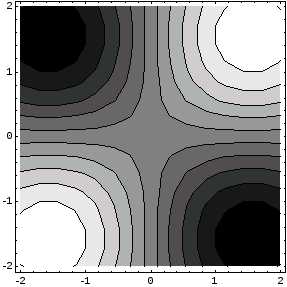
Out[7] = ContourPlot

10.3. Графики функции, заданной параметрически

Построение графика функции, заданной параметрически

ParametricPlot[{f1[t], f2[t], {t, tmin, tmax}],

где f1[t], f2[t] – функции, зависящие от параметра t, tmin, tmax – начальное и конечное значения изменения параметра. При построении графика значения f1 откладываются по горизонтальной оси, значения f2 откладываются по вертикальной оси.

In[7]:= ParametricPlot[{Sin[t], Sin[2*t]}, {t, 0, 2*Pi}]

Out[7] = -ParametricPlot-

Построение параметрически заданной функции в трехмерном пространстве.

In[8]:= ParametricPlot3D[{Sin[t], Cos[t], t/3}, {t, 0, 15}]

Out[8] = -ParametricPlot-

In[9]:= ParametricPlot3D[{t, u, Sin[t u]},

{t, 0, 3}, {u, 0, 3}]

Out[9] = -ParametricPlot-

Литература

1. Wolfram S. Mathematica: A system for doing mathematics. Addison-Wesley, second edition, 1991.

2. Аладьев В.З., Шишаков М.Л. Введение в среду пакета Mathematica 2.2 — М.: Информационно-издательский дом «Филинъ». 1997.

3. Хювенен Э., Сеппянен Й. Мир Лиспа. В 2-х томах. — М.:Мир. 1990.

26

studfiles.net

«Особенности построения графиков функций заданных неявно и параметрически»

Полякова О.Л.

Доклад

ОСОБЕННОСТИ Построения графиков функций

заданных неявно и параметрически

Из курса математического анализа известен стандартный алгоритм исследования явно заданных функций (область определения; множество значений; четность – нечетность; асимптоты; периодичность; нули; экстремумы; интервалы монотонности, выпуклости и вогнутости; точки перегиба). При параметрическом или неявном задании функции существует ряд специфических особенностей, отличающих построение графиков этих функций. Рассмотрим эти особенности на примерах.

Пример 1. Построить график функции 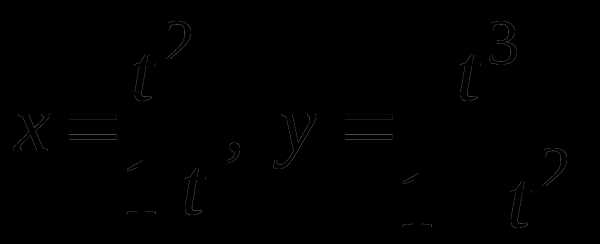[2, с. 126].

Сначала строим графики функций и соответственно в системах координат и .

1 а)

Рис. 1 б)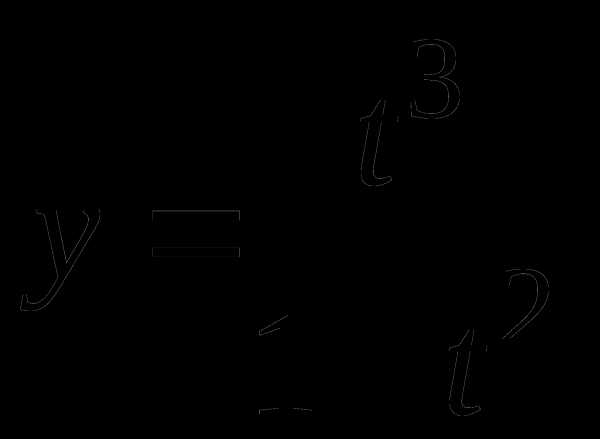

Учитывая графическое изображение функций и , исследуем функцию по схеме [3].

1. Область определения функции: .

2. Множество значений функции: .

3. Таккак — функция общего вида, а — нечетная функция, то симметрииграфик не имеет.

4. При исследовании функции заданной параметрически, необходимо найти

особые точки (точка особая точка кривой, если 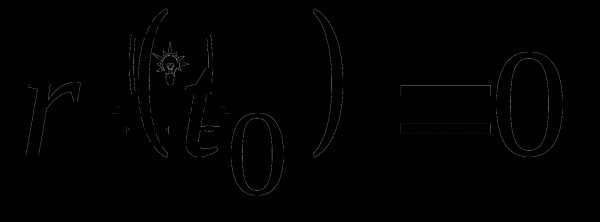) и определить их вид.

Пусть, — первая отличная от нуля производная и — первая из производных, не коллинеарных вектору . Тогда если:

Рис. 2 а)

Рис. 2 б)

Точка является особой точкой кривой, так как производные первого порядка: равны нулю при . Определяем тип особой точки, для этого вычисляем вторую и третью производные:

Таким образом, точка – точка возврата первого рода.

5. Точки самопересечения находим из условия , решая систему:

.

Так как , значит, кривая не имеет точек самопересечения.

7. Угловой коэффициент касательной:

.

При и при , т.е. в точках с координатами , и 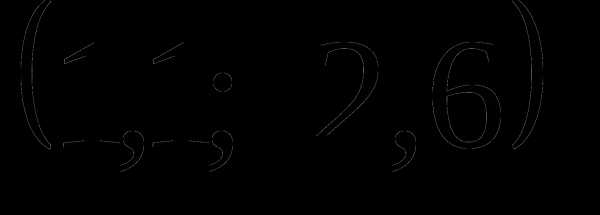касательные параллельны оси абсцисс; при , т.е. в точке с координатами касательная параллельна оси ординат.

7. Экстремумы функции и интервалы монотонности.

Точка – точка минимума; точки , 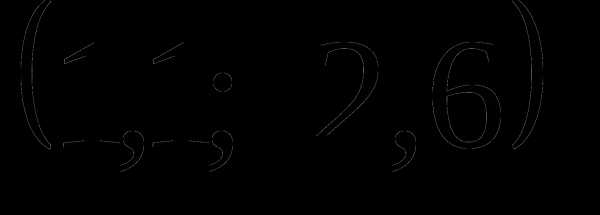– точки максимума; при и при функция убывает; при , и при функция возрастает.

7. Интервалы выпуклости и точки перегиба. Так как вторая производная

отлична от нуля, следовательно кривая не имеет точек перегиба; при и при кривая выпукла вверх; при и при кривая выпукла вниз.

7. Асимптоты.

Прямая является наклонной асимптотой, т.к.

; .

Прямая наклонная асимптота, так как пр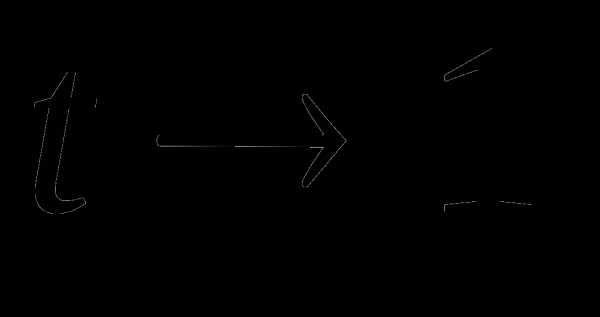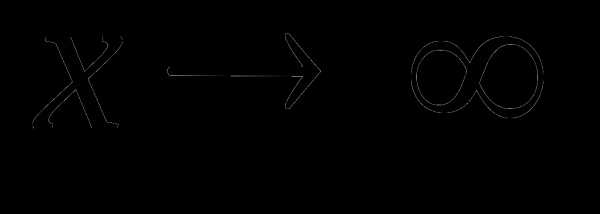и , , и .

Прямая  вертикальная асимптота, т.к. при .

Горизонтальных асимптот кривая не имеет.

7. График функции (рис. 3):

Рисунок 3 — График функции

При исследовании и построении графика функции заданной неявно также определяют особые точки кривой.

Точка кривой называется особой точкой, если ее координаты одновременно удовлетворяют трем уравнениям:

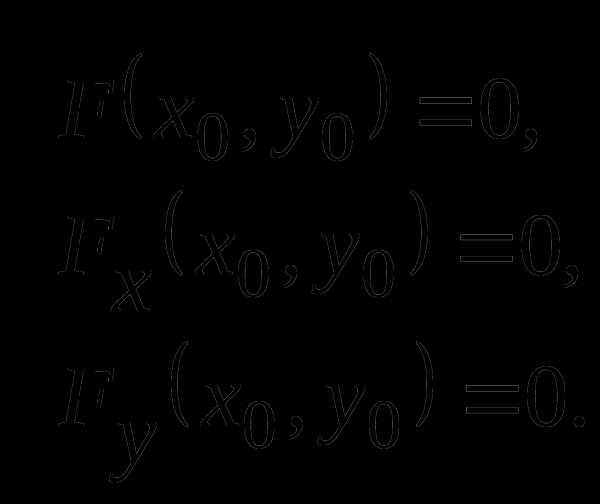
Если в особой точке производные второго порядка не равны одновременно нулю, тогда точка является

двойной точкой кривой, причем форма кривой у ее двойной точки зависит от знака определителя

.

Возможные случаи изображены на рисунке [1, с. 271]:

а) узловая точка

Рис. 4 б) изолированная точка

Рис. 4 в) точка возврата первого рода

4 г) точка возврата второго рода

Рис. 4 д) точка самокасания

Пример 2. Построить график функции [1, с.182].

1. Область определения находим, решая уравнение:

Откуда, область определения первой ветви , второй ветви —

2. Кривая симметрична относительно координатных осей.

3. Точки пересечения кривой с осями координат:

4. Асимптоты. Горизонтальных и вертикальных асимптот кривая не имеет, так как коэффициенты при высших степенях и постоянные величины. Наклонные асимптоты находим из условия:

,

приравнивая к нулю коэффициенты при , . Получаем и — наклонные асимптоты искомой кривой.

5. Особые точки:

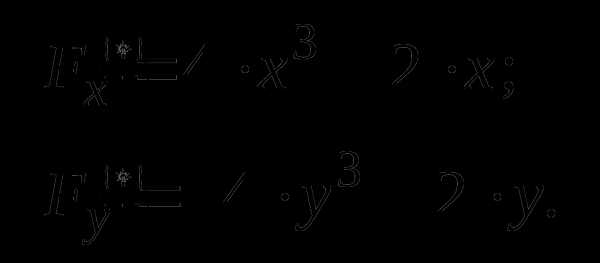
Точка является особой двойной точкой, так как и производные второго порядка в этой точке одновременно не равны нулю. Т.к. точка с координатами узловая точка.

Найдем касательные к кривой в особой точке, для этого приравняем к нулю коэффициенты при низших степенях:

,

Таким образом, прямые и – две касательные к кривой в особой точке.

6. Координаты точек, в которых касательные параллельны оси абсцисс, найдем, решив систему:

.

В точках , касательные параллельны оси абсцисс. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение

в точке с координатами принимает положительные значения, то в этой точке максимум; а в точках с координатами произведение , следовательно это точки минимума.

Координаты точек, в которых касательные параллельны оси ординат, найдем, решив систему:

.

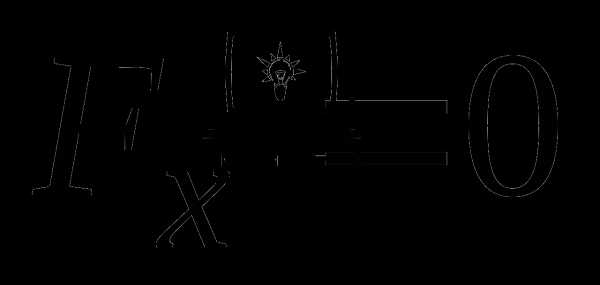В точках с координатами , касательные параллельны оси ординат. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение

в точке с координатами , принимает положительные значения, то в этой точке максимум; а в точке с координатами – минимум, так как произведение .

7. Точкиперегиба находим, приравняв к нулю вторую производную:

,

очевидно, точка перегиба.

8. График функции (рис. 5):

Рис. 5 — График функции

Исследовать кривую – значит выявить совокупность важнейших свойств, дающих исчерпывающую информацию для изображения графика этой кривой. В целом, алгоритм исследования параметрических и неявно заданных функций совпадает с алгоритмом исследования функций заданных явно. Однако, существуют следующая специфическая особенность отличающая исследование этих функций от функций заданных явно, заключающаяся в нахождении особых точек и точек самопересечения.

При исследовании параметрических функций часто возникают сложности при определении точек перегиба и промежутков вогнутости, так как это исследование требует нахождения второй производной функции, которая представляет собой громоздкое выражение и решить уравнение точными методами не удается, необходимо прибегать к численным методам. Аналогичные сложности возникают и при исследовании неявно заданных функций: из-за сложных выражений второй производной определять точки перегиба приходится методом подбора (интуитивно) или же не определять вовсе.

Библиографический список:

1. Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. – Киев: Наук. думка, 1979. – 320 с.

2. Райхмист Р. Б. Графики функций: Справ. пособие для вузов. – М., «Высшая школа», 1991. – 160 с.

infourok.ru