Система координат — Википедия
Материал из Википедии — свободной энциклопедии
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат —
ru.wikipedia.org
Декартова система координат: основные понятия и примеры
Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат.
Общая декартова система координат (аффинная система координат) может включать и не обязательно перпендикулярные оси. В честь французского математика Рене Декарта (1596-1662) названа именно такая система координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми.
Прямоугольная декартова система координат на плоскости имеет
две оси, а
Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.
Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.
С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a; b) удовлетворяют уравнению (x — a)² + (y — b)² = R².
Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей
образуют декартову прямоугольную систему координат на плоскости. Одна из этих
осей называется осью Ox, или осью абсцисс,
другую — осью Oy, или осью ординат.
Эти оси называются также координатными осями. Обозначим через
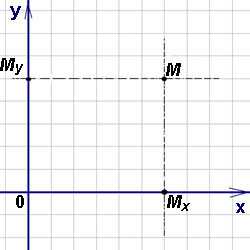
Декартовыми прямоугольными координатами x и y точки М будем называть соответственно величины направленных отрезков OMx и OMy. Величины этих направленных отрезков рассчитываются соответственно как x = x0 — 0 и y = y0 — 0. Декартовы координаты x
и y точки М называются соответственно её абсциссой и ординатой. Тот факт, что точка М имеет координаты x и y, обозначается так: M(x, y).Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.
Помимо декартовых прямоугольных координат на плоскости часто рассматривается также полярная система координат. О способе перехода от одной системы координат к другой — в уроке полярная система координат.
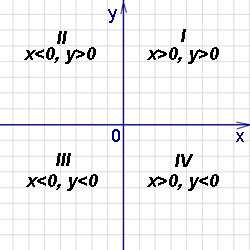
Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.
Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Одну из указанных осей называют осью Ox, или осью абсцисс, другую — осью Oy, или осью ординат, третью — осью Oz, или осью аппликат. Пусть Mx, My Mz — проекции произвольной точки М пространства на оси Ox, Oy и Oz соответственно.
Проведём через точку М плоскость, перпендикулярную оси Ox. Эта плоскость пересекает ось Ox в точке Mx. Проведём через точку М плоскость, перпендикулярную оси Oy
. Эта плоскость пересекает ось Oy в точке My. Проведём через точку М плоскость, перпендикулярную оси Oz. Эта плоскость пересекает ось Oz в точке Mz.
Декартовыми прямоугольными координатами x, y и z точки М будем называть соответственно величины направленных отрезков OMx, OMy и OMz. Величины этих направленных отрезков рассчитываются соответственно как x = x0 — 0, y = y0 — 0 и z = z0 — 0.
Декартовы координаты x, y и z точки М называются соответственно её абсциссой, ординатой и аппликатой.
Пример 1. В декартовой системе координат на плоскости даны точки
A(2; -3);
B(3; -1);
C(-5; 1).
Найти координаты проекций этих точек на ось абсцисс.
Решение. Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox, а следовательно имеет абсциссу, равную абсциссе самой точки, и ординату (координату на оси Oy, которую ось абсцисс пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось абсцисс:
Ax(2; 0);
Bx(3; 0);
Cx(-5; 0).
Пример 2. В декартовой системе координат на плоскости даны точкиA(-3; 2);
B(-5; 1);
C(3; -2).
Найти координаты проекций этих точек на ось ординат.
Решение. Как следует из теоретической части этого урока, проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy, а следовательно имеет ординату, равную ординате самой точки, и абсциссу (координату на оси Ox, которую ось ординат пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось ординат:
Ay(0; 2);
By(0; 1);
Cy(0; -2).
Пример 3. В декартовой системе координат на плоскости даны точки
A(2; 3);
C(-1; -1).
Найти координаты точек, симметричных этим точкам относительно оси Ox.
Решение. Поворачиваем на 180 градусов вокруг оси Ox направленный отрезок, идущий от оси Ox до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Ox, будет иметь такую же абсциссу, что и данная точка, и ординату, равную по абсолютной величине ординате данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Ox:
A’(2; -3);
B’(-3; -2);
C’(-1; 1).
Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения
Пример 4. Определить, в каких квадрантах (четвертях, рисунок с квадрантами — в конце параграфа «Прямоугольная декартова система координат на плоскости») может быть расположена точка M(x; y), если
1) xy > 0;
2) xy < 0;
3) x − y = 0;
4) x + y = 0;
5) x + y > 0;
6) x + y < 0;
7) x − y > 0;
8) x − y < 0.
Правильное решение и ответ.
Пример 5. В декартовой системе координат на плоскости даны точки
A(-2; 5);
B(3; -5);
C(a; b).
Найти координаты точек, симметричных этим точкам относительно оси Oy.
Правильное решение и ответ.
Продолжаем решать задачи вместе
Пример 6. В декартовой системе координат на плоскости даны точки
A(-1; 2);
B(3; -1);
C(-2; -2).
Найти координаты точек, симметричных этим точкам относительно оси Oy.
Решение. Поворачиваем на 180 градусов вокруг оси Oy направленный отрезок, идущий от оси Oy до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Oy, будет иметь такую же ординату, что и данная точка, и абсциссу, равную по абсолютной величине абсциссе данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Oy:
A’(1; 2);
B’(-3; -1);
C’(2; -2).
Пример 7. В декартовой системе координат на плоскости даны точки
A(3; 3);
B(2; -4);
C(-2; 1).
Найти координаты точек, симметричных этим точкам относительно начала координат.
Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:
A’(-3; -3);
B’(-2; 4);
C(2; -1).
Пример 8. В декартовой системе координат в пространстве даны точки
A(4; 3; 5);
B(-3; 2; 1);
C(2; -3; 0).
Найти координаты проекций этих точек:
1) на плоскость Oxy;
2) на плоскость Oxz;
3) на плоскость Oyz;
4) на ось абсцисс;
5) на ось ординат;
6) на ось апликат.
Решение.
1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy:
Axy(4; 3; 0);
Bxy(-3; 2; 0);
Cxy(2; -3; 0).
2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz:
Axz(4; 0; 5);
Bxz(-3; 0; 1);
Cxz(2; 0; 0).
3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz:
Ayz(0; 3; 5);
Byz(0; 2; 1);
Cyz(0; -3; 0).
4) Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox, а следовательно имеет абсциссу, равную абсциссе самой точки, а ордината и апликата проекции равны нулю (поскольку оси ординат и апликат пересекают ось абсцисс в точке 0). Получаем следующие координаты проекций данных точек на ось абсцисс:
Ax(4; 0; 0);
Bx(-3; 0; 0);
Cx(2; 0; 0).
5) Проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy, а следовательно имеет ординату, равную ординате самой точки, а абсцисса и апликата проекции равны нулю (поскольку оси абсцисс и апликат пересекают ось ординат в точке 0). Получаем следующие координаты проекций данных точек на ось ординат:
Ay(0; 3; 0);
By(0; 2; 0);
Cy(0; -3; 0).
6) Проекция точки на ось апликат расположена на самой оси апликат, то есть оси Oz, а следовательно имеет апликату, равную апликате самой точки, а абсцисса и ордината проекции равны нулю (поскольку оси абсцисс и ординат пересекают ось апликат в точке 0). Получаем следующие координаты проекций данных точек на ось апликат:
Az(0; 0; 5);
Bz(0; 0; 1);
Cz(0; 0; 0).
Пример 9. В декартовой системе координат в пространстве даны точки
A(2; 3; 1);
B(5; -3; 2);
C(-3; 2; -1).
Найти координаты точек, симметричных этим точкам относительно:
1) плоскости Oxy;
2) плоскости Oxz;
3) плоскости Oyz;
4) оси абсцисс;
5) оси ординат;
6) оси апликат;
7) начала координат.
Решение.
1) «Продвигаем» точку по другую сторону оси Oxy на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxy, будет иметь абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную по величине апликате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxy:
A’(2; 3; -1);
B’(5; -3; -2);
C’(-3; 2; 1).
2) «Продвигаем» точку по другую сторону оси Oxz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxz, будет иметь абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную по величине ординате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxz:
A’(2; -3; 1);
B’(5; 3; 2);
C’(-3; -2; -1).
3) «Продвигаем» точку по другую сторону оси Oyz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oyz, будет иметь ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную по величине абсциссе данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oyz:
A’(-2; 3; 1);
B’(-5; -3; 2);
C’(3; 2; -1).
По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.
4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:
A’(2; -3; -1);
B’(5; 3; -2);
C’(-3; -2; 1).
5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:
A’(-2; 3; -1);
B’(-5; -3; -2);
C’(3; 2; 1).
6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:
A’(-2; -3; 1);
B’(-5; 3; 2);
C’(3; -2; -1).
7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:
A’(-2; -3; -1);
B’(-5; 3; -2);
C’(3; -2; 1).
Поделиться с друзьями
Весь блок «Аналитическая геометрия»
- Векторы
- Плоскость
- Прямая на плоскости
function-x.ru
системы координат
2.1. Декартова система координат
Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости.
Одна из осей называется осью Ox, или осью абсцисс, другая – осью Oy, или осью ординат. Эти оси называют также координатными осями.
Обозначим через Mx и My соответственно проекции произвольной точки M плоскости на оси Ox и Oy.
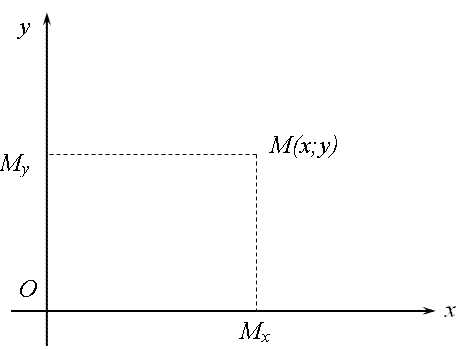
Декартовыми прямоугольными координатами x и y точки M будем называть соответственно величины направленных отрезков и:
— если направления иOx совпадают, то координата x равна длине ,
— если противоположны, то x равна длине , взятой со знаком «минус». Применяется обозначениеM(x, y).
Аналогично определяется координата y.
Три взаимно перпендикулярные оси в пространстве с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Одна из осей называется осью Ox, или осью абсцисс, другую – осью Oy, или осью ординат, третья – осью Oz или осью аппликат. Эти оси называют также координатными осями в пространстве.
Декартовы прямоугольные координаты точки в пространстве определяются так же как и на плоскости .
2.2. Полярная система координат
Полярная система на плоскости задается точкой О, называемой полюсом, лучом ОР, называемым полярной осью и вектором единичной длины и того же направления, что и луч ОР.
Возьмем на плоскости точку М. Положение точки М определяется двумя числами: её расстоянием r=|ОМ| от полюса О и углом j, образованным отрезком ОМ с полярной осью; при этом отсчет углов ведется в направлении, противоположном движению часовой стрелки.
Числа r, j называются полярными координатами точки М. Пишут М(r; j). При этом r называется полярным радиусом, j – полярным углом. Рассматривают главные значение полярного угла – из полуинтервала [0; 2p). Полярные координаты связаны с прямоугольными следующим образом (на рисунке полярная ось совпадет с осью абсцисс):
полярный радиус вычисляется по формуле ;
угол j в зависимости от значений x, y определяется по формулам
j = arctg(y/x), если x > 0, y ³ 0;
j = p – arctg(y/x), если x < 0, y < 0 или x < 0, y ³ 0;
j = 2p + arctg(y/x), если x > 0, y < 0;
j = p/2, если x = 0, y > 0;
j = 3p/2, если x = 0, y < 0.
Для начала координат О r=0, а угол j может быть произвольным.
Если же точка М задана в полярных координатах (r; j), а полярная ось совпадает с осью абсцисс, то
x = r cos j, y = r sin j.
2.3. Представление векторов в декартовой системе координат
Рассмотрим в пространстве декартову систему координат Oxyz. Выделим на координатных осях Оx, Оy и Oz единичные векторы (орты) и обозначим их ,и.
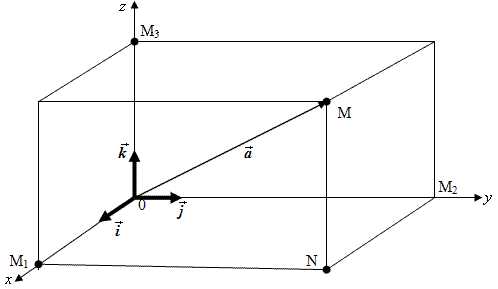
Выберем произвольный вектор и совместим его начало с началом координат=. Найдем проекцииax, ay, az вектора на координатные оси Оx, Оy и Oz. Для этого проведем через конец вектора плоскости параллельно координатным плоскостям. Точки пересечения этих плоскостей с осями координат обозначим соответственно М1, М2, М3. Получим прямоугольный параллелепипед. Имеем
=++.
Но = ax, = ay, = az, откуда
= ax+ ay+ az. (1)
Поскольку векторы ,инекомпланарные, то представление векторав виде линейной комбинации (1) единственно.
Формула (1) является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора , то есть координаты вектора – это его проекции на соответствующие координатные оси.
Векторное равенство (1) часто записывают в символическом виде:
= (ax, ay, az).
Модуль вектора равен
Пусть углы вектора с осями Оx, Оy и Oz, соответственно, равны α, β и γ. Тогда
Следовательно:
Числа cosα, cosβ и cosγ называются направляющими косинусами вектора . Очевидно, что
сos2α + cos2β + cos2γ = 1.
Пусть в пространстве задана прямоугольная декартова система координат Оxyz. Для любой точки М координаты вектора называются координатами точки М. Вектор называетсярадиус-вектором точки М, и обозначается =. Следовательно, координаты точки – это координаты её радиус-вектора(x, y, z) или = x+ y+ z. Координаты точки М записываются: М(x, y, z).
Даны две точки А(x1, y1, z1) и В(x2, y2, z2). Тогда
= =(x2 – x1, y2 – y1, z2 – z1).
Все приведенные выше определения и утверждения, касающиеся представления векторов в координатной форме, справедливы и для векторов на плоскости: в этом случае будут фигурировать не три, а лишь две координаты.
2.4. Действия над векторами в декартовой системе координат
Равенство векторов.
Два вектора иравны тогда и только тогда, если
.
Линейные операции над векторами.
Пусть векторы = (ax, ay, az) и = (bх; by; bz) заданы своими проекциями на оси координат Оx, Оy и Oz:
= ax+ ay+ az,
= bх+ by + bz
Операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
1) ±= (ах± bх)+ (аy ± by )+ (аz ± bz)
или
± = (ах ± bх; аy ± by ; аz ± bz)
2) λ= λax+ λay+ λazили λ= (λах; λаy; λаz)
Коллинеарность векторов
Теорема 1. Два заданных вектора = (ax, ay, az) и = (bх; by; bz) коллинеарные, если найдется такое действительное число l, что будет справедливо векторное равенство =l. При этом число l определяется единственным образом.
Равенство =lможно представить в виде пропорции
Таким образом проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: два вектора, имеющие пропорциональные координаты, коллинеарны.
Представление скалярного произведения в координатной форме
Даны два вектора =(ax, ay, az) и =(bх; by; bz). Их скалярное произведение в координатной форме:
(,) =ax bх + ay by + az bz .
Все приведенные в этом пункте определения и утверждения, справедливы и для векторов на плоскости: в этом случае будут фигурировать не три, а лишь две координаты.
studfiles.net
Система координат в геодезии, в топографии, в картографии
Пойдем прямым логическим путем, не отвлекаясь на многие современные международные и отечественные научные термины. Систему координат можно изобразить как некую систему отсчета ориентированную на плоскости двумя направлениями, а в пространстве тремя. Если вспомнить математическую систему, то она представлена двумя взаимно перпендикулярными направлениями, имеющими названия осей абсцисс (X) и ординат (Y). Ориентированы они в горизонтальном и вертикальном направлениях соответственно. Пересечение этих линий является началом координат с нулевыми значениями в абсолютной величине. А местоположение точек на плоскости определяется при помощи двух координат X и Y. В геодезии ориентирование осей на плоскости отличается от математики. Плоскостная прямоугольная система определена осью X в вертикальном положении (в направлении на север) и осью Y в горизонтальном (в направлении на восток).
Классификация систем координат
В геодезии все системы координат можно представить в виде двух групп:
- прямолинейная прямоугольная
- полярная
В обеих группах выделяют как плоские (двухмерные), так и пространственные (трехмерные) системы.
К прямолинейным прямоугольным системам относятся цилиндрическая проекция Гаусса-Крюгера, индивидуальные референцные и местные системы координат.
К полярным системам можно отнести географическую, астрономическую и геодезическую, геоцентрические и топоцентрические системы.
Географическая система координат
Замкнутая поверхность внешнего контура Земли представлена сфероидной геометрической формой. За основные направления ориентирования на ней можно принять дуги на поверхности шара. На упрощенно представленном уменьшенном макете нашей планеты в виде глобуса (фигура земли) можно зрительно увидеть принятые линии отсчета в виде Гринвичского меридиана и экваториальной линии.
В этом примере выражена общепринятая во всем мире именно пространственная система географических координат. В ней введены понятия долготы и широты. Имея градусные единицы измерения, они представляют угловую величину. Многим знакомы их определения. Следует напомнить, что географическая долгота конкретной точки представляет угол между двумя плоскостями, проходящими через нулевой (Гринвичский) меридиан и меридиан в определяемой точке расположения. Под географической широтой точки принят угол, образующийся между отвесной линией (или нормалью) к ней и плоскостью экватора.
Понятия астрономической и геодезической системы координат и их различия
Географическая система условно объединяет астрономическую и геодезическую системы. Для того чтобы было понятно какие все-таки существуют различия обратите внимание на определения геодезических и астрономических координат (долготы, широты, высоты). В астрономической системе широта рассматривается как угол между экваториальной плоскостью и отвесной линией в точке определения. А сама форма Земли в ней рассматривается как условный геоид, математически приближенно приравненный к сфере. В геодезической системе широта образовывается нормалью к поверхности земного эллипсоида в конкретной точке и плоскостью экватора. Третьи координаты в этих системах дают окончательное представление в их различиях. Астрономическая (ортометрическая) высота представляет собой превышение по отвесной линии между фактической и точкой на поверхности уровенного геоида. Геодезической высотой считается расстояние по нормали от поверхности эллипсоида до точки вычисления.
Система плоских прямоугольных систем координат Гаусса-Крюгера
Каждая система координат имеет свое теоретическое научное и практическое экономическое применение, как в глобальном, так и региональном масштабах. В некоторых конкретных случаях возможно использование референцных, местных и условных систем координат, но которые через математические расчеты и вычисления все равно могут быть объединены между собой.
Геодезическая прямоугольная плоская система координат является проекцией отдельных шестиградусных зон эллипсоида. Вписав эту фигуру внутрь горизонтально расположенного цилиндра, каждая зона отдельно проецируется на внутреннюю цилиндрическую поверхность. Зоны такого сфероида ограничиваются меридианами с шагом в шесть градусов. При развертывании на плоскости получается проекция, которая имеет название в честь немецких ученых её разработавших Гаусса-Крюгера. В таком способе проецирования углы между любыми направлениями сохраняют свои величины. Поэтому иногда ее называют еще равноугольной. Ось абсцисс в зоне проходит по центру, через условный осевой меридиан (ось X), а ось ординат по линии экватора (ось Y). Длины линий вдоль осевого меридиана передается без искажений, а вдоль экваториальной линии с искажениями к краям зоны.
Полярная система координат
Кроме выше описанной прямоугольной системы координат следует отметить наличие и использование в решении геодезических задач плоской полярной системы координат. За исходное отсчетное направление в ней применяется ось северного (полярного) направления, откуда и название. Для определения местоположения точек на плоскости используют полярный (дирекционный) угол и радиус-вектор (горизонтальное проложение) до точки. Напомним, что дирекционным углом считается угол, отсчитываемый от исходного (северного) направления до определяемого. Радиус-вектор выражается в определении горизонтального проложения. К пространственной полярной системе добавляется геодезические измерения вертикального угла и наклонного расстояния для определения 3D-положения точек. Этот способ практически ежедневно применяется в тригонометрическом нивелировании, топографической съемке и для развития геодезических сетей.
Геоцентрические и топоцентрические системы координат
По такому же полярному методу частично устроены и спутниковые геоцентрическая и топоцентрическая системы координат, с той лишь разницей, что основные оси трехмерного пространства (X, Y, Z) имеют отличные начала и направления. В геоцентрической системе началом координат является центр масс Земли. Ось X имеет направление по Гринвичскому меридиану к экватору. Ось Y располагают в прямоугольном положении на восток от X. Ось Z изначально имеет полярное направление по малой оси эллипсоида. Координатами в ней считаются:
- в экваториальной плоскости геоцентрическое прямое восхождение спутника
- в меридианной плоскости геоцентрическое склонение спутника
- геоцентрический радиус-вектор расстояние от центра тяжести Земли до спутника.
При наблюдении за движением спутников из точки стояния на земной поверхности используют топоцентрическую систему, оси координат которой расположены параллельно осям геоцентрической системы, а ее началом считается пункт наблюдения. Координаты в такой системе:
- топоцентрическое прямое восхождение спутника
- топоцентрическое склонение спутника
- топоцентрический радиус-вектор спутника
- геоцентрический радиус вектор в точке наблюдений.
В современные спутниковые глобальные системы отсчета WGS-84, ПЗ-90 входят не только координаты, но и другие параметры и характеристики важные для геодезических измерений, наблюдений и навигации. К ним относятся геодезические и другие константы:
- исходные геодезические даты
- данные земного эллипсоида
- модель геоида
- модель гравитационного поля
- значения величины гравитационной постоянной
- значение скорости света и другие.
geostart.ru
Адреса координат X Y Z A B C
Стр 1 из 3Следующая ⇒
Содержание
1. Системы ЧПУ
1.1. Декартовые системы координат
1.1.1. Плоские
1.1.2. Пространственные
1.2. Правила расположения осей
2. Программирование
2.1. Кадр, слово, адрес
2.2. Адреса координат
2.3. Специальные символы
3. Функции
3.1. G-функции
3.1.1. Группа 1 G90-G91, G17-G19, G00-G04
3.1.2. Группа 2 G40-G42, G53-G599
3.1.3. Группа 3 G94-G95, G96-G97, F, S, LIMS
3.2. М-функции
3.2.1. Управление исполнением программы
3.2.2. Управление электрооборудованием станка
3.2.2.1. Управление шпинделем
3.2.2.2. Управление инструментом
3.2.2.3. Управление СОЖ
4. Анализ листинга Управляющей Программы
5. Вопросы для самоконтроля
6. Краткие справочные сведения
Системы ЧПУ
Декартовые системы
Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. Каждой точке соответствует один и только один набор координат.
Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной).
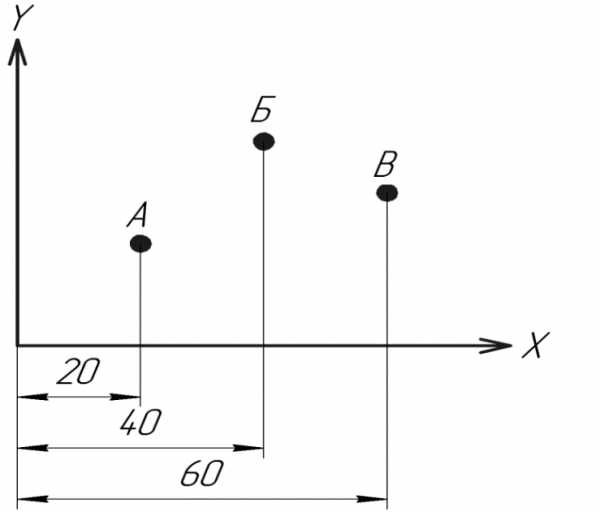
Плоские системы
Плоские прямоугольные координаты имеют в своей основе оси X и Y — перпендикулярные прямые, расположенные в одной плоскости.
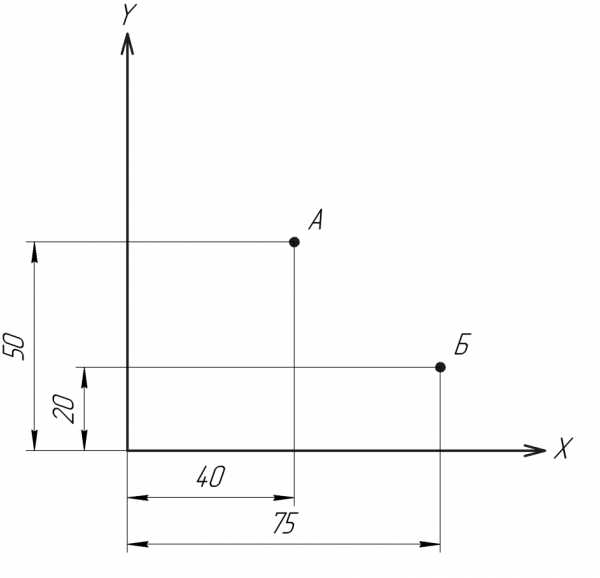
А: x=40, y=50
Б: x=75, y=20
Пространственные системы
Она образуется тремя взаимно перпендикулярными осями. Положение точки в пространстве в этой системе может быть задано тремя координатами — проекциями на эти оси
Положение любой точки задается тремя пространственными координатами — абсциссой X, ординатой У, аппликатой Z.
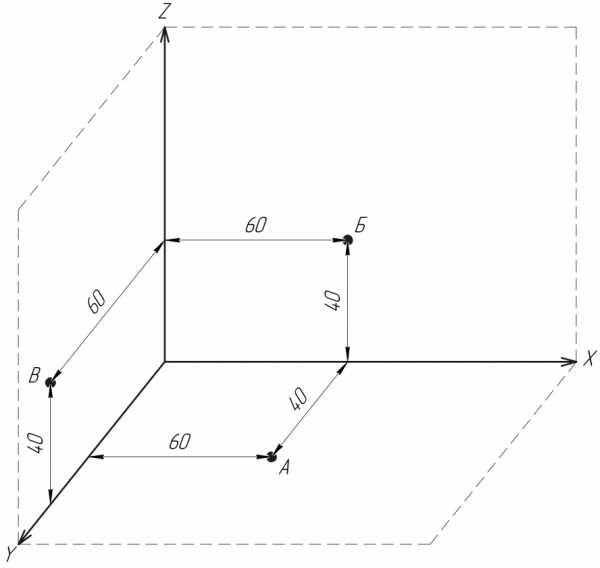
А: x=60, y=40, z=0
Б: x=60, y=0, z=40
В: x=0, y=60, z=40
Правила расположения осей
2. Оси всегда ориентированы параллельно направляющим станка. 
3. Ось Z всегда совмещена с осью вращения шпинделя. 
4. Положительное направление оси Z всегда совпадает с направлением перемещения от детали.
5. Направление остальных осей определяется по правилу правой руки. 
6. Положительное направление осей – удаление от детали.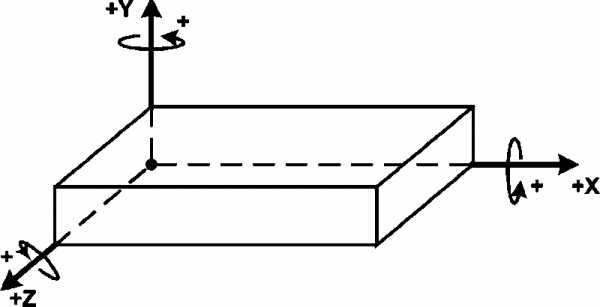 
Программирование
Кадр, слово, адрес
Кадр – структурная единица. Отрабатывается программой как единое целое – законченная команда станка ЧПУ.
Формат кадра – условная запись структуры и расположения слов в кадре.
Слово – команда – составная часть кадра, являющееся законченной и самостоятельной командой для системы ЧПУ. Слово состоит из адреса и числа.
Адрес – это фиксированный идентификатор – буква.
Число – значение определяющее адрес.
Пример:
N14 G01 X38 Y42 M8
| КАДР | Слово | Слово | Слово | Слово | Слово | ||||
| Адрес | Число | Адрес | Число | Адрес | Число | Адрес | Число | Адрес | Число |
| N | G | X | Y | M |
Адреса координат X Y Z A B C
Используются для обозначения координат точки, в которую необходимо осуществить перемещения.
Незначащие нули не записываются
Числа могут иметь знаки «+» и «-» . При отсутствии знака перемещение полагается положительным.
Движение вправо и вверх и по часовой стрелке – положительное.
Движение влево, вниз и против часовой стрелки – отрицательное.
Вращательные оси А, В, С идут вокруг осей X, Y, Z соответственно.
Специальные символы
N – имя кадра, номер кадра.
: — имя главного кадра (служит для выделения кадра из общей последовательности).
; — комментарий, исключает кадр из последовательности программы (служит для пояснения и документирования).
/ — пропускаемый кадр.
Функции
G-функции
Абсолютные/относительные системы счисления
G90 — режим абсолютного позиционирования.
В режиме абсолютного позиционирования перемещения исполнительных органов производятся относительно нулевой точки рабочей системы координат (программируется, куда должен двигаться инструмент). Код G90 отменяется при помощи кода относительного позиционирования G91.
G91 — режим относительного позиционирования.
В режиме относительного (инкрементального) позиционирования за нулевое положение каждый раз принимается положение исполнительного органа, которое он занимал перед началом перемещения к следующей опорной точке (программируется, на сколько должен переместиться инструмент). Код G91 отменяется при помощи кода абсолютного позиционирования G90.
М-функции
Вспомогательные (технологические) команды языка программирования начинаются с буквы М. Включают такие действия, как:
· Сменить инструмент
· Включить/выключить шпиндель
· Включить/выключить охлаждение
· Вызвать/закончить подпрограмму
Управление шпинделем
М0З — вращение шпинделя по часовой стрелке.
При помощи кода М03 включается прямое вращение шпинделя (по часовой стрелке, если смотреть со стороны шпинделя) с запрограммированным числом оборотов (S). Код М03 действует до тех пор, пока он не будет отменен с помощью М04 или М05.
М04 — вращение шпинделя против часовой стрелки.
При помощи кода М04 включается обратное вращение шпинделя (против часовой стрелки, если смотреть со стороны шпинделя) с запрограммированным числом оборотов (S). Код М04 действует до тех пор, пока он не будет отменен с помощью М03 или М05.
М05 — останов шпинделя.
Код М05 останавливает вращение шпинделя, но не останавливает осевые перемещения.
Управление инструментом
М06 — смена инструмента.
При помощи кода М06 инструмент, закрепленный в шпинделе, меняется на инструмент, находящийся в положении готовности в магазине инструментов.
Т— значение определяющее номер инструмента, который необходимо переместить в позицию смены, путем поворота инструментального магазина.
Управление СОЖ
М07 — включение охлаждения №2 (вспомогательного).
Код М07 включает подачу СОЖ в зону обработки в распыленном виде, если станок обладает такой возможностью.
М08 — включение охлаждения №1 (основного).
Код М08 включает подачу СОЖ в зону обработки в виде струи.
М09 — отключение охлаждения.
Код М09 выключает подачу СОЖ и отменяет команды М07 и М08.
4. Анализ листинга Управляющей Программы
Дана часть управляющей программы:
SKIQ-16NC SIN-840D
START
%_N_P341374_MPF
:9001 G71 G90 DIAMON T1 M6
N1 G97 M41 S9 M4
N2 G0 G94 X1405.976 Z499.35 V
N3 X1088.916 L
N4 Z449.56 M8 n
N5 X1089.7 Z449.55 L
N6 DIAMOFF G96 S30 LIMS=125
N7 G1 X1095.7 F0.1 T
N8 X1211.9 F0.15 L
N9 Z450.55 F2.
N10 DIAMON G0 G94 Z483.869
N11 X1097.942
N12 G0 X1123.319 Z444.84 M8
N13 G96 S30 LIMS=125 Dkp
N14 G1 Z443.64 F0.15 T
N15 Z430.54 F0.25 Fmin
N16 Z429.34 F2. Fob
N17 G0 G94 X1121.319
N18 Z444.84
N19 X1128.319
N20 G96 S60 LIMS=125
N21 G1 X443.64 F0.15 Fmin
N22 Z430.54 X1095.7 F0.25 T
N23 Z429.34 F2. Dkp
N24 G0 G94 X1126.319
N25 Z444.84
Необходимо вычислить: V (скорость резания), L (расстояние резания), T (время обработки), n (число оборотов), Dkp (критический диаметр), Fmin (минутная подача), Fob (оборотная подача).
1) Расчет скорости резания во втором кадре
Из N2: т.к. DIAMON, то D=х=1405,976 мм
n=9, т.к. в N1 S=9 – обороты шпинделя при G97
Подставляем в формулу:
2) Расчет расстояния резания в третьем кадре
Т.к. DIAMON , то х делим на 2 и получаем радиус
Х2=1088,916 (из N3)
Х1=1405,976 (из N2)
Z не меняется в N2 и N3, следовательно, Δz=0
Подставляем в формулу:
3) Расчет числа оборотов в четвертом кадре
Т.к. в N2 G96 (подача в мм/мин), то n=S=9 об/мин (из N1)
4) Расчет расстояния резания в пятом кадре
Т.к. DIAMON, то х делим на 2 и получаем радиус.
Х не меняется в N4 и N5, следовательно, Δх=0
z1=449.56 мм; z2=449,55 мм
Подставляем в формулу:
5) Расчет времени резания в седьмом кадре
Т.к. DIAMOFF, то х – это радиус и делить на 2 не надо.
l=x (из N7)-x (из N5) = 1095,7-1089,7=6 мм
т.к. G96 (обороты шпинделя в м/мин), то рассчитываем Fmin , где в N7 F0,1 – это Fob.
Fmin=Fob*n
Fob=0,1 об/мин
Рассчитываем
V=S=30 м/мин (из N6)
Dср=(D1+D2)/2=(1089,7+1095,7)/2=1092,7 мм
НО т.к. DIAMOFF, то дан радиус, следовательно, умножаем Dср на 2
Dср=2*1092,7=2185,4 мм
Подставляем в формулу:
Т=6/4,37=1,37 мин.
6) Расчет расстояния резания в восьмом кадре
Z не меняется в N7 и N8, следовательно, Δz=0
х1=1095,7 мм; х2=1211,9 мм
Подставляем в формулу:
7) Расчет критического диаметра в тринадцатом кадре
Т.к. G96, то V=S=30 м/мин
nкр=LIMS=125 об/мин
Подставляем в формулу:
8) Расчет времени резания в четырнадцатом кадре
Т.к. DIAMON, то х – это диаметр и делим на 2
l=444,64-443,64=1,2 мм
т.к. G96, то в N14 Fob=0,15 об/мин, следовательно, рассчитываем Fmin=Fob*n, где
V=S=30 м/мин, D=1123,319 мм
Подставляем в формулу:
Fmin=0,15*8,51=1,28 мм/мин
Т=1,2/1,28=0,9375 мин
9) Расчет минутной подачи в пятнадцатом кадре
Fmin=Fob*n
Fob=0,25 об/мин (из N15)
V=S=30 м/мин, D=1123,319 мм
Подставляем в формулу:
10) Расчет оборотной подачи в шестнадцатом кадре
Fob=2 (из N16), т.к G96, следовательно, G95 – подача в мм/об
11) Расчет минутной подачи в двадцать первом кадре
Fmin=Fob*n
Fob=0,15 об/мин (из N21)
V=S=60 м/мин, D=443,64 мм
Fmin=0,15*43,07=6,46 мм/мин
12) Расчет времени резания в двадцать втором кадре
Δх=1095,7-443,64=652,06 мм /2=326,03 мм, т.к. DIAMON
Δz=444,84-430,54=14,3 мм
Fmin=Fob*n
Fob=0,25 об/мин (из N22)
V=S=60 м/мин
Dср=(1095,7+443,64)/2=769,67 мм
Fmin=0,25*24,83=6,2 мм/мин
Т=326,37/6,2=52,64 мин
13) Расчет критического диаметра в двадцать третьем кадре
V=S=60 м/мин, т.к. G96 – обороты шпинделя в м/мин, то nкр=125 об (из N20)
Вопросы для самоконтроля
1. В чем отличие G90 от G91?
2. Напишите формат кадра для G02.
3. Напишите программу для круговой интерполяции.
4. Чему будет равен радиус при круговой интерполяции
X-.3976 Y-.4348 I-.015 J.1568 ?
5. Что такое трассировочная точка?
6. Где расположена точка трассировки у фрезы?
7. В чем заключается геометрический смысл команд G40 — G42?
8. Напишите формат кадра для G42.
9. 
Как изменится рисунок, если G41 заменить на G42?
10. 
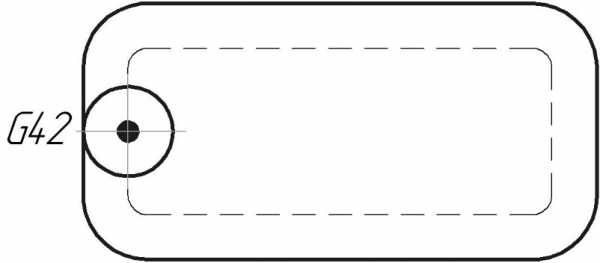Укажите направление движения инструмента при G42?
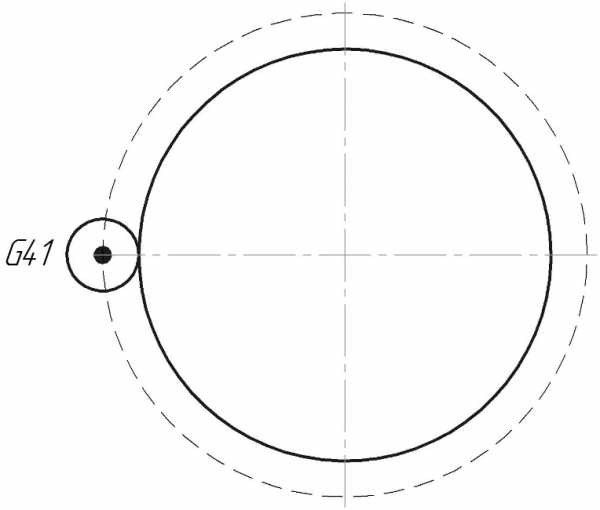
11. Укажите направление движения инструмента при G41?
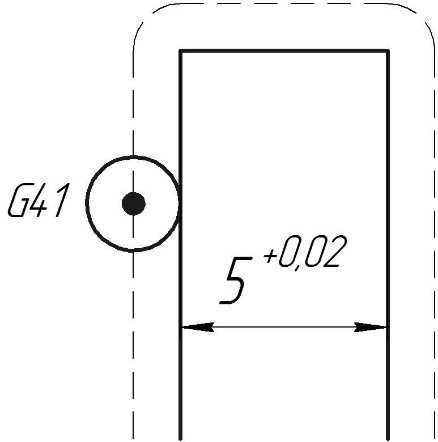
12. Задайте радиус инструмента с учетом допуска детали (определить значение корректора) – диаметр инструмента и фактическое значение размера .
13. Почему G95 используется с G96?
14. Почему при фрезерной обработке не используется G96?
15. Как перевести из мм/мин в об/мин?
16. Для чего нужен LIMS?
17. Укажите обязательную команду для выполнения команды M06.
18. Укажите формат кадра для G04?
19. Для чего необходимо смещение ноля?
20. Какой командой выбирается номер корректора на инструмент?
21. Какая плоскость интреполяции используется при токарной обработке?
22. В чем разница М00 и М01?
23. Назовите единицы измерения подачи при G94 и G95?
24. Для чего рассчитывают Dкр?
Краткие справочные сведения
| Код | Описание | Формат кадра |
| G — функции | ||
| G00 | ускоренное перемещение (холостой ход) | G00 X.. Y.. Z.. |
| G01 | линейная интерполяция с заданной скоростью подачи | G01 X.. Y.. Z..F.. |
| G02 | круговая интерполяция по часовой стрелке | G17 (G18, G19) G02/G03 X.. Y.. (Z..)I..J..(K..)F.. |
| G03 | круговая интерполяция против часовой стрелки | |
| G04 | пауза | G04 F.. – выдержка по времени G04 S.. – выдержка в оборотах |
| G17 | выбор плоскости XY | |
| G18 | выбор плоскости XZ | |
| G19 | выбор плоскости YZ | |
| G40 | отмена коррекции на радиус инструмента | |
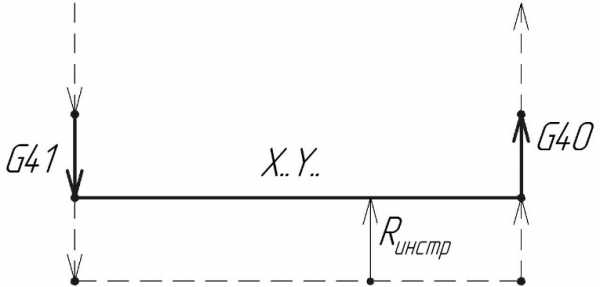
| G41 | левая коррекция на радиус инструмента | G17 (G18, G19) G41/G42 G01 X.. Y.. (Z..) F.. X.. Y.. (Z..) G40 X.. Y.. (Z..) |
| G42 | правая коррекция на радиус инструмента | |
| G53 | отмена заданного смещения | |
| G54-G599 | заданное смещение | |
| G90 | режим абсолютного позиционирования | |
| G91 | режим относительного позиционирования | |
| G94 | подача в мм/мин | G97 G94 S.. |
| G95 | подача в мм/об | G96 G95 S.. |
| G96 | задание значения оборотов шпинделя (S) в м/мин | G96 S.. |
| G97 | задание оборотов шпинделя в об/мин | G97 S.. |
| M — функции | ||
| M00 | безусловный останов | |
| M01 | условный останов (с подтверждением) | |
| M02 | конец программы с возвратом в начало (со сбросом модальных функций) | |
| M03 | вращение шпинделя по часовой стрелке | |
| M04 | вращение шпинделя против часовой стрелки | |
| M05 | останов шпинделя | |
| M06 | смена инструмента | |
| M07 | включение охлаждения №2 (вспомогательного) | |
| M08 | включение охлаждения №1 (основного) | |
| M09 | отключение охлаждения | |
| Специальные символы | ||
| F | задание подачи | |
| S | задание оборотов шпинделя | |
| LIMS | задание максимально допустимых оборотов шпинделя | |
| T | значение номера инструмента | |
| X, Y, Z | координаты точки траектории по осям X, Y, Z соответственно | |
| I, J, K | параметры дуги при круговой интерполяции по осям X, Y, Z соответственно |
Содержание
1. Системы ЧПУ
1.1. Декартовые системы координат
1.1.1. Плоские
1.1.2. Пространственные
1.2. Правила расположения осей
2. Программирование
2.1. Кадр, слово, адрес
2.2. Адреса координат
2.3. Специальные символы
3. Функции
3.1. G-функции
3.1.1. Группа 1 G90-G91, G17-G19, G00-G04
3.1.2. Группа 2 G40-G42, G53-G599
3.1.3. Группа 3 G94-G95, G96-G97, F, S, LIMS
3.2. М-функции
3.2.1. Управление исполнением программы
3.2.2. Управление электрооборудованием станка
3.2.2.1. Управление шпинделем
3.2.2.2. Управление инструментом
3.2.2.3. Управление СОЖ
4. Анализ листинга Управляющей Программы
5. Вопросы для самоконтроля
6. Краткие справочные сведения
Системы ЧПУ
Декартовые системы
Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. Каждой точке соответствует один и только один набор координат.
Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной).
Плоские системы
Плоские прямоугольные координаты имеют в своей основе оси X и Y — перпендикулярные прямые, расположенные в одной плоскости.
А: x=40, y=50
Б: x=75, y=20
Пространственные системы
Она образуется тремя взаимно перпендикулярными осями. Положение точки в пространстве в этой системе может быть задано тремя координатами — проекциями на эти оси
Положение любой точки задается тремя пространственными координатами — абсциссой X, ординатой У, аппликатой Z.
А: x=60, y=40, z=0
Б: x=60, y=0, z=40
В: x=0, y=60, z=40
Правила расположения осей
2. Оси всегда ориентированы параллельно направляющим станка.
3. Ось Z всегда совмещена с осью вращения шпинделя.
4. Положительное направление оси Z всегда совпадает с направлением перемещения от детали.
5. Направление остальных осей определяется по правилу правой руки.
6. Положительное направление осей – удаление от детали.
Программирование
Кадр, слово, адрес
Кадр – структурная единица. Отрабатывается программой как единое целое – законченная команда станка ЧПУ.
Формат кадра – условная запись структуры и расположения слов в кадре.
Слово – команда – составная часть кадра, являющееся законченной и самостоятельной командой для системы ЧПУ. Слово состоит из адреса и числа.
Адрес – это фиксированный идентификатор – буква.
Число – значение определяющее адрес.
Пример:
N14 G01 X38 Y42 M8
| КАДР | Слово | Слово | Слово | Слово | Слово | ||||
| Адрес | Число | Адрес | Число | Адрес | Число | Адрес | Число | Адрес | Число |
| N | G | X | Y | M |
Адреса координат X Y Z A B C
Используются для обозначения координат точки, в которую необходимо осуществить перемещения.
Незначащие нули не записываются
Числа могут иметь знаки «+» и «-» . При отсутствии знака перемещение полагается положительным.
Движение вправо и вверх и по часовой стрелке – положительное.
Движение влево, вниз и против часовой стрелки – отрицательное.
Вращательные оси А, В, С идут вокруг осей X, Y, Z соответственно.
Специальные символы
N – имя кадра, номер кадра.
: — имя главного кадра (служит для выделения кадра из общей последовательности).
; — комментарий, исключает кадр из последовательности программы (служит для пояснения и документирования).
/ — пропускаемый кадр.
Функции
G-функции
Рекомендуемые страницы:
lektsia.com
Системы координат — Электронный учебник K-tree
Из этой статьи Вы узнаете способы определения пространства, какие бывают системы координат
Задание пространства
Для определения местоположения точки в пространстве можно использовать любую систему координат, в зависимости от задачи. Например, если Вы проектируете светильник в форме шара, то Вы воспользуетесь сферическими координатами, если в Вашей задаче необходимо описать движение по спирали — Вы выберите цилиндрические координаты. Итак, впереди часто используемые системы координат.
Декартова система координат x, y, z
Декартова или прямоугольная система координат. В декартовой системе координат положение точки определяется с помощью координат по каждой из осей, в двухмерной системе координат — это пара чисел (x,y), в трёхмерном пространстве — группа из трёх чисел (x,y,z). Координаты декартовой системы принадлежат множеству вещественных чисел, т.е. x,y и z — это любое вещественное число (-∞;+∞)
Полярная система координат ρ, θ
Полярная система координат — плоская система координат, в которой положение любой точки определяется с помощью расстояния r от центра системы координат и угла между радиус-вектором к оси x. Полярная система координат используется когда расстояния между точками удобнее определять углом и расстоянием. Также полярная система координат используется для представления комплексных чисел. В полярной системе координат r ≥ 0, угол φ ∈ [0;2π), одноко, для удобства, угол φ можно записать и как отрицательное значение и как значения большие 2π. Полярные координаты связаны с декартовыми следующими выражениями:
Перевод полярных координат в декартовы:
x = r cosφ
y = r sinφ
Цилиндрические координаты r, φ, z
Цилиндрические координаты были введены для работы с цилиндрическими телами и поверхностями, цилиндрические координаты удобно использовать, например, для спирали, уравнения спирали в цилиндрической системе координат будет выглядеть значительно проще, нежели в декартовых координатах. В цилиндрических координатах плоскость XY определяется также, как и в полярных координатах: с помощью расстояния и угла между радиус-вектором и осью X, z-координата такая же, как и в декартовых координатах. Связь цилиндрических и декартовых координат:
Перевод цилиндрических координат в декартовы:
x = r cosφ
y = r sinφ
z = z
Сферические координаты ρ, φ, θ
Сферические координаты, как следует из названия, были введены для работы со сферическими телами, положение любой точки в сферических координатах определяется с помощью двух углов φ и θ и радиус-вектора ρ. Сферические координаты связаны с декартовыми координатами следующим образом:
Перевод сферических координат в декартовы:
x = ρ sinφ cosθ
y = ρ sinφ sinθ
z = ρ cosφ
k-tree.ru
Система координат
Определение положения точки в пространстве
Итак, положение какой-либо точки в пространстве может быть определено только по отношению к каким-либо другим точкам. Та точка, относительно которой рассматривается положение других точек, называется точкой отсчете . Мы так же применим и другое наименование точки отсчета – точка наблюдения . Обычно с точкой отсчета (или с точкой наблюдения) связывают какую-либо систему координат , которую и называют системой отсчета. В выбранной системе отсчета положение КАЖДОЙ точки определяется ТРЕМЯ координатами.
Правая декартова (или прямоугольная) система координат
Эта система координат представляет собой три взаимно перпендикулярных направленных прямых, называемых так же осями координат , пересекающихся в одной точке (начале координат). Точка начала координат обычно обозначается буквой О.
Оси координат носят названия:
1. Ось абсцисс – обозначается как OX;
2. Ось ординат – обозначается как OY;
3. Ось аппликат – обозначается как OZ
Теперь объясним, почему эта система координат называется правой. Давайте посмотрим на плоскость XOY с положительного направления оси OZ, например из точки А, как это показано на рисунке.
Предположим, что мы начинаем поворачивать ось OX вокруг точки О. Так вот – правая система координат имеет такое свойство, что, если смотреть на плоскость XOY из какой-либо точки положительной полуоси OZ (у нас – это точка А), то, при повороте оси OX на 90 против часовой стрелки, её положительное направление совпадет с положительным направлением оси OY.
Такое решение было принято в научном мире, нам же остается принимать это так, как оно есть.
Итак, после того, как мы определились с системой отсчета (в нашем случае – правой декартовой системой координат), положение любой точки описывается через значения её координат или другими словами – через величины проекций этой точки на оси координат.
Записывается это так: A(x, y, z), где x, y, z – и есть координаты точки А.
Прямоугольную систему координат можно представить себе, как линии пересечения трех взаимно перпендикулярных плоскостей.
Следует заметить, что ориентировать прямоугольную систему координат в пространстве можно как угодно, при этом надо выполнить только одно условие – начало координат должно совпадать с центром отсчета (или точкой наблюдения).
Сферическая система координат
Положение точки в пространстве можно описать и другим способом. Предположим, что мы выбрали область пространства, в котором располагается точка отсчета О (или точка наблюдения), и еще нам известно расстояние от точки отсчета до некоторой точки А. Соединим эти две точки прямой ОА. Эта прямая называется радиус-вектором и обозначается, как r . Все точки, имеющие одно и тоже значение радиус-вектора, лежат на сфере, центр которой находится в точке отсчета (или точке наблюдения), а радиус этой сферы равен, соответственно радиус-вектору.
Таким образом, нам становится очевидным, что знание величины радиус-вектора не дает нам однозначного ответа о положении интересующей нас точки. Нужны еще ДВЕ координаты, ведь для однозначного определения местоположения точки количество координат должно равняться ТРЕМ.
Далее мы поступим следующим образом – построим две взаимно перпендикулярные плоскости, которые, естественно, дадут линию пересечения, и эта линия будет бесконечной, потому как и сами плоскости ничем не ограничены. Зададим на этой линии точку и обозначим ее, ну например, как точка О1. А теперь совместим эту точку О1 с центром сферы – точкой О и посмотрим, что получается?
А получается очень интересная картина:
· Как одна, так и другая плоскости будут центральными плоскостями.
· Пересечение этих плоскостей с поверхностью сферы обозначат большие круги
· Один из этих кругов – произвольно, мы назовем ЭКВАТОРОМ , тогда другой круг будет называться ГЛАВНЫМ МЕРИДИАНОМ.
· Линия пересечения двух плоскостей однозначно определит направление ЛИНИИ ГЛАВНОГО МЕРИДИАНА.
Точки пересечения линии главного меридиана с поверхностью сферы обозначим, как М1 и М2
Далее мы поступаем следующим образом:
Через центр сферы точку О в плоскости главного меридиана проведем прямую, перпендикулярную линии главного меридиана. Эта прямая носит название ПОЛЯРНАЯ ОСЬ .
Полярная ось пересечет поверхность сферы в двух точках, которые называются ПОЛЮСАМИ СФЕРЫ. Обозначим эти точки, как Р1 и Р2.
Определение координат точки в пространстве
Теперь рассмотрим процесс определения координат точки в пространстве, а так же дадим наименования этим координатам. Для полноты картины, при определении положения точки, укажем основные направления, от которых производится отсчет координат, а так же положительное направление при отсчете.
1. Задаем положение в пространстве точки отсчета (или точки наблюдения). Обозначим эту точку буквой О.
2. Строим сферу, радиус которой равен длине радиус-вектора точки А. (Радиус-вектор точки А – это расстояние между точками О и А). Центр сферы располагается в точке отсчета О.
3. Задаем положение в пространстве плоскости ЭКВАТОРА, а соответственно плоскости ГЛАВНОГО МЕРИДИАНА. Следует напомнить, что эти плоскости взаимно перпендикулярны и являются центральными.
4. Пересечение этих плоскостей с поверхностью сферы определяет нам положение круга экватора, круга главного меридиана, а так же направление линии главного меридиана и полярной оси.
5. Определяем положение полюсов полярной оси и полюсов линии главного меридиана. (Полюса полярной оси – точки пересечение полярной оси с поверхностью сферы. Полюса линии главного меридиана – это точки пересечения линии главного меридиана с поверхностью сферы).
6. Через точку А и полярную ось строим плоскость, которую назовем плоскостью меридиана точки А. При пересечении этой плоскости с поверхностью сферы получится большой круг, который мы назовем МЕРИДИАНОМ точки А.
7. Меридиан точки А пересечет круг ЭКВАТОРА в некоторой точке, которую мы обозначим, как Е1
8. Положение точки Е1 на экваториальном круге определяется длиной дуги, заключенной между точками М1 и Е1. Отсчет ведется ПРОТИВ часовой стрелки. Дуга экваториального круга, заключенная между точками М1 и Е1 называется ДОЛГОТОЙ точки А. Долгота обозначается буквой .
Подведем промежуточный итог. На данный момент нам известны ДВЕ из ТРЕХ координат, описывающих положение точки А в пространстве – это радиус-вектор (r) и долгота (). Теперь мы будем определять третью координату. Эта координата определяется положением точки А на ее меридиане. Но вот положение начальной точки, от которой происходит отсчет, однозначно не определено: мы можем начинать отсчет как от полюса сферы (точка Р1), так и от точки Е1, то есть от точки пересечения линий меридиана точки А и экватора (или другими словами – от линии экватора).
В первом случае, положение точки А на меридиане называется ПОЛЯРНЫМ РАССТОЯНИЕМ (обозначается как р ) и определяется длиной дуги, заключенной между точкой Р1 (или точкой полюса сферы) и точкой А. Отсчет ведется вдоль линии меридиана от точки Р1 к точке А.
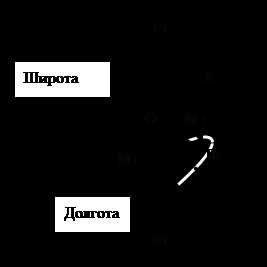
Во втором случае, когда отсчет ведется от линии экватора, положение точки А на линии меридиана называется ШИРОТОЙ (обозначается как и определяется длиной дуги, заключенной между точкой Е1 и точкой А.
Теперь мы можем окончательно сказать, что положение точки А в сферической системе координат определяется через:
· длину радиуса сферы ( r ),
· длину дуги долготы ( ),
· длину дуги полярного расстояния ( р )
В этом случае координаты точки А запишутся следующим образом: А(r, , p)
Если пользоваться иной системой отсчета, то положение точки А в сферической системе координат определяется через:
· длину радиуса сферы ( r ),
· длину дуги долготы ( ),
· длину дуги широты ( )
В этом случае координаты точки А запишутся следующим образом: А(r, , )
Способы измерения дуг
Возникает вопрос – как же нам измерить эти дуги? Самый простой и естественный способ – это провести непосредственное измерение длин дуг гибкой линейкой, и это возможно, если размеры сферы сравнимы с размерами человека. Но как поступить, если это условие не выполнимо?
В этом случае мы прибегнем к измерению ОТНОСИТЕЛЬНОЙ длины дуги. За эталон же мы примем длину окружности, частью которой является интересующая нас дуга. Как это можно сделать?
mirznanii.com