А в степени 1 матрица – Основные операции над матрицами (сложение, умножение, транспонирование) и их свойства.

Содержание

Обратная матрица с помощью алгебраических дополнений

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью алгебраических дополнений.

Обратной матрицей называется матрицы A^-1 при умножении на исходную матрицу A получается единичная матрица E.

A·A^-1 = A^-1 · A = E

Алгоритм нахождения обратной матрицы с помощью алгебраических дополнений:

Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
Найти матрицу миноров M.
Из матрицы M найти матрицу алгебраических дополнений C^*.
Транспонировать матрицу (поменяем местами строки со столбцами) C^*, получить матрицу C^*T.
По формуле найти обратную матрицу.

Пример

Рассмотрим данный метод на примере. Дана матрицы 3х3:

Найдем определитель (детерминант) матрицы, detA = 12 обратная матрица существует.

Найдем минор M₁₁ и алгебраическое дополнение A₁₁. В матрице А вычеркиваем строку 1 и столбец 1.

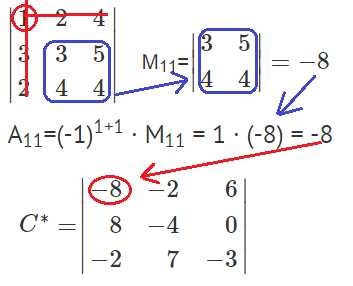
Найдем минор M₁₂ и алгебраическое дополнение A₁₂. В матрице А вычеркиваем строку 1 и столбец 2.

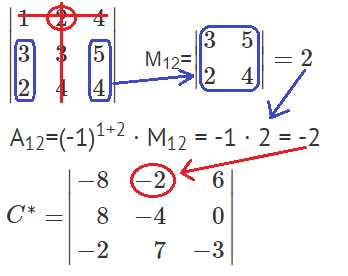
Остальные миноры и алгебраические дополнения находятся аналогично. В итоге получаем матрицу

C^*.

Найдем транспонированную союзную матрицу алгебраических дополнений C^*T.

Найдем обратную матрицу. Ответ:

mozgan.ru

матрицы

Основные понятия

Матрицы равны между собой если равны их соответствующие элементы А=В если аij=bij где аij bij-элементы матриц
Матрица у которой число строк равно числу столбцов называется квадратной
Квадратная матрица у которой все элементы равны нулю кроме главной диаконали называется диагональной
Диагональная матрица у которой все элементы равны еденицам называется еденичной
Квадратная матрица называется треугольной если все элементы расположенные по одну сторону диаконали равны нулю
Матрица все элементы которой равны нулю называется нулевой
Матрица содержащая в себе один столбец или строку называется вектор столбцом вектор строкой
Матрица полученная заменой строк столбцами называется транспонированной матрицей

Действия над матрицами

Операция сложения матриц вводится только для матриц одинаковых размеров
Суммой двух матриц А и B называется матрица С у которой элементы cij=aij+bij Анологично определяется разность матриц

Произведение матрицы на число называется матрица В у которой элементы bij=k*aij
Матрица–А=(-1)А называется противоположной матрице А.Разность матриц А-Вможно определить как А-В=А+(-В)

Операция умножения двух матриц вводится только тогда когда число столбцов первой матрицы равно числу строк второй матрицы m*n умножить на n*p равно матрицы m*p.
Умножение производиться следующим образом элементы iой строки и kго столбца матрицы произведения матрицы С равен сумме произведений элементов iй строки матрицы А на соответствующие элементы kго столбца матрицы В
Операции сложения и умножения матриц обладают следующими свойствами:

А+В=В+А
А+(В+С)=(А+В)+С
А+0=А
А-А=0
1*А=А
k*(A+B)=kA+kB
(k+c)*A=k*A+c*A
k*(c*A)=(k*c)*A

Элементарные преобразования матриц

Перестановка местами двух параллельных рядов матрицы
Умножение всех элементов ряда матрицы на число отличное от нуля
Прибавлением ко всем элементам ряда матрицы соответствующих элементов парралельного рада умноженных на одно и тоже число

Эквивалентными называются матрицы получиные с помощью элементарных преобразований одной в другую
Опрерация умножения матриц производится тогда и только тогда когда число столбцов одной матрицы равно числу строк матрицы другой m*n умножается на n*p и получается m*p
Произведением матрицы А на матрицу В называется матрица С у которой элемент i-строки и k-столбца равен сумме произведений элементов i-строки матрицы А на соответствующие элементы k-столбца матрицы В
Матрици А и В называют перестановычными если АВ=ВА

Свойства умножения матриц

A*(B*C)=(A*B)*C
A*(B+C)=A*B+A*C
(A+B)*C=A*C+B*C

Свойства определителей

Св-во 1: Определитель матрицы не изменится при транспонировании матрицы
Св-во2: При перестановке двух параллельных рядов определитель меняет знак на противоположный
Св-во 3: Определитель имеющий два одинаковых ряда равен нулю
Св-во 4: Общий множетель элементов какоголибо ряда определителя можно вынести за знак определителя
Св-во 5: Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых то определитель может быть разложен на сумму двух соответствующихз определителей
Св-во 6: Определитель не изменится если к элементам одного ряда прибавить соответствующие элементы паралельного ряда, умноженные на любое число
Теорема: определитель произведения двух квадратных матриц равен произведению определителей перемножаемых матриц det(A*B)=detA*detB
Минором некоторого элемента aij определителя n-го порядка называется определитель n-1го порядка полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент
Алгебраическим дополнением элемента aij определителя называется его минор взятый со знаком плюс если сумма i+j четное число и со знаком минус если эта сумма нечетная.

Св-во 7: Определитель равен сумме произведений элементов некоторого ряда на их алгебраическое дополнение
Св-во 8: Сумма произведений элементов какого либо ряда определителя на алгебраическое дополнение соответствующих элементов парралельного ряда равна нулю а11А21+а12А22+а13А23=0

Невырожденные матрицы

Невырожденная матрица матрица у которой определитель отличен от нуля
Вырожденная матрица матрица у которой определитель равен нулю
Рангом матрицы называется наибольший из порядков миноров отличных от нуля, Ранг канонической матрицы равен числу единиц стоящих на ее диагонали, Ранг матрицы равен максимальному числу линейно независимых строк матрицы А.
При транспонировании матрицы ее ранг не меняется
Если вычеркнуть из матрицы нулевой столбец, то ранг матрицы не изменится
Ранг матрицы не изменится при элементарных преобразованиях
Эквивалентными матрицами называются матрицы, когда одна матрица получена из другой с помощью элементарных преобразований матрицы ни являются равными, но их ранги равны
Теорема: Для того чтобы матрица А имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля
Док-во:
По определителю обратной матрицы А в минус первой степени = В; АВ=ВА=Е следует
А и А в минус первой степени перестановочные квадратные матрицы оного порядка по теореме о произведении обратных матриц имеем, что detA*detA в минус первой степени=det(A*A в минус первой степени)=detE=1=detA*detA в минус первой степени из этого следует, что ни один определитель не может быть нулевым, если матрица имеет обратную матрицу

Системы линейных уравнений

Совокупность n чисел C1,C2,Cn, называется решением системы уравнений, если каждое уравнение системы обращается в верное тождество (левая часть равна правой после подстановки n вместо Х)
Система уравнений называется совместной, если она имеет одно или множество решений, система является не совместной, если она ни имеет решения
Если система имеет множество решений, то каждое решение называется частным, а множество всех частных это общее решение системы
Эквивалентными системами называются такие системы, у которых решение одной системы является решением для другой и наоборот, все несовместные системы являются эквивалентными
Теорема: Крамера система из m уравнений и n неизвестных в случае, когда определитель этой системы отличен от нуля имеет решение и только одно это решение находится по формулам Х=deti/det для всех i

где det-определитель системы

deti-определитель матрицы полученной заменой i-го столбца столбцом свободных членов.

Если определитель отличен от нуля, это достаточно для того, чтобы матрица имела обратную А в минус первой степени

АХ=В; Х=В/А; Х=В*А-1степени, подставим в первое ур-е получим А*В*Ав –1степени=В А*А в минус первой

степени единичная матрица, следовательно, ЕВ=В; В=В

Допустим, что матрица А имеет множество решений (Х1, Х2, Хn) то АХ2=Ви АХ1=В следовательно АХ2=АХ1

Умножим обе части на обратную матрицу А получим ЕХ2=ЕХ1 следовательно, Х1=Х2 т.е. запись (Х1Х2Хn) не имеет смысла и все иксы равны. Формула Крамера ход: записать Х=А в минус первой *В где В вектор столбец свободных членов А в минус первой обратная к А запишем обратная матрица равна еденици деленой на определитель матрицы А умноженное на союзную матрицу,…

Базисным минором называется минор отличный от нуля r-го порядка где r ранг матрицы.

Всякий столбец матрицы есть линейная комбинация ее базисных столбцов сами базисные столбцы линейно независимы (верно для строк).

Обозначим аik элементы матрицы (k 1,…m строк, j=1,…n столбцов) пусть С1С2Сn столбцы матрицы пусть базисный минор находится в столбце (Cj1, Cj2,…Cjr) и в строках с номерами k1,…kr. Доказать что для любого столбца существует числа L1,…,Lr такие что столбец является линейной комбинацией столбцов Cj=L1Cj1+,…+LrCjr (1)

Для элементов матрицы А с учетом свойств матрицы уравнение (1) имеет вид (1<k<m) aij=L1aij1+,…,Lrakir где Lj не зависят от K.

Пусть система совместна ранг расширенной матрицы равен рангу системы.

1)показать что дополнительный вектор столбец является линейной комбинацией ( т.к. из совместной системы следует что Х1=С1б Хn=Cn при замене иксов на С получим что система уравнений является линейной комбинацией доп. столбца bjn т.к). системы это значит, что он не влияет на ранг по свойству ранга и это значит, что ранг расширенной матрицы равен рангу системы

2)ранги равны покажем что есть решение Пусть ранг расширенной матрицы равен рангу системы Выделим базис столбцы матрицы расширенной они же будут базис столбцами матрицы системы. Предположим что базисными являются первые r столбцов Согласно теореме о базисном миноре (всякий столбец матрицы есть линейная комбинация ее базисных столбцов) последний столбец может быть линейной комбинацией базисных столбцов, т.е. существуют числа С1,С1,Сr что С1аj1+C2aj2+,…,Crair=bir (2) если подставить в уравнение системы aj1X1,…,ajnXn=bjn (1) положим что Х1=С1, Хr=Cr, Xr+1=0получим что все уравнения системы (1) превратятся в (2) Т.е. получим Х=(С1С2Сr0000)”вектор столбец”- решение системы значит система разрешима.

Ранг не может быть больше числа столбцов: если ранг расширенной матрицы равен числу столбцов то у системы одно решение, если ранг меньше числа столбцов то у системы множество решений.

Метод Гауса (метод последовательного исключения неизвестных) если число базисных элементов соответствует числу строк то у системы единственное решение если число строк больше числа базисных элементов то у системы множество решений
Однородная система – система уравнений когда свободный член равен нулю и система неоднородна в противном случае aj1X1,…+…, ajnXn=0 или в матричном виде АХ=0. Любая однородная система имеет одно решение и совместна всегда
Теорема о существовании нетривиального решения: Для того чтобы существовало хотя бы одно ни тривиальное решение необходимо и достаточно чтобы ранг был меньше числа неизвестных
Док-во:

Система всегда имеет одно решение когда ранг меньше числа неизвестных система имеет множество решений одно из них тривиальное все остальные не тривиальные также ранг не может быть больше числа неизвестных.

Теорема о линейной комбинации решений однородной системы уравнений: если векторы С1, С2,…, Сn являются решением системы АХ=0 то любая их линейная комбинация С=L1C1+L2C2+…+LnCn является решением этой системы т.к. С1…Сn решение системы то АХ=0 следует что АС1=0… АСn=0 учитывая распределительный и сочетательный закон матричного умножения а также независимость произведения на число от порядка множителя имеем АС=А(L1C1+…LnCn)=L(AC1)+…L(Acn) из этого следует что С решение системы АХ=0.

Фундаментальной системой решений называется линейно зависимая система решений ч/з которую линейно выражается решение данной системы.

studfiles.net

Свойства определителя матрицы | Мозган калькулятор онлайн

Определитель единичной матрицы равен единице: det(E) = 1. Единичная матрица — это квадратная матрица, элементы главной диагонали которой равны единице, а все остальные элементы равны 0.
Определитель матрицы с двумя равными строками или столбцами равен нулю.
Определитель матрицы с двумя пропорциональными строками или столбцами равен нулю.
Определитель матрицы, содержащий нулевую строку или столбец, равен нулю.
Определитель матрицы равен нулю, если две или несколько строк или столбцов матрицы линейно зависимы.
При транспонировании значение определителя матрицы не меняется: det(A) = det(A^T).
Определитель обратной матрицы: det(A^-1) = det(A)^-1.
Определитель матрицы не изменится, если к какой-то его строке или столбцу прибавить другую строку или столбец, умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке или столбцу прибавить линейную комбинации других строк или столбцов.
Если поменять местами две строки или два столбца матрицы, то определитель матрицы поменяет знак.
Общий множитель в строке или столбце можно выносить за знак определителя:
Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени: B = k·A => det(B) = kⁿ·det(A), где A матрица n×n, k — число.
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
Определитель верхней или нижней треугольной матрицы равен произведению его диагональных элементов.
Определитель произведения матриц равен произведению определителей этих матриц: det(A·B) = det(A)·det(B).

Другой материал по теме

mozgan.ru

Умножение матрицы на матрицу онлайн

Умножение матрицы на матрицу

Операция умножения двух матриц А и В представляет собой вычисление результирующей матрицы С, каждый элемент c_ij которой равен сумме произведений элементов в соответствующей строке первой матрицы a_ik и элементов в столбце второй матрицы b_kj.

Две матрицы можно умножать между собой только тогда, когда количество столбцов в первой матрице совпадает с количеством строк во второй матрице. Другими словами первая матрица обязательно должна быть согласованной со второй матрицей. Таким образом, результатом операции умножения матрицы размера m×n на матрицу размером n×k является матрица размером m×k.

Итак, произведение матрицы А_m×n на матрицу В_n×k – это матрица С_m×k, элемент c_ij которой, находящийся в i-ой строке и j-ом столбце, равен сумме произведений i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В.

Каждый элемент матрицы С_m×k равен:

где k принимает значение от 1 до n.

Рассмотрим пример умножения двух матриц.

Даны две матрицы А и В.

Найти произведение матриц А × В.
Решение.

Свойства умножения матриц (свойства справедливы, если матрицы подходящего порядка):

Ассоциативность
(А × В) × С = А × (В × С)
Дистрибутивность
А × (В+С) = А×В + А×С
(А+В) × С = А×С + В×С
Ассоциативность и коммутативность относительно умножения на число
(k×A) × B = k × (A×B) = A × (k×B)
В общем случае умножение матриц не коммутативно
А×В ≠ В×А
Произведение коммутативно в случае умножения на единичную матрицу
E_m × A_m×n = A_m×n × E_n = A_m×n

Вы также можете

в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x (например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.