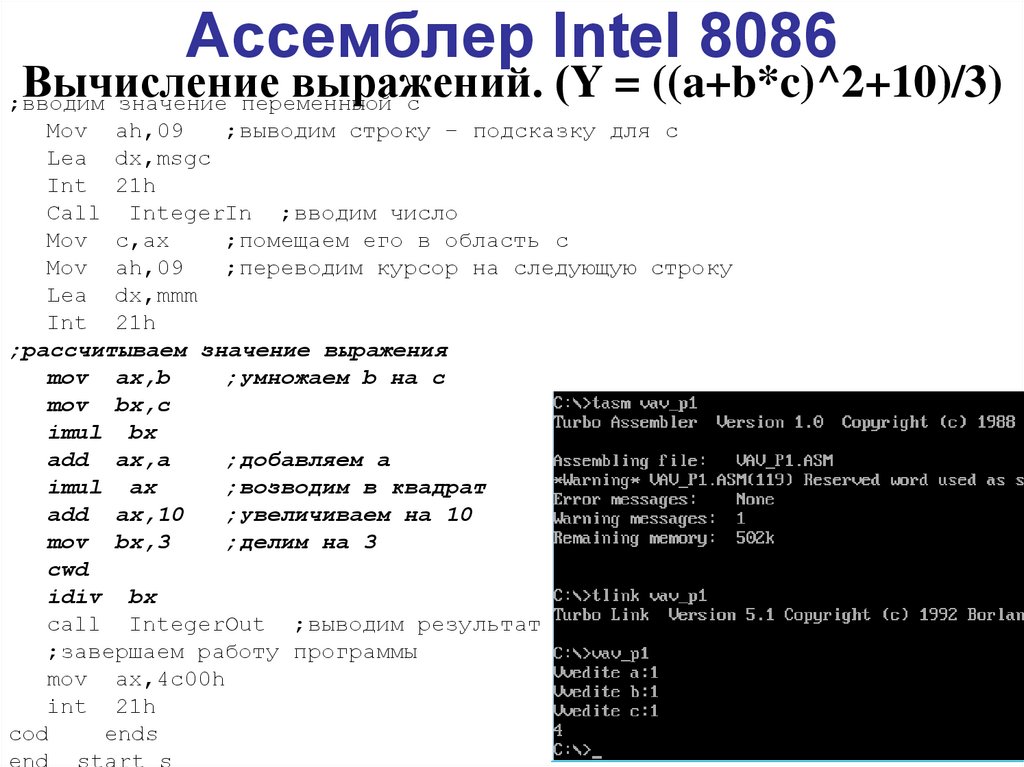
Деление и умножение в Assembler
Здравствуйте, уважаемые друзья! Продолжаем изучать нашу рубрику, на очереди тема умножения и деления в Assembler. Разберемся со всеми тонкостями этих операций, конечно же, на практическом примере.
Основные команды
- Для умножения в Assembler используют команду
mul - Для деления в Assembler используют команду
div
Правила умножения в Assembler
Итак, как мы уже сказали, при умножении и делении в Assembler есть некоторые тонкости, о которых дальше и пойдет речь. Тонкости эти состоят в том, что от того, какой размерности регистр мы делим или умножаем многое зависит. Вот примеры:
- Если аргументом команды mul является 1-байтовый регистр (например
mul bl), то значение этого регистра bl умножится на значение регистра al, а результат запишется в регистр ax, и так будет всегда, независимо от того, какой 1-байтовый регистр мы возьмем.
bl*al = ax - Если аргументом является регистр из 2 байт(например
mul bx), то значение в регистре bx умножится на значение, хранящееся в регистре ax, а результат умножения запишется в регистр eax.bx*ax = eax - Если аргументом является регистр из 4 байт(например
mul ebx), то значение в регистре ebx умножится на значение, хранящееся в регистре eax, а результат умножения запишется в 2 регистра: edx и eax.ebx*eax = edx:eax
Правила деления в Assembler
Почти аналогично реализуется и деление, вот примеры:
- Если аргументом команды div является 1-байтовый регистр (например
div bl), то значение регистра ax поделится на значение регистра bl, результат от деления запишется в регистр al, а остаток запишется в регистр ah.
ax/bl = al, ah - Если аргументом является регистр из 2 байт(например
div bx), то процессор поделит число, старшие биты которого хранит регистр dx, а младшие ax на значение, хранящееся в регистре bx. Результат от деления запишется в регистр ax, а остаток запишется в регистр dx.(dx,ax)/bx = ax, dx - Если же аргументом является регистр из 4 байт(например
div ebx), то процессор аналогично предыдущему варианту поделит число, старшие биты которого хранит регистр edx, а младшие eax на значение, хранящееся в регистре ebx. Результат от деления запишется в регистр eax, а остаток запишется в регистр edx.(edx,eax)/ebx = eax, edx
Программа
Далее перейдем к примеру: он не должен вызвать у вас каких либо затруднений, если вы читали наши предыдущие статьи, особенно важна статья про вывод на экран, советую вам с ней ознакомиться. Ну а мы начнем:
Ну а мы начнем:
.386 .model flat,stdcall option casemap:none include ..\INCLUDE\kernel32.inc include ..\INCLUDE\user32.inc includelib ..\LIB\kernel32.lib includelib ..\LIB\user32.lib BSIZE equ 15 .data ifmt db "%d", 0 ;строка формата stdout dd ? cWritten dd ? CRLF WORD ? .data? buf db BSIZE dup(?) ;буфер
Стандартное начало, в котором мы подключаем нужные нам библиотеки и объявляем переменные для вывода чисел на экран. Единственное о чем нужно сказать: новый для нас раздел .data? Знак вопроса говорит о том, что память будет выделяться на этапе компилирования и не будет выделяться в самом исполняемом файле с расширением .exe (представьте если бы буфер был большего размера) . Такое объявление — грамотное с точки зрения программирования.
.code start: invoke GetStdHandle, -11 mov stdout,eax mov CRLF, 0d0ah ;-------------------------деление mov eax, 99 mov edx, 0 mov ebx, 3 div ebx invoke wsprintf, ADDR buf, ADDR ifmt, eax invoke WriteConsoleA, stdout, ADDR buf, BSIZE, ADDR cWritten, 0 invoke WriteConsoleA, stdout, ADDR CRLF, 2, ADDR cWritten,0
В разделе кода, уже по традиции, считываем дескриптор экрана для вывода и задаем значения для перевода каретки. Затем помещаем в регистры соответствующие значения и выполняем деление регистра ebx, как оно реализуется описано чуть выше. Думаю, тут понятно, что мы просто делим число 99 на 3, что получилось в итоге выводим на экран консоли.
Затем помещаем в регистры соответствующие значения и выполняем деление регистра ebx, как оно реализуется описано чуть выше. Думаю, тут понятно, что мы просто делим число 99 на 3, что получилось в итоге выводим на экран консоли.
;-------------------------умножение mov bx, 4 mov ax, 3 mul bx invoke wsprintf, ADDR buf, ADDR ifmt, eax invoke WriteConsoleA, stdout, ADDR buf, BSIZE, ADDR cWritten, 0 invoke ExitProcess,0 end start
Думаю, что здесь тоже все понятно и без комментариев. Как производиться умножение в Assembler вы тоже можете прочитать чуть выше, ну и результат выводим на экран.
Просмотр консоли
Этот код я поместил в файл seventh.asm, сам файл поместил в папку BIN (она появляется при установке MASM32). Далее открыл консоль, как и всегда, с помощью команды cd перешел в эту папку и прописал amake.bat seventh. Скомпилировалось, затем запускаю исполняемый файл и в консоли получаются такие числа:
Как видите, мы правильно посчитали эти операции.
На этом сегодня все! Надеюсь вы научились выполнять деление и умножение на Assembler.
Скачать исходники
Команда MUL
|
Помощь в технических вопросах
Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. Подробнее… |
|
Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. |
Инструкция MUL в Ассемблере выполняет умножение без знака. Понять работу команды MUL несколько сложнее, чем это было для команд, рассмотренных ранее. Но, надеюсь, что я помогу вам в этом разобраться.
Итак, синтаксис команды MUL такой:
MUL ЧИСЛО
Выглядит всё очень просто. Однако эта простота обманчива.
Прежде чем разобраться в подробностях работы этой инструкции, давайте посмотрим, что может быть ЧИСЛОМ.
ЧИСЛОМ может быть один из следующих:
- Область памяти (MEM)
- Регистр общего назначения (REG)
Эта команда не работает с сегментными регистрами, а также не работает непосредственно с числами. То есть вот так
То есть вот так
MUL 200 ; неправильно
делать нельзя.
А теперь алгоритм работы команды MUL:
- Если ЧИСЛО — это БАЙТ, то AX = AL * ЧИСЛО
- Если ЧИСЛО — это СЛОВО, то (DX AX) = AX * ЧИСЛО
Вот такая немного сложноватая команда. Хотя сложно это с непривычки. Сейчас мы разберём всё “по косточкам” и всё станет ясно.
Для начала обратите внимание, что инструкция MUL работает либо с регистром АХ, либо с регистром AL. То есть перед выполнением этой команды нам надо записать в регистр АХ или в регистр AL значение, которое будет участвовать в умножении. Сделать это можно, например, с помощью уже известной нам команды MOV.
Затем мы выполняем умножение, и получаем результат либо в регистр АХ (если ЧИСЛО — это
байт), либо в пару регистров DX и AX (если ЧИСЛО — это слово). Причём в последнем
случае в регистре DX будет старшее слово, а в регистре AX — младшее.
А теперь, чтобы совсем всё стало понятно, разберём пару примеров — с байтом и словом.
Итак, например, нам надо умножить 150 на 250. Тогда мы делаем так:
MOV AL, 150 ; Первый множитель в регистр AL MOV BL, 250 ; Второй множитель в регистр BL MUL BL ; Теперь АХ = 150 * 250 = 37500
Обратите внимание, что нам приходится два раза использовать команду MOV, так как команда MUL не работает непосредственно с числами, а только с регистрами общего назначения или с памятью.
После выполнения этого кода в регистре АХ будет результат умножения чисел 150 и 250, то есть число 37500 (927С в шестнадцатеричной системе).
Теперь попробуем умножить 10000 на 5000.
MOV AX, 10000 ; Первый множитель в регистр AX MOV BX, 5000 ; Второй множитель в регистр BX MUL BX ; Теперь (DX АХ) = 10000 * 5000 = 50000000
В результате мы получили довольно большое число, которое, конечно, не поместится в
слово.
Если не верите — может перевести всё это в двоичное число и проверить.
Теперь о флагах.
После выполнения команды MUL состояния флагов ZF, SF, PF, AF не определены и могут быть любыми.
А если старшая секция результата (регистр AH при умножении байтов или регистр DX при умножении слов) равна нулю, то
CF = OF = 0
Иначе эти флаги либо не равны, либо равны 1.
В конце как обычно расскажу, почему эта команда ассемблера называется MUL.
Это сокращение от английского слова MULTIPLY, которое можно перевести как “умножить, умножать”.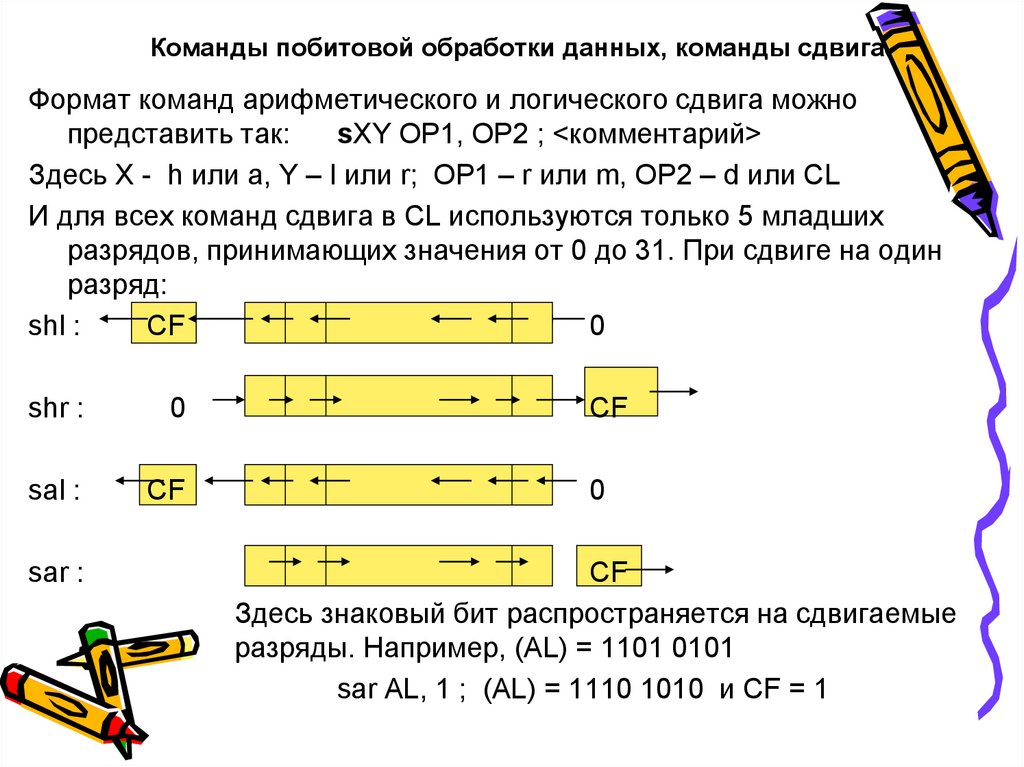
|
Подписаться на Дзен-канал
Вступить в группу «Основы программирования» Подписаться на рассылки по программированию |
|
Первые шаги в программирование
Главный вопрос начинающего программиста – с чего начать? Вроде бы есть желание, но иногда «не знаешь, как начать думать, чтобы до такого додуматься». У человека, который никогда не имел дело с информационными технологиями, даже простые вопросы могут вызвать большие трудности и отнять много времени на решение. Подробнее… |
Умножение и деление в ассемблере.
Умножение и деление в ассемблере. — it-black.ru Все мы знаем со школы что такое умножение и деление и конечно же в ассемблере эти команды присутствуют, и я расскажу Вам о них. В ассемблере умножение и деление для положительных и отрицательных чисел выполняются по-разному.
В ассемблере умножение и деление для положительных и отрицательных чисел выполняются по-разному.
Умножение положительных чисел
Для умножения положительных чисел в ассемблере предназначена команда “MUL”. У этой команды только один операнд — второй множитель, который должен находиться в регистре или в памяти. Местоположение первого множителя и результата задаётся неявно и зависит от размера операнда:
| Размер операнда | Множитель | Результат |
|---|---|---|
| Байт | AL | AX |
| Слово | AX | DX:AX |
Некоторые тонкости умножения:
- Если аргументом команды mul является 1-байтовый регистр (например mul bl), то значение этого регистра bl умножится на значение регистра al, а результат запишется в регистр ax, и так будет всегда, независимо от того, какой 1-байтовый регистр взять.
 bl*al = ax
bl*al = ax - Если аргументом является регистр из 2 байт (например mul bx), то значение в регистре bx умножится на значение, хранящееся в регистре ax, а результат умножения запишется в регистр eax. bx*ax = eax
- Если аргументом является регистр из 4 байт (например mul ebx), то значение в регистре ebx умножится на значение, хранящееся в регистре eax, а результат умножения запишется в 2 регистра: edx и eax. ebx*eax = edx:eax
Умножение отрицательных чисел
Для умножения чисел со знаком предназначена команда “IMUL”. Эта команда имеет три формы, различающиеся количеством операндов:
- С одним операндом — форма, аналогичная команде MUL. В качестве операнда указывается множитель. Местоположение другого множителя и результата определяется по таблице.
- С двумя операндами — указываются два множителя. Результат записывается на место первого множителя. Старшая часть результата в этом случае игнорируется. Эта форма команды не работает с операндами размером 1 байта.

- С тремя операндами — указывается положение результата, первого и второго множителя. Второй множитель должен быть непосредственным значением. Результат имеет такой же размер, как первый множитель, старшая часть результата игнорируется. Это форма тоже не работает с однобайтными множителями.
Деление положительных чисел
Деление целых двоичных чисел — это всегда деление с остатком. По аналогии с умножением, размер делителя, частного и остатка должен быть в 2 раза меньше размера делимого. Деление положительных чисел осуществляется с помощью команды “DIV”. У этой команды один операнд — делитель, который должен находиться в регистре или в памяти. Местоположение делимого, частного и остатка задаётся неявно и зависит от размера операнда:
| Размер операнда (делителя) | Делимое | Частное | Остаток |
|---|---|---|---|
| Байт | AX | AL | AH |
| Слово | DX:AX | AX | DX |
Некоторые тонкости деления:
- Если аргументом команды div является 1-байтовый регистр (например div bl), то значение регистра ax поделится на значение регистра bl, результат от деления запишется в регистр al, а остаток запишется в регистр ah.
 ax/bl = al, ah
ax/bl = al, ah - Если аргументом является регистр из 2 байт (например div bx), то процессор поделит число, старшие биты которого хранит регистр dx, а младшие ax на значение, хранящееся в регистре bx. Результат от деления запишется в регистр ax, а остаток запишется в регистр dx. (dx,ax)/bx = ax, dx
- Если аргументом является регистр из 4 байт (например div ebx), то процессор аналогично предыдущему варианту поделит число, старшие биты которого хранит регистр edx, а младшие eax на значение, хранящееся в регистре ebx. Результат от деления запишется в регистр eax, а остаток запишется в регистр edx. (edx,eax)/ebx = eax, edx
Деление отрицательных чисел
Для деления отрицательных чисел предназначена команда IDIV. Единственным операндом является делитель. Местоположение делимого и частного определяется также, как для команды DIV. Эта команда также генерирует прерывание при делении на ноль или слишком большом частном.
Поделиться в facebook
Поделиться в twitter
Поделиться в vk
VK
Поделиться в google
Google+
Группа в VK
Помощь проекту
Обнаружили опечатку?
Сообщите нам об этом, выделите текст с ошибкой и нажмите Ctrl+Enter, будем очень признательны!
Свежие статьи
Облако меток
Похожие статьи
Команды работы с битами.

Работать с отдельными битами операндов можно, используя логические операции и сдвиги. Также в системе команд x86 существуют специальные команды для работы с битами: это команды
Основы создания макросов в Assembler.
Макросы — это шаблоны для генерации кода. Один раз создав макрос, можно использовать его во многих местах в коде программы. Макросы делают процесс программирования на
Синтаксис объявления меток.
Метка в ассемблере – это символьное имя, обозначающее ячейку памяти, которая содержит некоторую команду. Метка может содержать следующие символы: Буквы (от A до Z и
Локальные переменные.
Локальные переменные в Assembler используются для хранения промежуточных результатов во время выполнения процедуры. В отличие от глобальных, эти переменные являются временными и создаются при запуске
Instagram Vk Youtube Telegram Odnoklassniki
Полезно знать
Рубрики
Авторы
© it-black.
 ru | 2016 — 2022
ru | 2016 — 2022
Assembler: div & mul. Приветствуем всех! С вами команда IT… | by ITRoot Corp
Приветствуем всех! С вами команда IT Root, и сегодня в планах у нас команды div и mul
- Для умножения в Assembler используют команду MUL
- Для деления в Assembler используют команду DIV
Умножение в Assembler
Для умножения чисел без знака предназначена команда MUL. У этой команды только один операнд — второй множитель, который должен находиться в регистре или в памяти. Местоположение первого множителя и результата задаётся неявно и зависит от размера операнда:
Отличие умножения от сложения и вычитания в том, что разрядность результата получается в 2 раза больше, чем разрядность сомножителей. Также и в десятичной системе — например, умножая двухзначное число на двухзначное, мы можем получить в результате максимум четырёхзначное. Запись «DX:AX» означает, что старшее слово результата будет находиться в DX, а младшее — в AX.
Если старшая часть результата равна нулю, то флаги CF и ОF будут иметь нулевое значение. В этом случае старшую часть результата можно отбросить. Это свойство можно использовать в программе, если результат должен быть такого же размера, как множители.
Если аргументом команды MUL является 1-байтовый регистр (например MUL bl), то значение этого регистра bl умножится на значение регистра al, а результат запишется в регистр ax, и так будет всегда, независимо от того, какой 1-байтовый регистр мы возьмем.
al * bl = ax;
Если аргументом является регистр из 2 байт(например MUL bx), то значение в регистре bx умножится на значение, хранящееся в регистре ax, а результат умножения запишется в регистр eax.
bx * ax = dx:ax
Если аргументом является регистр из 4 байт(например MUL ebx), то значение в регистре ebx умножится на значение, хранящееся в регистре eax, а результат умножения запишется в 2 регистра: edx и eax.
ebx * eax = edx:eax
Деление в Assembler
Для умножения чисел без знака предназначена команда DIV, которая относится к группе команд целочисленной арифметики и производит целочисленное деление с остатком беззнаковых целочисленных операндов.
Делимое, частное и остаток задаются неявно. Делимое является переменной в регистре (или регистровой паре) AX, DX:AX или EDX:EAX в зависимости от кода команды и размера операнда (что также определяет и разрядность делителя). Единственный явный операнд команды — операнд-источник (SRC), задающий делитель — может быть переменной в регистре или в памяти.
Целая часть частного помещается в регистр AL, AX или EAX в зависимости от заданного размера делителя (8, 16 или 32 бита). При этом остаток от целочисленного деления помещается в регистр AH, DX или EDX соответственно.
Действие команды DIV зависит от размера операнда-источника следующим образом:
Если частное, получаемое в результате деления, оказывается слишком велико, чтобы поместиться в целевом регистре-назначении (то есть имеет место переполнение), или если делитель равен нулю, то генерируется особая ситуация #DE.
Если аргументом команды div является 1-байтовый регистр (например DIV bl), то значение регистра ax поделится на значение регистра bl, результат от деления запишется в регистр al, а остаток запишется в регистр ah.
ax / bl = al:ah
Если аргументом является регистр из 2 байт(например DIV bx), то процессор поделит число, старшие биты которого хранит регистр dx, а младшие ax на значение, хранящееся в регистре bx. Результат от деления запишется в регистр ax, а остаток запишется в регистр dx.
(dx:ax) / bx = ax:dx
Если же аргументом является регистр из 4 байт(например DIV ebx), то процессор аналогично предыдущему варианту поделит число, старшие биты которого хранит регистр edx, а младшие eax на значение, хранящееся в регистре ebx. Результат от деления запишется в регистр eax, а остаток запишется в регистр edx.
Результат от деления запишется в регистр eax, а остаток запишется в регистр edx.
(edx:eax) / ebx = eax:edx
AfterWord
На этой ноте пост подходит к концу. Теперь вы знаете про команды умножения и деления в Assembler. В одном из следующих постов мы разберём умножение и деление чисел со знаком. Спасибо за внимание и до скорых встреч!)
Не забывайте, что множество интересных статей можно найти на нашем Telegram канале и в Telegram боте, также все статьи мы публикуем в Twitter и Facebook
Лекция 7. Арифметические команды языка Ассемблер: аддитивные и мультипликативные команды целочисленных операций.
7.1. Сложение и вычитание. 7.1.1. ADD – команда для сложения двух чисел. Она работает как с числами со знаком, так и без знака. ADD Приемник, Источник Логика работы команды: <Приемник> = <Приемник> + <Источник> Возможные
сочетания операндов для этой команды аналогичны команде MOV. По сути дела, это – команда сложения с присвоением, аналогичная принятой в языке C/C++: Приемник += Источник; Операнды должны иметь одинаковый размер. Результат помещается на место первого операнда. После выполнения команды изменяются флаги, по которым можно определить характеристики результата:
Примеры: add ax,5 ;AX = AX + 5 add dx,cx ;DX = DX + CX add dx,cl
;Ошибка: разный размер
операндов. 7.1.2. SUB — команда для вычитания одного числа из другого. Она работает как с числами со знаком, так и без знака. SUB Приемник, Источник Логика работы команды: <Приемник> = <Приемник> — <Источник> Возможные сочетания операндов для этой команды аналогичны команде MOV. По сути дела, это – команда вычитания с присвоением, аналогичная принятой в языке C/C++: Приемник -= Источник; Операнды должны иметь одинаковый размер. Результат помещается на место первого операнда. На самом деле вычитание в процессоре реализовано с помощью сложения. Процессор меняет знак второго операнда на противоположный, а затем складывает два числа. Примеры: sub ax,13 ;AX = AX — 13 sub ax,bx ;AX = AX + BX sub bx,cl ;Ошибка: разный размер операндов. 7.1.3. Инкремент и декремент. Эти команды содержит один операнд и имеет следующий синтаксис: INC Операнд DEC Операнд Логика работы команд: INC: <Операнд> = < Операнд > + 1 DEC: <Операнд> = < Операнд > — 1 В качестве инкремента допустимы регистры и память: reg, mem. Примеры: inc ax ;AX = AX + 1 dec ax ;AX = AX — 1 7.1.4. NEG – команда для изменения знака операнда. Синтаксис: NEG Операнд Логика работы команды: <Операнд> = – < Операнд > В качестве
декремента допустимы регистры и память: reg, mem. Примеры: neg ax ;AX = -AX 7.2. Сложение и вычитание с переносом. В системе команд процессоров x86 имеются специальные команды сложения и вычитания с учётом флага переноса (CF). Для сложения с учётом переноса предназначена команда ADC, а для вычитания — SBB. В общем, эти команды работают почти так же, как ADD и SUB, единственное отличие в том, что к младшему разряду первого операнда прибавляется или вычитается дополнительно значение флага CF. Они позволяют
выполнять сложение и вычитание многобайтных целых чисел, длина которых больше,
чем разрядность регистров процессора (в нашем случае 16 бит). Принцип
программирования таких операций очень прост — длинные числа складываются
(вычитаются) по частям. Младшие разряды складываются(вычитаются) с помощью
обычных команд ADD и SUB, а затем последовательно складываются(вычитаются)
более старшие части с помощью команд ADC и SBB. Так как эти команды учитывают
перенос из старшего разряда, то мы можем быть уверены, что ни один бит не
потеряется. На следующем рисунке показано сложение двух двоичных чисел командой ADD: При сложении происходит перенос из 7-го разряда в 8-й, как раз на границе между байтами. Если мы будем складывать эти числа по частям командой ADD, то перенесённый бит потеряется и в результате мы получим ошибку. К счастью, перенос из старшего разряда всегда сохраняется в флаге CF. Чтобы прибавить этот перенесённый бит, достаточно применить команду ADC:
Пример: #include <iostream.h> #include <iomanip.h> void main() { //Сложение двух чисел с учетом переноса: FFFFFFAA + FFFF int a, b; asm { mov eax, 0FFFFFFAAh mov ebx, 0FFFFh mov edx, 0 mov ecx, 0 add eax, ebx adc edx, ecx mov a, edx mov b, eax } cout << hex << a << setw(8) << setfill(‘0’) << b; //10000ffa9 } 7. 7.3.1. MUL – команда умножения чисел без знака. У этой команды только один операнд — второй множитель, который должен находиться в регистре или в памяти. Местоположение первого множителя и результата задаётся неявно и зависит от размера операнда:
Отличие умножения
от сложения и вычитания в том, что разрядность результата получается в 2 раза
больше, чем разрядность сомножителей. Примеры: mul bl ;AX = AL * BL mul ax ;DX:AX = AX * AX Если старшая часть результата равна нулю, то флаги CF и ОF будут иметь нулевое значение. В этом случае старшую часть результата можно отбросить. 7.3.2. IMUL – команда умножения чисел со знаком. Эта команда имеет три формы, различающиеся количеством операндов: 1. С одним операндом — форма, аналогичная команде MUL. В качестве операнда указывается множитель. Местоположение другого множителя и результата определяется по таблице. 2. С двумя операндами — указываются два множителя. Результат записывается на место первого множителя. Старшая часть результата в этом случае игнорируется. Кстати, эта форма команды не работает с операндами размером 1 байт. 3. С тремя операндами — указывается
положение результата, первого и второго множителя. Второй множитель должен быть
непосредственным значением. Результат имеет такой же размер, как первый
множитель, старшая часть результата игнорируется. Примеры: imul cl ;AX = AL * CL imul bx,ax ;BX = BX * AX imul cx,-5 ;CX = CX * (-5) imul dx,bx,134h ;DX = BX * 134h CF = OF = 0, если произведение помещается в младшей половине результата, иначе CF = OF = 1. Для второй и третьей формы команды CF = OF = 1 означает, что произошло переполнение. 7.3.3. DIV – команда деления чисел без знака. У этой команды один операнд — делитель, который должен находиться в регистре или в памяти. Местоположение делимого, частного и остатка задаётся неявно и зависит от размера операнда:
При выполнении команды DIV может возникнуть прерывание (в данном курсе прерывания мы рассматривать не будем поэтому старайтесь избегать таких случаев):
Примеры: div cl ;AL = AX / CL, остаток в AH div di ;AX = DX:AX / DI, остаток в DX 7.3.4. IDIV – команда деления чисел со знаком. Единственным операндом является делитель. Местоположение делимого и частного определяется также, как для команды DIV. Эта команда тоже генерирует прерывание при делении на ноль или слишком большом частном. 7.3.5. NOP – ничего не делающая команда. Синтаксис: NOP Примеры: nop
Пример. (5 + 8) / (2 * 3) #include <iostream.h> void main() { asm { mov bx, 5 //BL = 5 add bx, 8 //BL = BL + 8 | 13 sub bx, 1 //BL = BL — 1 | 12 mov al, 2 //AL = 2 mov cl, 3 //CL = 3 mul cl //AX = AL * CL | 6 //AX = 6, BL = 12 xchg bx, ax //AX = 12, BX = 6 mov dx, 0 div bx } }
|
1.
 1.5 Беззнаковое умножение: Команда mul
1.5 Беззнаковое умножение: Команда mulКоманда MUL умножает беззнаковые числа.
Пример:
n db 10
. . .
mov al,2
mul n ;ax=2*10=20=0014h: ah=00h al=14h
mov al,26
mul n ;ax=26*10=260=0104h: ah=01h al=04h
1.1.6 Знаковое умножение: Команда imul
Команда IMUL умножает знаковые числа.
mov ax,8
mov bx,-1
imul bx ; dx:ax=-8=0fffffff8h=0014h: dx=0ffffh ax=0fff8h
Таким образом, если множимое и множитель имеет одинаковый знаковый бит, то команды MUL и IMUL генерируют одинаковый результат. Но, если сомножители имеют разные знаковые биты, то команда MUL вырабатывает положительный результат умножения, а команда IMUL — отрицательный.
Повышение
эффективности умножения: При умножении
на степень числа 2 (2,4,8 и т. д.) более
эффективным является сдвиг влево на
требуемое число битов. Сдвиг более чем
на 1 требует загрузки величины сдвига
в регистр CL. В следующих примерах
предположим, что множимое находится в
регистре AL или AX:
д.) более
эффективным является сдвиг влево на
требуемое число битов. Сдвиг более чем
на 1 требует загрузки величины сдвига
в регистр CL. В следующих примерах
предположим, что множимое находится в
регистре AL или AX:
Умножение на 2: shl ax,1
Умножение на 8: mov ax,3
Shl ax,cl
1.1.7 Многословное умножение
Обычно умножение имеет два типа: «байт на байт» и «слово на слово». Как уже было показано, максимальное знаковое значение в слове ограничено величиной +32767. Умножение больших чисел требует выполнения некоторых дополнительных действий. Рассматриваемый подход предполагает умножение каждого слова отдельно и сложение полученных результатов.
Рассмотрим следующее умножение в десятичном формате:
1365
х12
2730
1365
16380
Представим, что
десятичная арифметика может умножать
только двухзначные числа. Тогда можно
умножить 13 и 65 на 12 раздельно, следующим
образом:
Тогда можно
умножить 13 и 65 на 12 раздельно, следующим
образом:
13 65
х12 х12
26 130
13 65
156 780
Следующим шагом сложим полученные произведения, но поскольку число 13 представляло сотни, то первое произведение в действительности будет 15600:
15600
+780
16380
Ассемблерная программа использует аналогичную технику за исключением того, что данные имеют размерность слов (четыре цифры) в шестнадцатеричном формате.
Умножение двойного
слова на слово (z=x*y).
X dd ?
Y dw ?
Z dw ? , ? , ?
. . .
wp equ word ptr
mov ax,wp x ;
mul y
mov z,ax
mov bx,dx
mov ax,wp x+2
mul y
add ax,bx
mov z+2,ax
adc dx,0
mov z+4,dx
1.1.8 Деление
Операция деления для беззнаковых данных выполняется командой DIV, a для знаковых — IDIV. Ответственность за подбор подходящей команды лежит на программисте. Существуют две основные операции деления:
Деление «слова
на байт». Делимое находится в регистре
AX, а делитель — в байте памяти или в
однобайтовом регистре. После деления
остаток получается в регистре AH, а
частное -в AL. Так как однобайтовое
частное очень мало (максимально+255
(шест.FF) для беззнакового деления и +127
(шест. 7F) для знакового), то данная операция
имеет ограниченное использование.
7F) для знакового), то данная операция
имеет ограниченное использование.
Деление «двойного слова на слово». Делимое находится в регистровой паре DX:AX, а делитель — в слове памяти или в регистре. После деления остаток получается в регистре DX, а частное в регистре AX. Частное в одном слове допускает максимальное значение +32767 (шест.FFFF) для беззнакового деления и +16383 (шест.7FFF) для знакового.
В единственном операнде команд DIV и IDIV указывается делитель. Рассмотрим следующую команду:
div divisor
Если поле DIVISOR определено как байт (DB), то операция предполагает деление слова на байт. Если поле DIVISOR определено как слово (DW), то операция предполагает деление двойного слова на слово.
При делении,
например, 13 на 3, получается результат
4 1/3. Частное есть 4, а остаток — 1.
Заметим, что ручной калькулятор (или
программа на языке BASIC) выдает в этом
случае результат 4,333. … Значение содержит
целую часть (4) и дробную часть (,333).
Значение 1/3 и 333… есть дробные части, в
то время как 1 есть остаток от деления.
… Значение содержит
целую часть (4) и дробную часть (,333).
Значение 1/3 и 333… есть дробные части, в
то время как 1 есть остаток от деления.
x86 — функция MUL в ассемблере
Они называются инструкциями и определяют операции , которые должны выполняться процессором. mov — это мнемоника для mov e, а mul — мнемоника для mul tiply. Другие общие инструкции включают добавить , sub и div . Я надеюсь, вы сможете понять, какую операцию они определяют!
Большинство инструкций принимают два параметра. На техническом жаргоне их часто называют 9.0003 операндов . Первый (слева) — это пункт назначения , а второй (справа) — источник . Таким образом, в случае mov bx, 5 это перемещает буквальное значение 5 в регистр назначения bx . Порядок этих параметров, конечно, имеет значение, потому что вы не можете переместить содержимое регистра bx в буквальное значение 5 !
Инструкция mul немного странная, потому что некоторые из ее операндов являются неявными. То есть они явно не указаны как параметры. Для
То есть они явно не указаны как параметры. Для mul , операнд назначения жестко запрограммирован как регистр x . Исходный операнд — это тот, который вы передаете в качестве параметра: это может быть либо регистр, либо ячейка памяти.
Таким образом, вы можете представить, что mul cx означает mul ax, cx , но вы не напишите это так, потому что регистр назначения ax является неявным.
Теперь инструкция mul дает процессору команду умножить операнд-адресат на операнд-источник и сохранить результат в адресате. В коде вы можете представить, что mul cx преобразуется в ax = ax * cx . И теперь вы должны увидеть проблему: вы не инициализировали содержимое регистра x , поэтому вы умножаете 10 (значение, которое вы поместили в cx ) на тот мусор, который остался в x . Таким образом, результат бессмысленен!
Если вы действительно хотите сделать 5 * 10, то вам достаточно изменить один символ в вашем коде:
mov ax, 5 ; топор = 5 мов сх, 10 ; сх = 10 мул сх ; топор = топор * сх; на самом деле dx:ax = ax * cx
Результат будет сохранен в x , который является неявным регистром назначения.
Ну, технически результат будет сохранен в dx:ax . Это пара регистров , и это означает, что старшая часть результата будет сохранена в dx , а младшая часть результата будет сохранена в x . Зачем это дополнительное усложнение? Потому что умножение двух 16-битных значений может привести к значению, превышающему 16 бит! Возврат полного результата умножения в 9Пара 0003 16-битных регистров позволяет инструкции mul возвращать 32-битный результат. Однако, когда вы только учитесь, вам не нужно беспокоиться об этом. Вы можете просто игнорировать возможность переполнения и извлечь нижнюю часть результата из x . (Но помните, что 16-битный mul перезаписывает dx , хотите вы этого или нет. На 386 и более поздних версиях вы можете использовать imul axe, cx , чтобы действительно сделать ax *= cx , не тратя время на запись dx .)
И хотя я уверен, что это всего лишь игрушечный пример, на самом деле нет причин писать код , который умножает две константы вместе. Это можно сделать во время сборки, либо используя калькулятор и жестко закодировав значение, либо записав умножение констант символически и позволив вашему ассемблеру выполнить вычисления. То есть
Это можно сделать во время сборки, либо используя калькулятор и жестко закодировав значение, либо записав умножение констант символически и позволив вашему ассемблеру выполнить вычисления. То есть mov ax, 50 . Или пусть ваш ассемблер сделает это за вас с mov ax, 5 * 10 . Но, как я уже сказал, я уверен, что вы уже знали это!
Если ничего не помогло, обратитесь к документации за инструкциями, которые вызывают у вас затруднения. Вы почти всегда можете найти это в Интернете, погуглив название инструкции и «x86». Например, документацию по mul можно найти здесь, а также на нескольких других сайтах. Эта информация может быть довольно сложной, но, приложив немного усилий, вы сможете извлечь нужную информацию. Вы также найдете много другой полезной информации и ссылок в вики по тегам x86.
, но по какой-то причине я не вижу изменения регистров, когда отмечена функция MUL.
Я также должен отметить, что если вы используете отладчик для пошагового выполнения вашего кода, текущая помеченная/выделенная строка — это строка, которая около для выполнения. Он еще не выполнен, поэтому его влияние на регистры, память и т. д. еще не будет видно. Вы должны перешагнуть инструкцию, чтобы метка/выделение было на следующей строке, и тогда вы увидите эффекты предыдущей (только что выполненной) инструкции.
Он еще не выполнен, поэтому его влияние на регистры, память и т. д. еще не будет видно. Вы должны перешагнуть инструкцию, чтобы метка/выделение было на следующей строке, и тогда вы увидите эффекты предыдущей (только что выполненной) инструкции.
Если вы поняли мое объяснение выше, после инструкции mul вы должны увидеть изменение содержимого регистров ax и dx . Вы также увидите изменение флагов и указателя инструкций, если ваш отладчик показывает какой-либо из них. Больше ничего не должно измениться! (Запись справочного руководства по инструкциям Intel для mul не перечисляет никаких других эффектов, влияющих на архитектурное состояние машины.)
Возможно ли умножение на непосредственное с mul в сборке x86?
спросил
Изменено 3 месяца назад
Просмотрено 50 тысяч раз
Часть коллектива Intel
Изучаю сборку для x86 с помощью эмулятора DosBox. Я пытаюсь выполнить умножение. Я не понимаю, как это работает. Когда я пишу следующий код:
Я пытаюсь выполнить умножение. Я не понимаю, как это работает. Когда я пишу следующий код:
м-н ал, 3 мул 2
Я получаю сообщение об ошибке. Хотя в справочнике, который я использую, говорится, что при умножении предполагается, что AX всегда является заполнителем, поэтому, если я напишу:
mul, 2
Умножает значение al на 2. Но у меня не работает.
Когда я пытаюсь сделать следующее:
mov al, 3 муль ал,2 целое 3
Я получаю результат 9 по оси. Смотрите эту картинку для пояснения:
Еще вопрос: Могу ли я умножать напрямую, используя ячейку памяти? Пример:
мов си, 100 мул [си],5
- сборка
- x86
- dos
- умножение
- непосредственный операнд
2
Не существует формы MUL , которая принимает непосредственный операнд.
Либо:
mov al,3 мов бл,2 мул бл ; продукт в топоре
или (требуется 186 для imul-immediate):
mov ax,3
имул топор,2 ; imul для умножения со знаком, но младшая половина такая же
; продукт в топоре. дх не изменен
дх не изменен
или:
мов ал,3 добавить аль, аль; то же самое, что умножить на 2
или:
мов ал,3 шл ал,1 ; то же самое, что умножить на 2
2
Руководство Intel
Руководство разработчика программного обеспечения для архитектур Intel 64 и IA-32 — Том 2 Справочник по набору инструкций — 325383-056US Сентябрь 2015 г.
раздел «MUL — Unsigned Multiply», столбец . Инструкция содержит только:
МУЛ р/м8 МУЛ р/м8* МУЛ р/м16 МУЛ р/м32 МУЛ р/м64
r/mXX означает регистр или память: поэтому непосредственные ( immXX ), такие как mul 2 , не допускаются ни в одной из форм: процессор просто не поддерживает эту операцию.
Это также отвечает на второй вопрос: можно ли умножать на память:
x:dd 0x12341234 мов акс, 2 многозначное двойное слово [x] ; еакс == 0x24682468
А также показывает, почему такие вещи, как mul al,2 , не будут работать: не существует формы, принимающей два аргумента.
Однако, как упоминал Майкл, imul имеет непосредственные формы, такие как IMUL r32, r/m32, imm32 и многие другие, которых нет у mul .
Непосредственного мул нет, но есть нерасширяемый имул -непосредственный в 186 и новее, и имул рег, р/м в 386 и новее. См. Ответ @phuclv о проблеме с пониманием инструкций mul и imul языка ассемблера для более подробной информации и, конечно же, справочные руководства по набору инструкций Intel для mul и imul:
- https://www.felixcloutier.com/x86/imul — расширение с одним операндом, восходящее к 8086, и более новые более эффективные и удобные формы, которые не используют DX:AX в качестве неявного адресата.
- https://www.felixcloutier.com/x86/mul — единственная форма расширения с одним операндом, существовавшая с 8086
Нет адресата памяти mul или imul даже на новейших процессорах.
Есть imul cx,[si],5 если хотите, правда, на 186 и новее, для 16-битного размера операнда и шире. А на 386 тоже
А на 386 тоже имул ди, [си] .
Но эти новые формы imul не существуют для 8-битного размера операнда, поэтому не существует imul cl, [si], 5 .
На 386 или новее обычно более эффективно использовать LEA для умножения на простую константу, хотя это требует немного больше размера кода.
; предполагая 16-битный режим
мов сх, [си] ; или лучше movzx ecx, слово [si] на более новых процессорах
lea cx, [ecx + ecx*4] ; СХ *= 5
Признано IntelТвой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
c — Эффективное умножение на ассемблере
Интересная часть этого упражнения — поиск способов использования 1 или 2 инструкций LEA, SHL и/или ADD/SUB для реализации умножения на различные константы.
На самом деле диспетчеризация на лету для одного умножения не очень интересна и будет означать либо фактическую JIT-компиляцию, либо то, что у вас уже есть все возможные последовательности в гигантской таблице крошечных блоков кода. (Например, операторы switch .)
Вместо этого я бы предложил написать C или Python или любую другую функцию, которая принимает 1 целочисленный аргумент, а на выходе выдает исходный текст asm, который реализует x * n , где n целочисленный аргумент. , то есть функция, которую вы можете найти в компиляторе, оптимизирующем умножение на константу.
Возможно, вы захотите придумать автоматизированный способ проверки этого, например. путем сравнения с чистым C x * n для пары разных значений x .
Если вы не можете выполнить работу за 2 инструкции (или 3, одна из которых mov ), она того не стоит . Современный x86 имеет смехотворно эффективное аппаратное умножение.
имул рег, р/м, имм — 1 мкп, задержка 3 цикла, полностью конвейерная. (AMD с Zen, Intel с Core2 или Nehalem или около того.) Это ваш запасной вариант для всего, что вы не можете сделать с длиной критического пути в 1 или 2 цикла (при условии, что перемещение с нулевой задержкой, если хотите, например, IvyBridge+ и Zen .)
Или вы можете установить более высокий порог перед откатом, если хотите исследовать более сложные последовательности, например. стремитесь к 64-битному умножению на семействе Bulldozer (задержка 6 циклов). https://agner.org/optimize/. Или даже P5 Pentium где imul занимает 9 циклов (не парные).
Образцы для поиска
Целочисленное умножение сводится к суммированию смещенных копий 1 операнда, где другой операнд имеет 1 бит. (См. алгоритм реализации умножения на значения переменных времени выполнения, путем сдвига и добавления, проверяющих каждый бит по одному.)
Самый простой шаблон, конечно, состоит только из одного установленного бита, т.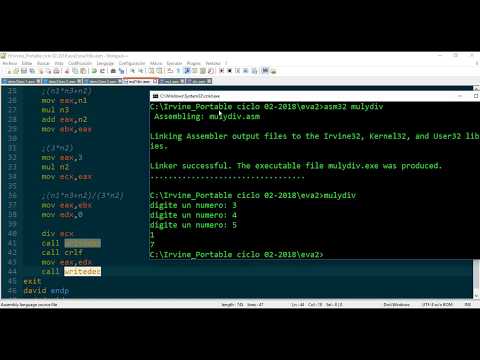 е. степени числа 2; то это просто сдвиг влево. Это легко проверить:
е. степени числа 2; то это просто сдвиг влево. Это легко проверить: n & (n-1) == 0 , когда n != 0 .
Все, что содержит ровно 2 установленных бита, представляет собой не более 2 сдвигов и добавление. (GNU C __builtin_popcount(n) подсчитывает установленные биты. В x86 asm, SSE4.2 popcnt ).
GNU C __builtin_ctz находит битовый индекс самого младшего установленного бита. Используя его для числа, которое, как вы знаете, не равно нулю, вы получите количество сдвигов для младшего бита. В x86 asm, bsf / tzcnt .
Чтобы очистить этот младший установленный бит и «открыть» следующий младший, вы можете сделать 9n — 1 способ:
mul15: # gcc -O3 -mtune=bdver2
мов акс, эди
Сал Эакс, 4
суб акс, эди
рет
clang более эффективен (для процессоров Intel, где масштабируемый индекс по-прежнему составляет всего 1 цикл):
mul15: # clang -O3 -mtune=bdver2
lea eax, [rdi + 4*rdi]
lea eax, [rax + 2*rax]
рет
Комбинирование этих шаблонов
Может быть, разложите свое число на простые множители и поищите способы использовать свои строительные блоки для создания комбинаций этих множителей.
Но это не единственный подход. Вы можете сделать x*11 как x*5*2 + x , как это делают GCC и Clang (что очень похоже на Как умножить регистр на 37, используя только 2 последовательных инструкции в x86?)
lea eax, [rdi + 4*rdi]
lea eax, [rdi + 2*rax]
Есть 2 подхода и для x*17. GCC и Clang делают это так:
mul17:
мов акс, эди
Сал Эакс, 4
добавить eax, edi
рет
Но есть еще один способ, который они не используют даже с -march=sandybridge (без перемещения-устранения, 1-цикл LEA [reg + reg*scale] ):
mul17:
lea eax, [rdi + 8*rdi] ; х*9
lea eax, [rax + 8*rdi] ; х*9 + х*8 = х*17
Итак, вместо умножения множителей мы добавляем разные множители, чтобы получить общий множитель.
У меня нет хороших предложений, как программно искать эти последовательности, кроме простых, таких как 2 установленных бита или 2 ^ n +- 1. Если вам интересно, посмотрите исходный код GCC или LLVM. для функций, выполняющих эти оптимизации; найти много хитрых из них.
Если вам интересно, посмотрите исходный код GCC или LLVM. для функций, выполняющих эти оптимизации; найти много хитрых из них.
Работа может быть разделена между нейтральными к цели проходами оптимизации для степеней двойки и целевым кодом, специфичным для x86, для использования LEA, а также для определения порога того, сколько инструкций стоит перед возвратом к imul -немедленно .
Отрицательные числа
x * -8 можно сделать с помощью x - x*9 . Я думаю, что может быть безопасным, даже если x * 9 переполняется, но вам придется перепроверить это.
#define MULFUN(c) int mul##c(int x) { return x*c; }
МУЛФУН(9)
МУЛФУН(10)
МУЛФУН(11)
МУЛФУН(12)
...
Я поместил это в обозреватель компилятора Godbolt для x86-64 System V ABI (первый аргумент в RDI, как в приведенных выше примерах). С помощью gcc и clang -O3. Я использовал -mtune=bdver2 (Piledriver), потому что умножение несколько медленнее, чем у Intel или Zen. Это побуждает GCC и Clang более агрессивно избегать
Это побуждает GCC и Clang более агрессивно избегать imul .
не пробовал если длинный / uint64_t изменит это (задержка 6 циклов вместо 4 и вдвое уменьшит пропускную способность). -mtune=bdver2 имеет ли значение по сравнению с по умолчанию tune=generic по крайней мере для GCC.
Если вы используете -m32 , вы можете использовать даже более старые версии uarch, такие как -mtune=pentium (в порядке P5). Я бы рекомендовал -mregparm=3 для этого, чтобы аргументы по-прежнему передавались в регистрах, а не в стеке.
8086 Инструкции по умножению целых чисел — программирование на языке ассемблера
В этом руководстве мы увидим инструкции умножения, поддерживаемые микропроцессором 8086, такие как инструкции умножения со знаком и без знака. В последнем уроке мы обсудили инструкции сложения и вычитания 8086.
Предыдущие учебные пособия в этой серии: 8086 Инструкции по передаче данных, 8086 Целочисленные арифметические инструкции, 8086 Режимы адресации микропроцессора
Соглашение о таблице
8086 Инструкции по умножению
Инструкции по умножению включают в себя:
- MUL
- IMUL
- AAM
8086 UNSGINED INTERCATION).
 Существуют виды умножения в зависимости от количества битов:
Существуют виды умножения в зависимости от количества битов:- Байт на байт
- Слово на слово
- Байт на слово
Байт с байтовым умножением: В этом умножении один операнд находится в регистре AL, а другой является исходным. Источником может быть регистр или адрес памяти.
Например:
MUL BL ;умножить данные в Bl на AL MUL 10[CL] ;Умножить данные, хранящиеся по адресу смещения CL+10, на данные в AL
Пример ассемблерного кода 1
Предположим, вы хотите умножить 35 на 15. Умножение 35 на 15 дает 525, шестнадцатеричное значение которого равно 20D. Результат сохраняется в регистре AX.
ОРГ 100ч .КОД МОВ АЛ, 35 МОВ БГ, 15 МУЛ ЧД РЕТ
Вывод:
Слово с умножением слов
В этом умножении один операнд загружается в регистр AX, а источником должен быть 16-битный регистр или адрес памяти. Два 16-битных слова при умножении могут дать 32-битное слово. Таким образом, в этом случае младшие байты слова хранятся в регистре AX, а старшие байты — в регистре DX.
Пример кода сборки
ORG 100h .МОДЕЛЬ МАЛЕНЬКАЯ .ДАННЫЕ VAR_1 DW 12DAH VAR_2 ДВ 3F24H .КОД MOV AX, VAR_1 MOV BX, VAR_2 МУЛ БХ РЕТ
Адрес VAR_2 — 0004h. Вы также можете проверить адрес по «LEA BX, VAR_2» или «MOV BX, OFFSET VAR_2». Обе команды дают адрес в регистре BX. Инструкция «MUL 20[VAR_2]» умножает содержимое по адресу памяти 0118h (0004h +14h) на AX, т. е. 90C3 x 12DA дает AA8 FC0E. FC0E переходит в регистр AX, а DX сохраняет AA8. Мы зарезервировали восемь байтов для смещения RES. При использовании команды MOV окончательный результат сохраняется в этих зарезервированных байтах.
Байт с умножением слов
Аналогично слову с умножением слов. Только регистр AH устанавливается в ноль, а AL загружается байтовым операндом. Результат сохраняется в регистрах DX и AX.
Пример кода ассемблера
Предположим код из примера 2. Только установите AH равным нулю. Вы можете сделать это, вычитая AH из AH или загрузив AH 0.
ORG 100h .МОДЕЛЬ МАЛЕНЬКАЯ .ДАННЫЕ VAR_1 DW 12DAH VAR_2 ДВ 3F24H RES DW 2 DUP(?); резервирует 8 байт неинициализированного пространства данных для смещения RES .КОД MOV AX,VAR_1 ;Загрузить 1-й опернд в AX СУБ АХ, АХ MUL 20[VAR_2] ;Загрузить 2-й операнд с эффективного адреса 20+VAR_2 ;умножить на AX MOV RES,AX ;копировать AX в младшие 2 байта RES MOV RES+2,DX ;копировать DX в 2 старших байта RES РЕТ
Вывод
Теперь в этом случае данные по адресу смещения 20[VAR_2] равны 0108h, поэтому операнды DA и 0108. Умножение двух операндов дает E0D0, который сохраняется в регистре AX.
8086 Singed Multiplication Instruction (IMUL)
Инструкция IMUL позволяет умножать два операнда со знаком. Операнды могут быть положительными или отрицательными. Когда операнд представляет собой байт, он умножается на регистр AL, а когда это слово — на регистр AX. Работа инструкций MUL и IMUL одинакова. Единственная разница между ними заключается в том, что одна работает с умножением чисел без знака, а другая — с операндами со знаком.
Если результат произведения множителя и множимого соответствует регистру назначения DX и AX, при этом некоторые биты остаются неиспользованными. Затем эти неиспользуемые биты заполняются копиями знакового бита и обнуляются флаги CF и OF.
Пример кода сборки
ORG 100h .МОДЕЛЬ МАЛЕНЬКАЯ .КОД MOV AL, 2AH ;Загрузить 1-й операнд в AX MOV BX, -26CH ;Загрузить 2-й операнд в BX ИМУЛ БХ РЕТ
Выход
Умножение дает отрицательный результат, поэтому старшие биты в DX равны FFFF.
Пример ассемблерного кода IMUL 2
Если заполнены только части регистров назначения, как при 16-битном умножении, один бит AH не заполнен или при 32-битном умножении части DX или DH остаются незаполненными, то и CF, и OF флаги установлены на 1.
ORG 100h .МОДЕЛЬ МАЛЕНЬКАЯ .КОД MOV AX, 2A45H ;Загрузить 1-й операнд в AX MOV BX, -26CH ;Загрузить 2-й операнд в BX ИМУЛ БХ РЕТ
Вывод
8086 Инструкция по умножению ASCII
AAM представляет собой мнемоническое обозначение «Умножение ASCII-настройки». Он исправляет или корректирует произведение двух неупакованных чисел BCD в правильное неупакованное число BCD. Это преобразование результата в число BCD выполняется инструкцией AAM. В случае умножения двух чисел ASCII нам нужно замаскировать старшие 4 бита обоих операндов, чтобы получить 1 цифру BCD на байт.
Он исправляет или корректирует произведение двух неупакованных чисел BCD в правильное неупакованное число BCD. Это преобразование результата в число BCD выполняется инструкцией AAM. В случае умножения двух чисел ASCII нам нужно замаскировать старшие 4 бита обоих операндов, чтобы получить 1 цифру BCD на байт.
Инструкция AAM работает с содержимым регистра AL и преобразует его в число BCD. Следовательно, произведение двух неупакованных двоично-десятичных чисел должно храниться в регистре AL. Умножьте числа BCD с помощью команды MUL. Сохраните продукт в регистре AX. Затем вызовите инструкцию AAM. Инструкция AAM делит данные в AL на 10. После этого она сохраняет частное в AH, а остаток в AL. AAM устанавливает флаги SF, ZF и AF в соответствии с результатом.
Пример кода сборки
Рассмотрим пример, в котором перемножаются два числа 7 и 9. Произведение равно 63 с шестнадцатеричным значением 3F. Инструкция AAM делит произведение на 10, что дает частное 06 и 03 в качестве остатка.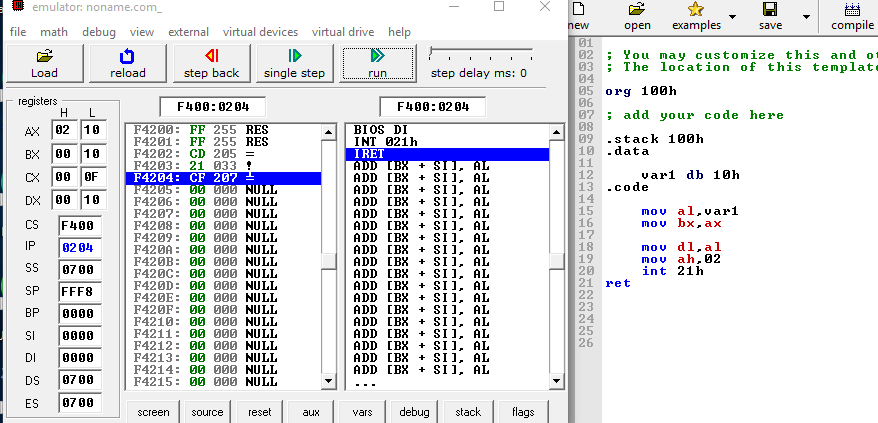 Вы можете видеть в окне регистра вывода, AH имеет 06, а AL имеет 03.
Вы можете видеть в окне регистра вывода, AH имеет 06, а AL имеет 03.
ORG 100h .МОДЕЛЬ МАЛЕНЬКАЯ .КОД MOV AX, 036H ;Загрузить 1-й операнд в AX MOV DX, 032H ;Загрузить 2-й операнд в DX МУЛ ДХ ААМ РЕТ
Выход
Категории Встраиваемые системыПодписаться на блог по электронной почте
Введите адрес электронной почты, чтобы подписаться на этот блог и получать уведомления о новых сообщениях по электронной почте.
Адрес электронной почты
Давайте напишем более сложный код на ассемблере!
Обучение ассемблеру — часть 4.2
Глядя на то, как выполнять умножение на 6502, мы можем дополнительно изучить, как писать код языка ассемблера
Фото Федерики Галли на Unsplash Написание языка ассемблера (я полагаю) требует, чтобы вы думали о написании кода по-другому. Я имею в виду, что все очень гранулировано. Что я имею в виду под , , так это то, что у вас есть очень тонкий контроль над тем, что происходит. Этот уровень контроля недоступен для нас в большинстве других языков. Недавно мы рассмотрели несколько небольших примеров (сложение и деление) того, как писать на этом языке. Однако, рассматривая только простые ситуации, мы ограничиваемся знанием лишь небольшого количества особенностей языка.
Этот уровень контроля недоступен для нас в большинстве других языков. Недавно мы рассмотрели несколько небольших примеров (сложение и деление) того, как писать на этом языке. Однако, рассматривая только простые ситуации, мы ограничиваемся знанием лишь небольшого количества особенностей языка.
Здесь мы рассмотрим более сложный пример — умножение. Это захватывающий пример, охватывающий гораздо больше набора инструкций. Это также заставит нас подумать о том, как выполнить более сложную процедуру, когда нам нужно будет сохранять несколько значений и выполнять циклы.
В сочетании с частью 4.1 это часть 4 серии «учебных сборок», которую я пишу. Однако везде, где это возможно, я стараюсь обеспечить независимость каждой части. Если вас интересуют только основы сборки, надеюсь, эти два поста подойдут и вам.
Умножать сложнее, чем складывать. В первую очередь потому, что у нас нет ни одной инструкции, которая может это сделать — нам нужно прокладывать свой собственный путь. Это действительно хороший пример для изучения, поскольку в нем используется множество различных инструкций и методов. Мы начнем с рассмотрения того, как мы обычно делаем умножение, и построим его оттуда.
Это действительно хороший пример для изучения, поскольку в нем используется множество различных инструкций и методов. Мы начнем с рассмотрения того, как мы обычно делаем умножение, и построим его оттуда.
12
*̲ ̲ ̲2̲3̲
36
+̲ ̲2̲4̲0̲
= 276
Это (надеюсь) выглядит знакомо. Вот как мы можем умножать обычные десятичные числа. В дальнейшем мы будем называть верхнее число множителем (MPD), а нижнее — множителем (MPR). Итак, 12 — это наш MPD, а 23 — наш MPR. Давайте попробуем разобраться, как именно мы могли сделать это умножение:
- Возьмите самую правую цифру из множителя (23), это 3. Затем умножьте это на 12. Теперь у нас есть 36
- Возьмите следующую цифру из множителя (23), это 2. Тогда, мы сдвигаем MPD (12) влево, что дает нам 120. Теперь перемножьте их вместе. Это дает нам 240.
- объединение этих чисел дает нам 276.
Это правильный результат. Сдвиг MPD влево, а затем умножение его на соответствующую цифру из множителя будет важным способом рассмотрения умножения в этом примере. Чтобы сделать это с двоичными числами, мы делаем ту же процедуру:
Чтобы сделать это с двоичными числами, мы делаем ту же процедуру:
101 (MPD)
*̲ ̲ ̲ ̲0̲1̲1̲ (MPR)
101
+ 1010
+ ̲ ̲0̲0̲0̲0̲0̲
= 01111
В этом примере мы сделаем 5 (101) Умножение на 3 (011). 101 — множимое (MPD), а 011 — множитель (MPR)
- Берем первый бит MPR (011). Это 1. Мы можем назвать бит, который мы используем, нашим значащим битом. Умножаем MPD (101) на это. У нас осталось 101
- Затем мы сдвигаем MPD влево, что дает нам 1010. Второй бит MPR также равен 1. Мы умножаем эти два вместе, и у нас остается 1010.
- Снова сдвигаем МУРЗ влево. В результате получается 10100. Последний бит MPR равен 0, что означает, что это дает нам 00000
- . Сложив их вместе, мы получим 01111, что равно 15.
Опять же, у нас есть правильный результат. Напомним, что если старший бит MPR (множитель) равен 1, вы сохраняете результат. Затем, независимо от этого, сдвигаем исходное (множимое — MPD) влево. Вы повторяете эту процедуру до тех пор, пока не убедитесь, что все биты вашего числа были проверены.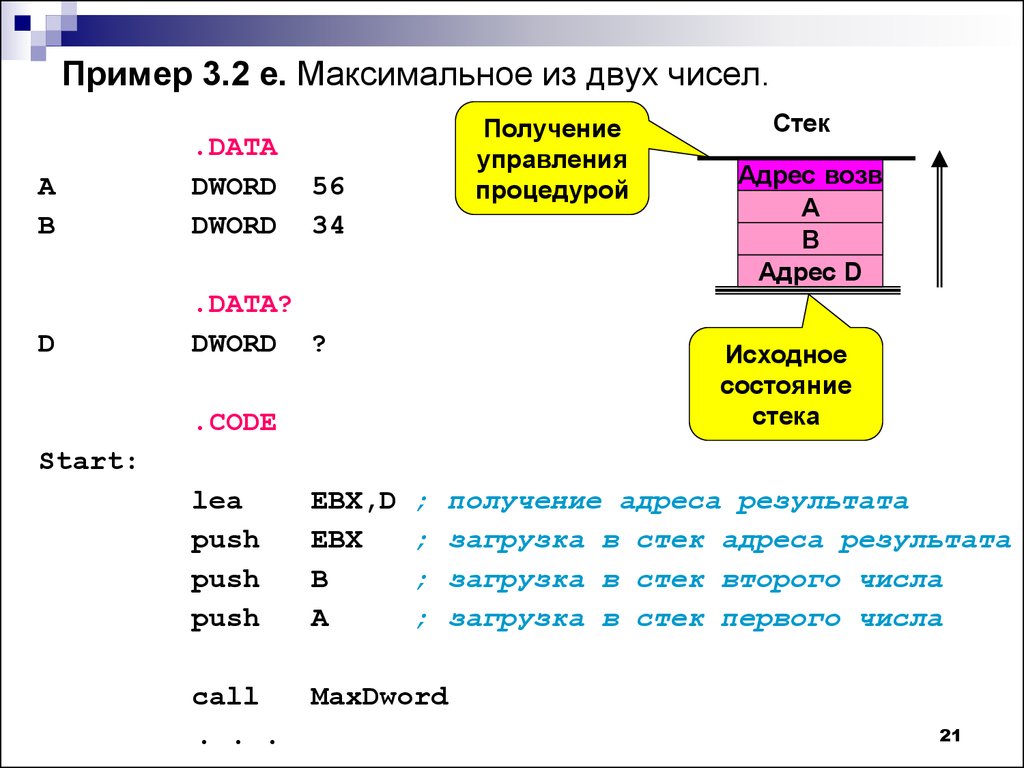
Блок-схемы
Это можно показать в блок-схеме. Это полезно сделать до того, как дело дойдет до написания кода, так как это может помочь вам визуализировать проблему, которую вы решаете. Это хорошо, поскольку по сравнению с нашими хорошими современными языками высокого уровня сложнее просто пойти на это и написать функцию.
Блок-схема того, как будет работать двоичное умножение. Сделано с помощью draw.ioПоначалу это может сбить с толку, но на этом рисунке показана та же логика, которую мы должны были использовать для умножения двоичных чисел выше. Стоит задуматься о графике и попытаться понять его. Это сбило меня с толку, пока я не подумал, что если значащий бит MPR = 0, то он никогда не будет влиять на результат.
Наш следующий шаг — преобразовать это в код. Давайте быстро рассмотрим некоторые проблемы/пограничные случаи, с которыми мы можем столкнуться при этом:
- Умножение двух 8-битных чисел может привести к 16-битному. Чтобы обойти это, нам нужно будет сохранить результат в двух 8-битных местах.
 Один для младших битов и один для старших битов. Например, мы можем сохранить 326 в виде двух 8-битных чисел, таких как
Один для младших битов и один для старших битов. Например, мы можем сохранить 326 в виде двух 8-битных чисел, таких как 00000001и01000110, а затем прочитать их все вместе, например00000001 01000110 9.0008 . - Нам нужно отслеживать много информации, чтобы сделать этот расчет. Мы будем вынуждены использовать больше, чем просто регистры (X, Y, A и т. д.), которые есть у 6502.
- Невозможно проверить и сравнить каждый бит числа одновременно. Для этого мы должны по отдельности переместить биты в аккумулятор (A) или регистр переноса (C) и провести там наши сравнения.
Код
Я просто представлю код, а затем мы пройдемся по нему построчно:
СТАРТ LDA #0 ; нулевой аккумулятор
STA TMP ; очистить адрес
STA RESULT ; очистить
STA RESULT+1 ; очистить
LDX #8 ; x — счетчик
MULT LSR MPR ; сдвиг mpr вправо - немного вдавить бит в C
BCC NOADD ; тестовый бит переноса
LDA RESULT ; нагрузка A с младшей частью результата
CLC
ADC MPD ; добавить mpd в res
STA RESULT ; сохранить результат
LDA RESULT+1 ; добавить отдых от сдвинутого mpd
ADC TMP
STA RESULT+1
NOADD ASL MPD ; сдвиг mpd влево, готовность к следующему "циклу"
ROL TMP ; сохранить бит из mpd в temp
DEX ; счетчик уменьшения
BNE MULT ; повторить, если счетчик 0
Теперь у нас есть несколько именованных блоков кода. Почему это полезно? Что ж, мы можем делать сравнения и переходить к этим блокам в зависимости от результата. Для этого подойдут
Почему это полезно? Что ж, мы можем делать сравнения и переходить к этим блокам в зависимости от результата. Для этого подойдут BCC и BNE . Если это содержимое бита переноса равно 0, BCC совершит прыжок. Инструкция BNE также может вызвать переход, если флаг Z равен 0. Зная это, мы можем пройтись по нашему коду, стараясь при этом помнить о нарисованной нами блок-схеме.
СТАРТ
Этот раздел предназначен для настройки на потом. Это эквивалент самого верхнего зеленого прямоугольника на приведенной выше блок-схеме. Мы хотим убедиться, что ячейки памяти, которые мы будем использовать, были очищены. Напомним, выше мы упоминали о проблеме, когда мы получили число, которое нельзя было удержать в 8-битном формате. Следовательно, у нас есть не 1, а 2 места для хранения наших результатов ( РЕЗУЛЬТАТ и РЕЗУЛЬТАТ+1 ).
СТАРТ LDA #0 ; нулевой аккумулятор
STA TMP ; очистить адрес
STA RESULT ; очистить
STA RESULT+1 ; очистить
LDX #8 ; x - это счетчик
👉 Строка 1 : мы загружаем аккумулятор с 0, это будет использоваться для установки областей в памяти пустыми.
👉 Строка 2/ 3/ 4 : Три ячейки памяти становятся пустыми путем переноса в них содержимого A. Эти места включают область временного хранения значений (TMP) и два места, где мы будем хранить результат (одно для старших 8 бит результата и одно для младших 8 бит).
👉 Строка 5 : Регистр X загружается со значением 8. Это будет использоваться для подсчета того, сколько раз мы сдвинули наши значения влево. Мы можем увеличить X вниз, используя инструкцию DEX .
MULT
Вспомните приведенные выше примеры того, как мы умножали выше. Мы проверили, равен ли значащий бит множителя 1, если это так, мы можем добавить множимое к результату. Эта часть кода обрабатывает один из таких циклов. Это эквивалент самого верхнего синего ромба (и зеленого прямоугольника под ним) на блок-схеме выше.
Во время работы программы мы посетим эту часть 8 раз, по одному разу для каждого бита множителя.
Мы упоминали, что для результата будет две области. Мы будем использовать содержимое регистра переноса, чтобы эффективно связать их вместе. Поэтому, если мы работаем с нижней половиной, нам не нужно беспокоиться о C, но когда мы работаем с более высокой половиной результата, мы будем — нам нужно знать, есть ли что-то, что нужно включить.
Мы будем использовать содержимое регистра переноса, чтобы эффективно связать их вместе. Поэтому, если мы работаем с нижней половиной, нам не нужно беспокоиться о C, но когда мы работаем с более высокой половиной результата, мы будем — нам нужно знать, есть ли что-то, что нужно включить.
МУЛЬТ ЛСР МПР ; сдвиг мпр вправо
BCC NOADD ; тестовый бит переноса
РЕЗУЛЬТАТ ЛДА ; загрузить a с низким разрешением
CLC
ADC MPD ; добавить mpd в res
STA RESULT ; сохранить результат LDA RESULT+1 ; add rest off shifted mpd
ADC TMP
STA RESULT+1
👉 Строка 1 : LSR — одна из смен, которые мы видели в предыдущей части. Это приведет к тому, что значащий бит нашего множителя попадет в регистр переноса.
👉 Строка 2 : BCC проверить содержимое переноски. Если это 1, мы продолжим со следующей строки и попытаемся включить наш расчет в наш результат. Однако, если это 0, мы перейдем к блоку кода, который мы назвали «NOADD». Это проигнорирует остальную часть блока MULT.
Это проигнорирует остальную часть блока MULT.
👉 Строка 3 : Предполагая, что содержимое регистра переноса равно 1, теперь мы помещаем текущее содержимое нижней части нашего результата в аккумулятор.
👉 Строка 4 : Поскольку нет необходимости что-либо переносить в нижнюю половину результата, мы можем сделать CLC , это очищает регистр переноса. Однако в этом нет необходимости, если вы заботитесь о верхней половине битов - нам нужно знать, перенеслось ли что-то из нижней части в верхнюю.
👉 Строка 5 : Поскольку MPR равен 1, мы можем включить MPD в результат. Текущий результат расчета находится в Аккумуляторе. АЦП здесь также добавит текущее множимое (MPD) к результату.
Добавление Result и MPD может дать число, превышающее 8 бит. Этот новый 9-й бит попадет в регистр переноса, где нам нужно будет добавить его в Result+1
👉 Строка 6 : Теперь мы сохраняем нижний результат обратно в RESULT. По мере выполнения вычислений здесь будет накапливаться нижняя половина результата.
По мере выполнения вычислений здесь будет накапливаться нижняя половина результата.
👉 Строка 7/8/9 : это делает то же самое, что и строки 3/5 и 6, но для верхних битов. Память TMP будет включать информацию о верхней половине (то, что не может быть сохранено в первых 8 битах) вычисления, как мы скоро увидим. Обратите внимание, что в этой части мы не очищали Carry, нам нужно знать, что произошло в нижней половине.
После этих строк мы, естественно, начинаем часть NOADD.
NOADD
Мы естественно входим в этот блок после каждого цикла через MULT. Однако, если мы не собираемся ничего добавлять к результату в конкретном цикле, нас также отправят сюда. Эта часть кода сдвинет множимое влево. Это также подготовит TMP , который помогает нам отслеживать старшие 8 бит вычисления. Наконец, здесь мы будем отслеживать, прошли ли мы каждый бит выходного множителя — если да, то умножение будет завершено. Это эквивалент двух нижних полей на блок-схеме выше.
NOADD ASL MPD ; сдвиг mpd влево
ROL TMP ; сохранить бит из mpd
DEX ; счетчик уменьшения
BNE MULT ; вернуться к МУЛЬТ
👉 Строка 1 : ASL сдвигает множимое влево. Это «противоположность» LSR . Это подготовит его к тому, когда мы зациклимся. Это помещает крайний левый бит MPD в регистр переноса
👉 Строка 2 : После строки 1 что-то попадет в перенос. Это можно восстановить в TMP с помощью инструкции ROL , которая поместит содержимое регистра переноса в самый правый бит TMP . Это сделано для того, чтобы этот бит можно было включить в старшие биты результата (см. MULT).
👉 Строка 3 : DEX уменьшает регистр X на 1. X отслеживает, сколько раз мы зациклились на коде.
👉 Строка 4 : Здесь мы определяем, нужно ли нам вернуться к началу MULT и продолжить наш расчет. Для этого используем инструкцию BNE .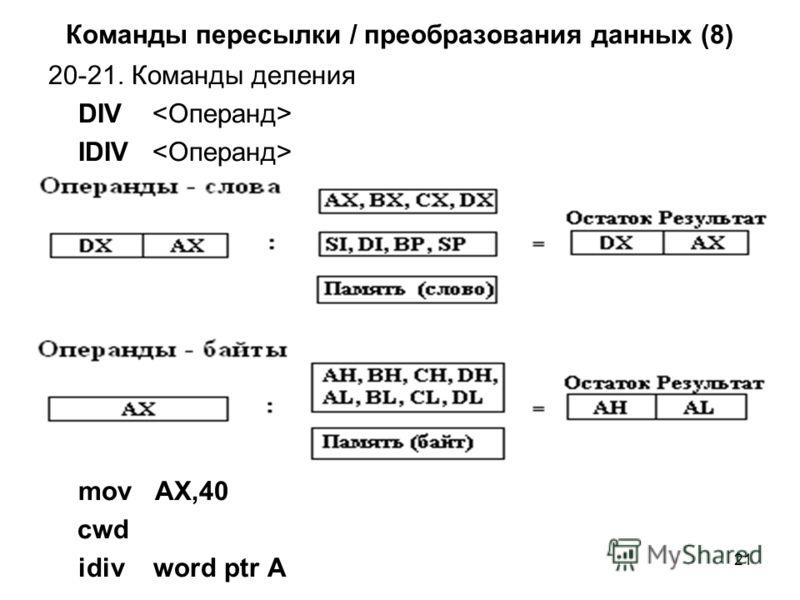
BNE выполняет разветвление, если содержимое регистра Z равно 0. Регистр Z будет автоматически установлен в 1 всякий раз, когда DEX устанавливает X в 0. Таким образом, если строка 3 уменьшает X до 0, Z будет установлен в 1, и поэтому мы не будем разветвляться. Программа завершится. Это произойдет после того, как все биты в MPR будут использованы и, следовательно, расчет будет завершен.
Если бы мы все еще находились в середине вычислений и достигли этой части, множимое было бы сдвинуто влево, и мы были бы готовы вернуться к началу. Там мы бы нашли следующий значащий бит множителя и проверили, нужно ли его прибавлять к результату.
Готово! Выполнение всей этой процедуры умножит 2 числа. Это немного сложно, правда? Тем не менее, он следует нашей блок-схеме, которая следует логике того, как мы делали умножение с самого начала. Это полезный пример, который стоит попытаться полностью понять, так как он содержит много важных инструкций и идей.
Теперь мы видели различные наборы инструкций 6502. Тем не менее, есть еще многое другое. Эти два примера показывают нам, какие инструкции доступны. В целом они относятся к следующим категориям:
Тем не менее, есть еще многое другое. Эти два примера показывают нам, какие инструкции доступны. В целом они относятся к следующим категориям:
- Обработка данных (ADC, DEX)
- Передача данных (LDA, STA, LDX)
- Сдвиги (ROL, LSR, ASL)
- Тестирование и разветвление (BCC, BNE)
- Контроль (CLC, CLD)
В каждой категории существует гораздо больше. На этом этапе большинству ресурсов потребуется время (обычно около 100 страниц) для обсуждения каждой инструкции. Такой справочный материал может быть очень полезным и обеспечит подробное описание каждого аспекта инструкций. Однако я не собираюсь делать это здесь. Писать скучновато, а читать не очень интересно. Многие инструкции, которые мы еще не видели, являются вариациями тех, которые у нас есть ( DEY уменьшает регистр Y, SBC вычитает...). Лучший способ узнать, как все они работают, — это использовать их или посмотреть, как они используются в примерах. Мы постараемся предоставить больше примеров в следующие недели. Несмотря на это, книги, которые я упоминаю внизу страницы (Закс и Левенталь), тоже являются фантастическими источниками.
Несмотря на это, книги, которые я упоминаю внизу страницы (Закс и Левенталь), тоже являются фантастическими источниками.
Это гораздо более сложный пример, чем мы видели ранее, однако он затрагивает множество различных особенностей языка. Мне потребовались годы, чтобы полностью понять, что происходит на каждом этапе кода, но я думаю, что это полезный (и забавный!) пример.
На следующей неделе мы сосредоточимся на том, чтобы заставить этот код работать. Мы сделаем это, установив ассемблер и эмулятор. Мы сможем получить представление о том, как происходила разработка программного обеспечения с использованием языка ассемблера 6502.
Это четвертая часть моей серии обучающих сборок.
- Часть 1. Введение в сборку 6502
- Часть 2. Знакомство с двоичными числами
- Часть 3. Как работают процессоры?
- Часть 4.1: Давайте напишем ассемблер!
- Часть 4.2: Давайте напишем более сложный ассемблер!
- Часть 5: Apple ii
Эта статья была адаптирована из моего личного блога.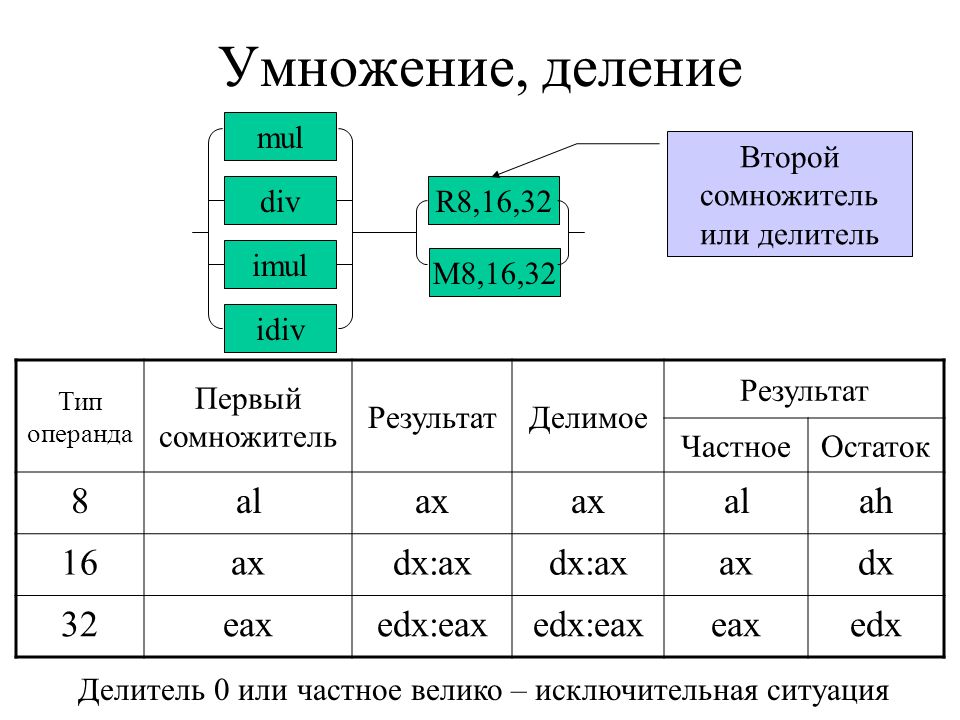 Большая часть материала, о котором я говорю, будет получена из двух основных источников: «Программирование на языке ассемблера 6502» Лэнса А. Левенталя и «Программирование 6502» Родни Закса.
Большая часть материала, о котором я говорю, будет получена из двух основных источников: «Программирование на языке ассемблера 6502» Лэнса А. Левенталя и «Программирование 6502» Родни Закса.
3.4: Умножение в сборке MIPS
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 27109
- Чарльз В. Канн III
- Геттисбергский колледж
Умножение и деление более сложны, чем сложение и вычитание, и требуют использования двух новых регистров специального назначения, регистров hi и lo. Регистры hi и lo не включены в 32 регистра общего назначения, которые использовались до этого момента, и поэтому не находятся под непосредственным контролем программиста. В этих разделах, посвященных умножению и сложению, будут рассмотрены требования к операциям умножения и деления, которые делают их необходимыми.
В этих разделах, посвященных умножению и сложению, будут рассмотрены требования к операциям умножения и деления, которые делают их необходимыми.
Умножение сложнее, чем сложение, потому что результат умножения может потребовать вдвое больше цифр, чем входные значения. Чтобы увидеть это, рассмотрим умножение по основанию 10. По основанию 10 9x9=81 (2 однозначных числа дают двузначное число) и 99x99=9801 (2 двузначных числа дают 4-значное число). Как видно из этого, в результате умножения требуется вдвое больше цифр, чем в исходных умножаемых числах. Тот же самый принцип применяется в двоичном формате. При перемножении двух 32-битных чисел для хранения результатов требуется 64-битное пространство.
Поскольку для умножения двух 32-битных чисел требуются 64-битные числа, требуются два 32-битных регистра. Всем компьютерам требуется два регистра для хранения результата умножения, хотя фактическая реализация этих двух регистров отличается. В MIPS используются регистры hi и lo, причем регистр hi используется для хранения большей 32-битной части умножения, а регистр lo используется для хранения меньшей 32-битной части умножения.
В MIPS все целочисленные значения должны быть 32-битными. Поэтому, если есть правильный ответ, он должен содержаться в младших 32 битах ответа. Таким образом, чтобы реализовать умножение в MIPS, два числа должны быть умножены с использованием 9.0007 множит оператор , а действительный результат перемещается из регистра lo . Это показано в следующем фрагменте кода, который умножает значение в $t1 на значение в $t2 и сохраняет результат в $t0 .
несколько $t1, $t2 mflo $t0
Однако что произойдет, если результат умножения слишком велик для хранения в одном 32-разрядном регистре? Снова рассмотрим арифметику с основанием 10. 3*2=06, и большая часть ответа равна 0. Однако 3*6=18, и большая часть ответа отлична от нуля. Это верно и для умножения MIPS. При перемножении двух положительных чисел, если hi регистр не содержит ничего, кроме 0, тогда переполнения нет, так как умножение не дало никакого значения в большей части результата. Если регистр hi содержит какие-либо значения 1, то результат умножения действительно имел переполнение, так как часть результата содержится в большей части результата. Это показано в двух примерах: 3*2=06 и 3*6=18 ниже.
Если регистр hi содержит какие-либо значения 1, то результат умножения действительно имел переполнение, так как часть результата содержится в большей части результата. Это показано в двух примерах: 3*2=06 и 3*6=18 ниже.
Итак, простая проверка на переполнение при перемножении двух положительных чисел, чтобы увидеть, hi 9В регистре 0008 все 0: если все 0, результат не переполняется, иначе результат переполняется.
Это нормально для двух положительных или двух отрицательных чисел, но что, если входные значения смешаны? Например, 2*(-3) = -6 и 2*(-8) = -18. Чтобы понять, что произойдет, эти задачи будут реализованы с использованием 4-битных регистров.
Помните, что 4-битные регистры могут содержать целые значения от -8 до 7. Таким образом, умножение 2*(-3) и 2*(-6) в 4-битах с 8-битным результатом показано ниже:
В первом примере старшие 4 бита равны 1111, что является расширением знака для -6. Это говорит о том, что пример не переполнился. Во втором примере старшие 4 бита равны 1110. Поскольку все 4 бита не равны 1, они не могут быть расширением знака отрицательного числа, и ответ переполнился. Таким образом, чрезмерно упрощенный взгляд может сказать, что если биты старшего разряда все 0 или все 1, переполнения нет. Хотя это необходимое условие для проверки на переполнение, этого недостаточно. Чтобы убедиться в этом, рассмотрим результат 6*(-2).
Поскольку все 4 бита не равны 1, они не могут быть расширением знака отрицательного числа, и ответ переполнился. Таким образом, чрезмерно упрощенный взгляд может сказать, что если биты старшего разряда все 0 или все 1, переполнения нет. Хотя это необходимое условие для проверки на переполнение, этого недостаточно. Чтобы убедиться в этом, рассмотрим результат 6*(-2).
Опять же, старшие 4 бита равны 1111, поэтому похоже, что переполнения нет. Но сложность здесь в том, что младшие 4 бита показывают положительное число, поэтому 1111 указывает, что младшая 1 (подчеркнутая) действительно является частью результата умножения, а не расширением знака. Этот результат показывает переполнение. Таким образом, для отображения переполнения в результате, содержащемся в регистре hi , должны совпадать все 0 или все 1, а также должен совпадать старший разряд (знак) бита lo 9.Регистр 0008.
Теперь, когда основы целочисленного умножения рассмотрены, мы рассмотрим пять операторов умножения MIPS.
 Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации.
Подробнее…
Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации.
Подробнее…

.jpg) Этот способ похож на сложение(вычитание) десятичных чисел в
столбик.
Этот способ похож на сложение(вычитание) десятичных чисел в
столбик. 3. Умножение и деление.
3. Умножение и деление.
