NoZDR — Перестановочные шифры
Это описание перестановочных шифров для начинающих составителей головоломок.
Простая перестановка
Простая перестановка без ключа — один из самых простых методов шифрования. Буквы перемешиваются по каким-либо правилам, но эти правила могут быть разными — и простыми и сложными.
Транспозиция
Допустим, у нас есть фраза: «МОЖНО, НО НЕЛЬЗЯ». И мы хотим её зашифровать. Самый простой способ — это записать всю фразу задом наперёд: «ЯЗЬЛЕН ОН, ОНЖОМ». Можно порядок слов в предложении оставить исходным, но каждое слово записать задом наперёд: «ОНЖОМ, ОН ЯЗЬЛЕН». А можно менять местами каждые две буквы: «ОМНЖ,ООНЕНЬЛЯЗ». Это называется «транспозиция» или простая перестановка в чистом виде.

Транспонирование
В этом шифре используется таблица. Сообщение записывается в таблицу по строкам, а для образования шифрованного текста считывается по столбцам. Ну или наоборот — записывается на столбцам, а считывается по строкам. Мы как бы переворачиваем таблицу относительно её диагонали, проходящей через верхний левый и нижний правый углы. Математики называют такой способ переворота таблицы транспонированием.
Для шифрования нужно нарисовать подходящего размера таблицу, вписать туда построчно шифруемый текст, а затем выписать его по столбцам в одну строку. Для расшифровки нужно лишь будет сообщить ключ шифра в виде размера таблицы. На рисунке ниже из ABCDEFGHIJKL получается ADGJBEHKCFIL. Согласитесь, понять без картинки, что это был алфавит, уже практически невозможно.
Итак, например, нам нужно зашифровать текст «Я памятник себе воздвиг нерукотворный, к нему не зарастёт народная тропа» . В нём 72 символа. 72 — удобное число, оно делится без остатка на 2,4,6,8,12,18,24,36, поэтому можно использовать таблицы 2х36, 3х24, 4х18, 6х12, 8х9, 9х8, 12х6, 18х4, 24х3, 36х2 :). Определяемся с ключом (размером таблицы), вписываем текст по строкам, а затем переписываем его по столбцам.

На рисунке выше показаны варианты с таблицами 9×8, 8×9, 4×18 и 18×4. Для третьего варианта (таблица 4×18) получится вот такой текст:
«Ямиеввнкой у атрар якбоиеор,н зс ояопт езгртн енатнд панс д увыкмерёанта (4:18)»
В данном случае я взял текст «как есть», то есть с пропусками между словами и со знаками препинания. Но если текст осмысленный, то знаки препинания и пропуски между словами можно и не использовать.
Штакетник
Упрощённый вариант транспонирования (с двухстрочной таблицей) — «штакетник». Напоминает «по конструкции» забор-шахматку.

Это очень простой способ шифровки, часто применяемый школьниками. Фраза записывается в две строки: в верхней пишутся нечётные буквы, в нижней — чётные. Затем нужно выписать подряд сначала верхнюю строку, затем нижнюю. Такое шифрование легко проделать и в уме, не выписывая сначала две строки.
«Я памятник себе воздвиг нерукотворный» превращается в «ЯАЯНКЕЕОДИНРКТОНЙ ПМТИСБВЗВГЕУОВРЫ».
Скитала
Известно, что в V веке до нашей эры правители Спарты, наиболее воинственного из греческих государств, имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью «скиталы», первого простейшего криптографического устройства, реализующего метод простой перестановки.

Шифрование выполнялось следующим образом. На стержень цилиндрической формы, который и назывался «скитала», наматывали спиралью (виток к витку) полоску пергамента и писали на ней вдоль стержня несколько строк текста сообщения. Затем снимали со стержня полоску пергамента с написанным текстом. Буквы на этой полоске оказывались расположенными хаотично. Для восстановления текста требовалась скитала такого же диаметра.
По сути скитала — это наша обычная плоская таблица, обёрнутая вокруг цилиндра.
Считается, что автором способа взлома шифра скиталы является Аристотель, который наматывал ленту на конусообразную палку до тех пор, пока не появлялись читаемые куски текста. Изначально древний аппарат использовался в качестве сохранения секретных рецептов. Сейчас вместо узкой полоски пергамента можно использовать серпантин, а роль скиталы выполнит карандаш.
Сдвиг
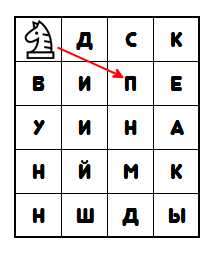
Похожий результат можно получить, если буквы сообщения писать через определенное число позиций до тех пор, пока не будет исчерпан весь текст. Ниже пример готовой головоломки, составленной по таким правилам. «Три дробь четыре» — это подсказка, что зашифровано три слова, читать надо каждую четвёртую букву (4-8-12-16-..), по достижению конца переходить снова к началу со сдвигом на 1 букву влево (3-7-11-15-..) и т.д. На рисунке ниже зашифровано «Идите назначенным маршрутом».

Одиночная перестановка по ключу
Более практический метод шифрования, называемый одиночной перестановкой по ключу, очень похож на предыдущий. Он отличается лишь тем, что колонки таблицы не сдвигаются, а переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы. Кодируемая фраза записывается в подходящую таблицу построчно. Затем над таблицей вставляется пустая строка и в неё вписывается ключевое слово/фраза/последовательность чисел. Затем это ключевое слово/фраза/последовательность сортируется по алфавиту/значению, вместе с ней сортируются столбцы, тем самым перемешивая всю таблицу. Затем зашифрованная фраза выписывается построчно из этой перемешанной таблицы.
Например, можно сделать головоломку на основе судоку. Разгадывающему даётся текст «-УРОМКУЛО ЬУЁЗЕБЯДЛ НЗЯАТЛЫЙА ЦЬБАДНЕПУ ЕММДНИТОЁ ИЧТЮКЬНОО УНЁЙВЫЧЁС ХИЕПОТОДЦ ПРМГОУИК-» и предлагается решить судоку, в которой одна из строк помечена.
Решать эту головоломку придётся так: сначала нужно записать текст в таблицу 9×9, затем разгадать судоку, нарисовать пустую таблицу 9×9, надписать над ней ключевую строку из помеченной строки, и затем в таблицу под номерами вписать столбцы согласно их порядковым номерам в исходной таблице.
Для детей можно использовать этот же метод, но попроще, даже без цифр, а сразу нарисовав порядок перестановки в виде путей.

Двойная перестановка
Для дополнительной скрытности можно повторно шифровать сообщение, которое уже было зашифровано. Этот способ известен под названием «двойная перестановка». Для этого размер второй таблицы подбирают так, чтобы длины её строк и столбцов были не такие, как в первой таблице. Лучше всего, если они будут взаимно простыми. Кроме того, в первой таблице можно переставлять столбцы, а во второй строки.
Маршрутная перестановка
Обычное транспонирование таблицы (заполняем по строкам, читаем по столбцам) можно усложнить и считывать не по столбцам, а змейкой, зигзагом, по спирали или каким-то другим способом, т.е. задавать маршрут обхода таблицы. Такие способы заполнения таблицы если и не усиливают стойкость шифра, то делают процесс шифрования гораздо более занимательным. Правда, процесс расшифровки при этом усложняется, особенно, если маршрут неизвестен, и его ещё надо узнать.
На рисунке сверху последовательность символов «АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,?» вписана построчно в таблицу 6×6, а затем считана по маршруту, указанному линиями. Получаются следующие шифровки:
АЁЛСЧЭБЖМТШЮВЗНУЩЯГИОФЪ.ДЙПХЫ,ЕКРЦЬ?
АЁЛСЧЭЮЯ.,?ЬЦРКЕДГВБЖМТШЩЪЫХПЙИЗНУФО
АБЁЛЖВГЗМСЧТНИДЕЙОУШЭЮЩФПКРХЪЯ.ЫЦЬ,?
АЁЛСЧЭЮШТМЖБВЗНУЩЯ.ЪФОИГДЙПХЫ,?ЬЦРКЕ
НЗВБАЁЖМЛСТШЧЭЮЯЩУФЪ.,?ЬЫХЦРПЙКЕДГИО
А здесь нужно обходить таблицу «ходом коня», причём маршрут уже нарисован, так что это совсем для маленьких 🙂

Но если подать эту головоломку так, как показано ниже, то будет уже совсем не просто, так как вариантов обхода ходом коня может быть много, и нужно будет найти из всех этих вариантов единственный правильный (ниже зашифровано «Пушкин. Медный всадник»).
Ещё один метод загадать маршрут — использовать мнемоническое стихотворение, в котором некими ключевыми словами заданы координаты обхода сетки. Допустим, есть шахматная доска, которую ходом шахматного коня нужно всю обойти клетка за клеткой так, чтобы побывать на каждой клетке только один раз. В результате получится маршрут длиной 64. Один из многих миллионов таких маршрутов показан на картинке ниже. Если в порядке обхода клеток вписать сообщение, то чтобы его разгадать, нужно будет восстановить этот самый маршрут.
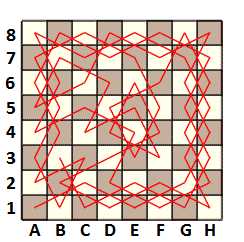
А вот загадать этот маршрут можно, например, вот таким стихотворением:
Алеет Осень Ценными Дарами, Еще Один Животворящий День. Хлеба Червонят Желтыми Шнурами, Хрустальных Вод Философична Сень. Два Вечера Цеплявшиеся Шишки Артист Писал, Бездонна Синева. Дорожный Шлак Целуют Червячишки, Еще Покрыта Флоксами Трава. Дымится Чай Эффектней Шоколада, Фарфоры Чашек Достаются Трем, Блондинке Девушка Дана Отрада Форшмак Делить Холодным Острием. Жена, Толкая Хилую Подругу, Желает Сняться Этим Выходным, Ценя Сама Арктическую Вьюгу, Бросает Шар Арбуза Четверым. Цикад Пяток, Едва Чревовещая, Дарует Дрему Фикусам Окна. Хотя Довольны Жаждавшие Чая, Хозяин Шумно Жертвует Вина. Фокстротами Шесть Девушек Пленились, Эстрадных Танцев Фантастичней Па, Едва Ступающий Цыпленок Вылез, А Селезень Блуждающий Пропал. Алеет Тело Бронзовой Осины, Царит Теней Ажурная Длина. Беззвучней, Чем Автомобиля Шины, Болоту Ветер Дарит Семена. Фонарь Восьмью Химерами Сияет, Жук Прилетает, Хлопая, Туда. Желанна Осень, Если Довершает Ценнейший Отдых Бодрого Труда.
Разгадывать его придётся так: «Алеет Осень» — это А1 (А Один), «Ценными Дарами» — C2 (Цэ Два), «Ещё Один» — E1 (E Один), «Животворящий День» — G2 (Жэ Два) и т.д.
Перестановка «Волшебный квадрат»
Волшебными (или магическими) квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами от 1 до n2 (где n — размерность квадрата), которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

В известном ещё в Древнем Китае квадрате Ло-Шу третьего порядка (3×3) константа квадрата 15 повторяется 8 раз:
по трём горизонталям: 2+9+4 = 7+5+3 = 6+1+8 = 15
по трём вертикалям: 2+7+6 = 9+5+1 = 4+3+8 = 15
по двум диагоналям: 2+5+8 = 4+5+6 = 15
Кстати, константу нечетного квадрата легко посчитать, умножив среднее число ряда, из которого составлен квадрат, на порядок квадрата. Для квадрата 3-го порядка (3×3) константа равна 123456789*3=15.
Далее, чтобы зашифровать какое-то послание, нужно сначала подобрать или составить подходящий по размеру волшебный квадрат, затем нарисовать пустую таблицу такого же размера, и вписать буквы текста по очереди в таблицу в соответствии с номерами в волшебном квадрате. Затем просто выписываем построчно буквы из таблицы в одну длинную строку. Порядок квадрата должен быть равен округлённому в большую сторону корню из длины шифруемой строки, чтобы строка полностью вошла в квадрат. Если строка короче, то остаток можно заполнить произвольными буквами или цифрами.
На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата. Так, существует лишь один магический квадрат размером 3х3, если не принимать во внимание его повороты и отражения. Счёт волшебным квадратам 4-го порядка уже идёт на сотни, 5-го — на сотни тысяч. Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени, так как ручной перебор всех вариантов ключа для этого шифра был немыслим.
Есть очень простой метод составления нечётных волшебных квадратов, т.е. размером 3×3, 5×5, 7×7 и т.д. Это метод «террас» или «пирамидок».
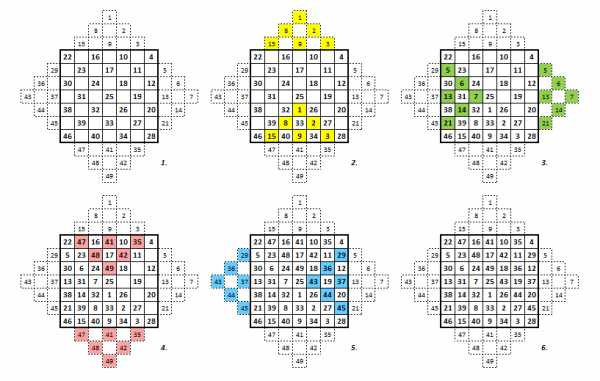
Рисуется квадрат нужного размера и к нему пририсовываются ступенчатые «террасы» (обозначены пунктиром). Далее по диагоналям сверху вниз направо квадрат заполняется последовательными числами. После этого «террасы» переносятся внутрь квадрата: правые — налево, левые — направо, верхние — вниз, а нижние — наверх. Получается волшебный квадрат!
На базе этого метода можно составлять разные головоломки. Если использовать метод напрямую, то получится вот такая головоломка:
Чтобы решить эту головоломку, нужно буквы из «террас» перенести в квадрат, тогда в квадрате прочитается полное сообщение. Здесь зашифрована фраза «За мостом засада, пройти нельзя, переходите речку в брод.»
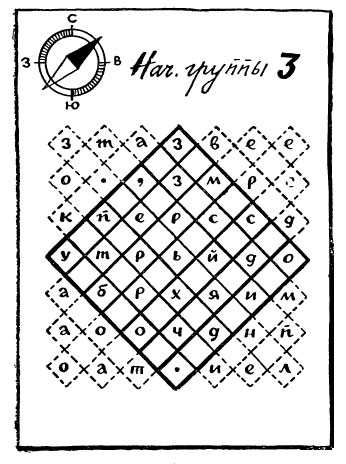
А если использовать метод наоборот, то получится головоломка типа такой.
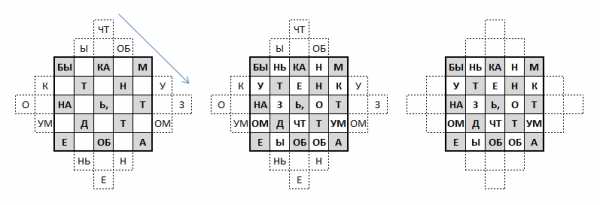
Чтобы её решить, надо вытащить соответствующие буквы из квадрата в «террасы».
Для квадратов 4×4, 6×6 и т.д. таких простых способов их составления не существует, поэтому проще использовать готовые. Например, квадрат Дюрера.

Вращающаяся решётка
Классическая решётка Кардано позволяет скрыть шифровку внутри мусорного текста и является хорошим примером стеганографии. Но если решётку Кардано использовать в качестве ключа для перестановочного шифра, то получим новый метод шифрования — вращающуюся решётку или сетку.
Решётка — это квадрат размером NxN клеток, некоторые из которых вырезаны. Вырезанные клетки могут касаться друг друга, в том числе вершинами, и даже сторонами. В одной клетке — одна буква. Вырезанные клетки должны располагаться таким образом, чтобы никакие две из них не оказывались в одном и том же месте при поворотах решётки.
При помощи конструктора, изображённого ниже, можно изготовить 416 (4 294 967 296) таких решёток. Для этого нужно вырезать строго одно из четырёх повторяющихся чисел. Для шифрования без мусора нужно вырезать все номера от 1 до 16, всего 16 клеток. Для шифрования с мусором некоторые числа можно не вырезать, оставшиеся места после шифрования заполнить любыми произвольными буквами, это и будет мусор.
Использовать полученную решётку надо следующим образом. Положить решётку на бумагу и в вырезанные клетки по одной букве начать вписывать шифруемый текст. Как только 16 букв будет вписано, решётка поворачивается на 90°, и вписываются следующие 16 букв, и так ещё два раза. В результате будет вписано 64 буквы. Если текст был короче, то в оставшиеся на бумаге пустые места нужно вписать произвольные буквы. Более длинный текст можно разбить на части по 64, и шифровать каждую отдельно. А можно вписывать в окошки и по две буквы.
Есть второй способ перекладывания решётки во время шифрования — не поворачивать решётку на 90° три раза, а в первый раз повернуть её на 180°, второй раз перевернуть обратной стороной относительно горизонтальной оси, в третий раз — снова повернуть на 180°.
Это были перестановочные шифры. А теперь можно почитать про Шифры замены.
Разное
games/quest/crypt/cipher/perestanovka.txt · Последние изменения: 2019/07/25 12:55 — NoZDR
nozdr.ru
Шифры перестановки
Шифрование перестановкой заключается в том, что символы открытого текста переставляются по определенному правилу в пределах некоторого блока этого текста. Рассмотрим перестановку, предназначенную для шифрования сообщения длиной n символов. Его можно представить с помощью таблицы
 ,
,
где i1 – номер места шифртекста, на которое попадает первая буква открытого текста при выбранном преобразовании, i2 — номер места для второй буквы и т. д. В верхней строке таблицы выписаны по порядку числа от 1 до n, а в нижней те же числа, но в произвольном порядке. Такая таблица называется перестановкой степени n.
Зная перестановку, задающую преобразование, можно осуществить как шифрование, так и расшифрование текста. В этом случае, сама таблица перестановки служит ключом шифрования.
Число различных преобразований шифра перестановки, предназначенного для шифрования сообщений длины n, меньше либо равно n! (nфакториал). Заметим, что в это число входит и вариант преобразования, оставляющий все символы на своих местах.
С увеличением числа n значение n! растет очень быстро. Для использования на практике такой шифр не удобен, так как при больших значениях n приходится работать с длинными таблицами. Поэтому широкое распространение получили шифры, использующие не саму таблицу перестановки, а некоторое правило, порождающее эту таблицу. Рассмотрим несколько примеров таких шифров.
Шифр перестановки «скитала».Известно, что в Vвеке до нашей эры правители Спарты, наиболее воинственного из греческих государств, имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью скитала, первого простейшего криптографического устройства, реализующего метод простой перестановки.
Шифрование выполнялось следующим образом. На стержень цилиндрической формы, который назывался скитала, наматывали спиралью (виток к витку) полоску пергамента и писали на ней вдоль стержня несколько строк текста сообщения (рис. 1.2). Затем снимали со стержня полоску пергамента с написанным текстом. Буквы на этой полоске оказывались расположенными хаотично.
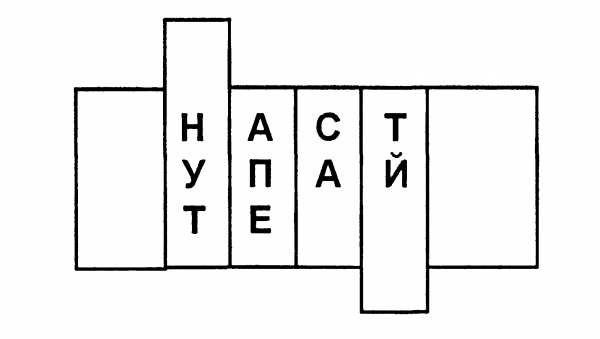
Рис. 1.2. Шифр «Скитала»
Такой же результат можно получить, если буквы сообщения писать по кольцу не подряд, а через определенное число позиций до тех пор, пока не будет исчерпан весь текст. Сообщение «НАСТУПАЙТЕ» при размещении его по окружности стержня по три буквы дает шифртекст: «НУТАПЕСА_ТЙ«.
Для расшифрования такого шифртекста нужно не только знать правило шифрования, но и обладать ключом в виде стержня определенного диаметра. Зная только вид шифра, но не имея ключа, расшифровать сообщение было непросто.
Шифрующие таблицы. С начала эпохи Возрождения (конец XIV столетия) начала возрождаться и криптография. В разработанных шифрах перестановки того времени применяются шифрующие таблицы, которые, в сущности, задают правила перестановки букв в сообщении.
В качестве ключа в шифрующих таблицах используются:
размер таблицы;
слово или фраза, задающие перестановку;
особенности структуры таблицы.
Одним из самых примитивных табличных шифров перестановки является простая перестановка, для которой ключом служит размер таблицы. Этот метод шифрования сходен с шифром скитала. Например, сообщение «ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ« записывается в таблицу поочередно по столбцам. Результат заполнения таблицы из 5 строк и 7 столбцов показан на рис. 1.3.
После заполнения таблицы текстом сообщения по столбцам для формирования шифртекста считывают содержимое таблицы по строкам. Если шифртекст записывать группами по пять букв, получается такое шифрованное сообщение: «ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ«.
Рис. 1.3. Заполнение шифрующей таблицы из 5 строк и 7 столбцов
Естественно, отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Следует заметить, что объединение букв шифртекста в 5-буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия выполняют в обратном порядке.
Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.
Применим в качестве ключа, например, слово «ПЕЛИКАН«, а текст сообщения возьмем из предыдущего примера. На рис. 1.4 показаны две таблицы, заполненные текстом сообщения и ключевым словом, при этом левая таблица соответствует заполнению до перестановки, а правая таблица – заполнению после перестановки.
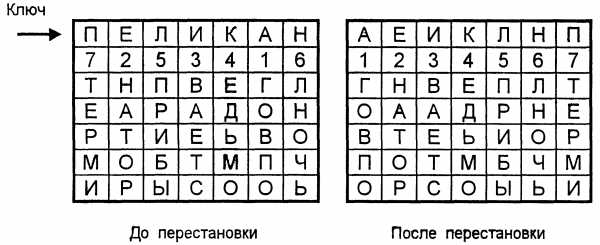
Рис. 1.4. Шифрующие таблицы, заполненные ключевым словом и текстом сообщения
В верхней строке левой таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были понумерованы слева направо. В правой таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа.
При считывании содержимого правой таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение: «ГНВЕП ЛТООА ДРНЕВ ТЕЬИО РПОТМ БЧМОР СОЫЬИ«.
Для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, а потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.
Пример выполнения шифрования методом двойной перестановки показан на рис. 1.5. Если считывать шифртекст из правой таблицы построчно блоками по четыре буквы, то получится следующее: «ТЮАЕ ООГМ РЛИП ОЬСВ«.
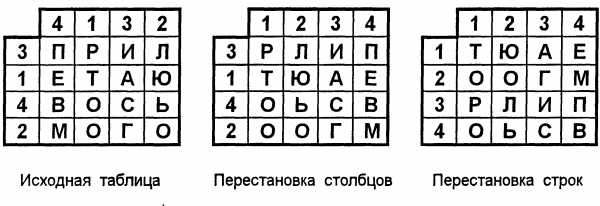
Рис. 1.5. Пример выполнения шифрования методом двойной перестановки
Ключом к шифру двойной перестановки служит последовательность номеров столбцов и номеров строк исходной таблицы (в нашем примере последовательности 4132 и 3142 соответственно).
Число вариантов двойной перестановки быстро возрастает при увеличении размера таблицы:
для таблицы 3×3 36 вариантов;
для таблицы 4×4 576 вариантов;
для таблицы 5×5 14400 вариантов.
Шифрование с помощью магических квадратов. В средние века для шифрования перестановкой применялись и магические квадраты. Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.
Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения.
Пример магического квадрата и его заполнения сообщением «ПРИЛЕТАЮ ВОСЬМОГО» показан на рис. 1.6.
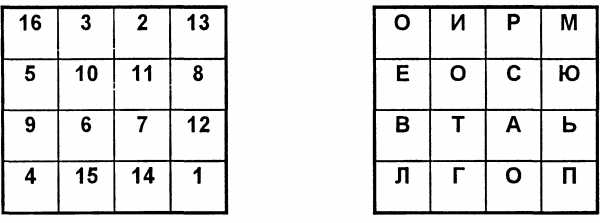
Рис. 1.6. Пример магического квадрата 4х4 и его заполнение сообщением
Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид: «ОИРМ ЕОСЮ ВТАЪ ЛГОП«.
Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3×3 (если не учитывать его повороты). Количество магических квадратов 4×4 составляет уже 880, а количество магических квадратов 5×5 – около 250000.
Магические квадраты средних и больших размеров могли служить хорошей базой для обеспечения нужд шифрования того времени, поскольку практически нереально выполнить вручную перебор всех вариантов для такого шифра.
studfiles.net
Перестановочный шифр — Википедия. Что такое Перестановочный шифр
Шифр перестано́вки — это метод симметричного шифрования, в котором элементы исходного открытого текста меняют местами. Элементами текста могут быть отдельные символы (самый распространённый случай), пары букв, тройки букв, комбинирование этих случаев и так далее. Типичными примерами перестановки являются анаграммы. В классической криптографии шифры перестановки можно разделить на два класса:
- Шифры одинарной (простой) перестановки — при шифровании символы открытого текста перемещаются с исходных позиций в новые один раз.
- Шифры множественной (сложной) перестановки — при шифровании символы открытого текста перемещаются с исходных позиций в новые несколько раз.
В качестве альтернативы шифрам перестановки можно рассматривать подстановочные шифры. В них элементы текста не меняют свою последовательность, а изменяются сами.
История
Точное время появления шифра перестановки не известно. Вполне возможно, что писцы в древности переставляли буквы в имени своего царя ради того, чтобы скрыть его подлинное имя или в ритуальных целях[1].
Одно из древнейших известных нам шифровальных устройств — Скитала. Бесспорно известно, что скитала использовалась в войне Спарты против Афин в конце V века до н. э.[2][3]
Прародителем анаграммы считают поэта и грамматика Ликофрона, который жил в Древней Греции в III веке до н. э. Как сообщал византийский автор Иоанн Цец, из имени царя Птоломея он составил первую из известных нам анаграмм: Ptolemaios — Аро Melitos, что в переводе означает «из мёда», а из имени царицы Арсинои — как «Ion Eras» (фиалка Геры)[4].
Шифры простой перестановки
Как правило, при шифровании и дешифровании шифра простой перестановки используется таблица перестановок:
Первая строка — позиция символа в открытом тексте, вторая строка — позиция в шифрограмме. Таким образом, при длине сообщения n{\displaystyle n} символов существует ровно n! {\displaystyle n!\ } ключей.
Шифры маршрутной перестановки
Широкое распространение получили так называемые маршрутные перестановки, использующие некоторую геометрическую фигуру (плоскую или объемную). Преобразования состоят в том, что отрезок открытого текста записывается в такую фигуру по некоторой траектории, а выписывается по другой траектории. Пример данного шифра — шифр Скиталы.
Шифр табличной маршрутной перестановки
Наибольшее распространение получили маршрутные шифры перестановки, основанные на прямоугольниках (таблицах). Например, можно записать сообщение в прямоугольную таблицу по маршруту: по горизонтали, начиная с верхнего левого угла, поочередно слева направо. Сообщение будем списывать по маршруту: по вертикалям, начиная с верхнего правого угла, поочередно сверху вниз.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки
| п | р | и | м | е |
| р | м | а | р | ш |
| р | у | т | н | о |
| й | п | е | р | е |
| с | т | а | н | о |
| в | к | и |
КРИПТОГРАММА: ешоеомрнрниатеаирмупткпррйсв
Обращение описанных шагов не представит труда при расшифровании[5].
Шифр вертикальной перестановки
Широкое распространение получила разновидность маршрутной перестановки — вертикальная перестановка. В этом шифре также используется прямоугольная таблица, в которую сообщение записывается по строкам слева направо. Выписывается шифрограмма по вертикалям, при этом столбцы выбираются в порядке, определяемом ключом.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки КЛЮЧ: (3, 1, 4, 2, 5)
| 3 | 1 | 4 | 2 | 5 |
| п | р | и | м | е |
| р | м | а | р | ш |
| р | у | т | н | о |
| й | п | е | р | е |
| с | т | а | н | о |
| в | к | и |
КРИПТОГРАММА: рмупткмрнрнпррйсвиатеаиешоео
Заполнять последнюю строку таблицы «нерабочими» буквами нецелесообразно, так как криптоаналитик, получивший данную криптограмму, получает сведения о длине числового ключа[6].
Шифр «поворотная решётка»
Решётка КарданоВ 1550 году итальянский математик Джероламо Кардано (1501—1576) в книге «О тонкостях» предложил новую технику шифрования сообщений — решётку.
Изначально решётка Кардано представляла собой трафарет с отверстиями, в которые записывали буквы, слоги или слова сообщения. Затем трафарет убирали, а свободное место заполняли более или менее осмысленным текстом. Такой метод сокрытия информации относится к стеганографии.
Позднее был предложен шифр «поворотная решётка» — первый транспозиционный (геометрический) шифр. Несмотря на то, что существует большая разница между изначальным предложением Кардано и шифром «поворотная решётка», методы шифрования, основанные на трафаретах, принято называть «решётками Кардано».
Четыре позиции решётки
Для шифрования и дешифрования с помощью данного шифра изготовляется трафарет с вырезанными ячейками. При наложении трафарета на таблицу того же размера четырьмя возможными способами, его вырезы полностью должны покрывать все клетки таблицы ровно по одному разу.
При шифровании трафарет накладывают на таблицу. В видимые ячейки по определённому маршруту вписывают буквы открытого текста. Далее трафарет переворачивают три раза, каждый раз проделывая операцию заполнения.
Шифрограмму выписывают из получившейся таблицы по определённому маршруту. Ключом являются трафарет, маршрут вписывания и порядок поворотов.
Данный метод шифрования использовался для передачи секретной информации нидерландскими правителями в 1740-х годах. Во время Первой мировой войны армия кайзера Вильгельма использовала шифр «поворотная решётка». Немцы использовали решётки разных размеров, однако очень недолго (четыре месяца), к огромному разочарованию французских криптоаналитиков, которые только-только начали подбирать к ним ключи. Для решёток разных размеров французы придумали собственные кодовые имена: Анна (25 букв), Берта (36 букв), Дора (64 буквы) и Эмиль (81 буква)[1][7].
Шифры сложной перестановки
В данном классе шифров перестановки используется идея многократной перестановки символов или повторного шифрования уже зашифрованного сообщения.
Шифр двойной перестановки
При шифровании шифром двойной перестановки в таблицу по определённому маршруту записывается текст, затем переставляются столбцы и строки. Далее по определённому маршруту выписывается шифрограмма.
Ключом к шифру являются размер таблицы, маршруты вписывания и выписывания, порядки перестановки столбцов и строк. Если маршруты являются фиксированными величинами, то количество ключей равно n!m!{\displaystyle n!m!}, где n{\displaystyle n} и m{\displaystyle m} — количество строк и столбцов в таблице[8].
ОТКРЫТЫЙ ТЕКСТ: двойная перестановка МАРШРУТ ВПИСЫВАНИЯ: слева - направо МАРШРУТ ВЫПИСЫВАНИЯ: сверху - вниз СТОЛБЦЫ: ( 3, 1, 4, 2) СТРОКИ: ( 3, 2, 4, 1, 5)
|
|
|
КРИПТОГРАММА: аавркопйстндевняоеа
Криптоанализ
При дешифровании текста используют частотные характеристики открытого текста. Однако для получения устойчивой картины длина послания должна быть существенно больше ключа. Одной из наиболее устойчивых характеристик осмысленного текста является отсутствие запретных биграмм (пара соседних букв). Например, биграммы «Ъ + Ь», «гласная + Ь», «пробел + Ь». Знание и использование частотной диаграммы открытого текста значительно упростит дешифрование шифра перестановки[9].
Примечания
- ↑ 1 2 Фред Б. Риксон, 2011.
- ↑ Фукидид. История I 131, 1.
- ↑ Дориченко, 1994.
- ↑ Lives of the Hellenistic Poets // Attalus: Sources for Greek and Roman history. (англ.)
- ↑ Алферов, 2002, с. 96.
- ↑ Алферов, 2002, с. 97.
- ↑ Бабаш, 2007.
- ↑ Алферов, 2002.
- ↑ Бабаш, 2007, с. 136.
Литература
- А. П. Алферов, А. Ю. Зубов, А. С. Кузьмин, А. В. Черёмушкин. Основы криптографии. — Гелиос АРВ, 2002. — ISBN 5-85438-137-0.
- А. В. Бабаш, Г. П. Шанкин. Криптография. — М. СОЛОН-ПРЕСС, 2007. — ISBN 5-93455-135-3.
- Фред Б. Риксон. Коды, шифры, сигналы и тайная передача информации. — Астрель, 2011. — ISBN 978-5-17-074391-9.
- Дориченко С. А., Ященко В. В. 25 этюдов о шифрах: Популярно о современной криптографии. — Теис, 1994. — ISBN 5-7218-0014-3.
wiki.sc
Шифр скользящей перестановки. Шифрование методом перестановки
Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки
Рассмотрим преобразование из ШП, предназначенное для зашифрования сообщения длиной символов. Его можно представить с помощью таблицы
где номер места шифртекста, на которое попадает первая буква исходного сообщения при выбранном преобразовании, номер места для второй буквы и т. д. В верхней строке таблицы выписаны по порядку числа от 1 до а в нижней — те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени
Зная подстановку, задающую преобразование, можно осуществить как зашифрование, так и расшифрование текста. Например, если для преобразования используется подстановка
и в соответствии с ней зашифровывается слово то получится Попробуйте расшифровать сообщение полученное в результате преобразования с помощью указанной выше подстановки.
В качестве упражнения читателю предлагается самостоятельно выписать подстановки, задающие преобразования в описанных ниже трех
примерах шифров перестановки. Ответы помещены в конце раздела.
Читатель, знакомый с методом математической индукции, может легко убедиться в том, что существует (обозначается читается факториал») вариантов заполнения нижней строки таблицы (6). Таким образом, число различных преобразований шифра перестановки, предназначенного для зашифрования сообщений длины меньше либо равно (заметим, что в это число входит и вариант преобразования, оставляющий все символы на своих местах!).
С увеличением числа значение растет очень быстро. Приведем таблицу значений для первых 10 натуральных чисел:
(см. скан)
При больших для приближенного вычисления можно пользоваться известной формулой Стирлинга
Примером ШП, предназначенного для зашифрования сообщений длины является шифр, в котором в качестве множества ключей взято множество всех подстановок степени а соответствующие им преобразования шифра задаются, как было описано выше. Число ключей такого шифра равно
Для использования на практике такой шифр не удобен, так как при больших значениях приходится работать с длинными таблицами.
Широкое распространение получили шифры перестановки, использующие некоторую геометрическую фигуру. Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного «маршрута», а затем по ходу другого выписывается с нее. Такой шифр называют маршрутной перестановкой. Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего угла поочередно слева направо и справа налево. Выписывать же сообщение будем по другому маршруту: по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.
Зашифруем, например, указанным способом фразу:
используя прямоугольник размера
(см. скан)
Зашифрованная фраза выглядит так:
Теоретически маршруты могут быть значительно более изощренными, однако запутанность маршрутов усложняет использование таких шифров.
Ниже приводятся описания трех разновидностей шифров перестановки, встречавшихся в задачах олимпиад.
Шифр «Сцитала». Одним из самых первых шифровальных приспособлений был жезл («Сцитала»), применявшийся еще во времена войны Спарты против Афин в V веке до н. э. Это был цилиндр, на который виток к витку наматывалась узкая папирусная лента (без просветов и нахлестов), а затем на этой ленте вдоль его оси записывался необходимый для передачи текст. Лента сматывалась с цилиндра и отправлялась адресату, который, имея цилиндр точно такого же диаметра, наматывал ленту на него и прочитывал сообщение. Ясно, что такой способ шифрования осуществляет перестановку местами букв сообщения.
Шифр «Сцитала», как видно из решения задачи 2.1, реализует не более перестановок по прежнему, — длина сообщения). Действительно, этот шифр, как нетрудно видеть, эквивалентен следующему шифру маршрутной перестановки: в таблицу, состоящую из столбцов, построчно записывают сообщение, после чего выписывают буквы по столбцам. Число задействованных столбцов таблицы не может превосходить длины сообщения.
Имеются еще и чисто физические ограничения, накладываемые реализацией шифра «Сцитала». Естественно предположить, что диаметр жезла не должен превосходить 10 сантиметров. При высоте строки в 1 сантиметр на одном витке такого жезла уместится не более 32 букв Таким образом, число перестановок, реализуемых «Сцита-лой», вряд ли превосходит 32.
Шифр «Поворотная решетка». Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера клеток. В трафарете вырезано тк клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.
Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке.
Поясним процесс шифрования на примере. Пусть в качестве ключа используется решетка приведенная на рис. 1.
Зашифруем с ее помощью текст
Наложив решетку на лист бумаги, вписываем первые 15 (по числу
вырезов) букв сообщения: Сняв решетку, мы увидим текст, представленный на рис. 2. Поворачиваем решетку на 180°. В окошечках появятся новые, еще не заполненные клетки. Вписываем в них следующие 15 букв. Получится запись, приведенная на рис. 3. Затем переворачиваем решетку на другую сторону и зашифровываем остаток текста аналогичным образом (рис. 4, 5).
Получатель сообщения, имеющий точно такую же решетку, без труда прочтет исходный текст, наложив решетку на шифртекст по порядку четырьмя способами.
Можно доказать, что число возможных трафаретов, то есть количество ключей шифра «решетка», составляет (см. задачу 1.1). Этот шифр предназначен для сообщений длины Число всех перестановок в тексте такой длины составит что во много раз
больше числа Однако, уже при размере трафарета число возможных решеток превосходит 4 миллиарда.
Широко распространена разновидность шифра маршрутной перестановки, называемая «шифром вертикальной перестановки» (ШВП). В нем снова используется прямоугольник, в который сообщение вписывается обычным способом (по строкам слева направо). Выписываются буквы по вертикали, а столбцы при этом берутся в порядке, определяемом ключом. Пусть, например, этот ключ таков: (5,4,1,7,2,6,3), и с его помощью надо зашифровать сообщение:
Впишем сообщение в прямоугольник, столбцы которого пронумерованы в соответствии с ключом:
(см. скан)
Теперь, выбирая столбцы в порядке, заданном ключом, и выписывая последовательно буквы каждого из них сверху вниз, получаем такую криптограмму:
Число ключей ШВП не более где число столбцов таблицы. Как правило, гораздо меньше, чем длина текста (сообщение укладывается в несколько строк по букв), а, значит, и много меньше
Пользуясь приведенной выше формулой Стирлинга при больших попытайтесь оценить, во сколько раз число возможных перестановок столбцами меньше числа всех перестановок на тексте длины кратном
В случае, когда ключ ШВП не рекомендуется записывать, его можно извлекать из какого-то легко запоминающегося слова или предложения. Для этого существует много способов. Наиболее распространенный состоит в том, чтобы приписывать буквам числа в соответствии с обычным алфавитным порядком букв. Например, пусть ключевым словом будет Присутствующая в нем буква А получает номер 1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает номер 2. Поскольку буквы в этом слове нет, то буква В получает номер 3 и так далее. Процесс продолжается до тех
пор, пока все буквы не получат номера. Таким образом, мы получаем следующий ключ:
Перейдем к вопросу о методах вскрытия шифров перестановки. Проблема, возникающая при восстановлении сообщения, зашифрованного ШП, состоит не только в том, что число возможных ключей велико даже при небольших длинах текста. Если и удастся перебрать все допустимые варианты перестановок, не всегда ясно, какой из этих вариантов истинный. Например, пусть требуется восстановить исходный текст по криптограмме и нам ничего не известно, кроме того, что применялся шифр перестановки. Какой вариант «осмысленного» исходного текста признать истинным:
lab-music.ru
Шифры перестановки
Этот метод заключается в том, что символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока символов, т.е. преобразования приводят к изменению только порядка следования символов исходного сообщения. Рассмотрим некоторые наиболее часто встречающиеся разновидности этого метода — простую, усложненную по таблице и усложненную по маршрутам перестановку.
Шифрование простой перестановкой (вертикальной перестановкой) осуществляется следующим образом:
выбирается ключевое слово с неповторяющимися символами;
шифруемый текст записывается последовательными строками под символами ключевого слова;
зашифрованный текст выписывается колонками в той последовательности, в которой располагаются в алфавите буквы ключа (или в порядке следования цифр в натуральном ряду, если ключ цифровой).
В качестве иллюстрации приведем пример шифрования способом простой перестановки сообщения: «БУДЬТЕ ОСТОРОЖНЫ С ПРЕДСТАВИТЕЛЕМ ФИРМЫ «ФЕНИКС». При этом применим цифровой ключ 5 – 8 – 1 – 3 – 7 – 4 – 6 – 2. В исходном тексте вместо пробелов используется буква а.
5 | 8 | 1 | 3 | 7 | 4 | 6 | 2 |
Б | У | Д | Ь | Т | Е | а | О |
С | Т | О | Р | О | Ж | Н | Ы |
А | С | а | П | Р | Е | Д | С |
Т | А | В | И | Т | Е | Л | Е |
М | а | Ф | И | Р | М | Ы | а |
Ф | Е | Н | И | К | С | а | а |
Выписывая текст по колонкам и группируя символы по пять, получаем зашифрованный текст в виде:
ДО ВФ
НОЫСЕ
ВФ
НОЫСЕ ЬРП
ИИИЕЖ ЕЕМСБ С
ЬРП
ИИИЕЖ ЕЕМСБ С ТМФ
ТМФ НДЛЫ
НДЛЫ TOPT
РКУТС A
TOPT
РКУТС A E
E .
.
Расшифрование выполняется в следующем порядке:
1) подсчитываем число знаков в зашифрованном тексте и делим на число знаков ключа;
2) выписываем ключевое слово и под его знаками в соответствующей последовательности выписываем символы зашифрованного текста в определенном выше количестве;
3) по строкам таблицы читаем исходный текст.
Число ключей не более m!, гдеm- число столбцов таблицы.
Слабость шифрования простой перестановкой обуславливается тем, что при большой длине шифруемого текста в зашифрованном тексте могут проявиться закономерности символов ключа. Для устранения этого недостатка можно менять ключ после зашифровки определенного числа знаков. При достаточно частой смене ключа стойкость шифрования можно существенно повысить. При этом, однако, усложняется организация процесса шифрования и расшифрования.
Для получения и запоминания числового ключа существуют различные методы. Один из самых распространенных состоит в том, чтобы приписывать буквам числа в соответствии с алфавитным порядком букв. Возьмем, например, слово ПЕРЕСТАНОВКА. Присутствующая в нем буква А получает №1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает №2. Буквы Б в этом слове нет, то буква В получает №3, и т.д.:
П | Е | Р | Е | С | Т | А | Н | О | В | К | А |
9 | 4 | 10 | 5 | 11 | 12 | 1 | 7 | 8 | 3 | 6 | 2 |
Усложнение перестановки по таблице заключается в том, что для записи символов шифруемого текста используется специальная таблица, в которую введены некоторые усложняющие элементы. Усложнение состоит в том, что определенное число клеток таблицы не используется (на рисунке они пусты). Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования. Шифруемый текст блоками по m х n –s элементов (mх n – размеры таблицы,s – число неиспользуемых элементов) записывается в таблицу. Далее шифрование аналогична простой перестановке.
2
6
1
3
8
0
5
9
4
7
Б
У
Д
Ь
Т
Е
а
О
С
Т
О
Р
О
Ж
Н
Ы
а
С
а
О
Р
Е
Д
С
Т
А
В
И
Т
Е
Л
Е
М
а
Ф
И
Р
М
Ы
а
Ф
Е
Н
И
К
С
а
а
а
а
А
а
а
Зашифрованный текст будет выглядеть
так: ДОПР БСВИК РРТМ
БСВИК РРТМ ОЫ
ОЫ
 Н
Н ЕНСЕФ
ЕНСЕФ  УТ
УТ И
СС
И
СС АФ
И
АФ
И ЬОЕ
ЕЫ
ЬОЕ
ЕЫ Т
МЕ
Т
МЕ ТЖДЛ.
ТЖДЛ.
При расшифровании знаки зашифрованного текста записываются столбцами таблицы в последовательности знаков ключа с пропуском неиспользуемых элементов. Исходный текст считывается по строкам. Варьируя размерами таблицы, последовательностью символов ключа, количеством и расположением неиспользуемых элементов, можно получить требуемую стойкость зашифрованного текста.
Еще один вариант — шифр «Поворотная решетка». предназначен для сообщений длины 4mk. Берется трафарет размером 2m*2kклеток, вырезаетсяm*kклеток так, что при наложении его на лист бумаги того же размера 4 различными способами (поворачивая на 90) его вырезы полностью покрывают всю площадь листа. Буквы сообщения последовательно вписываются в вырезы трафарета по строкам, в каждой строке слева направо, при каждом из 4-х его возможных положений в заранее установленном порядке. Число возможных трафаретов, т.е. количество ключей этого шифра составляет 4mk(при размере трафарета 8*8 число вариантов превосходит 4 миллиарда).
Весьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется несколько различных маршрутов. Для примера рассмотрим шифрование по маршругам Гамильтона при n =3. Структура и три маршрута показаны на Рис. 7, а пример шифрования – на Рис. 8.
Шифруемый текст: БУДЬТЕ ОСТОРОЖНЫ С ПРЕДСТАВИТЕЛЕМ ФИРМЫ ФЕНИКС
Зашифрованный текст: ТЕУБД ЬОаОС ОРТЖЫ НЕСПа …
Рис. 7 Пример структуры и маршрутов Гамильтона
Рис. 8 Пример шифрования по маршрутам Гамильтона
В 1991 г. В.М. Кузьмич предложил схему перестановки, основанную на кубике Рубика. Согласно этой схеме открытый текст записывается в ячейки граней куба по строкам. После осуществления заданного числа заданных поворотов слоев куба считывание шифртекста осуществляется по столбцам. Сложность расшифрования в этом случае определяется количеством ячеек на гранях куба и сложностью выполненных поворотов слоев. Перестановка, основанная на кубике Рубика, получила название объемной (многомерной) перестановки. В 1992 – 94 гг. идея применения объемной перестановки для шифрования открытого текста получила дальнейшее развитие. Усовершенствованная схема перестановок по принципу кубика Рубика, в которой наряду с открытым текстом перестановке подвергаются и функциональные элементы самого алгоритма шифрования, легла в основу системы «Рубикон». В качестве прообразов пространственных многомерных структур, на основании объемных преобразований которых осуществляются перестановки, в ней используются трехмерный куб и тетраэдр.
studfiles.net
Шифр вертикальной перестановки[править | править код]
Широкое распространение получила разновидность маршрутной перестановки — вертикальная перестановка. В этом шифре также используется прямоугольная таблица, в которую сообщение записывается по строкам слева направо. Выписывается шифрограмма по вертикалям, при этом столбцы выбираются в порядке, определяемом ключом.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки
КЛЮЧ: (3, 1, 4, 2, 5)
3 | 1 | 4 | 2 | 5 |
п | р | и | м | е |
р | м | а | р | ш |
р | у | т | н | о |
й | п | е | р | е |
с | т | а | н | о |
в | к | и |
КРИПТОГРАММА: рмупткмрнрнпррйсвиатеаиешоео
Заполнять последнюю строку таблицы «нерабочими» буквами нецелесообразно, так как криптоаналитик, получивший данную криптограмму, получает сведения о длине числового ключа[6].
Шифр вертикальной перестановки. Является разновидностью предыдущего шифра. К особенностям шифра можно отнести следующие:
— количество столбцов в таблице фиксируется и определяется длиной ключа;
— маршрут вписывания — строго слева-направо сверху-вниз;
— шифрограмма выписывается по столбцам в соответствии с их нумерацией (ключом).
Ключ | Д | Я | Д | И | Н | А |
2 | 6 | 3 | 4 | 5 | 1 | |
Текст | А | Б | Р | А | М | О |
В | _ | И | Л | Ь | Я | |
_ | С | Е | Р | Г | Е | |
Е | В | И | Ч | _ | _ |
Рис.5.5. Пример использования шифра вертикальной перестановки
В качестве ключа можно использовать слово или фразу. Тогда порядок выписывания столбцов соответствует алфавитному порядку букв в ключе. Например, если ключевым словом будет «ДЯДИНА», то присутствующая в нем буква А получает номер 1, Д – 2 и т.д. Если какая-то буква входит в слово несколько раз, то ее появления нумеруются последовательно слева направо. В примере первая буква Д получает номер 2, вторая Д – 3.
При шифровании сообщения «АБРАМОВ ИЛЬЯ СЕРГЕЕВИЧ» результат будет «ОЯЕ_АВ_ЕРИЕИАЛРЧМЬГ_Б_СВ».
studfiles.net
Перестановочный шифр — Википедия
Шифр перестано́вки — это метод симметричного шифрования, в котором элементы исходного открытого текста меняют местами. Элементами текста могут быть отдельные символы (самый распространённый случай), пары букв, тройки букв, комбинирование этих случаев и так далее. Типичными примерами перестановки являются анаграммы. В классической криптографии шифры перестановки можно разделить на два класса:
- Шифры одинарной (простой) перестановки — при шифровании символы открытого текста перемещаются с исходных позиций в новые один раз.
- Шифры множественной (сложной) перестановки — при шифровании символы открытого текста перемещаются с исходных позиций в новые несколько раз.
В качестве альтернативы шифрам перестановки можно рассматривать подстановочные шифры. В них элементы текста не меняют свою последовательность, а изменяются сами.
История
Точное время появления шифра перестановки не известно. Вполне возможно, что писцы в древности переставляли буквы в имени своего царя ради того, чтобы скрыть его подлинное имя или в ритуальных целях[1].
Одно из древнейших известных нам шифровальных устройств — Скитала. Бесспорно известно, что скитала использовалась в войне Спарты против Афин в конце V века до н. э.[2][3]
Прародителем анаграммы считают поэта и грамматика Ликофрона, который жил в Древней Греции в III веке до н. э. Как сообщал византийский автор Иоанн Цец, из имени царя Птоломея он составил первую из известных нам анаграмм: Ptolemaios — Аро Melitos, что в переводе означает «из мёда», а из имени царицы Арсинои — как «Ion Eras» (фиалка Геры)[4].
Шифры простой перестановки
Как правило, при шифровании и дешифровании шифра простой перестановки используется таблица перестановок:
Первая строка — позиция символа в открытом тексте, вторая строка — позиция в шифрограмме. Таким образом, при длине сообщения n{\displaystyle n} символов существует ровно n! {\displaystyle n!\ } ключей.
Шифры маршрутной перестановки
Широкое распространение получили так называемые маршрутные перестановки, использующие некоторую геометрическую фигуру (плоскую или объемную). Преобразования состоят в том, что отрезок открытого текста записывается в такую фигуру по некоторой траектории, а выписывается по другой траектории. Пример данного шифра — шифр Скиталы.
Шифр табличной маршрутной перестановки
Наибольшее распространение получили маршрутные шифры перестановки, основанные на прямоугольниках (таблицах). Например, можно записать сообщение в прямоугольную таблицу по маршруту: по горизонтали, начиная с верхнего левого угла, поочередно слева направо. Сообщение будем списывать по маршруту: по вертикалям, начиная с верхнего правого угла, поочередно сверху вниз.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки
| п | р | и | м | е |
| р | м | а | р | ш |
| р | у | т | н | о |
| й | п | е | р | е |
| с | т | а | н | о |
| в | к | и |
КРИПТОГРАММА: ешоеомрнрниатеаирмупткпррйсв
Обращение описанных шагов не представит труда при расшифровании[5].
Шифр вертикальной перестановки
Широкое распространение получила разновидность маршрутной перестановки — вертикальная перестановка. В этом шифре также используется прямоугольная таблица, в которую сообщение записывается по строкам слева направо. Выписывается шифрограмма по вертикалям, при этом столбцы выбираются в порядке, определяемом ключом.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки КЛЮЧ: (3, 1, 4, 2, 5)
| 3 | 1 | 4 | 2 | 5 |
| п | р | и | м | е |
| р | м | а | р | ш |
| р | у | т | н | о |
| й | п | е | р | е |
| с | т | а | н | о |
| в | к | и |
КРИПТОГРАММА: рмупткмрнрнпррйсвиатеаиешоео
Заполнять последнюю строку таблицы «нерабочими» буквами нецелесообразно, так как криптоаналитик, получивший данную криптограмму, получает сведения о длине числового ключа[6].
Шифр «поворотная решётка»
Решётка КарданоВ 1550 году итальянский математик Джероламо Кардано (1501—1576) в книге «О тонкостях» предложил новую технику шифрования сообщений — решётку.
Изначально решётка Кардано представляла собой трафарет с отверстиями, в которые записывали буквы, слоги или слова сообщения. Затем трафарет убирали, а свободное место заполняли более или менее осмысленным текстом. Такой метод сокрытия информации относится к стеганографии.
Позднее был предложен шифр «поворотная решётка» — первый транспозиционный (геометрический) шифр. Несмотря на то, что существует большая разница между изначальным предложением Кардано и шифром «поворотная решётка», методы шифрования, основанные на трафаретах, принято называть «решётками Кардано».
Четыре позиции решётки
Для шифрования и дешифрования с помощью данного шифра изготовляется трафарет с вырезанными ячейками. При наложении трафарета на таблицу того же размера четырьмя возможными способами, его вырезы полностью должны покрывать все клетки таблицы ровно по одному разу.
При шифровании трафарет накладывают на таблицу. В видимые ячейки по определённому маршруту вписывают буквы открытого текста. Далее трафарет переворачивают три раза, каждый раз проделывая операцию заполнения.
Шифрограмму выписывают из получившейся таблицы по определённому маршруту. Ключом являются трафарет, маршрут вписывания и порядок поворотов.
Данный метод шифрования использовался для передачи секретной информации нидерландскими правителями в 1740-х годах. Во время Первой мировой войны армия кайзера Вильгельма использовала шифр «поворотная решётка». Немцы использовали решётки разных размеров, однако очень недолго (четыре месяца), к огромному разочарованию французских криптоаналитиков, которые только-только начали подбирать к ним ключи. Для решёток разных размеров французы придумали собственные кодовые имена: Анна (25 букв), Берта (36 букв), Дора (64 буквы) и Эмиль (81 буква)[1][7].
Шифры сложной перестановки
В данном классе шифров перестановки используется идея многократной перестановки символов или повторного шифрования уже зашифрованного сообщения.
Шифр двойной перестановки
При шифровании шифром двойной перестановки в таблицу по определённому маршруту записывается текст, затем переставляются столбцы и строки. Далее по определённому маршруту выписывается шифрограмма.
Ключом к шифру являются размер таблицы, маршруты вписывания и выписывания, порядки перестановки столбцов и строк. Если маршруты являются фиксированными величинами, то количество ключей равно n!m!{\displaystyle n!m!}, где n{\displaystyle n} и m{\displaystyle m} — количество строк и столбцов в таблице[8].
ОТКРЫТЫЙ ТЕКСТ: двойная перестановка МАРШРУТ ВПИСЫВАНИЯ: слева - направо МАРШРУТ ВЫПИСЫВАНИЯ: сверху - вниз СТОЛБЦЫ: ( 3, 1, 4, 2) СТРОКИ: ( 3, 2, 4, 1, 5)
|
|
|
КРИПТОГРАММА: аавркопйстндевняоеа
Криптоанализ
При дешифровании текста используют частотные характеристики открытого текста. Однако для получения устойчивой картины длина послания должна быть существенно больше ключа. Одной из наиболее устойчивых характеристик осмысленного текста является отсутствие запретных биграмм (пара соседних букв). Например, биграммы «Ъ + Ь», «гласная + Ь», «пробел + Ь». Знание и использование частотной диаграммы открытого текста значительно упростит дешифрование шифра перестановки[9].
Примечания
- ↑ 1 2 Фред Б. Риксон, 2011.
- ↑ Фукидид. История I 131, 1.
- ↑ Дориченко, 1994.
- ↑ Lives of the Hellenistic Poets // Attalus: Sources for Greek and Roman history. (англ.)
- ↑ Алферов, 2002, с. 96.
- ↑ Алферов, 2002, с. 97.
- ↑ Бабаш, 2007.
- ↑ Алферов, 2002.
- ↑ Бабаш, 2007, с. 136.
Литература
- А. П. Алферов, А. Ю. Зубов, А. С. Кузьмин, А. В. Черёмушкин. Основы криптографии. — Гелиос АРВ, 2002. — ISBN 5-85438-137-0.
- А. В. Бабаш, Г. П. Шанкин. Криптография. — М. СОЛОН-ПРЕСС, 2007. — ISBN 5-93455-135-3.
- Фред Б. Риксон. Коды, шифры, сигналы и тайная передача информации. — Астрель, 2011. — ISBN 978-5-17-074391-9.
- Дориченко С. А., Ященко В. В. 25 этюдов о шифрах: Популярно о современной криптографии. — Теис, 1994. — ISBN 5-7218-0014-3.
wikipedia.green