Методы нахождения корней полинома в алгоритме пеленгования UCA Root Rare в пакете Mathcad
Рассмотрены два метода нахождения корней полинома, получаемого при выполнении алгоритма редукции ранга для пеленгования источников радиоизлучения UCA‑Root‑Rare. Продемонстрированы результаты численного моделирования. Приведён соответствующий листинг программ в пакете Mathcad.
Ключевые слова: UCA‑Root‑Rare, полином, Mathcad, polyroots, roots.
Введение. Определённый подкласс быстрых корреляционных алгоритмов оценивания координат источников излучения (ИИ), требует для своего применения выполнения поиска корней полиномов, степень, а соответственно и число корней, которых, в некоторых случаях, может быть более . В таких случаях, некоторые встроенные корни функции Mathcad не позволяют выполнить поиск решений.
Цель работы — используя свойства полинома, получаемого при выполнении алгоритма UCA‑Root‑Rare (Rare‑полином) [1], найти решения Rare‑полинома при помощи встроенных функций пакета Mathcad для произвольной степени полинома.
1.Алгоритм UCA‑Root‑Rare. Вычисление координат ИИ, в данном случае азимута, при помощи алгоритма UCA‑Root‑Rare, выполняется путём нахождения корней следующего полиномиального уравнения:
, (1)
где — определитель матрицы,
(2)
матрица размера ,
(3)
диагональная матрица размера , оператор диагонализации элементов,
. (4)
— это матрица отражений или антидиагональная единичная матрица:
. (5)
Используя (1)‑(3) и (5) матрица для будет иметь следующий вид:
. (6)
Матрица — это матрица собственных векторов, соответствующих подпространству шума корреляционной матрицы данных в пространстве лучей [2].
Исследование уравнения (1) показывает, что степень полинома будет , а следовательно уже для число корней Rare‑полинома будет равным .
2. Встроенные функции пакета Mathcad. Встроенные функции Mathcad в состоянии решить любое алгебраическое уравнение. Для решения уравнения с одним неизвестным можно использовать функции root и polyroots. Mathcad решает уравнения итерационным методом, поэтому перед решением необходимо задать начальное приближение для всех корней [3].
2.А. Функция root.
Функция root используется для решения одного уравнения с одним неизвестным. Обращение к функции: root(f(x)), где — выражение, равное нулю; — аргумент, варьируя который, система ищет значение, обращающее функцию в нуль. Функция и аргумент должны быть скалярами, то есть результат вычисления функции — число, а не вектор или матрица. Функция root использует итерационный метод секущих. Корень уравнения — ближайшее к начальному приближению значение , обращающее функцию в нуль. Если корней несколько, для отыскания каждого корня необходимо задавать свое начальное приближение. Если уравнение не имеет действительных корней, то есть функция нигде не равна нулю, то Mathcad выводит комплексное число [3].
2.А. Функция polyroots
Для нахождения корней полинома можно использовать функцию polyroots(K), которая определяет все корни полинома одновременно. Здесь — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. Если полином имеет корней (с учетом кратности), то вектор включает в себя коэффициент. Начальное приближение вводить не надо. Следует обратить внимание, что вектор должен содержать от до коэффициентов.
3. Получение оценок. Вэтом разделе рассматриваются оценки, получаемые при решении уравнения (1) при помощи функций polyroots и root.
3.А. Получение решений при помощи функции polyroots.
Как говорилось ранее, функция polyroots работает только с полиномами, степень которых не превышает . Накладываемое функцией polyroots ограничение позволяет применять её для решения уравнения (1) в случае, если параметр размера матрицы не превышает , что будет соответствовать корням. Для применение функции

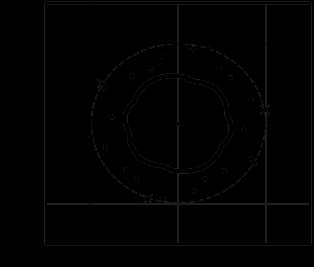
а) б)
Рис. 1. Решения Rare‑полинома при помощи функции: а) polyroots, ; б) root, . Азимут источников излучения , , .
3.А. Получение решений при помощи функции root.
Исследование уравнения (1) показывает, что истинными оценками азимута будут являться только те корни, которые максимально близко расположены к единичной окружности. Следовательно, для поиска корней полинома степени большей, чем можно применить функцию root, ограничив область поиска значениями, лежащими на единичной окружности взяв их с некоторым шагом. Для комплексной плоскости этим значениям будет соответствовать некоторый угол , косинус которого будет соответствовать действительной части числа, а синус мнимой. Ниже приведён листинг программы в пакете Mathcad реализующий поиск корней Rare‑полинома произвольной степени при помощи функции root.
Листинг 1. Нахождение корней Rare‑полинома произвольной степени
где — это соответствующий полном уравнения (1). В случае, если заданы только коэффициенты полинома, то необходимо преобразовать функцию в выражение, используя, например, следующий листинг:
Листинг 2. Преобразование коэффициентов полинома в выражение
где — это переменная полинома, — вектор столбец из действительных частей коэффициентов полинома, — вектор столбец из мнимых частей полинома. После применения листинга 2 необходимо выполнить листинг 1. Соответствующее решение уравнения (1) показаны на рисунке 1 б).
Одним из свойств корней Rare‑полинома, является то, что все его корни обладают так называемым свойством взаимной сопряжённости, которое означает, что если — это корень полинома, то также будет корнем полинома [4]. Иными словами, корни симметричны относительно единичной окружности, что можно наблюдать на рисунке 1 а). Для корней вблизи центра окружности, их парные корни находятся за пределами области построения графика, и охватывают окружность с наружи таким же плотным кольцом, как и корни вблизи центра окружности.
Поиск корней по методу, приведённому в листингах 1 и 2, даёт только один корень. Учитывать корень нет необходимости, однако при желании это возможно сделать, просто выполнив операцию для каждого найденного решения.
Следует также обратить внимание, на то, что полученные решения по листингам 1 и 2 получаются несколько искажёнными, а кольцо вблизи центра окружности на рисунке 1 б) имеет деформацию, в отличие от аналогичного кольца на рисунке 1 а). Такое различие может быть вызвано как большой дискретностью шага поиска, так и отличием методов поиска решений функций polyroots иroot.
Заключение. В статье были рассмотрены два варианта нахождения корней полинома, получаемого в результате нахождения определителя в уравнении (1). Приведён соответствующий листинг предлагаемых методов. На численном примере в графическом отображении показаны отличия, между нахождением корней полинома стандартными функциями пакета Mathcad polyroots иroot.
Литература:
1. Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.
2. Marple L. Digital spectral analysis with applications. New Jersey: Prentice-Hall, 1987. P. 492.
3. Макаров Е. Инженерные расчёты в Mathcad 15: Учебный курс — Спб.: Питер, 2011. — 400 с.: ил.
4. Li. H. Y., Xie J. L., He Z. S. A fast DOA estimation algorithm for uniform circular arrays in the presence of unknown mutual coupling // Progress In Electromagnetics Research C, 2011, Vol. 21, 257–271.
moluch.ru
Иллюстрированный самоучитель по MathCAD 12 › Нелинейные алгебраические уравнения › Уравнение с одним неизвестным: функция root [страница — 102] | Самоучители по математическим пакетам
Уравнение с одним неизвестным: функция root
Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.
- root(f(x),x);
- root (f (x), x, a, b):
- f(x) – скалярная функция, определяющая уравнение f(x)=0;
- х – имя скалярной переменной, относительно которой решается уравнение;
- а, b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.
Листинг 5.13. Два варианта уравнения методом секущих:
Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x),x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были «хорошими», т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.
samoychiteli.ru
функция root MathCAD 12 руководство
Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока
Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.
- root(f(x),x);
- root (f (x) , x, a, b);
- f(x) — скалярная функция, определяющая уравнение f(x)=0;
- х — имя скалярной переменной, относительно которой решается уравнение;
- а, b — границы интервала, внутри которого происходит поиск корня.
Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.
Листинг 5.13. Два варианта уравнения методом секущих
Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x) ,x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были «хорошими», т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.
Листинг 5.14. Пример уравнения, которое удается решить
только методом секущих
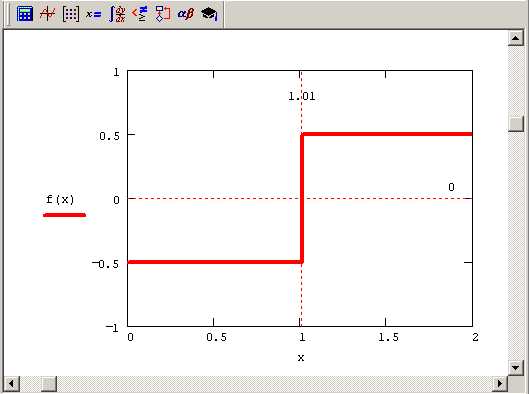
Рис. 5.5. Модельная функция f (х) (продолжение листинга 5.14)
Остается добавить, что f (х) может быть функцией не только х, а любого количества аргументов. Именно поэтому в самой функции
root необходимо определить, относительно какого из аргументов следует решить уравнение. Эта возможность проиллюстрирована листингом 5.15 на примере функции двух переменных f (x,y)=x2-y2+1. В нем сначала решается уравнение
f (х, 0) =0 относительно переменной х, а потом — другое уравнение
f (0, у) =0 относительно переменной у, причем, благодаря удачному подбору начальных значений, вычисляются все корни данного квадратичного уравнения.
Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой — как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки «This variable or function is not defined above», в данном случае говорящей о том, что другая переменная ранее не определена.
ПРИМЕЧАНИЕ
Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 5.3.3.
Листинг 5.15. Поиск корней уравнения, зависящего от двух
переменных
radiomaster.ru
функция root MathCAD 12 руководство
Итерационный алгоритм, реализованный в функции root, который называется методом секущих, состоит в следующем (рис. 5.7):
1. Начальное приближение принимается за 0-е приближение к корню: х0=х.
2. Выбирается шаг h=TOLх и определяется первое приближение к корню x1=x0+h. Если х=0, то принимается h=TOL.
3. Через эти две точки проводится секущая — прямая линия, которая пересекает ось х в некоторой точке х2. Эта точка принимается за второе приближение.
4. Новая секущая проводится через первую и вторую точки, тем самым определяя третье приближение, и т. д.
5. Если на каком-либо шаге оказывается, что уравнение выполнено, т. е. |f (х)|<TOL, то итерационный процесс прерывается, и х выдается в качестве решения.
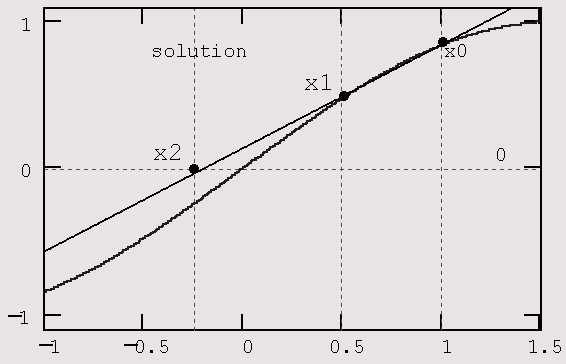
Рис. 5.7. Иллюстрация метода секущих
Результат, показанный на рис. 5.7, получен для погрешности вычислений, которой в целях иллюстративности предварительно присвоено значение
TOL=0.5. Поэтому для поиска корня с такой невысокой точностью оказалось достаточно одной итерации. В вычислениях, приведенных в листингах 5.13—
5.15 (см. разд. 5.2.2), погрешность TOL=0.001была установлена по умолчанию, и решение, выданное численным методом, лежало намного ближе к истинному положению корня. Иными словами, чем меньше константа TOL, тем ближе к нулю будет значение f (х) в найденном корне, но тем больше времени будет затрачено вычислительным процессором Mathcad на его поиск.
ПРИМЕЧАНИЕ
Соответствующий пример можно найти на компакт-диске, а также в Быстрых шпаргалках. Он расположен в разделе «Solving Equations» (Решение уравнений) и называется «Effects of TOL on Solving Equations» (Влияние константы TOL на решение уравнений).
Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума f (х). В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого положения корня. Для решения таких уравнений лучше применять другую встроенную функцию Minerr (см. разд. 6.2). Аналогичные проблемы могут возникнуть, если начальное приближение выбрано слишком далеко от настоящего решения или f (х) имеет особенности типа бесконечности.
radiomaster.ru