Правила перевода с использованием таблицы
Наиболее важные системы счисления (Таб. 1)
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. Пример. а) Перевести 305,48 в двоичную систему счисления. б) Перевести 7B2,E16 в двоичную систему счисления. Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) (Таб. 1) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой. Пример. а) Перевести 1101111001,11012 в восьмеричную систему счисления. б) Перевести 11111111011,1001112 в шестнадцатеричную систему счисления. Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад (Таб. Пример. Перевести 175.248 в шестнадцатеричную систему счисления. Результат: 175,248 = 7D,516. | |||||||||||||||||
4.9. Сводная таблица переводов целых чисел из одной системы счисления в другую
Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:
На этом рисунке использованы следующие обозначения:
в кружках записаны основания систем счисления;
стрелки указывают направление перевода;
номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 4.
 1.
1.
Например: означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.
Сводная таблица переводов целых чисел Таблица 4.1.
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
С л о ж е н и е
Таблицы сложения легко составить, используя Правило Счета.
Сложение в двоичной системе | Сложение в восьмеричной системе |
Сложение в шестнадцатиричной системе
При
сложении цифры суммируются по разрядам,
и если при этом возникает избыток, то
он переносится влево.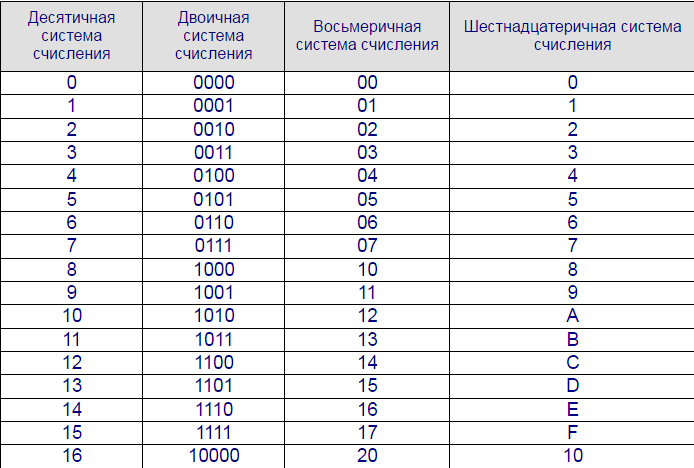
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
Шестнадцатеричная:F16+616 | Ответ:15+6 = 2110= 101012= 258= 1516.Проверка.Преобразуем полученные
суммы к десятичному виду:
101012= 24+ 22+ 20= 16+4+1=21,
258= 2.81+ 5.80= 16 +
5 = 21,
1516= 1.16 |
Пример 2. Сложим числа 15, 7 и 3.
Шестнадцатеричная:F16+716+316 | Ответ:5+7+3 = 2510= 110012= 318= 1916. |
Пример 3. Сложим числа 141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416Проверка. Преобразуем полученные суммы к десятичному
виду:
11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25
311,28 = 3.82 + 181 + 1.80 + 2.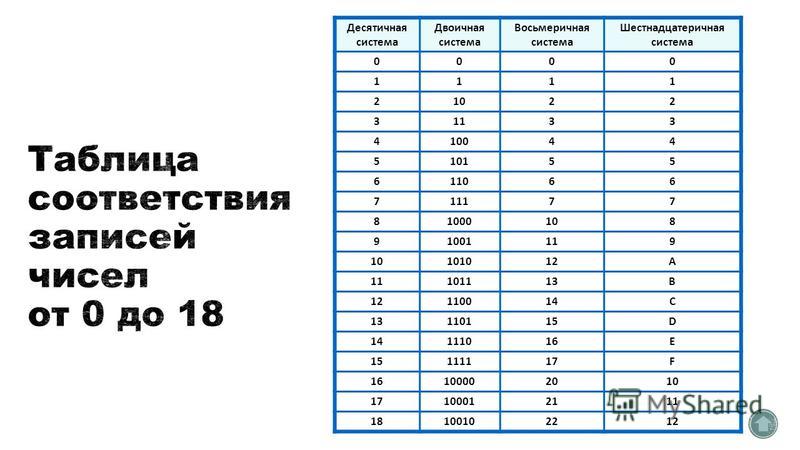 8-1 = 201,25
C9,416 = 12.161 + 9.160 + 4.16-1
8-1 = 201,25
C9,416 = 12.161 + 9.160 + 4.16-1
В ы ч и т а н и е
Пример 4. Вычтем единицу из чисел 102, 108 и 1016 Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016. Пример 6. Вычтем число 59,75 из числа 201,25.
Ответ: 201,2510 — 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816. Проверка. Преобразуем полученные разности к
десятичному виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2.82 + 1. 81 + 5.80 + 4. 8-1 = 141,5;
8D,816 = 8.161 + D.160 + 8.16-1 = 141,5.
81 + 5.80 + 4. 8-1 = 141,5;
8D,816 = 8.161 + D.160 + 8.16-1 = 141,5.
У м н о ж е н и е
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение в двоичной системе | Умножение в восьмеричной системе |
Ввиду чрезвычайной
простоты таблицы умножения в двоичной
системе, умножение сводится лишь к
сдвигам множимого и сложениям.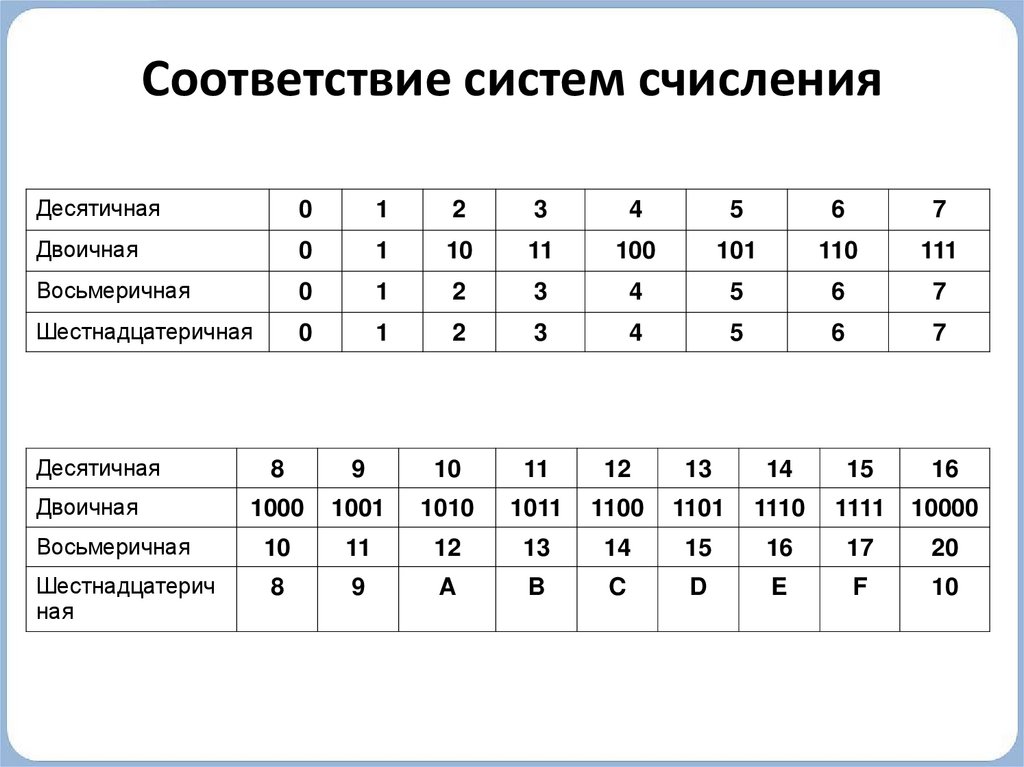
Пример 7. Перемножим числа 5 и 6.
Ответ: 5.6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду: 111102 = 24 + 23 + 22 + 21 = 30; 368 = 381 + 680 = 30.
Пример 8. Перемножим числа 115 и 51.
Ответ: 115.51 = 586510 = 10110111010012 = 133518. Проверка. Преобразуем полученные произведения
к десятичному виду:
10110111010012 = 212 + 210 + 2 9 + 27 + 26 + 25 + 23 + 20 = 5865;
133518 = 1.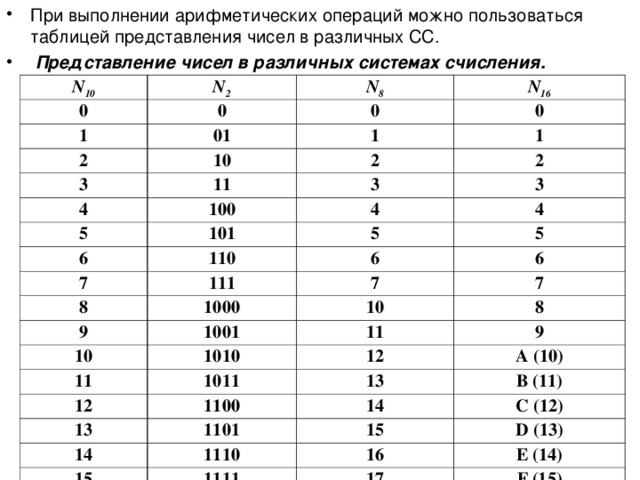 84 + 3.83 + 3.82 + 5.81 + 1.80 = 5865.
84 + 3.83 + 3.82 + 5.81 + 1.80 = 5865.
Д е л е н и е
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей. Пример 9. Разделим число 30 на число 6.
Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 10. Разделим число 5865 на число 115.
Восьмеричная: 133518 :1638
Ответ: 5865 : 115 = 5110 = 1100112 = 638.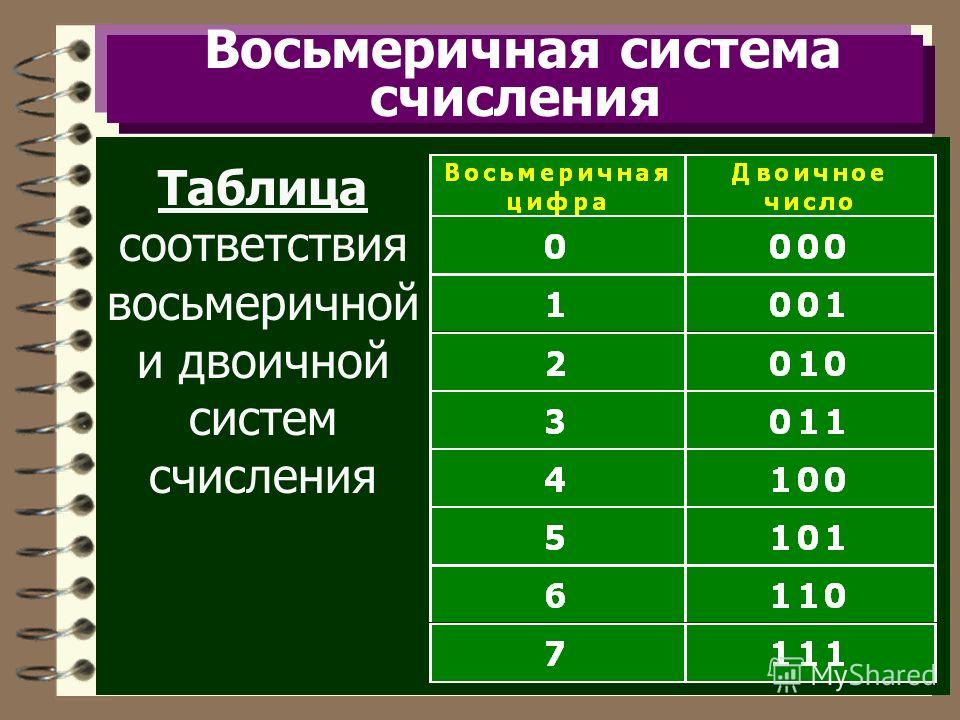 Проверка. Преобразуем полученные частные к
десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6.81 + 3.80 = 51.
Проверка. Преобразуем полученные частные к
десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6.81 + 3.80 = 51.
Пример 11. Разделим число 35 на число 14.
Восьмеричная: 438 : 168
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду: 10,1 2 = 21 + 2 -1 = 2,5; 2,48 = 2.80 + 4.8-1 = 2,5.
№ 2535: Таблицы умножения
Компьютерам легче всего работать с двумя цифрами — нулем и единицей. Эти «двоичные числа» называются «битами». Чтобы записать возраст Вселенной, требуется тридцать четыре бита. Это больше, чем одиннадцать в нашей десятичной системе, но у компьютера гораздо более простая таблица умножения: ноль умножить на ноль, ноль умножить на единицу и один умножить на единицу. Вот оно!
Эти «двоичные числа» называются «битами». Чтобы записать возраст Вселенной, требуется тридцать четыре бита. Это больше, чем одиннадцать в нашей десятичной системе, но у компьютера гораздо более простая таблица умножения: ноль умножить на ноль, ноль умножить на единицу и один умножить на единицу. Вот оно!
Широко распространено мнение, что мы используем десять цифр, потому что именно столько у нас пальцев. Это более чем необходимо для хорошей, работоспособной системы счисления. Я бы предпочел восьмерку. Но я просто рад, что мы не родились с двадцатью пальцами. Я бы никогда не разобрался со своей таблицей умножения.
Я Энди Бойд из Хьюстонского университета, где нас интересует, как работают изобретательные умы.
[аудио: три — магическое число]
Чтобы узнать о связанных эпизодах, см. БОЛЬШИЕ ЦИФРЫ и НОЛЬ среди многих других.
Системы счисления, обсуждаемые в этом выпуске, известны как позиционные системы . Позиционные системы счисления работают путем выбора базы , которая равна количеству цифр в системе. Положение цифры в строке цифр соответствует степени основания.
Позиционные системы счисления работают путем выбора базы , которая равна количеству цифр в системе. Положение цифры в строке цифр соответствует степени основания.
Например, в нашей стандартной десятичной системе счисления мы имеем
52 907 (с основанием десять) =
5 x 10 4 + 2 x 10 3 + 9 x 10 2 + 0 x 10 1 + 7 x 10 0
В базе восемь у нас есть
147 253 (с основанием восемь) =
1 x 8 5 + 4 x 8 4 + 7 x 8 3 + 2 x 8 2 + 5 x 8 1 + 3 x 8 0 .
Заметьте, что оба эти числа, 52 907 (с основанием десять) и 147 253 (с основанием восемь), представляют одно и то же количество; они просто выражаются в двух разных системах счисления.
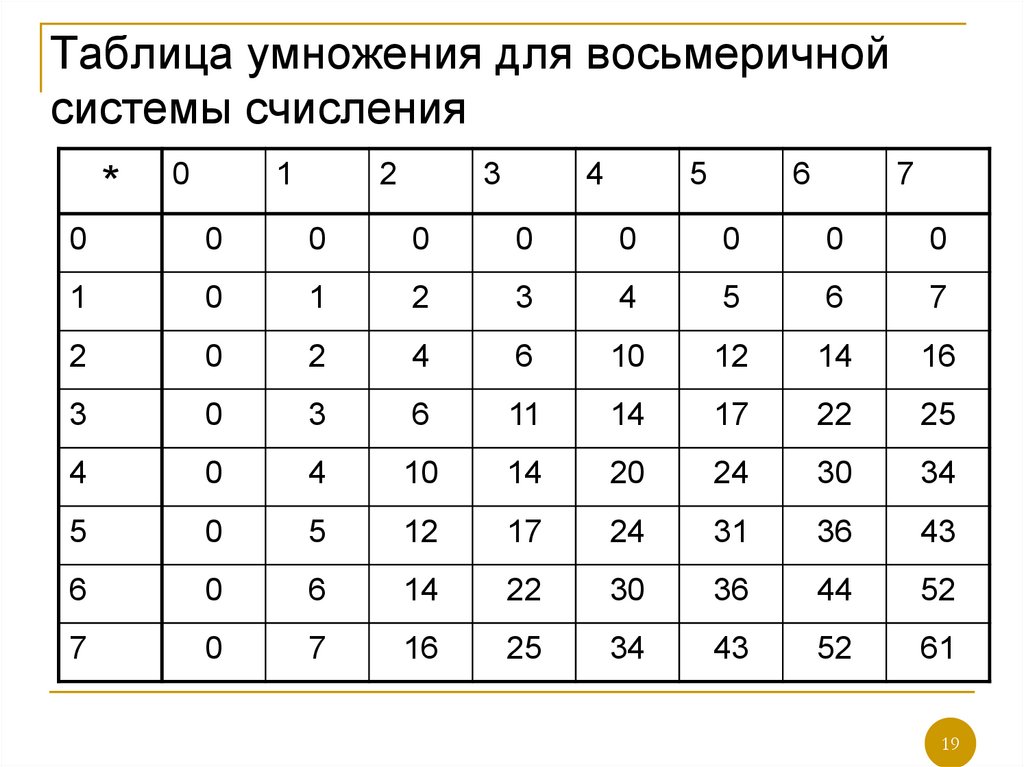
Таблицы времени для двоичной (с основанием два), четверичной (с основанием четыре), восьмеричной (с основанием восемь) и десятичной (с основанием десять) систем счисления показаны ниже.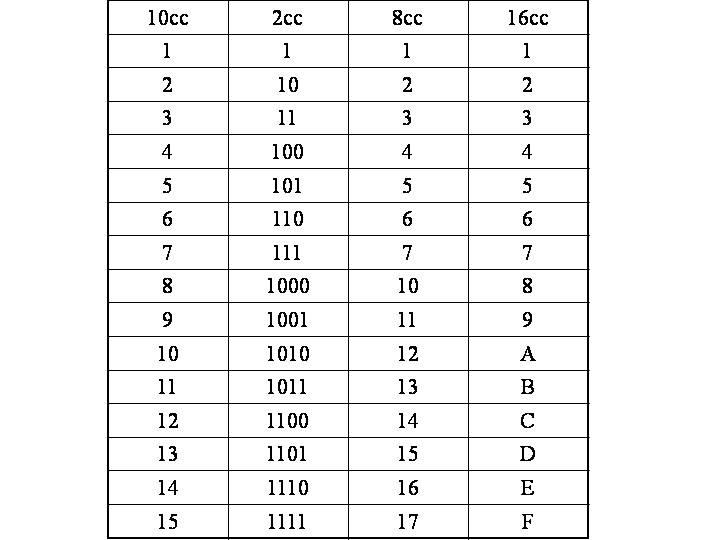 Обратите внимание, что нужно запомнить только немногим более половины значений в этих таблицах, поскольку изменение порядка умножения на обратный не меняет результат (например, 6 x 8 = 8 x 6).
Обратите внимание, что нужно запомнить только немногим более половины значений в этих таблицах, поскольку изменение порядка умножения на обратный не меняет результат (например, 6 x 8 = 8 x 6).
Следует отметить, что однозначные дополнительные таблицы, подобные таблицам умножения, также необходимы для овладения базовой арифметикой, но не обсуждаются в этом эпизоде. Большинство людей осваивают эти таблицы без особых проблем.
Для получения дополнительной информации о позиционных системах счисления см., например, http://en.wikipedia.org/wiki/Positional_notation.
Изображения таблиц умножения взяты с веб-сайта http://www.cut-the-knot.org/blue/SysTable.shtml.
Двигатели нашей изобретательности Copyright © 1988-2009 Джон Х. Линхард.
Предыдущий Эпизод | Индекс | Дом | Далее Эпизод
Система счисления и базовые преобразования
Электронные и цифровые системы могут использовать различные системы счисления (например, десятичную, шестнадцатеричную, восьмеричную, двоичную) или даже двенадцатеричную или менее известную, но лучше называемую унциальной. Все остальные базы, кроме Decimal, являются результатом использования компьютера. Унциал (названный от латыни для 1/12 «uncia», аналог десятичной системы с основанием двенадцати от латинского слова для 1/10 «decima»).
Все остальные базы, кроме Decimal, являются результатом использования компьютера. Унциал (названный от латыни для 1/12 «uncia», аналог десятичной системы с основанием двенадцати от латинского слова для 1/10 «decima»).
Число N по основанию или основанию b может быть записано как:
(N) b = d n-1 d n-2 -- -- -- -- d 1 d 0 . d -1 d -2 -- -- -- -- d -m
В приведенном выше примере от d n-1 до d 0 — целая часть, затем следует точка , а затем от d -1 до d -m — дробная часть.
d n-1 = старший бит (MSB)
d -m = младший значащий бит (LSB)
Как преобразовать число из одной базы в другую?
Следуйте Примеру Иллюстрации:
1. Десятичный до двоичного до двоичного
(10,25) 10
Примечание.
(0,25) 10 = (0,01) 2
Ответ: (10,25) 10 = (1010,01) 2
2. Двоично-десятичный
(1010,01) 2 1x2 3 + 0x2 2 + 1x2 1 + 0x2 0 + 0x2 -1 + 1x2 -2 = 8+0+2+0+1+0.0,0. (1010,01) 2 = (10,25) 10
3. От десятичной до восьмеричной
(10,25) 10 (10) 10 = (12) 8 Дробная часть: 0,25 x 8 = 2,00
Примечание: Продолжайте умножать дробную часть на 8, пока не получится десятичная часть 0,00.
(.25) 10 = (.2) 8
Ответ: (10,25) 10 = (12,2) 8
4. Octal to Decimal
998 (12.2)4. Octal to Decimal
98 (12.2)4.
1 x 8 1 + 2 x 8 0 +2 x 8 -1 = 8+2+0,25 = 10,25 (12.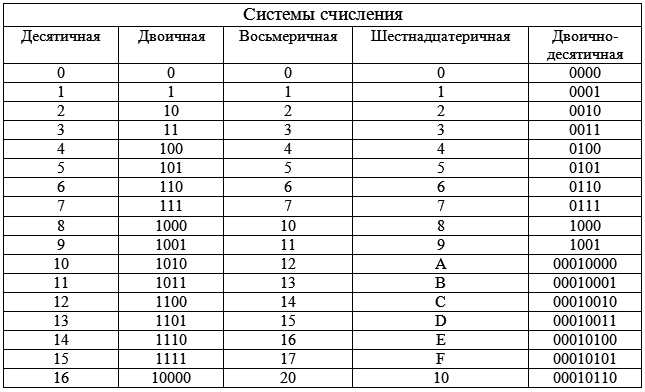 2) 8 = (10.25) 10
2) 8 = (10.25) 10 5. Шестнадцатеричное число в двоичное
Чтобы преобразовать шестнадцатеричное число в двоичное, напишите 4-битный двоичный эквивалент шестнадцатеричного числа.
(3A) 16 = (00111010) 2
6. Двоичный код в шестнадцатеричный
шестнадцатеричный для 4-битного двоичного кода. Добавьте дополнительные 0 слева, чтобы настроить группы.
1111011011 0011 1101 1011 (001111011011 ) 2 = (3DB) 16
7. Двоичный в восьмеричный
Чтобы преобразовать двоичное число в восьмеричное, начните группировать биты в группы по 3 с правого конца и запишите эквивалентное восьмеричное число для 3-битного
двоичного числа. Добавьте 0 слева, чтобы настроить группы.
Пример:
111101101
111 101 101
(111101101) 2 = (955)
.

 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.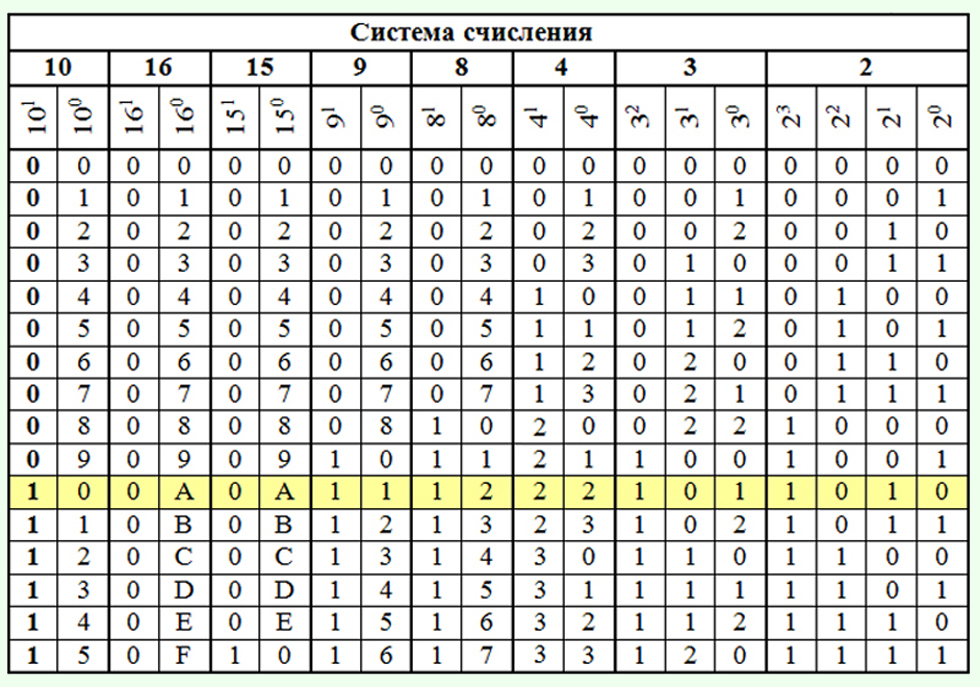 1).
1). Проверка:110012= 24+ 23+ 20= 16+8+1=25,
318=
3.81+ 1.80= 24 + 1 = 25,
1916= 1.161+ 9.16 0=
16+9 = 25.
Проверка:110012= 24+ 23+ 20= 16+8+1=25,
318=
3.81+ 1.80= 24 + 1 = 25,
1916= 1.161+ 9.16 0=
16+9 = 25.