This is the basic idea of the article. Ontological and epistemological limits of physical and mathematical formalization in landscape studies do not allow to say that the latter can be fully represented and interpreted within the framework of the so-called geophysical paradigm, which is the subject of the article of V. V. Sysuev. (Izvestiya RGO, 2019, vyp. 4, p. 6183).</p>landscape sciencemathematical formalizationtheory of setsexistencialismландшафтоведениематематическая формализациятеория множествэкзистенциализм1.Borzenkow V. G. Imeetsya li buduschee u reduktsii kak osnovaniya nauchnogo znaniya? // Buduschee fundamentalʼnoi nauki: Kotseptualʼnye, filosofskie i sotsialʼnye aspekty problemy. M.: KRASAND, 2011. S. 108-131.2.Burbaki N. Teoriya mozhestw. 2-е izd. M.: Knizhnyi dom «Librokom», 2010. 456 s.3.Veilʼ G. Matematicheskoe myshlenie. M.: Nauka, 1989. 400 s.4.Vopenka P. Alʼternativnaya teoriya mnozhestv: Novyi vzglyad na beskonechnostʼ. Novosibirsk: Izdatelʼstvo Instituta matematiki, 2004.
612 s.5.Grodzynsʼkyi M. D. Piznannya landshaftu: mistse i prostir. К.: Vydavnycho-poligrafichnyi tsentr «Kyїvsʼkyi universytet», 2005. T. 1. 431 s.6.Каntor G. Trudy po teorii mnozhestv. М.: Nauka, 1985. 430 s.7.Mesudi A. Kulʼturnaya evolyutsiya. Kak teoriya Darvina mozhet prolitʼ svet na chelovecheskuyu kulʼturu i obʼedenitʼ sotsialʼnye nauki. М.: Izdatelʼskii dom «Delo», 2019. 384 s.8.Neef E. Теоreticheskie osnovy landshaftovedeniya М.: Progress, 1974. 220 s.9.Peter R. Igra s beskonechnostʼyu. Matematika dlya nematematikow. М.: Prosveschenie, 1967. 272 s.10.Sysuev V. V. Geofizicheskaya paradigma landshaftovedeniya: postulaty i kontseptsii // Izvestiya RGO. 2019. T. 151, vyp. 4. S. 61-83.11.Turchin P. Istoricheskaya dinamika: na puti k teoreticheskoi istorii. 2-е izd. М.: Izdatelʼstvo «LKI», 2010. 368 s.12.Tyutyunnik Yu. G. Landshaft i landshaftnostʼ. К.: Institut evolyutsionnoi ekologii NAN Ukrainy, 2019. 124 s.13.Cherkashin A. K. Polisistemnyi analiz i sintez. Prilozhenie v geografii.
Novosibirsk: Nauka, 1997. 502 s.СТРУКТУРА (в математике) это
В алгебре наз. С. (или решеткой) множество М, рассматриваемое вместе с двумя двухместными операциями (первой, условно называемой часто сложением и обозначаемой знаком +, второй, условно называемой умножением и обозначаемой соответственно знаком + или отсутствием знака), если выполняются три пары тождеств: [тождества (1) наз. законами коммутативности, тождества (2) – законами ассоциативности, тождества (3) – законами поглощения]. С. часто наз. также упорядоченное множество (см. Порядка отношение), в к-ром для любых двух элементов а и b: (I) есть такой элемент sup (а, b), к-рый обладает свойствами: a ? sup (a, b), b ? sup (a, b), если a ? x и b ? x, то sup (a, b) ? x; и (II) есть такой элемент inf (a, b), к-рый обладает свойствами: inf (а, b) ? a, inf (a, b) ? b, если x ? a и x ? b, то x ? inf (a, b) [элемент sup (a, b) наз. точной верхней границей, или верхней гранью, элементов а и b, элемент inf (а, b) – их точной нижней границей, или нижней гранью].
Если множество M вместе с двумя операциями является С. в первом смысле, то, определив на M отношение x ? у ? df x + у = у (где ? df – знак тождественности по определению), мы получим упорядоченное множество, являющееся С. во втором смысле [а именно, sup (a, b) = a + b; inf (a, b) = ab]. И обратно: если в упорядоченном множестве, являющемся С. во втором смысле, определить операции х + у ? df sup (x, у), x · y ? df inf (x, y), мы получим С. в первом смысле. С. наз. дистрибутивной, если в ней выполняется тождество x (y + z) = xy + xz (4) Дистрибутивная С. наз. б у л е в о й, если в ней, во-первых, есть два спец. элемента (первый из них можно условно назвать нулем и обозначить знаком 0, второй – единицей и обозначить, соответственно, знаком 1 ) такие, что х + 0 = х, х · 1 = х (5) и, во-вторых, для любого элемента x есть такой элемент х´, что x + х´ = 1, х + х´ = 0 (6) (элемент х´ наз. дополнением элемента х). Булевы С. наз. также булевыми а л г е б р а м и (или алгебрами Буля, см. Алгебра логики).
Важнейшим примером булевой С. является система всех подмножеств произвольного множества А, рассматриваемая вместе с операциями теоретико-множественного объединения и пересечения. Единицей этой С. является само множество А, нулем – пустое множество ?, дополнением произвольного подмножества X множества А является их разность: А X. В трактате Н. Бурбаки «Начала математики» (пер. с франц., М., 1965) слово С. является частью термина «структура данного рода» и родств. терминов. В свою очередь, термин «структура данного рода» определяется контекстуально. Если элемент нек-рого множества M, построенного из каких-то исходных множеств при помощи двух операций (прямого произведения и перехода к множеству всех подмножеств), обладает определ. свойствами, то говорят, что этот элемент задает на исходных множествах С. данного рода. Примерами С., или точнее родов структур, являются алгебраич. С. (группы, кольца и т.д.), топологич. С., структуры упорядоченного множества и т.п. Лит.: Курош А.
Г., Лекции по общей алгебре, М., 1962; Бурбаки Н., Теория множеств, пер. с франц., М., 1965 (Начала математики, ч. 1, кн. 1). Ю. Шиханович. Москва.1.5.1. Понятие об алгебраических структурах
В математике и различных её приложениях важную роль играют такие математические объекты, которые называются алгебраическими структурами. Изучением их свойств занимается целый большой раздел математики – Высшая алгебра.
В широком смысле под алгебраической структурой понимают всякое множество, на котором заданы некоторые операции (т. е. законы, ставящие в соответствие одному или паре элементов по определённому правилу другой элемент), обладающие определёнными свойствами.
Примеры таких структур постоянно возникают в различных разделах математики. Это прежде всего:
1) Различные числовые множества с обычными операциями +, · на них.
2) Векторы с операциями [ · , · ], +, умножение на число.
3) Матрицы с операциями +, · , умножение на число.
4) Булева алгебра множеств с операциями , дополнение.
5) Множество функций (отображений) из R В R c операциями +, · , композиция.
6) Решётки (наличие sup и inf определяет наличие двух операций: (A,B) ® sup(A,B) и (A,B) ® inf(A,B) ).
Большинство свойств и результатов об этих множествах мы получаем, в основном опираясь на конкретную природу элементов этих множеств и на конкретный смысл операций над ними. В то же время многие результаты можно получить независимо от природы этих множеств и конкретного смысла операций, а исходя только из свойств этих операций.
Среди таких свойств таких операций рассматриваются: ассоциативность, коммутативность, дистрибутивность, наличие специальных элементов, обладающих определёнными свойствами (нулевой, единичный (нейтральный), обратный элемент к данному и т. д.).
В зависимости от количества операций и свойств, которыми они обладают, различают следующие алгебраические структуры.
1. Полугруппой Называется множество G, на котором задана бинарная операция * (часто её называют умножением и обозначают · ), для которой выполняется свойство ассоциативности, т. е.
« a, b,c Î G (A*B) *C = a*(B*C)
Примеры.
1. Множество отображений f : A®A с операцией произведение.
2. Множество отношений R A2 с операцией произведение отношений.
Если в полугруппе имеется нейтральный элемент Е (нулевой, единичный), т. е. такой, что A*E=e*A=a «AÎG, то полугруппа G называется Унитарной (полугруппой с нулём; полугруппой с единицей).
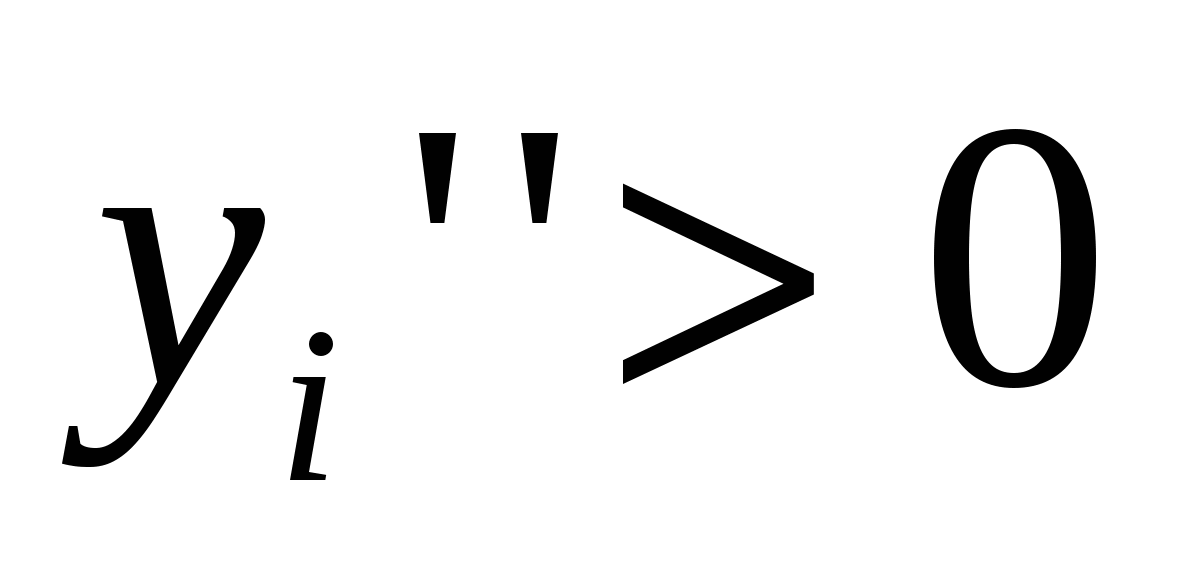
Унитарная полугруппа называется Группой, если «АÎG существует обратный элемент B G, т. е. такой, что A*B = b*A = e.
Таким образом, в группе G Должны выполняться три свойства:
1. Ассоциативность.
2. Существование нейтрального элемента.
3. Существование обратного элемента для любого элемента из G.
Если дополнительно выполняется свойство коммутативности, то группа называется Коммутативной (или Абелевой), и в этом случае обычно применяется аддитивная символика, т. е. операция обозначается +, нейтральный элемент 0, обратный элемент к A Называют противоположным и обозначается: -а.
Примеры.
1) Множество натуральных чисел N — унитарная абелевая полугруппа относительно обычной операции умножения чисел. В то же время N — абелевая полугруппа относительно сложения +.
2) Множество целых чисел Z — абелевая группа относительно +.
3) Q \{0} — абелевая группа относительно операции умножения чисел.
4) Sn – множество подстановокНа N Элементах с операцией произведение подстановок — группа, но не абелева. Эта группа называется симметрической группой степени N.
Множество элементов конечной группы называется ее порядком. Из подсчета количества различных подстановок следует, что порядок симметрической группы ½Sn½= n!
5) Пусть G – множество движений квадрата переводящих его в себя (к которым относятся повороты, симметрии и их композиции). Нетрудно проверить, что
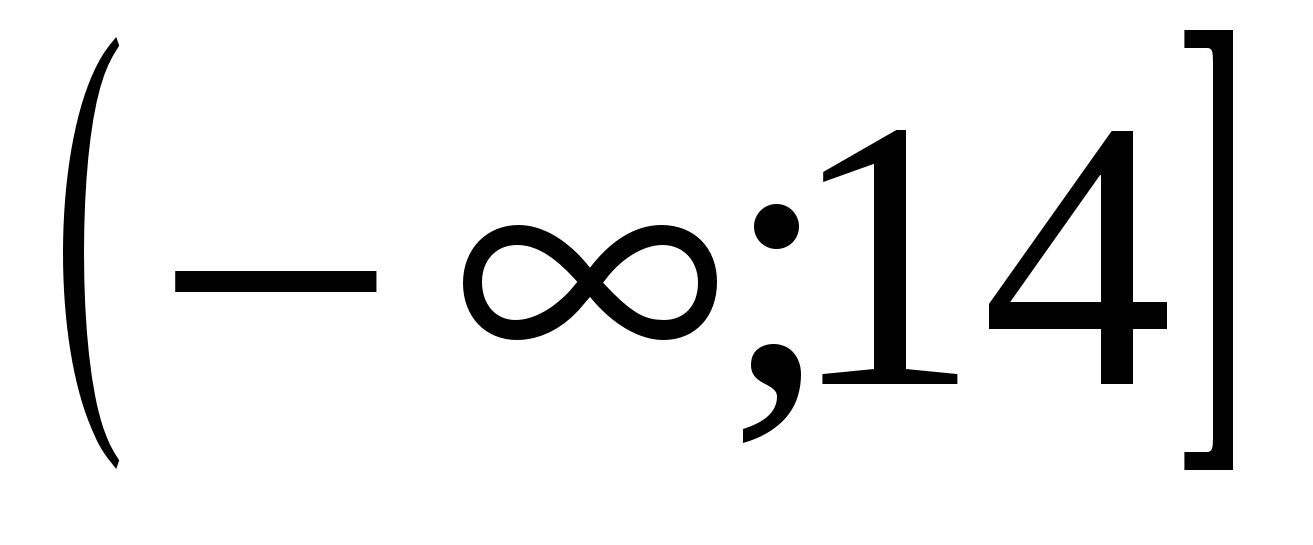Легко видеть также, что в данной группе выполняются соотношения: JI4 = e, si2 = e и все произведения поворотов и симметрий являются перечисленными поворотами и симметриями.2. Если в абелевой группе (К , +) наряду с операцией сложения + задана ещё одна операция: произведение * (или · ), которая связана с + дистрибутивными законами :
(A+b)*C=(A*C)+(B*C) , a* (B+c)=(A*B)+(A*C) » a,B,C K
и 0*A=A*0=0 » A K,
То К называется Кольцом.
Если в кольце (К, +, *) дополнительно для произведения * выполняется ассоциативный закон, т. е. если
(A* B) *C=A*(B*C) » A,B,C K,
То кольцо называется Ассоциативным.
А если кроме того $ единичный элемент 1, т. е. такой, что 1*A = A*1=A « aÎ K, то кольцо называется Унитарным (или кольцом с 1). Если в кольце выполняется коммутативный закон для *, то кольцо называется
Ассоциативное унитарное кольцо, в котором каждый ненулевой элемент A имеет обратный А-1, т. е. такой, что А*А-1 = А-1*А = 1 называется Телом.
Коммутативное тело называется Полем.
Примеры.
1) ( Z, +, · ) – коммутативное ассоциативное унитарное кольцо.
2) (Q, +, · ), (R, +, · ), (C, +, · ) – поля.
3) K[Х] – множество многочленов с коэффициентами из поля K c обычными операциями сложения и умножения многочленов – коммутативное ассоциативное унитарное кольцо.
4) Булеан (W(U), Å, Ç): нулевой элемент — Æ, единичный – U, противоположный элемент для множества А – само А, т.
к. А Å А = Æ, обратного элемента не существует. Таким образом это — ассоциативное коммутативное унитарное кольцо.
5) Тело кватернионов. Кватернионами называются выражения вида:
X = A + BI + CJ + DK ,
Где a, b, c, d Î R, и кроме того символы i, j, k Удовлетворяют соотношениям:
I2 = j2 = k2 = -1, ij = — ji = k,
jk = — kj = i,
ki = —Ik= J.
При этом A называется действительной (или скалярной) частью кватерниона X, а BI + cJ + dK — векторной частью. Два кватерниона складываются так же, как и векторы:
(A1 + B1I + C1J + D1K)+ (A2 + B2I + C2J + D2K) = (A1+ A2)
Соотношения между базисными элементами i, j, k позволяют естественным образом определить и операцию произведения кватернионов. Но уже из этих соотношений видно, что произведение – не коммутативно. Нетрудно, однако, проверить, что множество кватернионов с выше заданными операциями является телом. В частности обратным к кватерниону X = A + BI + CJ + DK Является кватернион
X-1= .
С помощью кватернионов очень изящно решаются задачи, связанные с композицией поворотов твердого тела в пространстве. Повороту вокруг вектора D = (B, c, d) на угол j поставим в соответствие кватернион a = A + bI
+ cJ + dK, где A = Cos. Если x = (X, y, z) – вектор, определяющий начальное положение тела, а вектор x’ = (X’, y’, z’) – после поворота, то можно показать, что x’ = a-1xa. Если совершается два поворота a и b, то общий результат определяется как произведение ab : x» = (ab)-1x(ab).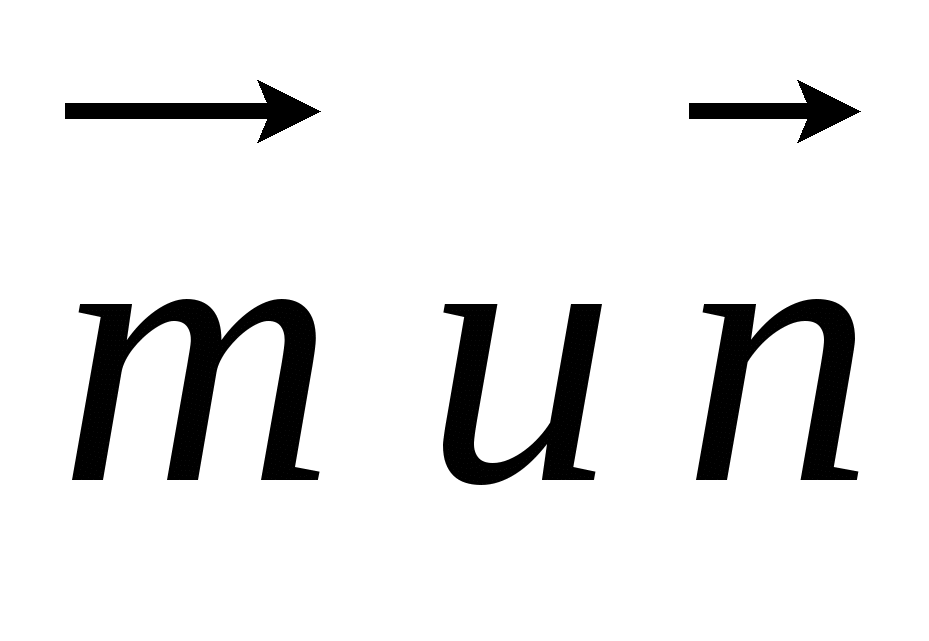
6) Пусть M – натуральное число. На множестве целых чисел определим следующее отношение эквивалентности: , если числа A и b имеют одинаковые остатки при делении на M (свойства рефлексивности, симметричности и транзитивности данного отношения очевидны). Обозначим через = – фактор-множество множества целых чисел Z по введенному отношению эквивалентности.
Определим на операции сложения и умножения определим следующим образом:
и
Можно показать, что определения корректны, т. е. результаты не зависят от выбора представителей классов – элементов
Если M – составное число, то в этом кольце существуют делители нуля. Пусть M = m1M2 , тогда , отсюда следует, что класс [M1] не имеет обратного (в противном случае получили бы . Значит, в данном случае кольцо классов вычетов не является полем. Но, если M = p – простое число, то – поле.
3. Алгебраические структуры с тремя операциями (и соответствующим набором свойств) называют Алгебрами.
Примеры.
1) Булева алгебра множеств с операциями (дополнение).
2) Алгебра матриц с операциями сложение, умножение и умножение на число.
Алгебраические структуры, на которых помимо операций заданы отношения, называются Алгебраическими системами.
Примером алгебраических систем могут служить решетки. В качестве операций можно рассматривать:
A+B = inf, A · B = sup
4. При изучении данных структур часто не важна природа элементов которые их составляют, а также конкретный смысл операций. В этом случае принято отождествлять алгебраические структуры, между которыми существует биекция, сохраняющая операции (т. е. такое отображение, при котором сумма переходит в сумму, произведение в произведение и т. д.):
Если F : GH – биекция структур (например, колец), причем
F(A + b) = f(A) + f(B) и F(Ab) = f(A) f(B) » a, b,c G,
То F Называется Изоморфизм, а G и H – Изоморфными (в этом случае пишут: GH).
Отношение изоморфности является отношением эквивалентности. Изоморфные структуры отождествляют, считают равными.
| < Предыдущая | Следующая > |
|---|
Норма, математика. Норма оператора A {\displaystyle A}
Пользователи также искали:
чебышевская норма,
кубическая норма,
l — норма,
норма градиента,
норма комплексного вектора,
норма матрицы,
норма вектора онлайн,
свойства нормы вектора,
Норма,
норма,
вектора,
кубическая норма,
чебышевская норма,
норма комплексного вектора,
норма градиента,
нормы,
норма матрицы,
норма вектора онлайн,
комплексного,
матрицы,
онлайн,
кубическая,
чебышевская,
градиента,
математика,
свойства,
Норма математика,
l — норма,
свойства нормы вектора,
норма (математика),
векторный анализ.
норма (математика),
ЕСТЬ ЛИ «ЦАРСКАЯ ДОРОГА» В МАТЕМАТИКЕ?
Даже если объяснять с предельнойясностью, кто-то все равно не поймет.
Следствие из третьего закона Чизхолма.
Наука и жизнь // Иллюстрации
Евклид — греческий математик, живший в IV—III веках до нашей эры.
Карл Теодор Вильгельм Вейерштрасс (1815—1897) — немецкий математик. Первым дал строгое доказательство основных свойств функций, непрерывных на отрезке.
Эдвин Эббот (1838 — 1926) — английский школьный учитель, который придумал страну Флатландию. Ее обитатели живут в двухмерном мире и не подозревают о существовании мира трехмерного.
Дионис Бюргер (1892 — 1987) — датский математик, автор книги “Сферландия”.
Персонажи мультфильма о Флатландии.
Ю. А. Данилов, благодаря переводам которого любители математики в нашей стране познакомились с книгами Эббота и Бюргера.
Треугольник ABC, который отсекает прямая от начала координат, после поворота на 90<SUP>°</SUP> переходит в треугольник А` В` С`. Его гипотенуза А` С` параллельна вектору нормали (a, b).
Эдвин Эббот (1838 — 1926) — английский школьный учитель, который придумал страну Флатландию. Ее обитатели живут в двухмерном мире и не подозревают о существовании мира трехмерного.
Дионис Бюргер (1892 — 1987) — датский математик, автор книги “Сферландия”.
Персонажи мультфильма о Флатландии.
Ю. А. Данилов, благодаря переводам которого любители математики в нашей стране познакомились с книгами Эббота и Бюргера.
Треугольник ABC, который отсекает прямая от начала координат, после поворота на 90<SUP>°</SUP> переходит в треугольник А` В` С`. Его гипотенуза А` С` параллельна вектору нормали (a, b).
‹
›
Те, кто изучал математику, наверное, помнят о Евклиде (в греческом написании — Eυκλειδης) — авторе фундаментального труда «Начала», в 15 книгах которого изложены аксиоматические основы геометрии (две книги, посвященные многогранникам, иногда приписывают Гипсилу Александрийскому).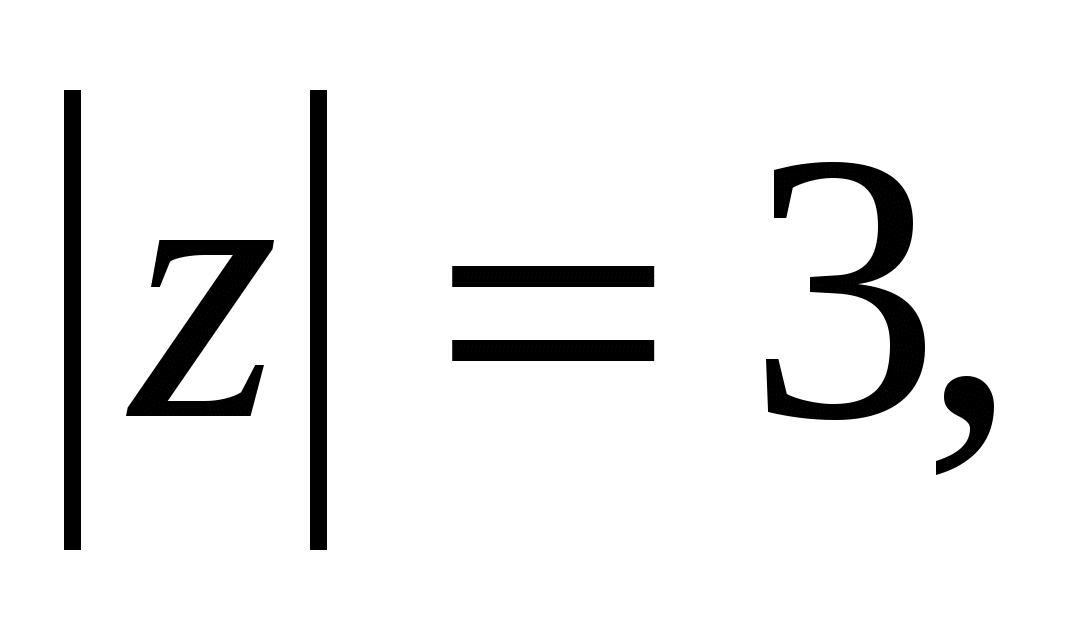
Предание гласит, что египетский правитель Птолемей I Сотер посетил мыслителя и поинтересовался, существует ли более короткий способ познания геометрии, чем тот, который изложен в «Началах». Ответ древнего мыслителя: «В науке нет царской дороги» — приводят как блестящий аргумент в пользу необходимости приложить немало усилий, чтобы освоить математику или любую другую науку.
А разве говорил великий Евклид, что изучение науки должно быть скучным? Конечно, нет. Но на практике получается, что многие предметы, в том числе и математика, ученикам кажутся неинтересными. Почему многие помнят историю про Евклида, а вот что такое логарифм, могут сформулировать с большим трудом? И стоит ли винить в этом нерадивых учеников, среди которых не то что царей, но и царских потомков малая доля?
В 1884 году увидела свет замечательная книга англичанина Эдвина Эббота «Флатландия» («Flatland» ), в увлекательной форме рассказавшая о многомерных пространствах. И хотя книга не предлагала «царского пути» в геометрии, она позволяла преодолеть эту дорогу с большими удобствами, чем классические учебники.
Вместо того чтобы формулировать теоремы и потом приводить их доказательства, автор создал образ необычной страны, обитатели которой не ведают о трехмерном пространстве так же, как нам не дано увидеть четырехмерный мир. Описание этого необычного государства занимает намного больше места, чем простая фраза вроде того, что «…в четырехмерном пространстве координаты точки задаются четырьмя числовыми значениями». Но зато у читателя появляется наглядное представление о том, как можно изучать четырехмерные пространства. Подчеркиваю, не наблюдать, а изучать. А когда такое представление получено, легче воспринять математический аппарат, который используется в строгом описании многомерных пространств.
СТРОГО, НО НЕПОНЯТНО
Наглядный подход облегчает понимание и других специальных понятий. В математике принято облекать в строгую абстрактную форму довольно простые вещи, которые можно объяснить «на пальцах» даже школьнику начальных классов. К сожалению, то, что просто показать, не всегда легко доказать.
В доказательствах не обойтись без развитого и сложного математического аппарата. Так, классическое определение непрерывной функции в математическом анализе выглядит не таким уж и легким:
Функция f(х) является непрерывной в точке х0, если:
1. Она определена в точке х0и некоторой окрестности этой точки.
2. Для любого числа ε > 0 можно указать такое число δ > 0, зависящее от е, что для всякого х, удовлетворяющего неравенству |х — х0| δ, следует, что |f(x) — f(х0)| ε.
Функция, непрерывная в каждой точке отрезка (интервала, полуинтервала и т.д.), называется непрерывной на этом отрезке (интервале, полуинтервале и т.д.).
Намного проще объяснить понятие непрерывной функции с помощью листа бумаги и карандаша. Достаточно нарисовать два графика: один — с непрерывной линией, другой — с точкой разрыва.
График гладкой непрерывной функции на отрезке [a, b].
График функции, имеющей разрыв в точке х0 отрезка [a, b].
Такой рисунок сразу позволяет понять: непрерывная функция потому и непрерывная, что ее график можно нарисовать одной линией, ни разу не отрывая карандаша от бумаги. Интересно, насколько меньше стало бы «хвостатых» студентов, если бы преподаватели уделяли часть времени наглядной подаче материала?
Возьмем другой пример — теорему Вейерштрасса. Она гласит:
Любая, непрерывная на отрезке функция является ограниченной и достигает на нем своего максимума и минимума.
Довольно очевидное утверждение, если подходить к нему с практических позиций. После одной-двух минут размышления любой студент скажет, что нарисовать график функции неограниченной и непрерывной на отрезке невозможно.
У непрерывной на отрезке функции всегда найдется минимум и максимум.
Но чтобы строго доказать это, нужно повторить ход рассуждений Карла Вейерштрасса — «отца» современного математического анализа.
Страдает отсутствием наглядности и классическое определение дифференцируемой, или, проще говоря, гладкой функции:
Функция f(х), определенная в некоторой окрестности точки х0, называется дифференцируемой в точке х0, если может быть представлена в виде
f(х)= f(х0) + C (х -х0) + о(x — х0),
где C — константа;
о(x — х0) — функция, пренебрежимо малая в сравнении с величиной (x — х0).
После такого определения быстренько доказывают теорему о том, что если функция дифференцируема в точке х0, то она имеет в этой точке конечную производную. Ну а затем объявляют функцию f(х) гладкой на интервале, если она дифференцируема в каждой точке этого интервала.
График функции, не дифференцируемой в точке х0.
Казалось бы, чего проще, нарисовать картинку с функцией, график которой имеет излом, а потом уже предложить вниманию учащихся строгое математическое определение? Но как раз на наглядное изложение материала времени в учебной программе обычно не предусмотрено.
Попробуйте нарисовать гладкую кривую, которая на концах отрезка принимает равные значения, но так, чтобы у нее не было точки, касательная к которой параллельна оси абсцисс. Не получается? Еще бы, такой кривой попросту не существует. Убедиться в этом с карандашом в руках может каждый. Но строгое доказательство приведено в теореме французского математика Мишеля Ролля (1652—1719):
Если функция, непрерывная на отрезке [a, b] и дифференцируемая внутри него, принимает на концах равные значения, то ее производная по крайней мере один раз обратится в ноль на интервале (a, b).
А ведь после математического анализа, где поначалу изучают функции одной переменной, переходят к функциям многих переменных. Там понятия непрерывности и гладкости тоже вводятся в виде строгих математических определений, но наглядности от этого не прибавляется.
ПРОЩЕ ПРЯМОЙ ТОЛЬКО ТОЧКА
Страдает отсутствием наглядности и такой раздел математики, как линейная алгебра.
После долгого изучения различных понятий и свойств матриц студенты обычно переходят к решению систем линейных уравнений вида
В этом уравнении — n-мерный вектор-столбец, b— m-мерный вектор-столбец, A — матрица размером m х n. Наглядный пример мог бы сильно помочь студентам в изучении линейной алгебры. Для этого достаточно взглянуть, как выглядит графическая интерпретация системы линейных уравнений с двумя неизвестными на плоскости. Уравнение прямой на плоскости имеет вид
ax + bx = c.
(Те, кто не любит букв, могут вместо a, b и c подставить какие-нибудь числа.)
Геометрическая интерпретация уравнения ax + by = c
Две прямые на плоскости описываются двумя линейными уравнениями:
Любой, даже далекий от математики человек догадывается, что две прямые на плоскости либо пересекаются, либо параллельны, либо просто совпадают. В первом, наиболее типичном случае точка пересечения двух прямых будет единственным решением системы линейных уравнений.
Координаты точки пересечения прямых будут решением системы двух линейных уравнений с двумя неизвестными.
Если прямые не пересекаются, значит, система линейных уравнений не имеет решений.
Когда две прямые параллельны — общих точек нет, и тогда система линейных уравнений решений не имеет. Ну а если две прямые совпадают, то у системы бесчисленное множество решений. Но геометрическая интерпретация хороша только тогда, когда надо понять, что такое система линейных уравнений. А вот чтобы находить эти решения, как раз и нужна строгая математика. Две прямые параллельны, если их уравнения можно представить в виде
Проще говоря, прямые параллельны (решения нет), если коэффициенты при неизвестных х и y пропорциональны. Если при этом еще и свободные члены пропорциональны, то вторая прямая попросту совпадает с первой (решений бесчисленное множество).
Кто бы мог подумать, что мы почти объяснили, о чем идет речь в теореме Кронекера — Капелли:
Система линейных уравнений имеет хотя бы одно решение тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Напомним, что расширенная матрица — это матрица системы, к которой добавили столбец, составленный из свободных членов, стоящих в правой части системы уравнений.
Когда прямые параллельны, т.е. коэффициенты при неизвестных пропорциональны, а свободные члены — нет, ранг матрицы системы равен 1, а вот ранг расширенной матрицы — 2.
ОТ ДВУХ ИЗМЕРЕНИЙ — К ТРЕМ
Для системы из трех линейных уравнений с тремя неизвестными ситуация немного сложнее. Одно линейное уравнение соответствует плоскости в трехмерном пространстве:
ax + bx + cz = d.
Геометрическая интерпретация уравнения
Система трех линейных уравнений также может иметь одно решение, не иметь решений или иметь бесчисленное множество решений.
Координаты точки пересечения трех плоскостей будут решением системы трех линейных уравнений с тремя неизвестными.
Решений нет, когда две плоскости из трех параллельны.
Ситуация, при которой решений нет, потому что две плоскости из трех параллельны, аналогична параллельным прямым на плоскости. Но в трехмерном пространстве решения может не быть еще из-за того, что прямая, образованная пересечением двух плоскостей, параллельна третьей плоскости.
Решений нет, когда прямая — пересечение двух плоскостей — параллельна третьей плоскости.
Теорема Кронекера — Капелли хотя и не является столь наглядной, как геометрические рисунки, зато предлагает очень удобный механизм, позволяющий вычислить, имеет система решения или нет.
От систем линейных уравнений перейдем к системам линейных однородных уравнений. Это такие системы, у которых свободные члены равны 0. В трехмерном пространстве каждое уравнение такой системы будет задавать плоскость, которая проходит через точку — начало координат. Понятно, что однородная система всегда имеет по крайней мере одно, нулевое, решение. Рассмотрим систему двух линейных уравнений с тремя неизвестными:
Координаты любой точки, лежащей на пересечении двух плоскостей, будут решением однородной системы двух уравнений с тремя неизвестными.
Если коэффициенты такой системы непропорциональны (в переводе на геометрический язык — плоскости совпадают), то две плоскости пересекаются. В таком случае решением системы будут точки прямой, образованной пересечением двух плоскостей. Размерность решения — 1. А ранг системы — 2. Обратите внимание, что 2 + 1 = 3 — количество неизвестных. Этот пример служит наглядным подтверждением известной теоремы:
Размерность пространства решений системы однородных линейных уравнений с n неизвестными равна n-r, где r — ранг матрицы системы.
ЛИНЕЙНО ПОПРОГРАММИРУЕМ
Переходя от уравнений к неравенствам, изобразим полуплоскость — множество точек, координаты которых удовлетворяют условиям
Геометрическая интерпретация неравенства ax + by = ≤c.
Системы линейных неравенств в геометрической интерпретации могут описывать довольно сложные множества точек на плоскости. Пересечение нескольких полуплоскостей образует выпуклые многоугольники, которые задают множество точек, удовлетворяющих нескольким линейным неравенствам:
Система линейных неравенств с двумя неизвестными в геометрической интерпретации зачастую представляет выпуклый многоугольник.
В линейном программировании занимаются изучением задачи поиска максимума линейной функции на множестве, образованном линейными неравенствами. Линейная функция, максимум которой ищут, в случае двух переменных выглядит следующим образом:
Если рассмотреть набор параллельных прямых, заданных уравнениями:
в которых значение свободного члена увеличивается (то есть с12 3), то из рисунка будет понятно, что максимум целевой функции достигается либо в вершине многогранника условий, либо на его стороне.
С ростом значения свободного члена прямые «удаляются» от начала координат.
В первом случае решение задачи линейного программирования будет единственным. Когда максимум целевой функции достигается в любой точке стороны выпуклого многоугольника, задача имеет бесчисленное множество решений. В этом случае у многоугольника целых две вершины будут решением исходной задачи.
На одной из вершин будет достигнут максимум целевой функции.
Отсюда можно сделать вывод, что одна из вершин многоугольника условий является решением задачи линейного программирования. К такому выводу и приходит одна из основных теорем линейного программирования:
Если существует решение задачи линейного программирования, то оно достигается в одной из угловых точек множества допустимых решений.
В трехмерном пространстве множество условий часто представимо в виде выпуклого многогранника. Целевая функция может достигать своего максимума как в вершине, так и на ребре или даже на целой грани многогранника. Но главный вывод остается неизменным: одна из вершин является решением задачи.
Геометрический способ поиска максимума целевой функции напрашивается сам собой: давайте попробуем последовательно перебрать все вершины многогранника условий. Одна из них и будет являться решением. Возможно, кого-то удивит, что знаменитый симплекс-метод как раз и занимается перебором угловых точек — вершин.
Именно этот способ зачастую эффективно используется при обработке многих экономических моделей, сводящихся к задачам линейного программирования.
О ФОРМАХ… КВАДРАТИЧНЫХ
При изучении высшей алгебры студенты занимаются изучением квадратичных форм n переменных. От выражения, которое предстоит изучать, холодеет в груди:
В матричном виде представление этого «монстра» несколько проще, но наглядности не добавляет:
Здесь = (х1, х2 …, хn) — вектор-строка, А — симметричная матрица. Интересно, что в случае двух переменных квадратичная форма имеет вид
a11x12 + 2a12x1x2 + a22x22.
Если рассмотреть набор точек, который удовлетворяет равенству
a11x12 + 2a12x1x2 + a22x22 = 1,
то это будет кривая второго порядка: эллипс, парабола или гипербола, в зависимости от значений коэффициентов квадратичной формы.
Квадратичная форма на плоскости — это кривая второго порядка.
В случае эллипса можно подобрать систему координат так, чтобы ее начало располагалось в центре эллипса, а оси координат были направлены по его главным осям. Для перехода к «удобной» системе координат потребуется перенести ее начало и повернуть на некоторый угол координатные оси (такие преобразования относятся к линейным).
Иметь дело с эллипсом намного удобнее в системе координат, центр которой совпадает с началом координат, а координатные оси направлены по главным осям.
В «удобной» системе координат уравнение кривой второго порядка станет намного проще. Для эллипса оно будет выглядеть так:
Такое уравнение эллипса называется каноническим. Размеры полуосей эллипса равны а1и а2. По сути, каноническое уравнение кривой второго порядка — частный случай квадратичной формы, матрица которой имеет диагональный вид:
Сравните полученный результат с известной теоремой:
Любую квадратичную форму можно с помощью невырожденного линейного преобразования привести к каноническому (или диагональному) виду.
В заключение я хотел бы принести извинения за нестрогость многих рассуждений. Главной целью статьи была наглядность. Думаю, что существует множество других интересных примеров, которые помогли бы преодолению совсем не «царской» дороги в математике. Автор будет признателен всем, кто сможет предложить свои примеры наглядного и доходчивого объяснения математических понятий.
Подробности для любознательных
О ЧЕТВЕРТОМ ИЗМЕРЕНИИ — ДОСТУПНО
Автор “Флатландии” англичанин Эдвин Эббот (Edwin Abbott) был школьным учителем. Родился он 10 декабря 1838 года, умер 12 октября 1926 года. Образование получил в Кембриджском университете. Занимаясь изучением и преподаванием математики и теологии, он написал несколько книг, но самой популярной стала вышедшая в 1884 году “Flatland”. В ней Эббот смог не только познакомить читателя с удивительной плоской страной, которую населяли геометрические фигуры. Ему удалось с легкой иронией передать атмосферу и модные воззрения своего времени.
Форма изложения оказалась настолько удачной, что спустя почти 70 лет датский математик Дионис Бюргер (Dionijs Burger) решил использовать ее для создания продолжения и написал не менее увлекательную “Сферландию” (“Bolland”). В 1957 году книга увидела свет, а в1965 году была издана на английском языке под названием “Sphereland”.
Популярность двухмерной страны оказалась столь высокой, что в 1965 году в Гарвардском университете был создан 11-минутный мультфильм о жизни геометрических фигур. Созданием ленты руководил художник Эрик Мартин (Eric Martin). Вторую попытку экранизировать “Флатландию” предпринял итальянский математик Мишель Эммер (Michele Emmer), который выпустил 22-минутный мультфильм.
В XXI веке появилось уже несколько проектов, в которых герои Флатландии предстают на экранах. В 30-минутной ленте, созданной специалистами Flat World Productions LLC в 2006 году, можно воочию увидеть, как живут герои Эдвина Эббота.
Самый крупный проект о двухмерной стране принадлежит корпорации Flatland Production Corp.
В 2007 году под управлением Лэда Элингера (Ladd Ehlinger Jr) создан 95-минутный мультфильм о приключениях геометрических фигур. Жизнь рисованных героев: треугольников, квадратов, сфер и других — на удивление напоминает наши будни, с той только разницей, что мы воспринимаем на одно измерение больше. Так же, как и у нас, у жителей Флатландии бьется сердце, течет по жилам кровь, только все это происходит на плоскости. И хотя рисованные герои совсем не похожи на людей, что-то человеческое в них все-таки есть.
На русском языке “Флатландия” и “Сферландия” впервые были изданы в 1976 году издательством “Мир”. Автор перевода — Юлий Александрович Данилов (1936—2003), профессор, ведущий научный сотрудник Российского научного центра “Курчатовский институт”. В его переводе в нашей стране выходили также популярные книги по математике Мартина Гарднера (“Математические новеллы”, “Математические досуги”, “Математические головоломки и развлечения” и другие), которые хорошо знакомы любителям математики.
За перевод книг американского физика-теоретика Георгия Гамова о мистере Томпкинсе Данилов получил в 1994 году премию и медаль имени Александра Беляева, присуждаемые за достижения в области научной фантастики.
Подробности для любознательных
РАНГ БЕЗ ТАБЕЛЯ
Понятие ранга матрицы тоже поддается наглядному объяснению. Для этого стоит напомнить, что вектор, координаты которого (a, b) составлены из коэффициентов в уравнении прямой ax + by = c, будет перпендикулярен ей. Обычно строгому доказательству этого факта посвящают целую теорему, но на плоскости это понятно из рисунка.
Для системы двух линейных уравнений с двумя неизвестными строки матрицы образуют два вектора нормалей. Если прямые, соответствующие уравнениям системы, параллельны, то векторы нормалей окажутся на одной прямой (размерность прямой 1). Такую пару векторов называют линейно зависимой.
Для системы из трех линейных уравнений с тремя неизвестными векторы нормалей будут располагаться в трехмерном пространстве.
Они линейно зависимы, если лежат вдоль одной прямой (размерность 1), или в одной плоскости (размерность 2).
Строгое определение линейной зависимости менее наглядно:
Векторы 1, 2 …n называют линейно зависимыми, если существуют коэффициенты α1, α2 …αn, не все равные нулю (то есть α12 + α22 + … + αn2 ≠ 0), такие, что α11 + α22+ …+ αnn= . Если это равенство выполняется только при α1= α2 = …= αn = 0, то система векторов называется линейно независимой.
Ранг матрицы системы линейных уравнений совпадает с размерностью множества, в котором располагаются векторы нормалей. Если все векторы нормалей направлены вдоль прямой, ранг матрицы — 1, если они лежат в плоскости, ранг равен 2. Классическое определение значительно строже, но его наглядность намного ниже:
Ранг матрицы — наивысший из порядков, отличных от нуля миноров этой матрицы.
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2),
Шпаргалка по дискретной математике и булевой алгебре.
Множества, логика, комбинаторика.Шпаргалка по дискретной математике и булевой алгебре содержит в себе:
1. Понятие множества. Принадлежность и включение. Аксиомы объёмности и абстракции.
2. Подмножества. Множество-степень. Операции над множествами и их основные свойства.
3. Дополнительные свойства операций над множествами. Вывод из основных.
4. Утверждения, эквивалентные включению.
5. Принцип двойственности.
6. Решение уравнений.
7. Прямое произведение множеств.
8. отношения на множествах. Бинарные отношения и их свойства (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность).
9. Обратные отношения, суперпозиция отношений, свойства.
10. Отношения эквивалентности. Фактор-множество.
11. Функциональное отношение. Инъекция, сюръекция, биекция.
12. Отношение порядка. Частично упорядоченные множества. Изоморфизм.
13. Наибольшее и наименьшее элементы множества, sup и inf.
14. Линейно упорядоченное множество.
15. Понятие мощности множества конечного и бесконечного.
16. Теоремы о счетных множествах.
17. Теорема о мощности множетва-степени конечного и бесконечного множества.
18. Теорема Кантора-Барнштейна.
19. Мощность континуум.
20. Общие правила( сложения и умножения).
21. Формулы для вычисления перестановок сочетаний и размещений с повторениями и без.
Размещение.
22. Биноминальная и полиноминальная теоремы.Биноминальная теорема.
23. Формула включений-исключений.
24. Высказывания. Основные логические связки. Таблицы истинности. Формулы и функции.
25. Общезначимость. Теоремы о получении общезначимых формул.
26. Получение отрицания формулы.
27. Логическое следствие. Логический вывод. Противоречивость системы высказываний.
28. Понятие предикатов. Кванторы всеобщности и существования. Общезначимые формулы.(см 25. Логическое следствие. Логический вывод.
Получение отрицания формулы.(см26)
29. Совершенные нормальные дизъюнктивные и конъюктивные формы.
Блестящая вики по математике и науке
Пусть xn x_n xn — последовательность действительных чисел. Для любых k, k, k пусть Sk = {xn : n≥k}. S_k = \ {x_n \ двоеточие n \ ge k \}. Sk = {xn: n≥k}. Тогда
lim infn → ∞xn = limk → ∞ (inf Sk) lim supn → ∞xn = limk → ∞ (sup Sk). \ Begin {align} \ liminf_ {n \ to \ infty} x_n & = \ lim_ {k \ to \ infty} (\ text {inf} S_k) \\\\ \ limsup_ {n \ to \ infty} x_n & = \ lim_ {k \ to \ infty} (\ text {sup} S_k). \ end {align} n → ∞liminf xn n → ∞limsup xn = k → ∞lim (inf Sk) = k → ∞lim (sup Sk).
−1,0, DNE, 0,1-1,0, \ text {DNE}, 0,1−1,0, DNE, 0,1 −1, −1,0,1,1-1, -1,0,1,1−1, −1,0,1,1 −21 / 2,0,0,0,2 -2 ^ {1/2}, 0, 0, 0, 2−21 / 2,0,0,0,2 −21 / 2, DNE, DNE, DNE, 2-2 ^ {1/2}, \ text {DNE}, \ text {DNE}, \ text {DNE}, 2−21 / 2, DNE, DNE, DNE , 2 -1, -1, DNE, 1,1 -1, -1, \ text {DNE}, 1, 1-1, -1, DNE, 1,1 −21 / 2, −21 / 2, DNE, 2,2 -2 ^ {1/2}, — 2 ^ {1/2}, \ text {DNE}, 2,2−21 / 2, −21 / 2, ДНЭ, 2,2 −21 / 2, −1, DNE, 1,2 -2 ^ {1/2}, -1, \ text {DNE}, 1, 2−21 / 2, −1, DNE, 1,2Пусть xn x_n xn — последовательность 12, −13,14, −15,… \ frac12, — \ frac13, \ frac14, — \ frac15, \ ldots21, −31, 41, −51,….Тогда inf Sk = −12ℓ + 1, \ text {inf} S_k = — \ frac1 {2 \ ell + 1}, inf Sk = −2ℓ + 11, где ℓ = ⌈k2⌉, \ ell = \ left \ lceil \ frac k2 \ right \ rceil, ℓ = ⌈2k ⌉ и sup Sk = 12m, \ text {sup} S_k = \ frac1 {2m}, sup Sk = 2m1, где m = ⌊k + 12⌋ .
m = \ left \ lfloor \ frac {k + 1} 2 \ right \ rfloor. m = ⌊2k + 1 ⌋. Предел обоих этих выражений при k → ∞ k \ to \ infty k → ∞ равен 0, 0, 0, что также является пределом последовательности. Итак
lim infn → ∞xn = lim supn → ∞xn = limn → ∞xn = 0. \ Liminf_ {n \ to \ infty} x_n = \ limsup_ {n \ to \ infty} x_n = \ lim_ {n \ to \ infty} x_n = 0.n → ∞liminf xn = n → ∞limsup xn = n → ∞lim xn = 0.
Обратите внимание, что inf xn = −13 \ text {inf} x_n = — \ frac13 inf xn = −31 и sup xn = 12. \ text {sup} x_n = \ frac12. sup xn = 21.
m = \ left \ lfloor \ frac {k + 1} 2 \ right \ rfloor. m = ⌊2k + 1 ⌋. Предел обоих этих выражений при k → ∞ k \ to \ infty k → ∞ равен 0, 0, 0, что также является пределом последовательности. ИтакПусть xn x_n xn будет последовательностью
2, −21/2, 21/3, −21/4, 21/5, −21/6,….
{1/6}, \ \ ldots.2, −21/2, 21/3, −21/4, 21/5, −21/6,….
Какие значения у
infxn, lim infn → ∞xn, limn → ∞xn, lim supn → ∞xn, supxn? \ Inf x_n, \ \ \ liminf_ {n \ to \ infty} x_n, \ \ \ lim_ {n \ to \ infty} x_n, \ \ \ limsup_ {n \ to \ infty} x_n, \ \ \ sup x_n \,? infxn, n → ∞liminf xn, n → ∞lim xn , N → ∞limsup xn, supxn?
Обозначение: В вариантах выбора DNE \ text {DNE} DNE означает «не существует».
Недвижимость:
(1) В отличие от предела последовательности, lim inf \ liminf liminf и lim sup \ limsup limsup всегда существуют, если мы допускаем −∞ — \ infty − ∞ и + ∞ + \ infty + ∞ в качестве возможных значений.Это потому, что последовательность tk = inf Sk t_k = \ text {inf} S_k tk = inf Sk является неубывающей последовательностью (((аналогично последовательность sup \ text {sup} sup не возрастает),), ), поэтому его предел либо существует, либо равен ± ∞ \ pm \ infty ± ∞.
(2) Предел limn → ∞xn \ lim \ limits_ {n \ to \ infty} x_nn → ∞lim xn существует тогда и только тогда, когда lim infn → ∞xn = lim supn → ∞xn ; \ liminf \ limits_ {n \ to \ infty} x_n = \ limsup \ limits_ {n \ to \ infty} x_n; n → ∞liminf xn = n → ∞limsup xn; если предел существует, все три значения равны.
(3) Если lim supn → ∞xn ≠ ∞, \ limsup \ limits_ {n \ to \ infty} x_n \ ne \ infty, n → ∞limsup xn = ∞, то это наименьшее вещественное число. число sss такое, что для любого ϵ> 0, \ epsilon> 0, ϵ> 0 только конечное число элементов последовательности> s + ϵ. > s + \ epsilon.> s + ϵ. Обратите внимание, что это может быть не так, что только конечное число элементов последовательности> s. > с. > с. (\ big ((Например, lim supn → ∞1n = 0.) \ limsup \ limits_ {n \ to \ infty} \ frac1 {n} = 0. \ big) n → ∞limsup n1 = 0 .) Итак, «каждое число, превышающее lim sup \ limsuplimsup, является конечной верхней границей.\ text {th} n-е простое число. Тогда
lim supn → ∞ (pn + 1 − pn) = ∞.
\ Limsup \ limits_ {n \ to \ infty} (p_ {n + 1} -p_n) = \ infty.n → ∞limsup (pn + 1 −pn) = ∞.
Доказательство: k! + 2, k! + 3,…, k! + K k! + 2, k! +3, \ ldots, k! + K k! + 2, k! + 3,…, k! + K все составные для любого k≥2. k \ ge 2. k≥2. Таким образом, для любых k, k, k существует бесконечно много значений nnn таких, что pn + 1 − pn≥k − 1 p_ {n + 1} -p_n \ ge k-1 pn + 1 −pn ≥k− 1. (((Возьмем pn p_n pn как наибольшее простое число, меньшее r! +2 r! + 2r! +2, где r≥kr \ ge kr≥k; тогда следующее простое число не меньше r − 1 r-1 r − 1 целых чисел прочь.))) Итак, k − 1 k-1 k − 1 не может быть конечной верхней границей, поэтому она не больше, чем lim sup. \ limsup.limsup. Поскольку это верно для всех k k k, результат следует.
С другой стороны,
lim infn → ∞ (pn + 1 − pn) \ liminf \ limits_ {n \ to \ infty} (p_ {n + 1} -p_n) n → ∞liminf (pn + 1 −pn)
пока неизвестен. Гипотеза о простых числах-близнецах эквивалентна утверждению, что оно равно 2, 2,2, но в настоящее время известно только то, что оно не превосходит 246.
246.246. (До 2013 года даже не было известно, что это конечно!)
справочный запрос — Характеристика наборов Inf и Sup
Я не верю, что есть хороший способ охарактеризовать $ \ Xi $.Более того, я не вижу причин отделять наборы с наименьшими верхними границами или наибольшими нижними границами от основного частичного упорядочивания. В этом ответе я приведу случаи, когда частичный порядок $ \ leq $ полностью определяется $ \ mathcal {A} $ и $ \ mathcal {B} $. В частности, поскольку $ \ mathcal {A} $ и $ \ mathcal {B} $ иногда полностью определяют частичный порядок $ X $, мы не получаем более простой структуры, когда наблюдаем множества $ \ mathcal {A} $ и $ \ mathcal {B} $ в отличие от частичного порядка $ \ leq $.{\ circ} y) $. Для доказательства этого результата нам понадобится простой факт об алгебрах Гейтинга. В алгебре Гейтинга, если существует $ \ bigvee R $ и $ a \ in X $, то
$ \ bigvee_ {r \ in R} (a \ wedge r) $ существует и $ a \ wedge \ bigvee R = \ bigvee_ {r \ in R} (a \ wedge r) $. 2010 Классификация предметов по математике: Начальная школа: 26A03 Средняя школа: 06A [MSN] [ZBL] Характеристики наборов на реальной линии. Наименьшая верхняя граница данного набора действительных чисел — это наименьшее число, ограничивающее этот набор сверху; его наибольшая нижняя граница — это наибольшее число, ограничивающее его снизу. Теперь это будет изложено более подробно. Пусть дано подмножество $ X $ действительных чисел. Примеры. $$ \ inf [a, b] = a, \ quad \ sup [a, b] = b; $$ $$ \ inf (a, b) = a, \ quad \ sup (a, b) = b; $$ если множество $ X $ состоит из двух точек $ a $ и $ b $, $ a $$ \ inf X = a, \ quad \ sup X = b. $$ Эти примеры показывают, в частности, что наименьшая верхняя граница (наибольшая нижняя граница) может либо принадлежать множеству (например, в случае интервала $ [a, b] $), либо не принадлежать ему (например, в случай интервала $ (a, b) $). Если набор имеет наибольший (наименьший) член, это число, очевидно, будет наименьшей верхней границей (наибольшей нижней границей) набора. Наименьшая верхняя граница (точная нижняя граница) множества, не ограниченного сверху (снизу), обозначается символом $ + \ infty $ (соответственно символом $ — \ infty $). Если $ \ mathbf N = \ {1,2, \ dots \} $ — множество натуральных чисел, то $$ \ inf \ mathbf N = 1, \ quad \ sup \ mathbf N = + \ infty. $$ Если $ \ mathbf Z $ — это набор всех целых чисел, как положительных, так и отрицательных, то $$ \ inf \ mathbf Z = — \ infty, \ quad \ sup \ mathbf Z = + \ infty. $$ Каждый непустой набор действительных чисел имеет уникальную наименьшую верхнюю границу (наибольшую нижнюю границу), конечную или бесконечную.Все непустые множества, ограниченные сверху, имеют конечные точные верхние границы, в то время как все ограниченные снизу имеют конечные точные нижние границы. Термины наименьшая верхняя (наибольшая нижняя) граница набора также иногда используются вместо наименьшей верхней границы (наибольшей нижней границы) набора в одном из значений, определенных выше. Под наименьшей верхней границей (наибольшей нижней границей) вещественнозначной функции, в частности последовательности действительных чисел, понимается наименьшая верхняя граница (наибольшая нижняя граница) множества ее значений (см.также верхний и нижний пределы). Обычно верхней границей набора действительных чисел $ S $ является такое число $ b $, что для всех $ x \ in S $ одно имеет $ x \ leq b $.Тогда точная верхняя граница $ S $ определяется как верхняя граница $ B $ такая, что для каждой верхней границы $ b $ один имеет $ B \ leq b $. Аналогичные определения справедливы для нижней границы и точной нижней границы. Если точная верхняя граница $ S $ принадлежит $ S $, то она называется максимумом $ S $. Если точная нижняя граница $ S $ принадлежит $ S $, то она называется минимумом $ S $. Основная аксиома системы действительных чисел или аксиома непрерывности может быть выражена в форме Каждый непустой набор действительных чисел, ограниченный выше, имеет верхнюю грань действительных чисел . Как процитировать эту статью: Aprs une form en intgr l’cole d’ingnieurs ENITIAA (Школа Nationale d’Ingnieurs des Techniques des Industries Agricoles et Alimentaires) Нант. roquette.fr специальной математики), я поступил в инженерное училище ENITIAA (Национальная школа инженерных технологий для сельскохозяйственной и пищевой промышленности) в Нанте. roquette.com dans l’arme de l’air et je suis devenue pilote de chasse. carlabrunisarkozy.org Итак, после выполнения carlabrunisarkozy.org Peu de temps aprs. Rencontr Сэмми, гитарист, исполняющий музыку, Stan laisse la musique rfimusique.com Вскоре после встречи с Сэмми, который был гитаристом, как и он сам, Стэн позволил музыке заменить rfimusique.com Ajouter les nouveaux termes dans une sorte de ineesite.org банк слов ineesite.org urantia-uai.org urantia-uai.org Ce dont nous avons besoin, dans beaucoup www2.parl.gc.ca www2.parl.gc.ca Nous Consuillons Aux Candidats de Bac STAV, SI un Excellent niveau scolaire est exig, de prendre contact avec lesecrtariat des admissions avant le dpt de leur кандидата для s’assurer de l’opportunit de celle-ci. purpan.fr Мы советуем кандидатам, имеющим , чтобы связаться с , прежде чем они отправят свою заявку, чтобы проверить их фактические возможности приема. purpan.fr taient peu prs les mmes pour les filles et les garons. ccsd.ca были примерно равны для девочек и мальчиков. ccsd.ca Pour Complter ce tableau, je n’avais pas non plus les moyens налей мне плательщик dsespr et j’tais toujours de mauvaise humeur. urantia-uai.org Кроме того, у меня не было средств заплатить всегда был в плохом настроении. urantia-uai.org Mes matires n5tn.com n5tn.com n5tn.com n5tn.com guyenneetgascogne.com guyenneetgascogne.com D’autres choisissent de ne pas investir dans un program de maintenance mais souhaitent une garantie de landesk.fr Другие могут не вкладывать средства в программу технического обслуживания, но landesk.co.uk Marie-Flore Bachelier в перевозке в группе AXA или в разных местах fonctions la Direction техника Vie d’AXA Assurances et au sein de la Direction immobilire du Groupe. mercialys2007.devmdg.com Бизнес-школа, Мари-Флора Башелье начала свою карьеру в AXA, где занимала несколько должностей в Техническом отделе страхования жизни AXA Assurances и в отделе инвестиций в недвижимость AXA Group. mercialys2007.devmdg.com Si vous explorez le concept actuel- je le vois avec mes propres enfants-, ils ont l’option www2.parl.gc.ca Если вы посмотрите на текущую конструкцию — я вижу ее со своим www2.parl.gc.ca L’idal serait de transformer les coles coraniques en medersas, qui ont un program africamission-mafr.org Идеальным было бы преобразовать эти школы Корана в медресе с нормальной программой религиозное образование в Коране и на арабском языке. africamission-mafr.org n5tn.com n5tn.com n5tn.com n5tn.com webawareness.ca webawareness.ca Комментарий faire pour ne pas bierengezondheid.com bierengezondheid.com un langage, o chaque фраза exprime une ide, annonce un rsultat, formule une demande. rivapublishers.com , в котором каждое предложение выражает какую-то идею, сообщает о результате или оформляет заказ. rivapublishers.com Mais ils ont la телосложение. jeuxcommonwealth.ca по математике, естествознанию и физике. jeuxcommonwealth.ca Conjointement avec les dirigeants et le gimv.com gimv.com Des donnes rcentes montrent que les tudiants de niveau 9 matrisent moins de la moiti des aptitude daccess-ods.un.org Последние данные показывают, что чем половина минимальных компетенций по естествознанию и математике. daccess-ods.un.org Dans tous les trois domaines, c’est — dire comptence de comprhension de lecture dans les Sciences naturelles (580), les lves qui travaillent dans leur premire langue ont obtenu des rsultats bien au dessus de ceux des meilleures pays. woluweparents.org Во всех трех областях, а именно, понимание прочитанного по естествознанию [580], студенты человек, которые работали на своем родном языке, показали более высокие результаты, чем представители лучших стран. woluweparents.org фр.playforia.com playforia.com Pourquoi tant de gens proclament-ils qu’ils com une matire qui leur fait насилия? rivapublishers.com Почему большинство школьников утверждают, что знают тяжело справляется со своими задачами? rivapublishers.com vous pouvez vous adressez au service de Relations customers ou nous tlphoner au T 041 784 07 84. belair.ch Если у вас по поводу вашего пребывания в клинике, пожалуйста, свяжитесь с нашим головным офисом или позвоните нам по телефону 041 784 07 84. belair.ch L’extension Render effectles traitements deposition ncessaire pour mlanger les fond de l’application. openbsd.gr Расширение Render обеспечивает необходимые операции композитинга на фоне приложения. openbsd.gr Si le produit ou un composant n? Est plus offert, nous le remplacerons par un produit hamiltonbeach.ca Если продукта или компонента больше нет в наличии, мы заменим его на hamiltonbeach.ca Топор Outre cet de la nouvelle socit. gimv.com gimv.com арабский
Немецкий
английский
испанский
Французский
иврит
Итальянский
Японский
нидерландский язык
Польский
португальский
румынский
русский
турецкий
китайский язык Синонимы
арабский
Немецкий
английский
испанский
Французский
иврит
Итальянский
Японский
нидерландский язык
Польский
португальский
румынский
русский
турецкий
китайский язык Эти примеры могут содержать грубые слова, основанные на вашем поиске. Эти примеры могут содержать разговорные слова, основанные на вашем поиске. Но когда после « Maths Sup » вас принимают в «Maths Spé», вы не бросаете все, чтобы поехать в Саутгемптон, не имея четкого представления о том, чем вы хотите заниматься в жизни. Предложите пример Его юность прошла между Савойей, Верхней Савойей и Греноблем, где он посещал уроки средней школы Шампольона Math sup . (Высшая математика). Результатов: 2. Точное: 1. Затраченное время: 99 мс. Réviser tes cours de prépa Maths Sup / Spé sur une application de révisions, c’est maintenant possible! Study Quizz t’aide et t’accompagne pendant tes deux années de classe prépa Maths Sup, Maths Spé pour réussir tes examens, tes concours et admissions. Prépa Maths Sup / Spé это приложение 100% бесплатно и без рекламы (et ça le restera)! + из 7500 организаций викторин по происхождению, по материалам и главам для 1 и 2 лет: Maths, Physique, Chimie, SI, Anglais, MPSI / PCSI / MP / PC / PSI, и т. Д. Dans le bus, dans le métro, aux toilettes, chez le coiffeur, à l’étranger: alors ne te fais pas devancer. Avec Study Quizz prépa Maths Sup / Spé, le concours est dans ta poche! T’as du mal à bosser? Tu n’arrives pas à réviser? Tu te laisses vite déconcentrer? Laisse toi guider et вдохновитель от Squizzy, notre super mascotte ultra motivée и super mignonne! Retrouve-nous sur les réseaux sociaux pour suivre tous nos tips de révisions: Проблема? Не вопрос? Контактная почта: [email protected] Factures ouv multipl impliqules 2 мембранная инф, мембранная инфо, мембранная суп, и мембранная инфа, а также кот и т. Д. Открытые множественные переломы обеих нижних конечностей, нижней конечности и верхней конечности, а также нижней конечности (-ей) с ребром (-ями) и грудиной Последнее обновление: 2014-12-09 
Предположим, что $ x \ not \ leq y $. Тогда $ y \ wedge x Верхняя и нижняя границы — Энциклопедия математики
Число $ \ beta $ называется его наименьшей верхней границей, обозначаемой $ \ sup X $ (от латинского supremum — наибольшее), если каждое число $ x \ in X $ удовлетворяет неравенству $ x \ leq \ beta $, и если для любого $ \ beta ‘<\ beta $ существует $ x' \ in X $ такое, что $ x '> \ beta’ $. Число $ \ alpha $ называется точной нижней границей $ X $, обозначаемой $ \ inf X $ (от латинского infimum — наименьшее), если каждое $ x \ in X $ удовлетворяет неравенству $ x \ geq \ alpha $, и если для любого $ \ alpha ‘> \ alpha $ существует $ x’ \ in X $ такое, что $ x ‘<\ alpha' $. Список литературы
[1] В.А. Ильин, Э. Позняк, «Основы математического анализа», 1-2 , МИР (1982) [2] Л.Д. Кудрявцев, «Курс математического анализа», 1 , Москва (1988) [3] С. Никольский, «Курс математического анализа», 1 , МИР (1977) Список литературы
[a1] T.M. Апостол, «Математический анализ», Addison-Wesley (1974) [a2] W. Rudin, «Принципы математического анализа», McGraw-Hill (1953) [a3] K.R. Стромберг, «Введение в классический реальный анализ», Wadsworth (1981)
Верхние и нижние границы. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Upper_and_lower_bounds&oldid=36143 maths sup — английский перевод — Linguee
После 2 -да r бутерброд c наш e (высшая математика — […] Donc, aprs un bac scientifique et al. fa i t maths sup ‘ e t maths j’ai pass le concours d’officier de carrire […] Ad d новый ter ms to a ‘Math […] J’tais un bon tudiant, mais je n’tais pas trs bo n e n maths . Я хорошо учился, но никогда не разбирался в математике. Во многих технических профессиях нам нужны люди с университетскими математическими навыками. E n математика , l es пропорции […] I n math, the pr oportions […] Мой любимый su bj ects are math and scie nc e. Сын дипломат e d e Sup d e C o Marseille en poche, Cdric rejoint son frre en 2004, avec la ferme de la de dvelopper. После завершения курса в бизнес-школе Марселя Кадрик присоединился к своему брату в 2004 году с твердым намерением развивать коммерческую сторону дела. Diplm e d e Sup d e C o Гавр-Кан, […] выпускник th e Le Havre-Caen […] J’ai de bons rsultats scolaires et j’aime la lecture et l e s maths . Я хорошо учусь и люблю читать и математику. J’tais fministe-et je voulais que ma fille soit bonn e e n maths . Я была феминисткой и хотела, чтобы моя дочь хорошо разбиралась в математике. Как я могу отслеживать свои единицы, не будучи вундеркиндом в математике? Un Cour s d e maths e s t aussi un Cours de langue: les mathmatiques sont […] Урок математики ic s i s также язык le ss on: математика — это a язык […] Но в конец мы ls или обучили их […] Вместе с руководством и персоналом OTN GIMV хочет развивать автономную компанию, инвестируя в дополнительные и дополняющие элементы портфеля, расширяя охват продаж и распределения и заполняя пробелы в функциях поддержки. L e s maths n ‘ ai deront pas, seulement votre force deduction! Вам не нужны математические навыки, только сила дедукции! Залить все ti o n sup — p l m entaire, […] Помимо этого сосредоточения на внутреннем росте, могут быть изучены дополнительные приобретения, чтобы обеспечить будущую лидирующую позицию новой компании. maths sup — Перевод на французский — примеры английский
английский Другие результаты
Prépa Maths Sup / Spé в App Store
Des corrections détaillées и упражнения, соответствующие специальным материалам для изменений, и оптимальной подготовке к соревнованиям, а также дополнительным экзаменам на время. Encore mieux que les khôlles!
Обзоры фильмов и адаптированные варианты исполнения викторины!
Découvre ton classement national parmi tous les кандидаты aux concours des Grandes Ecoles d’ingénieur de France, ainsi que celui de ta prépa.Tu veux savoir si tu déchires? Тональный класс актуализируется в тестах результатов викторины. Alors au boulot!
Challenge tes potes et les gens de ta class: пригласите les et défie les sur les quizz de ton choix. Qui sera le prochain majeur de l’X? T’es prêt.e à relver le défi?
https: // www.instagram.com/study_quizz/
https://www.facebook.com/studyquizz/
https://www.tiktok.com/@study_quizz Math sup et math spé на английском языке с контекстными примерами
Французский
Английский
Частота использования: 1
Качество:
Ссылка: IATE
Предупреждение: Это выравнивание может быть неправильным.