портфелей двух активов
портфелей двух активовСодержимое:
- Характеристики портфеля из двух активов
- Объединение безрискового актива с рискованным активом
- Объединение двух рискованных активов
- Объединение двух полностью положительно коррелированных рискованных активов
- Объединение несовершенно коррелированных рискованных активов
- Компромиссы между риском и доходностью в пространстве среднего отклонения
- Коэффициент Шарпа избыточного возврата
Обсужденных ранее формул и функций MATLAB достаточно для вычисления Характеристики любого портфеля. Однако, чтобы лучше понять экономику портфеля строительства полезно рассмотреть последствия объединения двух активов для формирования портфолио.
Для экономии обозначений мы опускаем круглые скобки. Таким образом, x1 и x2 будут пропорциями
вложены в активы 1 и 2 соответственно, а e1 и e2 будут их ожидаемой доходностью.
Стандартное отклонение доходности (sp), как всегда, будет квадратным корнем из дисперсия:
зр = кврт (вп)
В этом разделе мы будем предполагать, что актив 1 имеет меньший риск (v1<v2) и меньший ожидаемый доход (e1<e2). Нас будет интересовать компромисс между риском и доходностью. связаны с различными сочетаниями двух активов и, в частности, с формой кривые в пространстве средней дисперсии и среднего стандартного отклонения, которые получаются по мере увеличения количества денег. вложенный в рискованный актив (то есть по мере увеличения х2 и уменьшения х1).
На приведенном ниже рисунке показано геометрическое место комбинаций среднего стандартного отклонения для значений x2 между 0 и 1, когда e1=6, e2=10, s1=0, s2=15 и c12=0.
В этом случае, как и в любом случае, связанном с безрисковым и рискованным активом, отношение
является линейным.
, где abs(x2) обозначает абсолютное значение x2.
Этот результат можно распространить на случаи, когда можно открывать короткие позиции.
Во-первых, предположим, что можно либо открыть длинную позицию по безрисковому активу («ссуду»), либо открыть короткую.
позицию в нем («заем») по той же процентной ставке (e1). Формулы выше
затем подайте заявку напрямую. На рисунке ниже показаны результаты, полученные при использовании плечо таким образом. Например, точка с пометкой 1,5 связана с x2=1,5 и x1=-0,5.
Это указывает на то, что, «увеличив» инвестиции в актив 2 на 50%, инвестор
можно получить вероятностное распределение доходности начального капитала с ожидаемым значением
12% и стандартное отклонение 22,5%.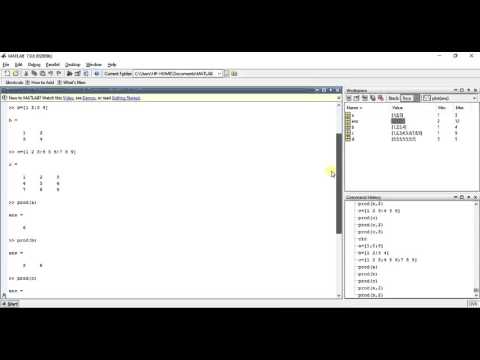
Что, если бы Инвестор мог продать рискованную ценную бумагу (x2<0) и инвестировать выручку получено от короткой продажи безрисковой ценной бумаги? Здесь тоже стандартные формулы применять. Однако обратите внимание, что дисперсия будет положительной, как и стандартное отклонение, поскольку отрицательное число (x2) в квадрате всегда положительно. На рисунке ниже показано эффекты отрицательных значений x2.
Требуется квалификация для этого анализа. Стратегия с короткими позициями может
требуют, чтобы был заложен дополнительный капитал для покрытия возможного дефицита между окончанием
стоимости активов и пассивов. В противном случае, как правило, будет взиматься более высокая ставка за
короткая позиция, поэтому доход кредитору в странах мира, в которых находится заемщик
растворителя будет достаточно высоким, чтобы компенсировать дефицит, связанный с
государства мира, в которых заемщик является неплатежеспособным.
На рисунке ниже показан простой случай такого рода, в котором средства могут быть взяты взаймы, но по более высокой ставке (8%), чем ставка, по которой они могут быть предоставлены взаймы (6%). Здесь местонахождение Комбинации ep,sp представляют собой две линии, первая из которых связана с более низкой процентной ставкой, второй с более высокой процентной ставкой. Как и прежде, рискованный актив предлагает ожидаемую доходность 10% и риск 15%. Эффективная граница показана сплошными линиями. пунктирная линия указывает варианты, которые были бы доступны, если бы Инвестор мог предоставить кредит по 8%. В то время как точки на нем невозможны, те, что строятся на его продолжении справа от точки, представляющие рискованный актив, являются одновременно осуществимыми и эффективными.
На практике ставка, взимаемая за заимствование, может увеличиваться вместе с суммой заимствования. В
В этом случае геометрическое место комбинаций ep,sp будет увеличиваться с уменьшающейся скоростью по мере увеличения риска.
(sp) превышает сумму, связанную с полными инвестициями без заемных средств в рискованные
актив (x2=1). В этих условиях в конечном итоге будет уменьшаться отдача от
принятие риска.
Когда портфель включает два рискованных актива, аналитик должен принять во внимание ожидаемая доходность, отклонения и ковариация (или корреляция) между активами возвращается. Отличия от предыдущего случая, когда один актив является безрисковым, заключаются в формула дисперсии портфеля. С точки зрения рисков и взаимосвязей это: 92
из чего следует что:
зр = абс (x1 * s1 + x2 * s2)
, где abs(..) обозначает абсолютное значение заключенного выражения. Пока х1 и x2 оба неотрицательны, само выражение будет неотрицательным, так как ни s1 ни s2 никогда не может быть отрицательным. Однако, если одно из двух значений x достаточно отрицательно, абсолютное значение должно использоваться явно.
Рассмотрим комбинации длинных позиций по двум активам (x1>=0, x2>=0).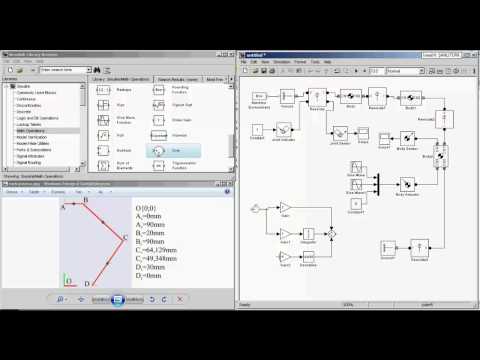
Для любого
такая комбинация:
зр = х1*с1 + х2*с2
И как всегда:
эп = х1*е1 + х2*е2
В таком случае и риск, и доходность будут пропорциональны x2:
sp = s1 + x2*(s2-s1) ep = e1 + x2*(e2-e1)
, и все такие портфели будут построены на прямой линии, соединяющей точки, представляющие два актива. На рисунке ниже e1=8,s1=5, e2=10, s2=15 и r12=1,0.
Это отношение можно расширить, разрешив x2 быть либо больше единицы, либо меньше чем ноль. Особый интерес представляет комбинация, дающая наименьший возможный риск: портфель минимальной дисперсии . В этом случае можно добиться отклонение ноль! Мы ищем значение x2, для которого:
sp = s1 + x2*(s2-s1) = 0
Это будет получено, когда:
x2 = -s1/(s2-s1)
и
х1 = 1-х2
= 1 + (s1/(s1+s2)
= с2/(с2-с1)
В нашем примере безрисковый портфель можно получить, установив:
х2 = -5/(15-5) = -0,5 х1 = 1-х2 = 1,5
Этого можно достичь, открыв короткую позицию по активу 2, равную половине
Средства инвестора и инвестирование выручки, а также первоначальной суммы денег в
актив 1.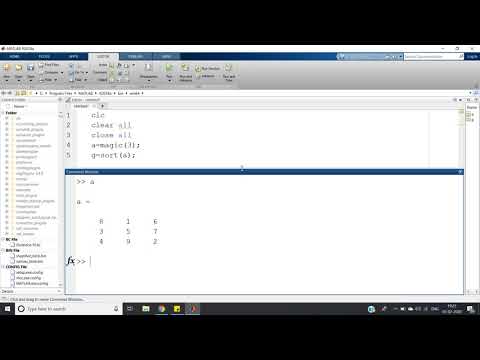
Способность формировать безрисковый портфель, занимая компенсирующие позиции в двух совершенно положительно коррелированные активы приводят непосредственно к цифре, аналогичной полученной раньше, когда безрисковый актив сочетался с рискованным. Пусть ожидаемая доходность портфель с нулевой дисперсией будет:
е0 = е1 + х2мин(*е2-е1)
где:
x2мин = -с1/(с2-с1)
В текущем примере e0 будет равно 7% (8-0,5*(10-8)). Набор портфельных рисков и Затем доходность может быть получена путем рассмотрения комбинаций этого безрискового актива (портфеля) и либо актив 1, либо актив 2. Любое представление предоставит знакомый график, связанный с рисковый и безрисковый актив. В данном случае:
Хотя все показанные комбинации возможны, только те, которые указаны в верхней строке, допустимы.
2))
Теперь представьте себе два случая, похожих во всех отношениях (x1,x2,e1,e2,s1,s2), но корреляция (р12). Пусть vp(1) — дисперсия одного портфеля, для которого r12=1, а vp(r) — дисперсия другого, для которого r12=r, где r меньше 1. Только средний член в уравнение для дисперсии портфеля будет различаться в двух расчетах. Поскольку все компоненты этого слагаемого, но r12 положительны, то vp(r)<vp(1). Более как правило, при прочих равных:
vp(r1) 0, x2>0
При прочих равных, чем меньше корреляция между двумя активами, тем меньше будет риск портфеля длинных позиций по двум активам.
На рисунке ниже показаны комбинации риска и доходности для таких портфелей, когда
e1=8,s1=5, e2=10 и s2=15. Каждая кривая относится к случаю с различной корреляцией
между доходностью двух активов. Неудивительно, что случаи совпадают в
конечные точки (x1=1,x2=0 и x1=0,x2=1). Для всех интерьерных комбинаций, когда соотношение
коэффициент меньше 1,0, риск менее чем пропорционален рискам двух
активов, причем степень снижения риска тем больше, чем меньше корреляция
коэффициент.
и
зр = абс (x1*s1 - x2*s2)
В таком случае портфель с минимальной дисперсией будет безрисковым. Чтобы получить его, мы желаем установить:
х1*с1 - х2*с2 = 0
дано: x1+x2 = 1
Решение:
х2 = с1/(с1+с2)
Таким образом, если s1=5 и s2=15 и два актива полностью отрицательно коррелированы, безрисковый портфель получится при x2=5/(5+15)=0,25 и x1=0,75. Ожидаемый доход будет равно 0,25*e1+0,75*e2 (здесь 8,5%). Следующий рисунок повторяет результаты предыдущего case и добавляет этот новый (белым цветом).
В очередной раз мы получили знакомую диаграмму, в которой присутствует безрисковый актив.
Это не должно быть сюрпризом. Длинные позиции в двух совершенно отрицательно коррелированных
активы аналогичны (1) длинной позиции в одном из двух совершенно положительно коррелированных
активы и (2) короткая позиция в другом.
В большинстве случаев корреляция активов находится в диапазоне от -1,0 до +1,0. Чтобы охватить все возможности нам нужна общая формула для портфеля с минимальной дисперсией. Для этого мы начинаем с уравнение в приведенной форме, в котором vp выражается как функция x2 (в предположении что x1=1-x2): 92)*(v1-2*c12+v2)
Производная по x2:
d(vp)/d(x2) = (c12-v1) + 2*x2*(v1-2*c12+v2)
Установка этого параметра на ноль дает:
x2мин = (v1-c12)/(2*(v1-2*c12+v2))
Портфель с минимальной дисперсией может иметь более низкий риск, чем любой из его компонентов. ресурсы. Он также может иметь более высокую доходность. Рассмотрим точку, в которой x2=0. Здесь:
d(ep)/d(x2) = e2-e1 d(vp)/d(x2) = c12-v1
и:
d(ep)/d(vp) = (e2-e1)/(c12-v1)
Как обычно, мы предполагаем, что e2>e1.
Чтобы наклон d(ep)/d(vp) был отрицательным, нам нужно:
c12-v1
То есть:
р12*с1*с2
или:
р12
Например, если s1=5, s2=15, e2>e1 и r12
На рисунке ниже показан случай, когда e1=8,s1=5, e2=10,s2=15 и r12=0,10. Здесь,
график риск-доходность «изгибается назад», так что x1=1 является неэффективным портфелем.
Портфель с минимальной дисперсией эффективен, как и портфели, сочетающие
это (в неотрицательных суммах) с активом 2.
Если r12 превышает s1/s2, портфель с минимальной дисперсией потребует короткой позиции в Актив 1. На рисунке ниже показан случай, когда e1=8,s1=5, e2=10,s2=15 и r12=0,80.
Как и прежде, все точки выше и правее точки, представляющей
Портфель с минимальной дисперсией эффективен. В этом случае актив 1 эффективен, как и все
комбинации с активом 2 в количестве, превышающем x2min.
Обратите внимание, что эффективное
граница увеличивается с убывающей скоростью, демонстрируя убывающую отдачу от принятия риска.
Мы видели, что эффективные комбинации двух активов строятся на кривой среднего стандартного пространство отклонений, которое увеличивается либо с постоянной скоростью, либо с убывающей скоростью по мере того, как стандартное отклонение увеличивается. Что можно сказать о форме границы в пространство средней дисперсии? 92
Таким образом:
d(vp) = 2*sp*d(sp)
и:
d(sp) = d(vp)/(2*sp)
Отсюда следует, что:
d(ep)/d(vp) = (d(ep)/d(sp))/(2*sp)
Если d(ep)/d(sp) остается постоянным при увеличении sp, то d(ep)/d(vp) будет
убывающая функция уд. На приведенных ниже рисунках показаны эффективные
границы в каждом из двух пространств, когда e1=6, s1=0, e2=10, s2=15 и два актива
совершенно положительно коррелированы.
.
Если два рискованных актива менее чем идеально коррелированы, d(ep)/d(sp) будет уменьшаться с sp и d(ep)/d(vp) в некотором смысле будут уменьшаться еще быстрее. Цифры ниже предоставить иллюстрации границы, представляющей неотрицательные комбинации двух активов в каждом из двух пространств, когда e1=6,s1=5, e2=10, s2=15 и r12=0,5.
Когда два актива объединяются в портфели, эффективная граница будет отображаться как кривая с уменьшающимся наклоном в пространстве средней дисперсии, независимо от того, какие активы характеристики. Это означает, что будет единственная точка касания с кривая безразличия (линия) из семьи, демонстрирующей постоянную толерантность к риску (т. какая полезность = ep-vp/t).
На рисунках ниже представлены иллюстрации с использованием активов в самом последнем примере и
толерантность к риску 50. На каждой диаграмме оптимальный портфель находится в точке, в которой
зеленая кривая безразличия касается границы эффективности.
Конечно, оптимально
портфель одинаков на каждой диаграмме. В этом случае оптимальная смесь имеет x1=0,5 и x2
=0,5. Ожидаемая доходность портфеля — 8,0%, его дисперсия — 81,25, стандартная
отклонение 90,0139, и это обеспечивает инвестору полезность в размере 6,375%. Последний
можно увидеть, изучив вертикальную точку пересечения зеленой кривой безразличия.
точки на синей кривой безразличия обеспечивают более низкий уровень полезности и, следовательно,
не подходит для этого Инвестора. Точки на красной кривой безразличия обеспечивают более высокую
уровень полезности, но в данном случае ни один из них невозможен.
Широко используемым (а иногда и неправильно) показателем эффективности инвестиций является Шарп.
Соотношение , первоначально названное его автором отношением вознаграждения к изменчивости , но
теперь часто дается это одноименное описание. В широком смысле это
отношение ожидаемой ценности стратегии с нулевыми инвестициями к стандартному отклонению
этой стратегии.
Важным частным случаем является стратегия нулевых инвестиций в
какие средства берутся взаймы по фиксированной ставке и инвестируются в рискованный актив.
Пусть x инвестируется в актив 2 и -x в актив 1. В наших предыдущих обозначениях это эквивалентно x2=x и x1=-x. Ожидаемый доход по отношению к базовому или условному значение х будет:
е = х*(е2-е1)
, а стандартное отклонение будет:
с = х * с2
Таким образом, коэффициент Шарпа для стратегии будет:
е/с = (х*(е2-е1))/(х*s2)
или:
(е2-е1)/с2
Обратите внимание, что e2-e1 — это ожидаемое значение разницы между доходностью актива 2
и доходность актива 1. Разница между доходностью рискованного актива и
доход безрискового актива называется избыточной доходностью рискованного актива :
хг2 = г2-г1
Поскольку r1 безрисковый, стандартное отклонение xr2 будет равно стандартному отклонению
р2.
Таким образом, коэффициент Шарпа для нашей стратегии будет:
е(хг2)/с(хг2)
, то есть ожидаемая избыточная доходность, деленная на стандартное отклонение избыточной доходности.
Для конкретности мы назовем этот актив 2 коэффициентом Шарпа избыточной доходности .
(xrsr), хотя его часто называют просто коэффициентом Шарпа актива.
Обратите внимание, что x, шкала стратегии нулевых инвестиций, не появляется в формула — все стратегии, использующие данный актив или портфель, имеют одинаковую ценность xrsr, независимо от их масштаба (при условии, конечно, что процентная ставка сумма займа не зависит). В этих условиях xrsr не зависит от масштаба .
Чтобы увидеть одно из следствий этой характеристики, рассмотрим выбор между двумя
рискованные активы, a и b, в которых можно выбрать только один, но могут быть открыты длинные или короткие позиции.
принято в безрисковый актив. Предположим, что актив b имеет более высокий коэффициент Шарпа избыточной доходности.
Как лучше? На рисунке ниже представлена иллюстрация.
Для любого желаемого уровня риска портфель, «основанный на» активе b, обеспечит более высокая ожидаемая доходность, чем та, которая основана на активе а. В этом контексте фраза «на основе on» означает комбинацию рассматриваемого актива и безрискового актива с количество последних положительное, отрицательное или нулевое, в зависимости от того, что требуется для получения желаемого уровня риск. Таким образом, если уровень риска, предлагаемый активом а, является желательным, комбинация актива b и кредитование, которое обеспечивает риск и доходность, показанные точкой z на диаграмме, должно быть выбран, так как он обеспечивает тот же уровень риска, но большую ожидаемую доходность. Это будет быть верным для любого желаемого уровня риска.
Еще один способ увидеть это — рассмотреть инвестиции в размере x1 в актив 1 и x2 в актив 2.
как (1) инвестиция в актив 1 и (2) решение открыть позицию размером x2 в
Стратегия без инвестиций, в которой актив 1 продается, а доходы от продажи
продажа, инвестированная в актив 2.
Институциональным механизмом для последнего является своп в котором Инвестор (сторона А) соглашается платить фиксированную ставку (доход от актива 1)
контрагента (сторона B), и последний соглашается платить ставку, основанную на возврате рискованного
актив (актив 2). Обе ставки умножаются на условную сумму, а затем сводятся для определения
окончательная стоимость, переданная от одной стороны («победителя») другой
(«неудачник»).
В этой ситуации Инвестор получит r1 на свои прямые инвестиции и x*(r1-r2) по свопу, где x — отношение номинальной стоимости свопа к стоимости первоначальных средств Инвестора. Итого возврат будет:
г1 + х*(г2-г1)
или:
г1*(1-х) + х*г2
Таким образом, x играет роль x2 в нашей исходной формулировке, а (1-x) играет роль
х1.
В то время как x представляет собой естественную меру для использования при заключении контракта с нулевыми инвестициями
стратегии, во многих случаях более полезной мерой масштаба является стандартное отклонение окончания
ценить.
В этом случае мы нормализуем его, разделив на сумму начального капитала Инвестора на
получить результирующее стандартное отклонение общего дохода:
сп = х*s2
Теперь мы готовы пересмотреть выбор между двумя взаимоисключающими рискованными активами.
исходя из предположения, что можно открывать длинные или короткие позиции по желанию,
либо прямо, либо косвенно с помощью производных стратегий, таких как свопы. в
В настоящее время необходимо выбирать между двумя стратегиями с нулевыми инвестициями. Один
обеспечивает e(xra)/s(xra) на единицу риска, а другой обеспечивает e(xrb)/s(xrb) на единицу
риска. Предположим, что желательна фиксированная величина риска sp. Тогда
ожидаемая доходность двух стратегий составит:
ea = e1+ ((e(xra)/s(sra))*sp
и
eb = e1+ ((e(xrb)/s(srb))*sp
Очевидно, что это стратегия с большим отношением ожидаемой избыточной доходности к стандартной.
отклонение избыточной доходности лучше.
Но это соотношение равно избыточному возврату Шарпа.
Соотношение. В ситуации такого рода следует выбрать альтернативу, которая
обеспечивает наивысшее вознаграждение за единицу изменчивости. Проще говоря: между взаимно
эксклюзивные рискованные портфели, выберите портфель с наибольшей ожидаемой доходностью
Коэффициент Шарпа.
Практики часто рассчитывают коэффициенты Шарпа избыточной доходности на основе исторической доходности для
взаимные фонды и другие инвестиционные продукты. Полезность таких мер может быть ограничена
из-за несоответствия предположениям, которые мы сделали в этом разделе. Первый,
распределение исторической доходности может быть плохой заменой распределения следующей
возврат периода. Во-вторых, невозможно получить кредит под ту же процентную ставку.
используется при расчете избыточного дохода. Наконец, Инвестор может иметь другие активы
и/или обязательств, и сравниваемые фонды могут иметь разную степень
корреляция с ними. Поскольку коэффициент Шарпа учитывает только ожидаемую доходность и
риск, это может не привести к лучшим инвестициям, если корреляции с важными активами и
обязательства существенно различаются между вариантами.
Несмотря на эти оговорки, коэффициент Шарпа является полезной мерой, которая может сочетать аспекты как ожидаемая доходность, так и риск в одном числе. Избыточная доходность Коэффициент Шарпа представляет собой один Применение более широкого понятия. В последующих разделах представлены другие примеры.
Пошаговый пример обратного распространения — Мэтт Мазур
Предыстория
Обратное распространение — это распространенный метод обучения нейронной сети. В Интернете нет недостатка в статьях, пытающихся объяснить, как работает обратное распространение ошибки, но лишь немногие из них содержат примеры с реальными числами. Этот пост — моя попытка объяснить, как это работает, на конкретном примере, с которым люди могут сравнить свои собственные расчеты, чтобы убедиться, что они правильно понимают обратное распространение.
Обратное распространение в Python
Вы можете поэкспериментировать с написанным мной Python-скриптом, который реализует алгоритм обратного распространения в этом репозитории Github.
Визуализация обратного распространения
Для интерактивной визуализации, показывающей нейронную сеть по мере ее обучения, ознакомьтесь с моей визуализацией нейронной сети.
Дополнительные ресурсы
Если вы считаете это руководство полезным и хотите продолжить изучение нейронных сетей, машинного обучения и глубокого обучения, я настоятельно рекомендую ознакомиться с новой книгой Адриана Роузброка «Глубокое обучение для компьютерного зрения с помощью Python». Мне книга очень понравилась, скоро будет полноценный обзор.
Обзор
В этом уроке мы будем использовать нейронную сеть с двумя входами, двумя скрытыми нейронами и двумя выходными нейронами. Кроме того, скрытые и выходные нейроны будут иметь смещение.
Вот базовая структура:
Чтобы иметь некоторые числа для работы, вот начальные веса, смещения и входные/выходные данные обучения:
Цель обратного распространения — оптимизировать веса так, что нейронная сеть может научиться правильно отображать произвольные входы в выходы.
В оставшейся части этого руководства мы будем работать с одним тренировочным набором: при входных данных 0,05 и 0,10 мы хотим, чтобы нейронная сеть выдавала значения 0,01 и 0,99.
Прямой проход
Для начала давайте посмотрим, что в настоящее время предсказывает нейронная сеть, учитывая приведенные выше веса и смещения и входные данные 0,05 и 0,10. Для этого мы будем передавать эти входные данные по сети.
Мы вычисляем суммарных входных данных для каждого нейрона скрытого слоя, сквош общий чистый ввод с использованием функции активации (здесь мы используем логистическую функцию ), затем повторите процесс с нейронами выходного слоя.
Общий чистый ввод также упоминается в некоторых источниках просто как чистый ввод .
Вот как мы вычисляем общий чистый ввод для:
Затем мы сжимаем его, используя логистическую функцию, чтобы получить результат:
Выполняя тот же процесс, мы получаем:
Мы повторяем этот процесс для нейронов выходного слоя, используя выходные данные нейронов скрытого слоя в качестве входных данных.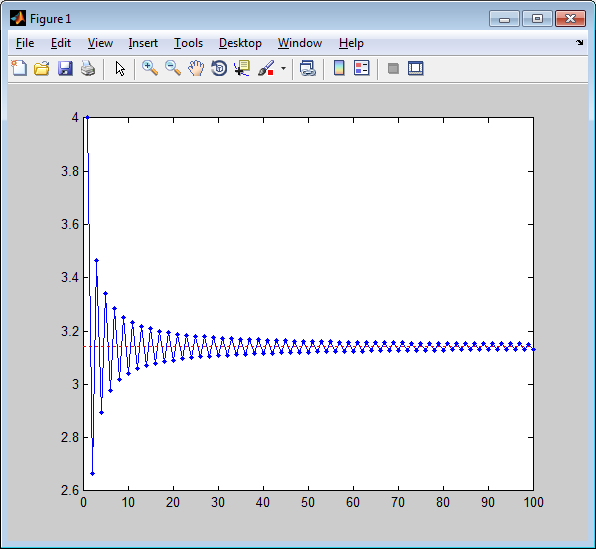
Вот результат для:
Выполняя тот же процесс для мы получаем:
Вычисление общей ошибки
900 ошибка в квадрате для каждой функции нейрона21 Теперь мы можем вычислить квадрат ошибки для каждой нейронной функции21 и суммируйте их, чтобы получить общую ошибку:В некоторых источниках цель называется идеальный и вывод как фактический .
Включено, чтобы показатель степени отменялся при дальнейшем дифференцировании. Результат в конечном итоге умножается на скорость обучения, поэтому не имеет значения, что мы вводим здесь константу [1].
Например, целевой вывод для равен 0,01, но вывод нейронной сети 0,75136507, поэтому ее ошибка:
Повторяя этот процесс для (помня, что цель равна 0,99), мы получаем:
Общая ошибка нейронной сети представляет собой сумму следующих ошибок:
Обратный проход
Наша цель с обратным распространением — обновить каждый из весов в сети, чтобы они привели к тому, что фактический результат будет ближе к целевому выходу, тем самым минимизируя ошибку для каждого выходного нейрона и сети в целом.
Выходной слой
Учитывать . Мы хотим знать, насколько изменение влияет на общую ошибку, также известную как .
читается как «частная производная по отношению к». Вы также можете сказать «градиент по отношению к».
Применяя цепное правило, мы знаем, что:
Визуально, вот что мы делаем:
Нам нужно вычислить каждую часть в этом уравнении.
Во-первых, насколько изменится общая ошибка по отношению к выходу?
иногда выражается как
Когда мы берем частную производную полной ошибки по , величина становится равной нулю, потому что не влияет на нее, что означает, что мы берем производную константы, которая равна нуль.
Далее, насколько изменится выпуск по отношению к общему чистому входу?
Частная производная логистической функции представляет собой выпуск, умноженный на 1 минус выпуск:
Наконец, насколько изменится общий чистый ввод по отношению к ?
Складываем все вместе:
Вы часто будете видеть этот расчет в виде дельта-правила:
В качестве альтернативы у нас есть и который может быть записан как , он же (греческая буква дельта) ака узел дельта .
Мы можем использовать это, чтобы переписать вычисление выше:
Следовательно:
Некоторые источники извлекают отрицательный знак, поэтому это будет записано как:
Чтобы уменьшить ошибку, мы затем вычитаем это значение. от текущего веса (необязательно умноженного на некоторую скорость обучения, eta, которую мы установим равной 0,5):
Некоторые источники используют (альфа) для представления скорости обучения, другие используют (эта), а третьи даже используют (эпсилон).
Мы можем повторить этот процесс, чтобы получить новые веса , и : мы используем исходные веса, а не обновленные веса, когда мы продолжаем алгоритм обратного распространения ниже).
Скрытый слой
Далее мы продолжим обратный проход, вычислив новые значения для , , и .
Общая картина, вот что нам нужно выяснить:
Визуально:
выход каждого нейрона скрытого слоя способствует выходу (и, следовательно, ошибке) нескольких выходных нейронов.
Мы знаем, что это влияет на оба, и поэтому необходимо учитывать его влияние на оба выходных нейрона:
Starting with :
We can calculate using values we calculated earlier:
And is equal to :
Plugging them in:
Following the same process for , we получаем:
Следовательно:
Теперь, когда у нас есть , нам нужно вычислить и затем для каждого веса:
как мы сделали для выходного нейрона:
Собирая все это вместе:
Вы также можете увидеть это:
Мы можем теперь обновление
2
.
Наконец-то мы обновили все наши веса! Когда мы изначально передавали входы 0,05 и 0,1, ошибка в сети была 0,298371109. После этого первого раунда обратного распространения общая ошибка снизилась до 0,29.1027924.