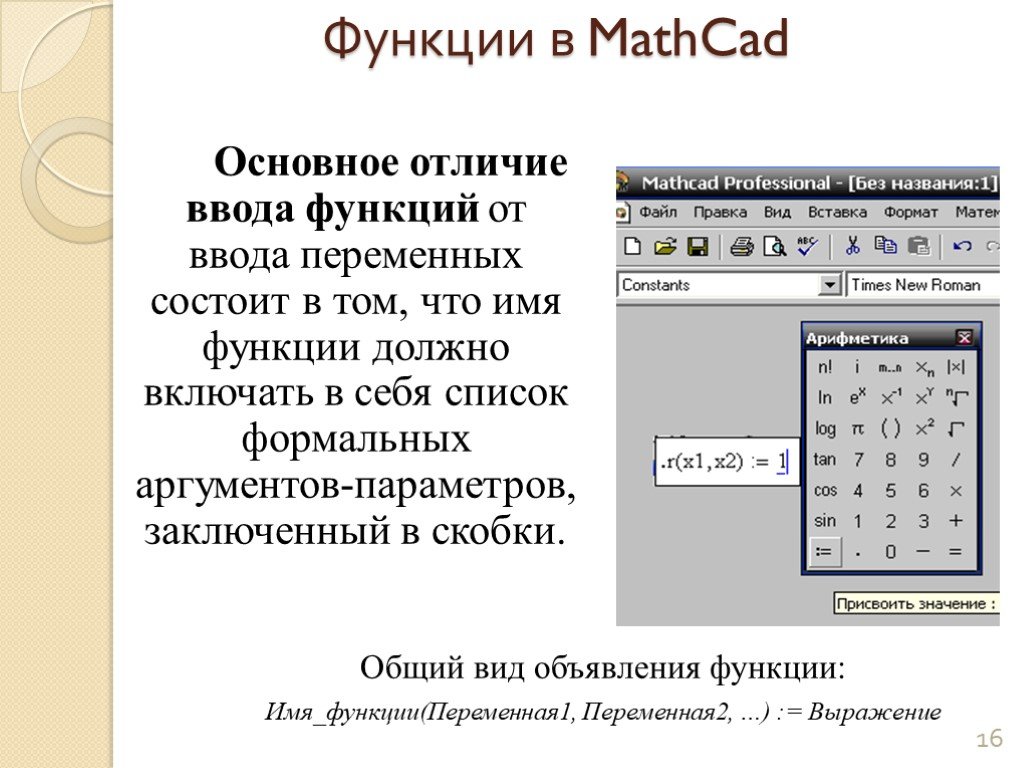
Функции в системе Mathcad — mathcad
Функции в системе Mathcad
|
Mathcad Express — бесплатный математический редактор, про который мало кто знает / Хабр
Прежде всего, приветствую первых посетителей моего блога. Это моя первая статья на Хабре и я надеюсь, что смогу рассказать вам здесь много полезного.
РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков. На протяжении последних лет Mathcad стал очень популярным, и его, на мой взгляд, по праву можно считать математическим пакетом №1 в мире.
Сначала несколько фактов о Mathcad, конечно, известных большинству читателей, т.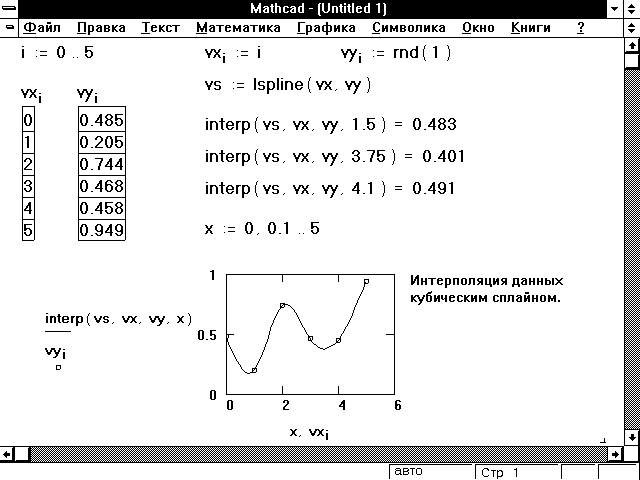 к. Mathcad у нас уже не один десяток лет используется в ВУЗовском обучении, научных и инженерных расчетах. Скорее всего, вы использовали «старую» версию Mathcad (последняя – за номером 15), мало изменившуюся еще с прошлого века. В наши дни она вполне успешно сосуществует с более молодым семейством Mathcad, которое носит имя Mathcad Prime. Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime. Дальше и в этой статье, и в моем блоге, будем говорить именно о Mathcad Prime.
к. Mathcad у нас уже не один десяток лет используется в ВУЗовском обучении, научных и инженерных расчетах. Скорее всего, вы использовали «старую» версию Mathcad (последняя – за номером 15), мало изменившуюся еще с прошлого века. В наши дни она вполне успешно сосуществует с более молодым семейством Mathcad, которое носит имя Mathcad Prime. Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime. Дальше и в этой статье, и в моем блоге, будем говорить именно о Mathcad Prime.
Сразу скажу, что русскоязычный дистрибутив, полнофункциональную 30-дневную версию Mathcad Prime вы можете скачать с сайта русского реселлера РТС. Если вы уже собрались попробовать ее в работе, мой совет – не торопитесь в Мастере установки согласиться с включением тестового 30-дневного периода. Дело в том, что Mathcad Prime, наряду с мощной полнофункциональной версией (окно которой вы видите сверху) имеет бесплатную ограниченную версию, которая называется Mathcad Express.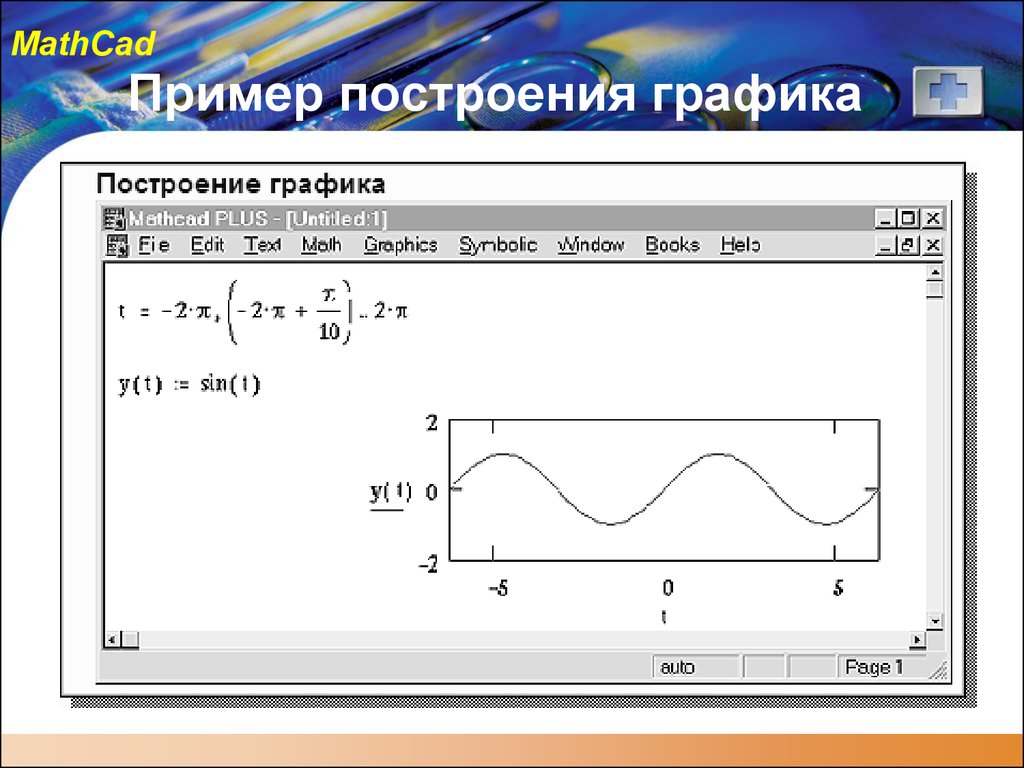 Особенность Mathcad Express заключается в том, что большинство функций в этой версии выключено и являются недоступными. Тем не менее, в программе Mathcad Express остается довольно богатый функционал, достаточный, по крайней мере, для того, чтобы изучать математику в школе и на 1-м курсе технического ВУЗа.
Особенность Mathcad Express заключается в том, что большинство функций в этой версии выключено и являются недоступными. Тем не менее, в программе Mathcad Express остается довольно богатый функционал, достаточный, по крайней мере, для того, чтобы изучать математику в школе и на 1-м курсе технического ВУЗа.
Формулы можно вводить в документы либо с клавиатуры (если подходящие символы на ней есть), либо при помощи меню Математика. Давайте ради примера посчитаем интеграл от функции cos(x). Для этого выбираем символ интеграла, а потом — в соответствующие местозаполнители вводим (с клавиатуры) пределы интегрирования и подынтегральную функцию cos(x). Остается нажать клавишу «равно», чтобы сразу получить ответ.
Надо хорошо себе представлять, что происходит, когда мы вводим знак равенства. А именно, запускается соответствующий численный алгоритм вычисления интеграла: интервал интегрирования разбивается на некоторое число отрезков, в определенных точках которых вычисляется массив значений подынтегральной функции, который потом пересчитывается в соответствующую аппроксимацию интегральной суммы.
Ключевые инструменты Mathcad – это операторы и функции. Например, в наших расчетах мы использовали оператор интегрирования и функцию косинуса. Для выбора нужной встроенной функции удобно использовать меню Функции.
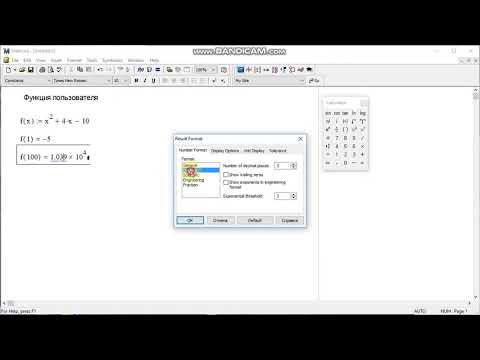
Давайте теперь определим пользовательскую функцию f(t), которая будет зависеть от переменной t. Будем использовать предназначенный для этого в Mathcad оператор присваивания (двоеточие со знаком равно).
Мы определили функцию f(t), как наш интеграл от cos(x) с переменным верхним пределом t. После того, как мы определили функцию f(t), можно посчитать ее значения в точках (для чего достаточно ввести аргумент и нажать клавишу «равно», чтобы вывести в документ ответ). Для ввода константы, например π, используется или меню Символы, или меню Константы.
В качестве аргумента можно использовать не только скалярную, но и векторную переменную.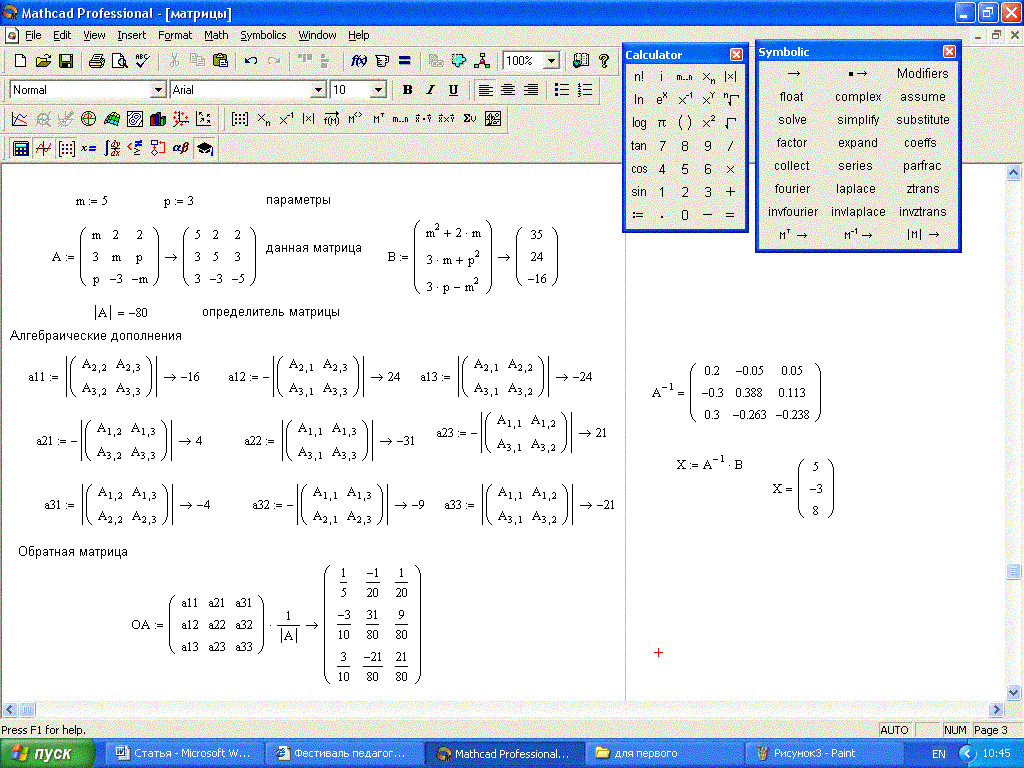
Тогда и результатом вычисления функции будет соответствующий вектор.
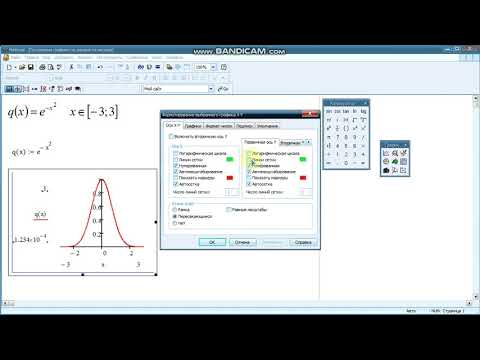
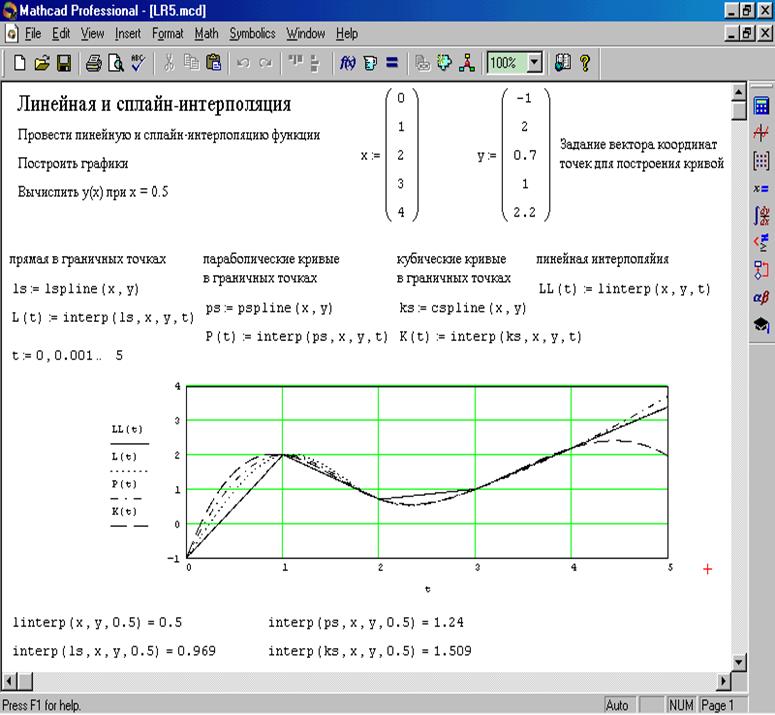
Наконец, одна из важных возможностей Mathcad Express – это возможность построения в документе графиков. Давайте выделим место в документе и вставим в это место XY-график (т.е. декартов график) нашей функции f(x).
Обозначаем на оси абсцисс имя переменной z (чтобы не путать с уже использованными ранее x и t), а на оси ординат – имя функции f(z), функцию, которую, как вы помните, мы определили, как интеграл от косинуса, равный конечно, sin(z). В итоге, получаем график этой функции.
Скажу еще, что в Mathcad Express (возможно, по недосмотру разработчика) остаются доступными матричные операции. Поэтому Mathcad Express — довольно мощный инструмент для решения задач линейной алгебры.
Переходя по документу вверх и вниз, мы можем просматривать свои расчеты, а управлять ими можно при помощи меню
 Если эту опцию отключить, то для того чтобы рассчитать документ вручную, достаточно нажить кнопку Рассчитать.
Если эту опцию отключить, то для того чтобы рассчитать документ вручную, достаточно нажить кнопку Рассчитать.Давайте я на этом остановлюсь, полагая, что задача знакомства читателя с Mathcad Express решена, и в следующих статьях блога, когда речь пойдет, собственно, о математике, я смогу использовать расчеты в Mathcad, не углубляясь в его интерфейс.
В заключение, адресую заинтересовавшегося читателя к своему видеокурсу по математическому анализу, который в формате МООС прошел на портале ИНТУИТ в 2014 году. Все лабораторные работы выполнены в Mathcad Prime и скачать их можно здесь. Все эти материалы на сайте Nerepetitor.ru бесплатные, регистрация не требуется.
PS. К своему удивлению столкнувшись с несколькими негативными комментариями, отмечу и несколько недостатков Mathcad (опять-таки, с моей точки зрения):
- имеется только Windows версия
- ресурсоемкий, работает медленнее«прошлых» Mathcad
- интерфейс мог бы быть и более удобным
- нельзя сохранить документ в прошлой версии (напр.
 из 3-й в формате 2-ю)
из 3-й в формате 2-ю) - документы из «прошлых» Mathcad не всегда удается импортировать в Prime
Сравнительная таблица версий PTC Mathcad
Сравните наши бесплатные и полные версии
PTC Mathcad Prime — это отраслевой стандарт программного обеспечения для инженерной математики, и покупка лицензии дает вам доступ ко всем последним разработкам продукта и полной функциональности продукта.
Однако с PTC Mathcad Express вы можете испытать полную функциональность в течение 30 дней, после чего вы получите базовую функциональность.
Используйте таблицу, чтобы понять, какие функции вы упустите, если не обновитесь до полной версии.
| ВОЗМОЖНОСТИ PTC MATHCAD | PTC Mathcad Express | PTC Mathcad Prime (ПОЛНАЯ ЛИЦЕНЗИЯ) | ||||
|---|---|---|---|---|---|---|
Удобство использования | ||||||
| Запишите уравнения, используя естественные математические обозначения | ||||||
| Проверка орфографии | ||||||
| Гиперссылки в тексте | ||||||
| Пользовательские размеры полей, верхнего и нижнего колонтитула | ||||||
| Предупреждения о переопределении | ||||||
| Водяной знак и стартовая страница | ||||||
Базовая математика | ||||||
| Автоматическое обновление расчетов | ||||||
| Операторы и функции алгебры и тригонометрии | ||||||
Документация | ||||||
| Полная документация | ||||||
| Стандартизация инженерных процессов с использованием шаблонов | ||||||
| Копирование областей рабочего листа в документ Word/PowerPoint | По одному | |||||
| Защита содержимого | ||||||
| Обтекание уравнения | ||||||
Заговор | ||||||
| Графики X-Y | ||||||
| Расширенные типы графиков: Полярный, Контурный, 3D | ||||||
Продвинутая математика | ||||||
| Программирование | ||||||
| Решение систем линейных, нелинейных и дифференциальных уравнений | ||||||
| Вычислять выражения символически | ||||||
Высшая инженерная математика: напр. План экспериментов, дифференциальные уравнения, решение регрессии План экспериментов, дифференциальные уравнения, решение регрессии | ||||||
| Расширенные числовые функции: напр. Преобразования Фурье, обработка сигналов, статистика и анализ данных | ||||||
Ввод, вывод | ||||||
| Руководство по API | ||||||
| Включить область рабочего листа | ||||||
| Компонент Excel | ||||||
| Поле со списком Управление вводом | ||||||
| Вставить объект | ||||||
Страница не найдена или в настоящее время переводится на запрошенный вами язык.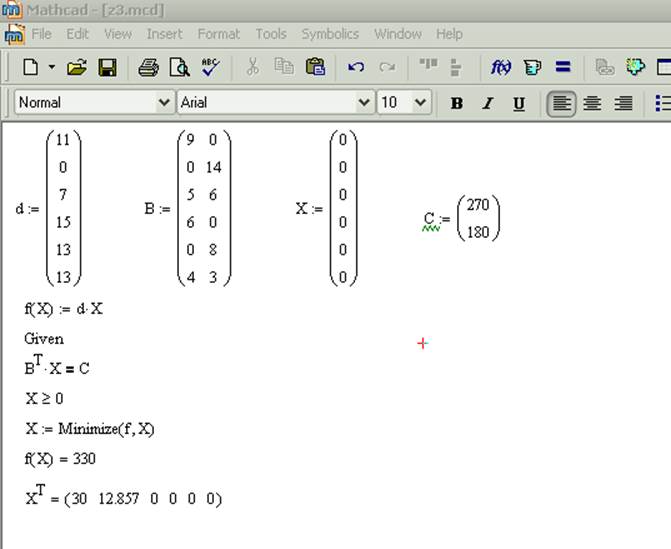 Если вы хотите перенаправить на английский язык, нажмите Да
Если вы хотите перенаправить на английский язык, нажмите Да
|
Основные инструкции. При использовании компьютерной алгебры системе часто возникают некоторые элементарные вопросы. Хотя они не тяжелые чтобы ответить, они могут представлять собой раздражающий порог для студентов. Преодолеть эти пороги, коллекция файлов ниже показывает, как решать те или иные задачи в Маткаде. Эти инструкции будут активными ссылками на файлы MathCAD в формате pdf. вариант моих модульных материалов.
Дополнительные инструменты. Приведенные ниже инструменты предназначены для создавать анимацию и визуализацию с помощью указанный пользователем функций и пользовательских доменов, центральных точек и т. д. Они могут также использоваться учащимися в качестве инструментов исследования. Разработка этих инструментов спонсировалась
Грант Совета регентов Луизианы за выдающиеся достижения в области инженерного образования «Математическая поддержка
для интегрированной инженерной учебной программы». Никакой гарантии правильности кода не делается и не подразумевается.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 2
2


 Анимация вращает график вокруг
данной центральной точки и отображает пересечение с плоскостью.
Анимация вращает график вокруг
данной центральной точки и отображает пересечение с плоскостью.

 Анимация увеличивает количество
Риман блокирует по указанному номеру.
Анимация увеличивает количество
Риман блокирует по указанному номеру.