Особенности двоичной системы счисления
Дата Автор ElectricianКомментироватьПросмотров: 10 395
В повседневной жизни мы используем десятичную систему счисления, которая состоит всего лишь из десяти цифр от 0 до 9, а все остальные числа являются комбинацией этих чисел. Данная комбинация получила название позиционной системы. Суть данной системы заключается в том, что число разбивают на части, кратные десяти, и записывают каждую часть на соответствующем месте, считая справа налево. Разберем на примере 365. Эта запись будет иметь следующий вид: где его разбивают на части и в такой же последовательности записывают множители при степенях десяти.
Если мы при построении счетчиков используем триггеры, то нам необходимо учитывать и то, что триггеры могут находится только в двух состояниях – либо единица, либо ноль. Поэтому любое число для них может быть записано только в двоичной системе счисления.
По аналогии с десятичной системой, каждое число разбивают на части, которые будут кратны уже не десяти, а двум. Такое выражение будет иметь вид:
Давайте рассмотрим на примере все того же 365 и определим все степени двойки, которые в этом числе могут быть:
20=1; 21=2; 22=4; 23=8; 24=16; 25=32; 26=64; 27= 128; 28=256; 29=512;
Поскольку 29=512 – а это больше чем 365, то мы берем ближайшее меньшее к 365 – а это 28=256. Последовательно отнимая от заданного числа степени двойки получим:
365 — 256(28)=109; 109 — 64(26)=45; 45 – 32(25)=13; 13 – 8(23) =5; 5 – 4(22) =1; 1 – 1(20)=0;
А это значит что:
365=256+64+32+8+4+1 =
То есть запись в позиционной системе будет иметь вид:
101101101
Проще переход к двоичной системе можно произвести еще таким способом:
Заданное число делят на два.
Если оно получается непарным, то от него отнимают единицу, которую записывают справа от числа за вертикальной чертой как показано выше. После того, как оно стало парным (365-1=364), его делят на два и результат записывают ниже заданного (364:2=182). Поскольку 182 парное, то справа записываем ноль и снова делим на два. Подобные действия проделывают до конца, а потом выписывают единицы и нули в направлении снизу вверх и получают 101101101.
Для перехода к десятичной системе счисления над каждой цифрой числа, записанного в двоичной системе, сверху надписывают справа налево степень двойки:
1 0 1 1 0 1 1 0 1
Подсчитывают степени соответствующие единице и суммируют результат:
28+26+25+23+22+20 = 256+ 64+32+8+4+1 =365
Каждый разряд двоичного числа называет «бит». В нашем случае использовано девять бит. Биты группируются в старшие разряды. Так, восемь битов составляют «байт».
Число, состоящее из байтов и битов называют «словом». Для записи больших чисел удобно использовать так называемую двоично – десятичную систему. Для осуществления этого каждую цифру в десятичной системе записывают в двоичном коде отдельно: 3 – 0011; 6 – 0110; 5 – 0101. Итак, 365 в двоично – десятичной системе будет иметь вид:
365 – 0011 0110 0101
При этом понадобится не девять бит, а двенадцать, но в таком виде гораздо удобней осуществлять перевод из одной системы в другую.
Posted in СхемотехникаКурс Harvard CS50 — Лекция: Двоичная система счисления
Harvard CS50
0 уровень , 3 лекция
Открыта
У нас 10 пальцев, и система — десятичная. То есть, любое, сколь угодно большое число мы можем представить с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В зависимости от того, где в числе стоит цифра, она может означать разное: если эта цифра последняя, то она расположена в разряде единиц, предпоследняя — разряд десятков, еще левее — разряд сотен и так далее.
По сути, любое число можно расписать в виде суммы цифр, каждая из которых умножена на десять в определенной степени. В случае единиц, эта степень — нулевая.
Например,
1573 = 3*100 + 7*101 + 5*102 + 1*103.
Число, на степень которого умножаются цифры называется базой системы счисления. Для десятичной системы базой, логично, является десятка.
У компьютера пальцев нет, но есть два состояния: условно «ток идет» и «ток не идет», нулик и единичка. Соответственно все числа (да и вообще информация) в памяти компьютера состоят только из двух цифр — 0 и 1. Их расположение, как и в случае десятичной системы счисления, указывает на разряд. Только теперь число можно разложить на сумму цифр, помноженных не на степени десятки, а степени двойки.
0 в двоичной системе = 0 1 в двоичной системе = 1 2 в двоичной системе = 10 710=1112
Научитесь переводить из двоичной системы в десятичую.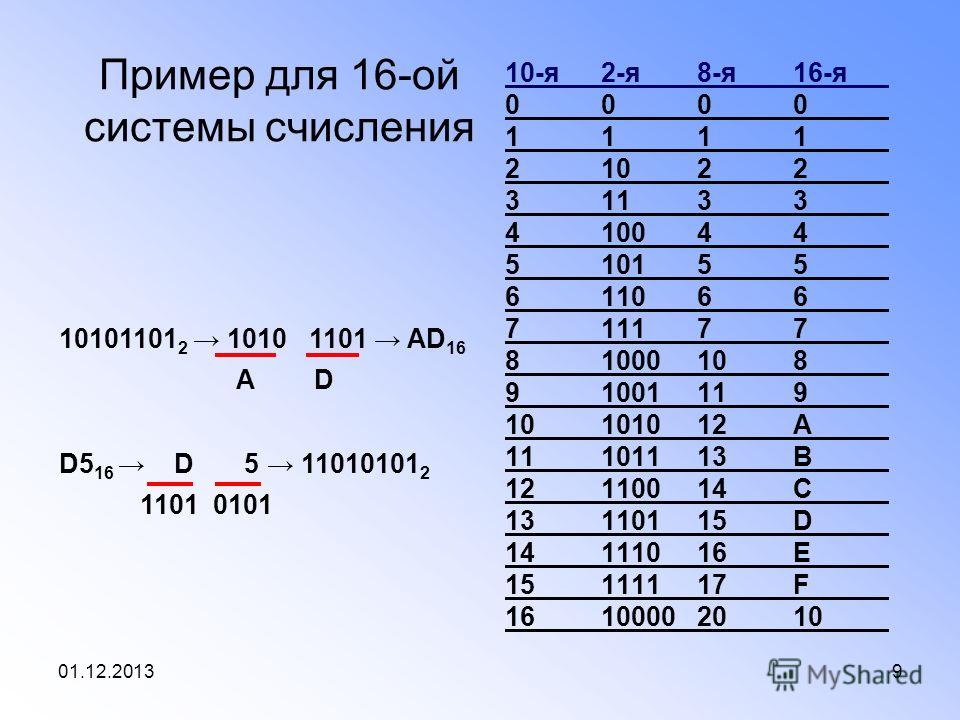
Вы, наверное, уже поняли, как это делается — просто берем цифру числа начиная с самой правой и умножаем её на базу системы счисления в степени, соответствующей её разряду, так с каждым разрядом. Затем складываем все получившиеся таким образом числа.
Пример:
Давайте найдем десятичный аналог двоичного числа 101101 2
- Самая правая единичка = 1*20
- Следующий нулик = 0*21
- Третья справа единичка = 1*22
- Четвертая = 1*23
- … и так далее
1011012 = 1*20 + 0*21 + 1*22 + 1*23 + 0*24 + 1*25 = 1 + 0 + 4 + 8 + 0 + 32 = 4510
Представьте восемь лампочек, выставленных в ряд. У каждой из них — свой собственный выключатель.
Каждая из лампочек — это разряд. Да что представлять, вспомните самую первую лекцию (там есть такой агрегат) или вот вам виджет: cdn.cs50.net/2016/x/psets/0/pset0/bulbs.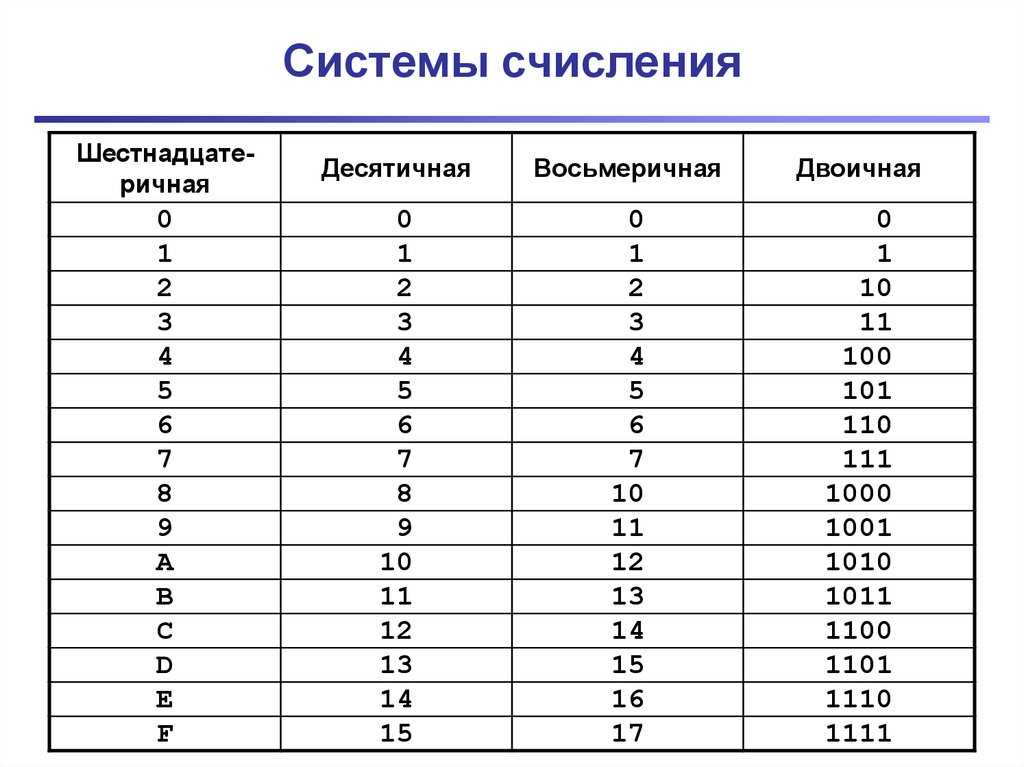
html
Поиграйтесь с ним, «прочувствуйте» двоичную систему.
Тут тоже всё просто, если понимать суть.
Пример:
У нас есть десятичное число 57
26 = 64. Это явно многовато. А вот 25 = 32.
Мы определили старший разряд. 3210 = 1000002. Теперь ищем следующий разряд. 57-32 = 25. Теперь для 25 ищем степень двойки, которая не превосходит 25. 24 = 16. Значит, следующий разряд у нас тоже равен 1. 32+16 = 4810 = 1100002. 57 – 48 = 9. 23 = 8, это меньше, чем 9. Значит следующий разряд тоже будет единичкой.
32 + 16 + 8 = 5610 = 1110002. 57 - 56 = 1, то есть осталась только одна степень 20. Таким образом, 5710 = 1110012.
На этом все =) Переходите к следующей лекции!
Что такое двоичная система?
Система нумерации представляет собой набор символов и правил, с помощью которых мы можем выразить все действительные числа в этой системе.
Например, десятичная система , которую мы используем чаще всего в повседневной жизни, использует число 10 в качестве основы и состоит из 10 различных чисел, с помощью которых вы можете представить все остальные: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Это позиционная система и поэтому значение каждого числа меняется в зависимости от его положения (единицы, десятки, сотни и т.д.).
Двоичная система , которая широко известна, потому что это система счисления, используемая компьютерами и другими электронными устройствами, является системой с основанием 2. Это означает, что он использует только две цифры для представления всех своих чисел, и в случае двоичного кода эти два числа равны 0 и 1. Компьютеры используют двоичную систему, потому что они работают только с двумя уровнями напряжения : ВЫКЛ или без присутствия электрического заряда (0) и ВКЛ или при наличии электрического заряда (1).
Существуют и другие системы счисления с различным назначением, такие как восьмеричная система (основание 8) и шестнадцатеричная система (основание 16), которые также используются в компьютерном мире, или шестидесятеричная система (основание 60), которая является другой системой нумерации.
система, которую мы используем каждый день для измерения времени (один час равен 60 минутам, а каждая минута равна 60 секундам).
Первые описания двоичной системы датируются 3 веком до н.э. и приписываются древнеиндийскому математику по имени Пингала . Первые представления двоичных чисел встречаются в классических трудах китайского происхождения, в частности, в философском труде « I Ching », который датируется между 1200 и 100 годами до нашей эры. в.
На протяжении следующих столетий мы также можем найти документы других математиков и других мыслителей, которые излагали идеи, связанные с двоичной системой. Например, сэр Фрэнсис Бэкон создал код Бэкона в начале 17 века, криптографический код, основанный на двоичной системе, в которой для шифрования сообщений использовались буквы A и B, сгруппированные в пятибуквенные комбинации.
Что касается современной двоичной системы, то математическая основа двоичной системы, какой мы ее знаем, была впервые задокументирована в 17 веке немецким математиком Готфридом Вильгельмом Лейбницем .
В 1703 году Лейбниц опубликовал статью « Explication de l’Arithmétique Binaire », в которой объяснялось, как числа могут быть представлены с помощью цифр 0 и 1. В то время его исследования не отвечали какой-либо конкретной цели, но с приходом первых компьютеров в начале 20-го века, почти 300 лет спустя, можно было понять, как все, что изложил Лейбниц в своей статье, применялось первыми программистами компьютеров.
Также важно отметить вклад британского математика Джорджа Буля , который в 1854 году опубликовал статью, в которой подробно описал систему логики, названную Булевой алгеброй, которая началась с теории двоичной системы и была ключ к разработке электронных схем.
Преобразование чисел из одной системы счисления в другую Возможно преобразование числа из одной системы счисления в другую, например из двоичной в десятичную или наоборот. В первом случае необходимо разложить двоичное число на множители (по основанию 2) и в дальнейшем мы можем преобразовать его в эквивалентное число в десятичной системе.
Если у нас есть двоичное число 10111101 и мы хотим преобразовать его в десятичное число, мы должны сначала разложить его на множители, используя число 2 и возведя его в степень, соответствующую каждой цифре, в соответствии с положением, которое она занимает в ряду чисел. В качестве показателей степени мы будем использовать 0, 1, 2, 3… пока не достигнем 7, и мы начнем факторизовать в порядке слева направо, начиная с наибольшей степени. Наконец, мы вычислим сложение и найдем эквивалентное десятичное число, которое в данном случае равно 189.:
10111101 = (1·2 7 ) + (0·2 6 ) + (1·2 5 ) + (1·2 4 ) + (1·2 3 ) + (1·2 3 ) (1·2 2 ) + (0·2 1 ) + (1·2 0 )
10111101 = (128) + (0) + (32) + (16) + (8) + ( 4) + (0) + (1)
10111101 = 189
Чтобы преобразовать целое число из десятичной системы и найти его эквивалент в двоичной системе, мы должны использовать число, которое мы хотим преобразовать (189), в качестве делимого и число 2 в качестве делителя, так как искомое число имеет основание 2.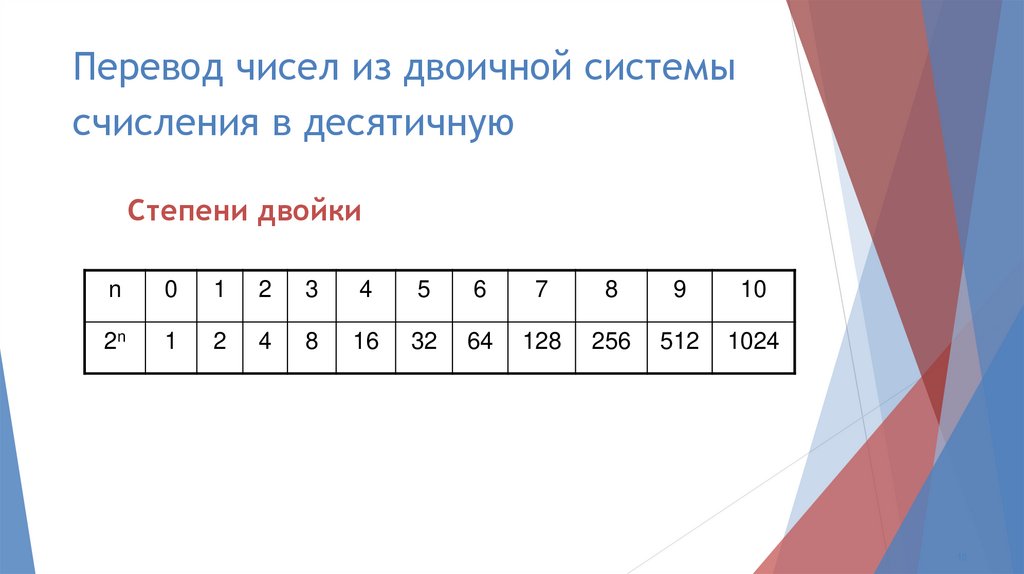
Затем мы возьмем результат этого первого деления и снова разделим его на 2 (и так далее с каждым полученным частным до тех пор, пока дальнейшее деление станет невозможным). ). Когда деление закончено, мы записываем числа, соответствующие остаткам каждого деления, в обратном порядке, то есть переводя их из последнего сделанного нами деления в первое. Таким образом мы получим эквивалентное двоичное число, которое на этот раз было 10111101.
Двоичный файл для чайников. «Все, что можно представить с помощью… | Уилл Бейнтон
«Все, что может быть представлено каким-либо шаблоном, может быть представлено набором битов».
-Клод Шеннон
Сам человек, возможно, наиболее известный своими Математическая теория связи, и основателем теории цифровых цепей, которая утверждает, что булева алгебра может передавать любые логические числовые отношения.
Что такое двоичный код?
Двоичная запись — это двухсимвольная система счета, способная сжимать сложные данные в длинную серию утверждений «да» или «нет».
Все процессы, выполняемые компьютером, и все данные, сохраненные в нем, в конечном итоге переводятся в двоичный или машинный код для чтения компьютером.
В 1689 году Готфрид Либниц написал статью под названием Explication de l’Arithmetique , в которой объяснял важность и область применения двоичной системы счисления. В нем он описывает основные методы двоичного счета, объясняя при этом, как его гибкость может быть полезна для ряда различных приложений.
«Здесь одним взглядом становится очевидной причина знаменитого свойства геометрической прогрессии на двойки целых чисел, состоящего в том, что если иметь только одно из этих чисел для каждой степени, то из них можно составить все остальные целые числа. ниже двойника высшей степени.
Ибо здесь все равно, что сказать, например, что 111, или 7, есть сумма четырех, двух и одного, а 1101, или 13, есть сумма восьми, четырех и одного. Это свойство позволяет оценщикам взвешивать все виды масс с небольшим весом и может использоваться при чеканке монет, чтобы получить несколько номиналов с помощью небольшого количества монет».
Здесь важно отметить, что с небольшим количеством монет, то есть с небольшим количеством символов, можно было бы производить удивительно сложные вычисления с минимальными ресурсами.
Как это работает?
Вместо использования системы счисления с основанием 10 (0–9) в двоичной системе счисления используется система счисления с основанием 2 (0–1). Это означает, что в десятичной системе счисления десять символов, а в двоичной — только два. В системе счисления с основанием 10 каждая добавленная цифра представляет значение, в десять раз превышающее предыдущую цифру, тогда как в системе с основанием 2 каждая добавленная цифра представляет собой значение, в два раза превышающее предыдущее. Все это говорит о том, что 0, 1 и цифровая позиция этих двух символов — это все, что используется для определения значения конкретной строки чисел.
Но почему?
Физические ограничения компьютеров диктуют необходимость двоичного кодирования. Компьютеры в основном состоят из транзисторов, которые работают, получая небольшой электрический заряд.
Большинство транзисторов работают, получая электрический заряд и включаясь или выключаясь подобно выключателю света. Сложите достаточное количество этих транзисторов вместе, и у нас есть основные компоненты схемы.
Хотя было бы сложно разработать схему, которая могла бы измерять градусов электрического заряда, относительно легче разработать компонент, который измеряет существование одного из них.
Все это приводит к риторическому вопросу:
«Что проще построить, выключатель или диммер?»
Транзисторы равны биту и, по сути, являются атомом или строительным блоком всех вычислений. В своей простейшей форме они могут только включаться или выключаться. На карте все переключатели, которые быстро включаются и выключаются в разной последовательности, определяют основные функции компьютера. Что делает двоичный код таким неотъемлемым элементом связи с компьютером, так это легкость, с которой мы можем создавать машины, которые распознают «истину» или «ложь», а не какой-то промежуточный диапазон.