Спектр фурье: Простыми словами о преобразовании Фурье / Хабр

Простыми словами о преобразовании Фурье / Хабр

Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

(с) xkcd

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:

• FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
• Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
• Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
• Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
• Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
• Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
• Как по цифровой последовательности восстанавливают исходный сигнал

Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):

Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике.

Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:

График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).

Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают.

Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.

Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.

Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:

Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:

Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.

Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.

Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.

Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.

Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi…pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).

Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).

Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:

Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции — тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени — это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:

Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.

Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный — достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать — это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T…1/2T и нулю — вне этого диапазона. Подобный Фурье-образ соответствует функции sinc(Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)

То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста”. Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное, но не необходимое условие для восстановления исходного сигнала. Все что нам требуется — это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.

Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) — непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.

Еще одно распространенное заблуждение, кстати, — это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:

Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.

На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.

Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке [0…1/T), поэтому часто этим отрезком спектр DTFT и ограничивают. При этом результат DTFT несмотря на то что это спектр дискретизированного сигнала — по-прежнему “аналоговая” функция. Кроме того, для “обычных” действительнозначных сигналов вторая половина этого спектра в силу свойства 6 зеркально повторяет левую половину, отраженную относительно частоты Найквиста 1/2T.

До сих пор мы предполагали что на вход наших преобразований поступает сигнал определенный от минус до плюс бесконечности. Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями. Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Однако часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.

Пользуясь уже хорошо нам знакомым свойством 5, несложно сообразить, что при подобном умножении исходный сигнал прсто сворачивается со спектром функции окна. Например если мы пытаемся измерить спектр синусоиды (дельта-функцию), но ограничиваем интервал измерений прямоугольным окном, то в получившимся спектре на месте дельта-функции мы увидим спектр окна — т.е. Tsinc(T(x-f)):

В данном случае T — это длина интервала которым мы ограничили наш сигнал, так что чем длиннее будет входной сигнал — тем “уже” и ближе к истинной дельта-функции будет наблюдаемый нами спектр. Конечная “ширина” главного лепестка приводит к невозможности уверенно различать наличие в исходном сигнале синусоид близких друг к другу по частоте, а наличие “боковых лепестков” вносит небольшие искажения и в далеко расположенные частоты, мешая точному измерению амплитуды отдельных частот, особенно если нужно измерять спектр в областях небольшой амплитуды при наличии в спектре на порядок более мощных компонент. Этот эффект называют “спектральной утечкой” и полностью победить его для бесконечных сигналов невозможно, но чем длиннее интервал на котором измеряется сигнал — тем меньше влияние этой утечки. Выбором функции окна можно контролировать “ширину” этой утечки, либо концентрируя её вокруг главной частоты (сильно “размывая” спектр, но зато не мешая соседним частотам), либо размазывая её повсюду (размытие пиков уменьшается но сильно растет “шум” и как следствие — погрешность измерения амплитуды отдельных частот). Заметьте, что выбранная частота дискретизации в спектральной утечке почти не играет роли — короткий отрезок сигнала можно сэмплировать хоть на 10 ГГц, но это увеличит только количество поддающихся измерению частот, тогда как точность определения каждой отдельной частоты все равно останется низкой.

Интересным частным случаем является ситуация, в которой сигнал с набором дискретных частот nF дискретизируется на частоте mF, где m,n — целые числа. В этом случае нули “окна” и расположение дельта-функций в спектре в точности совпадают и хотя частоты все равно “размазываются”, но их амплитуда в точках mF совпадает с истинной — “шум” равен нулю. Это свойство позволяет доказать аналог теоремы Котельникова для дискретного преобразования Фурье, но на практике такие сигналы, к сожалению, фактически не встречаются.

Итак, со “входом” мы разобрались — из непрерывной функции бесконечной длины мы получили конечное число дискретных отсчетов, с которыми можем работать а взамен получили ограничения по ширине спектра и утечку частот. Однако “выход” DTFT по-прежнему является непрерывной функцией, работать с которой компьютеру проблематично. На практике эту проблему решают очень просто — полный отрезок [0,1/T) делят на k равных частей и считают DTFT в точках fi=i/kT, где i = 0,1,… k-1. Получившуюся конструкцию называют “дискретным преобразованием Фурье” (DFT).

Последнее преобразование удобно нормализовать, убрав из него T и вопросы связанные с выбором “окна”. Эту нормализованную запись часто используют в качестве определения DFT как преобразования последовательности из N комплексных чисел:

Прелесть преобразования Фурье записанного в такой форме — в том что сохраняя все достоинства DTFT, подобное DTF для “гладких” k (например, степеней двойки) можно вычислять чрезвычайно быстро, за время порядка k log(k). Соответствующие алгоритмы называют “быстрым преобразованием Фурье” (БПФ, FFT) и их, вообще говоря, существует несколько. С практической точки зрения, впрочем, их все можно рассматривать как “черные ящики”, получающие последовательность комплексных чисел на входе и выдающих последовательность комплексных чисел на выходе. Таким образом, работа с дискретизированным сигналом конечной длины сводится к тому, что этот сигнал вначале умножается на подходящую взвешивающую функцию, затем дополняется нужным числом нулей справа и передается в алгоритм БПФ.

Как интерпретировать получившийся результат? С учетом всего вышеизложенного,

• Получившиеся значения есть равномерная сетка отсчетов по спектру DTFT. Чем больше отсчетов — тем мельче сетка, тем подробнее виден спектр. Дописывая к известной последовательности нужное число нулей можно посчитать сколь угодно близкое приближение к непрерывному спектру
• Спектр DTFT задан на отрезке частот от 0 до 1/T (где 1/T — частота дискретизации) и периодически повторяется на бесконечность вне этого отрезка
• Этот спектр задан комплексными числами (парами действительных). Амплитуда определяется как модуль комплексного числа, фаза — как аргумент.
• Для действительнозначного входного сигнала, спектр в диапазоне 1/2T…1/T просто зеркально повторяет спектр 0…1/2T и не несет соответственно полезной нагрузки (для визуализации спектра его можно просто обрезать)
• Если исходный сигнал содержал частоты выше половины частоты дискретизации, то они будут отображены в более низкие частоты (возможно накладываясь поверх уже существующего сигнала этой частоты) — алиасинг
• В спектре всегда присутствует “спектральная утечка” определяющаяся выбранной взвешивающей “оконной функцией”. Чем длиннее исходный сигнал (до дополнения нулями!) — тем эта утечка меньше.
• Спектральная утечка ограничивает осмысленность расчета БПФ с большим дополнением нулями. Однако дополнение все же часто бывает полезным, поскольку, например, позволяет точнее определить максимум узкополосного синусоидального сигнала, если он не попадает точно в одну из частот вида k/T.
• Синусоиде амплитуды A в амплитудном спектре (при выбранной мной нормировке преобразования Фурье) соответствует значение A*N/2, за исключением нулевой частоты, которая не раскладывается на “плюс” и “минус” частоту и потому имеет амплитуду A*N, а также частоты Найквиста 1/2T в которой касаются в предельном случае друг друга отдельные копии спектра (там тоже будет A*N, но, в отличие от нуля в выход БПФ это значение не попадает да и достоверным в реальных схемах все равно никогда не является). Здесь N = T1/T0, где T1 — это длина исходного сигнала (она определяет коэффициент перед спектром «окна»), а T0 — длина одного периода дискретизации (она определяет коэффициент у гребенки Дирака) и по смыслу это, как несложно видеть, попросту число отсчетов в исходном сигнале (до его дополнения нулями)

Ну вот, в общем, и всё. Надеюсь преобразование Фурье и алгоритмы БПФ будут теперь для Вас простыми, понятными и приятными в обращении инструментами.

Преобразование Фурье: самый подробный разбор

Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.

Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.

Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.

Здесь и пригодится знание преобразования Фурье.

Что такое звук в математическом смысле?

Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.

Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.

Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.

Запишем определение:

Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.

Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?

Геометрическая интерпретация преобразования Фурье

Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.

В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.

1. Наматываем сигнал

Давайте начнём с самого простого случая. Рассмотрим гармонический сигнал, совершающий 3 колебания в секунду (f₀ = 3с^-1):

g(t) = 1 + cos (6πt).

Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.

Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения f_В = 0.5 об/с.

Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная «намотка» сливается с началом координат, а при приближении к максимумам – отклоняется.

Пока выглядит не особо информативно, не так ли?

А теперь увеличим частоты намотки.

Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения f_В = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.

2. Ищем центр масс

Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).

Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.

Мы видим два пика: в точках f_В = 0 об/с и f_В = 3 об/с. На основании такого поведения центра масс уже можно судить о частоте исходного сигнала (он колеблется с f = 3с^-1).

Тогда что означает всплеск на низких частотах?

3. Анализируем влияние смещения

Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.

При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.

Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.

Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.

Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.

Таким образом, на графике остался только один резкий скачок.

Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.

4. Выделяем частоты полигармонического сигнала

Теперь рассмотрим сумму двух гармонических сигналов с частотой колебаний f₁ = 2 с^-1 и f₂ = 3 с^-1. Проделаем с ней те же операции – «намотаем» возле начала координат, и, меняя частоту вращения, построим график х-координаты центра масс.

Мы наблюдаем два пика в точках f_В = 2 об/с и f_В = 3 об/с, что соответствует частотному составу исходной суммы.

Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.

Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.

Вывод преобразования Фурье

В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:

e^iφ=cos(φ)+i·sin(φ).

Геометрически это соотношение означает, что при любом φ точка e^iφ на комплексной плоскости лежит на единичной окружности.

Построим радиус-вектор e^iφ при разных значениях φ.

При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.

Тогда намотка сигнала g(t) описывается как g(t)e^-2πift.

Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:

Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:

где t₁ и t₂ – границы интервала, на котором рассматривается сигнал.

Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.

Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.

Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.

Применение преобразования Фурье для фильтрации

Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.

При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.

После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.

Мы что-то упустили? Напишите об этом в комментариях 🙂

Что такое преобразование Фурье?

Добавлено 8 августа 2020 в 19:37

Данная статья даст вам важную информацию о математическом методе, который играет фундаментальную роль в проектировании систем и обработке сигналов.

Преобразование Фурье, названное в честь французского математика Жозефа Фурье, представляет собой математическую процедуру, которая позволяет нам определить частотный состав функции. Для инженеров-электронщиков преобразование Фурье обычно применяется к функциям времени, которые мы называем сигналами.

Разложение на синусоиды

График зависимости напряжения или тока от времени, который мы видим на экране осциллографа, представляет собой интуитивно понятное представление поведения сигнала. Однако это не единственное полезное представление.

Во многих случаях (например, при проектировании радиочастотных систем) нас в первую очередь интересует периодическое поведение сигналов. В частности, нас интересует понимание сигнала относительно синусоидальной периодичности, потому что синусоиды – это уникальное математическое выражение «чистой» частоты.

Преобразование Фурье выявляет элементарную периодичность сигнала, раскладывая этот сигнал на составляющие его синусоидальные частоты и определяя амплитуды и фазы этих составляющих частот.

Слово «разложение» здесь имеет решающее значение. Преобразование Фурье учит нас думать о сигнале во временной области как о сигнале, который состоит из базовых синусоидальных сигналов с различными амплитудами и фазами.

Например, прямоугольный сигнал может быть разложен на бесконечную последовательность синусоид с постоянно уменьшающимися амплитудами и постоянно увеличивающимися частотами. Точная последовательность для прямоугольного сигнала, с развязкой по постоянному току, с периодом T и амплитудой A, может быть записана следующим образом:

\[f_{прямоуг}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,. ..\}}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]

Мы можем преобразовать это в следующую форму, которая немного более интуитивна:

\[f_{прямоуг}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3}\sin(6\pi ft)+\frac{1}{5}\sin(10\pi ft)+\ …\right)\]

где f – частота прямоугольного сигнала в герцах.

На следующем графике синим цветом показан исходный прямоугольный сигнал и первые восемь синусоид в бесконечной последовательности.

Рисунок 1 – Прямоугольный сигнал и составляющие его синусоиды

Посмотрев на этот график, вы всё еще можете немного скептически относиться к тому, что эти синусоиды можно объединить в прямоугольный сигнал. Но следующий график вас убедит. Он показывает исходный прямоугольный сигнал и форму сигнала, полученную путем сложения всех составляющих синусоид, показанных выше.

Рисунок 2 – Исходный прямоугольный сигнал и результат сложения синусоид

Функции времени и частоты

Когда мы вычисляем преобразование Фурье, мы начинаем с функции времени f(t), а с помощью математического разложения получаем функцию частоты F(ω) (обычно в теоретических обсуждениях преобразования Фурье мы используем угловую частоту).

Оценка функции F(ω) на некоторой определенной угловой частоте, скажем 100 рад/с, дает нам величину и фазу синусоидальной составляющей f(t), частота которой равна 100 рад/с. Если f(t) не имеет синусоидальной составляющей на 100 рад/с, то ее амплитуда будет равна нулю.

Вам может быть интересно, как одна функция F(ω) может говорить и об амплитуде, и о фазе. Преобразование Фурье создает комплексную функцию, что означает, что результат самого преобразования не является ни амплитудами частотных компонентов в f(t), ни фазами этих компонентов. Как и с любым комплексным числом, чтобы определить амплитуду или фазу, мы должны выполнить дополнительные вычисления.

Идея комплексного преобразования несколько более интуитивна, когда мы работаем с дискретным преобразованием Фурье, а не со «стандартным» преобразованием, в котором мы начинаем с символической функции времени и заканчиваем символической функцией частоты. 2}\),.

Построение графика результатов преобразования Фурье

В технических описаниях, отчетах об испытаниях, учебниках и т.д. очень часто встречаются графики частотных составляющих. График зависимости амплитуды от частоты мы часто называем спектром – например, «давайте посмотрим на спектр сигнала» означает «давайте посмотрим на какое-то визуальное представление информации об амплитудах в результатах преобразования Фурье».

На следующем графике показан спектр прямоугольного сигнала, с развязкой по постоянному току, с амплитудой 1 и частотой 1 Гц.

Рисунок 3 – Спектр прямоугольного сигнала с амплитудой 1 и частотой 1 Гц

Если вы сравните нанесенные на график амплитуды частотных «всплесков» с амплитудами соответствующих синусоидальных составляющих в бесконечном ряду, описанном выше, то вы увидите, что они равны.

Вычисление преобразования Фурье

Мы почти подошли к концу этой статьи, и я все еще не рассказал вам, как мы на самом деле математически выполняем преобразование Фурье определенного сигнала. { — j\omega t}}dt}\]

Заключение

Я надеюсь, что данная статья дала вам четкое, интуитивно понятное объяснение того, что такое преобразование Фурье и как оно дает нам дополнительное понимание сути сигнала.

Преобразование Фурье – это только начало обширного массива связанных тем. Если вы хотите узнать больше, ознакомьтесь со статьями, перечисленными ниже.

Материалы для дальнейшего чтения

• Как выполнить анализ в частотной области с помощью Scilab
• Учимся жить в частотной области

Оригинал статьи:

• Robert Keim. What Is the Fourier Transform?

Теги

Преобразование ФурьеПрямоугольный сигналРадиочастотная системаРазложение на синусоиды

Преобразование Фурье

Содержание

Предельный переход от ряда Фурье к преобразованию Фурье Пояснения понятия спектральной плотности сигнала Связь спектральной плотности непериодического сигнала и огибающей коэффициентов ряда Фурье Условия существования преобразования Фурье Выводы Список литературы

DSPL-2. 0 — свободная библиотека алгоритмов цифровой обработки сигналов Распространяется под лицензией LGPL v3 Страница проекта на SourceForge

Обнаружили ошибку? Выделите ее мышью и нажмите

Предельный переход от ряда Фурье к преобразованию Фурье

Использование периодических функций для представления периодических сигналов выглядит вполне логичным и позволяет перевести анализ в частотную область. Таким образом, мы можем заменить сигнал набором спектральных гармоник , путем разложения в ряд Фурье:

Жан-Батист Жозеф Фурье
1768–1830

(1)

где  — период повторения сигнала. Спектр состоит из дискретных гармоник, равноотстоящих по частоте с шагом рад/с.

Однако, периодические функции могут быть использованы и для частотного представления непериодических сигналов. В данном разделе мы произведем переход от ряда Фурье (1) к интегральному преобразованию Фурье для непериодических сигналов .

Для начала рассмотрим, что будет происходить, если мы будем увеличивать период повторения периодического сигнала. На рисунке 1 показаны временные осциллограммы периодической последовательности прямоугольных импульсов , а также амплитудный спектр , при различном периоде повторения с, с и с, при амплитуде сигнала равной 2 В.

Рисунок 1. Амплитудный спектр периодической последовательности прямоугольных импульсов
при увеличении периода повторения

Из рисунка 1 видно, что при увеличении периода , гармоники спектра приближаются друг к другу, потому что расстояние между гармониками  обратно пропорционально периоду . Амплитуды гармоник при этом уменьшаются из-за уменьшения средней мощности сигнала на одном периоде повторения.

При увеличении периода повторения до бесконечности, периодический сигнал становится непериодическим, расстояние между гармониками  уменьшатся до нуля (дискретные гармоники сольются в одну сплошную линию), а амплитуды гармоник уменьшатся до бесконечно-малых значений.

Подставим в уравнение (1) для сигнала выражение для коэффициентов ряда Фурье :

(2)

Непериодический сигнал можно получить как предельный переход периодического сигнала (2) при стремящимся к бесконечности:

(3)

Учитывая, что , множитель переходит в бесконечно-малое приращение частоты:

(4)

Значения частот дискретных гармоник:

(5)

и (3) с учетом (4) и (5):

(6)

Сумма бесконечно-малых площадей, где  — основание прямоугольника переходит в интеграл, а переходит в непрерывную переменную :

(7)

Окончательно, из выражения (7) можно выделить пару интегральных преобразований Фурье для непериодического сигнала:

(8)

(9)

Уравнение (8) определяет прямое преобразование Фурье непериодического сигнала. Прямое преобразование Фурье обозначается оператором , ставит в соответствие сигналу непрерывную функцию частоты , которая носит название спектральной плотности сигнала .

Выражение (9) представляет собой обратное преобразование Фурье, которое обозначается оператором и позволяет восстановить сигнал  по его спектральной плотности .

В терминах частоты , выраженной в Гц, с учетом , уравнения (8) и (9) принимают вид:

(10)

(11)

Пояснения понятия спектральной плотности сигнала

Часто спектральную плотность непериодического сигала называют спектром, что не совсем корректно, потому что не определяет конечные амплитуды гармоник сигнала, как это было при разложении периодического сигнала в ряд Фурье, а задает распределение энергии сигнала по оси частот. Для пояснения отличия понятия спектра периодического сигнала от спектральной плотности непериодического сигнала рассмотрим следующую аналогию.

Пусть имеется стержень длины м, единичной площади , который состоит из сегментов сплава меди и алюминия в различных пропорциях, как это показано на рисунке 2.

Рисунок 2. Стрежень состоящий из сегментов
сплава меди и алюминия в различных пропорциях

Каждый сегмент имеет постоянную плотность , где , но различные сегменты имеют различную плотность. Масса стержня может быть представлена как сумма масс всех сегментов:

(12)

где  — конечные массы отдельных сегментов.

Также как стержень в приведенном примере состоит из отдельных сегментов конечных масс, так и периодический сигнал состоит из суммы дискретных гармоник конечной амплитуды, в соответствии с рядом Фурье.

Предположим теперь, что такой же стержень представляет собой непрерывно-меняющийся по длине сплав меди и алюминия, как это показано на рисунке 3.

Рисунок 3. Стрежень состоящий из непрерывного по длине
сплава меди и алюминия

Плотность такого стержня непрерывно уменьшается по длине. Тогда массу мы не можем представить как сумму конечных дискретных масс, а только как интеграл плотности по длине стержня:

(13)

Другими словами, конечная масса состоит из бесконечного числа бесконечно-малых масс . Размерность плотности при постоянной площади стержня можно выразить в единицах кг/м.

Аналогично, спектральная плотность непериодического сигнала есть непрерывная функция частоты . При этом каждой бесконечно-малой полосе соответствует амплитуда , по аналогии бесконечно-малых масс из которых состоит полная масса стержня.

Единица измерения плотности в приведенном примере кг/м, тогда единица измерения равна сигнал/(единицу полосы), или Вс, если характеризует изменение напряжения. Таким образом, размерность спектральной плотности непериодического сигнала отличается от размерности спектра периодического сигнала и эти два термина отождествлять не следует.

Иоганн Петер Густав Лежён-Дирихле
1805–1859

Связь спектральной плотности непериодического сигнала и огибающей коэффициентов ряда Фурье

В предыдущем параграфе мы привели пояснения понятия спектральной плотности непериодического сигнала физической аналогией с плотностью непрерывного сплава двух металлов. Мы говорили, что спектральная плотность непериодического сигнала представляет собой непрерывную функцию частоты . При этом каждой частоте соответствует бесконечно-малая амплитуда , спектра сигнала.

И хотя физический смысл спектральной плотности отличается от физического смысла спектра периодического сигнала, равно как масса стержня отличается от плотности, но оба этих представления находятся в тесной связи друг с другом. Эту взаимосвязь спектра периодического сигнала и спектральной плотности мы проследим на примере одиночного импульса длительности и его периодических копий.

Пример одиночного импульса показан на рисунке 4 сплошной линией. Обратим внимание, что исходный импульс ограничен по длительности, т.е. при .

Рисунок 4. Периодическое повторение одиночного импульса

Периодический сигнал , показанный на рисунке 4 пунктиром, представляет собой бесконечную сумму копий сигнала , сдвинутых друг относительно друга по времени на величину (чтобы импульсы не перекрывались во времени).

Преобразование Фурье одиночного импульса равно:

(14)

Периодический сигнал имеет дискретный спектр , где , , который равен:

(15)

Сравнивая (14) и (15) на фиксированной секте частот , можно заключить, что:

(16)

Таким образом, если периодический сигнал представляет собой повторенный импульс длительности , то его спектр на сетке частот равен значению спектральной плотности одиночного импульса , деленного на период повторения . При этом приводит размерность спектральной плотности к размерности спектра (равно как объем тела приводит размерность плотности к размерности массы тела).

Непрерывная по частоте спектральная плотность, деленная на период повторения задает непрерывную огибающую дискретного спектра , как это показано на рисунке 5 пунктирной линией.

Рисунок 5. Cпектральная плотность как непрерывная огибающая дискретного спектра

Забегая немного вперед, можем заметить, что периодическое повторение одиночного импульса привело к дискретизации непрерывной по частоте огибающей и переходу к дискретному спектру . Мы еще будем подробно рассматривать этот вопрос в следующих главах.

Условия существования преобразования Фурье

Мы осуществили передельный переход от периодического сигнала к непериодическому при устремлении периода повторения к бесконечности. При увеличении периода длительность сигнала не увеличивалась. Это можно видеть на рисунке 1, длительность импульса остается постоянной при увеличении периода повторения .

Таким образом мы можем утверждать, что преобразование Фурье (8) и (9) существует для всех ограниченных во времени сигналов , для которых выполняется условие Дирихле [1, стр. 165].

Представим теперь, что сигнал не является ограниченным во времени, но затухает настолько быстро, что выполняется условие:

(17)

Говорят, что  — абсолютно интегрируемая функция времени [2, стр. 510], если выполняется (17).

Леонард Эйлер
1707–1783

Рисунок 6. График функции

В качестве примера абсолютно интегрируемой функции можно привести , график которой показан на рисунке 6. Поскольку затухает достаточно быстро, то всегда найдется такое конечное , при котором ошибка представления в виде ряда Фурье функции на интервале (при отбрасывании «затухающих хвостов») будет меньше любой конечной величины. Другими словами, «затухающие хвосты» с ростом периода будут оказывать исчезающе слабое влияние.

Таким образом, функция может быть бесконечной, но носить затухающий характер, и при условии абсолютной интегрируемости функции , мы можем использовать преобразование Фурье для расчета ее спектральной плотности.

Можно заметить, что всякий ограниченный во времени сигнал, удовлетворяющий условиям Дирихле также является абсолютно интегрируемым.

Приведенные рассуждения не являются строгим математическим доказательством условий существования преобразования Фурье, а скорее дают интуитивно-понятное разъяснение (17). Строгое доказательство условий существования преобразования Фурье можно найти [1, стр. 199] или в [2, стр. 511].

Выводы

В данном разделе мы рассмотрели предельных переход от периодического сигнала к непериодическому и получили выражения для прямого и обратного интегрального преобразования Фурье.

Мы отметили, что в отличии от спектра периодических сигналов, преобразование Фурье непериодического сигнала возвращает спектральную плотность сигнала, выраженную в единицах измерения сигнала, деленного на частоту. Были даны необходимые пояснения к понятию спектральной плотности.

Также были рассмотрены условия существования преобразования Фурье.

В следующих разделе мы рассмотрим свойства преобразования Фурье, a также спектральные плотности некоторых сигналов.

Вопросы, замечания и пожелания вы можете оставить настранице обсуждения статьи

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов

Информация была полезна? Поделитесь с друзьями!

Список литературы

[1] Воробьев Н.Н. Теория рядов. Москва, Наука, Главная редакция физико-математической литературы, 1979, 408 с.

[2] Будак, Б.М., Фомин, С.В. Кратные интегралы и ряды. Москва, Наука, 1965, 608 c.

[3] Баскаков, С.И. Радиотехнические цепи и сигналы. Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[4] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[5] Дёч, Г. Руководство по практическому применению преобразования Лапласа. Москва, Наука, 1965, 288 c.

[6] Bracewell R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 12.05.2022 (19:42:44)

Страница создана Latex to HTML translator ver. 5.20.11.14

Спектральный анализ (Spectral analysis) · Loginom Wiki

Синонимы: Фурье-анализ, Гармонический анализ, Frequency analysis

Разделы: Алгоритмы

Спектральный анализ — это широкий класс методов обработки данных, в основе которых лежит их частотное представление, или спектр. Спектр получается в результате разложения исходной функции, зависящей от времени (временной ряд) или пространственных координат (например, изображения), в базис некоторой периодической функции. Наиболее часто для спектральной обработки используется спектр Фурье, получаемый на основе базиса синуса (разложение Фурье, преобразование Фурье).

Основной смысл преобразования Фурье в том, что исходная непериодическая функция произвольной формы, которую невозможно описать аналитически и поэтому сложно обрабатывать и анализировать, представляется в виде набора синусов или косинусов с различной частотой, амплитудой и начальной фазой.

Иными словами, сложная функция преобразуется в множество более простых. Каждая синусоида (или косинусоида) с определенной частотой и амплитудой, полученная в результате разложения Фурье, называется спектральной составляющей или гармоникой. Спектральные составляющие образуют спектр Фурье.

Визуально спектр Фурье представляется в виде графика, на котором по горизонтальной оси откладывается круговая частота, обозначаемая греческой буквой «омега», а по вертикали – амплитуда спектральных составляющих, обычно обозначаемая латинской буквой A. Тогда каждая спектральная составляющая может быть представлена в виде отсчета, положение которого по горизонтали соответствует ее частоте, а высота – ее амплитуде. Гармоника с нулевой частотой называется постоянной составляющей (во временном представлении это прямая линия).

Даже простой визуальный анализ спектра может много сказать о характере функции, на основе которой он был получен. Интуитивно понятно, что быстрые изменения исходных данных порождают в спектре составляющие с высокой частотой, а медленные – с низкой. Поэтому если в нем амплитуда составляющих быстро убывает с увеличением частоты, то исходная функция (например, временной ряд) является плавной, а если в спектре присутствуют высокочастотные составляющие с большой амплитудой, то исходная функция будет содержать резкие колебания. Так, для временного ряда это может указывать на большую случайную составляющую, неустойчивость описываемых им процессов, наличие шумов в данных.

В основе спектральной обработки лежит манипулирование спектром. Действительно, если уменьшить (подавить) амплитуду высокочастотных составляющих, а затем на основе измененного спектра восстановить исходную функцию, выполнив обратное преобразование Фурье, то она станет более гладкой за счет удаления высокочастотной компоненты.

Для временного ряда, например, это означает убрать информацию об ежедневных продажах, которые сильно подвержены случайным факторам, и оставить более устойчивые тенденции, например, сезонность. Можно, наоборот, подавить составляющие с низкой частотой, что позволит убрать медленные изменения, а оставить только быстрые. В случае временного ряда это будет означать подавление сезонной компоненты.

Применяя спектр таким образом, можно добиваться желаемого изменения исходных данных. Наиболее часто используется сглаживание временных рядов путем удаления или уменьшения амплитуды высокочастотных составляющих в спектре.

Для манипуляций со спектрами используются фильтры – алгоритмы, способные управлять формой спектра, подавлять или усиливать его составляющие. Главным свойством любого фильтра является его амплитудно-частотная характеристика (АЧХ), от формы которой зависит преобразование спектра.

Если фильтр пропускает только спектральные составляющие с частотой ниже некоторой граничной частоты, то он называется фильтр нижних частот (ФНЧ), и с его помощью можно сглаживать данные, очищать их от шума и аномальных значений.

Если фильтр пропускает спектральные составляющие выше некоторой граничной частоты, то он называется фильтром верхних частот (ФВЧ). С его помощью можно подавлять медленные изменения, например, сезонность в рядах данных.

Кроме этого, используется множество других типов фильтров: фильтры средних частот, заградительные фильтры и полосовые фильтры, а также более сложные, которые применяются при обработке сигналов в радиоэлектронике. Подбирая тип и форму частотной характеристики фильтра, можно добиться желаемого преобразования исходных данных путем спектральной обработки.

Выполняя частотную фильтрацию данных с целью сглаживания и очистки от шума, необходимо правильно указать полосу пропускания ФНЧ. Если ее выбрать слишком большой, то степень сглаживания будет недостаточной, а шум будет подавлен не полностью. Если она будет слишком узкой, то вместе с шумом могут оказаться подавленными и изменения, несущие полезную информацию. Если в технических приложениях существуют строгие критерии для определения оптимальности характеристик фильтров, то в аналитических технологиях приходится использовать в основном экспериментальные методы.

Спектральный анализ является одним из наиболее эффективных и хорошо разработанных методов обработки данных. Частотная фильтрация – только одно из его многочисленных приложений. Кроме этого, он используется в корреляционном и статистическом анализе, синтезе сигналов и функций, построении моделей и т.д.

В Loginom есть специализированный обработчик Сглаживание, предназначенный для сглаживания численных рядов данных и выделения трендовой составляющей.

Преобразование Фурье

Двумерное преобразование Фурье доступно в меню Обработка данных → Интегральные преобразования → 2D БПФ, где реализовано быстрое преобразование Фурье (БПФ, FFT). Преобразование Фурье раскладывает сигнал на его гармонические составляющие, и, таким образом, его можно использовать при изучении спектральных частот, присутствующих в данных СЗМ.

Модуль 2D БПФ предлагает несколько вариантов вывода данных:

• Модуль — абсолютное значение комплексного коэффициента Фурье, пропорциональное квадратному корню функции спектральной плотности мощности (ФСПМ).
• Фаза — фаза комплексного коэффициента (используется редко).
• Действительное — действительная часть комплексного коэффициента.
• Мнимое — мнимая часть комплексного коэффициента.

и некоторые их сочетания для удобства.

Радиальные сечения двумерной ФСПМ можно удобно получить с помощью операции 2D PSDF. Несколько других функций, рассчитывающих спектральные плотности описаны в разделе Статистический анализ. Также возможно фильтровать изображения в частотном представлении (Фурье-пространстве) используя одномерный или двумерный фильтры на основе быстрого преобразования Фурье (БПФ) или простое разделение частот.

Для не зависящего от масштаба и поворота сравнения текстур может оказаться полезным преобразовать ФСПМ из декартовых координат частот в координаты, состоящие из логарифма пространственной частоты и её направления. Масштабирование и поворот в новых координатах становятся простыми смещениями. Функция Обработка данных → Статистика → Log-Phi ФСПМ непосредственно расчитывает преобразованную ФСПМ. Безразмерная горизонтальная координата это угол (от 0 до 2π), вертикальная это логарифм частоты. Также возможно сгладить ФСПМ гауссовым фильтром заданной ширины перед преобразованием.

Следует отметить, что преобразование Фурье считает данные бесконечно протяженными, и, следовательно, накладывает некоторые периодические граничные условия. Поскольку реальные данные не обладают этими свойствами, необходимо использовать некоторую оконную функцию для подавления данных на границах изображения. Если вы этого не сделаете, БПФ будет считать данные обработанными прямоугольной функцией окна, которая имеет действительно скверный Фурье-образ, что приводит к искажению Фурье-спектра.

Gwyddion предлагает на выбор несколько функций окна. Большинство из них образовано набором синусов и косинусов, которые корректно приглушают данные на краях. В следующей таблице формул для функций окна независимая переменная x лежит в диапазоне [0, 1], что соответствует нормализации абсциссы; для простоты переменная ξ = 2πx используется в ряде формул. Доступные виды оконных функций включают в себя:

Одномерная фильтрация БПФ

Обработка данных → Исправить данные → Одномерная фильтрация БПФ

Одним из наиболее удачных способов удаления шума на определённых частотах из изображения является Фурье-фильтрация. Сначала вычисляется прямое преобразование Фурье изображения. Затем к результату преобразования применяется фильтр. После этого обратное преобразование используется для получения отфильтрованного изображения. Gwyddion использует быстрое преобразование Фурье (БПФ или FFT) для существенного ускорения этого большого расчёта.

При использовании одномерного фильтра БПФ частоты, которые должны быть удалены со спектра (тип подавления: убрать) или подавлены до значения соседних частот (тип подавления: выровнять), могут быть выбраны отметкой нужных областей на графике спектра мощности. Выбранная область может быть легко инвертирована использованием опции «тип фильтра». Одномерная фильтрация БПФ может использоваться как для горизонтального, так и для вертикального направления.

Двумерная фильтрация БПФ

Обработка данных → Исправить данные → Двумерный фильтр БПФ

Двумерная фильтрация БПФ работает подобно одномерному варианту (см. выше), но использует двумерное преобразование Фурье. Следовательно, пространственные частоты, которые нужно отфильтровать должны быть выбраны в двумерном пространстве с использованием редактора маски. Поскольку частоты измеряются относительно центра изображения (который соответствует нулевой частоте), маску можно прикрепить к центру (началу координат) в процессе редактирования. Также доступны различные режимы отображения и вывода результата, которые не требуют разъяснений – модуль может выводить изображение или коэффициенты БПФ (или оба).

Разделение частот

Обработка данных → Выравнивание → Разделение частот

Простой альтернативой двумерной фильтрации с помощью БПФ будет разделение изображение на составляющие с низкими и высокими пространственными частотами используя простые фильтры нижних и верхних частот. В зависимости от выбранной опции тип вывода модуль разделения частот может создавать либо низкочастотное, либо высокочастотное изображение, либо оба

Порог задаёт пространственную частоту, которая показывается как относительная доля частоты Найквиста и также как соответствующая пространственная длина волны. Если Ширина пороговой функции задаётся нулевой, фильтр будет иметь узкий порог частоты. Для ненулевых значений переход будет иметь форму функции ошибки erf с заданной шириной.

Фильтрация в частотной области может приводить к артефактам вдоль границ изображения. Вследствие этого модуль предлагает несколько вариантов работы с граничной областью помимо варианта Нет, который годится только для периодических данных (или другим способом непрерывных при переходе через границу изображения). По Лапласу и Зеркально расширяют изображение решением уравнения Лапласа или зеркальным отображением, соответственно, точно таким же способом, как и функция Расширить. Гладкий переход применяет к строкам и колонкам изображения одномерный гладкий метод расширения, который используется в инструменте измерения шероховатости для подавления артефактов на границе.

Понимание спектров Фурье — В центре внимания фотоники

Главная	Викторина	Руководство покупателя
Поиск	Категории	Глоссарий	Реклама

You can also receive this as a newsletter.»> Прожектор фотоники

Учебники

Показать статьи A-Z

Опубликовано 11 октября 2007 г. в рамках информационного бюллетеня Photonics Spotlight (доступен как информационный бюллетень по электронной почте!)

Постоянная ссылка: https://www.rp-photonics.com/spotlight_2007_10_11.html

Автор: д-р Рюдигер Пашотта, RP Photonics AG

Резюме: Статья создает интуитивное понимание спектров Фурье путем обсуждения ряда физические примеры в контексте ультракоротких импульсов.

Эта статья изначально была частью Энциклопедии лазерной физики и техники, но так как ее общий подход и стиль не совсем соответствовали этой среде, я решил представить этот материал как статью журнала Photonics Spotlight. Это очень редкий случай, когда статья из энциклопедии удаляется; старый URL-адрес перенаправляется на эту статью.

Преобразования Фурье широко используются в области оптики, как и в контексте других волновых явлений. Эта статья представляет собой дидактическое упражнение, иллюстрирующее временные спектры Фурье, а статья о расходимости луча дает пример использования пространственных преобразований Фурье. Основная цель состоит в том, чтобы создать интуитивное понимание спектров Фурье, продемонстрировав их тесную связь с элементарными физическими эффектами. В энциклопедии эта тема в основном рассматривается в контексте ультракоротких импульсов, генерируемых лазерами с синхронизацией мод.

Спектр одиночного импульса

Рассмотрим простой случай, когда импульс формируется путем умножения синусоидальной функции на огибающую Гаусса:

Это описывает (реальное) электрическое поле E в зависимости от времени t , где частота колебаний ν ₀ , фаза колебаний φ и полная ширина на полувысоте (FWHM) длительности импульса (определена для профиля интенсивности , пропорциональна квадрату модуля E ) есть τ.

Непрерывное преобразование Фурье (названное в честь французского математика и физика Жана Батиста Жозефа Фурье) определяется как

(в соответствии с электротехническим соглашением), а спектр Фурье обычно отождествляется с этой функцией. Его квадрат модуля представляет собой спектр интенсивности или спектр мощности (→ спектральная плотность мощности), а его фаза называется спектральной фазой.

Хорошо известно, что спектр интенсивности гауссовского импульса, как определено выше, также является гауссовым, и что произведение времени на ширину полосы (т. е. произведение половины максимума полной ширины во временной и частотной области) составляет ≈0,44. Это означает, что чем короче такой импульс, тем шире его спектр.

Поучительно напомнить, что примерный импульс был сгенерирован базовой синусоидальной функцией. Таким образом, мгновенная частота этого импульса постоянна и равна ν ₀ , если φ считается постоянным. По этой причине можно было бы ожидать, что «реальная» ширина спектра равна нулю, поскольку задействована только одна частота. С этой точки зрения можно было бы воспринимать конечную ширину спектра Фурье как своего рода математический артефакт.

Однако при ближайшем рассмотрении обнаруживается тесная связь преобразования Фурье с физической реальностью. Для этого необходимо рассматривать конкретную физическую реализацию спектрального анализа, а не только математические уравнения. В следующем «мысленном эксперименте» (воображаемом эксперименте) мы исследуем спектральный состав импульса на определенной частоте ν, воздействуя на генератор с узкой полосой пропускания. Настроим резонансную частоту генератора на значение ν и примем, что время затухания значительно больше длительности импульса. Сначала мы останавливаем осциллятор, затем подвергаем его воздействию импульса, а затем измеряем амплитуду осциллятора. Оказывается, эта амплитуда как раз пропорциональна соответствующей амплитуде в спектре Фурье. Амплитуда Фурье велика для резонансных частот в конечном диапазоне около ν ₀ . Вышеупомянутое условие достаточно большого времени затухания подразумевает, что ширина линии генератора значительно меньше ширины спектра импульса.

Физическую реальность конечной ширины полосы импульса можно дополнительно проиллюстрировать, рассмотрев, почему значительное рассогласование резонансной частоты генератора ν с мгновенной частотой ν ₀ импульса оказывает лишь слабое влияние на результирующее возбуждение генератора: это связано с тем, что генератор может значительно не совпадать по фазе с импульсом только тогда, когда несоответствие угловой частоты, умноженное на время воздействия (ограниченное длительностью импульса), приводит к фазовому рассогласованию порядка 1 рада или больше.

Двойные импульсы

Следующий пример представляет собой двойной импульс, т. е. наложение двух одиночных импульсов с временным интервалом T , который предполагается значительно большим, чем длительность импульса. Спектр Фурье двойного импульса демонстрирует спектральную интерференционную картину (рис. 1):

Рис. 1: Фурье-спектр двойного импульса. Оба импульса имеют длительность 120 фс и центральную частоту 300 ТГц, а интервал между ними составляет 1 пс. Спектр (сплошная кривая) модулируется с частотой 1 ТГц, что является обратным интервалом между импульсами. Для сравнения пунктиром показан спектр одиночного импульса.

Эта модуляция может показаться математическим артефактом, но ее можно понять как иллюстрацию физической реальности, если снова рассмотреть тестовый осциллятор, как описано выше. Сначала мы предполагаем, что время затухания генератора значительно превышает интервал между импульсами. Настроенный на 300 ТГц, центральную частоту импульсов, генератор будет сначала сильно возбуждаться первым импульсом, а затем еще больше возбуждаться вторым импульсом, который (в этом примере) находится точно в фазе. При расстройке генератора на 300,5 ТГц возбуждение от первого импульса почти такое же, но в промежутке между импульсами осциллятор выходит из фазы со вторым импульсом, что затем полностью разрушает возбуждение. Это соответствует нулевой спектральной интенсивности, наблюдаемой на графике. Дальнейшая расстройка до 301 ТГц создает ситуацию с все еще почти резонансным возбуждением первым импульсом, относительным изменением фазы на 2π между импульсами и дальнейшим возбуждением вторым импульсом – таким образом, вторым максимумом. Легко видеть, что спектральная модуляция имеет период, обратный интервалу между импульсами.

В модифицированной ситуации, когда время затухания тестового генератора конечно, а интервал между импульсами больше, чем это время затухания, генератор «забудет» о первом импульсе, когда на него поступит второй. Затем колебательная частотная зависимость возбуждения осциллятора исчезает. В частотной области понятно, что большой ширины линии осциллятора недостаточно для разрешения быстрых спектральных колебаний.

Рассмотрим еще раз ситуацию малых интервалов между импульсами, реализованную в эксперименте по сверхбыстрой оптике. Генератор может представлять собой квантовую точку, возбуждаемую парой пикосекундных импульсов. В ситуации, когда спектральная интенсивность минимальна (например, для 300,5 ТГц на рис. 1), квантовая точка будет ослаблять первый импульс (извлекая из него энергию), но усиливать второй и после этого оставаться невозбужденной. Это показывает, что нулевая спектральная интенсивность двойного импульса составляет , а не подразумевают, что он не будет взаимодействовать с поглотителем на этой частоте. Скорее это означает, что его общая энергия двойного импульса не изменится. Передача энергии от первого импульса ко второму фактически описывается частотно-зависимым фазовым сдвигом (т. е. изменением фазы спектра), который можно рассчитать с помощью соотношений Крамерса–Кронига.

Последовательности импульсов

Еще одним расширением является бесконечная регулярно расположенная последовательность импульсов, предполагающая, что все импульсы взаимно когерентны. Обычно это в значительной степени верно для последовательностей импульсов, генерируемых в лазерах с синхронизацией мод (однако, с некоторыми осложнениями в контексте гармонической синхронизации мод). Спектр Фурье такой последовательности импульсов состоит из (теоретически без лазерных помех) бесконечно узких линий, интервал частот которых равен частоте следования импульсов, т. е. обратному интервалу между импульсами. Это называют частотной гребенкой, и в соответствующей статье дается гораздо больше деталей.

Чиркающие импульсы

Сильно модулированные спектры возникают не только для двойных (или множественных) импульсов, но и для чирпированных импульсов, что может привести, например, к от сильной фазовой самомодуляции. В качестве примера см. рис. 2 в статье о фазовой самомодуляции. В такой ситуации оптическая интенсивность во временной области показывает один импульс, но мгновенная частота претерпевает большие отклонения. Может быть несколько раз, когда мгновенная частота совпадает с определенной частотой Фурье. Интеграл Фурье, таким образом, получает множественные вклады, которые суммируются и могут (для определенных частот) компенсировать друг друга. Это снова можно объяснить с помощью представленной выше модели тестового генератора: тестовый генератор может входить в резонанс с импульсом в течение нескольких коротких интервалов времени внутри импульса, так что он также добавляет несколько вкладов, которые могут быть или не быть в фазе. в зависимости от частоты генератора.

Оптический спектр произвольного источника света

Обратите внимание, что оптический спектр источника света не всегда можно точно отождествить с квадратом модуля его спектра Фурье. Это связано с тем, что во многих случаях излучение света в значительной степени является случайным. Тогда оптический спектр представляет собой усредненный по спектр интенсивности , в то время как спектральная фаза может быть случайной. Это тот случай, например. для суперлюминесцентных источников.

Выводы

Надеюсь, я вас убедил

• что спектры Фурье тесно связаны с физической реальностью,
• что тщательное изучение их очевидных «артефактов» приводит к более глубокому пониманию,
• , что выполняется следующее уравнение: опыт = 2 × знания + 3 × мышление, и
• , что у RP Photonics есть опыт для четкого анализа физических эффектов, лазерных конструкций, инновационных идей и т. д., а также способность четко объяснить их!

---

Эта статья является публикацией журнала Photonics Spotlight, автором которого является доктор Рюдигер Пашотта. Вы можете ссылаться на эту страницу и цитировать ее, потому что ее местоположение постоянно. См. также энциклопедию RP Photonics.

Обратите внимание, что вы также можете получать статьи в форме информационного бюллетеня или с помощью RSS-канала.

Вопросы и комментарии от пользователей

Здесь вы можете задать вопросы и комментарии. Если они будут приняты автором, они появятся над этим абзацем вместе с ответом автора. Автор принимает решение о принятии на основе определенных критериев. По существу, вопрос должен представлять достаточно широкий интерес.

Пожалуйста, не вводите здесь личные данные; в противном случае мы бы удалили его в ближайшее время. (См. также нашу декларацию о конфиденциальности.) Если вы хотите получить личную обратную связь или консультацию от автора, свяжитесь с ним, например. по электронной почте.

Ваш вопрос или комментарий:

Проверка на спам:

  (Пожалуйста, введите сумму тринадцати и трех в виде цифр!)

Отправляя информацию, вы даете свое согласие на возможную публикацию ваших материалов на нашем веб-сайте в соответствии с нашими правилами. (Если вы позже отзовете свое согласие, мы удалим эти материалы.) Поскольку ваши материалы сначала просматриваются автором, они могут быть опубликованы с некоторой задержкой.

Если вы хотите разместить ссылку на эту статью на каком-либо другом ресурсе (например, на своем сайте, в социальных сетях, на дискуссионном форуме, в Википедии), вы можете получить необходимый код здесь.

HTML-ссылка на эту статью:

  
 Статья о понимании Фурье-спектров — обзор фотоники 
 в < a href="https://www.rp-photonics.com/encyclopedia.html"> 
 Энциклопедия RP Photonics 

С предварительным изображением (см. рамку чуть выше):

  
  alt="статья"> 

Преобразование Фурье

Введение в преобразование Фурье Серия Фурье Преобразование Фурье — свойства Пары преобразования Фурье Приложения преобразования Фурье Математический фон Внешние ссылки Преобразование Фурье — это инструмент, который разбивает сигнал (функцию или сигнал) на альтернативное представление, характеризующееся функциями синуса и косинуса различной частоты. Преобразование Фурье показывает, что любой сигнал может быть переписан как сумма синусоид. Если вы ничего не знаете о преобразованиях Фурье, начните со ссылки «Введение» слева. если ты хотите освежить в памяти, проверьте ссылку «Свойства преобразования Фурье». И если вы просто ищете стол преобразований Фурье с выводами, перейдите по ссылке Пары преобразований Фурье.

Вот более подробные описания вышеупомянутых Преобразование Фурье связанные темы: 1. Введение в преобразование Фурье В разделе «Введение» дается обзор того, почему стоит изучить преобразование Фурье. Это оказывается, преобразование Фурье требуется, чтобы понять один из фундаментальных секретов Вселенной….. 2. Ряд Фурье Ряд Фурье дает нам метод разложения периодических функций на их синусоидальные составляющие. Ряд Фурье также можно рассматривать как частный вводный случай преобразования Фурье, поэтому нет Учебное пособие по преобразованию Фурье завершено без изучения рядов Фурье. 3. Преобразование Фурье — теория 90–201. Раздел теории содержит доказательства и список основных свойств преобразования Фурье. 4. Пары преобразования Фурье В этом разделе приводится список пар преобразования Фурье, а также их производные во многих случаях. 5. Приложения преобразования Фурье Что хорошего в теории, если она не применима к чему-то практическому? В разделе приложений преобразования Фурье показано преобразование Фурье. в действии в реальном мире. 6. Математическая основа В этом разделе приводятся математические основы, полезные для понимания преобразования Фурье. Смотрите также Преобразование Фурье.

Этот веб-сайт предназначен для того, чтобы стать источником знаний для изучения и понимание Преобразование Фурье . Цель состоит в том, чтобы представить всеобъемлющее руководство по преобразованию Фурье и смежным темам. В духе Эйнштейна: «Все должно быть сделано как можно проще, но не проще.» Этот веб-сайт будет стремиться сделать Преобразование Фурье понятным, без излишней сложности.

Посетите наш партнерский сайт, антенну-theory.com, лучшую страницу об антеннах в мире! Интересный факт: знаете ли вы, что диаграмма направленности антенны часто просто преобразование Фурье текущего распределения антенны? 1. Введение в преобразование Фурье Практически все в мире можно описать волновой формой — функцией времени, пространства или какой-либо другой переменной. Например, звуковые волны, электромагнитные поля, высота холма в зависимости от местоположения, график VSWR в зависимости от частоты, цена вашей любимой акции в зависимости от времени и т. д. Преобразование Фурье дает нам уникальный и мощный способ просмотра этих сигналов. Целью всего этого веб-сайта является объяснение следующего фундаментального факта: Один из фундаментальных секретов Вселенной Все волновые формы, независимо от того, что вы рисуете или наблюдаете во Вселенной, на самом деле просто сумма простых синусоид разных частот. Приведенный выше факт, как мы увидим, чрезвычайно крут. Преобразование Фурье разлагает сигнал — в основном любая форма волны реального мира, в синусоидах. То есть преобразование Фурье дает нам другой способ представления сигнала. (Нужно освежить в памяти синусоиды? См. Свойства синусоиды) В качестве примера давайте разобьем сигнал на Рисунке 1 на его «строительные блоки» (или составляющие частоты). Это разложение может быть выполнено с помощью преобразование Фурье (или ряд Фурье для периодических сигналов), как мы увидим. Первый компонент представляет собой синусоидальную волну с периодом T=6,28 (2*pi) и амплитудой 0,3, как показано на рисунке 1.

Рис. 1. Сравнение первой основной частоты (слева) и исходной формы волны (справа).

Вторая частота будет иметь период, вдвое меньший, чем первая (удвоенная частота). Секунда компонент показан слева на рис. 2 вместе с суммой первых двух частот по сравнению с оригинальная форма волны.

Рис. 2. Вторая основная частота (слева) и форма исходного сигнала в сравнении с первыми двумя частотными компонентами.

Мы видим, что сумма первых двух частот начинает напоминать исходную форму волны. Третья частотная составляющая в 3 раза больше частоты, чем первая. Сумма первых трех компонентов показана на рисунке 3.

Рис. 3. Третья основная частота (слева) и исходная форма волны по сравнению с первыми тремя частотными компонентами.

Наконец, добавив четвертую частотную составляющую, мы получим исходную форму волны, показанную на рис. 4.9.0038

Рис. 4. Четвертая основная частота (слева) и исходная форма сигнала по сравнению с первыми четырьмя частотными компонентами (перекрываются).

Хотя это кажется выдуманным, это верно для всех волновых форм. Это касается телевизионных сигналов, сигналов сотовых телефонов, звуковых волн, которые распространяются, когда вы говорите. Как правило, сигналы состоят не из дискретного числа частот, а из непрерывного диапазона частот. Преобразование Фурье — это математический инструмент, который показывает нам, как разложить сигнал на синусоидальные составляющие. Это имеет множество применений, помогает понять вселенную и просто делает жизнь намного проще. для практикующего инженера или ученого. Чтобы начать изучение преобразования Фурье, мы начнем с изучения чего-то очень близкого — ряда Фурье. Далее: ряд Фурье Вверху: преобразование Фурье Преобразование Фурье Введение Видео-лекция Об этом сайте: Преобразование Фурье всегда было для меня увлекательной темой, и именно это волнение это побудило меня представить этот учебник по преобразованию Фурье. В своей жизни я обнаружил, что как только я полностью разбираюсь в предмете, Я поражен тем, насколько простым это кажется, несмотря на первоначальную сложность. Это я нашел верным для широкого круга деятельность, будь то езда на мотоцикле, изучение преобразования Фурье или понимание физических явлений например, электромагнетизм. Имея это в виду, я стараюсь писать этот учебник по преобразованию Фурье самым простым из всех возможных способов. В частности, рассмотрите это утверждение: Сложность не является признаком интеллекта; упростить . У меня есть нашел в этом бесценную мудрость. В этом отношении нет необходимости знать тонкости Лебега. интегрирование или комплексные интегралы, включающие вычеты Коши, чтобы полностью понять преобразование Фурье. Преобразование Фурье лучше всего понять интуитивно; ведь физики давно заявили, что вся материя на самом деле представляет собой волны (постулат де Бройля) или явление волнового типа. Фурье Трансформация, по сути, состоит из другого способа видения вселенной (то есть трансформация из во временной области в частотную область ). А так как, согласно преобразованию Фурье, все волны можно просматривать одинаково точно во временной или частотной области, у нас есть новый способ просмотра мира. И этот взгляд иногда гораздо более интуитивен и прост для понимания. чем исходное представление домена. С учетом сказанного, я рад начать этот урок по преобразованию Фурье. На этих страницах вы не найдет строгого математического анализа того, когда и когда не существует преобразования Фурье; Я просто констатирую факт: все формы сигналов, возникающие в реальной жизни (т.е. в природе, на вашем компьютере, в вашем сетевом анализаторе звук, свет, радиоволны и т. д. и т. д.) имеют преобразования Фурье. И в качестве инженер, конечной целью является применение знаний в реальном мире, а не споры о математически неясные точки. Следовательно, я, честно говоря, не забочусь о формах сигналов, для которых преобразования Фурье не существует; Я знаю, что не столкнусь с таким на практике, и поэтому Мне все равно. Преобразование Фурье не только дает нам особое представление о том, как устроен мир, но и проявляется в реальных приложениях, таких как МРТ (магнитно-резонансная томография), обработка сигналов, электромагнетизм, квантовая физика и теоретическая математика. Как таковой, Я не могу вспомнить ни одного серьезного ученого или инженера, который мог бы оправдать карьеру без знаний. преобразования Фурье. На этих страницах я постараюсь провести исследование Фурье. Преобразование максимально интуитивное и без математики; однако всегда возникают интегралы, поэтому можно посоветовать переподготовку по исчислению. Обо мне: Я практикующий инженер, имею докторскую степень в этой области и работаю на многих лет в обороне, университете и области бытовой электроники. Мой бэкграунд и работа опыт переплетается с обработкой сигналов, медицинской визуализацией и теорией линейных систем. которые поднимают повторяющуюся тему преобразования Фурье. Кроме того, приняв Классы по преобразованию Фурье, проводимые профессорами со страстью к преобразованию Фурье, это страсть передалась мне. И мои познания в электромагнетизме/антеннах быть зияюще неполным без глубокого понимания интуиции и практики преобразования Фурье. Преобразование Фурье шутка: О чем говорит преобразование Фурье треугольного импульса в Преобразование Фурье функции sinc? Ответ: Ты такой квадратный! Хотя вышеизложенное забавно только в том случае, если вы уже немного знаете о преобразовании Фурье, тогда Я буду считать успехом, если этот сайт хотя бы научит вас достаточному количеству преобразований Фурье. так что это понятно. Связаться с автором: [email protected] Работа над этим учебным пособием по преобразованию Фурье защищена авторским правом. На страницу можно ссылаться и использовать по желанию, просто процитируйте работу, если вы ее используете. Copyright 2010-2022 TheFourierTransform.com. Главная: Преобразование Фурье

Интерактивное руководство по преобразованию Фурье — BetterExplained

Преобразование Фурье — одно из самых глубоких открытий, когда-либо сделанных. К сожалению, смысл скрыт в плотных уравнениях:

Да ладно. Вместо того, чтобы прыгать в символы, давайте испытаем ключевую идею на собственном опыте. Вот простая английская метафора:

• Что делает преобразование Фурье? Получив смузи, он находит рецепт.
• Как? Пропустите смузи через фильтры, чтобы извлечь каждый ингредиент.
• Почему? Рецепты легче анализировать, сравнивать и изменять, чем сам смузи.
• Как вернуть смузи? Смешайте ингредиенты.

Вот «математическая английская» версия приведенного выше:

• Преобразование Фурье берет шаблон, основанный на времени, измеряет каждый возможный цикл и возвращает общий «рецепт цикла» (амплитуда, смещение и скорость вращения для каждого найденный цикл).

Время для уравнений? Нет! Давайте запачкаем руки и испытаем , как любой шаблон может быть построен с помощью циклов, с помощью живых симуляций.

Если все пойдет хорошо, у нас будет ага! момент и интуитивно понять, почему преобразование Фурье возможно. Мы сохраним подробный математический анализ для последующих действий.

Это не марш-бросок по уравнениям, это непринужденная прогулка, о которой я мечтаю. Вперед!

От смузи к рецепту

Математическое преобразование — это изменение точки зрения. Мы меняем наше представление о количестве с «отдельных предметов» (линии на песке, счетная система) на «группы по 10» (десятичные числа) в зависимости от того, что мы считаем. Забить игру? Подсчитайте это. Умножение? Десятичные, пожалуйста.

Преобразование Фурье меняет нашу точку зрения с потребителя на производителя, 9 лет0060 Что у меня есть? в Как это было сделано?

Другими словами: есть смузи, давайте найдем рецепт.

Почему? Что ж, рецепты — отличное описание напитков. Вы бы не поделились анализом по каплям, вы бы сказали: «У меня был апельсиново-банановый смузи». Рецепт легче классифицировать, сравнивать и модифицировать, чем сам объект.

Итак… учитывая смузи, как нам найти рецепт?

Представьте, что у вас завалялось несколько фильтров:

• Пролить через «банановый» фильтр. Извлекается 1 унция бананов.
• Пролить через «оранжевый» фильтр. 2 унции апельсинов.
• Пролить через «молочный» фильтр. 3 унции молока.
• Пролить через фильтр «Вода». 3 унции воды.

Мы можем реконструировать рецепт, отфильтровав каждый ингредиент. Улов?

• Фильтры должны быть независимыми . Банановый фильтр должен улавливать бананы и ничего больше. Добавление большего количества апельсинов никогда не должно влиять на показания бананов.

• Фильтры должны быть в комплекте . Мы не получим настоящего рецепта, если опустим фильтр («Были и манго!»). Наша коллекция фильтров должна улавливать все возможные ингредиенты.

• Ингредиенты должны быть совместимы . Смузи можно без проблем разделять и снова комбинировать (печенье? Не очень. Кому нужны крошки?). Ингредиенты, разделенные и объединенные в любом порядке, должны давать одинаковый результат.

Посмотрите на мир как на циклы

Преобразование Фурье использует особую точку зрения: Что, если бы любой сигнал можно было бы отфильтровать в виде множества круговых путей?

Вау. Эта концепция ошеломляет, и бедному Жозефу Фурье сначала отказали в его идее. ( Правда, Джо, из кругов можно сделать даже лестницу? )

И, несмотря на десятилетия дебатов в математическом сообществе, мы ожидаем, что учащиеся без проблем усвоят эту идею. Фу. Пройдемся по интуиции.

Преобразование Фурье находит рецепт сигнала, как в нашем процессе смузи:

• Начните с сигнала, основанного на времени
• Применение фильтров для измерения каждого возможного «кругового ингредиента»
• Собрать полный рецепт, указав количество каждого «кругового ингредиента»

Стоп. Вот где большинство учебных пособий взволнованно бросают вам в лицо инженерные приложения. Не пугайтесь; думайте о примерах как «Вау, мы наконец-то видим исходный код (ДНК) за ранее сбивающими с толку идеями».

• Если вибрации землетрясения можно разделить на «ингредиенты» (вибрации с разной скоростью и амплитудой), можно спроектировать здания так, чтобы избежать взаимодействия с наиболее сильными.

• Если звуковые волны можно разделить на составляющие (низкие и высокие частоты), мы сможем усилить важные части и скрыть ненужные. Треск случайного шума может быть удален. Возможно, можно сравнить похожие «звуковые рецепты» (сервисы распознавания музыки сравнивают рецепты, а не необработанные аудиоклипы).

• Если компьютерные данные могут быть представлены в виде осциллирующих шаблонов, возможно, наименее важные из них можно игнорировать. Это «сжатие с потерями» может значительно уменьшить размеры файлов (и почему файлы JPEG и MP3 намного меньше, чем необработанные файлы .bmp или .wav).

• Если нашим сигналом является радиоволна, мы можем использовать фильтры для прослушивания определенного канала. В мире смузи представьте, что каждый человек обращает внимание на разные ингредиенты: Адам ищет яблоки, Боб ищет бананы, а Чарли получает цветную капусту (извини, приятель).

Преобразование Фурье, конечно, полезно в технике, но это метафора поиска первопричин наблюдаемого эффекта.

Думайте кругами, а не только синусоидами

Одной из моих больших путаниц было разделение определений «синусоида» и «окружность».

• «Синусоида» — это особый возвратно-поступательный паттерн (синусоидальная или косинусоидальная волна), и в 99% случаев он относится к движению в одном измерении.
• «Круг» — это круглый двухмерный узор, который вы, вероятно, знаете. Если вам нравится использовать 10-долларовые слова для описания 10-центовых идей, вы можете назвать круговой путь «сложной синусоидой».

Обозначение кругового пути как «сложной синусоиды» похоже на описание слова как «многобуквенного». Вы выбрали неправильный уровень детализации. Слова — это понятия, а не буквы, на которые их можно разделить!

Преобразование Фурье касается круговых траекторий (а не одномерных синусоид), и формула Эйлера представляет собой умный способ их создания:

Должны ли мы использовать воображаемые показатели для движения по кругу? Неа. Зато удобно и компактно. И конечно, мы можем описать наш путь как скоординированное движение в двух измерениях (реальном и воображаемом), но не забывайте общую картину: мы просто движемся по кругу.

Круговые пути

Допустим, мы разговариваем по телефону, и, как обычно, я хочу, чтобы мы одновременно нарисовали один и тот же круг. ( Ты обещал! ) Что мне сказать?

• Насколько большой круг? (Амплитуда, т.е. размер радиуса)
• Как быстро мы его нарисуем? (Частота. 1 круг/сек соответствует частоте 1 Герц (Гц) или 2*пи радиан/сек)
• С чего начнем? (Фазовый угол, где 0 градусов — ось x)

Я мог бы сказать: «Радиус 2 дюйма, начните с 45 градусов, 1 круг в секунду, вперед!». Через полсекунды каждый из нас должен указывать на: начальную точку + пройденное расстояние = 45 + 180 = 225 градусов (на 2-дюймовом круге).

Каждому круговому пути нужны размер, скорость и начальный угол (амплитуда/частота/фаза). Мы даже можем комбинировать пути: представьте крошечные автомобили, которые едут по кругу с разной скоростью.

Комбинированное положение всех циклов — это наш сигнал, точно так же, как сочетание вкуса всех ингредиентов — это наш смузи.

Вот симуляция простого кругового пути:

(Исходный код основан на этой анимации. Требуется современный браузер. Щелкните график, чтобы приостановить/возобновить паузу.)

Величина каждого цикла указана по порядку, начиная с 0 Гц. Циклы [0 1] означает

• 0 амплитуда для цикла 0 Гц (0 Гц = постоянный цикл, застрявший на оси X на нуле градусов)
• 1 амплитуда для цикла 1 Гц (завершает 1 цикл за интервал времени)

Теперь сложная часть:

• Синий график измеряет действительную часть цикла . Еще одна милая математическая путаница: реальная ось круга, которая обычно горизонтальна, имеет величину, показанную на вертикальной оси. Можно мысленно вращать круг 90 градусов, если хотите.
• Моменты времени расположены с максимальной частотой . Сигналу с частотой 1 Гц требуется 2 точки времени для запуска и остановки (одна точка данных не имеет частоты). Значения времени [1 -1] показывают амплитуду в этих равноотстоящих интервалах.

Со мной? [0 1] — это чистый цикл 1 Гц.

Теперь давайте добавим в микс цикл 2 Гц. [0 1 1] означает «Ничего на 0 Гц, 1 Гц амплитуды 1, 2 Гц амплитуды 1»:

Ого. Маленькие автомобили сходят с ума: зеленые линии — это циклы 1 Гц и 2 Гц, а синяя линия — объединенный результат. Попробуйте переключить зеленый флажок, чтобы четко увидеть окончательный результат. Комбинированный «аромат» представляет собой влияние, которое начинается с максимума и опускается вниз до конца интервала.

Желтые точки — это когда мы фактически измеряем сигнал. При заданных 3 циклах (0 Гц, 1 Гц, 2 Гц) каждая точка составляет 1/3 пути прохождения сигнала. В этом случае циклы [0 1 1] генерируют значения времени [2 -1 -1] , который начинается с максимума (2) и опускается до минимума (-1).

О! Мы не можем забыть фазу, начальный угол! Используйте величина: угол , чтобы установить фазу. Итак, [0 1:45] — это цикл 1 Гц, который начинается с 45 градусов:

Это сдвинутая версия [0 1] . На временной стороне мы получаем [0,7 - 0,7] вместо [1 -1] , потому что наш цикл не совсем совпадает с нашими интервалами измерения, которые все еще находятся на полпути (это может быть желанный!).

Преобразование Фурье находит набор циклических скоростей, амплитуд и фаз для соответствия любому временному сигналу.

Наш сигнал становится абстрактным понятием, которое мы рассматриваем как «наблюдения во временной области» или «ингредиенты в частотной области».

Хватит болтать: попробуйте! В симуляторе введите любое время или шаблон цикла, который вы хотите увидеть. Если это временные точки, вы получите набор циклов (которые объединяются в «волну»), которые соответствуют вашим желаемым точкам.

Но… не имеет ли комбинированная волна странные значения между желтыми временными интервалами? Конечно. Но кто может сказать, распространяется ли сигнал по прямым линиям, по изгибам или по другим измерениям, когда мы его не измеряем? Он ведет себя именно так, как нам нужно, в равноотстоящие моменты, о которых мы просили.

Всплеск во времени

Можем ли мы сделать всплеск во времени, как (4 0 0 0) , используя циклы? Я буду использовать круглые скобки () для последовательности временных точек и скобки [] для последовательности циклов.

Хотя шип кажется нам, обитателям времени, скучным ( одна точка данных, и все? ), подумайте о сложности мира циклов. Ингредиенты нашего цикла должны сначала выровняться (при максимальном значении, 4), а затем «взорваться наружу», каждый цикл с партнерами, которые отменяют его в будущем. Каждая оставшаяся точка равна нулю, что представляет собой сложный баланс с множеством циклов (мы не можем просто «отключить их»).

Пройдемся по каждой временной точке:

• В момент времени 0, в первый момент, каждый ингредиент цикла находится на максимальном уровне. Игнорируя другие моменты времени, (4 ? ? ?) можно составить из 4 циклов (0 Гц 1 Гц 2 Гц 3 Гц), каждый с амплитудой 1 и фазой 0 (т. е. 1 + 1 + 1 + 1 = 4) .

• В каждой будущей точке (t = 1, 2, 3) сумма всех циклов должна аннулироваться.

Вот в чем хитрость: когда два цикла находятся на противоположных сторонах круга (север и юг, восток и запад и т. д.), их общая позиция равна нулю (3 цикла могут отмениться, если они распределены равномерно по точкам 0, 120 и 240 градусов).

Представьте себе созвездие точек, движущихся по кругу. Вот положение каждого цикла в каждый момент времени:

 Время 0 1 2 3
------------
0 Гц: 0 0 0 0
1 Гц: 0 1 2 3
2 Гц: 0 2 0 2
3 Гц: 0 3 2 1
 

Обратите внимание, как цикл 3 Гц начинается с 0, достигает позиции 3, затем позиции «6» (всего 4 позиции, 6 по модулю 4 = 2), затем позиции «9» (9 по модулю 4 = 1).

Когда наш цикл имеет длину 4 единицы, скорости цикла, разделенные полупериодом (2 единицы), будут либо выстроены в линию (разница 0, 4, 8…), либо на противоположных сторонах (разница 2, 6, 10…) .

ОК. Давайте углубимся в каждую временную точку:

• Время 0: все циклы на максимуме (всего 4)
• Время 1: 1 Гц и 3 Гц отменяются (положения 1 и 3 противоположны), 0 Гц и 2 Гц также отменяются. Чистая 0.
• Время 2: 0 Гц и 2 Гц выстраиваются в позиции 0, а 1 Гц и 3 Гц выстраиваются в позиции 2 (противоположная сторона). Итого по-прежнему 0.
• Время 3: 0 Гц и 2 Гц отменяются. 1 Гц и 3 Гц отменяются.
• Время 4 (повторение t=0): все циклы совпадают.

Хитрость заключается в отмене отдельных скоростей (0 Гц против 2 Гц, 1 Гц против 3 Гц) или в отмене выстроенных пар (0 Гц + 2 Гц против 1 Гц + 3 Гц).

Когда каждый цикл имеет одинаковую мощность и 0 фаз, мы начинаем выравнивание и затем отменяем. (У меня пока нет хорошего доказательства — есть берущие? — но вы сами можете его увидеть. сигналы, которые мы генерируем: (2 0) , (3 0 0) , (4 0 0 0) ).

В уме я называю эти сигналы «всплесками времени»: они имеют значение для одного момента и равны нулю в противном случае (причудливое название — дельта-функция).

Вот как я визуализирую начальное выравнивание, после по чистой отмене:

Перемещение пика времени

Не все происходит при t=0. Можем ли мы изменить наш шип на (0 4 0 0) ?

Похоже, что ингредиенты цикла должны быть похожи на (4 0 0 0) , но циклы должны выровняться при t=1 (одна секунда в будущем). Вот где начинается фаза.

Представьте себе гонку с 4 бегунами. В обычных гонках все выстраиваются у стартовой линии по схеме времени (4 0 0 0) . Скучный.

Что, если мы хотим, чтобы все закончили одновременно? Легкий. Просто перемещайте людей вперед или назад на соответствующее расстояние. Может быть, бабушка может стартовать за 2 фута до финиша, Усэйн Болт может стартовать за 100 метров, и они могут пересечь ленту, держась за руки.

Фазовые сдвиги, начальный угол, являются задержками во вселенной циклов. Вот как мы настраиваем начальную позицию, чтобы задерживать каждый цикл на 1 секунду:

• Цикл 0 Гц не перемещается, поэтому он уже выровнен
• Цикл 1 Гц делает 1 оборот за все 4 секунды, поэтому задержка в 1 секунду соответствует четверти оборота. Фаза сдвигается на 90 градусов назад (-90), и она достигает фазы = 0, максимального значения, при t = 1.
• Цикл 2 Гц в два раза быстрее, поэтому задайте ему вдвое больший угол охвата (фазовый сдвиг -180 или 180 — в любом случае это пересечение круга).
• Цикл 3 Гц в 3 раза быстрее, поэтому дайте ему 3-кратное расстояние перемещения (фазовый сдвиг -270 или +90)

Если моменты времени (4 0 0 0) состоят из циклов [1 1 1 1] , то моменты времени (0 4 0 0) состоят из [1 1:-90 1:180 1:90] . (Примечание: я использую «1 Гц», но имею в виду «1 цикл за весь период времени»).

Ого, мы прокручиваем циклы в голове!

Визуализация интерференции похожа, за исключением того, что выравнивание выполняется при t=1.

Проверьте свою интуицию: сможете ли вы сделать (0 0 4 0) , т.е. 2-секундная задержка? 0 Гц не имеет фазы. 1 Гц имеет 180 градусов, 2 Гц — 360 (он же 0), а 3 Гц — 540 (он же 180), так что это [1 1:180 1 1:180] .

Полное преобразование

Большое открытие: наш сигнал — это просто набор временных всплесков! Если мы объединим рецепты для каждого пика времени, мы должны получить рецепт для полного сигнала.

Преобразование Фурье строит рецепт по частоте:

• Разделите полный сигнал (a b c d) на «временные пики»: (a 0 0 0) (0 b 0 0) (0 0 c 0) (0 0 0 г)
• Для любой частоты (например, 2 Гц) предварительный рецепт выглядит следующим образом: «a/4 + b/4 + c/4 + d/4» (амплитуда каждого выброса делится на все частоты)
• Подожди! Нам нужно компенсировать каждый всплеск фазовой задержкой (угол для «задержки в 1 секунду» зависит от частоты).
• Фактический рецепт для частоты = a/4 (без смещения) + b/4 (смещение на 1 секунду) + c/4 (смещение на 2 секунды) + d/4 (смещение на 3 секунды).

Затем мы можем перебрать каждую частоту, чтобы получить полное преобразование.

Вот преобразование «математического английского» в полную математику:

Несколько замечаний:

• N = количество временных выборок, которые у нас есть
• n = текущий образец, который мы рассматриваем (0 .. N-1)
• x _n = значение сигнала в момент времени n
• k = текущая частота, которую мы рассматриваем (от 0 Гц до N-1 Гц)
• X _k = количество частот k в сигнале (амплитуда и фаза, комплексное число)
• Коэффициент 1/N обычно переносится на 9-ix — это наш обратный круговой путь. Комбинация — это то, как далеко мы продвинулись для такой скорости и времени.
• Необработанные уравнения для преобразования Фурье просто говорят «сложите комплексные числа». Многие языки программирования не могут обрабатывать комплексные числа напрямую, поэтому вы конвертируете все в прямоугольные координаты и добавляете их.

Далее

Это была моя самая сложная статья. Преобразование Фурье имеет несколько видов (дискретное/непрерывное/конечное/бесконечное), охватывает глубокую математику (дельта-функции Дирака), и в нем легко потеряться в деталях. Я постоянно натыкался на край своих знаний.

Но всегда есть простые аналогии — я отказываюсь думать иначе. Будь то смузи или Усэйн Болт и бабушка, пересекающие финишную черту, возьмите простое понимание и усовершенствуйте его. Аналогия ошибочна, и это нормально: это плот, который можно использовать и оставить, как только мы пересечем реку.

Я понял, насколько слабым было мое собственное понимание, когда я не мог вычислить в уме преобразование числа (1 0 0 0) . Для меня это было все равно, что сказать, что я знаю сложение, но, черт возьми, я не уверен, что такое «1 + 1 + 1 + 1». Почему бы и нет? Разве у нас не должно быть интуиции для простейших операций?

Этот дискомфорт побудил меня бродить по сети, чтобы развить свою интуицию. В дополнение к ссылкам в статье я хотел бы поблагодарить:

• Скотта Янга за первоначальный импульс для этого поста
• Шахин Ганди, Роджер Ченг и Брит Круз за обсуждение идей и уточнение аналогии
• Стив Лехар за отличные примеры преобразования Фурье на изображениях
• Чаран Лэнгтон за подробное прохождение
• Джулиусу Смиту за фантастическое пошаговое руководство по дискретному преобразованию Фурье (то, что мы рассмотрели сегодня)
• Брет Виктор за методы визуализации обучения

Сегодняшней целью было испытать преобразование Фурье. Мы сохраним расширенный анализ для следующего раза.

Счастливая математика.

Приложение: Проектирование на циклы

У Стюарта Риффла есть великолепная интерпретация преобразования Фурье:

Представьте, что вы вращаете свой сигнал в центрифуге и проверяете смещение. У меня поправка: надо раскрутить назад 9{-i 2 \pi…}$). Вы уже знаете, почему: нам нужна фаза , задержка , чтобы в будущем появились всплески .

Приложение: Еще одна замечательная визуализация

Лукас Виейра, автор превосходных анимаций из Википедии, вдохновился на создание этой интерактивной анимации: Преобразование Фурье — это циклы, добавленные к циклам, добавленным к циклам. Попробуйте создать «всплеск времени», установив амплитуду 1 для каждого компонента (нажимайте Enter после ввода каждого числа). Забавный факт: при наличии достаточного количества терминов вы можете нарисовать любую фигуру, даже Гомера Симпсона.

Посетите http://www.jezzamon.com/fourier/, чтобы найти отличный инструмент для рисования любой формы с помощью эпициклов.

Приложение: Статья с образцами кода R

Жоао Нето сделал отличный отчет с примерами технического кода (R) здесь:

http://www. di.fc.ul.pt/~jpn/r/ Fourier/fourier.html

Приложение: Использование кода

Весь код и примеры имеют открытый исходный код (лицензия MIT, делайте, что хотите).

• Интерактивный пример (исходный код)
• Гитхаб суть
• Обсуждение деталей расчета на Reddit, я pb_zeppelin

Другие сообщения из этой серии

1. Наглядное интуитивное руководство по воображаемым числам
2. Интуитивная арифметика с комплексными числами
3. Понимание того, почему сложное умножение работает
4. Интуитивное руководство по углам, градусам и радианам
5. Интуитивное понимание формулы Эйлера
6. Интерактивное руководство по преобразованию Фурье
7. Интуитивное руководство по свертке
8. Интуитивное понимание синусоиды
9. Интуитивное руководство по линейной алгебре
10. Интуиция программиста для умножения матриц
11. Мнимое умножение против мнимых показателей
12. Интуитивное руководство по гиперболическим функциям

Обработка сигналов Python — Real Python

Преобразование Фурье — это мощный инструмент для анализа сигналов , который используется во всем, от обработки звука до сжатия изображений. SciPy обеспечивает зрелую реализацию в своих scipy.fft , и в этом руководстве вы узнаете, как его использовать.

Модуль scipy.fft поначалу может показаться пугающим, так как в нем много функций, часто с похожими именами, а в документации используется много технических терминов без пояснений. Хорошей новостью является то, что вам нужно только понять несколько основных концепций, чтобы начать использовать модуль.

Не волнуйтесь, если вам не нравится математика! Вы познакомитесь с алгоритмом на конкретных примерах, и там будут ссылки на дополнительные ресурсы, если вы хотите погрузиться в уравнения. Для визуального ознакомления с тем, как работает преобразование Фурье, вам может понравиться видео 3Blue1Brown.

В этом уроке вы узнаете:

• Как и когда использовать преобразование Фурье
• Как выбрать правильную функцию из scipy.fft для вашего варианта использования
• Как просмотреть и изменить частотный спектр сигнала
• Какие различные преобразования доступны в scipy. fft

Если вы хотите, чтобы краткое изложение этого руководства сохранилось после того, как вы закончите чтение, загрузите шпаргалку ниже. Он имеет объяснения всех функций в 9Модуль 0625 scipy.fft , а также разбивка различных типов доступных преобразований:

Модуль

scipy.fft

Преобразование Фурье является важным инструментом во многих приложениях, особенно в научных вычислениях и науке о данных. Таким образом, SciPy уже давно предоставляет его реализацию и связанные с ним преобразования. Первоначально SciPy предоставила модуль scipy.fftpack , но с тех пор они обновили свою реализацию и переместили его в 9Модуль 0625 scipy.fft .

SciPy обладает полной функциональностью. Более общее знакомство с библиотекой см. в статье Scientific Python: Using SciPy for Optimization.

Удалить рекламу

Установить SciPy и Matplotlib

Прежде чем вы сможете начать, вам необходимо установить SciPy и Matplotlib. Вы можете сделать это одним из двух способов:

1. Установка с Anaconda: Загрузите и установите Anaconda Individual Edition. Он поставляется с SciPy и Matplotlib, поэтому, как только вы выполните шаги в программе установки, все готово!

2. Установить с pip : Если у вас уже установлен pip , вы можете установить библиотеки с помощью следующей команды:

    $ python -m pip install -U scipy matplotlib
    

Вы можете убедиться, что установка работает, набрав python в своем терминале и выполнив следующий код:

>>>

 >>> импорт scipy, matplotlib
>>> печать (scipy.__file__)
/usr/local/lib/python3.6/dist-packages/scipy/__init__.py
>>> печать (matplotlib.__file__)
/usr/local/lib/python3.6/dist-packages/matplotlib/__init__.py
 

Этот код импортирует SciPy и Matplotlib и печатает расположение модулей. Ваш компьютер, вероятно, покажет разные пути, но пока он печатает путь, установка работает.

SciPy теперь установлен! Теперь пришло время взглянуть на различия между scipy.fft и scipy.fftpack .

scipy.fft против scipy.fftpack

При просмотре документации SciPy вы можете обнаружить два очень похожих модуля:

1. scipy.fft
2. scipy.fftpack

Модуль scipy.fft новее, и его следует предпочесть scipy.fftpack . Вы можете прочитать больше об изменении в примечаниях к выпуску для SciPy 1.4.0, но вот краткий обзор:

• scipy.fft имеет улучшенный API.
• scipy.fft позволяет использовать несколько рабочих процессов, что в некоторых ситуациях может обеспечить повышение скорости.
• scipy.fftpack считается устаревшим, и SciPy рекомендует вместо него использовать scipy. fft .

Если у вас нет веских причин для использования scipy.fftpack , вам следует придерживаться scipy.fft .

scipy.fft против numpy.fft

Реализация быстрого преобразования Фурье (БПФ) SciPy содержит больше функций и с большей вероятностью исправит ошибки, чем реализация NumPy. Если у вас есть выбор, вы должны использовать реализацию SciPy.

NumPy поддерживает реализацию БПФ для обратной совместимости, хотя авторы считают, что такие функции, как преобразования Фурье, лучше всего реализованы в SciPy. Дополнительные сведения см. в разделе часто задаваемых вопросов по SciPy.

Преобразование Фурье

Анализ Фурье — это область, изучающая, как математическая функция может быть разложена на ряд более простых тригонометрических функций . Преобразование Фурье — это инструмент из этой области для разложения функции на составляющие ее частоты.

Хорошо, это определение довольно сложное. Для целей этого руководства преобразование Фурье — это инструмент, который позволяет вам взять сигнал и увидеть мощность каждой частоты в нем. Взгляните на важные термины в этом предложении:

• Сигнал — это информация, которая меняется со временем. Например, звуковые, видеосигналы и кривые напряжения — все это примеры сигналов.
• Частота — это скорость, с которой что-то повторяется. Например, часы тикают с частотой один герц (Гц) или одно повторение в секунду.
• Мощность , в данном случае просто означает силу каждой частоты.

На следующем изображении показана частота и мощность некоторых синусоидальных волн:

Пики высокочастотной синусоиды расположены ближе друг к другу, чем пики низкочастотной синусоиды , поскольку они повторяются чаще. Синусоидальная волна малой мощности имеет меньшие пики, чем две другие синусоидальные волны.

Чтобы сделать это более конкретным, представьте, что вы использовали преобразование Фурье для записи того, как кто-то играет три ноты на фортепиано одновременно. В результате частотный спектр показал бы три пика, по одному для каждой из нот. Если бы человек играл одну ноту тише, чем другие, то сила частоты этой ноты была бы ниже, чем у двух других.

Вот как этот пример пианино будет выглядеть визуально:

Самая высокая нота на фортепиано была сыграна тише, чем две другие ноты, поэтому результирующий частотный спектр для этой ноты имеет более низкий пик.

Удалить рекламу

Зачем вам нужно преобразование Фурье?

Преобразование Фурье полезно во многих приложениях. Например, Shazam и другие службы идентификации музыки используют преобразование Фурье для идентификации песен. Сжатие JPEG использует вариант преобразования Фурье для удаления высокочастотных компонентов изображения. Распознавание речи использует преобразование Фурье и связанные с ним преобразования для восстановления произнесенных слов из необработанного звука.

В общем, вам нужно преобразование Фурье, если вам нужно посмотреть частоты в сигнале. Если работа с сигналом во временной области затруднена, то стоит попробовать использовать преобразование Фурье для его перемещения в частотную область. В следующем разделе вы рассмотрите различия между временной и частотной областями.

Временная область и частотная область

В остальной части руководства вы встретите термины во временной области и в частотной области . Эти два термина относятся к двум различным способам рассмотрения сигнала, либо как частоты его компонентов, либо как информация, которая меняется во времени.

Во временной области сигнал представляет собой волну, амплитуда которой (ось Y) меняется во времени (ось X). Скорее всего, вы привыкли видеть графики во временной области, такие как этот:

Это изображение какого-то звука, представляющего собой сигнал временной области . Горизонтальная ось представляет время, а вертикальная ось представляет амплитуду.

В частотной области сигнал представляется как последовательность частот (ось X), каждая из которых имеет соответствующую мощность (ось Y). Следующее изображение представляет собой приведенный выше звуковой сигнал после преобразования Фурье:

.

Здесь предыдущий звуковой сигнал представлен составляющими его частотами. Каждая частота внизу имеет соответствующую мощность, производя спектр, который вы видите.

Для получения дополнительной информации о частотной области ознакомьтесь с записью глоссария DeepAI.

Типы преобразований Фурье

Преобразование Фурье можно разделить на различные типы преобразования. Самое основное подразделение основано на типе данных, с которыми работает преобразование: непрерывные функции или дискретные функции. Этот учебник будет иметь дело только с дискретным преобразованием Фурье (DFT) .

Даже в этом руководстве вы часто будете видеть, что термины ДПФ и БПФ взаимозаменяемы. Однако это не совсем одно и то же. быстрое преобразование Фурье (БПФ) — это алгоритм вычисления дискретного преобразования Фурье (ДПФ), тогда как ДПФ — это само преобразование.

Еще одно различие, которое вы увидите в библиотеке scipy.fft , касается разных типов ввода. fft() принимает комплексные входные данные, а rfft() принимает вещественные входные данные. Перейдите к разделу Использование быстрого преобразования Фурье (БПФ) для объяснения комплексных и действительных чисел.

Два других преобразования тесно связаны с ДПФ: дискретное косинусное преобразование (DCT) и дискретное синусоидальное преобразование (DST) . Вы узнаете о них в разделе Дискретные косинусные и синусоидальные преобразования.

Практический пример: удаление нежелательного шума из звука

Чтобы помочь вам лучше понять преобразование Фурье и то, что вы можете с ним делать, вы собираетесь отфильтровать звук. Сначала вы создадите звуковой сигнал с высокочастотным гудением, а затем удалите гудение с помощью преобразования Фурье.

Создание сигнала

Синусоидальные волны иногда называют чистыми тонами , потому что они представляют одну частоту. Вы будете использовать синусоидальные волны для генерации звука, поскольку они будут формировать четкие пики в результирующем частотном спектре.

Еще одна замечательная особенность синусоид — это то, что их легко генерировать с помощью NumPy. Если вы раньше не использовали NumPy, вы можете проверить, что такое NumPy?

Вот код, генерирующий синусоиду:

 импортировать numpy как np
из matplotlib импортировать pyplot как plt
SAMPLE_RATE = 44100 # Гц
ПРОДОЛЖИТЕЛЬНОСТЬ = 5 # секунд
def generate_sine_wave (частота, частота дискретизации, продолжительность):
    x = np.linspace(0, продолжительность, sample_rate * продолжительность, конечная точка = False)
    частоты = x * частота
    # 2pi, потому что np. sin принимает радианы
    y = np.sin((2 * np.pi) * частоты)
    вернуть х, у
# Генерируем синусоиду частотой 2 Гц, которая длится 5 секунд
x, y = generate_sine_wave(2, SAMPLE_RATE, DURATION)
plt.plot(x, y)
plt.show()
 

После импорта NumPy и Matplotlib вы определяете две константы:

1. SAMPLE_RATE определяет, сколько точек данных использует сигнал для представления синусоиды в секунду. Таким образом, если бы сигнал имел частоту дискретизации 10 Гц и представлял собой пятисекундную синусоидальную волну, то он имел бы 10 * 5 = 50 точек данных.
2. DURATION — длина сгенерированной выборки.

Затем вы определяете функцию для генерации синусоидальной волны, поскольку позже вы будете использовать ее несколько раз. Функция принимает частоту, freq , а затем возвращает значения x и y , которые вы будете использовать для построения волны.

X-координаты синусоиды равномерно распределены между 0 и DURATION , поэтому код использует NumPy linspace() для их генерации. Он принимает начальное значение, конечное значение и количество генерируемых выборок. Установка endpoint=False важна для правильной работы преобразования Фурье, поскольку оно предполагает, что сигнал является периодическим.

np.sin() вычисляет значения функции синуса в каждой из координат x. Результат умножается на частоту, чтобы синусоида колебалась на этой частоте, а произведение умножается на 2π для преобразования входных значений в радианы.

Примечание: Если вы раньше мало занимались тригонометрией или вам нужно освежить свои знания, ознакомьтесь с курсом тригонометрии Академии Хана.

После того, как вы определите функцию, вы используете ее для создания двухгерцовой синусоидальной волны, которая длится пять секунд, и строите ее с помощью Matplotlib. Ваш график синусоиды должен выглядеть примерно так:

Ось X представляет время в секундах, и, поскольку на каждую секунду приходится два пика, вы можете видеть, что синусоида колеблется дважды в секунду. Эта синусоидальная волна имеет слишком низкую частоту, чтобы ее можно было услышать, поэтому в следующем разделе вы сгенерируете несколько высокочастотных синусоидальных волн и увидите, как их смешивать.

Удалить рекламу

Микширование аудиосигналов

Хорошей новостью является то, что микширование аудиосигналов состоит всего из двух шагов:

1. Суммирование сигналов
2. Нормализация результата

Прежде чем вы сможете микшировать сигналы, вам нужно их сгенерировать:

 _, nice_tone = generate_sine_wave(400, SAMPLE_RATE, DURATION)
_, Noise_tone = generate_sine_wave(4000, SAMPLE_RATE, DURATION)
шумовой_тон = шумовой_тон * 0,3
смешанный_тон = приятный_тон + шумовой_тон
 

В этом примере кода нет ничего нового. Он генерирует тон средней и высокой тональности, назначенный переменным nice_tone 9.0626 и Noise_Tone соответственно. Вы будете использовать высокий тон в качестве нежелательного шума, поэтому он умножается на 0,3 , чтобы уменьшить его мощность. Затем код складывает эти тона вместе. Обратите внимание, что вы используете символ подчеркивания ( _ ), чтобы отбросить значения x , возвращаемые функцией generate_sine_wave() .

Следующим шагом является нормализация или масштабирование сигнала, чтобы он соответствовал целевому формату. Из-за того, как вы будете хранить звук позже, ваш целевой формат — 16-битное целое число, которое имеет диапазон от -32768 до 32767:

 normalized_tone = np.int16((mixed_tone/mixed_tone.max()) * 32767)
plt.plot(normalized_tone[:1000])
plt.show()
 

Здесь код масштабирует mixed_tone , чтобы он точно соответствовал 16-битному целому числу, а затем приводит его к этому типу данных, используя NumPy np. int16 . Разделив Mixed_Tone на его максимальное значение, вы получите масштаб между -1 и 1 . Когда этот сигнал умножается на 32767 , он масштабируется между -32767 и 32767 , что примерно соответствует диапазону np.int16 . Код отображает только первые 1000 выборок, чтобы вы могли более четко увидеть структуру сигнала.

Ваш график должен выглядеть примерно так:

Сигнал выглядит как искаженная синусоида. Синусоида, которую вы видите, — это сгенерированный вами тон 400 Гц, а искажение — это тон 4000 Гц. Если присмотреться, то видно, что искажение имеет форму синусоиды.

Чтобы прослушать аудио, вам нужно сохранить его в формате, который может прочитать аудиоплеер. Самый простой способ сделать это — использовать метод SciPy wavfile.write, чтобы сохранить его в файле WAV. 16-битные целые числа являются стандартным типом данных для файлов WAV, поэтому вы нормализуете свой сигнал до 16-битных целых чисел:

.

 из scipy.io.wavfile импорт записи
# Помните, что SAMPLE_RATE = 44100 Гц — это наша частота воспроизведения
write("mysinewave.wav", SAMPLE_RATE, normalized_tone)
 

Этот код запишет в файл mysinewave.wav в каталоге, где вы запускаете свой скрипт Python. Затем вы можете прослушать этот файл с помощью любого аудиоплеера или даже с помощью Python. Вы услышите более низкий тон и более высокий тон. Это синусоидальные волны 400 Гц и 4000 Гц, которые вы смешали.

После того, как вы выполните этот шаг, у вас будет готовый аудиосэмпл. Следующий шаг — удаление высокого тона с помощью преобразования Фурье!

Использование быстрого преобразования Фурье (БПФ)

Пришло время использовать БПФ для сгенерированного звука. БПФ — это алгоритм, который реализует преобразование Фурье и может вычислять частотный спектр сигнала во временной области, например, ваш звук:

 из scipy.fft импортировать fft, fftfreq
# Количество семплов в normalized_tone
N = SAMPLE_RATE * ПРОДОЛЖИТЕЛЬНОСТЬ
yf = fft (normalized_tone)
xf = fftfreq(N, 1/SAMPLE_RATE)
plt. plot (xf, np.abs (yf))
plt.show()
 

Этот код вычисляет преобразование Фурье сгенерированного звука и отображает его. Прежде чем разбирать его, взгляните на сюжет, который он производит:

Вы можете видеть два пика на положительных частотах и ​​зеркала этих пиков на отрицательных частотах. Пики положительной частоты находятся на частотах 400 Гц и 4000 Гц, что соответствует частотам, которые вы вкладываете в звук.

Преобразование Фурье взяло ваш сложный, шаткий сигнал и превратило его только в частоты, которые он содержит. Поскольку вы вводите только две частоты, получается только две частоты. Отрицательно-положительная симметрия является побочным эффектом помещения действительных входных данных в преобразование Фурье, но вы услышите об этом позже.

В первых нескольких строках вы импортируете функции из scipy.fft , которые будете использовать позже, и определяете переменную, N , в котором хранится общее количество выборок в сигнале.

После этого следует самый важный раздел, вычисляющий преобразование Фурье:

 yf = fft(normalized_tone)
xf = fftfreq(N, 1/SAMPLE_RATE)
 

Код вызывает две очень важные функции:

1. fft() вычисляет само преобразование.

2. fftfreq() вычисляет частоты в центре каждого бин в выводе fft() . Без этого невозможно было бы построить ось X на вашем частотном спектре.

Ячейка представляет собой диапазон значений, которые были сгруппированы, как на гистограмме. Дополнительные сведения о бинах см. в этом вопросе об обмене стеками обработки сигналов. Для целей этого руководства вы можете думать о них как об отдельных значениях.

Когда у вас есть результирующие значения преобразования Фурье и соответствующие им частоты, вы можете построить их:

 plt.plot(xf, np. abs(yf))
plt.show()
 

Интересной частью этого кода является обработка, которую вы выполняете для yf перед построением графика. Вы вызываете np.abs() на yf , потому что его значения комплексные .

Комплексное число — это число, состоящее из двух частей: реальной части и мнимой части . Есть много причин, по которым полезно определять такие числа, но все, что вам нужно знать прямо сейчас, это то, что они существуют.

Математики обычно записывают комплексные числа в виде a + bi , где a — действительная часть, а b — мнимая часть. i после b означает, что b — мнимое число.

Примечание: Иногда вы увидите комплексные числа, записанные с использованием i , а иногда вы увидите их с использованием j , например, 2 + 3 i и 2 + 3 j . Оба одинаковые, но i больше используется математиками, а j больше инженерами.

Чтобы узнать больше о комплексных числах, ознакомьтесь с курсом Академии Хана или страницей «Математика — это весело».

Поскольку комплексные числа состоят из двух частей, для их построения в зависимости от частоты на двумерной оси требуется вычислить из них одно значение. Вот тут-то и появляется np.abs() . Он вычисляет √(a² + b²) для комплексных чисел, что является общей величиной для двух чисел вместе и, что важно, одним значением.

Примечание: Кстати, вы могли заметить, что fft() возвращает максимальную частоту чуть более 20 тысяч герц, а точнее 22050 Гц. Это значение составляет ровно половину нашей частоты дискретизации и называется частотой Найквиста.

Это фундаментальная концепция обработки сигналов, которая означает, что частота дискретизации должна быть как минимум в два раза выше самой высокой частоты вашего сигнала.

Удаление рекламы

Ускорение с помощью

rfft()

Спектр частот, выдаваемый функцией fft() , был отражен относительно оси Y, так что отрицательная половина была зеркалом положительной половины. Эта симметрия была вызвана вводом действительных чисел (не комплексных чисел) для преобразования.

Вы можете использовать эту симметрию, чтобы ускорить преобразование Фурье, вычислив только его половину. scipy.fft реализует этот хак скорости в форме rfft() .

Самое замечательное в rfft() заключается в том, что это замена fft() . Помните код БПФ, который был раньше:

.

 yf = fft(normalized_tone)
xf = fftfreq(N, 1/SAMPLE_RATE)
 

Замена в rfft() , код остается почти таким же, только с парой ключевых изменений:

 из scipy.fft импортировать rfft, rfftfreq
# Обратите внимание на лишний 'r' впереди
yf = rfft(normalized_tone)
xf = rfftfreq(N, 1/SAMPLE_RATE)
plt. plot (xf, np.abs (yf))
plt.show()
 

С rfft() возвращает только половину вывода, который делает fft() , он использует другую функцию для получения отображения частоты, rfftfreq() вместо fftfreq() .

rfft() по-прежнему выдает сложный вывод, поэтому код для построения результата остается прежним. График, однако, должен выглядеть следующим образом, так как отрицательные частоты исчезнут:

Вы можете видеть, что изображение выше — это только положительная сторона частотного спектра, который fft() производит. rfft() никогда не вычисляет отрицательную половину частотного спектра, что делает его быстрее, чем использование fft() .

Использование rfft() может быть в два раза быстрее, чем использование fft() , но некоторые длины ввода быстрее, чем другие. Если вы знаете, что будете работать только с реальными числами, то этот лайфхак стоит знать.

Теперь, когда у вас есть частотный спектр сигнала, вы можете перейти к его фильтрации.

Фильтрация сигнала

Одна из замечательных особенностей преобразования Фурье заключается в том, что оно обратимо, поэтому любые изменения, которые вы вносите в сигнал в частотной области, будут применяться при обратном преобразовании во временную область. Вы воспользуетесь этим, чтобы отфильтровать звук и избавиться от высоких частот.

Предупреждение: Метод фильтрации, продемонстрированный в этом разделе, не подходит для реальных сигналов. Объяснение причин см. в разделе Как избежать ловушек при фильтрации.

Значения, возвращаемые функцией rfft() , представляют мощность каждого частотного бина. Если вы установите мощность данного бина на ноль, то частоты в этом бине больше не будут присутствовать в результирующем сигнале во временной области.

Используя длину xf , максимальную частоту и тот факт, что ячейки частот равномерно распределены, вы можете вычислить индекс целевой частоты:

 # Максимальная частота равна половине частоты дискретизации
points_per_freq = длина (xf) / (SAMPLE_RATE / 2)
# Наша целевая частота 4000 Гц
target_idx = int(points_per_freq * 4000)
 

Затем вы можете установить yf на 0 в индексах вокруг целевой частоты, чтобы избавиться от нее:

 yf[target_idx - 1 : target_idx + 2] = 0
plt. plot (xf, np.abs (yf))
plt.show()
 

Ваш код должен вывести следующий график:

Поскольку пик только один, похоже, это сработало! Затем вы примените обратное преобразование Фурье, чтобы вернуться во временную область.

Удаление рекламы

Применение обратного БПФ

Применение обратного БПФ аналогично применению БПФ:

 из scipy.fft импортировать irfft
new_sig = irfft(yf)
plt.plot(new_sig[:1000])
plt.show()
 

Поскольку вы используете rfft() , вам нужно использовать irfft() , чтобы применить обратное. Однако, если бы вы использовали fft() , то обратная функция была бы ifft() . Теперь ваш график должен выглядеть так:

Как видите, теперь у вас есть одна синусоида, колеблющаяся с частотой 400 Гц, и вы успешно удалили шум 4000 Гц.

Еще раз, вам нужно нормализовать сигнал перед записью в файл. Вы можете сделать это так же, как и в прошлый раз:

 norm_new_sig = np. int16 (new_sig * (32767 / new_sig.max ()))
write("clean.wav", SAMPLE_RATE, norm_new_sig)
 

Когда вы прослушаете этот файл, вы услышите, что раздражающий шум исчез!

Как избежать ошибок при фильтрации

Приведенный выше пример предназначен больше для образовательных целей, чем для реального использования. Воспроизведение процесса на реальном сигнале, таком как музыкальное произведение, может создать больше шумихи, чем убрать.

В реальном мире вы должны фильтровать сигналы, используя функции разработки фильтра в пакете scipy.signal . Фильтрация — сложная тема, требующая большого количества математических вычислений. В качестве хорошего введения взгляните на Руководство для ученых и инженеров по цифровой обработке сигналов.

Дискретные косинусные и синусоидальные преобразования

Учебное пособие по модулю scipy.fft было бы неполным без изучения дискретного косинусного преобразования (DCT) и дискретного синусоидального преобразования (DST). Эти два преобразования тесно связаны с преобразованием Фурье, но работают исключительно с действительными числами. Это означает, что они принимают функцию с действительным знаком в качестве входных данных и производят другую функцию с действительным знаком в качестве выхода.

SciPy реализует эти преобразования как dct() и dst() . Варианты i* и *n являются обратными и n -мерными версиями функций соответственно.

DCT и DST немного похожи на две половины, которые вместе составляют преобразование Фурье. Это не совсем так, поскольку математика намного сложнее, но это полезная ментальная модель.

Итак, если DCT и DST подобны половинкам преобразования Фурье, то зачем они нужны?

Во-первых, они быстрее, чем полное преобразование Фурье, поскольку фактически выполняют половину работы. Они могут быть даже быстрее, чем rfft() . Кроме того, они работают исключительно с действительными числами, так что вам никогда не придется беспокоиться о комплексных числах.

Прежде чем вы сможете научиться выбирать между ними, вам нужно понять четные и нечетные функции. Четные функции симметричны относительно оси Y, тогда как нечетные функции симметричны относительно начала координат. Чтобы представить это наглядно, взгляните на следующие диаграммы:

Вы видите, что четная функция симметрична относительно оси Y. Нечетная функция симметрична относительно y = - x , что описывается как -симметричная относительно начала координат .

Когда вы вычисляете преобразование Фурье, вы делаете вид, что функция, для которой вы его вычисляете, бесконечна. Полное преобразование Фурье (ДПФ) предполагает бесконечное повторение входной функции. Однако DCT и DST предполагают, что функция расширяется за счет симметрии. DCT предполагает, что функция расширена с четной симметрией, а DST предполагает, что она расширена с нечетной симметрией.

На следующем рисунке показано, как каждое преобразование представляет функцию, расширяющуюся до бесконечности:

На изображении выше ДПФ повторяет функцию как есть. DCT отражает функцию по вертикали, чтобы расширить ее, а DST — по горизонтали.

Обратите внимание, что симметрия, подразумеваемая DST, приводит к большим скачкам в функции. Они называются разрывами и производят более высокочастотные компоненты в результирующем частотном спектре. Поэтому, если вы не знаете, что ваши данные имеют нечетную симметрию, вам следует использовать DCT вместо DST.

Очень часто используется DCT. Есть еще много примеров, но все стандарты JPEG, MP3 и WebM используют DCT.

Удалить рекламу

Заключение

Преобразование Фурье — это мощная концепция, которая используется в самых разных областях: от чистой математики до аудиотехники и даже финансов. Теперь вы знакомы с дискретным преобразованием Фурье и хорошо подготовлены для применения его к задачам фильтрации с использованием модуля scipy.fft .

В этом уроке вы узнали:

• Как и когда использовать преобразование Фурье
• Как выбрать правильную функцию из scipy. fft для вашего варианта использования
• В чем разница между временной областью и частотной областью
• Как просмотреть и изменить частотный спектр сигнала
• Как использовать rfft() может ускорить ваш код

В последнем разделе вы также узнали о дискретном косинусном преобразовании и дискретном синусоидальном преобразовании . Вы увидели, какие функции вызывать для их использования, и узнали, когда использовать одну вместо другой.

Если вам нужен краткий обзор этого руководства, вы можете скачать шпаргалку ниже. В нем есть объяснения всех функций в модуле scipy.fft , а также разбивка различных типов доступных преобразований:

Продолжайте изучать эту увлекательную тему и экспериментировать с трансформациями, и обязательно поделитесь своими открытиями в комментариях ниже!

OpenCV: преобразование Фурье

Цель

В этом разделе мы узнаем

• Чтобы найти преобразование Фурье изображений с использованием OpenCV
• Чтобы использовать функции БПФ, доступные в Numpy
• Некоторые применения преобразования Фурье
• Мы увидим следующие функции: cv. dft() , cv.idft() и т. д.

Теория

Преобразование Фурье используется для анализа частотных характеристик различных фильтров. Для изображений 2D дискретное преобразование Фурье (DFT) используется для нахождения частотной области. Для расчета ДПФ используется быстрый алгоритм под названием Быстрое преобразование Фурье (БПФ) . Подробности об этом можно найти в любых учебниках по обработке изображений или обработке сигналов. См. раздел Дополнительные ресурсы_.

Для синусоидального сигнала \(x(t) = A \sin(2 \pi ft)\), мы можем сказать, что \(f\) - это частота сигнала, и если взять его частотную область, мы можем увидеть всплеск в \(f\). Если сигнал дискретизируется для формирования дискретного сигнала, мы получаем ту же частотную область, но периодическую в диапазоне \([- \pi, \pi]\) или \([0,2\pi]\) (или \ ([0,N]\) для N-точечного ДПФ). Вы можете рассматривать изображение как сигнал, который дискретизируется в двух направлениях. Таким образом, преобразование Фурье в обоих направлениях X и Y дает вам частотное представление изображения.

Более интуитивно понятно, что для синусоидального сигнала, если амплитуда изменяется так быстро за короткое время, можно сказать, что это высокочастотный сигнал. Если он изменяется медленно, это низкочастотный сигнал. Вы можете распространить ту же идею на изображения. Где амплитуда сильно различается на изображениях? На краевых точках или шумах. Таким образом, мы можем сказать, что края и шумы являются высокочастотными составляющими изображения. Если нет больших изменений амплитуды, это низкочастотная составляющая. (Некоторые ссылки добавлены в Дополнительные ресурсы_, которые интуитивно объясняют частотное преобразование с примерами).

Теперь посмотрим, как найти преобразование Фурье.

Преобразование Фурье в Numpy

Сначала мы увидим, как найти преобразование Фурье с помощью Numpy. У Numpy есть пакет FFT для этого. np.fft.fft2() предоставляет нам преобразование частоты, которое будет представлять собой сложный массив. Его первым аргументом является входное изображение в градациях серого. Второй аргумент является необязательным и определяет размер выходного массива. Если он больше, чем размер входного изображения, входное изображение дополняется нулями перед вычислением БПФ. Если оно меньше входного изображения, входное изображение будет обрезано. Если аргументы не переданы, размер выходного массива будет таким же, как и входной.

Теперь, когда вы получили результат, нулевая частотная составляющая (постоянная составляющая) будет в верхнем левом углу. Если вы хотите поместить его в центр, вам нужно сдвинуть результат на \(\frac{N}{2}\) в обоих направлениях. Это просто делается с помощью функции np.fft.fftshift() . (Легче анализировать). Как только вы нашли преобразование частоты, вы можете найти спектр амплитуды.

импортировать cv2 как cv

импортировать numpy как np

из matplotlib импортировать pyplot как plt

img = cv.imread('messi5.jpg',0)

f = np. fft.fft2(img)

fshift = np.fft.fftshift(f)

величина_спектр = 20*np.log( np.abs(fshift))

plt.subplot(121),plt.imshow(img, cmap = 'grey')

plt.title('Входное изображение'), plt.xticks([]), plt. yticks([])

plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'grey')

plt.title('Спектр магнитуды'), plt.xticks([]), plt.yticks( [])

plt.show()

Результат выглядит следующим образом:

image

Видите, вы можете увидеть более белую область в центре, показывающую более низкочастотный контент.

Итак, вы нашли частотное преобразование. Теперь вы можете выполнять некоторые операции в частотной области, такие как фильтрация верхних частот и реконструировать изображение, т.е. найти обратное ДПФ. Для этого вы просто удаляете низкие частоты, маскируя их прямоугольным окном размером 60x60. Затем примените обратный сдвиг, используя np.fft.ifftshift() , чтобы компонент постоянного тока снова попал в верхний левый угол. Затем найдите обратное БПФ, используя np.ifft2() функция. Результат, опять же, будет комплексным числом. Вы можете взять его абсолютное значение.

rows, cols = img.shape

crow,ccol = rows//2 , cols//2

fshift[crow-30:crow+31, ccol-30:ccol+31] = 0

f_ishift = np.fft.ifftshift(fshift)

img_back = np.fft.ifft2(f_ishift)

img_back = np.real(img_back)

plt.subplot(131),plt.imshow(img, cmap = 'серый' )

plt.title('Входное изображение'), plt.xticks([]), plt.yticks([])

plt.subplot(132),plt.imshow(img_back, cmap = 'grey')

plt.title('Изображение после HPF'), plt.xticks([]), plt.yticks([])

plt.subplot(133),plt.imshow(img_back)

plt.title('Результат в JET'), plt.xticks([]), plt.yticks([])

plt.show()

Результат выглядит следующим образом:

image

Результат показывает, что фильтрация верхних частот является операцией обнаружения границ. Это то, что мы видели в главе «Градиенты изображения». Это также показывает, что большая часть данных изображения находится в низкочастотной области спектра. Во всяком случае, мы видели, как найти DFT, IDFT и т. д. в Numpy. Теперь давайте посмотрим, как это сделать в OpenCV.

Если вы внимательно посмотрите на результат, особенно на последнее изображение в цвете JET, вы можете увидеть некоторые артефакты (один экземпляр я отметил красной стрелкой). Он показывает некоторые волнообразные структуры и называется эффектами звона . Это вызвано прямоугольным окном, которое мы использовали для маскирования. Эта маска преобразуется в синусоидальную форму, что вызывает эту проблему. Таким образом, прямоугольные окна не используются для фильтрации. Лучший вариант — гауссовские окна.

Преобразование Фурье в OpenCV

OpenCV предоставляет для этого функции cv.dft() и cv.idft() . Он возвращает тот же результат, что и предыдущий, но с двумя каналами. Первый канал будет иметь действительную часть результата, а второй канал будет иметь мнимую часть результата. Входное изображение должно быть сначала преобразовано в np.float32. Мы увидим, как это сделать.

импортировать numpy как np

импортировать cv2 как cv

из matplotlib импортировать pyplot как plt

img = cv.imread('messi5.jpg',0)

dft = cv.dft(np.float32(img),flags = cv.DFT_COMPLEX_OUTPUT)

dft_shift = np.fft.fftshift(dft)

величина_спектр = 20*np.log(cv.magnitude(dft_shift[: ,:,0],dft_shift[:,:,1]))

plt.subplot(121),plt.imshow(img, cmap = 'grey')

plt.title('Входное изображение'), plt .xticks([]), plt.yticks([])

plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'grey')

plt.title('Спектр магнитуды'), plt.xticks ([]), plt.yticks([])

plt.show()

Примечание

Вы также можете использовать cv.cartToPolar() , который возвращает и амплитуду, и фазу за один раз

Итак, теперь нам нужно выполнить обратное ДПФ. В предыдущем сеансе мы создали HPF, на этот раз мы увидим, как удалить высокочастотное содержимое в изображении, т. е. мы применим LPF к изображению. Это действительно размывает изображение. Для этого мы создаем маску сначала с высоким значением (1) на низких частотах, т.е. пропускаем НЧ-содержимое, и 0 на ВЧ-области.

rows, cols = img.shape

crow,ccol = rows/2 , cols/2

# сначала создайте маску, центральный квадрат равен 1, остальные нули

mask = np.zeros((rows,cols ,2),np.uint8)

mask[crow-30:crow+30, ccol-30:ccol+30] = 1

# применить маску и обратное ДПФ

fshift = dft_shift*mask

f_ishift = np .fft.ifftshift(fshift)

img_back = cv.idft(f_ishift)

img_back = cv.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'grey')

plt.title('Входное изображение'), plt.xticks([]), plt.yticks([])

plt.subplot(122),plt.imshow(img_back, cmap = 'grey')

plt.title('Спектр магнитуды'), plt.xticks([]), plt.yticks([])

plt. show()

См. результат:

image

Note

Как обычно, функции OpenCV cv. dft() и cv.idft() быстрее, чем аналоги Numpy. Но функции Numpy более удобны для пользователя. Дополнительные сведения о проблемах с производительностью см. в разделе ниже.

Производительность расчета ДПФ лучше для некоторого размера массива. Это быстрее всего, когда размер массива равен степени двойки. Массивы, размер которых является произведением 2, 3 и 5, также обрабатываются достаточно эффективно. Поэтому, если вы беспокоитесь о производительности своего кода, вы можете изменить размер массива до любого оптимального размера (дополняя нулями), прежде чем находить ДПФ. Для OpenCV вам нужно вручную заполнить нули. Но для Numpy вы указываете новый размер расчета БПФ, и он автоматически дополняет вас нулями.

Так как же найти этот оптимальный размер? OpenCV предоставляет для этого функцию cv.getOptimalDFTSize() . Это применимо как к cv.dft() , так и к np.fft.fft2() . Давайте проверим их производительность с помощью волшебной команды IPython timeit.

В [16]: img = cv.imread('messi5.jpg',0)

В [17]: rows,cols = img.shape

В [18]: print("{} {}" .format(rows,cols))

342 548

В [19]: nrows = cv.getOptimalDFTSize(rows)

В [20]: ncols = cv.getOptimalDFTSize(cols)

В [21]: print("{} {}".format(nrows,ncols))

360 576

См. размер (342 548 ) изменяется на (360, 576). Теперь давайте дополним его нулями (для OpenCV) и найдем их производительность вычисления ДПФ. Вы можете сделать это, создав новый большой нулевой массив и скопировав в него данные, или использовать cv.copyMakeBorder() .

nimg = np.zeros((nrows,ncols))

nimg[:rows,:cols] = img

ИЛИ:

right = ncols - cols

bottom = nrows - rows

bordertype = cv.BORDER_CONSTANT # просто чтобы избежать разрыва строки в файле PDF

nimg = cv.copyMakeBorder(img,0,bottom,0,right,bordertype, value = 0)

Теперь мы вычисляем сравнение производительности DFT функции Numpy:

В [22]: %timeit fft1 = np. fft.fft2(img)

10 циклов, лучший из 3: 40,9 мс на цикл

В [23]: %timeit fft2 = np.fft.fft2(img,[nrows,ncols])

100 циклов, лучшее из 3: 10,4 мс на цикл

Показывает ускорение в 4 раза. Теперь попробуем то же самое с функциями OpenCV.

В [24]: %timeit dft1= cv.dft(np.float32(img),flags=cv.DFT_COMPLEX_OUTPUT)

100 циклов, лучшее из 3: 13,5 мс на цикл

В [27]: %timeit dft2= cv.dft(np.float32(nimg),flags=cv.DFT_COMPLEX_OUTPUT)

100 циклов, лучшее из 3: 3,11 мс на цикл

Это также показывает 4-кратное ускорение. Вы также можете видеть, что функции OpenCV примерно в 3 раза быстрее, чем функции Numpy. Это можно проверить и для обратного БПФ, и это остается вам в качестве упражнения.

Почему лапласиан является фильтром верхних частот?

Подобный вопрос был задан на форуме. Вопрос в том, почему лапласиан является фильтром высоких частот? Почему Sobel является HPF? и т. д. И первый ответ на него был с точки зрения преобразования Фурье. Просто возьмите преобразование Фурье лапласиана для большего размера БПФ. Проанализируйте это:

import cv2 as cv

import numpy as np

from matplotlib import pyplot as plt

# простой фильтр усреднения без параметра масштабирования

mean_filter = np.ones((3,3))

# создание фильтра Гаусса

x = cv.getGaussianKernel(5,10)

gaussian = x*x.T

# различные фильтры обнаружения границ8 scharr в направлении x

scharr = np.array([[-3, 0, 3],

[-10,0,10],

[-3, 0, 3]])

# sobel в направлении x

sobel_x= np.array([[-1, 0, 1],

[-2, 0, 2],

[-1, 0, 1]])

# sobel в y направление

sobel_y= np.array([[-1,-2,-1],

[0, 0, 0],

[1, 2, 1]])

# лапласиан

лапласиан=np .array([[0, 1, 0],

[1,-4, 1],

[0, 1, 0]])

фильтры = [mean_filter, гауссов, лапласиан, sobel_x, sobel_y, scharr ]

filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', \

'sobel_y', 'scharr_x']

fft_filters = [np. fft.fft2(x) для x в фильтрах ]

fft_shift = [np.fft.fftshift(y) для y в fft_filters]

mag_spectrum = [np.log(np.abs(z)+1) для z в fft_shift]

для i в диапазоне (6):

plt.subplot(2,3,i+1),plt. imshow(mag_spectrum[i],cmap = 'grey')

plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])

plt.show()

См. результат:

image

Из изображения видно, какую частотную область блокирует каждое ядро ​​и какую область оно проходит. Из этой информации мы можем сказать, почему каждое ядро ​​является HPF или LPF

9.0049 Дополнительные ресурсы

1. Интуитивное объяснение теории Фурье Стивена Легара
2. Преобразование Фурье в HIPR
3. Что означает частотная область в случае изображений?

Упражнения

Введение в преобразование Фурье

Введение в преобразование Фурье

ОСНОВНЫЕ ФУНКЦИИ:

Преобразование Фурье (в данном случае двумерное преобразование Фурье) представляет собой разложение в ряд функции изображения ( по двумерному пространству домен ) в терминах базисных функций «косинусоидальных» изображений (ортонормированных).

Определения преобразования (в коэффициенты разложения) и обратное преобразование приведено ниже:

F(u,v) = SUM{f(x,y)*exp(-j*2*pi*(u*x+v*y)/N)}
    а также
f(x,y) = SUM{F(u,v)*exp(+j*2*pi*(u*x+v*y)/N)}
    где u = 0,1,2,...,N-1 и v = 0,1,2,...,N-1
х = 0,1,2,...,N-1 и у = 0,1,2,...,N-1
j = КОРЕНЬ(-1)
а SUM означает двойное суммирование по правильному
диапазоны x, y или u, v
 

Сначала мы исследуем «базисные» функции для Фурье Преобразование (FT). FT пытается представить все изображения как сумму косинусоподобных изображений. Следовательно, изображения, являющиеся чистыми косинусами, имеют особенно простые ФП.

Это показывает 2 изображения с их преобразованиями Фурье непосредственно под ними. Образы представляют собой чистый горизонтальный косинус из 8 циклов и чистый вертикальный косинус 32 циклов. Обратите внимание, что FT для каждого только что один компонент, представленный 2 яркими пятнами симметрично расположен примерно в центре изображения FT. Центр изображения находится начало системы координат частоты. Ось U проходит влево вправо через центр и представляет собой горизонтальную составляющую частота. Ось v проходит снизу вверх через центр и представляет собой вертикальную составляющую частоты. В обоих случаях есть точка в центре, представляющая частотный член (0,0) или средняя стоимость изображения. Изображения обычно имеют большой средний значение (например, 128) и много информации о низких частотах, поэтому FT изображения обычно имеют яркое пятно компонентов около центра. Обратите внимание, что высокие частоты в вертикальном направлении вызовут яркие точки от центра в вертикальном направлении. И что высокие частоты в горизонтальном направлении вызовут яркие точки от центра в горизонтальном направлении.

Вот 2 изображения более общих компонентов Фурье. Это изображения двумерных косинусов с горизонтальными и вертикальными компонентами. Тот самый слева имеет 4 цикла по горизонтали и 16 циклов по вертикали. один справа имеет 32 цикла по горизонтали и 2 цикла по вертикали. (Примечание: вы видите серую полосу, когда функция проходит серый = 128 что происходит дважды за цикл.) Вы можете начать замечать, что существует много симметрии. Для всех НАСТОЯЩИХ (в отличие от ВООБРАЖАЕМЫХ или СЛОЖНЫХ) изображений, FT симметричен о происхождении, поэтому 1-й и 3-й квадранты одинаковы, а 2-й и 4-й квадранты одинаковы. Если изображение симметрично относительно оси x (поскольку косинусные изображения are) результаты 4-кратной симметрии.

ВЕЛИЧИНА ПРОТИВ. ФАЗА:

Напомним, что определение преобразования Фурье:

F(u,v) = SUM{f(x,y)*exp(-j*2*pi*(u*x+v*y)/N)}
    а также
f(x,y) = SUM{F(u,v)*exp(+j*2*pi*(u*x+v*y)/N)}
    где u = 0,1,2,...,N-1 и v = 0,1,2,...,N-1
х = 0,1,2,...,N-1 и у = 0,1,2,...,N-1
а SUM означает двойное суммирование по правильному
диапазоны x, y или u, v
 

Обратите внимание, что f(x,y) является изображением и РЕАЛЬНО, но F(u,v) (сокращенно F) является ФТ и является, в общем, СЛОЖНЫМ. Как правило, F представляет собой его ВЕЛИЧИНА и ФАЗА, а не его РЕАЛЬНАЯ и ВООБРАЖАЕМАЯ части, где: 92 ) ФАЗА(F) = АТАН(ВООБРАЖАЕМАЯ(F)/РЕАЛЬНАЯ(F)) Вкратце, ВЕЛИЧИНА говорит, «сколько» определенной частотной составляющей присутствует, и ФАЗА сообщает, «где» находится частотная составляющая. изображение. Чтобы проиллюстрировать это, рассмотрим следующее.

Обратите внимание, что изображения FT, на которые мы смотрим, — это просто изображения MAGNITUDE. Отображаемые изображения представляют собой горизонтальные косинусы 8 периодов, различающихся только тем, что одно смещено в сторону от другого на 1/2 цикла (или по фазе PI). Обратите внимание, что оба имеют одинаковый FT ВЕЛИЧИНА изображения. Конечно, изображения PHASE будут другими. Обычно мы не показываем изображения PHASE, потому что большинство людей, которые видят вскоре после этого они поддаются галлюциногенам или попадают в Тибетский монастырь. Тем не менее разумно помнить, что когда человек смотрит на обычное изображение FT и думает о «высокой» частоте мощность и мощность "низкой" частоты, это только часть ВЕЛИЧИНЫ кража.

Кстати, вы, возможно, слышали о БПФ и задавались вопросом, отличается ли оно от из ФТ. БПФ расшифровывается как «быстрое» преобразование Фурье и представляет собой просто быстрый алгоритм вычисления преобразования Фурье.

ВРАЩЕНИЕ И КРАЕВЫЕ ЭФФЕКТЫ:

В общем, поворот изображения приводит к эквивалентному повороту его ФТ. Чтобы убедиться, что это так, возьмем FT простого косинуса а также FT повернутой версии той же функции. результаты можно увидеть:

Поначалу результаты кажутся довольно неожиданными. Горизонтальный косинус имеет свой нормальный, очень простой FT. Но повернутый косинус кажется иметь ФТ гораздо сложнее, с сильной диагональю компоненты, а также прочный «плюс» в форме горизонтальных и вертикальные компоненты. Вопрос в том, откуда взялись эти горизонтальные а вертикальные компоненты берутся? Ответ заключается в том, что FT всегда обрабатывает изображение, как если бы оно было частью периодически воспроизводимого массив одинаковых изображений, простирающийся по горизонтали и вертикали до бесконечность. И есть сильные краевые эффекты между соседями такой периодический массив, как можно увидеть:

Таким образом, то, что мы видим как FT на «наклонном» изображении (нижний правый угол позапрошлое изображение) на самом деле комбинация фактического FT функции косинуса и это вызвано краевыми эффектами взгляда на конечную часть изображение. Эти краевые эффекты могут быть значительно уменьшены путем "окно" изображения с функцией, которая медленно сужается до средний серый по краю. Результат можно увидеть:

Изображение в окне показано в левом верхнем углу.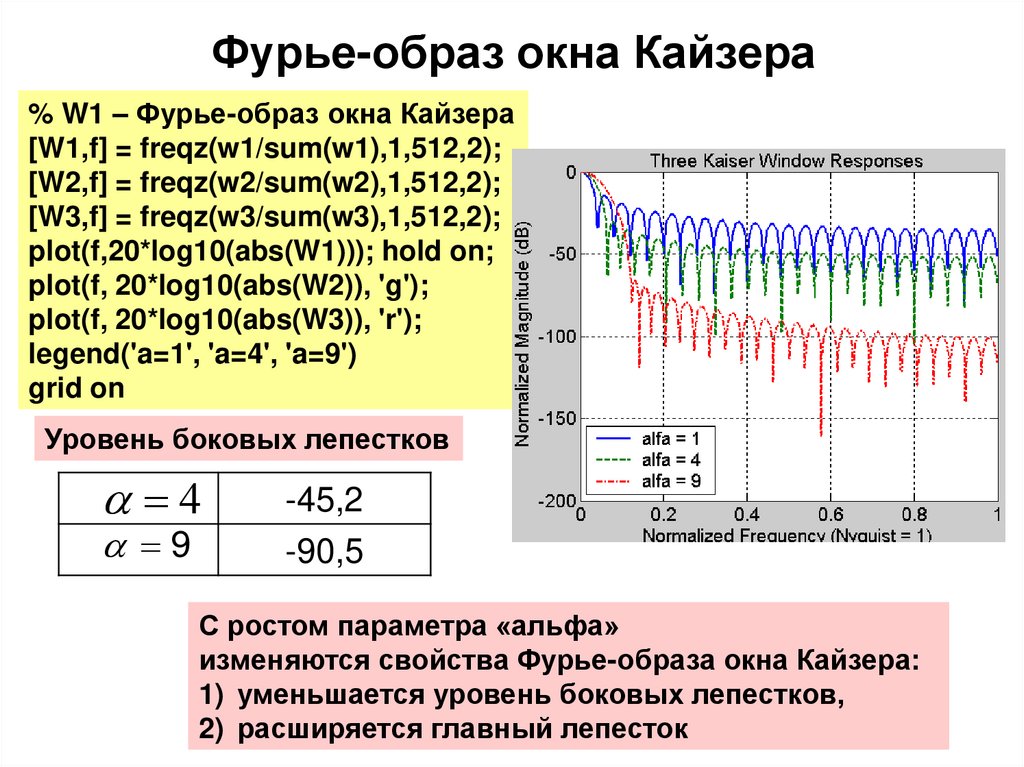 Его FT показан на нижний левый. Неоконный FT показан в правом верхнем углу. а фактическая истинная FT косинуса показана в правом нижнем углу. Все эти изображения масштабируются по-разному, и сравнение только качественно, но видно, что оконное изображение FT гораздо ближе к истинному FT и устраняет многие краевые эффекты.

НЕКОТОРЫЕ ИЗОБРАЖЕНИЯ ТРАНСФОРМИРУЮТ:

Теперь, после приведенного выше введения, лучший способ познакомиться с Преобразование Фурье — это увидеть множество изображений и множество их FT. Во-первых, интересная пара снимков, один резкий и четкий, а другой размыто и шумно.

Есть 2 изображения, тупой и деградировавший тупой, с FT под каждым. Обратите внимание, что оба страдают от краевых эффектов, о чем свидетельствует сильное вертикальная линия через центр. Основной эффект, который следует заметить, заключается в том, что в преобразовании деградировавшего тупого высокие частоты в горизонтальное направление значительно ослаблено. Это до к тому, что искаженное изображение формировалось сглаживанием только в горизонтальное направление. Также, если внимательно посмотреть видно, что у деградированного гуфи фон немного больше уровень шума на высоких частотах. Это трудно увидеть и, возможно, даже не имеет смысла, потому что изображения масштабируются по-разному, но если действительно там, это из-за случайного шума, добавленного к деградировавшему тупому. Заметьте также, что трудно найти смысл в низком уровне. информация о частоте. Это характерно для реальных изображений.

На следующих изображениях показаны эффекты краев на изображениях:

Обратите внимание на сильную периодическую составляющую, особенно в вертикальном направлении для изображения кирпичей. Горизонтальные компоненты кажутся ближе друг к другу в FT. На изображении блоков обратите внимание на яркая линия, идущая к высоким частотам перпендикулярно сильной края на изображении. Каждый раз, когда изображение имеет высокую контрастность, резкость края значения серого должны изменяться очень быстро. Требуется много высоких частотная мощность, чтобы следовать за таким краем, поэтому обычно есть такая линия в своем амплитудном спектре.

Теперь давайте посмотрим на кучу различных форм и их FT.

Обратите внимание, что буквы имеют совершенно разные FT, особенно в конце. более низкие частоты. FT также имеет тенденцию иметь яркие линии, которые перпендикулярно линиям исходного письма. Если в письме есть круговые сегменты, то и FT тоже.

Теперь давайте посмотрим на некоторые коллекции подобных объектов:

Обратите внимание на концентрическое кольцо структура в FT изображения белых гранул. Это индивидуально для каждого гранула. То есть, если бы мы взяли ФТ всего одной пули, мы бы все равно получить этот образец. Помните, мы смотрим только на величину спектр. Дело в том, что существует множество пеллет и информации о точно, где каждый из них содержится в основном в фазе. Кофе бобы имеют меньшую симметрию и более окрашены по-разному, поэтому они не показывают одинаковую кольцевую структуру. Ты может быть в состоянии обнаружить слабый "ореол" в кофе FT. Что Вы думаете это откуда?

Вот наши первые по-настоящему общие изображения. Заметьте, очень мало структура. Вы можете увидеть наклонную линию сверху слева вниз справа на образ девушки FT. Вероятно, это из-за края между ее шляпой и ее волосы. В обоих случаях также присутствуют небольшие краевые эффекты. картинки. Изображение мандрила имеет более высокую частоту. власть, вероятно, из-за волос.

На изображении морского веера много маленьких дырочек примерно одинакового размера. размера и несколько случайно ориентированы. Размер отверстий примерно 2 пикселя в ширину, что соответствует частотным компонентам около 1/2 выход на максимум. Сильные горизонтальные компоненты в озере изображение, вероятно, связано с краями ствола дерева.

Итак, вот ваша первая викторина. Рассмотрим изображение, которое полностью черное за исключением полосы шириной в один пиксель слева вверху вниз Правильно. Какой у него ФТ? Кроме того, рассмотрите изображение, которое полностью случайный. То есть каждый пиксель представляет собой некоторую случайную величину, независимую от всех другие пиксели. Какой у него ФТ?

Ты веришь в это? Если нет, можете проверить сами. Кстати, обратите внимание на единственную яркую точку в середине шумового FT-изображения. Почему это там? Почему шум FT выглядит темно-серым?

НЕКОТОРЫЕ ФИЛЬТРЫ:

Теперь мы начинаем иллюстрировать использование некоторых фильтров на изображении девушки. Первый фильтр нижних частот. Верхний левый - оригинал изображение. Нижний левый производится:

fft2d 128 девушкаффт
mag2d 128 девушкамаг
 

Затем нижний правый создается:

fftfilt 128 низкий идеал 50 lpgirlfft
mag2d 128 lpgirlmag
 

Наконец, верхний правый создается:

ifft2d 128 lpgirl
 

Чтобы увидеть результаты:

Левую часть изображения мы уже видели. В правом нижнем углу обратите внимание, как резко обрезаются высокие частоты у "идеала" фильтр нижних частот. Заметьте также, что не так уж много энергии выбрасывается. далеко за пределы круга, который отрезан. В правом верхнем углу реконструированное изображение явно более размыто из-за потери высокого частоты. Общий контраст по-прежнему довольно хорош из-за этого факта. что не так много сил было выброшено. Заметьте также, что есть явные «звенящие» артефакты на реконструированном изображении. Это из-за очень резкой среза "идеального" фильтра. Баттерворт или Экспоненциальный фильтр с достаточно низким порядком их не вызовет.

Теперь мы сделаем фильтр верхних частот. Следующее изображение создается в аналогично предыдущему, за исключением:

fftfilt 128 высокое масло 50 hpgirlfft
 

Другими словами, используется фильтр Баттерворта 1-го порядка.

Обратите внимание, что в правом нижнем углу этот фильтр не обрезает резко. в точке 50%, как это сделал фильтр нижних частот. Тем не менее, центр яркий пятно, на которое приходится большая часть силы изображения, явно прошло. Изображение в правом верхнем углу, которое выглядит полностью черным, в на самом деле не совсем черный. Если вы используете возможности цветовой карты "dym", чтобы растянуть значения серого от 0 до 20 по всему диапазон, вы можете видеть, что этот фильтр высоких частот сохранил информация об изображении с очень быстрыми изменениями уровня серого. Такой процесс часто требуется в детекторе краев. Однако это не является улучшением изображения. Есть 2 проблемы. Во-первых, слишком темно. Это можно исправить изменением масштаба или повторным контрастированием. растягивание изображения после фильтрации. Это обычно делается и легкий. Во-вторых, и это сложнее, это тот факт, что слишком много тональная информация о частоте исчезла.

Для повышения резкости изображения требуется фильтр повышения резкости или высокая частота акцентный фильтр. Этот тип фильтра сохраняет некоторые из низких частот. информацию о частоте, но относительно повышает более высокие частоты. Для этого мы создадим собственный фильтр, который будет кусочно-линейный. Фильтр будет симметричным по окружности и будет имеют следующие коэффициенты:

0 0,5
96 4.0
127 4,0
 

Другими словами, коэффициенты Фурье частоты-расстояния 0 от происхождение будет умножено на 0,5. Когда вы уходите от источника или нулевая частота, выход на частоту-расстояние 96, множитель будет вставлен между 0,5 и 4,0. С этого момента наружу множитель будет 4.0. Таким образом, более высокие частотные коэффициенты умножаются на значения больше 1,0 и более низкие частотные коэффициенты умножается на значения меньше 1,0. Общий чистый эффект на сила образа в том, что он неизменен. Указанные выше значения находятся в файле называется "filter_coeffs". Чтобы применить фильтр, выполните следующие действия. выполненный:

filttabler filter_file
fftfilt 128 файловых фильтровфайл mfgirlfft
 

Остальная часть изображения строится, как и раньше. Чтобы увидеть результат:

Обратите внимание на относительную яркость высоких частот в нижних частотах. правильное изображение. Какое верхнее изображение четче? Какое верхнее изображение выглядит лучше? Портреты — одно из немногих противоречий общему Принципиально что острее тем лучше.

Фильтрация также может использоваться для уменьшения шума. Это особенно эффективен, когда шум ограничивается несколькими частотами:

Изображение в левом верхнем углу выглядит глупо с наложенным косинусом. добавляется к нему, представляя шум. В левом нижнем углу обратите внимание на сильные косинусные «точки» слева и справа от начала координат. В правом нижнем углу эти "точки" убраны ( я собственно и сделал это с возможностью «трассировки» в dym ). Полученная величина Затем файл используется с командой «filter» для фильтрации Фурье. коэффициенты. Затем файл коэффициентов подвергается обратному преобразованию Фурье, чтобы получить верхнее правое изображение. Косинусный "шум" исчез.

Жизнь не всегда так проста, как показано в следующем примере:

В этом случае сетка была помещена поверх гуфи. Нижний левый показывает полученный FT. Обратите внимание, что сетка довольно четкая, поэтому имеет много высоких частот, поэтому его влияние на частотную область очень раскидан. Дым снова использовался для «закрашивания» сетки. частоты как можно больше. Правая половина нижнего правого изображение не закрашивается, потому что оно является симметричным отражением левая половина и не используется фильтром.

 ВАШЕ ЗАДАНИЕ: (ЕСЛИ ВЫ РЕШИТЕ ​​ПРИНЯТЬ ЕГО)
(1) Выберите изображение.
(2) БПФ и найдите спектр величин.
см. человека для fft2d и mag2d
(3) Сделайте что-нибудь со спектром или фф.
пример: фильтр
fffilt
что-то типа:
см
двойной
умножить на чередующиеся +1,-1
взять только фазу
принимать только величину
(4) Восстановите изображение с помощью обратного БПФ.
см. человека для ifft2d
(5) Объедините результаты, как показано на изображениях выше, используя «группу».
см человека для группы
(6) Объясните свои результаты (1-2 страницы).
 Больше внимания будет уделено воображению того, что вы делаете, чем
 правильности вашего объяснения.