Разное

Сопряжение прямой и окружности дугой заданного радиуса: Сопряжение прямой с окружностью

Содержание

Федеральное агентство по образованию — Васин С.А. Основы черчения и начертательной геометрии

приобрести
Васин С.А. Основы черчения и начертательной геометрии
скачать (7486.5 kb.)
Доступные файлы (1):

1.1. Введение. Предмет и метод начертательной геометрии 5

1.2. Центральное проецирование 5

1.3. Параллельное проецирование 6

2.1. Инвариантные свойства параллельного проецирования 7

2.2. Прямоугольное (ортогональное) проецирование 8

3.1. Аксонометрические проекции. Общие положения 11

3.2. Аксонометрическое проецирование 11

3.3. Коэффициенты искажения 12

3.4. Виды аксонометрических проекций 12

4.1. Стандартные аксонометрические проекции 14

4.2. Прямоугольная изометрическая проекция 14

4.3. Прямоугольная диметрическая проекция 15

4.4. Косоугольная фронтальная диметрическая проекция 15

5.1. Комплексный чертеж точки 17

5. 2. Проекции прямых общего положения 18

6.1. Проекции прямых уровня 20

6.2. Проекции проецирующих прямых 22

6.3. Определение натуральной величины отрезка
прямой общего положения 23

6.4. Деление отрезка прямой в данном отношении 24

7.1. Параллельные прямые 25

7.2. Пересекающиеся прямые 25

7.3. Скрещивающиеся прямые 25

8.1. Проекции плоскостей общего положения 27

8.1.1. Проекции плоскостей уровня 27

8.1.2. Проекции проецирующих плоскостей 29

9.1. Взаимное расположение двух плоскостей 31

9.2. Пересечение плоскостей общего положения 31

10.1. Взаимное расположение прямой и плоскости 34

10.2. Пересечение прямой линии с плоскостью 35

10.3. Условие видимости на чертеже 37

ПЕРПЕНДИКУЛЯРНОСТЬ ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ 40

11.1. Главные линии плоскости 40

11.2. Прямая, перпендикулярная к плоскости. Теорема о проецировании прямого угла 42

12.1. Перпендикулярные плоскости 44

12. 2. Перпендикулярные прямые 46

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ 47

ПОСТРОЕНИЕ ТЕНЕЙ 48

13.1. Основы теории теней 48

13.2. Тени от точки, линии и плоской фигуры 49

13.2.1. Падающая тень от точки 49

13.2.2. Падающая тень от прямой линии 51

13.2.3. Тень от плоской фигуры 53

13.2.4. Тень от диска (окружности) 55

14.1. 57

14.1. Тень, падающая от одной фигуры на другую 57

14.1.1. Метод обратных лучей 57

14.1. 59

15.1. Тени геометрических тел 60

15.1.1 Тени многогранников 60

15.1.2. Тени цилиндра 62

15.1.3. Тени конуса 63

16.1. 65

Тени пересекающихся многогранников (от здания) 65

17.1. 68

Тени на фасадах зданий 68

17.1.1. Построение теней в нишах 68

17.1.2. 70

Тени от выступов 70

МЕТОДЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА 72

18.1. Общие сведения 72

18. 2. Замена плоскостей проекций 72

19.1. Вращение вокруг оси, перпендикулярной плоскости проекций 75

19.2. Плоско-параллельное движение 75

ЛИНИИ И ПОВЕРХНОСТИ 77

20.1. ЛИНИЯ 77

20.1.1. Винтовая линия 78

20.2. ПОВЕРХНОСТИ 79

20.2.1. Поверхности линейчатые 80

20.2.2. Поверхности линейчатые развертывающиеся 81

20.2..3. Поверхности линейчатые неразвертывающиеся 82

20.2.4. Поверхности нелинейчатые 85

20.2.5. Поверхности параллельного переноса, вращения и винтовые 86

21.1. Поверхности вращения 88

21.2. Поверхности винтовые 91

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ 93

22.1. Пересечение плоскости с поверхностью многогранника 93

22.2. Пересечение плоскостью поверхности вращения 94

23.3. Конические сечения 96

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ 100

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ 101

24.1. Общие положения 101

24. 2. Пересечение прямой с поверхностью многогранника 101

24.3. Пересечение прямой с поверхностью вращения 102

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ 104

25.1. Общие положения 104

25.2. Пересечение многогранников 105

25.3. Способ секущих плоскостей 106

Лекция № 26. Пересечение поверхностей 110

26.1.. Способ концентрических сфер 110

26.2. Способ эксцентрических сфер 111

26.3. Особые случаи пересечения. Теорема Монжа 114

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ 117

27.1. Общие положения 117

27.2. Аналитический способ 118

27.3. Способ триангуляции (треугольников) 118

27.4. Способ нормального сечения 119

28.1. Способ раскатки 121

28.2. Приближенные построения разверток 122

СПИСОК РЕКОМЕНДОВАНОЙ
ЛИТЕРАТУРЫ К РАЗДЕЛАМ 1 9 126

Введение в черчение 127

ОСНОВНЫЕ РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ ЧЕРТЕЖА 128

29.1. Инструмент и материал 128

29.2. Форматы 129

29. 3. Масштабы 129

30.1. Линии 130

30.2. Шрифты чертежные 131

ОСНОВНАЯ НАДПИСЬ 137

Порядок выполнения основной надписи 137

30.3.1. Порядок заполнения основной надписи 137

СОПРЯЖЕНИЯ 141

31.1. Общие положения 141

31.2. Построение касательных и касание окружностей 142

31.2.1. Построение касательной к окружности 142

31.2.2. Касание окружностей 143

31.2.3. Построение касательных к двум окружностям 144

Рис. 181 145

СОПРЯЖЕНИЯ С ПОМОЩЬЮ ДУГИ ОКРУЖНОСТИ 146

31.2.4. Сопряжение двух прямых дугой окружности 146

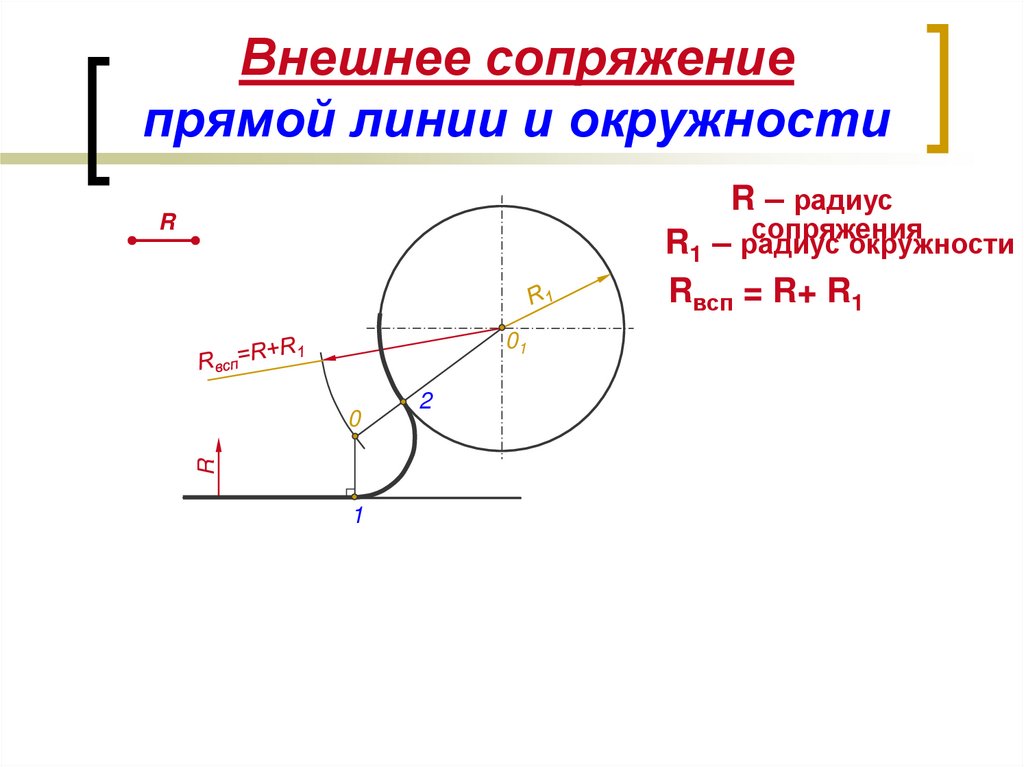
31.2.5. Сопряжение дуги и прямой дугой окружности заданного радиуса 147

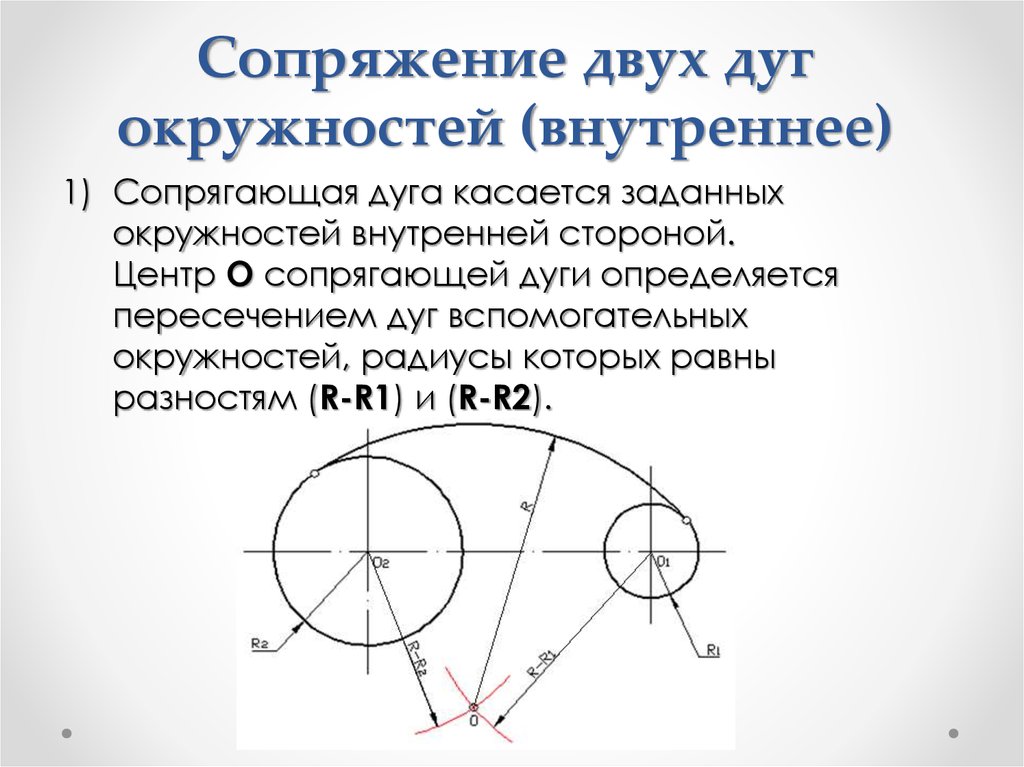
31.2.6. Сопряжение двух дуг дугой окружности заданного радиуса 147

32.1.Вычерчивание контуров деталей 149

32.2. Архитектурные обломы 151

ПЛОСКИЕ КРИВЫЕ 153

33.1 циркульные кривые 153

33.1.1 завитки 153

33.2. Коробовые кривые 154

33. 3. Лекальные кривые 157

33.3.1. Порядок вычерчивания лекальных кривых 157

33.3.2. Способы построения некоторых лекальных кривых 158

НАНЕСЕНИЕ РАЗМЕРОВ 170

34.1. Правила и рекомендации при простановке размеров 170

“Паук совершает операции, напоминающие операции ткача, и пчела постройкой своих восковых ячеек посрамляет некоторых людей-архитекторов. Но и самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что прежде чем строить ячейку из воска, он уже состроил ее в своей голове” (К.Маркс, “Капитал”, т.1, с.189).

Задуманная инженером конструкция выявляется посредством чертежей. Чертеж – язык техники. Начертательная геометрия – грамматика этого интернационального языка.

2. Построение с помощью проекций обратимого чертежа. (Обратимый чертеж позволяет воспроизвести оригинал, то есть определить форму и размеры фигуры, изображенной на чертеже).

3. Способы решения на чертеже позиционных и метрических задач. Позиционные задачи – на определение взаимного расположения фигур. Метрические задачи – на определение метрических характеристик геометрических фигур (расстояния, углы).

МЕТОД начертательной геометрии – проецирование пространственных фигур на плоскость.

Редакция девизі: БІЗ ҰСТАЗДАР ҮШІН ҚЫЗМЕТ ЕТЕМІЗ ! — E-mail: [email protected] — Тел: 8 777 087 6843

Жаңа сабақтар

Редакция

ГРИВКОВА НАТАЛЬЯ АЛЕКСАНДРОВНА
ЖЫЛКАЙДАРОВА ЖАНАР ОРАЛТАЕВНА
НАХОВА УЛДАНА МУРАТБЕКҚЫЗЫ
ДЕМЕУБАЕВА МАЛИКА ШЫМЫРАЛИЕВНА
КОНУСОВА АЛТЫНАЙ АБДЫДЖЕЛИЛОВНА
УТЕПОВА ЖУПАР АМИРХАНОВНА
ШКУТОВА ВИКТОРИЯ МИХАЙЛОВНА
ШЕВЧЕНКО ЕЛЕНА ВЛАДИМИРОВНА
БИСЕНАЛИН МУРАТБАЙ МУСАЕВИЧ
ЗЕЛЕНЮК ЕЛЕНА АЛЕКСАНДРОВНА
СЕРАЛИЕВА НУРЖАМАЛ УМИРЗАКОВНА
БЕГАЛИН МИРАС БУРТЕБАЕВИЧ

2023-03Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

БАТЫРГОЖИНА ГУЛЬБАРШИН ЖАНИБЕКОВНА
САДЫБЕКОВА УЛЖАН ТУРАРБЕКОВНА
РЫСПАЕВА ЭЛЬВИРА АБЫЛХАЙРОВНА
ЖАМАНГАРИНА МАЙРА САЛИМБЕКОВНА
МАРАТОВА ЖУЛДЫЗ МАРАТҚЫЗЫ
РАХИМОВА КАМИЛЯ НҰРЛЫБЕКҚЫЗЫ
ДАРИБАЕВА НУРГУЛ РЫСБЕКОВНА
ХАЖАТ ЛИЗА
КАЖКЕНОВА ЖАННА КЕНЖЕГУЛОВНА

orleutv-2023-02Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

СЕРАЛИЕВА АЙЖАН БАЗАРАЛИЕВНА
ИСА ГУЛМИРА БАЗАРХАНҚЫЗЫ
САДЫБЕКОВА УЛЖАН ТУРАРБЕКОВНА
АБУХАНОВА НАГИМА ХАСАНХАНОВНА

2023-02-01Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

УСМАНОВА МИНАВАР ҚАЛБЕКОВНА
БЕГЕЕВА АНАР САГИНБАЕВНА
ИСА ГУЛМИРА БАЗАРХАНҚЫЗЫ
САТБЕРГЕНОВА ШЫНАР НҰРМАҒАМБЕТҚЫЗЫ

2023-02Скачать

Понравилось это:

Нравится Загрузка. ..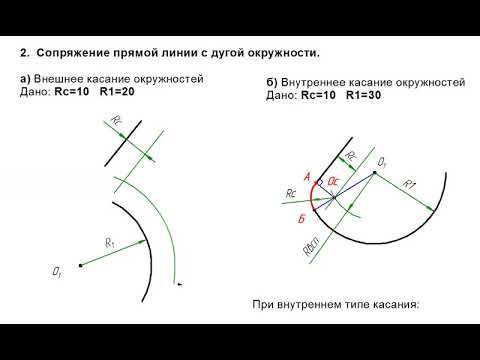

Оставьте комментарий Жаңа сабақтар

Редакция

МӘЛІК ЕЛДАНА ЕРТАЙҚЫЗЫ
ШАГРАЕВА ТАЛШЫН УРЫНБАСАРОВНА
УБИШЕВА ЭЛЕОНОРА БОЛАТОВНА
КАЛИЕВА НУРГУЛЬ БАЛГАБЕКОВНА
ШӘМШІДІН АРАЙЛЫМ САРБАЙҚЫЗЫ
АБУХАНОВА НАГИМА ХАСАНХАНОВНА
СЕРАЛИЕВА АЙЖАН БАЗАРАЛИЕВНА

orleutv-2023-01Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

ШАГРАЕВА ТАЛШЫН УРНБАСАРОВНА
ТУЯКПАЕВА БАКЫТГУЛ САТКАЛИЕВНА
УТЕУГАЛИЕВА ГУЛНАЗ МАРАТОВНА
ЖҮСІПБЕКОВА БӨБЕК ЕСЕНЖОЛҚЫЗЫ
БЕГЕЕВА АНАР САГИНБАЕВНА

2023-01Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

САРСЕНОВА ЗАРИПА САНСЫЗБАЕВНА
МАСАТОВА УЛБОЛСЫН ТАБЫЛДИЕВНА
КАЗИХАНОВА ЖАНЫЛСЫН ГАЙНЕДЕНОВНА
АЙСАГАЛИЕВА АЙЫМГУЛ НУРСУЛТАНОВНА
ИСМАГУЛОВА ЖУМАГУЛ РАХМАНОВНА
САРКУЛОВА АЛТЫН СИСЕНОВНА
КАЗИЕВА КУЛЯШ БЕРДЕШЕВНА
ЖАХИНА ДИНАРА ТАУФИХОВНА
МОЛДАШЕВА АЙГУЛЬ НҰХЕСҚЫЗЫ
ДАУЛЕТОВА АКМАРАЛ ДЕМЕУОВНА
ДАУЛЕТОВА АЙГУЛЬ КЕНЕСОВНА
БАҚЫТОВА ЭЛЬЗА ЕРБОЛҚЫЗЫ
ХАЛИДУЛЛИНА АЛЬБИНА ФАЙЗУЛЛАЕВНА
БИЖАНОВА ГУЛДЕН АЛЬБИЕВНА

СУФАЛДИЯРОВА АКТОЛКЫН ДАРСКАЛИЕВНА
КАБАСОВА АЙНУР ЧАПАЕВНА

adis-12Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

БЕРДИЕВА КАЛАМКАС ИБРАГИМОВНА
ШАГРАЕВА ТАЛШЫН УРНБАСАРОВНА
РЫСБАЕВА ДИАНА НҰРЛАНҚЫЗЫ
ХУТТУБАЕВА БИБИГУЛЬ ЖАНАБАЕВНА
ТУЯКПАЕВА БАКЫТГУЛ САТКАЛИЕВНА

adis-11Скачать

Понравилось это:

Нравится Загрузка. ..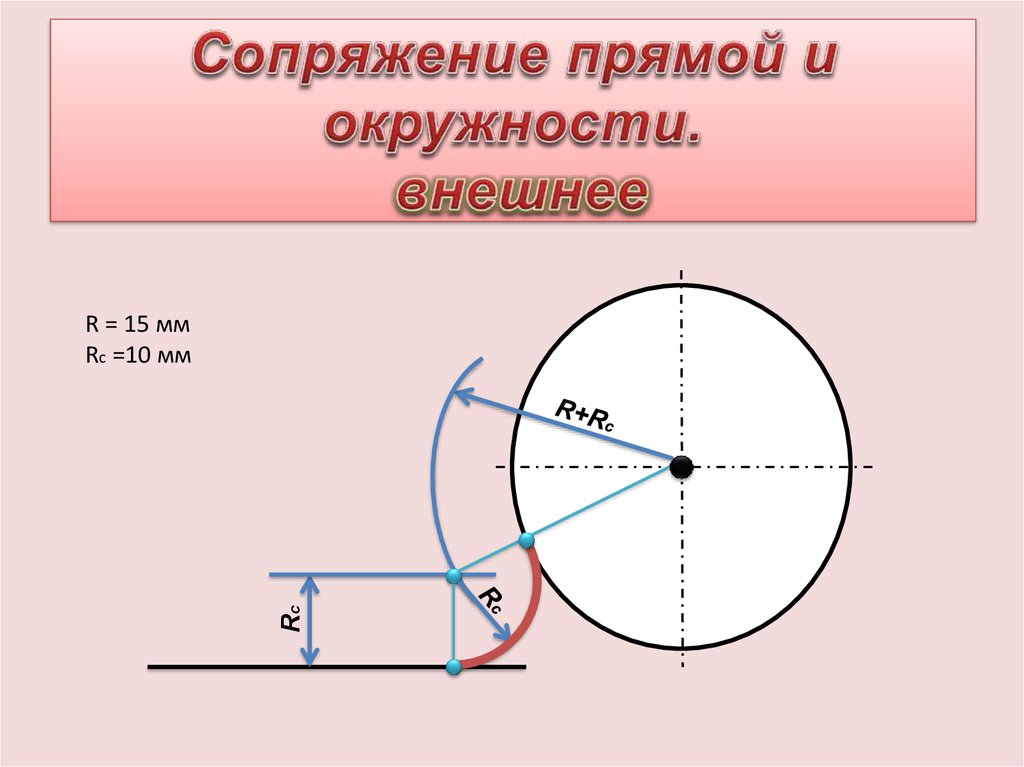

Оставьте комментарий Жаңа сабақтар

Редакция

Құрметті ұстаздар мен оқушылар !!!

2022-2023 оқу жылына арналған «ОҚУШЫЛАР ШЫҒАРМАШЫЛЫҒЫ» республикалық шығармашылық байқауына қатысуға шақырамыз!
Байқау 04.01.2023-28.02.2023 жылдар аралығында өтеді.

Қатысушылар: мектепке дейінгі, жалпы орта және қосымша білім беру мекемелерінің ұстаздары мен білім алушылары қатыса алады.
Жеке, сыныппен және топ болып қатыса алады.
Өткізілген іс-шаралар, балалар жұмыстары, суреттер, қолөнер бұйымдары, эссе, өлеңдер

Байқау тақырыбы:
«Қыс келбеті» сурет салу
«Менің қызықты каникулым» эссе жазу
Қол өнер «Қыс мезгілі» жапсырмалау,қолөнер
«Қыс қызығы» сурет салу
«Көңілді қыс» сурет салу
Қағаздан ақ ұлпа қар жасау. Қолөнер
«Менің өнерім» Қолөнер
«Қыс ғажайыптары» сурет салу

Байқауға қатыстырған жетекшіге сертификат, оқушыға диплом беріледі.
Шығармашылық жұмыстар, суреттер республикалық
45 minut. kz газетінде жарияланады. 45 minut.kz газеті ПДФ нұсқада беріледі.

Барлық жұмыстар ватцап желісі және e-mail: zaytunae @mail.ru арқылы қабылданады.

Байланыс телефоны, ватцап: +77754956519 87757524063(KASPI GOLD)
e-mail: zaytunae @mail.ru
«Білім жолы – Нұрлы жол» журналының жауапты тілшісі: Есмагамбетова З.Т.

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

«Назарбаев Зияткерлік мектептері» дербес білім беру ұйымы 2023-2024 оқу жылында Назарбаев Зияткерлік мектептерінің 7-сыныптарында білім алу үшін «Өркен» білім грантын тағайындау конкурсын өткізуде. Байқауға жалпы білім беретін мектептердің 6-сынып оқушылары қатыса алады. 

Алматы қаласындағы химия-биология бағытындағы Назарбаев Зияткерлік мектебіне үміткерлер

10 қаңтарға дейін келесі құжаттарды қабылдау комиссиясына өткізулері тиіс:
— Конкурсқа қатысу үшін өтініш;
— Сауалнама;
— Үміткердің туу туралы куәлігінің көшірмесі, үміткердің ЖСН-і, бар болған жағдайда жеке бас құжатының көшірмесі, заңды өкілдің ЖСН-і көрсетілген жеке куәлігінің көшірмесі;

— Үміткердің 6-сыныптың I жарты жылдығындағы үлгерімі мен тәртібі туралы табелінің көшірмесі. Талап етілген құжаттар оқитын мектеп басшысының қолымен расталып, тиісті білім беру ұйымының мөрімен бекітілуі керек.
— Үміткердің графикалық файл түріндегі 1 МБ (мегабайт) кем емес көлемі 3х4 см. цифрлі фотосуреті немесе үміткердің фототүсірілімі құжат тапсыру кезінде қабылдау комиссиясында жасалынады.

Көрсетілген барлық құжаттар пластикалық тезтікпеге жинақталып, қабылдау комиссиясына ұсынылады.

Құжат қабылдау комиссиясы Алматы  қаласы Қалқаман-2 ш/ауданы Ә.Елібаев к-сі, 2  мекен-жайы бойынша дүйсенбі-жұма аралығында сағат 9.00-ден 18.00-ге дейін, ал сенбі күні 9.00-ден 13.00-ге дейін жұмыс жасайды. Үзіліс уақыты: 12.00-13.00.

7 қаңтар 2023 жыл — мерекелік күн.

Айта кету керек, келушілер ағымын реттеу үшін арнайы онлайн брондау қызметі іске қосылған.

Қабылдау комиссиясына құжаттарын қаңтардың 10-на дейін толық өткізген үміткерлерге кешенді тестілеуге қатысу рұқсатнамасы беріледі. Рұқсатнаманы кешенді тестілеуге келгенде көрсетеді.  Кешенді тестілеу 2023 жылдың 2 және 3 наурызда өтеді.

Тестілеу нәтижелері кешенді тестілеудің екінші күнінен 40 календарлық күн өткеннен кейін www.nis.edu.kz сайтында жарияланады. Соңғы шешім «Өркен» білім беру грантын тағайындау жөніндегі Республикалық комиссиямен қабылданады.

Байланыс телефондары: 8 (727) 338-33-00

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

АОО «Назарбаев Интеллектуальные школы» проводит конкурс на присуждение образовательного гранта «Өркен» для обучения в 7-классах NIS на 2023-2024 учебный год.

Для участия в конкурсе ученикам 6-классов общеобразовательных школ необходимо по 10 января 2023 года предоставить в приемную комиссию следующие документы:
— Заявление на участие в конкурсе (можно скачать на сайте)
— Анкета претендента;
— Копии свидетельства о рождении претендента, ИИН претендента, удостоверения личности претендента (в случае наличия), копия удостоверения личности законного представителя с указанием ИИН;
— Копия табеля успеваемости и поведения претендента за первое полугодие 6-класса. Требуемые документы должны быть заверены подписью руководителя и скреплены печатью соответствующей организации образования.
— Цифровая фотография претендента размером 3х4 см. в виде графического файла не более 1 МБ (мегабайт) или выполнить фотосъемку претендента в приемной комиссии при подаче документов.

Все указанные документы подшиваются в пластиковый скоросшиватель.

Конкурсная комиссия работает по адресу город Алматы, улица Елибаева , 2. Режим работы с понедельника по пятницу с 9.00 до 18.00 часов, в субботу — с 9.00 до 13.00 часов, перерыв: 12.00-13.00 часов.
7 января 2023 года- праздничный день.
Стоит отметить, в целях обеспечения регулирования потока посетителей, функционирует сервис онлайн-бронирования, который позволит заранее забронировать дату и время посещения школы для подачи документов на конкурсный отбор.

Претенденты, зарегистрировавшиеся на конкурсный отбор, получат пропуск на участие в комплексном тестировании, который пройдет 2 и 3 марта 2023 года.

Результаты тестирования будут известны не более чем через *40 календарных дней* со дня окончания последнего комплексного тестирования и опубликованы на сайте www.nis.edu.kz Окончательное решение по итогам конкурса принимается Республиканской комиссией по присуждению образовательного гранта «Өркен».

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

СИСЕНБАЙ САОДАТ АМАНКЕЛДІҚЫЗЫ
БЕРДИЕВА КАЛАМКАС ИБРАГИМОВНА
РЫСБЕКОВА БАНУ АМИРХАНОВНА
ИСАХАНОВА КУЛПЫНАЙ СЕРИКБАЕВНА
КУЛМУРАТОВА НАЗИРА КУДАКЕЛДИЕВНА

2022-27Скачать

Понравилось это:

Нравится Загрузка…

Оставьте комментарий Жаңа сабақтар

Редакция

ШУАҚБАЕВА АЙНҰР НУРАБЫЛЛАЕВНА
СИСЕНБАЙ САОДАТ АМАНКЕЛДІҚЫЗЫ
САДУАКАСОВА ЖАНАТ СЫРЫМОВНА
АБДУЛЛАЕВА АКБОТА ТОЙШИБАЕВНА
БЕРДИЕВА КАЛАМКАС ИБРАГИМОВНА

orleutv-2022-41Скачать

Понравилось это:

Нравится Загрузка.

..

Оставьте комментарий

Материал іздеу

Найти:

Youtube

«Республикалық 45minut.kz» газеті

Республикалық “Білім жолы Нұрлы жол” журналы

[instagram-feed]

Мои твиты

«КҮНТІЗБЕ ЖОСПАРЫ — 2015-2016»

Январь 2023
ПнВтСрЧтПтСбВс
 1
2345678
9101112131415
16171819202122
23242526272829
3031 

РЕДАКЦИЯ ТӨСБЕЛГІЛЕРІ

Рубрики

  • «45minut — Vox populi»
  • «45minut. kz — Электронды нұсқа»
  • «45minut.org — Конкурстар»
  • «Арманы асқақ оқушы» байқауы
  • «Жаңа білім — Жаңа ғасыр» Республикалық конкурс
  • «Интернет сұхбат»
  • «КҮНТІЗБЕ ЖОСПАРЫ — 2015-2016»
  • «МЕКТЕПТЕГІ БІР МЕЗЕТ»
  • «Мастер класс»
  • «Мектептегі бір мезет» бәйгесі
  • «Отряды правопорядка»
  • «Топтамалар»
  • «Ekiбастұз қаласы. Семинар материалдары»
  • Жаңалықтар
  • 2017-2018
  • «БОЛАШАҚТЫ БІРГЕ ЖАСАЙМЫЗ» КОНКУРСЫ
  • BAQ-SEMINAR
  • DISTANCE
  • БАСТАУЫШ БІЛІМ БЕРУ ДЕҢГЕЙІНІҢ ОҚУ ПӘНДЕРІ БОЙЫНША ҮЛГІЛІК ТАҚЫРЫПТЫҚ ЖОСПАРЛАРЫ (1-4 СЫНЫПТАР)
  • БАҚ ӨКІЛІ
  • БАҚ өкілі-Тілшілер
  • Бастауыш сынып
  • Баяндамалар
  • Биология
  • Бәйге — Конкурс
  • География
  • Жаратылыстану
  • Жаңа сабақтар
  • Жаңалықтар
  • Интернет сұхбат
  • КОНКУРС
  • Мектептен тыс үйірмелер
  • Оқушылар шығармашылығы
  • Педагогика
  • Реферат
  • Русский язык и литература КТП
  • Сертификаттар
  • Технология
  • Түсінік хат
  • Физиология
  • Филология
  • Хабарландыру
  • Химия
  • Экономика
  • EEAS. EUROPA.EU
  • English
  • face=»Times New Roman
  • konkurs
  • konkurs032018
  • konkurs042018
  • konkurs052018
  • lang=»en-US»>
  • metodist.kz
  • NIS
  • Ғылыми жобалар
  • ҚР БҒМ — МОН РК
  • ҚР БҒМ БАСПАСӨЗ
  • Қазақ тілі
  • Қазақ әдебиеті
  • Құқықтану
  • Өзін-өзі тану пәні
  • Ұстаздар
  • SDU
  • TULEKTER MEDIA
  • ULAGATTY USTAZ
  • USTAZ UNIVERSITY

Республикалық 45minut.kz басылымы туралы ақпарат

МББ аты: «Республикалық 45minut.kz» газеті
Куәлік: № 12341-Г 19.03.2012 ж
БАҚ қайта тіркеу: № KZ48VPY00013618. Дата: 08.08.2019 жыл
Тарату аумағы: Қазақстан Республикасы
МББ тілі: қазақша, орысша, ағылшынша
Негізгі тақырыптық бағыты: білім беретін, ғылыми, танымдық, жарнамалық
Редактор: Нағиев ІЗГІЛІК Байдрахманұлы

«Бұқаралық ақпарат құралдары туралы» ҚР Заңы
45minut. kz басылымы. Министрліктен берілген куәлік туралы
СЕРТИФИКАТ, АЛҒЫС ХАТ, ТОПТАМА ҚҰЖАТТАРЫНЫҢ ЗАҢДЫЛЫҚТАРЫ ТУРАЛЫ

Редакция мекен-жайы

11 микрорайон, дом 115, Актобе 030000, Казахстан

8-777-087-6843

[email protected]

Часы работы: понедельник — суббота
10:00 — 17:00

«ҰСТАЗДАР ӘНІ»

Педагогтің ғылыми-әдістемелік қызметі туралы куәландыратын құжаттар:

Ғылыми-практикалық конференцияларға, шығармашылық конкурстарға, семинарларға, дөңгелек үстелдерге, әртүрлі деңгейдегі педагогикалық оқуларға қатысу; мерзімді басылымдардағы, бұқаралық ақпарат құралдарындағы ғылыми-әдістемелік материалдар жарияланымдарының көшірмелері;

Документы, свидетельствующие о научно-методической деятельности педагога:

участие в научно-практических конференциях, творческих конкурсах, семинарах, круглых столах, педагогических чтениях различного уровня; копии публикаций научно-методических материалов в периодической печати, средствах массовой информации;

Қазақстан Республикасы нормативтік құқықтық актілерінің ақпараттық-құқықтық жүйесі: http://adilet. zan.kz/kaz/docs/V1300008678

Презентациялар

45minut.kz Редакцияның семинардағы презентациясы. 2012-2013 жұмыс нәтижесі. Презентация және 2014 жыл жұмыс жоспары, Интернетте жұмыс істеудің ережелері Презентациялары жарияланды. Қарап танысыңыздар.

Хабарландыру

English Ағылшын тілі Бастауыш сынып Баяндамалар Биология География Жаңа сабақтар Жаңа сабақтар Информатика История Математика Мектепке дейінгі ұйым Мероприятия Начальные класссы Новости Психология Русский язык и литература Сызу және бейнелеу пәні Тарих пәні Технология Тәрбие сағаттары Физика Филология Филология (тілдер) Хабарландыру Химия диля сер Ғылыми жобалар Өзін-өзі тану пәні

Yandex.Metrika informer

геометрия — преобразование сегмента линии в дугу

Задать вопрос

спросил

Изменено 2 года, 2 месяца назад

Просмотрено 246 раз

$\begingroup$ 92$, переводящий отрезок $AA’$ с двумя конечными точками $A=(x_A,y_A)$ и $A=(x_{A’},y_{A’})$ в дугу $BB’$ с радиуса $r$ с центром в $O$, с конечными точками $B=(x_B,y_B)$ и $B’=(x_{B’},y_{B’})$.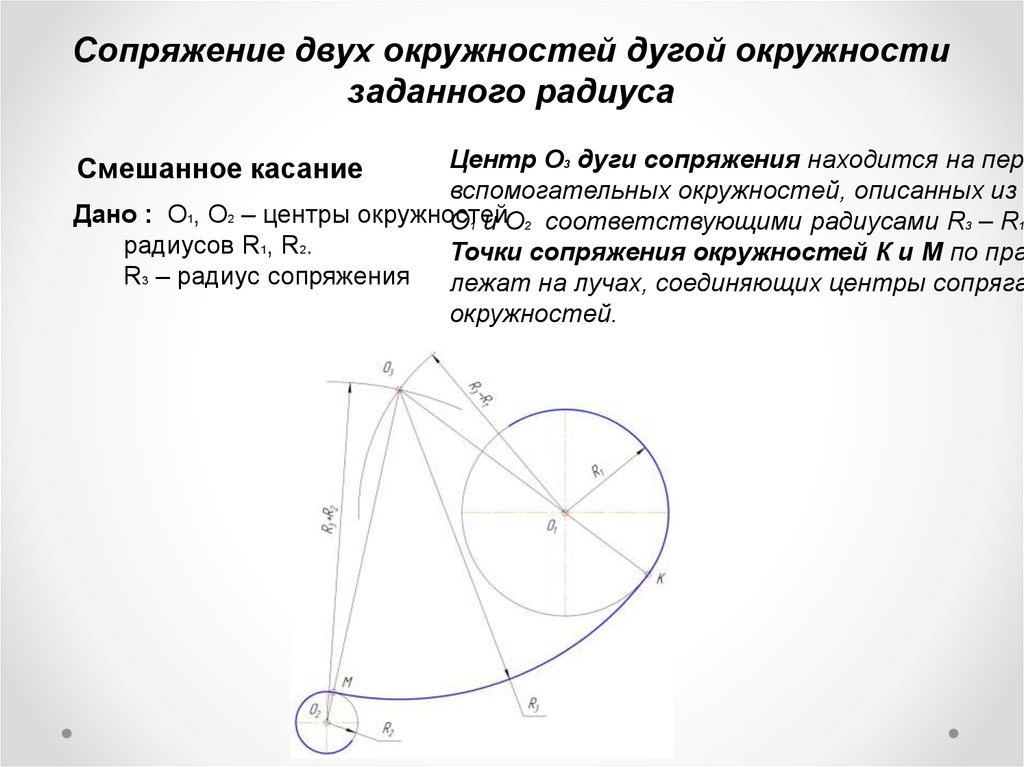

Это отображение должно отображать $A$ в $B$ и $A’$ в $B’$. Кто-нибудь знает отношение закрытой формы для такого отображения?

Я знаю, что такие отображения, как $w=1/z$ в комплексной плоскости, могут преобразовывать линии в окружности. Но я не знаю, как изменить это, чтобы преобразовать определенный сегмент линии в дугу с учетом конечных точек и радиуса.

  • геометрия
  • аналитическая геометрия
  • вычислительная геометрия

$\endgroup$

$\begingroup$

Рассматривайте все как комплексные числа, пусть $P$ будет точкой на отрезке $AA’$. Отображение $$P \mapsto \frac{1}{A’-A}\left( P — \frac{A+A’}{2}\right)$$ переводит отрезок $AA’$ в отрезок, соединяющий $-\frac12$ с $\frac12$. Команда Multiply $B’-B$ повернет и масштабирует отрезок прямой до параллельной копии $BB’$. После очередного перевода карта 92}{\bar{P}’ — \bar{N}}$$ Обратите внимание, что в знаменателе приведенного выше выражения необходимо взять комплексное сопряжение для $P’$ и $N$.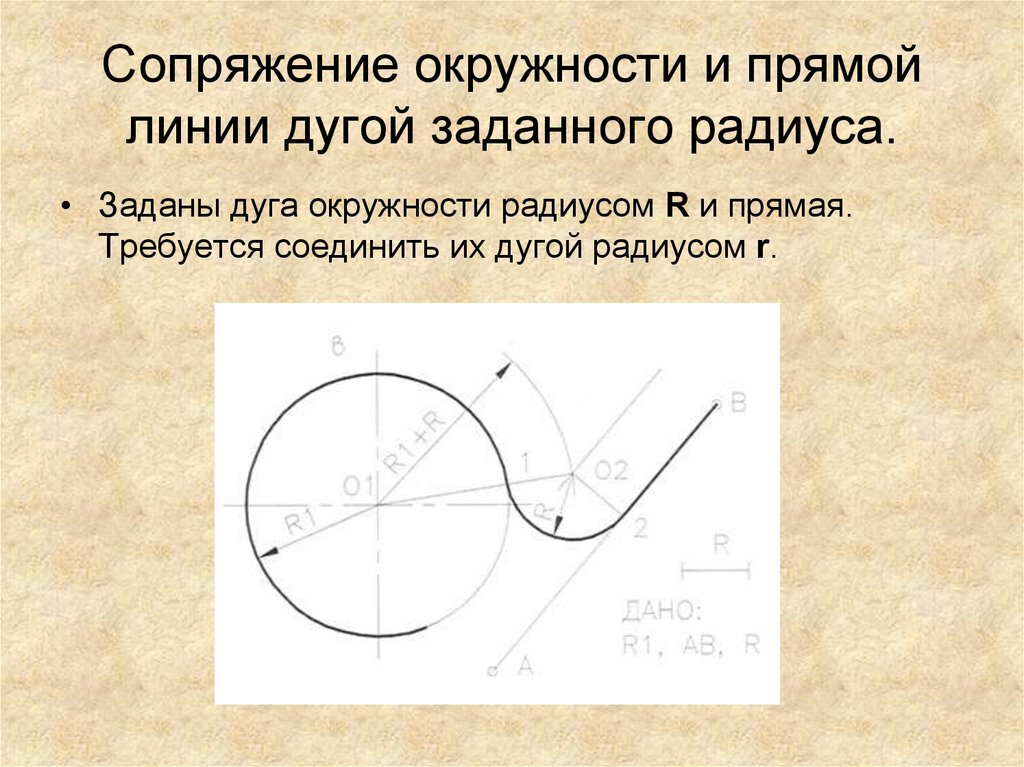

$\endgroup$

2

$\begingroup$

ВНИМАНИЕ: У меня есть большая часть ответа, кроме последней карты в конце. Я обновлю, как только разберусь с этим

Давайте рассматривать как сложный самолет.

Во-первых, обратите внимание, что единичный отрезок $L=[0,1]$ может быть отображен как дуга единичной окружности от угла $\theta_1$ до $\theta_2$, где $0 \leq \theta_1 \leq \theta_2 \ leq 2\pi$, обозначаемый $S(\theta_1 , \theta_2)$, через параметризацию $f(t ; \theta_1, \theta_2) : L \to S(\theta_1 , \theta_2)$, определяемую формулой $$ f(t; \theta_1, \theta_2) = \exp[ i ( \theta_1 (1-t) + \theta_2 t)] .$$

Итак, ваша дуга $BB’$ радиуса $r$ с центром в начале координат получается из $\mathbf{L}$ по карте $$ t \mapsto r \cdot f(t ; \theta_1, \theta_2) .$$

Осталось выяснить, как отобразить $AA’$ в $L$.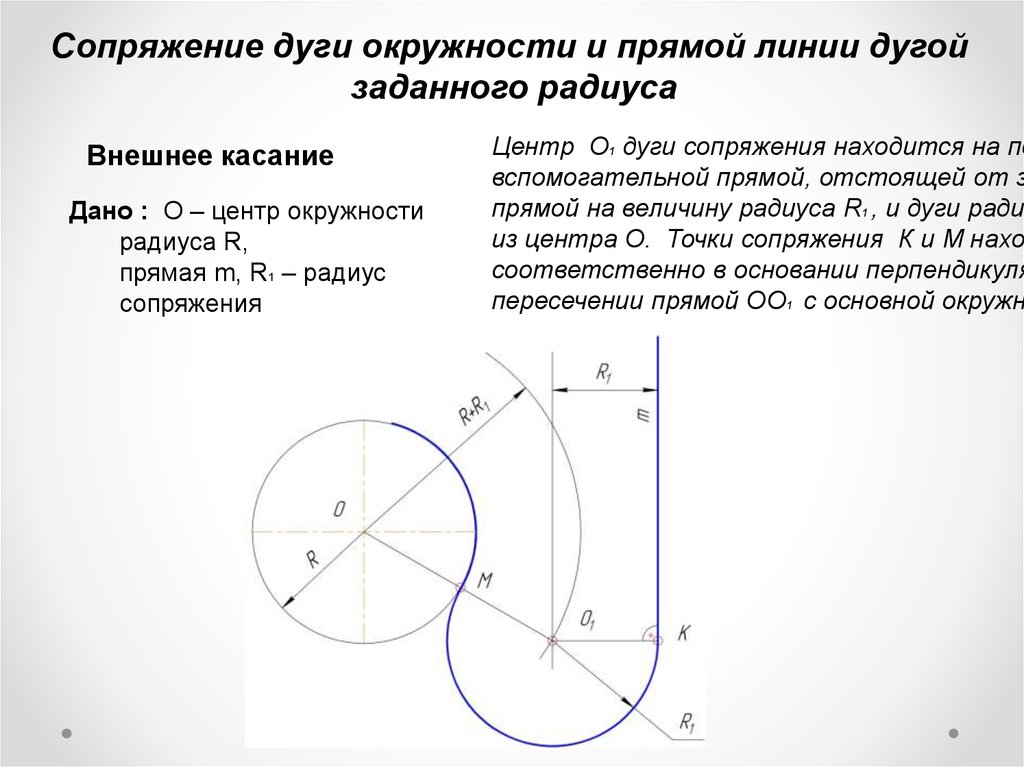 Все еще работаю над этим, должно быть какое-то вращение, перемещение и масштабирование

$\endgroup$

геометрия — Малоизвестные/оригинальные/интересные исследования/приложения инверсии (геометрического преобразования)

92} \ \vec{CM} $$

Это «инволютивное» преобразование: $M’$ является образом $M$ тогда и только тогда, когда $M$ является образом $M’$. Это объясняет двойную стрелку.

Это преобразование, приписываемое Магнусу и более или менее одновременно Плюкеру в начале 1830-х годов, подробно описано во многих книгах/сайтах.

См. комментарий о свойствах инверсии, показанных на рис. 1, в Приложении 1.

Рис. 1. : Инверсия с центром $C$ и мощностью 1. Фигуры, выделенные черным, заменяются посредством инверсии фигурами, выделенными красным. Синий круг, называемый «кругом инверсии», представляет собой геометрическое место инвариантных точек.

Но есть малоизвестные особенности, которые я хотел бы собрать.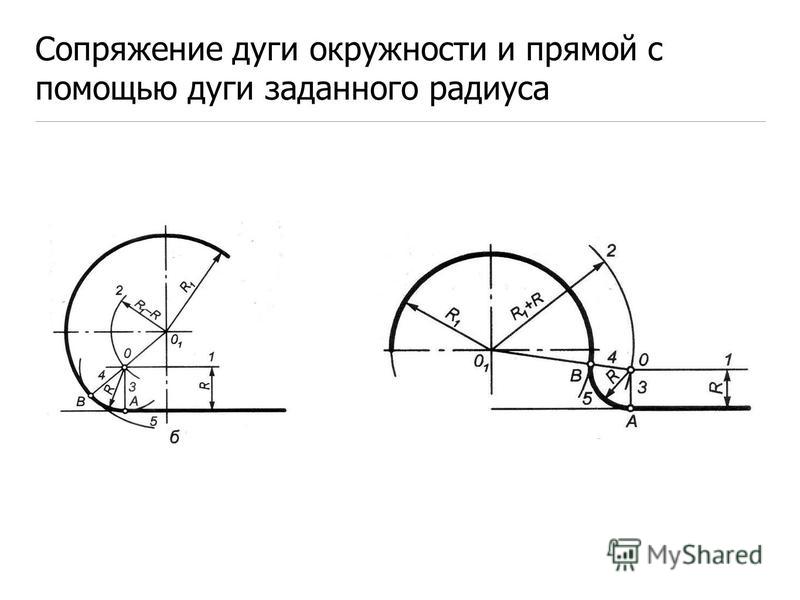 {-1}$ относительно параболоида $\Pi$ , где: 92)$, где $(a,b)$ — координаты точки $C$.

Этот неклассический способ описания инверсии заслуживает пояснения, которое мы поместили в Приложение 2.

Рис. 2. Инверсия конической проекцией $\Pi \to \Pi$.

  1. «Пузырьковая инверсия» Это двоюродное представление первого со сферой вместо параболы (см. рис. 3). Необходимо использовать 2 шага с двумя стереографическими проекциями $S_N$ и $S_S$ с северного и южного полюсов соответственно. относительно экваториальной плоскости. Взгляните на рис. 3.

Рассмотрим определенную фигуру, скажем, красный кружок. Превращается $S_N$ в окружность на единичной сфере, материализованную черными ромбиками; этот круг, в свою очередь, преобразуется $S_S$ в синий круг на экваториальной плоскости… который является прообразом исходного красного круга. Кратко:

$$\tag{$\star$}I=S_S \circ S_N$$

Это не должно вызывать удивления, потому что стереографические проекции сами по себе являются трехмерными инверсиями.

См. (композиция стереографических проекций — инверсия через шар — геометрический способ) для доказательства.

Рис. 3. Инверсия (плоскостная), реализуемая путем объединения двух стереографических проекций (формула ($\star$)).

  1. « Как инверсионное преобразование связано с линейной алгеброй » (фактически связано с пунктом 1) ; этот вопрос выглядит парадоксальным, поскольку инверсия точно не является линейным преобразованием. На самом деле существует группа аналлагматиков с линейным представлением $4 \times 4$ (также называемая группой конформной геометрии). Кроме того, в эту группу входит еще одна категория нелинейных преобразований — переводы. Ссылка: очень хорошая книга «Риманова геометрия» С. Галло, Д. Халлина, Ж. Лафонтена, 2-е издание 1993. Universitext, Springer, стр. 175-176. Вот как осуществляется это соответствие (Пояснения можно найти в этой книге или в очень интересной разработке @MvG, приведенной в 4а):

$$\text{Если} \ J \ \text{является основной инверсией (центр 0, степень 1):}$$ $$[J]:=\begin{pmatrix}0&0&0&1\\0&1&0&0\\0&0&1&0\\1&0&0&0\end{pmatrix}. 2\end{pmatrix}.$$ 92-x_0x_3$$

где $x_0$ следует рассматривать как однородную координату (т.е. учитывать ли проективную размерность). Поскольку сигнатура $q$ равна $(+++-)$, мы имеем дело с элементами группы, классически обозначаемой $O(3,1)$.

Это соответствие с 2D-преобразованиями может быть прямо расширено до более высоких размерностей (для $n$D-преобразований соответствие выполняется с матрицами $(n+2) \times (n+2)$).

  1. Этот справочник (переход к слайдам, начиная со слайда 130) использует линейную алгебру в $SL(2,\mathbb{C})$. 9{-i \theta}} \circ I$).

    Если мы возьмем $\theta=0$ в (%%), то получим:

    $$1+ \frac{1}{\overline{-1 + \frac{1}{\overline{1 + \frac {1}{\overline{z}}}}}} = — \overline{z}. \tag{%%%}$$

    (обратите внимание на спряжение).

    1. Сохранение перекрестного соотношения:

    $$\dfrac{AC.BD}{BC.AD}=\dfrac{A’C’.B’D’}{B’C’.A’D’}$$

    (см. рис. 4) .

    Рис. 4: Сохранение кросс-отношения.

    Это свойство (сохранение перекрестного отношения) является общим с проективными преобразованиями.

    (обратите внимание: изображение отрезка $AB$, например, не является отрезком $A’B’$). Для доказательства см. очень дидактическую презентацию здесь, где кросс-отношение используется для определения гиперболического геометрического расстояния.

    1. Сборник интересных документов/вопросов

    • а) См. слайд-шоу (http://www.cis.umac.mo/~fstitl/2013geometry/sterograph.pdf).

    • b) Углубленный анализ MvG в (https://math.stackexchange.com/q/866403), связанный с конформной группой, проанализированной в 3).

    • c) Изучение торов, циклид Дюпена и т. д. в связи с трехмерной инверсией: (обращение конуса в тор).

    • d) Ответы, которые я сделал (https://math.stackexchange.com/q/3599762) и (https://math.stackexchange.com/q/2621344), объясняющие, почему локально, в непосредственной близости от круга инверсия, инверсия ведет себя как симметрия. 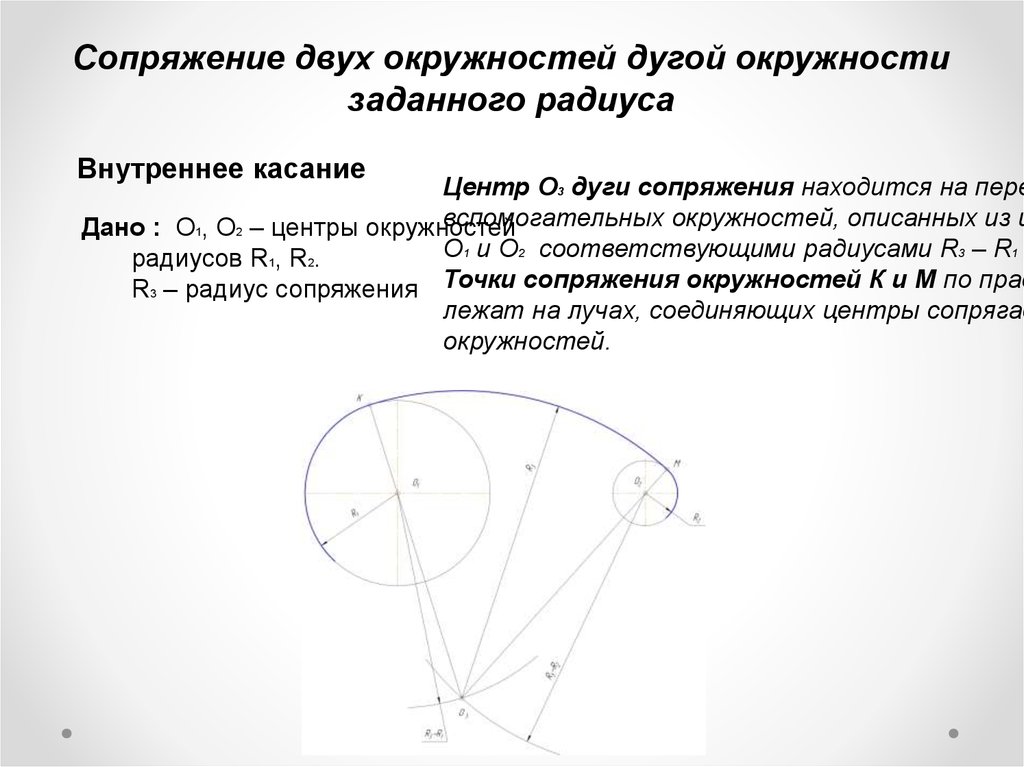Это также элегантно трактуется в исх. 3а).

    • д) Заявление в центры Вороного (https://math.stackexchange.com/q/2378365).

    • f) Расширение задачи ИМО, решаемой с помощью инверсии/стереографической проекции (https://pdfs.semanticscholar.org/3bcb/00d463fceb26ab103c9a3757ee85398eb187.pdf).

    • g) Документ MAA для обучения математическим олимпиадам инверсии: https://www.maa.org/sites/default/files/pdf/ebooks/pdf/EGMO_chapter8.pdf

    • h) Еще одна статья MAA «Основы инверсивной геометрии», Алан Дж. Хоффманн (1951): https://www.ams.org/journals/tran/1951-071-02/S0002-9947-1951-0044137-1/S0002-9947-1951-0044137-1.pdf

    • i) Другие: этот отличный документ, или этот, или этот вики-документ, или этот другой вики-документ. Этот вопрос и ответы на него.

    • j) Инверсия по отношению к (другим) коникам: см. это (на французском языке).

    • k) Две статьи J.B. Wilker et al. «Аполлоновы октеты и инверсионная форма теоремы Краузе» и «Аполлоний инверсией» (Mathematics Magazine)

    • l) Другие: http://jwilson. coe.uga.edu/EMT600/STORAGE/Inversion/inversion.html

    Мой (расширенный) вопрос: можете ли вы привести примеры (свои) интересных, возможно, необычных применений инверсии?

    Приложение 1: Вспомнить свойства инверсии, как показано на рис. 1:

    • Образ прямой линии в общем случае представляет собой окружность, проходящую через полюс $C$ ; в исключительных случаях, когда прямая проходит через начало координат, ее образом является сама прямая (осторожно: в последнем случае прямая «глобально» инвариантна, но ее точки, вообще говоря, не инвариантны).

    • Образ $\Gamma’$ окружности $\Gamma$, не проходящей через начало координат, является окружностью того же типа (внимание: центр $\Gamma’$ не является образом центра $\Gamma $ , тем не менее эти центры совпадают с полюсом инверсии). Образ окружности, проходящей через начало координат, представляет собой прямую линию, как было сказано ранее.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *