Сложение матриц
1) Определение матрицы— Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Вектор-строкой называют матрицу, состоящую из одной строки. Вектор-столбцом — из одного столбца. Матрица, у которой количество столбцов равно количеству строк, называется квадратной матрицей n-ого порядка. Элементы матрицы, у которых номер строки и номер столбца совпадает, называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы матрицы равны нулю, то матрицу называют диагональной. Если у диагональной матрицы n-ого порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е. Матрица любого размера, все элементы которой равны 0, называется нуль-матрицей.
Сложение и вычетание матриц— Сложение 2-х матриц
Суммой 2-х матриц
А и В называется матрица С=А+В, каждый
элемент которой находится по формуле Сij=aij+bij.
Для того, чтобы сложить 2 матрицы,
необходимо складывать между собой
элементы, стоящие на одинаковых местах.Умножение матрицы на число- условий нет, умножить на число можно любую матрицу. Произведением матрицы А на число l называется матрица В, равная lА, каждый элемент которой находится по формуле: bij =l x aij. Для того, чтобы умножить матрицу на число необходимо умножить на это число каждый элемент матрицы.
Произведения
матриц—
умножение А на В возможно тогда и только
тогда, когда число столбцов А равно
числу строк В; произведением матрицы А
размера mxk на
матрицу В размера kxn называется матрица С размера mxn, каждый
элемент которой равен сумме произведений
элементов i-ой
строки матрицы А на соответствующие
элементы j-ого
столбца матрицы В.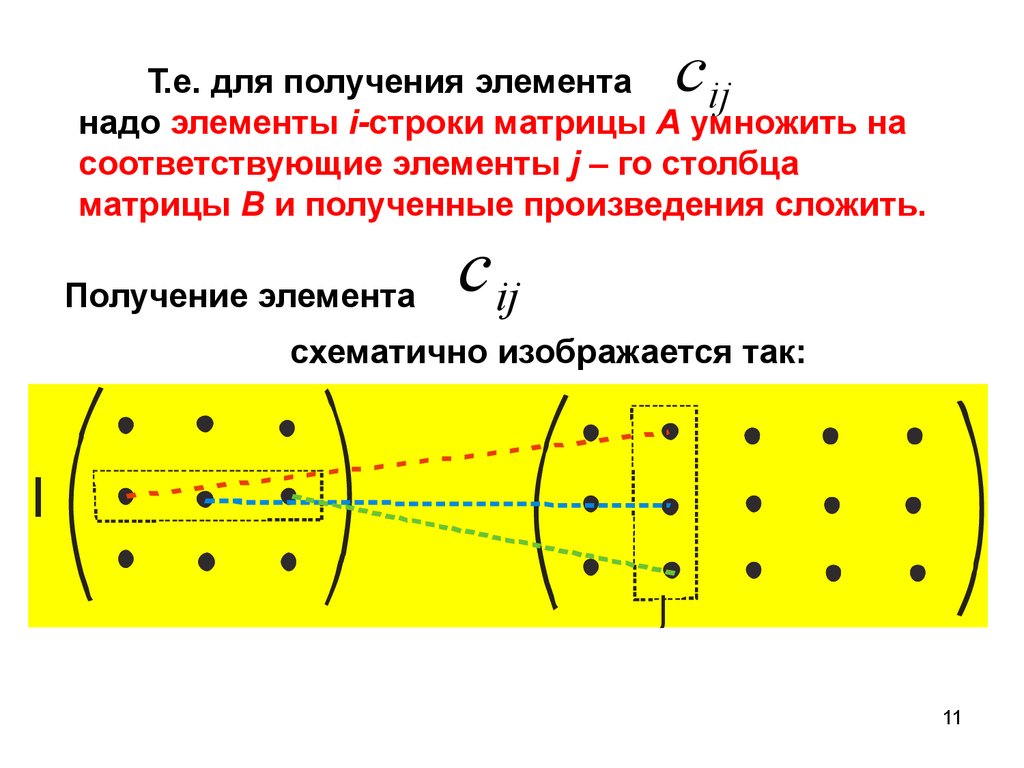
Определители 2-го и 3-го порядка— Определитель— число, характеризующее матрицу. Определителем матрицы 1-го порядка А=(а11) является единственный элемент этой матрицы. Определителем 2-го порядка называется число, характеризующее матрицу 2-го порядка, которое находится по следующему правилу: из произведений элементов главной диагонали вычитается произведение элементов второй диагонали матрицы А.
Обратная
матрица- Матрица
А-1 называется обратной по отношению к
квадратной матрице А, если при умножении
её на заданную как справа так и слева
получатся единичная матрица. Теорема
(необходимое и достаточн.условие сущ-я
обратн.матрицы): обратная матрица А-1
сущ-т и единственна тогда и только тогда,
когда заданная матрица не вырожденная. 
3)Алгебраические
дополнения всех элементов транспонированной
матрицы. 4) Присоед.матрица А@
(на месте каждого эл-та Ат его
алгебраич.доп-я). 5) А-1=
1/DА
*A@.
6) Проверка=>А-1 *А=Е.
Понятие о матрице
Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:
a ij, I – номер строки, j – номер столбца.
Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.
пример 1.
Элементы главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
пример 2.
Если
количество строк m
матрицы не равно количеству столбцов
n,
то матрица называется прямоугольной
(пример 2).
Если количество столбцов матрицы совпадают с количеством строк, то матрица называется квадратной (пример 1).
Количество строк или столбцов в квадратной матрице называются ее порядком.
Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной (пример 3).
пример3
Если все числа главной диагонали равны единице, то матрица называется единичной (пример 4).
пример 4
Если в прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT = (2 3 5). пример 5.
Если n=1, то получается матрица-столбец (пример 6).
пример 6.
Матрицы-строки матрицы-столбцы называются векторами.
Свойства матриц:
Действия с матрицами
Матрицы
одинакового размера можно складывать.
Суммой двух таких матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Символически будем записывать так: А+В=С.
Пример.
Легко видеть, что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.
Вычитание матриц.
Разностью двух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Обозначается разность матриц А и В так: С=А – В.
Пример.
3.
Умножение матрицРассмотрим правило умножения двух квадратных матриц второго порядка.
Произведением матрицы А на матрицу В называется матрица С=АВ.
Правила умножения прямоугольных матриц:
Умножение матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.
В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов было во второй матрице.
4. Умножение матрицы на число
При
умножении матрицы A на число a
все числа, составляющие матрицу A,
умножаются на число a.
Например, умножим матрицу на число 2. Получим ,
т.е. при умножении матрицы на число
множитель «вносится» под знак матрицы.
Транспонирование матрицы
Транспонированная матрица – матрица AТ, полученная из исходной матрицы A заменой строк на столбцы.
Формально, транспонированная матрица для матрицы A размеров m*n – матрица AT размеров n*m, определённая как AT[i, j] = A [j, i].
Например,
Свойства транспонированных матриц
1. (AT)T = A
2. (A + B)T = AT + BT
3. (AB)T = BTAT
4. detA = detAT
Определители 2-го и 3-го порядков.
Будем рассматривать квадратные матрицы
Определители являются основными числовыми характеристиками квадратных матриц.
Определителем (детерминантом) матрицы ,
состоящей
из одного числа ,
называется само это число.
Определителем матрицы А= второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:
Рассмотрим матрицу третьего порядка:
Определителем матрицы A третьего порядка называется число
Данная формула называется формулой разложения определителя 3 порядка по элементам первой строки.
Пример 6. Вычислить определители заданных матриц:
1.
Решение :
2.
Решение:
3.
Решение.
В
первой строке определителя уже есть
два нулевых элемента. Преобразуем
определитель так, чтобы еще два элемента
этой строки обратились в ноль. Сделать
это можно путем преобразований столбцов.
Оставим без изменения 2-й и 5-й столбцы
(там уже стоят нули). К 3-му столбцу
прибавим 1-й, умноженный на -2, к 4-му ~
первый, умноженный на 1. При этом первый
столбец в преобразованном определителе
останется без изменения.
Теперь разложим определитель по элементам первой строки:
В полученном определителе четвертого порядка преобразуем к нулю первые три элемента 1-й строки с помощью последнего 4-гo столбца: к 1-му прибавим 4-й, умноженный на 3, 2-ой преобразовывать не нужно, к 3-му прибавим 4-ый, умноженный на -1.
Разложим этот определитель по элементам первой строки:
Полученный определитель третьего порядка можно вычислить по правилу треугольников, однако проще и здесь, получив нули (легче всего в первом столбце), свести дело к определителю второго порядка. Ко 2-ой строке прибавим 1-ю, умноженную на -4, 3-й – первую, умноженную на 3:
Разлагаем определитель по элементам первого столбца:
И здесь можно упростить вычисления: ко 2-ой строке прибавим 1-ую, затем ко 2-му столбцу прибавим 1-ый, умноженным на 2:
Замечание
4.При
использовании свойства 8, следует иметь
в виду, что в преобразованном определителе
меняется только та строка, к которой
прибавляется другая (аналогично для
столбцов).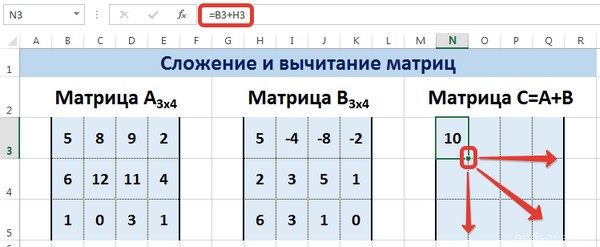
Так, если, например, к 3-ий
строке прибавляется 1-ая, умноженная на
2, то в преобразованном определителе
первая строка останется в неизменном
виде, меняется только 3-я строка.
Действия над матрицами. Сложение и вычитание
Определение 1Если у матриц совпадает количество столбцов и строк, то, считается, что у таких матриц одинаковая размерность (одинаковый порядок).
А=1-204-21 и В=10-20-4-21
Данные матрицы одинакового порядка, т.к. у них одинаковое количество строк и столбцов (3 строки и 2 столбца).
Сложение матриц
ЗамечаниеМатрицы одинаковой размерности можно складывать и вычитать.
Определение 2А=(αij)m×n и B=(bij)m×n — сумма матриц. Сумма этих матриц представлена выражением С=(сij) той же размерности, причем ее элементы вычисляются, как сумма соответствующих элементов исходных матриц:undefined. Сумма матриц имеет обозначение: А+B
Пример 2Найти сумму матриц:
1). А=2-131, В= 12-1-35;
2). А=2-131, В=-103-1253
Решение:
1).
А+В=2-131+12-1-35=2+12-1+(-1)3+(-3)1+5=14-206
2). Сложить данные матрицы нельзя, потому что они разной размерности
Свойства сложения матриц
Определение 3Исходная матрица А=(aij)m×n. Противоположной матрицей считается выражение -А=(-аij)m×n,где все элементы противоположны исходным.
Свойства сложения матриц:
- А + В = В + А — коммуникативный закон сложения;
- (А + В) + С = А + (В + С) — ассоциативный закон сложения;
- А + 0 = 0 + А = А;
- А + (-А) = -А + А = 0.
Вычитание матриц
Определение 4Разностью матриц А=(αij)m×n и B=(bij)m×n является матрица С=(сij), у которой такая же размерность. Ее элементы вычисляются как сумма соответствующих элементов матриц:
А=(aij)m×n и -В=(-bij)m×n; cij=(aij)+(-bij)
Разность матриц обозначается как А — В.
Пример 3Найти разность матриц:
1). А=2-131, В= 12-1-35;
2). А=2-131, В=-103-1253
Решение:
1).
А-В=2-131-12-1-35=2+(-12)-1+(-(-1))3+(-(-3))1+(-5)=2-12-1+13+31-5=-1006-4
2).Найти разность во втором варианте невозможно, потому что матрица разно размерные.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Арифметические корни натуральной степени
Следующая статья
Определитель матрицы
- Определитель матрицы
- Равенство матриц
- Ранг матрицы
- Умножение матриц
- Все темы по математике
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
тестовые задания
Вид работы:
Домашняя работа
Выполнена:
6 октября 2022 г.
Стоимость:
800 руб
Заказать такую же работу
правельных ответов Экзамен попытки часа на выполнения
Заказать такую же работу
Разработка алгоритма метода многокритериального выбора средств защиты ПДн в ЛВС
Заказать такую же работу
Дифференциальные уравнения
Вид работы:
Решение задач
Выполнена:
5 мая 2022 г.
Стоимость:
1 100 руб
Заказать такую же работу
сделать контрольную работу по экономикоматематическому моделированию
Вид работы:
Контрольная работа
Выполнена:
23 апреля 2022 г.
Стоимость:
2 200 руб
Заказать такую же работу
http решить задания
Вид работы:
Домашняя работа
Выполнена:
19 апреля 2022 г.
Стоимость:
1 600 руб
Заказать такую же работу
Смотреть все работы по алгебре
Операции со строками матрицы
Над строками используются 3 основные операции. матрица когда вы используете матрицу для решить систему линейных уравнений . Обычно цель состоит в том, чтобы левая часть матрицы выглядела как единичная матрица .
Три операции:
- Переключение строк
- Умножение строки на число
- Добавление строк
Переключение строк
Вы можете поменять местами строки матрицы, чтобы получить новую матрицу.
[ 2 3 − 2 6 0 0 3 − 6 1 0 2 − 3 ] → [ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ]
В примере, показанном выше, мы перемещаем строку
1
грести
2
, Строка
2
грести
3
, и Строка
3
грести
1
.
(Причина для этого состоит в том, чтобы получить
1
в левом верхнем углу.)
Умножение строки на число
Вы можете умножить любую строку на число. (Это означает умножение каждой записи в строке на одно и то же число.)
[ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ] → р 3 : 1 3 р 3 [ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]
В этом примере мы умножили строку
3
матрицы на
1
3
.
(Это дает нам
1
нам нужно в строке
3
, Столбец
3
.)
Добавление строк
Вы также можете добавить две строки вместе и заменить строку результатом.
Например, в матрицу, полученную в последнем примере, мы можем добавить строки 2 и 3 вместе, запись за записью:
[ 2 3 − 2 6 ] + [ 0 0 1 − 2 ] _ [ 2 3 − 1 4 ]
Затем мы заменяем строку
2
с результатом.
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + р 3 [ 1 0 2 − 3 2 3 − 1 4 0 0 1 − 2 ]
Добавление нескольких строк
Мы сказали, что было всего три операции, и они есть.
Но, используя последние две операции в сочетании, мы можем добавлять целые кратные строки к другим строкам, чтобы ускорить работу.
Шаг назад, поэтому у нас есть матрица:
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]
Теперь вместо того, чтобы просто добавить строку 2 + Строка 3 , Добавить ряд 2 + ( 2 × Строка 3 ) :
[ 2 3 − 2 6 ] + [ 0 0 2 − 4 ] _ [ 2 3 0 2 ]
Затем замените строку
2
с результатом.
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + 2 р 3 [ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ]
Таким образом, мы получаем
0
в строке
2
, Столбец
3
.
Мы можем сделать это снова, чтобы получить 0 в строке 2 , Столбец 1 . Здесь мы умножаем ряд 1 к − 2 , добавьте строку 2 и замените строку 2 с результатом.
[ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ] → р 2 : − 2 р 1 + р 2 [ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ]
Мы покажем еще несколько шагов, чтобы получить
3
×
3
единичная матрица слева (и, таким образом, решить систему).
Следующим шагом является добавление Строка 2 + ( 4 × Строка 3 ) чтобы получить 0 в строке 2 , Столбец 3 .
[ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ] → р 2 : р 2 + 4 р 3 [ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ]
Далее нам нужен ноль в строке
1
, Столбец
3
.
[ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ] → р 1 : р 1 − 2 р 3 [ 1 0 0 1 0 3 0 0 0 0 1 − 2 ]
Последний шаг — это просто применение второй операции, умножение строки на число.
[ 1 0 0 1 0 3 0 0 0 0 1 − 2 ] → 1 3 р 3 [ 1 0 0 1 0 1 0 0 0 0 1 − 2 ]
Теперь у нас есть решение в виде заказанной тройки ( 1 , 0 , − 2 ) .
Важная заметка: Если уравнения, представленные вашей исходной матрицей, представляют собой одинаковые или параллельные линии, вы не сможете получить единичную матрицу, используя эти операции со строками.
В этом случае решения либо не существует, либо существует бесконечно много решений системы.
python 3.x — Как заполнить матрицу равной суммой строк и столбцов?
У меня есть матрица N x N с целыми элементами.
У нас есть два входа: n и k.
Для решения этой задачи есть два условия:
1- сумма столбцов и строк матрицы должна быть равна k .
2- Разница между максимальным и минимальным числом в матрице должна быть минимальной.
Я написал код на Python, но он не работает.
n , k = карта (целое, ввод (). Разделить ())
матрица = [[k//n]*n для i в диапазоне (n)]
def row_sum (матрица, строка):
возвращаемая сумма (матрица [строка])
def col_sum (матрица, столбец):
разрешение = 0
для i в матрице:
разрешение += я [столбец]
вернуть разрешение
для я в диапазоне (n):
для j в диапазоне (n):
если (row_sum(matrix,i) != k) и (col_sum(matrix,j) != k):
матрица[i][j] += 1
для i в матрице:
печать (*я)
например, у нас есть матрица 5×5, сумма столбцов и строк которой должна быть равна 6:
ввод: 5 6 вывод : 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2
но это не работает:
ввод: 6 11 вывод: 2 2 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 1 1 1 1 1 2
Я трачу на это много времени и не могу решить.
Пожалуйста помоги!
(Эта задача не домашнее задание или что-то в этом роде. Это вопрос из конкурса алгоритмов, и конкурс окончен!)
- python-3.x
- алгоритм
- матрица
1
Решение состоит в том, чтобы обработать первую строку (используя код, который у вас уже есть), а затем установить каждую строку как строку над ней, повернутую на одну позицию.
Так, например, если первая строка имеет значения
a b c d e
, затем вы поворачиваете одну позицию в каждой строке, чтобы получить
a b c d e б в г д а в г д а б г д а б в а б в г
Поскольку каждое значение помещается в каждый столбец после того, как столбцы будут содержать по одному из каждого значения и, таким образом, в сумме дают одинаковую сумму, и поскольку в каждой строке есть одни и те же значения, только что перемещенные, все строки также складываются одинаково.
Код:
n , k = map(int,input().
