Двоичные и шестнадцатеричные значения | FreeBSD
Будучи системным администратором, вы частенько будете встречать такие термины, как 48-битовый адрес или 18-битовая сетевая маска. Я часто встречал системных администраторов, которые только кивают и улыбаются, когда слышат нечто подобное, и при этом думают: «Да неважно, ты прямо скажи, что я должен делать». К сожалению, математика — это неотъемлемая часть работы, и вы обязаны знать двоичное исчисление. Понимание этой области является одним из признаков, которые отличают любителей от профессионалов. Вам не нужно читать эту книгу, если вы хотите остаться любителем.
Возможно, вы уже бормочете себе под нос: «Но я знаю это!» Тогда просто пропустите этот раздел. Но не обманывайте себя, если вы этого еще не знаете.
Возможно, вы уже знаете, что компьютер интерпретирует данные как нули и единицы и что одна единица или один ноль составляют один бит. Когда протокол задает биты, он указывает это число согласно представлениям компьютера.
Десятичная математика (числа с основанием 10) ежедневно используется нами при покупке пиццы или для подсчета баланса чековой книжки. В ней задействованы цифры от 0 до 9. Чтобы получить число, превышающее самую большую цифру, слева к этой цифре добавляется другая, а текущая становится равной нулю. Это правило «переноса единицы», которое вы изучили много лет назад и сейчас используете неосознанно. В двоичной математике есть только цифры 0 и 1. Чтобы получить число, превышающее самую большую цифру, слева к этой цифре добавляется другая, а текущая становится равной 0. Та же самая десятичная математика, только с восемью пропавшими пальцами.
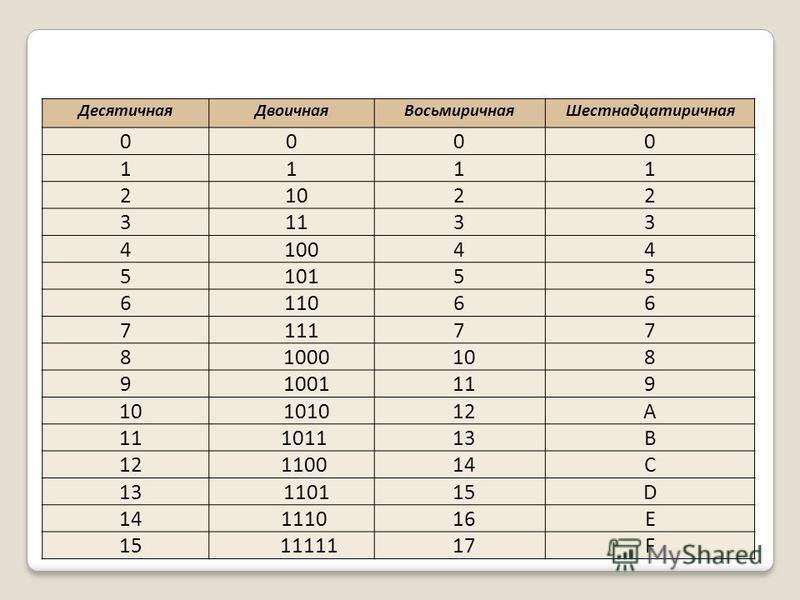
Таблица 6.1. Десятичные и двоичные числа
| Десятичные | Двоичные |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
Число из 32 бит, например IP-адрес, представляет собой строку из 32 нулей и единиц. MAC-адреса, используемые протоколом Ethernet, представляют собой 48-битовые числа и состоят из 48 нулей и единиц.
Ради интереса могу заметить, что в UNIX в некоторых случаях используются шестнадцатеричные числа (например, МАС-адреса и сетевые маски). Шестнадцатеричные числа имеют длину 4 бита. Двоичное число 1111, в котором все четыре бита представлены единицами, эквивалентно десятичному числу 15, а это означает, что в шестнадцатеричной системе используются цифры от 0 до 15. Сейчас некоторые из вас, глядя на двузначное число 15, которое должно представлять единственную цифру, думают — какую травку я курю и нельзя ли организовать поставку такой замечательной травки себе. Для представления чисел от 10 до 15 в шестнадцатеричной системе счисления используются символы от A до F. Когда счет доходит до самой большой цифры и нужно добавить еще единицу, текущая цифра устанавливается равной нулю, а слева добавляется еще одна цифра. Например, последовательность чисел от 1 до 17 в шестнадцатеричной системе выглядит следующим образом: «1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11». Снимайте обувь и считайте на пальцах, пока не поймете.
Сейчас некоторые из вас, глядя на двузначное число 15, которое должно представлять единственную цифру, думают — какую травку я курю и нельзя ли организовать поставку такой замечательной травки себе. Для представления чисел от 10 до 15 в шестнадцатеричной системе счисления используются символы от A до F. Когда счет доходит до самой большой цифры и нужно добавить еще единицу, текущая цифра устанавливается равной нулю, а слева добавляется еще одна цифра. Например, последовательность чисел от 1 до 17 в шестнадцатеричной системе выглядит следующим образом: «1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11». Снимайте обувь и считайте на пальцах, пока не поймете.
Шестнадцатеричные числа обычно помечаются префиксом 0x. Например, число 0×12 — это шестнадцатеричный эквивалент десятичного числа 18, тогда как 18 — это просто число 18. Если шестнадцатеричное число не помечено префиксом 0x, значит оно находится на месте, где допустимы только шестнадцатеричные числа, например в MAC-адресе. Наличие символов от А до F однозначно говорит о том, что число шестнадцатеричное, но это не самый надежный признак, потому что шестнадцатеричные числа могут не содержать шестнадцатеричных цифр, так же как многие десятичные числа могут состоять только из двоичных цифр.
Наличие символов от А до F однозначно говорит о том, что число шестнадцатеричное, но это не самый надежный признак, потому что шестнадцатеричные числа могут не содержать шестнадцатеричных цифр, так же как многие десятичные числа могут состоять только из двоичных цифр.
Когда вы работаете с шестнадцатеричными, десятичными и двоичными числами, было бы желательно пользоваться научным калькулятором. Современные средние калькуляторы имеют функции преобразования чисел между этими тремя системами счисления, как и большинство программных калькуляторов.
Биты по байтам
Компьютеры преимущественно работают с байтами, где каждый символ представлен 8-битовым числом. Единственное исключение — сетевой стек, где все сущее представлено отдельными битами. Так, например, файл размером 5 мегабайтов может находиться в компьютере, подключенном к сети со скоростью передачи данных 10 мегабитов (в секунду — прим. научн. ред). Не путайте их!
Шестнадцатеричная система счисления
Для написания программ на Ассемблере,
необходимо разобраться с шестнадцатеричной системой счисления.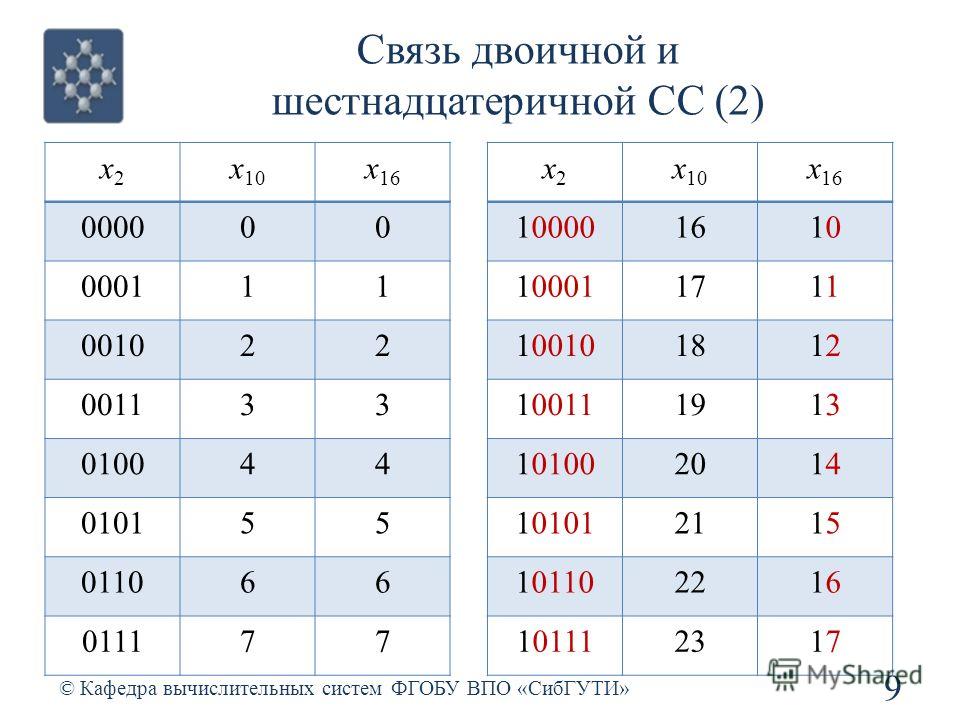 Ничего сложного
в ней нет. Мы используем в жизни десятичную систему. Уверен, что Вы все ее
знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя
аналогию с десятичной.
Ничего сложного
в ней нет. Мы используем в жизни десятичную систему. Уверен, что Вы все ее
знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя
аналогию с десятичной.
Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).
В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. Таблицу 1).
Таблица 1. Десятичная и шестнадцатеричная
системы счисления.
|
Десятичное число |
0 1 2 3 4 … 8 9 10 11 12 13 14 15 16 17 |
|
Шестнадцатеричное число |
0 1 2 3 4 … 8 9 A B C D E F 10 11 |
|
Десятичное число |
26 27 28 29 30 … 158 159 160 161 162 … 254 255 256 257 |
|
Шестнадцатеричное число |
1A 1B 1C 1D 1E … 9E 9F A0 A1 A2 … FE FF 100 101 |
Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.
Пример 1
- 1 х 16 = 10;
- 10 х 16 = 100;
- 100 х 16 = 1000 и т.д.
Вы смогли отличить в Примере 1
шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8,
19? Это могут быть как шестнадцатеричные, так и десятичные.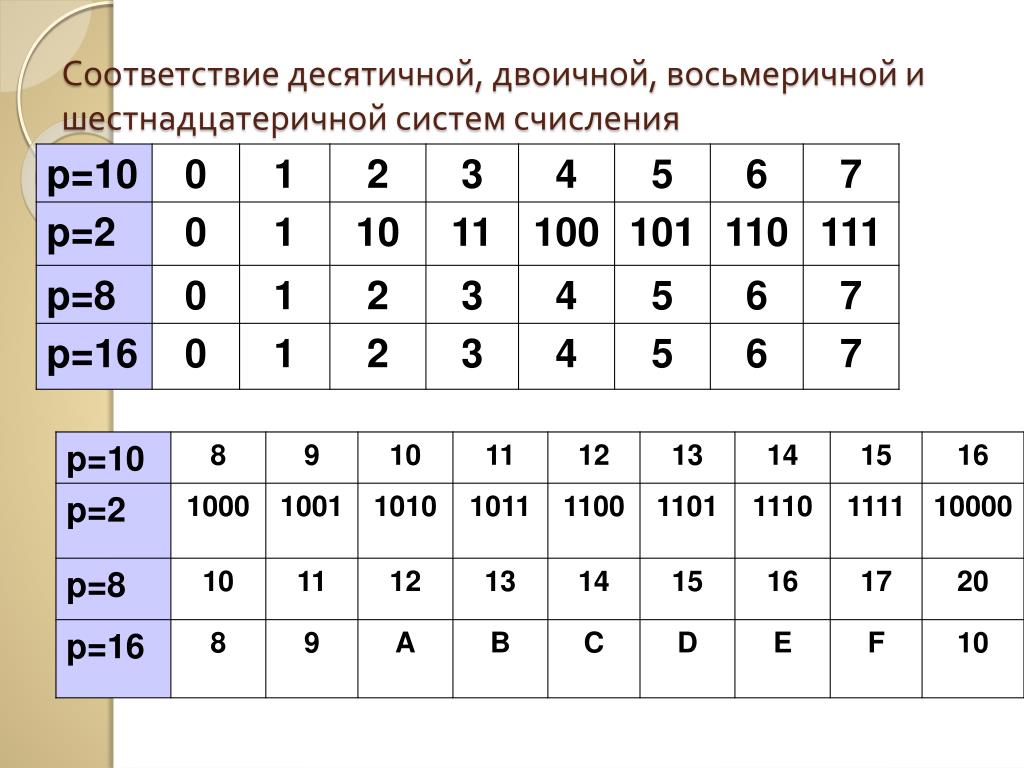
Т.о. Пример 1 (см. выше) правильнее записать шестнадцатеричные числа будет так:
- 1 х 16 = 10h;
- 10h х 16 = 100h;
- 100h х 16 = 1000h и т.д.
Либо так:
- 1h х 10h = 10h;
- 10h х 10h = 100
- 100h х 10h = 1000h
Для чего нужна шестнадцатеричная система — мы
рассмотрим в последующих главах. А в данный момент для нашего примера
программы, который будет рассмотрен ниже, нам необходимо знать о существовании
шестнадцатеричных чисел.
Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему, так как мы будем постоянно использовать ее при написании программ.
Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их сплошным текстом в книге, поэтому сперва будет идти сам код программы с пронумерованными строками, а сразу же после него — объяснения и примечания.
Примерно так:
(01)mov ah,9
(02)mov al,8
…
(15)mov dl,5Ah
Как интерпретировать шестнадцатеричные числа, такие как 0x0A?
Как уже было сказано, 0x0A равно десятичному 10 (десять). Это равно коду ASCII для LF (перевод строки), который является новой строкой во многих системах.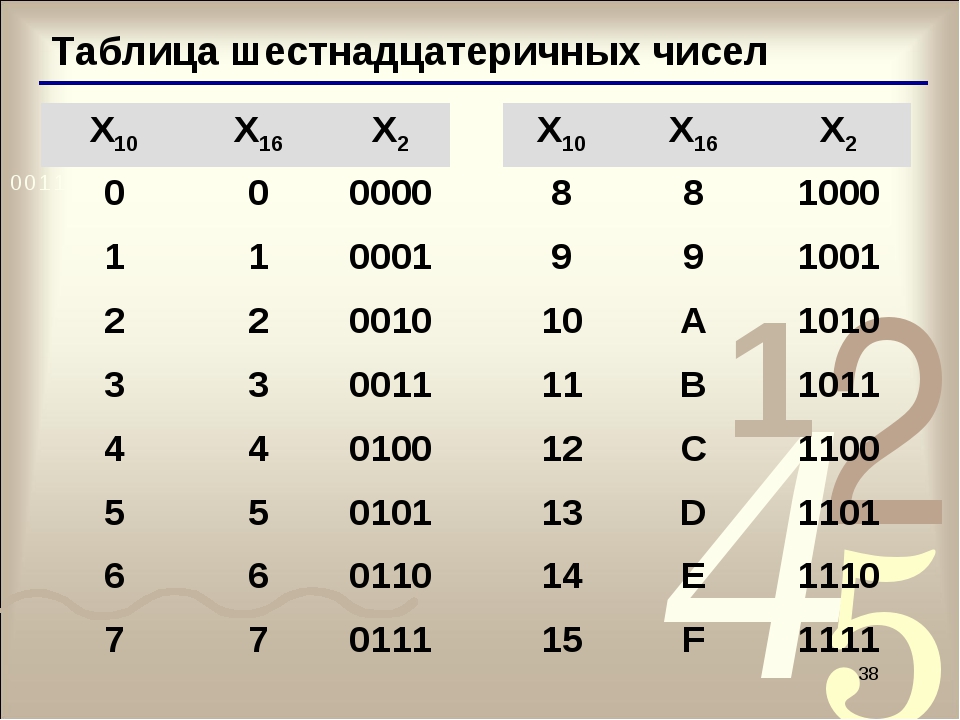 Но в вашем случае вы используете
Но в вашем случае вы используете DisconnectClient , что требует ULONG . Пройдете ли вы 0xA или просто 10 , не имеет значения.
Значение этого числа в данном случае- интерфейс, к которому подключается клиент .
EDIT: если еще раз взглянуть на ваш код, то ваша функция disconnectClient отличается от функции MSDN. Если это пользовательский метод, то для выяснения значения 0x0A требуется проверить сам этот метод или его документацию (хотя вполне возможно , что это просто заглушка для «real»
Понимание шестнадцатеричного
EDIT: если вам интересно, как все ответчики здесь, кажется, знают, что шестнадцатеричное 0x0A равно десятичному 10, читайте дальше:
Шестнадцатеричные числа имеют основание-16 (hexa = 6, deca = 10). В настоящее время мы привыкли к базе-10, но история показывает, что база-20 (во Франции все еще есть quatre-vingt), база-5 (Россия) и другие использовались еще до того, как двоичные (база-2) числа стали обычными для компьютеров. База-16 такая же, как база-10, но теперь у вас не 10 пальцев, а 16.
База-16 такая же, как база-10, но теперь у вас не 10 пальцев, а 16.
Компьютеры могут мыслить только битами, четыре бита (кусочек) могут составить числа 0-15. Чтобы облегчить чтение и запись битов, была использована шестнадцатеричная нотация. Это добавляет A-F к вездесущим цифрам 0-9, где A равно 10, B равно 11, пока F не будет равно 15.
В языках программирования принято начинать число с x, 0x или &h (в зависимости от языка), чтобы обозначить шестнадцатеричное число. Ведущие нули, как и десятичные числа, можно игнорировать. Нули Trailing имеют свое очевидное значение.
Преобразование шестнадцатеричного числа в десятичное
Итак, как бы вы перешли от шестнадцатеричного числа к десятичному? Каждая цифра должна быть умножена на степень 16, а не на степень 10 для десятичной дроби. Есть простое общую формулу, чтобы сделать из любой базы-X на любое основание-й, но здесь оно применяется для идущих от основания-16 на базу-10. 0 = 0 * 1 = 0
——- +
35616
0 = 0 * 1 = 0
——- +
35616
Довольно утомительно делать это вручную, но, надеюсь, вы уловили суть. Если у вас есть Windows, введите Calc в окне запуска или поле поиска (Vista, W7) и нажмите кнопку Просмотреть > Scientific. Теперь вы можете вводить шестнадцатеричные числа (нажмите F5) и переключаться между десятичными (F6), восьмеричными (F7) и двоичными (F8).
Есть еще много чего сказать о числах и их основаниях, но если вам нужно больше, я предлагаю вам взглянуть на часто задаваемые вопросы математического форума или на Википедию (более общую) . Чтобы конвертировать между многими базами, попробуйте этот онлайн-калькулятор base-X .
Обновление: добавлены разделы о понимании и преобразовании шестнадцатеричных чисел, подумал, что это, возможно, применимо 😉
Вывод шестнадцатеричного числа в C++
Это пример в «A Complete Guide to Programming in C++» (Улла Кирх-принц & Питер принц)
Пример:
cout << dec << -1 << " " << hex << -1;
Этот оператор вызывает следующий вывод в 32-разрядной системе:
-1 ffffffff
Не мог бы кто-нибудь объяснить, почему второй выход равен ffffffff ?
У меня есть проблемы с объяснением в книге, которая говорит::
c++Когда выводятся восьмеричные или шестнадцатеричные числа, биты выводимого числа всегда интерпретируются как беззнаковые! Другими словами, выходные данные показывают битовый шаблон числа в восьмеричном или шестнадцатеричном формате.
Поделиться Источник Ng. 25 мая 2018 в 07:10
3 ответа
- Форматирование шестнадцатеричного числа до короткого UUID в JavaScript
У меня есть шестнадцатеричное число в javascript. Для целей отображения я хотел бы отформатировать строку следующим образом: ffffffff-ffff-ffff 00000000-0000-01ff (8 digits)-(4 digits)-(4 digits) с мягкими нулями спереди Я пытался написать свой собственный цикл для форматирования произвольного…
- Преобразование шестнадцатеричного числа в двойное
Строка шестнадцатеричного числа выглядит следующим образом: 0X1.05P+10 Реальное значение этого шестнадцатеричного числа is:1044.0 Я могу преобразовать его с помощью языка C с помощью метода strtod. Но я не могу найти способ преобразовать его в PHP. Может кто-нибудь показать мне, как это делается?…
5
Это потому,что большинство современных машин используют представление целых чисел со знаком дополнения two .
В дополнении двойки старший бит используется как знаковый бит. Если оно задано, то число считается отрицательным , и чтобы получить его абсолютное (положительное) значение, нужно вычесть его из 2 N, то есть взять дополнение к двум.
Если бы у вас было 8-битное число 00000001, то его дополнение к двум было бы 100000000-00000001 = 11111111 (или 0xFF hex). Таким образом, -1 представляется как все 1 в двоичной форме.
Это очень удобная система, потому что вы можете выполнять арифметику, как если бы числа были без знака (позволяя им переполняться), а затем просто интерпретировать результат как знак, и он будет правильным.
Поделиться rustyx 25 мая 2018 в 07:23
0
компилятор реализует отрицательные числа для подписанных переменных следующим образом: если старший бит равен true, то ваше число реализует like (VALUE_RANGE-variable)
вот пример по 8-битным числам, надеюсь, вы его расширите.
char 0 1 2 ... 10 ... 126 127 -128 -127 -126 ... -10 ... -2 -1
uchar 0 1 2 ... 10 ... 126 127 128 129 130 ... 246 ... 254 255
hex 0 1 2 ... A ... 7E 7F 80 81 82 ... F6 ... FE FF
Поделиться bobra 25 мая 2018 в 07:25
0
Текст, который вы выделили, говорит о том, что вывод эквивалентен
cout << dec << -1 << " " << hex << (unsigned)-1;
В системе дополнения 2 (которой в наши дни является любой настольный компьютер PC) битовый шаблон для -1 имеет все биты, установленные на 1.
Таким образом, для 32-битного int выход будет равен ffffffff .
Наконец, обратите внимание, что если int (и, следовательно, unsigned ) являются 32 битами, то тип литерала 0xffffffff равен unsigned .
Рекомендации:
http://en.cppreference.com/ж/КПП/язык/integer_literal
https://en.wikipedia.org/wiki/ два%27s_complement
Поделиться Bathsheba 25 мая 2018 в 07:29
- Длина шестнадцатеричного числа
Как мы можем получить длину шестнадцатеричного числа в языке Python? Я пытался использовать этот код, но даже он показывает некоторую ошибку. i = 0 def hex_len(a): if a > 0x0: # i = 0 i = i + 1 a = a/16 return i b = 0x346 print(hex_len(b)) Здесь я просто использовал 346 в качестве…
- C++ endl вывод шестнадцатеричного числа
После компиляции большого количества программ с g++, внезапно endl; демонстрирует странное поведение. В дополнение к новой строке я также получаю консольный вывод шестнадцатеричного числа. Подумав, что, возможно, у меня возникла какая-то проблема с утечкой памяти, я перезагрузил свою версию Linux.
 ..
..
Похожие вопросы:
Запись шестнадцатеричного числа в файл
Как я могу записать строковое представление шестнадцатеричного числа в файл? Например, если у меня есть шестнадцатеричное значение 0x001A (которое равно 26 в десятичной системе счисления) Я хочу,…
lisp программа для преобразования шестнадцатеричного числа в десятичное
как написать программу lisp для преобразования заданного шестнадцатеричного числа в десятичное. может кто — нибудь дать мне подсказку? спасибо
Как перевести из шестнадцатеричного числа в строку в C?
Как перейти от шестнадцатеричного к строковому в C?
Форматирование шестнадцатеричного числа до короткого UUID в JavaScript
У меня есть шестнадцатеричное число в javascript. Для целей отображения я хотел бы отформатировать строку следующим образом: ffffffff-ffff-ffff 00000000-0000-01ff (8 digits)-(4 digits)-(4 digits) с. ..
..
Преобразование шестнадцатеричного числа в двойное
Строка шестнадцатеричного числа выглядит следующим образом: 0X1.05P+10 Реальное значение этого шестнадцатеричного числа is:1044.0 Я могу преобразовать его с помощью языка C с помощью метода strtod….
Длина шестнадцатеричного числа
Как мы можем получить длину шестнадцатеричного числа в языке Python? Я пытался использовать этот код, но даже он показывает некоторую ошибку. i = 0 def hex_len(a): if a > 0x0: # i = 0 i = i + 1 a…
C++ endl вывод шестнадцатеричного числа
После компиляции большого количества программ с g++, внезапно endl; демонстрирует странное поведение. В дополнение к новой строке я также получаю консольный вывод шестнадцатеричного числа. Подумав,…
Regex отрицательного и положительного шестнадцатеричного числа
Что такое регулярное выражение для шестнадцатеричного числа (отрицательное или положительное)? мне нужен код, который может распознать, является ли введенное мной число шестнадцатеричным (это может. ..
..
Преобразование шестнадцатеричного числа в двоичное в программировании c
Я прошу пользователя ввести текст, а затем сохраняю его в input. Затем я печатаю шестнадцатеричное значение каждого символа в тексте. Однако мне также нужен двоичный код шестнадцатеричного числа,…
uint16_t преобразования шестнадцатеричного числа в десятичное в C
Я просмотрел так много вопросов, касающихся преобразования шестнадцатеричного числа в десятичное, но я не мог найти способ преобразовать шестнадцатеричное число uint_16t в десятичное. Вы можете мне…
Шестнадцатеричная система счисления
Содержание:Что такое шестнадцатеричная система счисления
Как перевести целое десятичное число в шестнадцатеричную систему счисления
Как перевести десятичную дробь в шестнадцатеричную систему счисления
Как перевести число из шестнадцатеричной системы счисления в десятичную
Как перевести дробное шестнадцатеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в шестнадцатеричной системе счисления
Что такое шестнадцатеричная система счисления
шестнадцатеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в шестнадцатеричной системе счисления используется десять цифр и шесть
букв 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F.
Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.
Например, F24516 или 123A16
Для записи числа в шестнадцатеричной системе счисления используется десять цифр и шесть
букв 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F.
Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.
Например, F24516 или 123A16Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в шестнадцатеричную систему счисления
Для того, чтобы перевести целое десятичное число в шестнадцатеричную систему счисления нужно десятичное число делить на 16 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 32394710 в шестнадцатеричную систему счисления:
323947 : 16 = 20246 остаток: 11, 11 = B
20246 : 16 = 1265 остаток: 6
1265 : 16 = 79 остаток: 1
79 : 16 = 4 остаток: 15, 15 = F
4 : 16 = 0 остаток: 4
32394710 = 4F16B16
Как перевести десятичную дробь в шестнадцатеричную систему счисления
Для того чтобы перевести десятичную дробь в шестнадцатеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в шестнадцатеричную систему счисления, а затем дробную часть, последовательно умножать на 16, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
В результате будет получено число из целых частей произведений, записанное слева направо.Например, переведем десятичное число 842.99082088510 в шестнадцатеричную систему счисления:
Переведем целую часть
842 : 16 = 52 остаток: 10, 10 = A
52 : 16 = 3 остаток: 4
3 : 16 = 0 остаток: 3
84210 = 34A16
Переведем дробную часть
0.990820885 · 16 = 15.85313416, 15 = F
0.85313416 · 16 = 13.65014656, 13 = D
0.65014656 · 16 = 10.40234496, 10 = A
0.40234496 · 16 = 6.43751936
0.43751936 · 16 = 7.00030976
0.00030976 · 16 = 0.00495616
0.00495616 · 16 = 0.07929856
0.07929856 · 16 = 1.26877696
0.26877696 · 16 = 4.30043136
0.30043136 · 16 = 4.80690176
0.99082088510 = 0.FDA670014416
842.99082088510 = 34A.FDA670014416
Шестнадцатеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть
представлена конечной шестнадцатеричной.
В данном примере получается бесконечная шестнадцатеричная дробь, поэтому умножение на 16 можно производить бесконечное число раз
и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 842.99082088510 не может быть точно представлена в шестнадцатеричной системе счисления.
Не всегда конечная десятичная дробь может быть
представлена конечной шестнадцатеричной.
В данном примере получается бесконечная шестнадцатеричная дробь, поэтому умножение на 16 можно производить бесконечное число раз
и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 842.99082088510 не может быть точно представлена в шестнадцатеричной системе счисления.
Как перевести число из шестнадцатеричной системы счисления в десятичную
Для того, чтобы перевести число из шестнадцатеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число на 16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем число AE1916 в десятичную систему счисления:
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | A | F | 2 | D | 6 |
A16 = 1010
D16 = 1310
F16 = 1510
AF2D616 = 10 ⋅ 164 + 15 ⋅ 163 + 2 ⋅ 162 + 13 ⋅ 161 + 6 ⋅ 160 = 71752610
Как перевести дробное шестнадцатеричное число в десятичное
Для того, чтобы перевести дробное шестнадцатеричное число в десятичное, необходимо записать дробное шестнадцатеричное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число на
16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Необходимо последовательно умножить каждое число на
16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.Например, переведем дробное шестнадцатеричное число 69.F316 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 6 | 9 | F | 3 |
F16 = 1510
69.F316 = 6 ⋅ 161 + 9 ⋅ 160 + 15 ⋅ 16-1 + 3 ⋅ 16-2 = 105.9492187510
Таблица значений десятичных чисел от 0 до 100 в шестнадцатеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в шестнадцатеричной системе счисления |
| 010 | 016 |
| 110 | 116 |
| 210 | 216 |
| 310 | 316 |
| 410 | 416 |
| 510 | 516 |
| 610 | 616 |
| 710 | 716 |
| 810 | 816 |
| 910 | 916 |
| 1010 | A16 |
| 1110 | B16 |
| 1210 | C16 |
| 1310 | D16 |
| 1410 | E16 |
| 1510 | F16 |
| 1610 | 1016 |
| 1710 | 1116 |
| 1810 | 1216 |
| 1910 | 1316 |
| 2010 | 1416 |
| 2110 | 1516 |
| 2210 | 1616 |
| 2310 | 1716 |
| 2410 | 1816 |
| 2510 | 1916 |
| 2610 | 1A16 |
| 2710 | 1B16 |
| 2810 | 1C16 |
| 2910 | 1D16 |
| 3010 | 1E16 |
| 3110 | 1F16 |
| 3210 | 2016 |
| 3310 | 2116 |
| 3410 | 2216 |
| 3510 | 2316 |
| 3610 | 2416 |
| 3710 | 2516 |
| 3810 | 2616 |
| 3910 | 2716 |
| 4010 | 2816 |
| 4110 | 2916 |
| 4210 | 2A16 |
| 4310 | 2B16 |
| 4410 | 2C16 |
| 4510 | 2D16 |
| 4610 | 2E16 |
| 4710 | 2F16 |
| 4810 | 3016 |
| 4910 | 3116 |
| 5010 | 3216 |
| Значение числа в десятичной системе счисления | Значение числа в шестнадцатеричной системе счисления |
| 5110 | 3316 |
| 5210 | 3416 |
| 5310 | 3516 |
| 5410 | 3616 |
| 5510 | 3716 |
| 5610 | 3816 |
| 5710 | 3916 |
| 5810 | 3A16 |
| 5910 | 3B16 |
| 6010 | 3C16 |
| 6110 | 3D16 |
| 6210 | 3E16 |
| 6310 | 3F16 |
| 6410 | 4016 |
| 6510 | 4116 |
| 6610 | 4216 |
| 6710 | 4316 |
| 6810 | 4416 |
| 6910 | 4516 |
| 7010 | 4616 |
| 7110 | 4716 |
| 7210 | 4816 |
| 7310 | 4916 |
| 7410 | 4A16 |
| 7510 | 4B16 |
| 7610 | 4C16 |
| 7710 | 4D16 |
| 7810 | 4E16 |
| 7910 | 4F16 |
| 8010 | 5016 |
| 8110 | 5116 |
| 8210 | 5216 |
| 8310 | 5316 |
| 8410 | 5416 |
| 8510 | 5516 |
| 8610 | 5616 |
| 8710 | 5716 |
| 8810 | 5816 |
| 8910 | 5916 |
| 9010 | 5A16 |
| 9110 | 5B16 |
| 9210 | 5C16 |
| 9310 | 5D16 |
| 9410 | 5E16 |
| 9510 | 5F16 |
| 9610 | 6016 |
| 9710 | 6116 |
| 9810 | 6216 |
| 9910 | 6316 |
| 10010 | 6416 |
Число шестнадцатеричное — Справочник химика 21
Ранее отмечалось, что перевод числа из двоичной системы счисления в шестнадцатеричную и наоборот не представляет трудностей. Это объясняется тем, что основания этих систем кратные, поэтому необходимо лишь заменить коды одной системы кодами другой. Переход от десятичной записи числа к двоичной или шестнадцатеричной и наоборот осуществляется сложнее. При этом необходимо считаться с тем, что конечная дробь в одной системе счисления может оказаться бесконечной или периодической в другой, что в свою очередь приведет к потере точности. Например, [c.160]Алгоритмы перевода отличаются тем, как устанавливается соответствие между числами с различными основаниями. При переводе числа из десятичной системы в производную от двоичной системы целесообразно сначала записать его в шестнадцатеричной, а затем перейти, например, к двоичной. В этом случае потребуется выполнить меньшее количество операций. Рассматриваемые ниже алгоритмы достаточно просты, чтобы ими можнО было воспользоваться для оперативного сопоставления чисел в различных системах счисления. При решении задач на ЭВМ перевод числовой информации осуш ествляется либо по специальным программам, либо с по-мош ью команд машины. [c.161]
Для восьмибитового кода символов КОИ-8 также используется шестнадцатеричное представление- Однако в отличие от ДКОИ символы КОИ-8 записываются двумя десятичными числами. Для этого кода также используется понятие зонного формата. Таблица символов КОИ-8 (табл. 3.3) представляет собой матрицу из 16 столбцов, пронумерованных десятичными числами 00, 01, 02,. . ., 09, 10, 11, 12, 13, 14, 15 и 16 строк, пронумерованных числами 0,1,. . ., 15. [c.163]
Адресом загрузки фазы с именем КВВ является адрес первого двойного слова после конца предыдущей фазы (или адрес начала соответствующего раздела, как в первом примере), увеличенный на 3 Кбайт (К = 1024 байт). Смещение, равное 3 Кбайта, может быть задано со знаком + или — . Оно может задаваться также шестнадцатеричным числом длиной от одного до шести знаков (например, Х 5700 ) или десятичным числом длиной от одного до восьми знаков. [c.217]
Двоичные данные с плавающей точкой в памяти представляются как нормализованные шестнадцатеричные числа с плавающей точкой. Если объявляемая разрядность меньше 21, то они занимают слово, а если больше 21 — то двойное слово. Их значения находятся в диапазоне от 2 до 2+ » . [c.247]
Шестнадцатеричная константа записывается как шестнадцатеричное число, перед которым стоит буква X. При этом один байт памяти содержит две шестнадцатеричные цифры. Если количество цифр в константе нечетное, то слева добавляется нуль до заполнения байта. [c.342]
При передаче шестнадцатеричных данных по формату Zw усечение и добавление пробелов при несоответствии количества позиций числа и позиций w поля производится слева. [c.397]
Отметим, что очень компактное представление числа можно получить при помощи шестнадцатеричной системы счисления. Шестнадцатеричные числа можно легко преобразовать в двоичные (подробности здесь не рассматриваются). [c.571]
Например, шестнадцатеричное число 1 3 0 9 переводится в десятичную систему следующим образом [c.10]
Перевести в десятичную систему счисления целые шестнадцатеричные числа [c.11]
Арифметические действия над числами, представленными в форме с фиксированной запятой, в двоичной, восьмеричной и шестнадцатеричной системах счисления [c.12]
Выполнить операцию вычитания над шестнадцатеричными числами [c.18]
Перевести в шестнадцатеричную систему счисления целые двоичные числа [c.22]
Представить в форме с плавающей запятой шестнадцатеричные числа [c.24]
Нормализовать шестнадцатеричные числа [c.25]
Преобразовать шестнадцатеричные числа из нормальной формы в форму с фиксированной запятой [c.26]
Выполнить операцию сложения шестнадцатеричными числами [c.30]
Выполнить операцию вычитания над нормализованными шестнадцатеричными числами [c.30]
Сдвиг осуществляется на Ь разрядов. Число Ь в адресной части команды за писывается как двузначное шестнадцатеричное число, целое без знака. [c.52]
Команды при записи их на бланках представляются шестнадцатеричными числами, причем код операции — двузначным числом, а адрес — четырехзначным числом. Порядок выполнения команд естественный. Фрагмент системы команд этой машины приведен в табл. 9.11. [c.58]
Печатание результатов производится с помощью стандартного рулонного телетайпа со скоростью одно число в 2,5 сек. Выводимые результаты печатаются в виде таблиц 8-значных чисел в десятичной или шестнадцатеричной системах счисления. Печать таблиц осуществляется в три или четыре столбца в зависимости от положения специального тумблера на печатающем устройстве. Каждое десятичное число печатается в следующем порядке знак числа, семь цифр числа, пробел, восьмая цифра (порядок), знак порядка. [c.320]
Как уже отмечалось, для перехода от двоичной записи числа к шестнадцатеричной необходимо в двоичном коде выделить группы по четыре двоичных цифры и заменить их соответствующими шестнадцатеричными цифрами. При этом для целой части числа выделение групп производится справа палево от запятой, а для дробной — слева направо. Неполные тетрады дополняются нуля- [c.159]
Мантисса числа не превышает единицы. Считается, что число нормализовано, если старшая шестнадцатеричная цифра мантиссы отлична от нуля, т. е. 1/16 Л получения истинного значения числа мантиссу необходимо умножить на 16 в степени порядка. Однако для более точного представления как больших, так и малых по абсолютной величине чисел к действительной величине порядка добавляется число 64. Полученный таким образом порядок носит название характеристики. Значит, чтобы получить истинное значение числа, необходимо мантиссу умножить на 16 в степени характеристика минус 64. ДианаЕО-ном значений порядка в этом случае являются числа от —64 до -1- 63 (характеристики соответственно от О до 127), диапазон десятичных чисел — от 10 до 10 . Следовательно, характеристика, отсчитываемая относительно числа 64, всегда положительная. Знак порядка нет необходимости учитывать. [c.176]
Мантисса короткого числа состоит из шести шестнадцатеричных цифр и обеснечивает точность семи десятичных цифр. Мантисса длинного числа содержит 14 шестнадцатеричных цифр и дает точность в 17 десятичных цифр. [c.177]
Адресом загрузки фазы с именем КВВ будет адрес раздела переднего плана, равный 2000. Он может задаваться в виде пКбайт шестнадцатеричным числом длиной от четырех до шести знаков или десятичным числом длиной от пяти до восьми знаков. [c.217]
В шестнадцатеричной системе счисления в качестве цифр можно использовать символы О, 1, 2, 3, 4, 5, 6, 7, 8, 9, О, 1, 2, 3, 4, 5, означающие соответственно числа от нуля до пятнадцати, а в качестве основания — последовательность символов 16, означающую число шестнадцать. [c.10]
Глава 15 Байты и шестнадцатеричные числа . Код. Тайный язык информатики
Две усовершенствованные счетные машины, описанные в предыдущей главе, хорошо иллюстрируют концепцию потоков данных. Восьмибитные значения перемещаются по цепи от одного компонента к другому. Эти значения подаются на входы сумматоров, защелок и селекторов, а также появляются на выходах этих устройств. Кроме того, 8-битные значения задаются с помощью переключателей и отображаются рядом лампочек. Таким образом, поток данных в этих схемах имеет ширину восемь бит. Но почему? Почему не шесть, не семь, не девять и не десять?
Можно было бы ответить, что основой наших усовершенствованных счетных машин является исходный сумматор из главы 12, работающий с 8-битными значениями. Однако нет никаких особых причин конструировать эту машину именно так. Просто при ее создании мы сочли эту величину удобной. Как бы то ни было, признаю, что схитрил, поскольку с самого начала знал (возможно, и вы тоже), что восемь бит данных соответствуют одному байту.
Слово «байт» (byte) возникло в компании IBM примерно в 1956 году. Оно произошло от слова bite («кусок»), но его было решено писать через букву y, чтобы не путать со словом bit («бит»). В течение некоторого времени слово «байт» обозначало просто число битов в конкретном потоке данных. Однако в середине 1960-х, в связи с разработкой семейства компьютеров System/360 в компании IBM, это слово стало обозначать группу из восьми бит.
Как 8-разрядное число, байт может принимать значения в диапазоне от 00000000 до 11111111. Эти значения могут описывать положительные целые числа от 0 до 255, а при использовании дополнения до двойки для представления отрицательных чисел они могут отображать как положительные, так и отрицательные целые числа в диапазоне от ?128 до 127. Кроме того, конкретный байт может просто представлять одну из 28, или 256, разных вещей.
Число 8 оказалось весьма удобной величиной. Компания IBM отдала предпочтение 8-битным байтам в связи с простотой хранения чисел в формате BCD (о котором я расскажу в главе 23). Однако, как мы увидим далее, байт идеально подходит для хранения текста, поскольку большую часть языков мира (за исключением идеограмм, использующихся в китайском, японском и корейском) можно представить менее чем 256 символами. Кроме того, байт идеально подходит для представления оттенков серого на черно-белых фотографиях, поскольку человеческий глаз различает примерно 256 оттенков этого цвета. А там, где не хватает одного байта (например, для представления вышеупомянутых идеограмм китайского, японского и корейского языков), как правило, можно использовать два байта, которые позволяют выразить 216, или 65 536, различных элементов.
Половина байта, то есть четыре бита, иногда называется тетрадой, однако это слово употребляется гораздо реже, чем «байт».
Поскольку байты часто используются при описании работы компьютеров, нам требуется как можно более лаконичный способ записи их значения. Например, запись числа, состоящего из восьми двоичных цифр 10110110, безусловно, является корректной, но едва ли лаконичной.
Разумеется, мы всегда можем обращаться к байтам, используя их десятичные эквиваленты, но это потребует преобразования двоичного числа в десятичное, что хоть и несложно, но весьма обременительно. В главе 8 я продемонстрировал один довольно простой подход. Поскольку каждая двоичная цифра соответствует степени 2, мы можем просто записать цифры двоичного числа, а под ними — степени 2, после чего перемножить числа в каждом столбце и сложить результаты. Далее представлен процесс преобразования числа 10110110.
Процесс преобразования десятичного числа в двоичное менее удобен и предполагает деление десятичного числа на убывающие степени двойки. Частное от каждого деления — двоичная цифра, а остаток делится на следующую в порядке убывания степень двойки. Вот как десятичное число 182 преобразуется в двоичное.
В главе 8 эта техника описана подробно. Тем не менее для преобразования двоичных чисел в десятичные и обратно обычно требуется бумага, карандаш и практика.
Мы уже узнали о восьмеричной системе счисления — системе счисления с основанием 8, где используются только цифры 0, 1, 2, 3, 4, 5, 6 и 7. Преобразовать восьмеричное число в двоичное легко. Все, что нужно, — это запомнить 3-битный эквивалент каждой восьмеричной цифры.
Двоичное число
Восьмеричное число
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
Если у вас есть двоичное число (например, 10110110), начинайте преобразование с правого края. Каждая группа из трех бит соответствует восьмеричной цифре.
Таким образом, байт 10110110 можно выразить в виде восьмеричного числа 266. Это выражение, безусловно, является более лаконичным, значит, восьмеричная система действительно подходит для представления байтов. Однако у нее есть небольшой недостаток.
В двоичной системе байты выражаются значениями в диапазоне от 00000000 до 11111111, в восьмеричной — значениями в диапазоне от 000 до 377. Как было показано в предыдущем примере, средней и крайней справа восьмеричным цифрам соответствуют группы из трех бит, однако крайней слева восьмеричной цифре соответствуют только два бита. Это означает, что восьмеричное представление 16-разрядного числа не совпадает с восьмеричными представлениями двух байтов, составляющих это 16-разрядное число.
Чтобы согласовать представления многобайтных значений с представлениями отдельных байтов, нужна система, в которой каждый байт делится на равное количество битов. Следовательно, нам требуется разделить каждый байт на четыре значения по два бита каждое (система счисления с основанием 4) или на два значения по четыре бита каждое (система счисления с основанием 16).
Систему счисления с основанием 16 мы еще не рассматривали, и на то есть причины. Система счисления с основанием 16 называется шестнадцатеричной[18], — даже название труднопроизносимо. В десятичной системе счисления считаем так:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
В восьмеричной системе, как вы помните, не используются цифры 8 и 9:
0 1 2 3 4 5 6 7 10 11 12 …
В системе с основанием 4 не требуются цифры 4, 5, 6 и 7:
0 1 2 3 10 11 12 …
Наконец, в двоичной системе достаточно только 0 и 1:
0 1 10 11 100 …
Однако шестнадцатеричная система отличается тем, что в ней используется больше цифр, чем в десятичной. В шестнадцатеричной системе подсчет происходит примерно так:
0 1 2 3 4 5 6 7 8 9 ? ? ? ? ? ? 10 11 12 …
В данном случае 10 соответствует числу 16ДЕСЯТЬ. Вопросительные знаки говорят о том, что нам нужны еще шесть символов для представления шестнадцатеричных чисел. Что это за символы? Откуда их брать? Что ж, поскольку они не достались нам в наследство, подобно другим традиционным числовым символам, мы можем придумать их самостоятельно, например такие.
В отличие от символов, используемых для обозначения большинства чисел, у этих обозначений есть преимущество: они легко запоминаются и отождествляются с теми величинами, которые представляют. Существует так называемая десятигаллонная ковбойская шляпа, мяч для американского футбола (11 игроков в команде), дюжина пончиков (12 штук), черная кошка (с которой ассоциируется несчастливое число 13), полная луна (появляется на небе через 14 дней после новолуния) и кинжал (напоминающий об убийстве Юлия Цезаря в 15-й день марта). Каждый байт можно выразить в виде двух шестнадцатеричных цифр. Другими словами, шестнадцатеричная цифра эквивалентна четырем битам, или одной тетраде. В следующей таблице показаны соответствия двоичных, шестнадцатеричных и десятичных чисел.
Вот как можно представить двоичное число 10110110 в шестнадцатеричной системе.
И не важно, имеем ли мы дело с многобайтными числами.
Один байт всегда представляется парой шестнадцатеричных цифр.
К сожалению (а может быть, к счастью), мы не собираемся использовать футбольные мячи и пончики для записи шестнадцатеричных чисел, хотя они, безусловно, могли бы сгодиться для этой цели. Вместо них в шестнадцатеричной системе применяются обозначения, приводящие многих в замешательство. Дело в том, что шесть недостающих шестнадцатеричных цифр представляют шестью первыми буквами латинского алфавита:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 …
В следующей таблице показано реальное соответствие между двоичными, шестнадцатеричными и десятичными числами.
Двоичное число
Шестнадцатеричное число
Десятичное число
0000
0
0
0001
1
1
0010
2
2
0011
3
3
0100
4
4
0101
5
5
0110
6
6
0111
7
7
1000
8
8
1001
9
9
1010
A
10
1011
B
11
1100
C
12
1101
D
13
1110
E
14
1111
F
15
Таким образом, двоичное число 10110110 можно представить шестнадцатеричным числом B6, не рисуя футбольный мяч. Как вы помните, в предыдущих главах я указывал основание системы счисления с помощью нижнего индекса, например: 10110110ДВА — для двоичной системы; 2312ЧЕТЫРЕ — для четвертичной; 266ВОСЕМЬ — для восьмеричной; 182ДЕСЯТЬ — для десятичной.
По аналогии мы можем использовать обозначение B6ШЕСТНАДЦАТЬ для шестнадцатеричной системы.
Однако такое выражение чересчур громоздко. К счастью, для шестнадцатеричных чисел существуют и другие, более краткие, обозначения. Вы можете записать такое число следующим образом:
B6HEX.
В этой книге я буду использовать распространенный способ представления шестнадцатеричных чисел, предполагающий добавление к числу строчной латинской буквы h:
B6h.
В шестнадцатеричном числе положение каждой цифры соответствует степени числа 16.
Шестнадцатеричное число 9A48Ch можно представить так:
9A48Ch = 9 ? 10000h +
A ? 1000h +
4 ? 100h +
8 ? 10h +
C ? 1h.
Это выражение можно записать, используя степени числа 16:
9A48Ch = 9 ? 164 +
A ? 163 +
4 ? 162 +
8 ? 161 +
C ? 160.
Или десятичные эквиваленты этих степеней:
9A48Ch = 9 ? 65 536 +
A ? 4096 +
4 ? 256 +
8 ? 16 +
C ? 1.
Обратите внимание на отсутствие двусмысленности при записи отдельных цифр числа (9, А, 4, 8 и C) без нижнего индекса, обозначающего основание системы счисления. Девять — это 9, будь то десятичная или шестнадцатеричная система счисления. С другой стороны, А очевидно представляет шестнадцатеричный эквивалент десятичного числа 10.
По сути, преобразование всех цифр в десятичные числа позволяет выполнить расчет итогового значения:
9A48Ch = 9 ? 65 536 +
10 ? 4096 +
4 ? 256 +
8 ? 16 +
12 ? 1.
В итоге получается число 631 948. Таким образом шестнадцатеричные числа преобразуются в десятичные.
Шаблон для преобразования любого четырехзначного шестнадцатеричного числа в десятичное выглядит следующим образом.
В качестве примера преобразуем число 79ACh. Имейте в виду, что шестнадцатеричные цифры A и C эквивалентны десятичным числам 10 и 12.
Преобразование десятичных чисел в шестнадцатеричные обычно предполагает выполнение операций деления. Число меньшее или равное 255 можно представить одним байтом, состоящим из двух шестнадцатеричных цифр. Чтобы вычислить эти две цифры, нужно разделить число на 16, в результате чего получится частное и остаток. Вернемся к примеру с десятичным числом 182. Разделив 182 на 16, получим 11 (что соответствует цифре B в шестнадцатеричной системе) и 6 в остатке. Так, шестнадцатеричным эквивалентом десятичного числа 182 является B6h. Если десятичное число, которое вы хотите преобразовать, меньше 65 536, то шестнадцатеричный эквивалент будет состоять не более чем из четырех цифр. Шаблон для преобразования такого числа в шестнадцатеричное следующий.
Сначала поместите десятичное число в верхний левый прямоугольник. Это наше первое делимое. Разделим число на 4096 (первый делитель). Частное впишем в прямоугольник, расположенный под делимым, а остаток — в прямоугольник справа от делимого. Этот остаток — новое делимое, которое мы разделим на 256. Вот как число 31 148 преобразуется в шестнадцатеричный формат.
Десятичные числа 10 и 12 соответствуют шестнадцатеричным цифрам A и C, поэтому результат равен 79ACh.
Одна из проблем этой техники заключается в том, что для деления вы, вероятно, решите использовать калькулятор, а калькуляторы не показывают остаток от деления. Если вы разделите 31 148 на 4096 на калькуляторе, то получите 7,6044921875. Чтобы рассчитать остаток, нужно умножить 4096 на 7 (получится 28 672) и вычесть это значение из 31 148. Или умножить 4096 на 0,6044921875 — дробную часть результата от деления. (Правда, некоторые калькуляторы предусматривают функцию преобразования десятичных чисел в шестнадцатеричные и обратно.)
Другой способ преобразования десятичных чисел от 0 до 65 535 в шестнадцатеричные предполагает разделение числа на два байта путем его деления на 256. Затем каждый байт делится на 16. Шаблон для этого следующий.
Начнем сверху. После каждой операции деления частное помещается в прямоугольник, расположенный слева от делителя, а остаток — в прямоугольник справа. Например, число 51 966 преобразуется таким образом.
Шестнадцатеричными эквивалентами чисел 12, 10, 15 и 14 являются буквы С, А, F и Е, поэтому результат скорее напоминает слово, чем число.
Далее представлена таблица сложения для шестнадцатеричной системы счисления.
Используя эту таблицу и обычные правила сложения в столбик, можно складывать шестнадцатеричные числа.
В главе 13 я упоминал, что для представления отрицательных чисел можно применять дополнение до двойки. Если вы имеете дело с 8-битными двоичными числами со знаком, то отрицательные числа начинаются с 1. В шестнадцатеричной системе счисления двузначные числа со знаком отрицательные, если они начинаются с цифр 8, 9, A, B, C, D, E или F, поскольку их двоичные эквиваленты начинаются с 1. Например, число 99h может соответствовать либо десятичному числу 153 (если вы знаете, что имеете дело с однобайтными числами без знака), либо десятичному числу –103 (если вы знаете, что это число со знаком).
Кроме того, байт 99h может соответствовать и десятичному числу 99. Это интересно, но, похоже, противоречит всему, о чем мы говорили до сих пор. В главе 23 объясню, как это работает, а теперь остановимся на памяти.
в шестнадцатеричной системе счисления
Шестнадцатеричное число основано на числе 16
16 различных значений
Имеется 16 шестнадцатеричных цифр. Они такие же, как десятичные цифры до 9, но есть буквы A, B, C, D, E и F вместо десятичных чисел от 10 до 15:
| Шестнадцатеричный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | B | С | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Таким образом, одна шестнадцатеричная цифра может отображать 16 различных значений вместо обычных 10.
Подсчет
Выберите «Шестнадцатеричный» ниже и посмотрите, как он подсчитывает:
После того, как позиция «Единицы» заполнена (после F ), они начинаются с 0 , и мы добавляем 1 к следующей позиции слева (чтобы показать 1 лот из 16).
И после позиция достигает F , мы делаем то же самое, и так далее.
По мере продвижения влево каждое числовое место будет 16 раз больше .
Пример: какое десятичное значение шестнадцатеричного числа «D1CE»
= 53 248 + 256 + 192 + 14
= 53 710 в десятичной системе счисления
(Протестируйте его в преобразователе двоично-десятичного в шестнадцатеричный.)
The Point!
Пример: 2E6.A3
Это 2 × 16 × 16 + 14 × 16 + 6 + 10/16 + 3 / (16 × 16)
= 742,63671875 в десятичном формате
Прочтите ниже, чтобы узнать, почему
Цифры можно размещать слева или справа от точки, чтобы отображать значения больше единицы или меньше единицы:
| Число слева от точки
целое число. По мере продвижения влево каждое числовое место будет 16 раз больше . | |
| Первая цифра справа от точки означает шестнадцатых. (1/16). По мере продвижения вправо каждое число ставит в 16 раз меньше (одна шестнадцатая больше). |
Другие примеры
Пример 1: Что такое 4B5 (шестнадцатеричный)?- «4» находится в позиции «16 × 16», то есть 4 × 16 × 16
- Буква «B» (11) находится в положении «16», что означает 11 × 16
- «5» находится в позиции «1», что означает 5.
- Ответ: 4B5 = 4 × 16 × 16 + 11 × 16 + 5 (= 1205) в десятичном формате
- Слева стоит цифра «2», то есть целое число. часть.
- Число 3 находится в позиции «шестнадцатая», что означает «3». шестнадцатая «, или 3/16
- Итак, 2,3 — это «2 и 3 шестнадцатые» (= 2,1875 в десятичной системе)
Слово «шестнадцатеричное»
Слово «шестнадцатеричный» означает «основанный на 16». (От греческого hexa: «шесть» и латинского decima : «десятая часть» ).
Конвертер десятичной системы в шестнадцатеричную
Из Двоичный Десятичный Шестнадцатеричный
К Двоичный Десятичный Шестнадцатеричный
= Конвертировать × Сброс Менять Hex подписал дополнение 2Группировка цифр
Шаги вычисления от десятичного к шестнадцатеричному
Разделите на основание 16, чтобы получить цифры из остатка:
| Деление на 16 | Частное | Остаток (цифры) | Цифра № |
|---|
Конвертер шестнадцатеричного в десятичный ►
Как преобразовать десятичное в шестнадцатеричное
Шаг преобразования:
- Разделите число на 16.
- Получить целое частное для следующей итерации.
- Получите остаток от шестнадцатеричной цифры.
- Повторяйте эти шаги, пока частное не станет равным 0.
Пример № 1
Преобразовать 7562 10 в шестнадцатеричное:
| Подразделение по 16 | Частное (целое) | Остаток (десятичный) | Остаток (шестигранник) | Цифра № |
|---|---|---|---|---|
| 7562/16 | 472 | 10 | А | 0 |
| 472/16 | 29 | 8 | 8 | 1 |
| 29/16 | 1 | 13 | D | 2 |
| 1/16 | 0 | 1 | 1 | 3 |
Итак 7562 10 = 1D8A 16
Пример # 2
Преобразовать 35631 10 в шестнадцатеричное:
| Подразделение по 16 | Частное | Остаток (десятичный) | Остаток (шестигранник) | Цифра № |
|---|---|---|---|---|
| 35631/16 | 2226 | 15 | F | 0 |
| 2226/16 | 139 | 2 | 2 | 1 |
| 139/16 | 8 | 11 | B | 2 |
| 8/16 | 0 | 8 | 8 | 3 |
Итак, 35631 10 = 8B2F 16
Таблица преобразования десятичных чисел в шестнадцатеричные
| Десятичное с основанием 10 | Hex основание 16 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | А |
| 11 | B |
| 12 | С |
| 13 | D |
| 14 | E |
| 15 | F |
| 16 | 10 |
| 17 | 11 |
| 18 | 12 |
| 19 | 13 |
| 20 | 14 |
| 21 | 15 |
| 22 | 16 |
| 23 | 17 |
| 24 | 18 |
| 25 | 19 |
| 26 | 1A |
| 27 | 1Б |
| 28 | 1С |
| 29 | 1D |
| 30 | 1E |
| 40 | 28 |
| 50 | 32 |
| 60 | 3C |
| 70 | 46 |
| 80 | 50 |
| 90 | 5A |
| 100 | 64 |
| 200 | C8 |
| 1000 | 3E8 |
| 2000 | 7D0 |
Конвертер шестнадцатеричного в десятичный ►
См. Также
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ НОМЕРА
БЫСТРЫЕ СТОЛЫ
Этот веб-сайт использует файлы cookie для улучшения вашего опыта, анализа трафика и отображения рекламы.Учить большеОбъяснение шестнадцатеричной системы счисления
Шестнадцатеричные числа, часто сокращаемые до «шестнадцатеричных чисел» или «шестнадцатеричных», представляют собой числа, представленные по основанию 16, а не по основанию 10, которые мы используем для повседневной арифметики и счета.
На практике это означает, что каждый столбец числа, записанного в шестнадцатеричном формате, может представлять до 16 значений.
Цифры в шестнадцатеричном формате используют стандартные символы 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 для представления соответствующего значения и используют первые шесть букв алфавита для представления значений от 10 до 15 (Е.G: A, B, C, D, E, F).
В программировании мы ставим перед шестнадцатеричными константами префикс 0x , за некоторыми исключениями.
0x1 == 1
0xF == 15
0xFF == 255
0xFFF == 4095
0x1000 == 4096 В стандартной системе с основанием 10 каждый столбец представляет возрастающую степень 10, а в системе счисления 16 каждый столбец представляет возрастающую степень 16.
Как видно из приведенного выше примера таблицы, с помощью одной шестнадцатеричной цифры мы можем представляют собой числа до 15 включительно.Добавьте еще один столбец, и мы можем представить числа до 255, 4095 с другим столбцом и так далее.
Использование шестнадцатеричного числа в низкоуровневом программированииШестнадцатеричное число впервые нашло свое применение в информатике как удобная функция.
Данные в наших компьютерах имеют самую низкую общую единицу хранения — байт. Каждый байт содержит 8 бит и может хранить число от 0 до 255 включительно.
Шестнадцатеричный формат имеет то преимущество, что он краток и имеет четко определенные границы.
Один байт всегда представлен двумя шестнадцатеричными цифрами от 0x00 до 0xFF, последняя из которых является наибольшим байтовым значением 255.
Краткость и побайтовый характер шестнадцатеричных чисел делают их популярным выбором для работающих инженеров-программистов. на низкоуровневых базах кода или встроенном программном обеспечении.
Использование шестнадцатеричных чисел в JavaScriptJavaScript поддерживает использование шестнадцатеричной записи вместо любого целого числа, но не десятичных.
В качестве примера, число 2514 в шестнадцатеричном формате — это 0x9D2, но не существует поддерживаемого языком способа представления 25,14 в виде шестнадцатеричного числа.
Использование шестнадцатеричного числа в вашем коде является личным и стилистическим выбором и не влияет на базовую логику, реализуемую вашим кодом.
Использование шестнадцатеричных чисел в CSSCSS долгое время использовала шестнадцатеричную нотацию для представления значений цвета. Рассмотрим следующий селектор:
.my-container {
цвет фона: # 112233;
цвет: #FFFFFF;
} Значение background-color фактически составляет три шестнадцатеричных байта.
Процессор CSS обрабатывает их как три отдельных байта, представляющих красный, зеленый и синий.
В нашем примере 11 соответствует компоненту красного цвета, 22 соответствует компоненту зеленого цвета, а 33 — компоненту синего цвета.
В настоящее время в CSS3 нет способа определить цвет с альфа-компонентом с использованием шестнадцатеричного кода. Предлагаемый проект CSS4 1 включает предложение о разрешении дополнительного байта для определения альфа-значений.
На данный момент рекомендуется использовать стандартную функцию rgba () для добавления альфа-значения к вашим цветам.
Шестнадцатеричное число — обзор
5.2.7 Шестнадцатеричное-двоичное преобразование
Шестнадцатеричное число — это число с основанием (или основанием) 16, а его величина является суммой произведения значения каждой цифры в числе. (h) и его положение (n). Это позволяет создавать числа с цифрами в наборе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Позиция сразу для левая часть десятичной точки равна нулю (0). При перемещении влево из позиции 0 (в целой части числа) позиция увеличивается на 1.Значение цифры имеет вес 16 n , где n — номер позиции. При перемещении вправо от нулевой позиции (в дробную часть числа) позиция уменьшается на 1. Шестнадцать возможных цифр объединяются для создания целых и действительных чисел. В десятичном эквиваленте шестнадцатеричные цифры от A 16 до F 16 представляют собой числа от 10 10 до 15 10 . Таблица 5.7 показывает таблицу преобразования.
Таблица 5.7. Шестнадцатеричное десятичное без знака четырехбитное двоичное преобразование
| Шестнадцатеричное число | Десятичное число | 4-битное двоичное число без знака |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 110 0 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Величина числа (в виде десятичного числа) определяется по формуле:
Величина = (h n .16 n ) + (h n – 1 .16 n – 1 ) + (h n – 2 .16 n – 2 ) + + (h 0 .16 0 ) + (h –1 .16 –1 ) + + (h –n .16 –n )
Здесь шестнадцатеричное число записывается как h n h n – 1 h n – 2 h 0 .h –1 h –n (с использованием десятичного эквивалента шестнадцатеричного числа).
Вот некоторые примеры шестнадцатеричных чисел:
8 16 — [(8 × 16 0 )] 10
A8 16 [(10 × 16 ) + (8 × 16 0 )] 10
2A8 16 это [(2 × 16 2 ) + (10 × 16 1 ) + (8 × 16 0 )] 10
218.F 16 — это [(2 × 16 2 ) + (1 × 16 1 ) + (8 × 16 0 ) + (15 × 16 –1 )] 10
218.F7 16 равно [(2 × 16 2 ) + (1 × 16 1 ) + (8 × 16 0 ) + (15 × 16 –1 ) + (7 × 16 –2 )] 10 .
Для двоичных чисел каждое шестнадцатеричное число представляет четыре бита. Следовательно, 8-битное двоичное число представлено двумя шестнадцатеричными числами, 16-битное двоичное число представлено четырьмя шестнадцатеричными числами и так далее.Например, 8 16 — это 1000 2 , а A8 16 — это 10101000 2 .
Вот некоторые примеры шестнадцатеричных чисел:
8 16 is 1000 2
A8 16 is 10101000 2
25
25
2218.F 16 — 001000011000.1111 2
218.F7 16 — 001000011000.11110111 2 .
Десятичный эквивалент шестнадцатеричного числа создается путем вычисления величины шестнадцатеричного числа с использованием десятичного эквивалента шестнадцатеричных чисел от A до F в виде десятичного числа:
Величина = (h n .16 n ) + (h n – 1 .16 n – 1 ) + (h n – 2 .16 n – 2 ) + + (h 0 .16 0 ) + (ч –1 .16 –1 ) + + (h –n .16 –n )
Преобразование из десятичного числа в шестнадцатеричное выполняется аналогично преобразованию из десятичного числа в двоичное, за исключением того, что теперь делится на 16, а не на 2, и используя буквы от A до F для значений десятичного остатка от 10 до 15. Рассмотрим число 7 10 . Процедура преобразования:
Начните с числа (d) Деление Остаток Цифра шестнадцатеричного числа Начните с десятичного числа (d = 7) Разделить на 16 d / 16 = 7/16 = 0 7 h 0 = 7 Шестнадцатеричное число можно прочитать как: 7 10 = (h 0 ) 16 = 7 16 .
Рассмотрим число 100 10 . Процедура преобразования:
Действие Раздел Остаток Шестнадцатеричная цифра Начните с десятичного числа (d = 100) Делить на 16 d / 16 = 100/16 = 6 4 h 0 = 4 Разделить на 16 d / 16 = 6/16 = 0 6 h 1 = 6 Шестнадцатеричное число можно прочитать как: 100 10 = (h 1 h 0 ) 16 = 64 16 .
Рассмотрим число 255 10 . Процедура преобразования:
Начните с числа (d) Деление Остаток Цифра шестнадцатеричного числа Начните с десятичного числа (d = 255) Разделить на 16 d / 16 = 255/16 = 15 15 h 0 = F Разделить на 16 d / 16 = 15/16 = 0 15 h 1 = F Шестнадцатеричное число можно прочитать как: 255 10 = (h 1 h 0 ) 16 = FF 16 .
Преобразование из шестнадцатеричного в восьмеричное или наоборот осуществляется преобразованием числа в двоичный или десятичный эквивалент и из восьмеричного в шестнадцатеричное число.
Сводная таблица для систем счисления показана в Таблице 5.8. Здесь рассматриваются беззнаковые десятичные числа от 010 до 1510.
Таблица 5.8. Сводка числовых систем
Десятичное Двоичное без знака Восьмеричное Шестнадцатеричное BCD 0 0000 0 0 0000 1 1 1 0001 2 0010 2 2 0010 3 0011 3 3 0011 4 0100 4 4 0100 5 0101 5 5 0101 6 0110 6 6 0110 7 0111 7 7 0111 8 1000 10 9 0016 81000 9 1001 11 9 1001 10 1010 12 A 00010000 11 1011 13 B 00010001 12 1100 14 C 00010010 13 1101 15 D 00010011 14 1110 16 E 00010100 15 1111 17 F 00010101 И двоичные, и десятичные числа могут быть только целыми или действительными числами.В таблице 5.9 показаны двоичные и десятичные числа для действительного числа, представленного 40 битами в двоичном формате, при этом 24 бита представляют собой целую часть числа, а 16 битов представляют собой дробную часть числа.
Таблица 5.9. Таблица десятично-двоичного преобразования с положительной позицией слева от десятичной точки и отрицательной позицией справа от десятичной точки
Двоичная позиция Беззнаковое двоичное число Двоичное взвешивание Десятичное значение 23 100000000000000000000000.0000000000000000 2 23 8,388,608 22 0100000000000000000000.0000000000000000 2 22 4,194,304 21 010000000000000000000000.0016000017 0048000000000000 000100000000000000000000.0000000000000000 2 20 1,048,576 19 000010000000000000000000.0000000000000000 2 19 524,288 18 000001000000000000000000.0000000000000000 2 18 262,144 17 000000100000000000000000.0000000000000017 000000010000000000000000.0000000000000000 2 16 65,536 15 000000001000000000000000.0000000000000000 2 15 32,768 14 000000000100000000000000.0000000000000000 2 14 16,384 13 0000000000100700000000000.0000000000000000 12 000000000001000000000000.0000000000000000 2 12 4,096 11 000000000000100000000000.0000000000000000 2 11 2048 10 000000000000010000000000.0000000000000000 2 10 1,024 9 00000000000000100000048 000000000000000100000000.0000000000000000 2 8 256 7 000000000000000010000000.0000000000000000 2 7 128 6 000000000000000001000000.0000000000000000 2 6 64 5 000000000000000000100000,00 32000000000000 000000000000000000010000.0000000000000000 2 4 16 3 000000000000000000001000.0000000000000000 2 3 8 2 000000000000000000000100.0000000000000000 2 2 4 1 000000000000000000000010.00000000000000 2 000000000000000000000001.0000000000000000 2 0 1 Десятичная точка (.) –1 000000000000000000000000.1000000000000000 2 –1 0,5 –2 000000000000000000000000.0100000000000000 2 –2 0,25 –3 00000000 000000000.0010000000000000
0000000000000000.0010000000000000 00000000 –4 000000000000000000000000.0001000000000000 2 –4 0,0625 –5 000000000000000000000000.0000100000000000 2 –5 0,03125 –6 00000000000000000000.0000010000000000 2 –6 0,015625 –7 00000000000000000000,00200000 –8 000000000000000000000000.0000000100000000 2 –8 0.003 –9 000000000000000000000000.0000000010000000 2 –9 0.001953125 –10 00000000000000000000.0000000001000000 2 –10 0.0009765625 –11 000000000000170000000000 –12 000000000000000000000000.0000000000010000 2 –12 0.00024414063 –13 000000000000000000000000.0000000000001000 2 –13 0,00012207031 –14 00000000000000000000.0000000000000100 2 –14 0.000061035156 005 001600001700000000
–15 00000000170000 –16 000000000000000000000000.0000000000000001 2 –16 0.000015258789 Ты положил мне шестигранник
Помимо десятичной и двоичной систем счисления, шестнадцатеричная система счисления является следующей наиболее часто используемой системой счисления в информатике. В сегодняшнем посте мы рассмотрим эту многоцелевую систему счисления, исследуя сходство между ней и вышеупомянутыми системами счисления двоичных и десятичных чисел, прежде чем изучать некоторые приемы преобразования чисел в шестнадцатеричную систему и обратно.
Что такое шестнадцатеричная система счисления?
В некоторых из моих предыдущих постов мы узнали о том, как можно писать разные числа, используя разные обозначения.Мы узнали о десятичной системе счисления и о том, как в ней используется основание (или основание системы счисления) 10 и символы 0–9 для записи чисел. Мы также узнали о второй системе счисления, двоичной, и о том, как вместо системы счисления 10 используется система счисления 2 и символы 0 и 1 для выражения чисел в этой системе счисления. Мы также видели, как, хотя эти обозначения различны, они оба основывались на общей концепции, в которой числа в соответствующих обозначениях выражались в единицах степени основания системы счисления или основания счисления.
В компьютерных науках шестнадцатеричная система чисел (также известная как шестнадцатеричная система) является еще одним таким обозначением. Где шестнадцатеричный отличается от десятичного, а двоичный — это его основание числа. Шестнадцатеричный формат основан на системе счисления или системе счисления 16. В шестнадцатеричных числах используются символы 0–9 и AF (или a — f), а иногда они записываются с основанием в качестве нижнего индекса, чтобы отличить их от чисел, записанных в двоичном или десятичном формате. . Например:
Десятичное число Шестнадцатеричный эквивалент 0 10 0 16 1 10 1 16 2 10 2 16 3 10 3 16 4 10 4 16 5 10 5 16 6 10 6 16 7 10 7 16 8 10 8 16 9 10 9 16 10 10 А 16 11 10 В 16 12 10 С 16 13 10 Д 16 14 10 E 16 15 10 Ф. 16 Чаще всего шестнадцатеричный код используется для выражения цветов, и вы, возможно, видели это раньше, особенно если вы когда-либо писали свою собственную веб-страницу или использовали какие-либо графические приложения.Когда шестнадцатеричный формат используется таким образом, 24-битная информация о цвете (представляющая относительные пропорции красного, зеленого и синего, составляющих цвет) записывается в виде трех пар шестнадцатеричных цифр в форме #RRGGBB, где RR представляет красный компонент. , GG представляет зеленый компонент, а BB представляет синий компонент. Включено несколько примеров: шестнадцатеричное число # DFFFF8, которое представляет сине-зеленый цвет, и шестнадцатеричное число # 7334A4, которое представляет фиолетовый цвет. В этих примерах символ # (решетка — наш знак фунта) используется для обозначения шестнадцатеричного числа.
Основное преимущество использования шестнадцатеричной записи состоит в том, что она позволяет нам записать значение байта в удобочитаемом формате, используя только два символа. Эти два символа по-прежнему могут представлять все 256 возможных значений байта.
В основе всего этого по-прежнему действуют те же правила, которые мы узнали, рассматривая двоичные и десятичные числа. По сути, числа, выраженные в шестнадцатеричном формате, выражаются степенями 16. Различные числовые столбцы:
Мощность 16 6 16 5 16 4 16 3 16 2 16 1 16 0 Десятичный эквивалент 16777216 1048576 65536 4096 256 16 1 В следующих нескольких разделах мы рассмотрим, как мы используем эти числовые столбцы и преобразуем числа между разными основами счисления.
Преобразование десятичной системы в шестнадцатеричную
Процесс преобразования десятичного числа в шестнадцатеричное является итеративным.
В одном из моих предыдущих постов мы уже узнали, как выполнять деление вручную (вам действительно стоит вернуться и прочитать его, если вы все еще не уверены), поэтому я не собираюсь подробно описывать все этапы деления. Вместо этого я просто опишу те шаги, которые имеют отношение к преобразованию десятичной системы в шестнадцатеричную.
Примеры всегда лучше, поэтому, чтобы проиллюстрировать шаги, мы собираемся преобразовать десятичное число 43894 в шестнадцатеричную систему счисления.
Преобразование из шестнадцатеричной системы в десятичную
Процесс преобразования шестнадцатеричного числа в десятичный намного проще, чем наоборот. Как мы уже узнали ранее, используя как двоичную, так и десятичную нотацию, вместо того, чтобы выражать шестнадцатеричное число только как множители, мы также можем записать его в развернутой форме. Например:
89AB 16 = (8 x 16 3 ) + (9 x 16 2 ) + (A x 16 1 ) + (B x 16 0 )
Если затем преобразовать каждый из отдельных множителей в двоичные, мы получим:
89AB 16 = (8 x 16 3 ) + (9 x 16 2 ) + (10 x 16 1 ) + (11 x 16 0 )
Если теперь перемножить все и просуммировать результат:
89AB 16 = (8 x 4096) + (9 x 256) + (10 x 16) + (11 x 1) = 32768 + 2304 + 160 + 11 = 35243 10
Преобразование двоичного числа в шестнадцатеричное
Преобразование двоичного числа в его шестнадцатеричный эквивалент также является относительно простым процессом.Первый шаг — разделить двоичное число на группы из четырех цифр и добавить любые ведущие нули, которые необходимы, чтобы сделать эти группы до четырех цифр.
Если мы воспользуемся примером 101101011 2 , мы получим следующее (нам нужно будет добавить три ведущих нуля):
0001 0110 1011
Следующим шагом в процессе преобразования является выделение каждой четырехзначной группы по отдельности и вычисление ее десятичного эквивалента.
Отсюда вычислите эквивалентное шестнадцатеричное представление.Я расширил нашу предыдущую таблицу, чтобы помочь вам с этим преобразованием. Как только вы познакомитесь с двоичными и шестнадцатеричными числами, вы можете пропустить промежуточное преобразование в десятичное и выполнить преобразование непосредственно из двоичного в шестнадцатеричный.
4-значное двоичное число Десятичный эквивалент Шестнадцатеричный эквивалент 0000 2 0 10 0 16 0001 2 1 10 1 16 0010 2 2 10 2 16 0011 2 3 10 3 16 0100 2 4 10 4 16 0101 2 5 10 5 16 0110 2 6 10 6 16 0111 2 7 10 7 16 1000 2 8 10 8 16 1001 2 9 10 9 16 1010 2 10 10 А 16 1011 2 11 10 В 16 1100 2 12 10 С 16 1101 2 13 10 Д 16 1110 2 14 10 E 16 1111 2 15 10 Ф. 16 После того, как вы выполнили преобразование для каждой из отдельных групп битов, вы можете затем объединить все вычисленные шестнадцатеричные цифры, чтобы сформировать окончательное число.Если мы сделаем это с нашим примером выше, мы получим:
0001 2 = 1 10 = 1 16
0110 2 = 6 10 = 6 16
1011 2 = 11 10 = B 16
А потом, когда мы к ним присоединимся, мы получим:
101101011 2 = 16B 16
Преобразование из шестнадцатеричного в двоичное
Последнее, что мы рассмотрим сегодня, — это преобразование шестнадцатеричного числа в двоичное.
Есть два основных подхода, которые вы можете использовать для этого:
Первый подход к преобразованию шестнадцатеричного числа в двоичное — сначала преобразовать шестнадцатеричное число в десятичное, а затем выполнить второе преобразование из десятичного представления в двоичное. Ранее в этом посте мы видели, как выполнить первое из этих преобразований, а в предыдущем посте мы видели, как выполнить второе. Хотя этот подход работает, лично я считаю его довольно длинным и предпочитаю второй подход — прямое преобразование в двоичный код.
Если вы собираетесь преобразовать шестнадцатеричное число непосредственно в его двоичный эквивалент, мы в основном выполняем шаги из предыдущего раздела в обратном порядке. Возьмем для примера шестнадцатеричное число 5AF2 16 .
Мы уже знаем, что каждый шестнадцатеричный символ представляет четыре двоичных бита, поэтому мы возьмем каждый из шестнадцатеричных символов по очереди. Начиная с наиболее значимого символа, мы имеем:
5 16 = 0101 2
А 16 = 1010 2
Факс 16 = 1111 2
2 16 = 0010 2
Если мы теперь возьмем каждый из двоичных результатов и объединим их, мы получим результат:
5AF2 16 = 101 1010 1111 0010 2
Сводка
Я оставлю это на сегодня.В этом посте мы узнали, что шестнадцатеричная запись является еще одним из ключевых чисел, используемых в информатике. Мы увидели, чем он отличается от двоичного и десятичного числа, используя систему счисления или основание системы счисления 16, и как числа, выраженные в шестнадцатеричной системе счисления, представлены с использованием символов 0-9 и A — F. Затем мы также увидели, как преобразовывать числа. в шестнадцатеричную, двоичную и десятичную системы счисления и обратно. Как всегда, если у вас есть какие-либо вопросы или вы хотите что-то добавить, оставьте сообщение в комментариях ниже.
Почему мы используем шестнадцатеричный формат ?. Если вы программист, вы, вероятно,… | Нико Савас
Если вы программист, вы, вероятно, привыкли видеть, как шестнадцатеричные числа появляются во множестве мест. Например, шестнадцатеричный используется для обозначения цветов в «шестнадцатеричной» схеме.
Для считывания из памяти значения также часто являются шестнадцатеричными. Даже шрифт Брайля закодирован в шестнадцатеричном формате.
Есть несколько очевидных причин, по которым шестнадцатеричный формат предпочтительнее стандартного двоичного кода, который компьютеры хранят на низком уровне.
- Читаемость. В шестнадцатеричном формате используются цифры, которые больше напоминают нашу обычную систему счета по основанию 10, и поэтому легче сразу определить, насколько велико число, такое как e7, по сравнению с 11100111.
- Более высокая плотность информации. С помощью двух шестнадцатеричных цифр мы можем выразить любое число от 0 до 255. Чтобы сделать то же самое в двоичном формате, нам нужно 8 цифр. По мере того, как мы становимся все больше и больше, нам нужно все больше и больше цифр, и с этим становится все труднее работать.
Почему мы не используем десятичную дробь?
Кажется, что простое использование нашей системы подсчета по умолчанию, основание 10, могло бы решить все эти проблемы.Это определенно самый простой для чтения, поскольку это то, что мы узнаем в детстве, и он также относительно хорошо сжимает числа. Основная проблема с десятичными числами может быть проиллюстрирована следующим графиком:
Каждая пурпурная отметка — это когда новая цифра добавляется при представлении чиселОбратите внимание, что двоичное и десятичное число никогда не совпадают, тогда как шестнадцатеричное и двоичное составляют , на самом деле они совпадают. это каждые 4 двоичных цифры. На практике это означает, что одна шестнадцатеричная цифра всегда может быть представлена четырьмя двоичными цифрами.Десятичная дробь не работает. Ключевое свойство, которое позволяет шестнадцатеричному числу работать таким образом, состоит в том, что его основание кратно 2. (2⁴ для шестнадцатеричного). По этой причине в любой системе счисления, которую мы выбираем для сжатия двоичных данных, должна иметь основание, кратное 2 .
Почему мы не используем более высокие основания, такие как 128 или 256?
Base 128 и 256 следуют правилу, описанному выше (2⁷ и 2⁸ соответственно), почему бы нам не использовать их?
Это полностью сводится к удобочитаемости.В шестнадцатеричном формате используются арабские цифры 0–9 и английские буквы a-f. У нас есть врожденное понимание того, что «a» стоит перед «e», а «c» стоит перед «d», потому что мы выучили алфавит в очень молодом возрасте. Если бы мы использовали весь английский алфавит (26 букв, a-z) и арабские цифры (10 цифр, 0–9), у нас получилось бы 36 символов. Чтобы представить базу 128, нам нужно будет добавить новые символы, такие как / или (. Представьте, что вы пытаетесь решить, какое число больше, $ # @ / или $ * (). Поскольку у нас нет внутреннего упорядочения в нашем сознании относительно того, является ли @ или) чем больше, тем труднее рассуждать о числах, в которых используются символы, не входящие в стандартный алфавит.
Кодировка Base 64 решает эту проблему, используя заглавные буквы для дополнительных 26, а затем также используя + и / для заполнения последних двух мест.
Сопоставления Base 64 (Фото)Отлично! Значит, мы должны просто использовать базу 64, не так ли? Легко понять и хорошо сжимает информацию!
Ну, не совсем. Здесь все становится интересно. Наши базы на самом деле говорят нам еще кое-что, что важно учитывать, особенно при программировании. Одна цифра с основанием 32 (2⁵) соответствует 5 двоичным цифрам.Одна цифра с основанием 64 (2⁶) соответствует 6 двоичным цифрам.
Базовых двоичных цифр на символ
2 1
4 2
8 3
16 4
32 5
64 6
128 7
256 8Байт
Байт — это единицы информации, состоящие из 8 бит. Почти все компьютеры имеют байтовую адресацию, что означает, что вся память обращается по байтам, а не по битам. Это означает, что при программировании байты появляются постоянно. Использование системы подсчета, которая может легко конвертироваться в байты, является еще одним важным требованием для нашего двоичного представления.База 256 идеально подходит для этого, так как она равна 2⁸, что означает, что одна цифра составляет ровно один байт. К сожалению, по причинам, которые мы рассмотрели выше, 256 будет иметь другие проблемы с удобочитаемостью и будет очень громоздким в использовании.
И теперь мы понимаем, почему мы используем шестнадцатеричные числа. Шестнадцатеричный код с основанием 16 или основанием 2 base представляет ровно половину байта. Каждый байт может быть полностью представлен двумя шестнадцатеричными цифрами, не больше и не меньше. Шестнадцатеричный формат также соответствует всем остальным нашим спецификациям:
- Он успешно сжимает данные.одна шестнадцатеричная цифра может представлять 0–15, что намного лучше, чем 0–1, предлагаемые двоичным кодом.
- Легко читать. Всем известно, что C стоит перед E, а 4 — перед 9.
- Он легко конвертируется в байты. Две шестнадцатеричные цифры = 1 байт.
Но подождите! Мы еще не закончили! Если мы собираемся проследить этот вопрос до конца, мы должны спросить:
Почему байт равен 8 битам?
Причина этого довольно интересна и восходит к заре компьютерной эры.Еще в 1960-х годах люди осознали, что для кодирования текста в двоичную форму нам потребуется система, которая отображает английские символы в двоичные представления.
Алфавит кода Бодо (кредит)Еще в 1870 году Эмиль Бодо придумал код Бодо, 5-битную схему отображения для использования на ручных клавиатурах. К сожалению, 5-битные коды действительно поддерживают только буквы и некоторые знаки препинания, чего недостаточно для требований компьютеров. (5 бит = 2⁵ = 32 символа)
IBM 1620, компьютер с 6-битной архитектурой (кредит)По мере того, как компьютеры становились все более сложными, появились 6-битные архитектуры, такие как BCD.6-битная кодировка символов позволяет использовать 2⁶ = 64 символа, что означает, что мы можем уместить числа, а также символы пунктуации или строчные буквы. Поскольку не было возможности уместить прописные и строчные буквы, числа и знаки препинания в 64-битные архитектуры, 6-битные архитектуры не задерживались надолго.
7-битная таблица ASCII (кредит)Теперь мы переходим к настоящему соку. ASCII был формализован в 1963 году и включает 7-битный набор символов, в котором было место для всех упомянутых выше групп, а также несколько дополнительных кодов, которые можно было использовать для таких вещей, как 32 системных кода в позициях 0–31, такие вещи, как «Начало текста» или даже «Синхронный режим ожидания».7-битные архитектуры в конечном итоге уступили место 8-битным по нескольким причинам:
- Поскольку компьютеры являются двоичными, рекомендуется иметь все в степени двойки, поэтому 2³ = 8 имеет больше смысла, чем 7 бит.
- Наличие этого дополнительного бита также использовалось для «бита четности» — ведущий бит символа будет указывать, было ли количество единиц в следующих 7 битах четным или нечетным. Это использовалось для обнаружения ошибок в подверженных ошибкам машинах, существовавших на ранних этапах вычислений.
Я полагаю, мы могли бы проследить этот вопрос еще дальше, чтобы определить, почему английский язык является стандартом для программирования или почему в английском языке 26 символов, но я оставлю это здесь и предоставлю вам возможность провести собственное исследование.
Что такое шестнадцатеричный? — Определение с сайта WhatIs.com
ОтШестнадцатеричная система счисления описывает систему счисления с основанием 16. То есть он описывает систему нумерации, содержащую 16 последовательных чисел в качестве основных единиц (включая 0) перед добавлением новой позиции для следующего числа. (Обратите внимание, что мы используем здесь «16» как десятичное число, чтобы объяснить число, которое будет «10» в шестнадцатеричном формате.) Шестнадцатеричные числа — это 0–9, а затем используются буквы A – F. Мы показываем эквивалентность двоичных, десятичных и шестнадцатеричных чисел в таблице ниже.
Шестнадцатеричный формат — это удобный способ выражения двоичных чисел в современных компьютерах, в которых байт почти всегда определяется как содержащий восемь двоичных цифр. При отображении содержимого компьютерной памяти (например, при получении дампа памяти для отладки новой компьютерной программы или при отображении строки текстовых символов или строки двоичных значений при кодировании программы или HTML-страницы) один шестнадцатеричная цифра может представлять собой расположение четырех двоичных цифр. Две шестнадцатеричные цифры могут представлять восемь двоичных цифр или байт.
Двоичный Десятичное Шестнадцатеричный 0 0 0 1 1 1 10 2 2 11 3 3 100 4 4 101 5 5 110 6 6 111 7 7 1000 8 8 1001 9 9 1010 10 А 1011 11 B 1100 12 С 1101 13 D 1110 14 E 1111 15 F 10000 16 10 10001 17 11 и т.
