Графики в «Маткаде» — построение и исследование
Программа MathCAD обеспечивает стабильное поддержание своих функций уже долгие годы. В этой вычислительной среде работают экономисты, ученые, студенты и другие специалисты, владеющие прикладной и аналитической математикой. Так как математический язык понятен не всем, и не каждый способен за быстрое время его изучить, программа становится сложной для восприятия начинающих пользователей. Нагруженный интерфейс и большое количество нюансов отталкивают людей от использования этого продукта, но на самом деле разобраться в любой рабочей среде возможно — достаточно иметь желание. В этой статье разберем такую важную тему, как построение графиков функций в «Маткаде». Это несложная процедура, которая очень часто помогает при расчетах.
Типы графиков
Помимо того что в MathCAD определены быстрые графики, которые вызываются с помощью горячих клавиш, существуют и другие графические приложения. Например, пользователь может в шапке программы найти раздел «Вставка», а в ней — подраздел «График», в котором можно просмотреть все доступные графики в «Маткаде»:
- График X-Y — показывает зависимость одной величины от другой. Самый распространенный тип, который позволяет быстро оценить и исследовать зависимости.
- Полярный график — использует полярные координаты. Суть графика — показать зависимость одной переменной от другой только в полярной координатной плоскости.
- График поверхности — создает поверхность в пространстве.
- Векторное поле, 3-D график разброса, столбчатая 3-D диаграмма используются для других специальных целей.
Построение графика функции
Невозможно научиться работать с вычислительной средой без примеров, поэтому будем разбираться в MatchCAD на шаблоне.
Допустим, задана функция f(x) = (e^x/(2x-1)^2)-10 в интервале [-10;10], которую необходимо построить и провести исследование. Прежде чем приступить к построению графика функции, необходимо данную функцию перевести в математический вид в самой программе.
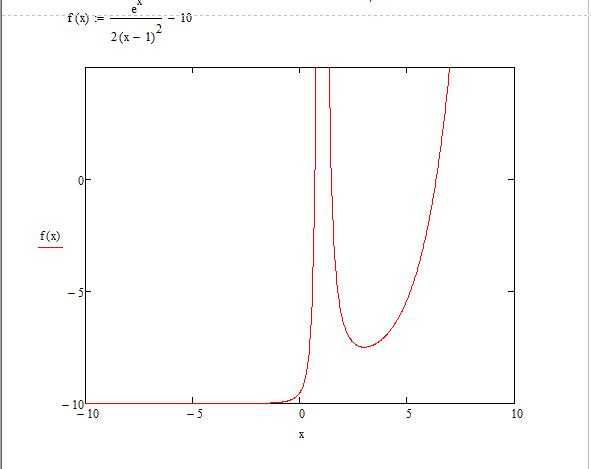
- После того как функция была задана, следует вызвать окно быстрого графика клавишей Shift + 2. Появляется окошечко, в котором расположены 3 черных квадратика по вертикали и горизонтали.
- По вертикали: самый верхний и нижний отвечают за интервалы значений, которые можно регулировать, средний задает функцию, по которой пользователь может построить график в «Маткаде». Крайние черные квадратики оставляем без изменения (значения автоматически присвоятся после построения), а в средний пишем нашу функцию.
- По горизонтали: крайние отвечают за интервалы аргумента, а в средний нужно вписать «х».
- После проделанных шагов нарисуется график функции.
Построение графика по точкам в «Маткаде»
Иногда тяжело задать функцию или посчитать ее значение, поэтому для ее построения используют метод диапазонов. В техническом задании может быть дан только диапазон значений, по которому необходимо воспроизвести изображение.
- Зададим диапазон значений для аргумента, в рассматриваемом случае x:=-10,-8.5.. 10 (символ «..» ставится при нажатии на клавишу «;»).
- Для удобства можем отобразить получившиеся значения «х» и «у». Для первого случая используем математическую формулировку «х=», а для второго — «f(x)». Наблюдаем два столбика с соответствующими значениями.
- Построим график, используя сочетание клавиш Shift + 2.
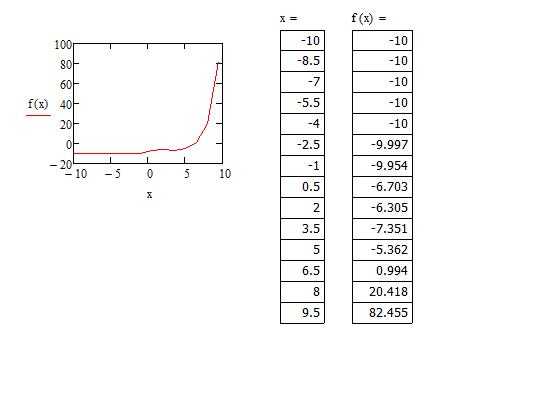
Заметим, что та часть графика, которая устремлялась вверх, исчезла, а на месте нее образовалась непрерывная функция. Все дело в том, что в первом построении функция претерпевала разрыв в некой точке. Второй график был построен по точкам, но, очевидно, что точка, которая не принадлежала графику, не отображена здесь — это одно из особенностей построения графиков по принципу точек.
Табуляция графика
Чтобы избавится от ситуации, где функция претерпевает разрыв, необходимо протабулировать график в «Маткаде» и его значения.

- Возьмем известный нам интервал от -10 до 10.
- Теперь запишем команду для переменного диапазона — x:=a,a + 1 .. b (не стоит забывать, что двоеточие — результат нажатия клавиши «;»).
- Смотря на заданную функцию, можно сделать вывод о том, что при значении «х=1» будет происходить деление на ноль. Чтобы без проблем протабулировать функцию, стоит исключить эту операцию так, как показано на картинке.
- Теперь можно наглядно отобразить значения в столбиках, как мы это делали с построением по точкам. Табуляция выполнена, теперь все значения с шагом в одну единицу соответствуют своим аргументам. Обратите внимание, что на «х=1» значение аргумента не определенно.
Минимум и максимум функции
Чтобы найти минимум и максимум функции на выбранном участке графика в «Маткаде», следует использовать вспомогательный блок Given. Применяя этот блок, необходимо задать интервал поиска и начальные значения.

- В рассматриваемом случае начальное значение x:=9.
- Запишем рабочую команду для поиска максимального значения — Xmax=Maximize(f,x) и вычисляем значение через знак равенства.
- Через блок Given запишем условие для x.
- Задаем минимум функции по аналогии с максимумом.
- Результаты получились следующими: значение минимума на графике с указанным интервалом f(x) = 2,448*10198, а значение минимума f(x) = -10.
fb.ru
Построение графиков в MathCad
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Постановка задачи:
1. Построить график функции f(x) согласно варианту из таблицы №1. Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.
2. Построить два совмещенных графика f1(x) и f2(x), где f1(x)-f2(x)=f(x) на одной координатной плоскости. Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.
3. Скопировать график функции f(x), на нем изменить стиль осей с ограничения на пересечение.
4. Найти точные корни уравнения f(x)=0, используя функцию root.
Типовой пример:
Задание 1. Построить график функции . Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.
1. Выбираем на Панели инструментов графики (Graph) кнопку Координаты X-Y (X-Y-Plot) – появится пустой шаблон графика.
2. Вводим в метку оси y – функцию , а в метку оси x – неизвестную переменную x, нажимаем Enter – появится график функции.
3. Там, где функция пересекается с осью ox, там находятся корни уравнения. Отформатируем график для нахождения приближенных значений корней. Для этого:
3.1. щелкаем по графику левой кнопкой мыши, изменяем минимальные и максимальные пределы изменения по x (-5;5), по y (-3;3) и нажимаем Enter;
3.2. два раза щелкаем мышью по графику – появится диалоговое окно Formatting Currently Selected X-Y Axes. Окно содержит 4 корешка: Оси X-Y (X-Y Axes), Следы (Traces), Ярлыки (Labels), По умолчанию (Defaults).
3.3. в корешке Оси X-Y (X-Y Axes) расположены пункты для выбора форматирования осей графика:
Мерн. линейка (Log Scale) – нумерует оси в логарифмической последовательности;
Линии сетки (Grid Lines) – выводит вспомогательные линии сетки;
Пронумеровать (Numbered) – выводит нумерацию осей;
Автомасштаб (Autoscale) – устанавливает автоматический масштаб;
Показать маркеры (Show Markers) – устанавливает режим показа меток;
Авторешетка (Auto Grid) – устанавливает число вспомогательных линий сетки =2.
Число клеток решетки (Number Of Grid) – установка числа вспомогательных линий сетки.
Стиль осей (Axes Style) – позволяет выбрать стиль изображения осей графика:
Блочный (Boxed) – выводит график в рамке без осей;
Скрещив. (Crossed) – выводит график с осями;
Нет (None) – выводит график без осей и рамки.
Равные веса (Equal Scale) – устанавливает одинаковый масштаб по оси x и y.
Для нашего графика ставим галочки по каждой оси: Линии сетки (Grid Lines), Пронумеровать (Numbered), устанавливаем Число клеток решетки (Number of Grids) по оси x – 10, по оси y – 6, выбираем стиль осей — Блочный (Boxed).
3.4. в корешке Traces (Следы) находятся пункты для форматирования линий графика.
Подпись (Legend Label) – условный номер линии графика;
Символ (Symbol), Линия (Line), Цвет (Color), Тип (Type), Ширина (Weight) – устанавливают характеристики линии на графике.
Скрыть аргументы (Hide Arguments) – убирает с экрана подписи осей x и y;
Скрыть легенду (Hide Legend) – убирает с экрана подпись линии графика.
Для нашего графика меняем Цвет (Color) на голубой (blue) и ширину (Weight) делаем =2.
4. С помощью трассировки находим приближенные корни уравнения. Для этого щелкаем правой кнопкой по графику, выбираем команду Трассировка (Trace). С появлением окна X-Y-Trace щелкаем по кривой левой кнопкой мыши в точке пересечения кривой графика и оси x – в окне появляются значения x,y, где x – приближенный корень уравнения.
5. Оформить задание 1 как показано на рис. 1.
Рис. 1. График функции f(x)
Задание 2. Построить два совмещенных графика f1(x) и f2(x), где f1(x)-f2(x)=f(x) на одной координатной плоскости. Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.
1. Разобьем функцию на две, перенеся в правую часть, получим . Построим на одном графике две функции y= и y= . Для этого выбираем кнопку X-Y-Plot – появится пустой шаблон графика.
2. Вводим в метку оси y — , затем ,, затем , а в метку оси x – неизвестную переменную x, нажимаем Enter – появится совмещенный график двух функций.
3. Там, где функции и пересекаются, там находятся корни уравнения. Отформатируем график аналогично, как в прошлом задании. С помощью трассировки найдем приближенные корни уравнения.
4. Оформить задание 2 как показано на рис. 2.
Рис. 2. Совмещенный график функций
Задание 3. Скопировать график функции f(x), на нем изменить стиль осей с ограничения на пересечение.
1. Выделяем график функции , обведя вокруг него рамку. В меню Правка (Edit) выбираем команду Копировать (Copy). Устанавливаем курсор там, где будет располагаться копируемый график. Выбираем в меню Правка (Edit) команду Вставить (Paste).
2. Два раза щелкаем мышью по графику – появится диалоговое окно Formatting Currently Selected X-Y Axes. В корешке Оси X-Y (X-Y Axes) галочку сменим с Блочный (Boxed) на Скрещив. (Crossed)
3. Оформить задание 3 как показано на рис. 3.
Рис. 3. График функции с осями
Задание 4. Найти точные корни уравнения f(x)=0, используя функцию root.
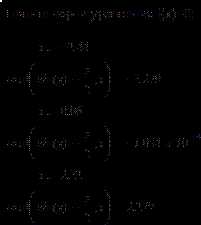
Варианты заданий:
Таблица 1
| № | Вид функции f(x) | № | Вид функции f(x) |
| 1. | sin(x) + 4x – 1 | 19. | x1/2– 2sin(x) |
| 2. | x3 + 5x – 3 | 20. | 1/(2x) – cos(x) |
| 3. | ex + x2 – 3 | 21. | 3sin(x) – x2 + 1 |
| 4. | ex + 2x – 2 | 22. | cos(x) – 2x2 |
| 5. | x3 + 5x2 – 1 – x | 23. | x1/3 – cos(3x) |
| 6. | x2 — 20sin(x) | 24. | tg(x) – 2x |
| 7. | ctg(x) – x/10 | 25. | lg(x) – 2cos(x) |
| 8. | x3 – 3x2 – 9x + 2 | 26. | 2ln(x) – x3 + 6 |
| 9. | x3 – 6x – 8 | 27. | 3ln(x) – x/4 – 1 |
| 10. | tg(0,5x ) – x2 | 28. | 2ln(x) – 1/x |
| 11. | 5x – 1 – 2cos(x) | 29. | ex + x2 – 2 |
| 12. | ctg(x) – x/2 | 30. | x3 + 4x2 – 8 |
| 13. | e-x – (x – 1)2 | 31. | ln(x) + 7/(2x + 6) |
| 14. | x×ln(x) – 1 | 32. | e-x — x2 |
| 15. | 2x – 2x2 + 1 | 33. | ln(x) – x-2 |
| 16. | x — 0,5sin(x) – 2 | 34. | x — sin(x) – 0,25 |
| 17. | 2cos(x) – (x2)/2 | 35. | x — 3cos2(x) |
| 18. | x2 – (x)–2 + 10x |
Контрольные вопросы:
Уметь:
- Изменять максимальные и минимальные пределы по оси x и по оси y.
- Изменять размер сетки по оси x и по оси y.
- Строить вспомогательные линии по оси x и по оси y.
- Изменять цвет и толщину кривой графика.
- Найти корни а) приближенные с помощью трассировки и б) точные.
megapredmet.ru
Построение графиков в MathCad | Cl-Box
При решении задач в MathCad часто возникает необходимость построить график, будь то график функции или график по каким либо расчетным данным. В этой статье мы разберем как строятся графики в MathCad. В этой статье мы не будем рассматривать само решение задач, его Вы можете найти в других статьях, ссылка в конце статьи.
Построение графика функции в MathCad
1.1. Рассмотрим построение на примере функции sin, для этого введем в Маткад следующее (думаю как пользоваться инструментами ввода информации подробно рассматривать не надо, а если вдруг возникнут какие-либо трудности с вводом советую почитать статью Расчаты в MathCad ):
Не забываем что необходимо ставить не знак «равно» а именно знак «определения».
1.2. Теперь нам нужно создать сам график, для этого нажимаем на пункт меню Добавить, выбираем строку Графики, и в появившемся списке выбираем X—Y график
1.3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)
После ввоза названий полей кликаем в любой области вне поля графика
В итоге мы получаем готовый график функции синуса:
Построение графика в MathCad по данным
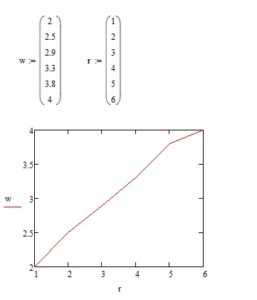
2.1. Для начала введем данные графика, для этого вводим определитель (у меня это w и r) и добавляем матрицу нужным размером (в моем случае 6х1, это 6 строк, 1 столбик) и вводим в нее свои данные для графика. Вот что получилось у меня:
2.2. Теперь повторяем действия указанные в пункте 1.2. этой статьи (т.е. добавляем график)
2.3. Как и в пункте 1.3. этой статьи заполняем название осей, только на этот раз у нас будут определители наших данных
2.4. При необходимости совместить два графика на одном делаем следующее: добавляем еще один блок данных, ставим курсор после определителя w в графике и нажимаем поставить запятую (напоминаю, что запятая на русской раскладке и на английской раскладке это разные клавиши, и так как мы работаем в Маткаде используя английскую раскладку нам нужна запятая именно английской раскладки), после этого вводим определитель во вторую (появившеюся) строку на нашем графике.
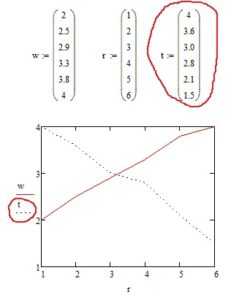
Теперь у нас получилось два пересекающихся графика (конечно же то как он будет выглядеть зависит от данных)
Форматирование графика в MathCad
Созданный график по умолчанию очень бледный и Вам наверное захочется сделать его немого поярче.
3.1. На графике нажимаем ПКМ (правой клавишей мыши) и в контекстном меню выбираем пункт Формат…
В открывшемся диалоговом окне переходим на вкладку Графики
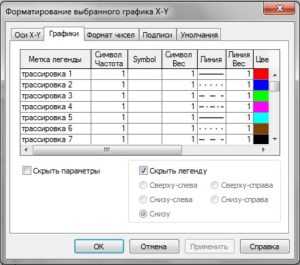
Тут мы видим табличку строка трассировка 1 соответствует первой кривой нашего графика, трассировка 2 соответственно второй. Столбик Линия соответствует типу линии на нашем графике (сплошная, прерывистая, точка-тире и т.п.). Столбик Линия Вес соответствует толщине нашей линии. И Цвет соответственно цвету. Я в своем примере изменю только толщину линии, и по второму графику тип линии с точек на пунктир для этого в двух верхних строках столбика Линия Вес поставлю цифру 2 и в столбике Линия поменяю тип линии, после чего нажму Применить
Вот что получилось:
Я думаю не надо объяснять как изменять размер графика, если это необходимо.
автор: Admin
cl-box.ru
Графики в «Маткаде» — построение и исследование
Программа MathCAD обеспечивает стабильное поддержание своих функций уже долгие годы. В этой вычислительной среде работают экономисты, ученые, студенты и другие специалисты, владеющие прикладной и аналитической математикой. Так как математический язык понятен не всем, и не каждый способен за быстрое время его изучить, программа становится сложной для восприятия начинающих пользователей. Нагруженный интерфейс и большое количество нюансов отталкивают людей от использования этого продукта, но на самом деле разобраться в любой рабочей среде возможно — достаточно иметь желание. В этой статье разберем такую важную тему, как построение графиков функций в «Маткаде». Это несложная процедура, которая очень часто помогает при расчетах.
Типы графиков
Помимо того что в MathCAD определены быстрые графики, которые вызываются с помощью горячих клавиш, существуют и другие графические приложения. Например, пользователь может в шапке программы найти раздел «Вставка», а в ней — подраздел «График», в котором можно просмотреть все доступные графики в «Маткаде»:
- График X-Y — показывает зависимость одной величины от другой. Самый распространенный тип, который позволяет быстро оценить и исследовать зависимости.
- Полярный график — использует полярные координаты. Суть графика — показать зависимость одной переменной от другой только в полярной координатной плоскости.
- График поверхности — создает поверхность в пространстве.
- Векторное поле, 3-D график разброса, столбчатая 3-D диаграмма используются для других специальных целей.
Построение графика функции
Невозможно научиться работать с вычислительной средой без примеров, поэтому будем разбираться в MatchCAD на шаблоне.
Допустим, задана функция f(x) = (e^x/(2x-1)^2)-10 в интервале [-10;10], которую необходимо построить и провести исследование. Прежде чем приступить к построению графика функции, необходимо данную функцию перевести в математический вид в самой программе.
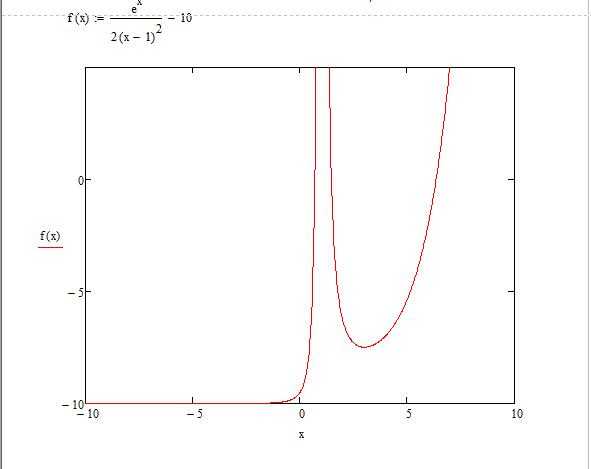
Построение графика по точкам в «Маткаде»
Иногда тяжело задать функцию или посчитать ее значение, поэтому для ее построения используют метод диапазонов. В техническом задании может быть дан только диапазон значений, по которому необходимо воспроизвести изображение.
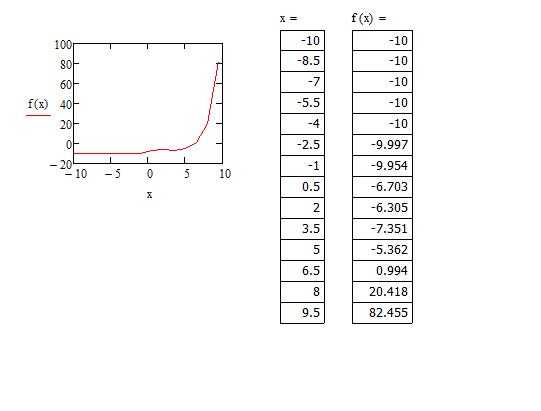
Заметим, что та часть графика, которая устремлялась вверх, исчезла, а на месте нее образовалась непрерывная функция. Все дело в том, что в первом построении функция претерпевала разрыв в некой точке. Второй график был построен по точкам, но, очевидно, что точка, которая не принадлежала графику, не отображена здесь — это одно из особенностей построения графиков по принципу точек.
Табуляция графика
Чтобы избавится от ситуации, где функция претерпевает разрыв, необходимо протабулировать график в «Маткаде» и его значения.

Минимум и максимум функции
Чтобы найти минимум и максимум функции на выбранном участке графика в «Маткаде», следует использовать вспомогательный блок Given. Применяя этот блок, необходимо задать интервал поиска и начальные значения.

Источник
ruud.ru
Лабораторная работа №3 Построение графиков функций в MathCad
Цель работы
Овладеть навыками построения графиков в MathCAD.
Задачи:
— умение применять различные способы построения двумерных графиков в Mathcad;
Порядок выполнения
Задание №1: Построить график функции заданный в виде:
а) таблицы:
x | -3.5 | -3 | -1.7 | 0 | 1.1 | 3.7 |
y | 11.21 | 9.99 | 3.6 | 0.65 | -5 | -8.7 |
б) функции y=f(x),
где 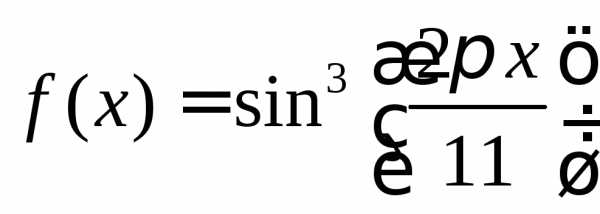 ,
на отрезке [
,
на отрезке [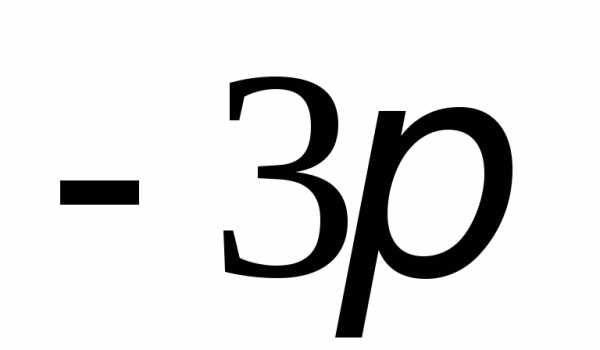 ;
; ]
]
а). 1. Сформировать векторы данных X и Y.
2. Выполнить команды: Добавить – Графики – X—Y график.( рис.10).
3. Ввести исходные данные т.е. в поле оси абсцисс ввести x, а в поле оси ординат y.
4. Нажать Enter (рис.10).
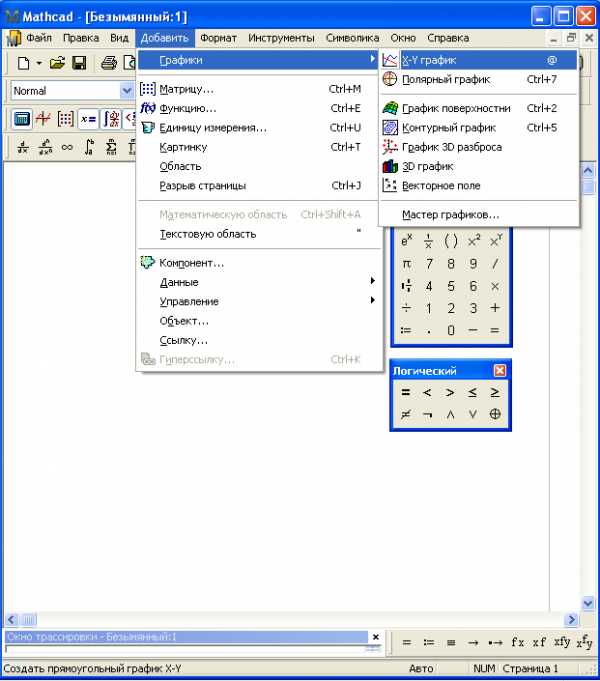
Рис 10. Операции над числами
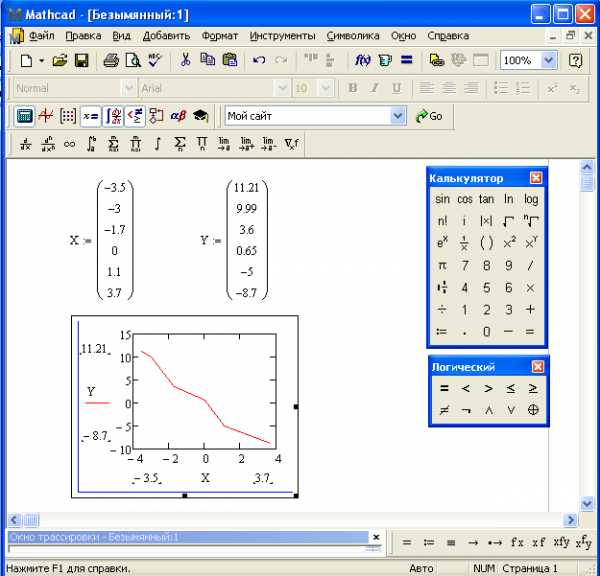
Рис 11. Построение графика
б). 1. Выбрать команды: Добавить – Графики – X—Y график..
2. на оси абсцисс
указать интервал от 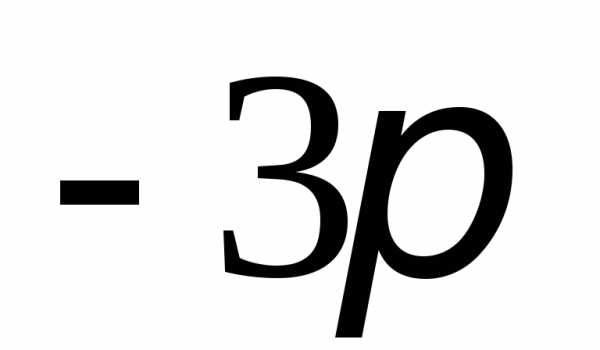 до
до ,
на оси ординат задать функцию.
,
на оси ординат задать функцию.
3. Для ввода 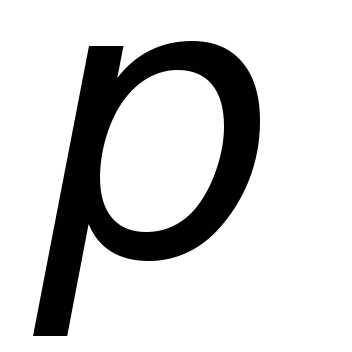 ,
необходимо выбрать:Вид
– панели инструментов – греческая.
,
необходимо выбрать:Вид
– панели инструментов – греческая.
4. Нажать Enter (рис.12).
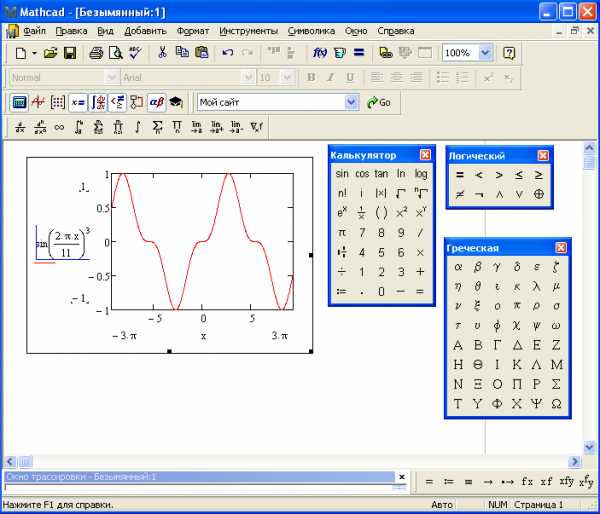
Рис 12. Построение графика
Самостоятельно:
Построить графики функций, заданные в виде таблицы и аналитически:
1.
X | -7.7 | -5 | -3.4 | -2.5 | -1 | 0.8 | 1.3 | 2 | 5 |
Y | 0 | 11 | -5.55 | -6.6 | 6 | 23 | 0 | -7 | -9 |
2.
X | 12 | 11.54 | 8 | 3.43 | 2.54 | 1 | 0.99 | 2.55 | 4.54 |
Y | 11 | 4.876 | 2 | 1.51 | 0 | -3.43 | -5 | -7.76 | -10 |
y=f(x), где
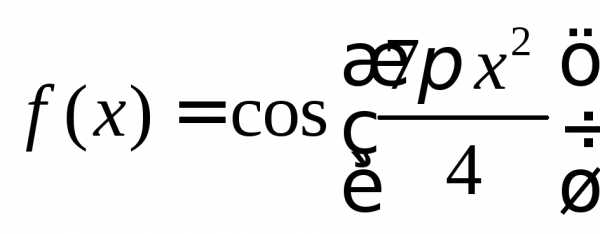 ,
на отрезке [
,
на отрезке [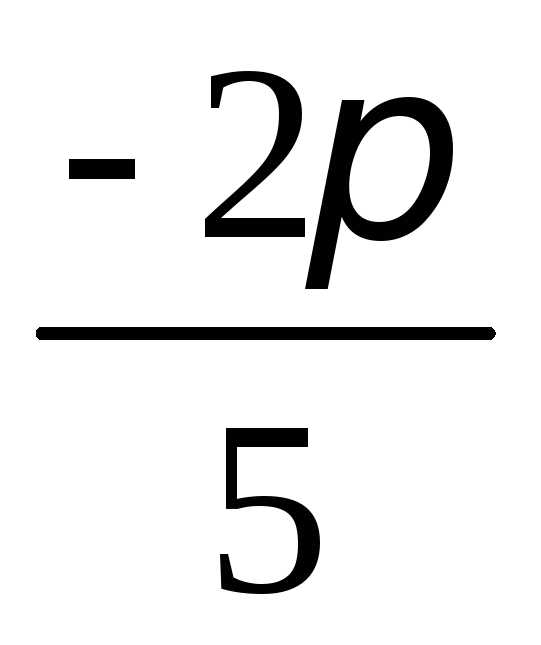 ;
;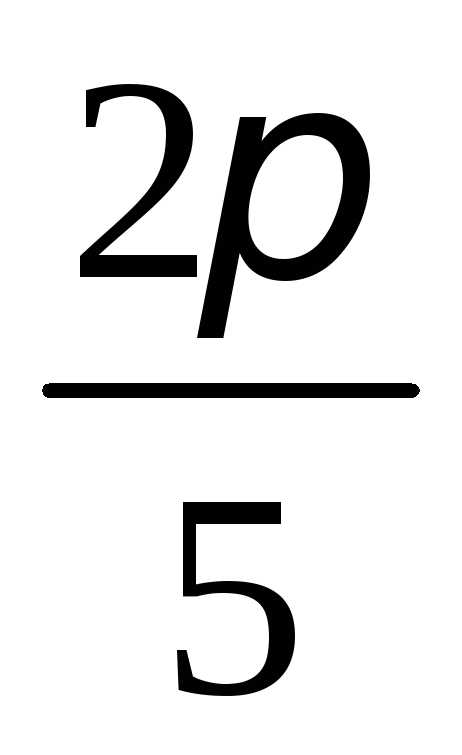 ]
]y=f(x), где
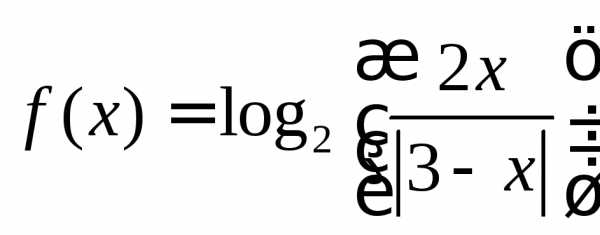 ,
на отрезке [
,
на отрезке [ ;
;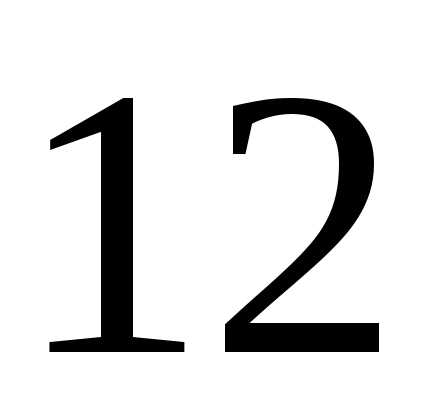 ].
].y=f(x), где
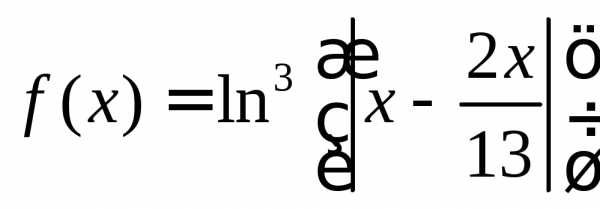 ,
на отрезке [
,
на отрезке [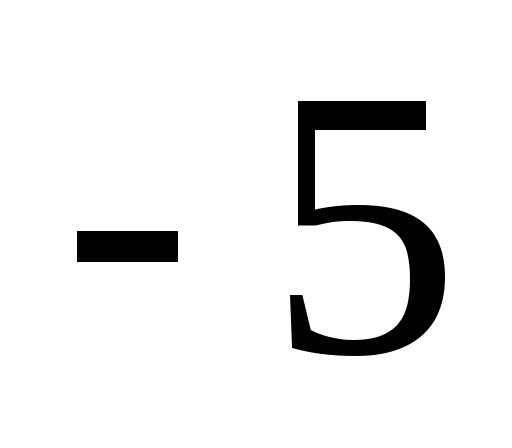 ;
; ].
].Построить на одном графике следующие функции:
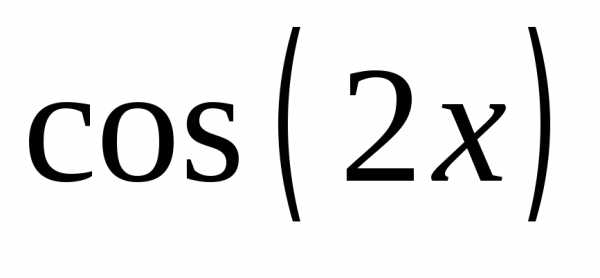 ,
,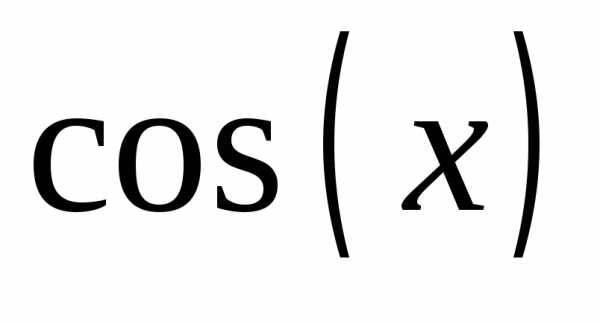 ,
,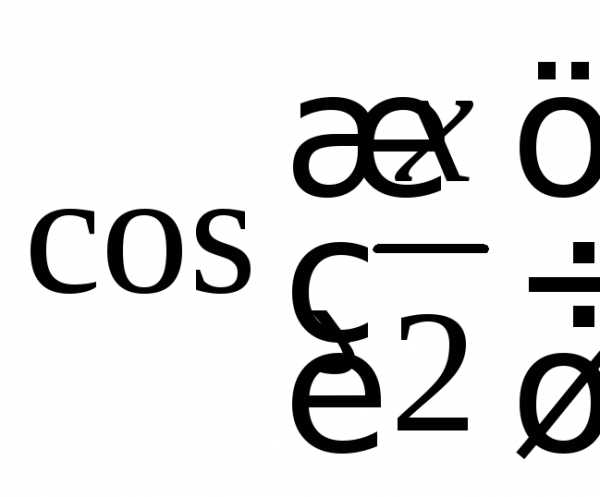 ,
(рис. 13). Функции перечислить через
запятую.
,
(рис. 13). Функции перечислить через
запятую.
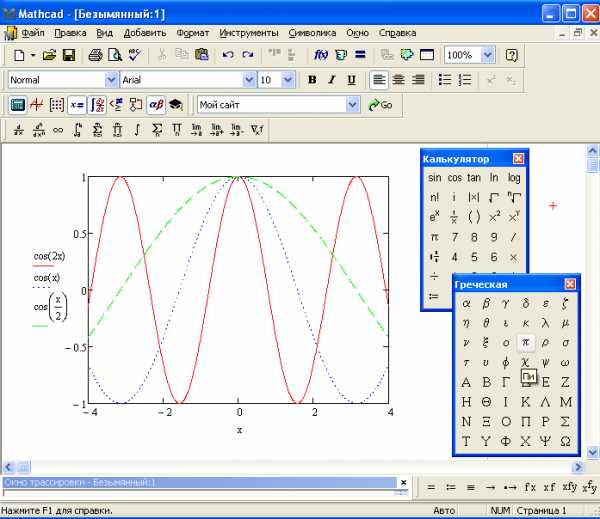
Рис 13. График тригонометрической функции
Задание №2: Построить график функции в полярной системе координат:
Полярная система координат состоит из полюса О и лучей, выходящих из точки О, один из которых, ОХ, называется полярной осью.
График строится
аналогично графику в декартовой системе
координат. Задается: 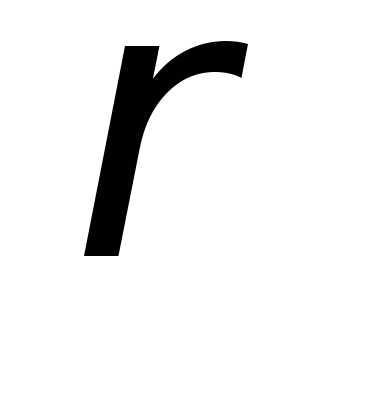 и
и ,
полярными координатами.
,
полярными координатами.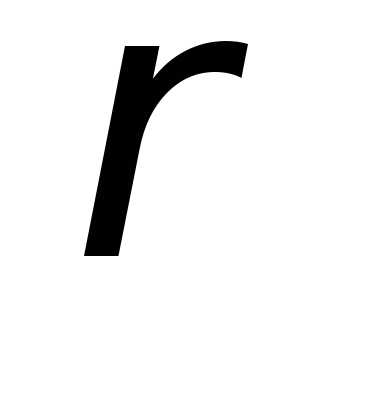 — полярный радиус,
— полярный радиус, — полярный угол.
— полярный угол.
Пример: Построить
график функции: 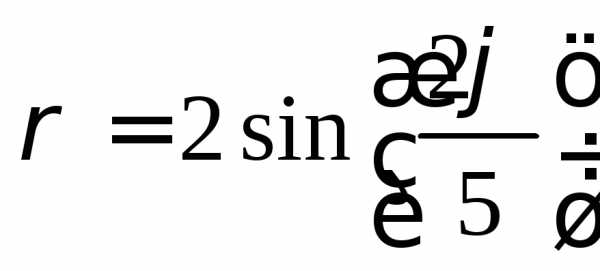 (рис.14).
(рис.14).
Самостоятельно:
Построить график функции:
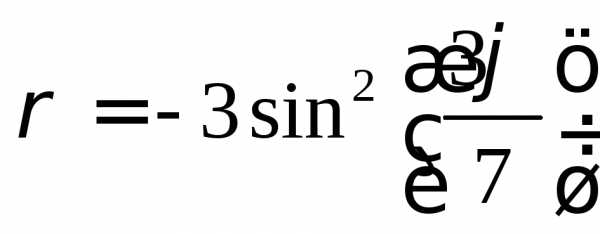
Построить график функции:
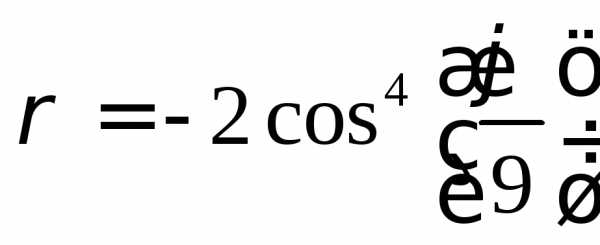
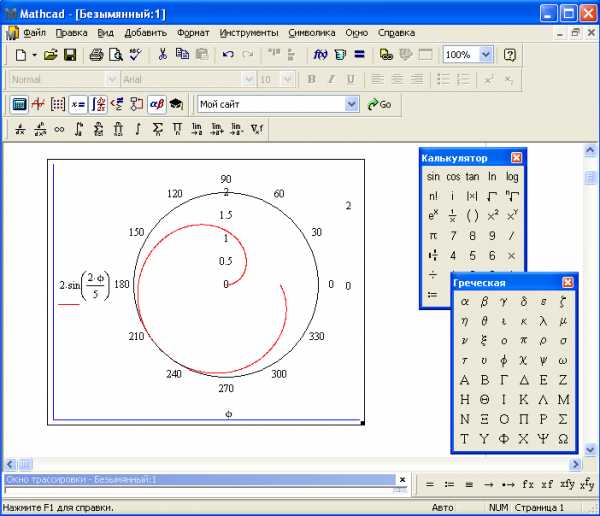
Рис 14. График функции
Задание №3: Построить график функции, заданной параметрически:
Задание функции
при помощи равенств 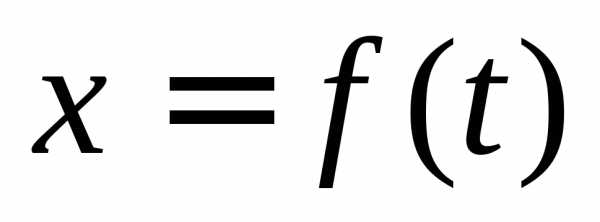 и
и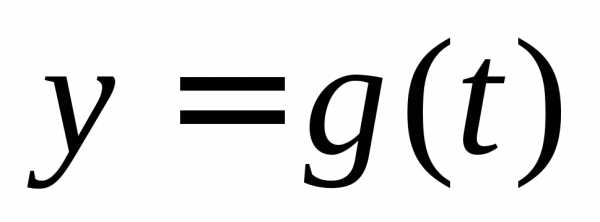 ,
когда
,
когда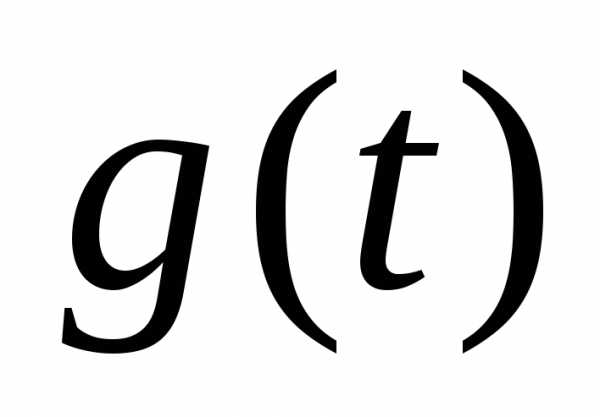 зависит
от
зависит
от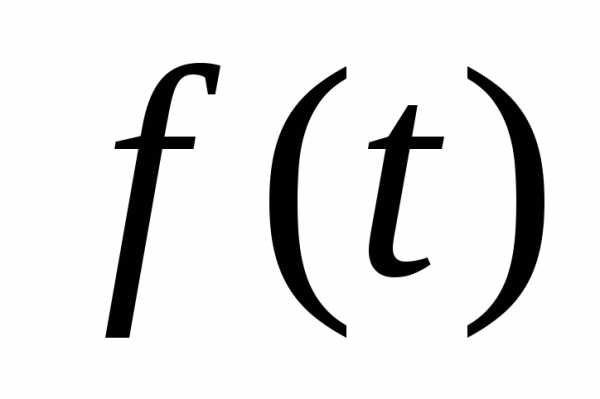 или наоборот, называют параметрическим,
а
или наоборот, называют параметрическим,
а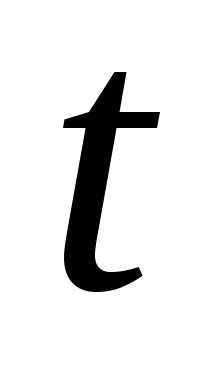 — параметром.
— параметром.
Пример: полукубическая
парабола:
,
параметрически представляется в виде: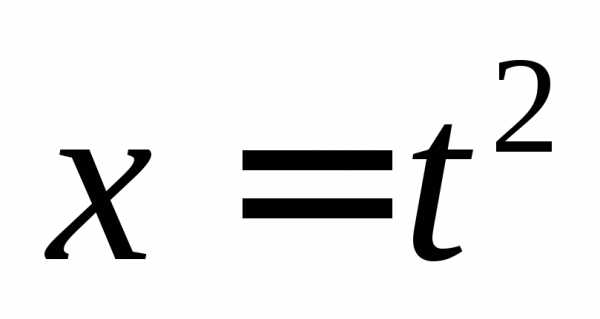 ,
,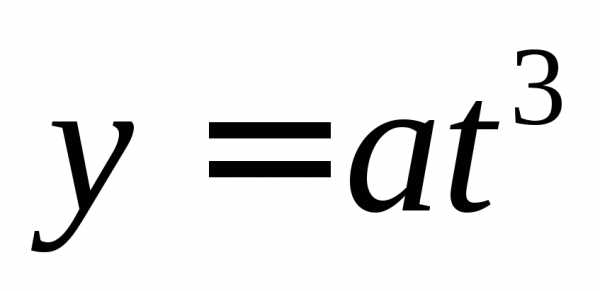 ,
при
,
при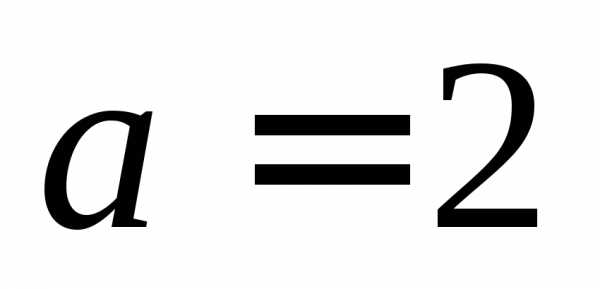 (рис.15).
(рис.15).
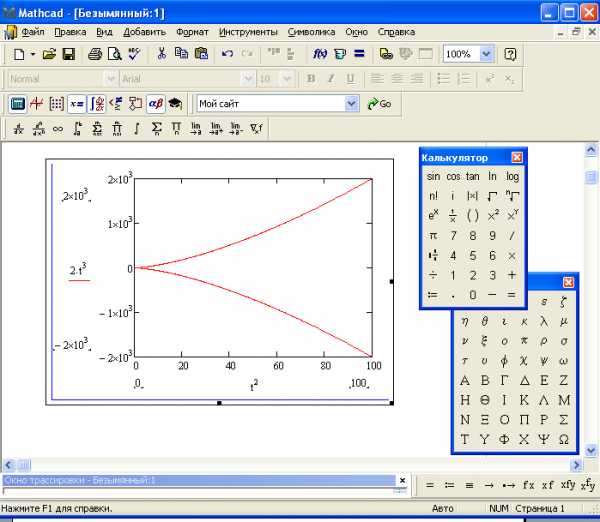
Рис 15. График функции, заданной параметрически
Самостоятельно:
1. Изучить команды трассировки и увеличения построенных графиков.
2. Построить графики функций:
а). 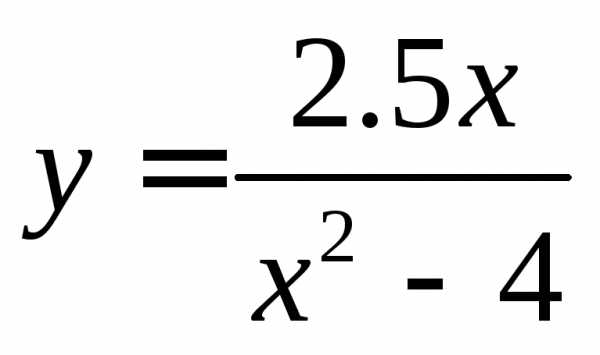
б). 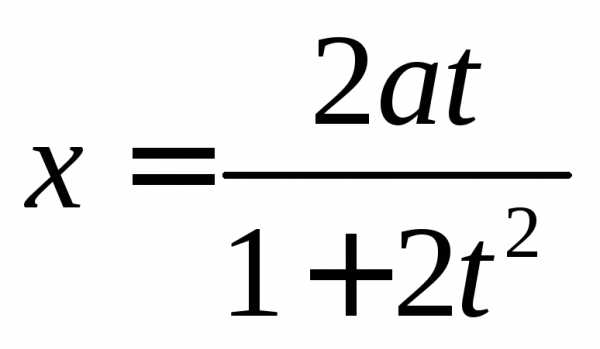 и
и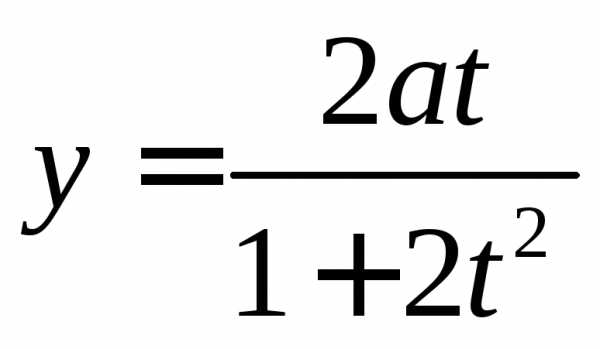 ,
еслии
,
еслии
в). 
Лабораторная работа №4 Построение трехмерных графиков функций в MathCad
Цель работы
Овладеть навыками построения графиков в MathCAD.
Задачи:
— умение применять различные способы построения трехмерных графиков в Mathcad;
Порядок выполнения
График поверхности (трехмерный) – это график, положение точки в котором определяется значениями трех координат. Прямоугольная система координат в пространстве состоит из начала координат и трех перпендикулярных прямых пространства, не лежащих в одной плоскости и пересекающихся в начале координат.
Функция в пространственной системе координат задается:
1. формулой, функция бывает как явной так и неявной.
2. таблицей с двойным входом, т.е. в верхней строке значения одного аргумента, в левом столбце значения другого, а на пересечении записывают соответствующее значение функции.
3. пространственным графиком, представляет собой поверхность в пространственной системе координат, проекция любой точки поверхности на плоскость служит изображением пары значений аргументов x,y, а аппликата данной точки изображает соответствующее значение функции.
Задание №1:
Построить график функции, заданной в виде таблицы:
1. Для вставки таблицы необходимо выполнить следующие команды: Добавить – Данные – Таблицу.
2. Заполнить таблицу числовыми значениями.
3. Для построения графика необходимо выбрать: Добавить – Графики – График поверхности.( рис. 16).
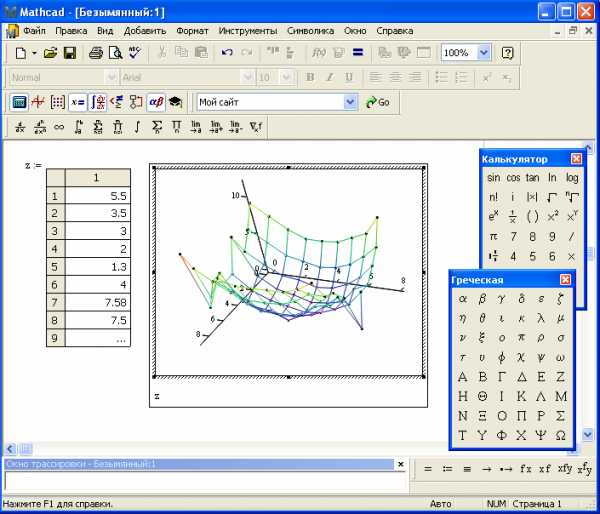
Рис 16. График поверхности
Можно форматировать получившийся график с помощью диалогового окна ( рис. 17) со следующими вкладками:
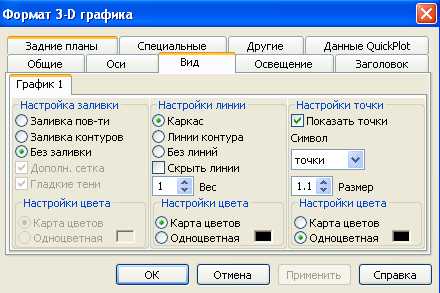
Рис 17. Форматирование графика
Вкладка «Вид» позволяет менять фон графика, заливку, линии. На вкладке «Общие» можно задать угол поворота, угол наклона и вращения, тип графика.
Задание №2:
Построить график функции:
Сначала ввести функцию, затем выбрать Добавить – Графики – График поверхности.( рис. 18).
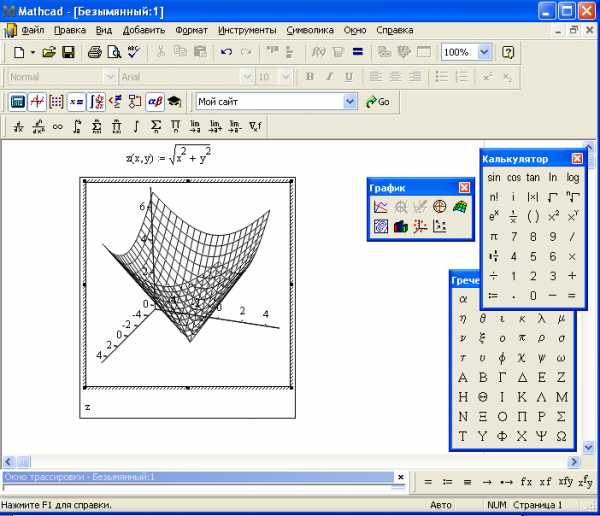
Рис 18. Форматирование графика
Типы графиков:
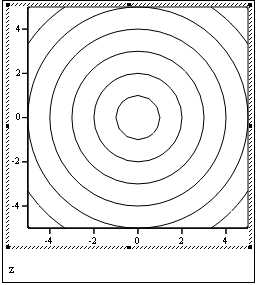
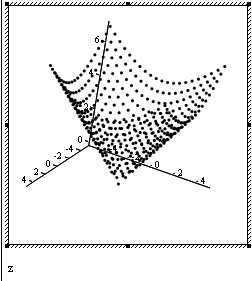
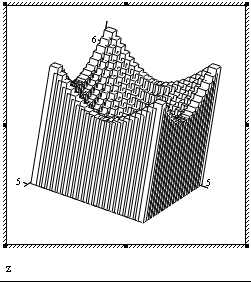
Контурный график Точечные данные График полосы
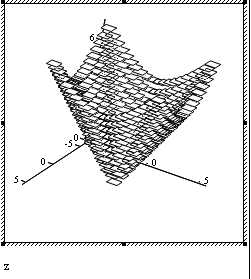
График исправления
Самостоятельно:
1. Построить график функции
2. Построить график функции
3. Построить график функции:
4. Построить график функции:
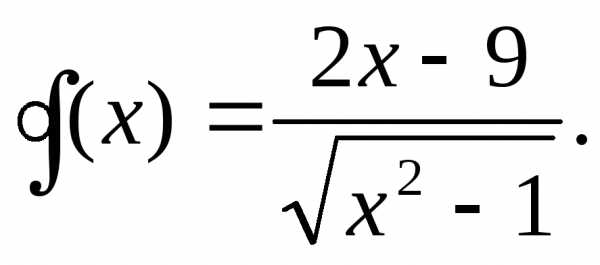
5. Изобразить график:
6. Построить график двух функций в одной области:
7. Изобразить линии, заданные неявно:
8. Построить фигуру, заданную линией:
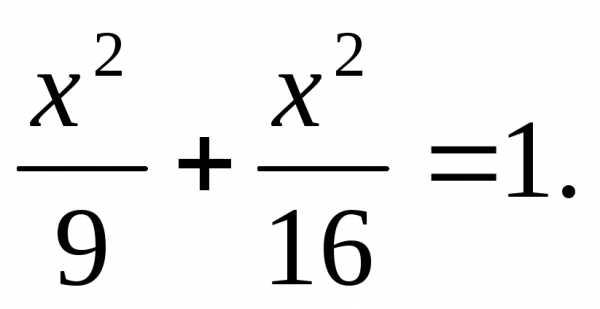
9. Построить на плоскости кривую, заданную в параметрическом виде:
10. Изобразить кривые, заданные в полярных координатах:
studfiles.net
Построение графиков в Маткаде?
Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. «Маткад» способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в «Маткаде»? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в «Маткаде» построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.
Быстрый график в Mathcad
Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.
Итак, перед тем как построить график в «Маткаде», нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.
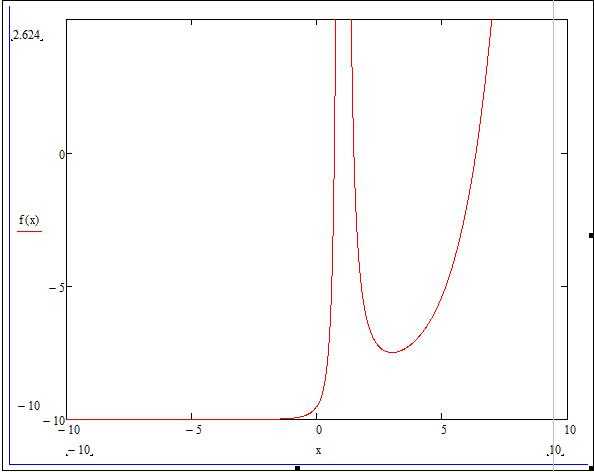
- Для этого необходимо нажать сочетание клавиш Shift+2. Появится окно, в котором будет построен график нашей функции, но предварительно следует ввести все необходимые данные.
- Напротив вертикальной линии находятся 3 черных квадратика: верхний и нижний определяют интервал построения, а средний задает функцию, по которой будет построен график. Зададим функцию f(x) в среднем квадрате, а верхний и нижний оставим без изменения (они отрегулируются автоматически).
- Под горизонтальной чертой также три черных квадратика: крайние отвечают за интервал аргумента, а средний — за переменную. Введем в крайние поля наше значение интеграла от -10 до 10, а в средний — значение «x».
Построение дополнительных графиков
Чтобы понять, как построить несколько графиков в «Маткаде», добавим к нашему техническому заданию небольшое дополнение: построить график производной от заданной функции. Единственное, что нам нужно — в поле графика добавить производную по переменной «x».
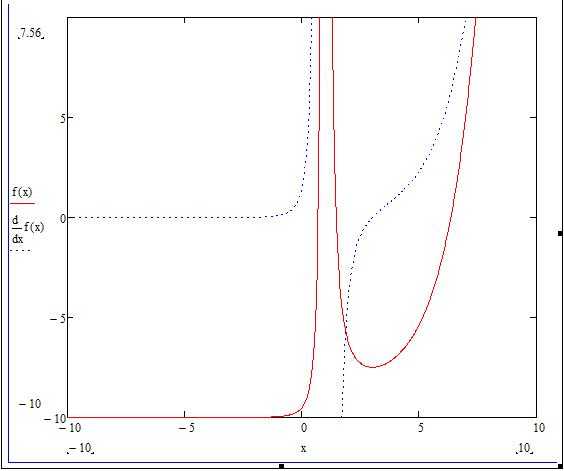
- Открываем наш график и там, где писали функцию, необходимо поставить «,» (запятую). Следом отобразится новая строка снизу, где нам нужно вписать производную: df(x)/dx.
- Отобразился график производной, но для наглядности стоит поменять цвет линии и ее форму. Для этого дважды кликаем по графику — открывается окно с настройками.
- Нам необходим раздел «Трассировка», где в таблице будут перечисляться кривые.
- Выбираем вторую кривую и меняем форму линии на пунктир.
График, построенный по набору значений
Перед тем как построить график в «Маткаде» по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.
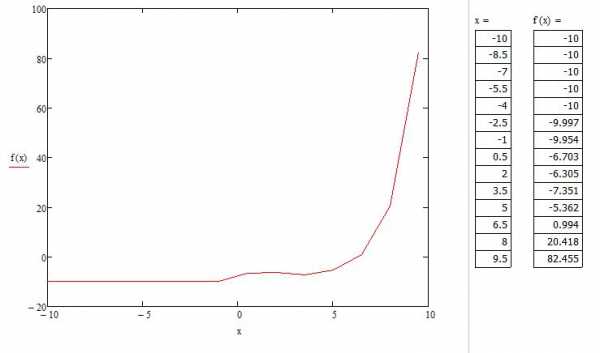
Нам необходимо задать диапазон значений. Для этого присвоим значения переменной (x:=-10,-8.5.. 10). Когда пользователь будет задавать диапазон, ему следует знать, что двоеточие ставится через символ «;». Теперь для визуального восприятия отобразим все значения «х» и «f(x)» в программе. Для этого необходимо ввести «х=» и, соответственно, «f(x)=». Теперь заново построим график функции, только в этот раз по точкам.
- С помощью горячих клавиш Shift+2 вновь вызываем окно с построением графика.
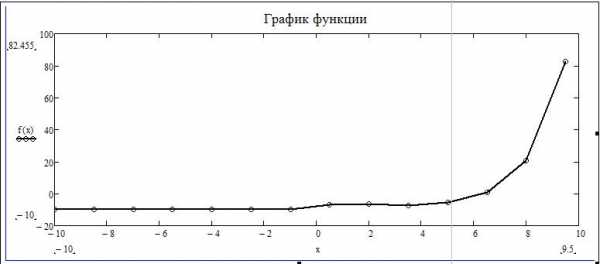
- Зададим функцию f(x), интервал по оси ординат от -20 до 100, интервал по оси абсцисс от -10 до 10, обозначаем переменную «х».
- Происходит автоматическое построение графика, который отличается в некоторых частях от графика функции, построенного аналитически.
Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.
Настройка отображения графика
В этой статье мы уже затрагивали настройки графика. Окно с настройками вызывается двойным нажатием левой кнопкой мыши по графику. В окне форматирования графика есть пять разделов. «Оси X, Y» — содержит информацию про координатные оси, а также отображения вспомогательных элементов. Второй раздел «Трассировка» связан с кривыми линиями построения графика, здесь можно корректировать их толщину, цвет и другое. «Формат числа» отвечает за отображение и расчет единиц. В четвертом разделе можно добавлять подписи. Пятый раздел » По умолчанию» выводит все настройки в стандартную форму.
autogear.ru
Как построить график в «Маткаде»? Советы и рекомендации
Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. «Маткад» способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в «Маткаде»? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в «Маткаде» построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.
Быстрый график в Mathcad
Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.
Итак, перед тем как построить график в «Маткаде», нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.
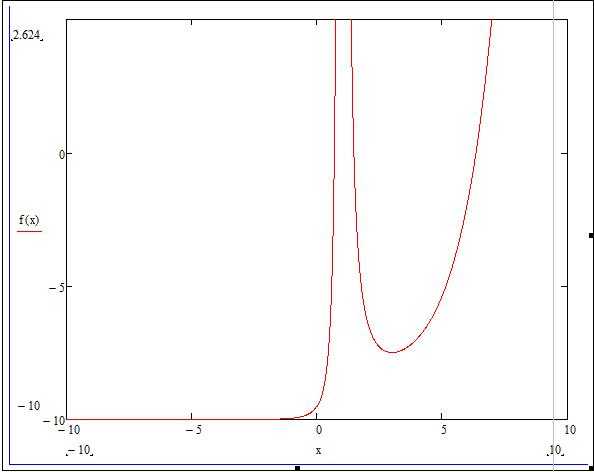
- Для этого необходимо нажать сочетание клавиш Shift+2. Появится окно, в котором будет построен график нашей функции, но предварительно следует ввести все необходимые данные.
- Напротив вертикальной линии находятся 3 черных квадратика: верхний и нижний определяют интервал построения, а средний задает функцию, по которой будет построен график. Зададим функцию f(x) в среднем квадрате, а верхний и нижний оставим без изменения (они отрегулируются автоматически).
- Под горизонтальной чертой также три черных квадратика: крайние отвечают за интервал аргумента, а средний — за переменную. Введем в крайние поля наше значение интеграла от -10 до 10, а в средний — значение «x».
Построение дополнительных графиков
Чтобы понять, как построить несколько графиков в «Маткаде», добавим к нашему техническому заданию небольшое дополнение: построить график производной от заданной функции. Единственное, что нам нужно — в поле графика добавить производную по переменной «x».
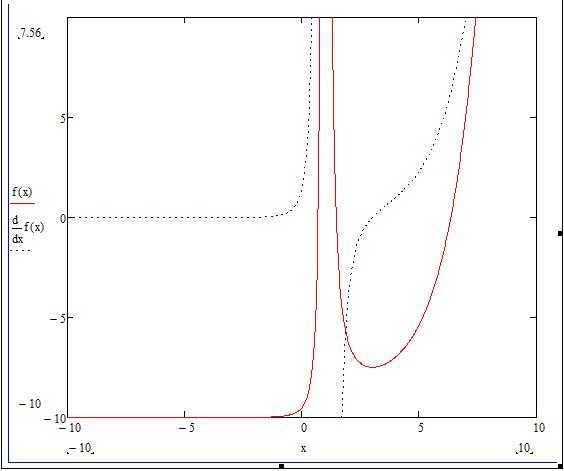
- Открываем наш график и там, где писали функцию, необходимо поставить «,» (запятую). Следом отобразится новая строка снизу, где нам нужно вписать производную: df(x)/dx.
- Отобразился график производной, но для наглядности стоит поменять цвет линии и ее форму. Для этого дважды кликаем по графику — открывается окно с настройками.
- Нам необходим раздел «Трассировка», где в таблице будут перечисляться кривые.
- Выбираем вторую кривую и меняем форму линии на пунктир.
График, построенный по набору значений
Перед тем как построить график в «Маткаде» по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.
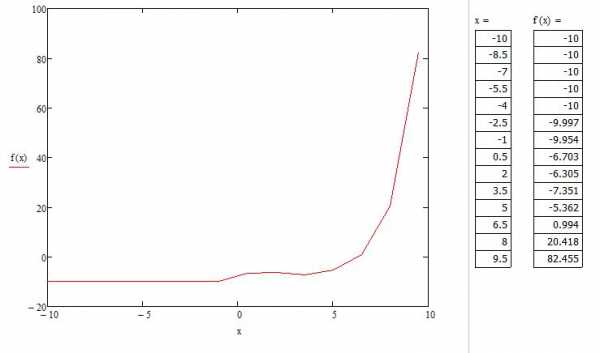
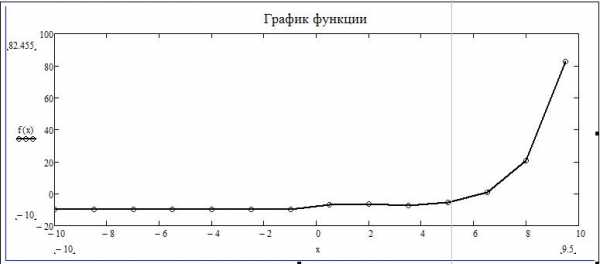
Нам необходимо задать диапазон значений. Для этого присвоим значения переменной (x:=-10,-8.5.. 10). Когда пользователь будет задавать диапазон, ему следует знать, что двоеточие ставится через символ «;». Теперь для визуального восприятия отобразим все значения «х» и «f(x)» в программе. Для этого необходимо ввести «х=» и, соответственно, «f(x)=». Теперь заново построим график функции, только в этот раз по точкам.
- С помощью горячих клавиш Shift+2 вновь вызываем окно с построением графика.
- Зададим функцию f(x), интервал по оси ординат от -20 до 100, интервал по оси абсцисс от -10 до 10, обозначаем переменную «х».
- Происходит автоматическое построение графика, который отличается в некоторых частях от графика функции, построенного аналитически.
Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.
Настройка отображения графика
В этой статье мы уже затрагивали настройки графика. Окно с настройками вызывается двойным нажатием левой кнопкой мыши по графику. В окне форматирования графика есть пять разделов. «Оси X, Y» — содержит информацию про координатные оси, а также отображения вспомогательных элементов. Второй раздел «Трассировка» связан с кривыми линиями построения графика, здесь можно корректировать их толщину, цвет и другое. «Формат числа» отвечает за отображение и расчет единиц. В четвертом разделе можно добавлять подписи. Пятый раздел » По умолчанию» выводит все настройки в стандартную форму.
fb.ru