Решение полиномиальных матричных уравнений MatLab
Урок 16. Численные методы
Элементарные средства решения СЛУ
Функции для решения систем линейных уравнений с ограничениями
Решение СЛУ с разреженными матрицами
Точное решение, метод наименьших квадратов и сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Устойчивый двунаправленный метод
Метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Метод минимизации обобщенной невязки
Квазиминимизация невязки — функция qmr
Вычисление нулей функции одной переменной
Минимизация функции одной переменной
Минимизация функции нескольких переменных
Аппроксимация производных
Аппроксимация Лапласиана
Аппроксимация производных конечными разностями
Вычисление градиента функции
Численное интегрирование
Метод трапеций
Численное интегрирование методом квадратур
Работа с полиномами
Умножение и деление полиномов
Вычисление полиномов
Вычисление производной полинома
Разложение на простые дроби
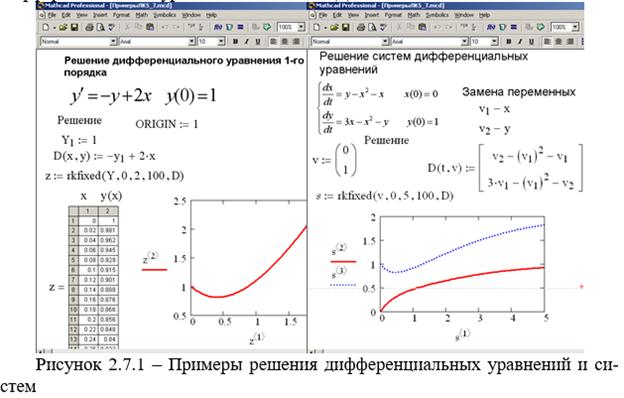
Решение обыкновенных дифференциальных уравнений
Решатели ОДУ
Использование решателей систем ОДУ
Описание системы ОДУ
Дескрипторная поддержка параметров решателя
Пакет Partial Differential Equations Toolbox
Что нового мы узнали?
Приведенная
ниже функция вычисляет собственные значения матричного полинома.
[Х.е] = polyeig(AO,Al,…Ap) — решает задачу собственных значений для матричного полинома степени р вида:
где степень полинома р — целое неотрицательное число, а А 0 , А 1 ,…, А p —
входные матрицы порядка п. Выходная матрица X размера nхnр содержит собственные векторы в столбцах. Вектор е размером пр содержит собственные значения.Пример:
» А=[1:4:5:8:9:12:13:16]
А =
|
|
3
4
|
|||
|
5
6
|
7
8
|
|||
|
9
10
|
11
12
|
|||
|
1314
|
15
16
|
|||
|
»
В=[4:7
|
;2:5;10:13;23:26]
|
|||
|
3
-
|
||||
|
4
5
|
6
7
|
|||
|
2
3
|
4
5
|
|||
|
1011
|
12
13
|
|||
|
2324
|
25
26
|
|||
|
»
[F. |
polyeig(A.B)
|
|||
|
F
=
|
||||
|
0.4373
|
0. |
-0.5426 |
-0.7594 |
|
|
-0.3372
|
-0.4969
|
0.6675
|
-0.1314 |
|
|
-0. |
0.7870
|
0.2927
|
-0.1314 |
|
|
0.5374
|
-0.3591
|
-
0.4176
|
0. |
|
|
a
=
|
||||
|
4.4048
|
||||
|
0. |
||||
|
-0.3229
|
||||
|
-1.0000
|
||||
Нравится
Твитнуть
Благодарю всех за помощь (в т. Суть задачи, приведшей ко всем этим уравнениям, следующая: есть экспериментальные данные (Yex — двумерный массив, Xex — одномерный массив) и некоторый физический закон, позволяющий найти эти данные путем расчета, но с неизвестными параметрами: a, Z, b, X, Y (формулы для расчета записана в числителе E и отнимается от Yex). Эти параметры надо опрелить так, чтобы минимизировать величину E, указанную вами и мной в начале. Но что более важно — необходимо, чтобы ОТНОСИТЕЛЬНАЯ погрешность между любой парой экспериментальных данных (Yex) и расчетных (полученных с использованием a, Z, b, X, Y) была меньше 10% (заданный фиксированный порог). Задача осложняется последним обстоятельством (необходимостью сделать отн. пог. меньше 10%), а также наличием пропусков в исходных экспериментальных значениях Yex.. Для решения задачи я нахожу частные проихзводные по неизвестным параметрам, приравниваю их к нулю, нахожу оптимальные значения параметров и по ним нахожу расчетные значения и сопоставляю с экспериментальными. ————————————————————————————————————————— В связи с этим несколько вопросов: 1) На ваш взгляд, правильно ли (оптимально ли) выбран критерий для минимизации- выражение E (с учетом 10% ограничения)? 2) Поскольку получающаяся система нелинейная и решается численными методами (я это делаю в Matlab), то есть вероятность плохой обусловленности якобиана. Для улучшения обусловленности я проводил нормировку якобиана по столбцам (делил элементы каждого столбца на евклидову норму столбца), получал решение и возвращался к исходному множеству путем домножения на матрицу, обратную матрице якобиана. Обусловленность улучшалась на 10 порядков. Может, есть какие-то еще способы улучшения обусловленности системы? 3) Пока мне не удается для всех случаев получить относительную погрешность в пределах 10%. 4) Какой, на ваш взгляд, оптимальный способ заполнения пропусков с учетом моего критерия (10% относительная погрешность между любой парой эксп. и расчетных данных)? ——————————————————————————————— Я уверен, что та задача, с которой я столкнулся, уже неоднократно решалась. часто требуется сделать относит. погрешногсть между эксперим. и расч. данными меньшей некоторого числа. Заранее признателен за компетентную помощь и советы. С уважением, Dmitry |
решатель сложных уравнений — Googlesuche
AlleBilderVideosBücherMapsNewsShopping
suchoptionen
Калькулятор сложных уравнений — Symbolab
www.symbolab.com › . .. › Алгебра › Уравнения
.. › Алгебра › Уравнения
Бесплатный калькулятор сложных уравнений — шаг за шагом решайте сложные уравнения -шаг.
Решатель уравнений — Wolfram|Alpha
www.wolframalpha.com › калькулятор-решатель уравнений
Бесплатный онлайн-калькулятор уравнений помогает решать линейные, квадратичные и полиномиальные системы уравнений. Ответы, графики, альтернативные формы. 92… · Решить {3x-5y==2,x+2y==-1} · Системы уравнений
Решение уравнений с комплексными числами — Калькулятор онлайн
www.solumaths.com › рассчитать › complexe_solve
Комплексное решение, онлайн-исчисление. Резюме: Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
Решатель уравнений — Mathway
www.mathway.com › Калькулятор › Решатель уравнений
Введите уравнение, которое вы хотите решить, в редактор. Калькулятор уравнений позволяет вам взять простое или сложное уравнение и решить его наилучшим методом.
Решатель систем уравнений с комплексными коэффициентами
www.mathforengineers.com › math-calculators › sys…
Представлен онлайн-калькулятор для решения систем уравнений с комплексными коэффициентами. Калькулятор принимает любое количество уравнений с числом …
Equation Solver — Number Empire
www.numberempire.com ›equationsolver
Окончательный результат решения уравнения упрощен, поэтому он может быть в другом форме, чем вы ожидаете. Оба уравнения с комплексными решениями и …
Синхронные уравнения (сложные) Калькулятор
keisan.casio.com › exec › system
Вычисляет решение одновременных линейных уравнений с n переменными. В переменную разрешен ввод комплексных чисел.
Другой запрос
Какое приложение решает сложные уравнения?
Как решить сложное квадратное уравнение?
Какой самый лучший решатель уравнений?
Калькулятор комплексных чисел — HackMath. net
net
www.hackmath.net › калькулятор › комплексное число
Вычислите выражение с комплексными числами с помощью онлайн-калькулятора. Сделайте базовое комплексное число …, которое удовлетворяет основному уравнению i2 = −1 или j2 = −1.
Комплексные числа: Решение уравнений — с примерами — YouTube
www.youtube.com › смотреть
24.11.2019 · Поддержите канал на Steady: https://steadyhq.com/ru/brightsideofmathsИли поддержите меня через . ..
Дауэр: 16:06
Прислан: 24.11.2019
Как решить СЛОЖНУЮ СИСТЕМУ УРАВНЕНИЙ с помощью … — YouTube
www.youtube.com › смотреть
27.06.2022 · Вот как я решаю сложную систему уравнений с помощью калькулятора Casio FX570.
Дата: 10:51
Прислан: 27.06.2022
Ähnlichesuchanfragen
Решатель уравнений с шагами
Wolfram|Alpha решить систему уравнений
Решить уравнение matlab
Решатель уравнений для x
Решатель уравнений онлайн
Решатель уравнений Wolfram|Alpha
Решатель систем уравнений
Онлайн-решатель математических уравнений
numpy.
 linalg.lstsq — NumPy v1.24 Manual
linalg.lstsq — NumPy v1.24 Manual- linalg.lstsq( a , b , rcond=’warn’ )[источник]
Возвращает решение линейного матричного уравнения методом наименьших квадратов.
Вычисляет вектор x , который приблизительно решает уравнение
а @ х = б. Уравнение может быть недоопределенным, хорошо или переопределенным. (т. е. количество линейно независимых строк из a может быть меньше, равно или больше, чем его количество линейно независимых столбцов). Если и квадратные и имеют полный ранг, то x (но для ошибки округления) является «точным» решением уравнения. В противном случае, x сводит к минимуму Евклидова 2-норма \(||b — ax||\). Если существует несколько минимизирующих решений, возвращается вариант с наименьшей 2-нормой \(||x||\).- Параметры:
- a (M, N) array_like
Матрица «Коэффициент».
- b {(M,), (M, K)} array_like
Значения ординат или «зависимых переменных».
 Если b двумерное,
решение методом наименьших квадратов вычисляется для каждого из K столбцов б .
Если b двумерное,
решение методом наименьших квадратов вычисляется для каждого из K столбцов б .- rcond с плавающей запятой, опционально
Коэффициент отсечки для малых сингулярных значений a . Для целей определения ранга рассматриваются сингулярные значения. как ноль, если они меньше rcond раза больше единственного числа значение a .
Изменено в версии 1.14.0: Если не установлено, выдается FutureWarning. Предыдущее значение по умолчанию из
-1будет использовать машинную точность как параметр rcond , новое значение по умолчанию будет использовать машинную точность, умноженную на max(M, N) . Чтобы отключить предупреждение и использовать новое значение по умолчанию, используйтеrcond=None, чтобы продолжать использовать старое поведение, используйтеrcond=-1.
- Возвращает:
- x {(N,), (N, K)} ndarray
Решение методом наименьших квадратов.
 Если b двумерное,
решения находятся в столбцах K размером x .
Если b двумерное,
решения находятся в столбцах K размером x .- остатки {(1,), (K,), (0,)} ndarray
Сумма квадратов остатков: Квадрат евклидовой 2-нормы для каждого столбца в
б - а @ х. Если ранг a < N или M <= N, это пустой массив. Если b является одномерным, это массив формы (1,). В противном случае форма (K,).- ранг int
Ранг матрицы a .
- s (min(M, N),) ndarray
Сингулярные значения a .
- Повышение:
- LinAlgError
Если вычисления не сходятся.
См. также
-
scipy.linalg.lstsq Аналогичная функция в SciPy.
Примечания
Если b является матрицей, то все результаты массива возвращаются в виде матриц.

 a]=
a]=
 0689
0689
 6375
6375
 3771
3771
 4425
4425
 ч. посредством личных сообщений)!!!
ч. посредством личных сообщений)!!! Пропуски заполняю методом средних, регрессией, а также учетом динамики других непропущенных значений (для даной задачи это имеет смысл).
Пропуски заполняю методом средних, регрессией, а также учетом динамики других непропущенных значений (для даной задачи это имеет смысл).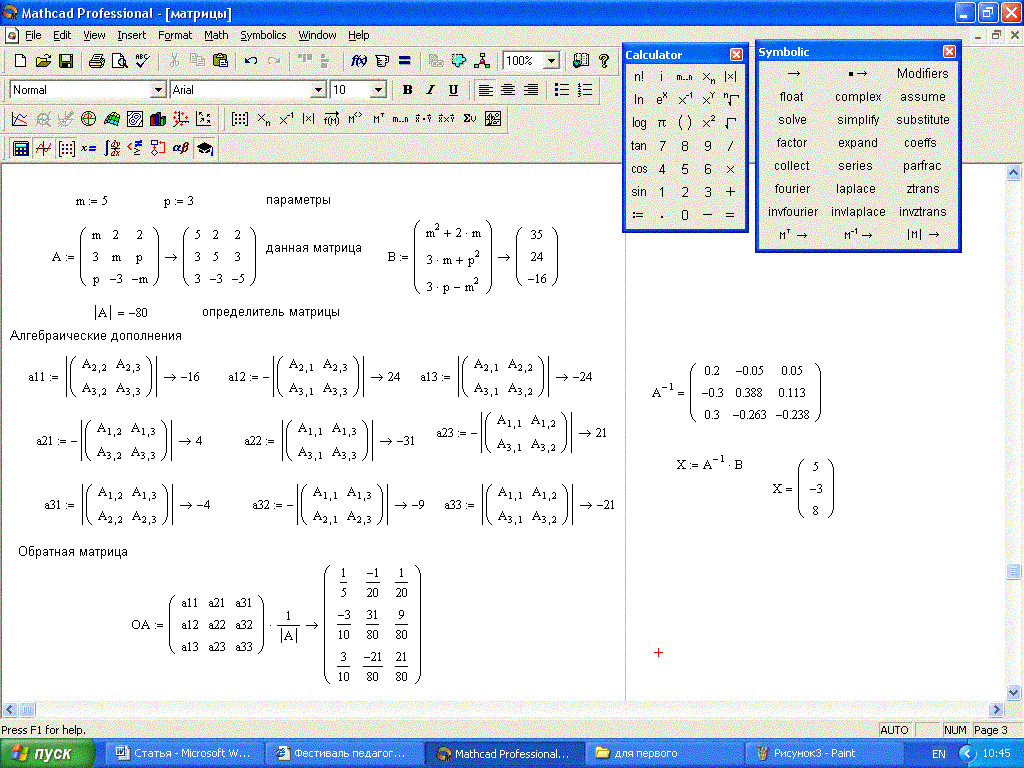 Может, есть какие-то методы уточнения решения системы нелинейныхх уравнений? Например, я пробовал итерационное уточнение, но результат не сильно улучшался.
Может, есть какие-то методы уточнения решения системы нелинейныхх уравнений? Например, я пробовал итерационное уточнение, но результат не сильно улучшался.