Многозначные числа. Классы и разряды. Сумма разрядных слагаемых.
Многозначные числа.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:
13 миллиардов 562 миллионов 6 тысяч 891.
Сумма разрядных слагаемых.
Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.
4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать
4062=4 ⋅1000+0 ⋅100+6 ⋅10+2
Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0
Вопросы по теме:
Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.
Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.
Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.
Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)
Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)
Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.
Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.
Примеры на задачи.
Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)
Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.
Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.
Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6
tutomath.ru
Разряды и классы чисел по математике
В начальных классах дети изучают «Разряды и классы чисел», однако эта тема вызывает много вопросов у родителей.
В этой статье Вы сможете «освежить» свои знания и объяснить ребенку эту тему.
Числа и цифры
ЧИСЛА — это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Для записи чисел используются специальные знаки — ЦИФРЫ.
Цифр десять: 1 2 3 4 5 6 7 8 9 0
Натуральные числа
НАТУРАЛЬНЫЕ ЧИСЛА — это числа, которые используются при счёте.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …,
1 — самое маленькое число, а самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль НЕ является натуральным числом.
Разряды и классы натуральных чисел
Для записи чисел используется
Каждая новая единица счёта больше предыдущей ровно в 10 раз:
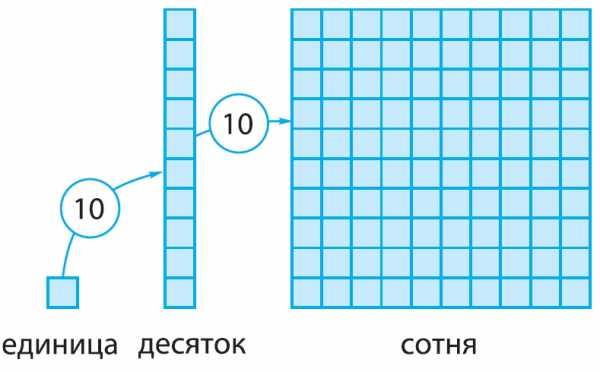
Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).
Позиция (место) цифры в записи числа называется РАЗРЯДОМ. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.
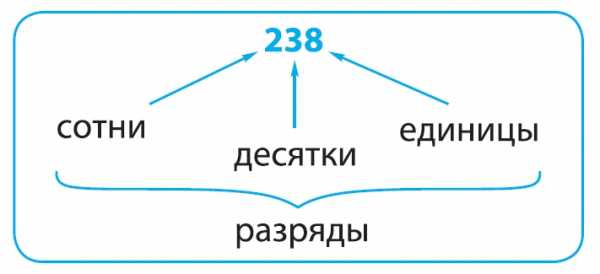
Каждые три разряда натуральных чисел образуют КЛАСС.
 Плакат «Сделай уроки сам!» 3-4 класс https://делайурокисам.рф
Плакат «Сделай уроки сам!» 3-4 класс https://делайурокисам.рфОсновной вопрос, который родители часто задают: зачем ребенку эти знания? Ответ на этот вопрос очень простой — после изучения этого материала, дети переходят к таким темам как сложение и вычитание в столбик, где обязательно необходимо знать разряды числа, чтобы правильно вычислить примеры.
И если ребенок не освоит эту тему, тогда он не сможет правильно решать в столбик.
Складываем и вычитаем через разряды
Сложение столбиком
А) Складываем единицы: 4 + 3 = 7.
Записываем под единицами.
Б) Складываем десятки: 4 + 3 = 7.
Записываем под десятками.
В) Складываем сотни: 4 + 3 = 7.
Записываем под сотнями.
Ответ: 777
Вычитание столбиком
А) Вычитаем единицы: 9 – 3 = 6.
Записываем под единицами.
Б) Вычитаем десятки: 0 меньше,
чем 2, занимаем в сотнях (тысячах).
10 – 2 = 8. Записываем под десятками.
В) Вычитаем сотни: 9 – 4 = 5.
Ответ: 586
Опубликовано: 25.04.2018
Разговоры с детьми о детях.Читать далее
нет комментариев
Опубликовано: 18.02.2018
Положительные и отрицательные числа — это не абстрактные математические понятия, а часто встречающиеся в современной жизни явления.Читать далее
нет комментариев
Опубликовано: 20.04.2018
Жизнь каждого школьника — постоянный круговорот: школа, секции, репетиторы. Из-за того, что ребёнок занят и каждый час его расписан, у него не хватает времени на отдых и общение с друзьями.Читать далее
нет комментариев
Опубликовано: 31.03.2018
В статье собрана подборка всех правил имени прилагательного + морфологический разбор.Читать далее
нет комментариев
Опубликовано: 20.04.2018
Школьные уроки закончились. И ваш радостный ребенок бежит вприпрыжку домой. Как помочь распланировать день — все эти вопросы в голове родителей не дают им покоя. Но вот несколько советов, которые все расставят по своим местам, в прямом и переносном смысле.Читать далее
нет комментариевРазряды и классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
Первый класс справа называют классом единиц, второй – тысяч, третий – миллионов, четвёртый – миллиардов, пятый – триллионов, шестой – квадриллионов, седьмой – квинтиллионов, восьмой – секстиллионов.
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
148 951 784 296
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
При чтении класса единиц в конце обычно не добавляют слово единиц
.
Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа – цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 – цифра второго разряда, 2 – цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
единицы называют единицами 1-го разряда (или простыми единицами)
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.
Все единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. – составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда. Например, сотня содержит 10 десятков, десяток – 10 простых единиц.
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра – 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде. Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен – отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
172 526 – сто семьдесят две тысячи пятьсот двадцать шесть.
102 026 – сто две тысячи двадцать шесть.
naobumium.info
Название чисел | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
В названиях арабских чисел каждая цифра принадлежит своему разряду, а каждые три цифры образуют класс. Таким образом, последняя цифра в числе обозначает количество единиц в нем и называется, соответственно, разрядом единиц. Следующая, вторая с конца, цифра обозначает десятки (разряд десятков), и третья с конца цифра указывает на количество сотен в числе – разряд сотен. Дальше разряды точно также по очереди повторяются в каждом классе, обозначая уже единицы, десятки и сотни в классах тысяч, миллионов и так далее. Если число небольшое и в нем нет цифры десятков или сотен, принято принимать их за ноль. Классы группируют цифры в числах по три, нередко в вычислительных приборах или записях между классами ставится точка или пробел, чтобы визуально разделить их. Это сделано для упрощения чтения больших чисел. Каждый класс имеет свое название: первые три цифры – это класс единиц, далее идет класс тысяч, затем миллионов, миллиардов (или биллионов) и так далее.
Поскольку мы пользуемся десятичной системой исчисления, то основная единица измерения количества – это десяток, или 101. Соответственно с увеличением количества цифр в числе, увеличивается и количество десятков 102,103,104 и т.д. Зная количество десятков можно легко определить класс и разряд числа, например, 1016 – это десятки квадриллионов, а 3×1016 – это три десятка квадриллионов. Разложение чисел на десятичные компоненты происходит следующий образом – каждая цифра выводится в отдельное слагаемое, умножаясь на требуемый коэффициент 10n, где n – положение цифры по счет слева направо.
Например:
253 981=2×106+5×105+3×104+9×103+8×102+1×101
Также степень числа 10 используется и в написании десятичных дробей: 10(-1) – это 0,1 или одна десятая. Аналогичным образом с предыдущим пунктом, можно разложить и десятичное число, n в таком случае будет обозначать положение цифры от запятой справа налево, например: 0,347629= 3×10(-1)+4×10(-2)+7×10(-3)+6×10(-4)+2×10(-5)+9×10(-6)
Названия десятичных чисел. Десятичные числа читаются по последнему разряду цифр после запятой, например 0,325 – триста двадцать пять тысячных, где тысячные – это разряд последней цифры 5.
geleot.ru
Разряды счётных единиц. Видеоурок. Математика 3 Класс
Рассмотрим, как связаны между собой счётные единицы (рис. 1).
Рис. 1. Взаимосвязь счетных единиц (Источник)
При записи числа каждая счётная единица записывается на своём месте (табл. 1).
Таблица 1. Запись трёхзначных чисел
|
3 разряд |
2 разряд |
1 разряд |
|
сотни |
десятки |
единицы |
Разряды считаются справа налево, начиная с первого разряда – единицы. Второй разряд – десятки. И третий разряд – сотни.
Запишите числа, отложенные на счётах, (рис. 2, 3, 4) и прочитайте их.
Рис. 2. Числа
Рис. 4. Числа
Рис. 3. Числа
Решение: 1. На счётах отложено семь единиц, два десятка и три сотни. Получается число триста двадцать семь.
327
2. В следующем числе (рис. 3) единицы отсутствуют. Если нет какого-либо разряда, можно поставить ноль. Всё число – триста двадцать.
320
3. На рисунке 4 в числе семь единиц, нет десятков и три сотни. Получается число триста семь.
307
Прочитайте числа и объясните, что обозначает каждая цифра в записи числа:
1. 894 3. 480
2. 809 4. 900
Решение: 1. Число восемьсот девяносто четыре. В этом числе цифра 4 обозначает четыре единицы. Цифра 9 означает девять десятков. А цифра 8 означает восемь сотен.
2. В числе восемьсот девять цифра 9 означает, что в первом разряде девять единиц. Цифра 0 означает, что единицы второго разряда отсутствуют. А Цифра 8 показывает, что единиц третьего разряда восемь.
3. В числе четыреста восемьдесят цифра 0 указывает, что единицы отсутствуют, десятков восемь, а сотен четыре.
4. В числе девятьсот отсутствуют единицы и десятки, а сотен девять.
Разделите данные числа на 3 группы по какому-либо признаку: 100, 4 , 43, 606, 8 ,61, 999, 250, 3, 57.
Решение: 1. Внимательно посмотрим на числа и разделим их на группы (табл. 2).
Таблица 2. Задание № 4
|
1 группа |
2 группа |
3 группа |
|
4 8 3 |
43 61 57 |
100 606 999 250 |
Так, в первой группе оказались все однозначные числа. Во второй группе – двузначные, а в третьей группе все числа трёхзначные.
Запишите числа и прочитайте их:
1. 283 3. 501
2. 460 4. 700
Решение: 1. В числе двести восемьдесят три 2 сотни 8 десятков и 3 единицы.
2. В числе четыреста шестьдесят 4 сотни 6 десятков и нет единиц.
3. В числе пятьсот один 5 сотен 0 десятков и 1 единица.
4. В числе семьсот 7 сотен 0 десятков и 0 единиц.
Выразите данные величины в более крупных единицах измерения:
1. 125 см 3. 86 мм
2. 540 см 4. 42 дм
Решение: 1. Для того чтобы выполнить такой перевод одних единиц измерения в другие, необходимо вспомнить взаимосвязь этих единиц (рис. 5). Применим данные знания к первому выражению. В числе 125 одна сотня – 1 м, два десятка – 2 дм, и пять единиц – 5 см.
125 см = 1 м 2 дм 5 см
Рис. 5. Взаимосвязь единиц измерения (Источник)
2. Во второй величине пятьсот сорок сантиметров. В этом числе 5 сотен – 5 м и 4 десятка – 4 дм, а единицы отсутствуют, следовательно, сантиметров не будет.
540 см = 5 м 4 дм
3. Восемьдесят шесть миллиметров. В одном сантиметре десять миллиметров, значит, в этой величине будет восемь сантиметров и шесть миллиметров.
86 мм = 8 см 6 мм
4. В последнем числе (42 дм) видно четыре десятка и известно, что в 1 м – 10 дм.
42 дм = 4 м 2 дм
Выразите данные величины в более мелких единицах измерения:
1. 1 м 75 см
2. 2 дм 8 мм
Решение: 1. Для решения задания воспользуемся рисунком 5, на котором изображена взаимосвязь между единицами измерения длины.
1 м 75 см = 175 см
2. Переведём второе число.
2 дм 8 мм = 208 мм
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- All-schools.pp.ua (Источник).
- Urokonline.com (Источник).
- Uchu24.ru (Источник).
Домашнее задание
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., стр. 44, 45 № 1–7.
- Выразите в миллиметрах
а) 22 см б) 1 м в) 3 дм 1 см г) 7 см 8 мм - Разделите числа на три группы по какому-либо признаку: 100, 210, 15, 7, 8, 123, 458, 33, 49, 1, 99, 8.
- *Прочитай числа и объясни, что обозначает каждая цифра в записи числа:
а) 219 б) 380 в) 407 г) 800.
interneturok.ru
Разряды числа
1. Числа второго десятка (двадцаток).
2. Числа первой сотни.
3. Числа первой тысячи.
4. Многозначные числа.
5. Системы счисления.
1. Числа второго десятка (двадцаток)
Числа второго десятка (11, 12, 13, 14, 15, 16, 17, 18, 19, 20) -двузначные числа.
Для записи двузначного числа используются две цифры. Первая цифра справа в записи двузначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа — цифрой второго разряда или разряда десятков.
Числа второго десятка во всех учебниках математики для начальных классов рассматриваются отдельно от других двузначных чисел. Это объясняется тем, что названия чисел второго десятка противоречат способу их записи. Поэтому многие дети некоторое время путают порядок записи цифр в числах второго десятка, хотя называть их при этом могут правильно.
Например, при записи на слух числа 12 (две-на-дцать) ребенок первым словом слышит «две(а)», поэтому он может записать цифры в таком порядке 21, но прочитать эту запись как «двенадцать».
Формирование представления о двузначных числах строится на основе понятия «разряд».
Понятие разряда является базовым в десятичной системе счисления. Под разрядом понимается определенное место в записи числа в позиционной системе счисления (разряд — это позиция цифры в записи числа).
Каждая позиция в этой системе имеет свое название и свое условное значение: цифра, стоящая на первой позиции справа, означает количество единиц в числе; цифра, стоящая на второй позиции справа, означает количество десятков в числе и т. д.
Цифры от 1 до 9 называют значащими, а нуль является незначащей цифрой. При этом его роль в записи двузначных и других многозначных чисел очень важна: нуль в записи двузначного (и т. д.) числа означает, что число содержит обозначенный нулем разряд, но значащих цифр в нем нет, т. е. наличие нуля справа в числе 20, обозначает, что цифра 2 должна восприниматься как символ десятков, и при этом число содержит только два целых десятка; запись 23 будет означать, что кроме 2 целых десятков число содержит еще 3 единицы, дополнительно к целым десяткам.
Понятие «разряд» играет большую роль в системе изучения нумерации, а также является основой для освоения так называемых «нумерационных» случаев сложения и вычитания, в которых действия производятся целыми разрядами:
27 — 20 365 — 300
27-7 365-60
20+7 305+ 60
Умение узнавать и выделять в числах разряды является основой умения раскладывать числа на разрядные слагаемые: 34 = 30 + 4.
Для чисел второго десятка понятие «разрядный состав» совпадает с понятием «десятичный состав». Для двузначных чисел, содержащих более одного десятка — эти понятия не совпадают. Для числа 34 десятичный состав — это 3 десятка и 4 единицы. Для числа 340 разрядный состав — это 300 и 40, а десятичный — это 34 десятка.
Знакомство с числами второго десятка (11—20) удобно начинать со способа их образования и названия чисел, сопровождая его сначала моделью на палочках, а затем чтением числа по модели:
Запоминание названий двузначных чисел в этом случае не будет затруднено для детей противоречащей названию записью: 11, 13,17. (Ведь в соответствии с традицией чтения в европейских письменностях слева направо в названии этих чисел сначала должна была бы идти цифра десятков, а потом цифры единиц!) В связи с такой особенностью чисел второго десятка, многие дети в первом классе долго путаются при записи их на слух и чтении по записи. Раннее введение символики играет в данном случае отрицательную роль как для запоминания названий чисел второго десятка, так и для понимания их структуры. Для формирования правильного представления о структуре двузначного числа следует всегда класть десятки слева, а единицы справа. Таким образом ребенок зафиксирует во внутреннем плане правильный образ понятия, без специальных многословных и не всегда понятных ему объяснений.
На следующем этапе предлагаем ребенку соотнесение вещественной модели и символической записи:
один-на-дцать три-на-дцать сем-на-дцать
Затем переходим на графические модели и к чтению чисел по графической модели:
Далее вводятся схематические разрядные модели:
а затем символическая запись разрядного состава чисел второго десятка:
17 = 10 + 7.
В дальнейшем в школе вводят понятие разряда и знакомят детей с понятием «разрядные слагаемые»:
37 = 30 + 7; 624 = 600 + 20 + 4.
Использование десятичной модели вместо разрядной для знакомства со всеми двузначными числами позволяет без введения понятия «разряд» познакомить ребенка как со способом образования этих чисел, так и научить его читать число по модели (и наоборот, строить модель по названию числа), а затем и записывать:
При изучении детьми чисел второго порядка рекомендуем педагогу использовать следующие виды заданий:
1) на способ образования чисел второго десятка:
Покажи тринадцать палочек. Сколько это десятков и сколько еще отдельных палочек?
2) на принцип образования натурального ряда чисел:
Сделай рисунок к задаче и реши ее устно. «В городе было 10 кинотеатров. Построили еще 1. Сколько кинотеатров стало в городе?»
Уменьши на 1: 16, 11, 13, 20
Увеличь на 1:19, 18, 14, 17
Найди значение выражения: 10+ 1; 14+ 1; 18— 1;20— 1.
(Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.)
3) на поместное значение цифры в записи числа:
Что обозначает каждая цифра в записи числа: 15, 13, 18, 11, 10,20?
(В записи числа 15 цифра 1 обозначает количество десятков, а цифра 5 — количество единиц. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет.)
4) на место числа в ряду чисел:
Вставь пропущенные числа: 12………16 17 … 19 20
Вставь пропущенные числа: 20 … 18 17………13 … 11
(При выполнении задания ссылаются на порядок чисел при счете.)
5) на разрядный (десятичный) состав:
10 + 3 = … 13-3 = … 13-10 = …
12=10 + … 15 = … + 5
При выполнении задания ссылаются на разрядную (десятичную) модель числа из десятка (пучка палочек) и единиц (отдельных палочек),
6) на сравнение чисел второго десятка:
Какое из чисел больше: 13 или 15? 14 или 17? 18 или 14? 20 или 12?
При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 13 две единицы получим 15, значит 15 больше, чем 13).
Сравнивая числа второго десятка с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные:
Назови самое большое и самое маленькое из этих чисел: 12 6 18 10 7 20.
При сравнении чисел второго десятка удобно пользоваться линейкой.
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Сравнивая длины соответствующих отрезков, ребенок наглядно определяет постановку знака сравнения: 17 < 19.
studfiles.net
Десятичная система счисления, классы и разряды чисел
Так как десятичная система счисления поместная, то число зависит не только от записанных в нем цифр, но и от места записи каждой цифры.
Определение: Место записи цифры в числе называется разрядом числа.
Например, число состоит из трех цифр: 1, 0 и 3. Поместная, или разрядная, система записи позволяет из этих трех цифр составить трехразрядные числа: 103, 130, 301, 310 и двухразрядные числа: 013, 031. Приведенные числа расположены в порядке возрастания: каждое предыдущее число меньше последующего.
Следовательно, цифры, которые используются для записи числа, не определяют полностью это число, а служат только инструментом его записи.
Само число строится с учетом разрядов, в которых записана та или иная цифра, т. е. нужная цифр должна еще и занимать нужное место в записи числа.
Правило. Разряды натуральных чисел именуются справа налево от 1 к большему числу, каждый разряд имеет свой номер и место в записи числа.
Наиболее употребляемые числа имеют до 12 разрядов. Числа, имеющие более 12 разрядов, относятся к группе больших чисел.
Количество занятых цифрами мест при условии, что цифра наибольшего разряда не 0, определяет разрядность числа. О числе можно сказать, что оно: однозначное (одноразрядное), например 5; двузначное (двухразрядное), например 15; трехзначное (трехразрядное), например 551, и т. д.
Кроме порядкового номера каждый из разрядов имеет свое наименование: разряд единиц (1-й), разряд десятков (2-й), разряд сотен (3-й), разряд единиц тысяч (4-й), разряд десятков тысяч (5-й) и т. д. Каждые три разряда, начиная с первого, объединены в классы. Каждый класс тоже имеет свой порядковый номер и наименование.
Например, первые 3 разряда (от 1-го до 3-го включительно) — это класс единиц с порядковым номером 1; третий класс — это класс миллионов, он включает 7-й, 8-й и 9-й разряды.
Приведем структуру разрядного построения числа, или таблицу разрядов и классов.
| Классы | Разряды |
| 1-й класс единицы |
|
| 2-й класс тысячи |
|
| 3-й класс миллионы |
|
| 4-й класс миллиарды |
|
Число 127 432 706 408 — двенадцатиразрядное и читается так: сто двадцать семь миллиардов четыреста тридцать два миллиона семьсот шесть тысяч четыреста восемь. Это многозначное число четвертого класса. Три разряда каждого класса читаются как трехзначные числа: сто двадцать семь, четыреста тридцать два, семьсот шесть, четыреста восемь. К каждому классу трехзначного числа добавляется наименование класса: «миллиардов», «миллионов», «тысяч».
У класса единиц наименование опускается (подразумевается «единиц»).
Числа от 5-го класса и выше относятся к большим числам. Большие числа используются только в специфических отраслях Знаний (астрономии, физике, электронике и т. д.).
Приведем ознакомительно названия классов от пятого до девятого: единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — септиллионы.
shkolo.ru