Как записать число в двоичной системе – Двоичные числа, цифры и двоичная система счисления. Перевод числа в двоичную систему счисления из десятичной.

Иллюстрированный самоучитель по цифровой графике › Системы счисления › Запись целых чисел в двоичной системе счисления. Двоичные коды десятичных чисел. [страница — 39] | Самоучители по графическим программам

Запись целых чисел в двоичной системе счисления. Двоичные коды десятичных чисел.

Настало время разобраться, каким же образом можно записывать любые целые числа с помощью двоичной системы счисления, т. е. с помощью всего двух цифр «0» и «1».

Замечание
Разумеется, что записывать можно не только целые, но и дробные, а также любые другие числа, однако это выходит за рамки, необходимые для того, чтобы в конечном счете понять, как происходит кодирование и обработка любой интересующей нас информации, в частности изображений и цвета. Пока же мы не выходим за рамки арифметики, поэтому – терпение: мы уже на пути к этому.

Исходя из этой задачи, попробуем составить таблицу чисел, которые «состоят» из цифр «0» и «1».

Замечание
Как эту задачу можно определить «обычными» словами (наука наукой, однако за скучными, точными фразами надо уметь находить обычный план изложения)? То, что мы сказали («кодировать в двоичной системе счисления»), на самом деле означает – «как с помощью всего двух цифр написать любое целое число». Можно также сформулировать нашу задачу фразой «как преобразовать десятичные числа в двоичные»

.

Тогда давайте, рассуждая, заполнять строки таблицы, у которой в левом столбце будут располагаться привычные нам десятичные числа, а в правом – их эквивалент в двоичной системе счисления (табл. 4.2).

С нуля начинается числовая ось натуральных целых чисел. Последующие целые числа получаются с помощью последовательного прибавления единицы к предыдущему числу.

Итак, число «ноль» в десятичной и двоичной системах счисления совпадает и обозначается одной и той же цифрой «0».

Далее переходим к единице, которая получается прибавлением единицы к нулю. В двоичной системе счисления, как и в десятичной, используется также одна и та же цифра «1».

Замечание
Еще раз напомним, что «цифра» и «число» не всегда совпадают. Цифра – это просто знак, количество цифр ограничено. Число – это математическая категория количества, чисел бесконечное множество

.

Таблица 4.2. Начало таблицы преобразования десятичных чисел в двоичные.

Десятичная система счисления	Двоичная система счисления
0	0
1	1

Затем любой первоклассник скажет, что после единицы на числовой оси следует двойка, получаемая прибавлением еще одной единицы.

Для обозначения числа «два» в десятичной системе счисления предусмотрен специальный знак – цифра «2». А в двоичной системе счисления весь, прямо скажем, небогатый запас знаков («цифр») мы уже исчерпали. Как же быть в этой ситуации?

Читатели, надеюсь, не обидятся, если мы снова напомним некоторые сведения первого класса начальной школы. Итак, вспомним сложение.

2 + 1 = 3;

8 +

1 = 9;

9 + 1 =...

Мы получили число «9» и попытались к нему прибавить «1». Почему же мы остановились? У нас опять кончились цифры! До этого момента каждое число получало свой особенный знак или символ – цифру. Последовательно прибавляя «1», мы каждый раз использовали для этого шага особый знак.

И вот после числа «9» особые знаки закончились. Цифр больше нет, а числа-то продолжают возрастать, т. к. числовая ось бесконечна…

Теперь следует вспомнить позиционный принцип, который мы обсуждали ранее, попробуем применить его и к двоичной системе счисления.

Информация о позиционном принципе – в разд. «Позиционный метод записи» данной главы.

samoychiteli.ru

Двоичная система счисления

Главная / Ассемблер / Для чайников / Системы счисления /

Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа. А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два состояния – вЫключено и включено (или нет напряжения – есть напряжение). Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо, потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете почитать здесь: Структура процессора.

Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.

Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.

Каждая цифра в двоичном числе называется бит (или разряд). Четыре бита – это полубайт (или тетрада), 8 бит – байт, 16 бит – слово, 32 бита – двойное слово. Запомните эти термины, потому что в программировании они используются очень часто. Возможно, вам уже приходилось слышать фразы типа

слово данных или байт данных. Теперь, я надеюсь, вы понимаете, что это такое.

Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например,

101 – это десятичное число
101b – это двоичное число, которое эквивалентно десятичному числу 5.

А теперь попробуем понять, как формируется двоичное число.

Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду. Тетрада (или полубайт) имеет 4 бита.

Двоичное	Десятичное	Пояснения
0000	0	—
0001	1	В младший бит устанавливается 1.
0010	2	В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается.
0011	3	В младший бит устанавливается 1.
0100	4	В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются.
0101	5	В младший бит устанавливается 1.
0110	6	Продолжаем в том же духе…
0111	7	…
1000	8	…
1001	9	…
1010	10	…
1011	11	…
1100	12	…
1101	13	…
1110	14	…
1111	15	…

Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:

Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе:

0…9
10 – очищаем младший разряд, а в старший добавляем 1

Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).

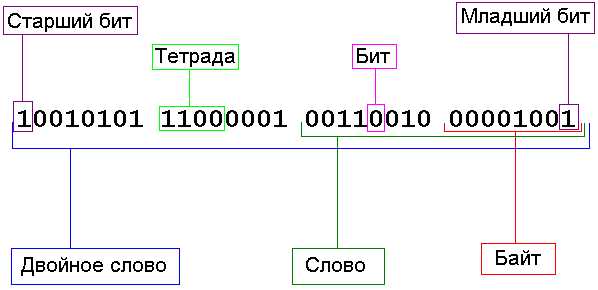
Рис. 2.2. Двоичное число.

av-assembler.ru

Двоично-десятичный код — Википедия

Материал из Википедии — свободной энциклопедии

Перевод десятичных цифр в двоично-десятичный код

Двоично-десятичный код (англ. binary-coded decimal), BCD, 8421-BCD  — форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода.

Например, десятичное число 311₁₀ будет записано в двоичной системе счисления в двоичном коде как 1 0011 0111₂, а в двоично-десятичном коде как 0011 0001 0001_BCD.

При помощи 4 бит можно закодировать 16 цифр. Из них используются 10. Остальные 6 комбинаций в двоично-десятичном коде являются запрещёнными. Таблица соответствия двоично-десятичного кода и десятичных цифр:

Двоично-десятичный код также применяется в телефонной связи. В этом случае кроме десятичных цифр кодируются символы ‘*’ или ‘#’, или любые другие. Для записи этих символов в двоично-десятичном коде используются запрещенные комбинации:

Преимущества и недостатки[править |

ru.wikipedia.org

Двоичная система счисления

Рейтинг:   / 1

Подробности

Просмотров: 4474

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:

0 – это ноль

1 – это один (и это предел разряда)

10 – это два

11 – это три (и это снова предел)

100 – это четыре

101 – пять

110 – шесть

111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 10³ + 4 * 10² + 7 * 10¹ + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 137₁₀

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания. 

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)

38 / 2 = 19 (0 остаток)

19 / 2 = 9 (1 остаток)

9 / 2 = 4 (1 остаток)

4 / 2 = 2 (0 остаток)

2 / 2 = 1 (0 остаток)

1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

• < Назад
• Вперёд >

palkins.ru

2.2.3. Двоично-десятичная система счисления

Эта система имеет основание S = 10, но каждая цифра изображается четырехразрядным двоичным числом, называемым тетрадой. Обычно данная система счисления используется в ЭВМ при вводе и выводе информации. Однако в некоторых типах ЭВМ в АЛУ имеются специальные блоки десятичной арифметики, выполняющие операции над числами в двоично-десятичном коде. Это позволяет в ряде случаев существенно повышать производительность ЭВМ.

Например, в автоматизированной системе обработки данных чисел много, а вычислений мало. В этом случае операции, связанные с переводом чисел из одной системы в другую, существенно превысили бы время выполнения операций по обработке информации.

Перевод чисел из десятичной системы в двоично-десятичную весьма прост и заключается в замене каждой цифры двоичной тетрадой.

Пример.

Записать десятичное число 572.38₍₁₀₎в двоично-десятичной системе счисления.

Обратный перевод также прост: необходимо двоично-десятичное число разбить на тетрады от точки влево (для целой части) и вправо (для дробной), дописать необходимое число незначащих нулей, а затем каждую тетраду записать в виде десятичной цифры.

Пример.

Записать двоично-десятичное число 10010.010101_(2-10)в десятичной системе счисления.

Перевод чисел из двоично-десятичной в двоичную систему осуществляется по общим правилам, описанным выше.

2.3. Восьмеричная система счисления

В восьмеричной системе счисления употребляются всего восемь цифр, т.е. эта система счисления имеет основание S = 8. В общем виде восьмеричное число выглядит следующим образом:

,

где .

Восьмеричная система счисления не нужна ЭВМ в отличие от двоичной системы. Она удобна как компактная форма записи чисел и используется программистами (например, в текстах программ для более краткой и удобной записи двоичных кодов команд, адресов и операндов). В восьмеричной системе счисления вес каждого разряда кратен восьми или одной восьмой, поэтому восьмиразрядное двоичное число позволяет выразить десятичные величины в пределах 0-255, а восьмеричное охватывает диапазон 0-99999999 (для двоичной это составляет 27 разрядов).

Поскольку 8=2³, то каждый восьмеричный символ можно представить трехбитовым двоичным числом. Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.

Пример.

Двоичное число 10101011111101₍₂₎записать в восьмеричной системе счисления.

Пример.

Двоичное число 1011.0101₍₂₎ записать в восьмеричной системе счисления.

Перевод из восьмеричной системы счисления в двоичную осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом (триадой).

2.4. Шестнадцатеричная система счисления

Эта система счисления имеет основание S = 16. В общем виде шестнадцатеричное число выглядит следующим образом:

,

где .

Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=2⁴. Шестнадцатеричная система также применяется в текстах программ для более краткой и удобной записи двоичных чисел.

Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.

Пример.

Двоичное число 10101011111101₍₂₎записать в шестнадцатеричной системе.

Пример.

Двоичное число 11101.01111₍₂₎записать в шестнадцатеричной системе.

Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо, наоборот, каждую цифру этого числа заменить тетрадой.

В заключение следует отметить, что перевод из одной системы счисления в другую произвольных чисел можно осуществлять по общим правилам, описанным в разделе “Двоичная система счисления”. Однако на практике переводы чисел из де­сятичной системы в рассмотренные системы счисления и обратно осуществляются через двоичную систему счисления.

Кроме того, следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления больших двоичных чисел, которыми фактически оперирует процессор. При этом шестнадцатеричная система оказывается предпочтительнее, поскольку в современных ЭВМ процессоры манипулируют словами длиной 4, 8, 16, 32 или 64 бита, т.е. длиной слов, кратной 4. В восьмеричной же системе счисления предпочтительны слова, кратные 3 битам, например слова длиной 12 бит (как в PDP-8 фирмы DEC).

studfiles.net

Электронный справочник по ИНФОРМАТИКЕ (Автор Панов В.А.)

Двоичная система счисления

 

 

 

 

 

 

 

 

 

 

 

Двоичная система счисления является основной системой представления информации в памяти компьютера.

В этой системе счисления используются две цифры: 0 и 1.

Двоичную цифру называют битом.

Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу ( 1670 г .). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г . В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие. Большинство современных электронно-вычислительных машин используют в своей работе именно эту систему чисел.

 

Ей было тысяча сто лет. Она в сто первый класс ходила, В портфеле по сто книг носила — Всё это правда, а не бред. Когда пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий. Она ловила каждый звук Своими десятью ушами, И десять загорелых рук Портфель и поводок держали. И десять тёмно-синих глаз Рассматривали мир привычно… Но станет всё совсем обычным, Когда поймёте наш рассказ. ———————

С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе.

Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.

Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.

Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово «килобайт», вообще говоря, означает «1000 байт». (Напомним, что приставка «кило» означает «тысяча».)

Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.

Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.

Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более

Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.

1 Мбайт = 1024 Кбайт = 1 048 576 байт.

Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт.

имеет в двоичной форме объём 25 байт: 23 буквы и 2 символа «пробел» по 1 байту.

Пример. Измерим в байтах объём текстовой информации в книге из 258 страниц, если на одной странице размещается в среднем 45 строк по 60 символов (включая пробелы). Один символ в двоичной форме содержит 1 байт. Строка будет содержать 61 байт, учитывая и служебный символ окончания строки. Тогда

61 байт * 45 строк = 2745 байт.

Так как в книге 258 страниц текста и на каждой странице в среднем по 2745 байт информации, то объём алфавитно-цифровой информации в книге

2745 байт * 258 страниц = 708210 байт » 692 Кбайт

Таким образом, текст книги имеет объём около 692 Кбайт.

 

Перевод чисел

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

73₁₀ = 1001001₂

А вот как происходит перевод двоичного числа в десятичное:

 

 

В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.

Запишем формулу представления дробного числа в позиционной системе счисления:

 

A_p = a_n-1·p^n-1+a_n-2·p^n-2 + … + a₁·p¹+a₀·p⁰ +a_-1·p^-1+a_-2·p^-2 + … + a_-m·p^-m,       

В случае десятичной системы счисления получим:

24,73₁₀ = (2·10¹+4·10⁰+7·10^-1+3·10^-2)₁₀

Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:

101101,101₂ = (1·2⁵+0·2⁴+1·2³+1·2²+0·2¹+1·2⁰+1·2^-1+0·2^-2+1·2^-3)₁₀=45,625₁₀

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

·  Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

·  Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

·  В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

·  Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

 

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.612

.612 • 2 = 1.224

.224 • 2 = 0.448

.448 • 2 = 0.896

.896 • 2 =1.792

.792 • 2 = 1.584

и т.д.

Получим: 206,116₁₀=11001110,0001110011₂

Таблицу степеней первых восьми отрицательных степеней двойки

 

Степень основания	2	8	16
0	1	1	1
1	2	8	16
2	4	64	256
3	8	512	4096
4	16	4096	65536
5	32	32768	1048576
6	64	262144	16777216
7	128	2097152	268435456
8	256	16777216	4294967296
9	512	134217728	68719476736
10	1024	1073741824	1099511627776
11	2048	8589934552	17592186044416
12	4096	68719476736	281474976710656
13	8192	549755813888	4503599627370496
14	16384	4398046511104	72057594037927936
15	32768	35184372088832	1152921504606846976
16	65536	281474976710756	18446744073709551616

 

Отрицательные числа

Перейдем теперь к вопросу представления отрицательных чисел. Для определенности рассмотрим тип byte, в котором любое число занимает ровно восемь бит. Из записи в двоичной системе счисления равенства (- 1) + 1 = 0 легко найти, какой вид должно иметь неизвестное нам пока двоичное представление xxxxxxxx числа — 1:

    xxxxxxxx + 00000001 = 00000000      

Ясно, что на месте символов xxxxxxxx должно быть расположено число 11111111. Правильным результатом при этом, конечно, следовало бы считать 100000000, а не 00000000, но ведь мы имеем дело с типом byte и, так как результат обязан разместиться в байте, единица <<исчезает>>.

Итак, число — 1 должно кодироваться как 11111111. Дальнейшее уже совсем просто: для получения — 2 нужно — 1 уменьшить на единицу, что даст 11111110; число — 3 представляется как 11111101 и т.д.

Отрицательные числа всегда имеют в своем двоичном представлении единицу в самом старшем разряде, который поэтому называют знаковым, а абсолютная величина кодируемого числа получается как двоичное дополнение остальных бит (нули нужно заменить на единицы и наоборот), увеличенное на один.

Легко видеть, что при этом самым маленьким отрицательным числом, которое принадлежит типу byte, является число — 128 (двоичное представление 10000000), а самым большим — число 127 (представление 01111111). Все представимыe числа (а их 256) в данном случае могут быть получены как пересечение двух множеств: множества Z всех целых чисел и отрезка [ — 128; 127 ].

Интересным является следующее наблюдение: если число 01111111 увеличить на единицу, то получится 10000000, что означает следующее:

127 + 1 = — 128 !!!

Итак, множество элементов типа byte можно представлять себе в виде свернутого в кольцо отрезка
[ — 128; 127 ].

То, что для элементов множества , являющегося машинным аналогом Z, нарушено фундаментальное свойство целых чисел X + 1 > X, способно привести к различным невероятным на первый взгляд результатам, однако гораздо более странные вещи происходят при работе с вещественными числами.

 

 

Двоичная арифметика

Над числами в двоичной системе счисления можно выполнять арифметические действия.

При этом используются следующие таблицы:

Сложение	Вычитание	Умножение
0+0=0	0-0=0	0*0=0
1+0=1	1-0=1	1*0=0
0+1=1	1-1=0	0*1=0
1+1=10	10-1=1	1*1=1

Рассмотрим примеры:

1 1 0 1 0 12 + 1 1 0 1 12
1 1 0 1 12 — 1 1 0 12
1 1 0 1 12 * 1 0 12

Для деления в двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать. Посмотри деление на анимированном примере

Пример:

Еще несколько примеров:
Несколько примеров для тренировки:

 

konsulytant-inf.narod.ru

Учебный курс «Информатика»

Кодирование информации без компьютеров Системы кодирования числовой информации Двоичная система счисления Перевод чисел из одной системы счисления в другую Кодирование информации на компьютере Вопросы и упражнения     Вопреки распространённому заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, ещё в 17 веке. Великий немецкий учёный Лейбниц считал:     «Вычисление с помощью двоек… является для науки основным и порождает новые открытия… При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок».     Впервые двоичная система появилась в 1605 году в работах Томаса Хэрриота (он изобрёл знаки > и ). Позже двоичная система была забыта, и только в 1936-1938 гг. американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.     Двоичная система удобна для компьютера, но неудобна для человека — числа получаются очень длинными и их трудно записывать и запоминать. Она используется, как правило, для «внутренних нужд» компьютера. Двоичная система счисления позволяет достаточно просто организовать числа, и для того, чтобы представить число в ЭВМ, достаточно иметь устройство, которое обладает только двумя устойчивыми состояниями, одно из которых соответствует логической «1», а другое — «0». Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. Для десятичной системы счисления понадобилось бы, к примеру, устройство с 10 устойчивыми состояниями. Это значительно усложнило бы схему ЭВМ.     Другим важным достоинством двоичной системы является простота вычислений. Рассмотрим, как выполняются арифметические действия в двоичной системе. Для этого проведём анализ таблиц сложения и умножения в двоичной системе. Примеры сложения двоичных чисел: Примеры умножения двоичных чисел:     Следует обратить внимание на аналогию в правилах выполнения арифметических действий в двоичной и десятичной системах счисления: например, если при сложении двух двоичных чисел сумма цифр окажется больше единицы, то возникает перенос в старший разряд.     Вычитание двоичных чисел осуществляется следующим образом: Вычитаемое число преобразуется в дополнительный код. Например, если надо вычесть из числа 10110 число 01000, то вычитаемое 01000 преобразуется в дополнительный код так: в числе вместо 0 пишется 1, а вместо 1 пишется 0, следовательно, получим из вычитаемого число 10111. Затем преобразованное число складывается с уменьшаемым:     И вычитаемое, и уменьшаемое состоят из 5 разрядов, а результат суммы — число 6-разрядное. Старший разряд суммы отнимается от числа и складывается с результатом:     Такой приём часто используется в практике вычислений. Например, в десятичной системе числа можно вычесть так. Допустим требуется найти разность 842-623. Представим число 623 в дополнительный вид, отняв его от 1000. Получим число 377. Затем найдём сумму: 842+377=1219. Отбросим перенос в старший разряд и получим число 219. Мы нашли решение этого примера.      Деление двоичных чисел выполняется аналогично делению десятичных чисел. Вычитание и умножение в процессе деления необходимо выполнять рассмотренными ранее способами.     Важнейшее преимущество двоичной арифметики заключается в том, что она позволяет все арифметические действия свести к одному — сложению, а это значительно упрощает устройство процессора ЭВМ. Отметим недостаток, характерный для двоичной системы счисления — значительный рост числа разрядов при увеличении числа. Но все достоинства этой системы делают такой недостаток не столь существенным.

infolike.narod.ru