Разложить функцию в ряд тейлора в окрестности точки: Ряд Тейлора. Разложение функции в ряд Тейлора.

2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

Разложение функций в ряды Тейлора и Маклорена

Разложение заданной функции f(x) в ряд Тейлора в окрестности точки распадается на два этапа

1. Сначала вычисляются значения функции f(x) и ее производных в точке и составляется ряд Тейлора для функции f(x). При этом предполагается, что функция f(x) бесконечное число раз дифференцируема.

2. Находится интервал, в котором составленный ряд Тейлора сходится к функции f(x), то есть устанавливается для каких значений х остаточный член ряда будет стремиться к нулю при . При этом можно воспользоваться следующей теоремой.

Теорема

Если в некотором интервале, окружающем точку , абсолютные величины всех производных функции

f(x) ограничены одним и тем же числом, то функция в этом интервале разлагается в ряд Тейлора.

Доказательство

Нужно установить, что для всех точек интервала при .

По условию теоремы во всех точках интервала , где М – постоянная, не зависящая от n. Тогда в силу неравенства (***) . Но отношение при , то есть радиус сходимости . Следовательно, для всех точек х, рассматриваемого интервала, что и требовалось доказать.

Особенно часто используется разложение функции в ряд по степеням х. Полагая , получаем ряд . Такой ряд называется рядом Маклорена.

Разложение в ряды элементарных функций

1. Показательная функция

Разложим эту функцию в ряд Маклорена. Все производные функции равны и обращаются в 1 при

х=0. По формуле Тейлора . Рассмотрим интервал [-N,N], где N – любое фиксированное число. Для всех значений х из этого интервала . Следовательно, все производные в этом интервале ограничены одним и тем же числом и по доказанной теореме . По предположению N – любое число, следовательно, функция разлагается в ряд Маклорена при всех значениях х, то есть на всей числовой оси.

Итак

В частности при х=1 находим ряд для числа е

2. Тригонометрические функции sinx и cosx

Разложим в ряд Маклорена функцию sinx. Для этого последовательно находим значения ее производных в точке х=0

и т.д.

Значения производных повторяются и образуют периодическую последовательность

0,1,0,-1,0,1,0,-1,.

..

Любая производная функции sinx (то есть следовательно ряд функции sinx сходится к ней на всей числовой оси.

Итак

Аналогично для функции cosx

3. Биноминальный ряд

Рассмотрим функцию , где m – любое число. Разложим функцию в ряд Маклорена.

…

поэтому . Следовательно, ряд запишется в виде:

Установим область сходимости ряда. Найдем предел абсолютной величины отношения последующего элемента к предыдущему

согласно признака Даламбера ряд сходится, если |x|<1

и расходится, если |x}>1.

Исследуем , ограничившись случаем, когда 0<x<1. В этом интервале для всех n>m-1 имеем и поэтому

Воспользуемся неравенством (***) . Правая часть неравенства есть абсолютная величина (n+1)-го члена степенного ряда, сходящегося при |x|<1. Следовательно, . Соответствующее доказательство для интервала

(-1,0) более сложное и оно не приводится.

Таким образом, биноминальный ряд представляет функцию в интервале (-1,1)

Если m – целое положительное число, то ряд справа содержит всего (m+1) слагаемых и превращается в форму бинома Ньютона. Заметим, что ряд сходится к функции во всем замкнутом интервале [-1,1].

Приведем биноминальные ряды, соответствующие значениям m=-1, m=1/2, m=-1/2.

(это геометрическая прогрессия)

Замечание

Разложение отдельных функций в ряды могут быть получены из уже известных разложений с помощью свойств степенных рядов.

4. Функции ln(1+x) и arctgx

Для разложения в ряд Маклорена функции f(x)=ln(1+x) воспользуемся формулой для суммы геометрической прогрессии

Применим теорему об интегрировании степенных рядов и проинтегрируем ряд в пределах от 0 до х. Поскольку , то интегрируя поэлементно ряд, получим .

Совершенно аналогично получается разложение функции arctg x в ряд Маклорена. Для этого, заменим в формуле для суммы элементов геометрической прогрессии x на . Получим . Проинтегрируем ряд в пределах от 0 до х. Считая, что |x|<1 получаем

Замечание

Разложения (1)-(6) могут быть использованы для разложения в ряды других функций. Примеры:

1. Разложим в ряд Маклорена гиперболические функции chx и shx

Для ряда (1) заменим на получим . Далее, по правилу сложения и вычитания рядов находим искомое разложение

2. Разложим в ряд Маклорена функцию

Возьмем разложение функции и вместо , подставим получим

3. Разложим в ряд Маклорена функцию

Воспользуемся разложением биноминального ряда, где

m=-1/2 и, для заменим x на , получим

(*). Умножим обе части на

4. Разложим в ряд Маклорена функцию

Так как . То разложение arcsinx получается интегрированием ряда (*)

5. Разложим в ряд Маклорена функцию

Так как ряды для и sinx сходятся абсолютно, то, перемножая их по правилу, рассмотренному ранее получим искомое разложение

(первые коэффициенты, так как закон подметить трудно).

Курс по математическому анализу

• 1. Предел числовой последовательности.

• 2. Методы вычисления пределов последовательностей.

• 3. Предел функции в точке.

• 4. Бесконечно малые функции. Сравнение бесконечно малых функций.

• 5. Методы вычисления пределов функций.

• 6. Непрерывность функции в точке, на отрезке.

• 7. Классификация точек разрыва

• 8. Производная, ее вычисление, геометрический смысл.

• 9. Производные сложных, обратных функций.

• 10. Дифференцируемость, дифференциал.

• 11. Производные и дифференциалы высших порядков.

• 12. Исследование функций и построение графиков.

• 13. Кривые на плоскости.

• 14. Формула Тейлора.

• 15. Неопределенный интеграл, простейшие методы интегрирования.

• 16. Интегрирование некоторых классов функций.

• 17. Определенный интеграл. Формула Ньютона-Лейбница.

• 18. Применение определенного интеграла для площадей и длин дуг.

• 19. Несобственные интегралы.

• 20. Числовые ряды.

• 21. Сходимость знакоположительных рядов.

• 22. Сходимость знакопеременных рядов.

• 23. Функциональные ряды, равномерная сходимость.

• 24. Ряд Тейлора.

• 25. Ряд Фурье.

• 26. Сходимость ряда Фурье.

• 27. Функции многих переменных.

• 28. Частные производные, градиент.

• 29. Неявные функции.

• 30. Формула Тейлора для многих переменных.

• 31. Исследование на экстремум.

• 32. Условный экстремум.

• 33. Двойной и тройной интегралы.

• 34. Замена переменных в кратных интегралах.

• 35. Сферические и цилиндрические координаты.

• 36. Поверхностный интеграл по площади поверхности.

• 37. Криволинейный интеграл по длине дуги.

• 38. Скалярное поле.

• 39. Векторное поле.

• 40. Поток векторного поля.

• 41. Формула Остроградского.

• 42. Криволинейный интеграл в векторном поле.

• 43. Формула Стокса.

• 44. Потенциальное поле.

 

 

Наверх

1. Предел числовой последовательности.

Последовательность  — это функция, заданная на множестве натуральных чисел . Число  называется пределом последовательности , если для любого положительного числа , как бы мало оно ни было, существует такой номер, что для всех  c номерами  справедливо неравенство . Неравенство , эквивалентное неравенству , означает, что для любого существует такой номер , что все  c номерами расположены между и . Последовательность, предел которой — конечное число , называется сходящейся, и ее предел обозначают. Если изобразить элементы последовательности на плоскости точками с координатами  , то неравенства означают, что все точки  с номерами расположены между параллельными оси абсцисс прямыми и .

 

Бесконечно малая последовательность. Последовательность  , предел которой равен нулю , называется бесконечно малой.   

Бесконечно большая последовательность. Последовательность называется бесконечно большой, если для любого положительного числа  , как бы велико оно ни было, существует такой номер  , что для всех с номерамисправедливо неравенство  , записываем .

 

 

Наверх

2. Методы вычисления пределов последовательностей.

Пусть заданы две последовательности  и . Если существуют  и , то существуют и пределы суммы и произведения последовательностей, а при и предел частного, причем   ,        ,  . Для правильного применения этих теорем очень важно существование пределов каждой последовательности.

Неопределенности и их раскрытие.

Если    и  , то может существовать  . В этом случае говорят, что имеем неопределенность типа  . Также может существовать   , в этом случае имеем неопределенность типа  . Если   и  , то может существовать . В этом случае говорят, что имеем неопределенность типа   . Поскольку в перечисленных случаях не применимы теоремы о пределе суммы, произведения и частного, используют другие способы вычисления, которые называют методами раскрытия неопределенностей. Это, как правило, алгебраические преобразования, приводящие выражения к виду, при котором можно пользоваться упомянутыми теоремами.

 

 

Наверх

3. Предел функции в точке.

 

Рассмотрим функцию , определенную в некоторой окрестности точки  , , , за исключением, быть может, самой точки  . Число  называется пределом функции  при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех   , удовлетворяющих неравенству  , справедливо неравенство . Говорят “предел функции  в точке  ” и обозначают  . Неравенство  для всех , эквивалентное неравенствам , , означают, что для любого существует такое , что для  график функции   расположен на плоскости в прямоугольнике . При вычислениях на компьютере мы имеем дело с дискретными значениями переменных. Поэтому удобнее пользоваться другим, эквивалентным приведенному, определением предела. А именно:  , если для любой, сходящейся к  последовательности значений аргумента , соответствующая последовательность значений функции  сходится к числу . Отсюда следует, в частности, что для любого существует такое , что для любой последовательности , сходящейся к , точки с координатами  находятся на плоскости внутри прямоугольника   . 

Бесконечно большие функции.

Если для любой последовательности  значений аргумента соответствующая последовательность значений функции бесконечно большая, то функция называется бесконечно большой в точке . Если  бесконечно большая в точке , то для любого положительного числа , как бы велико оно ни было, существует такое число , что для всех , удовлетворяющих неравенству , справедливо неравенство ; обозначают  .

 

 

Наверх

4. Бесконечно малые функции. Сравнение бесконечно малых функций.

Рассмотрим функцию, определенную в некоторой окрестности точки , ,  за исключением, быть может, самой точки . Функция  называется бесконечно малой при , стремящемся к , если . Если — бесконечно малая в точке , то для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех , удовлетворяющих неравенству , справедливо неравенство . Неравенства  для всех , эквивалентные неравенствам , , означают, что для любого существует такое , что для график функции расположен на плоскости в прямоугольнике . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию.  При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.   

Сравнение бесконечно малых функций.

Пусть и  — две функции, бесконечно малые в точке . Если , то говорят, что  более высокого порядка малости, чем и обозначают . Если же , то  более высокого порядка малости, чем ; обозначают . Бесконечно малые функции  и называются бесконечно малыми одного порядка малости, если  , обозначают  .  И, наконец, если   не существует, то бесконечно малые функции и  несравнимы.   

Эквивалентные бесконечно малые функции.

Если , то бесконечно малые функции и  называются эквивалентными, обозначают ~ .

 

 

Наверх

5. Методы вычисления пределов функций.

Пусть заданы две функции и . Если существуют  и  , то существуют и пределы суммы и произведения этих функций, а при и предел частного, причем        

,

,      

 .

Для правильного применения этих теорем очень важно существование пределов каждой функции. Не трудно доказать, что предел постоянной функции равен этой постоянной, то есть   . Из приведенных формул следует полезное утверждение: 

 , то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной , то вычисление предела при  всегда можно свести к вычислению предела при . Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке  в выражение для функции. 

 

Неопределенности и их раскрытие.

Существуют случаи, когда не применимы теоремы о пределах суммы, произведения, частного, но предел существует и может быть вычислен. Если  и   , то может существовать . В этом случае говорят, что имеем неопределенность типа . Также может существовать   , в этом случае имеем неопределенность типа   . Если   и   , то может существовать  .   В этом случае говорят, что имеем неопределенность типа . Если     и   , то может существовать  — неопределенность типа  . Рассматривают также неопределенности типа , и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой в выражение для функции. Полезно запомнить замечательные пределы: 

      (е = 2.71828… — основание натуральных логарифмов) — неопределенность типа .

       — неопределенность типа .

Использование эквивалентных бесконечно малых.

Если мы имеем неопределенность типа    , то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке  равен нулю. Пусть, , ,  — бесконечно малые функции при  , причем эквивалентна  , т.е. ~ , ~ (напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда, т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную. 

Правило Лопиталя.

Неопределенности типа  или удобно раскрывать с помощью правила Лопиталя. Пусть  и  две бесконечно малые или бесконечно большие функции при  и существует предел отношения их производных при . Тогда  . Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз.  

 

Формула Тейлора.

Пусть функция имеет в точке  производные всех порядков до -го включительно. Тогда для    справедлива формула Тейлора:

где  называется остаточным членом формулы Тейлора.

 

 

Наверх

6. Непрерывность функции в точке, на отрезке.

Рассмотрим функцию , определенную на некотором промежутке . Функция  непрерывна в точке , если предел функции в точке  равен значению функции в этой точке,. 

Свойства функций, непрерывных на отрезке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Для функции, непрерывной на отрезке , справедливы следующие утверждения. 

Функция, непрерывная на отрезке  , достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке  существуют точки  такие, что

. 

Если функция  непрерывна на отрезке  и принимает на концах значения разных знаков, то на интервале  существует точка   , в которой функция обращается в нуль, т. е.   . Это утверждение применяют для отделения корней уравнений  с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.

Если функция   непрерывна на отрезке    , дифференцируема хотя бы на интервале  , то на интервале  существует точка , такая, что  . Это свойство называют формулой Лагранжа или формулой конечных приращений.

 

 

Наверх

7. Классификация точек разрыва

Рассмотрим функцию  , определенную на некотором промежутке . Функция непрерывна в точке , если предел функции в точке  равен значению функции в этой точке, . 

Односторонние пределы функции в точке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Если функция определена на промежутке , , то при исследовании поведения функции в окрестности точки  имеет смысл говорить о пределе функции  в точке  справа, а при исследовании в окрестности точки — о пределе функции в точке  слева. Число называется пределом справа функции при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех  , удовлетворяющих неравенству , справедливо неравенство  . Говорят “предел справа функции в точке ” и обозначают . Аналогично говорят “предел слева функции в точке ” и обозначают , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство  . Для существования предела функции в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы функции в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Функция, определенная на отрезке , , непрерывна справа в точке , если и непрерывна слева в точке  , если. Для того чтобы функция была непрерывна в точке  необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:. Если хотя бы одно из равенств нарушается, говорят о разрыве в точке . 

Классификация разрывов.

Если хотя бы одно из равенств  нарушается, говорят о разрыве в точке . Если  и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

 

 

Наверх

8. Производная, ее вычисление, геометрический смысл.

Производная функции в точке — Пусть функция  определена на промежутке . Точка — произвольная точка из области определения функции,   — приращение функции в точке , вызванное приращением независимой переменной .  Производной функции по независимой переменной  в точке ,  называется предел отношения приращения функции к приращению  при стремлении  к нулю, т. е.   

,  

— производная функции в точке . 

Односторонние производные — Если определена при , то можно определить правую производную функции в точке :

Аналогично, если  определена при , определяется левая производная функции в точке :

 Функция  имеет в точке  производную тогда и только тогда, когда в точкесовпадают ее левая и правая производные:  . 

Секущая графика функции — Пусть — функция, определенная на промежутке . Прямая, проходящая через точки , , ,  называется секущей графика функции  . Угловой коэффициент  секущей равен   и ее уравнение имеет вид  . 

Касательная и нормаль к графику функции — Касательной к графику функции  в точке  называется предельное положение секущей, проходящей через точки  , , когда . Угловой коэффициент касательной равен значению производной в точке и ее уравнение имеет вид . Нормалью к графику функции  в точке называется прямая , проходящая через эту точку перпендикулярно касательной. Угловой коэффициент нормали равен    и ее уравнение имеет вид  .

 

 

Наверх

9. Производные сложных, обратных функций.

Пусть    — функция, дифференцируемая в точке  ,   — функция, дифференцируемая в точке   , причем  . Тогда   — сложная функция независимого переменного , дифференцируема в точке    и ее производная в этой точке вычисляется по формуле   .

Обычно    называют внешней функцией, а — внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции. 

Производная обратной функции.

Пусть функция дифференцируема и строго монотонна на . Пусть также в точке производная . Тогда в точке   определена дифференцируемая функция , которую называют обратной к  , а ее производная вычисляется по формуле .

 

 

Наверх

10. Дифференцируемость, дифференциал.

Дифференцируемость функции в точке.

Пусть функция  определена в некоторой окрестности точки  . Рассмотрим приращение функции в этой точке:  . Функция называется дифференцируемой в точке , если ее приращение можно записать в виде , где — приращение независимой переменной, А – постоянная, не зависящая от , — бесконечно малая функция при . 

Дифференциал функции.

Дифференциалом функции  в точке называется линейная по  часть приращения . Дифференциал обозначается   , то есть  . Рассматривая функцию , нетрудно убедиться, что  , если  — независимая переменная. 

Связь дифференциала и производной.

Воспользуемся определением производной для дифференцируемой функции в точке : . Таким образом, дифференциал функции выражается формулой  , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на  . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная. 

 

 

Наверх

11.

Производные и дифференциалы высших порядков.

Производные высших порядков.

Рассмотрим функцию  , определенную на некотором промежутке   . Вычислим производную , которая также является функцией на . Производной второго порядка от функции  называется производная от ее производной:   . Аналогично определяют производную любого порядка:  . 

Дифференциалы высших порядков.

Рассмотрим дифференциал функции  в произвольной точке промежутка : . Здесь  — приращение независимой переменной, которое является числом и не зависит от . Сам же дифференциал есть функция от , и можно вычислить дифференциал от этой функции:   При  этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле Аналогично вычисляется дифференциал любого порядка .

Понятие инвариантности формы дифференциала.

Рассмотрим дифференциал функции  в произвольной точке промежутка : . Здесь — приращение независимой переменной, которое является числом и не зависит от . Пусть теперь   — функция независимого переменного , определенная на промежутке  . Тогда  — сложная функция переменного . Вычислим ее дифференциал, используя формулу для производной сложной функции: . Заметим, что и выражение для дифференциала принимает ту же форму , хотя здесь  уже функция переменного  . Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что  — функция переменного  . Поэтому и форма второго (а также и всех следующих) дифференциала неинвариантна.

 

 

Наверх

12. Исследование функций и построение графиков.

Рассмотрим функцию , определенную на промежутке (возможно,  ) . Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения. 

Если , то график функции пересекает ось абсцисс в точке  . 

Если , то график функции пересекает ось ординат в точке  .

Если в точке  функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту  (Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты стремится к нулю при справа, слева или с обеих сторон). 

Если , или , существуют и конечны пределы и , то прямая — асимптота графика функции. 

Если , то график функции имеет на левой границе области сходимости вертикальную асимптоту  ; аналогично, если , то график функции имеет на правой границе области сходимости вертикальную асимптоту . 

Если и существует такое число , что для любого , то исследуемая функция периодична с периодом ; в этом случае достаточно построить график функции на промежутке  и доопределить его по периодичности на всю числовую ось.

Если , то исследуемая функция четная; этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке и отобразить его симметрично относительно оси ординат на . 

Если  , то исследуемая функция нечетная; этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке  и отобразить его симметрично относительно начала координат на .  

Исследование функций с помощью производной.

Если функция дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения. 

Для того, чтобы дифференцируемая на функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы () на . 

Пусть в точке  производная  или не существует. Если существует окрестность точки , такая, что для  из этой окрестности при  и при , то функция имеет в точке максимум. Если же при  и  при  , то функция имеет в точке  минимум (в этом случае говорят, что “производная меняет знак при переходе через точку ”).

Если непрерывная в точке функция дифференцируема на , при этом на  и на , то функция имеет в точке максимум; если же при  и  при , то функция имеет в точке  минимум.   

Исследование функций с помощью второй производной.

Если функция дважды дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.

График функции называется выпуклым (выпуклым вниз) на промежутке , если он расположен выше касательной, проведенной в любой точке , . Если же график функции лежит ниже касательной, — то он называется вогнутым (выпуклым вверх). 

Если дважды дифференцируемая на промежутке  функция имеет на нем положительную вторую производную, то функция выпуклая на . Если же вторая производная отрицательна на промежутке , то функция на нем вогнута. 

Если вторая производная равна нулю в точке , а слева и справа от нее имеет значения разных знаков, точка  — точка перегиба.

 

 

Наверх

13. Кривые на плоскости.

Кривые на плоскости в декартовых координатах.

Кривая на плоскости в прямоугольных (декартовых) координатах — это множество точек, координаты которых связаны соотношениями , , , или ; первые два соотношения задают кривую явно, последнее — неявно. Кривая, заданная уравнением  , , называется гладкой, если функция дифференцируема на промежутке . В каждой точкегладкой кривой можно провести касательную , уравнение которой . Уравнение нормали в той же точке имеет вид  или  . Кривая, заданная неявно уравнением , называется гладкой, если на ней нет особых точек (точка линии называется особой, если в ней одновременно обращаются в нуль обе частные производные функции : ). Уравнения касательной и нормали к такой кривой, проходящих через точку , , имеют соответственно вид   и

Кривые, заданные параметрически.

Уравнения , , устанавливающие зависимость декартовых координат точки плоскости от значения параметра , определяют на плоскости кривую, заданную в параметрической форме (говорят еще — заданную параметрически). Поскольку производная функции , заданной параметрически уравнениями , в точке, которая не является особой точкой кривой, вычисляется по формуле , то уравнения касательной и нормали к кривой, проходящих через точку , имеют соответственно вид: .   

Кривые в полярных координатах.

Декартовы координаты точки  на плоскости связаны с полярными координатамисоотношениями . Многие кривые на плоскости удобно описывать как функции радиуса-вектора и полярного угла — в полярных координатах. Так, уравнение единичной окружности в полярных координатах имеет вид  . Уравнение кривой в полярных координатахобычно имеет вид . Угловой коэффициент касательной к графику функции, заданной уравнением , в точке   равен   , а декартовы координаты точки равны соответственно  и   .

 

 

Наверх

14. Формула Тейлора.

Остаточный член формулы Тейлора — Пусть функция имеет в точке  производные всех порядков до -го включительно. Тогда для справедлива формула Тейлора:

 ,

где ,  называется остаточным членом формулы Тейлора в форме Пеано; — бесконечно малая более высокого порядка малости, чем . Если отбросить остаточный член, то получится приближенная формула Тейлора

 

,

правая часть которой называется многочленом Тейлора функции ; его обозначают . Приближенная формула позволяет заменять в различных математических расчетах (аналитических и численных) произвольную функцию ее многочленом Тейлора. 

Из формулы Тейлора видно, что чем точка  ближе к точке , тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена. Это означает, в свою очередь, что чем больше производных имеет функция в некоторой окрестности точки , тем выше точность, с которой многочлен Тейлора аппроксимирует функцию в этой окрестности. 

Разложение основных элементарных функций — Положив  и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций: 

• ; 

• ;

• ;

• ;

• ; 

•  ; 

• .

Разложение функций с использованием стандартных разложений — Для разложения по формуле Тейлора функции в окрестности произвольной точки необходимо сделать замену переменной , то есть  , и воспользоваться одним из приведенных выше разложений основных функций в окрестности точки  .

 

 

Наверх

15. Неопределенный интеграл, простейшие методы интегрирования.

Первообразная и неопределенный интеграл — Рассмотрим функцию , определенную на промежутке (здесь возможно ). Дифференцируемая на промежутке     функция , производная которой в каждой точке равна , называется первообразной функции  : . Поскольку  , то можно говорить о семействе первообразных — множестве функций вида  , . Семейство первообразных   функции называется неопределенным интегралом функции  и обозначается символом : для всех . Здесь    — знак интеграла, — подынтегральное выражение,  — подынтегральная функция,  — переменная интегрирования, — значение неопределенного интеграла, семейство первообразных функции , . То есть производнаянеопределенного интеграла равна подынтегральной функции. Наоборот,    , следовательно, дифференцирование и вычисление неопределенного интеграла, – взаимно обратные операции. Не представляет труда с помощью таблицы производных составить таблицу неопределенных интегралов. Важным свойством неопределенного интеграла является линейность: , здесь    — постоянные. Вычисление неопределенного интеграла обычно сводится к преобразованию подынтегрального выражения так, чтобы можно было воспользоваться таблицей интегралов. 

Интегрирование заменой переменной — Если — непрерывно дифференцируемая функция, то, полагая   , получим формулу интегрирования заменой переменной    . Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному. 

Интегрирование по частям — Пусть   — непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям . Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть”     подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида   ,  ,  ,  и некоторых других.

 

 

Наверх

16.

Интегрирование некоторых классов функций.

Интегрирование рациональных функций — Функция называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: . Если , рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого: 

Если , выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена   , а именно: 

Каждому действительному корню кратности 1 в разложении соответствует член   . 

Каждому действительному корню  кратности  в разложении соответствует набор из  членов     . 

Каждой паре комплексно сопряженных корней   кратности 1 в разложении соответствует член    ( — корни уравнения ).

Каждой паре комплексно сопряженных корней кратности  в разложении соответствует набор из членов       .  

В приведенных выражениях — неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю , приравнивая полученные коэффициенты при степенях   к соответствующим коэффициентам  и решая систему относительно  . 

Наконец, полученное разложение интегрируем почленно. 

Интегрирование тригонометрических функций — Интегралы вида , где  — рациональная функция своих аргументов, вычисляются с помощью универсальной замены переменной  . При этом . Однако универсальная замена обычно связана с большими вычислениями, поэтому в некоторых случаях можно ее избежать. 

Интегралы вида   вычисляются с помощью замены  . Интегралы вида  вычисляются с помощью замены  . Интегралы вида  , если , то есть четная рациональная функция своих аргументов вычисляются с помощью замены    . 

Интегралы вида  вычисляются с помощью формул понижения степени  . 

Интегрирование иррациональных функций — Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен. 

Интегралы вида , где  — рациональная функция своих аргументов, вычисляются заменой . 

Интегралы вида   вычисляются заменой или . 

Интегралы вида   вычисляются заменой   или . Интегралы вида вычисляются заменой или .

 

 

Наверх

17. Определенный интеграл. Формула Ньютона-Лейбница.

Определенный интеграл, его геометрический смысл.

Рассмотрим функцию , определенную на промежутке . Разобьем промежуток на  произвольных частей точками   и обозначим , , . На каждом промежутке    возьмем произвольную точку  и вычислим в ней значение функции. Выражение   называется интегральной суммой функции на  .Если при  существует и конечен предел последовательности частичных сумм  , не зависящий ни от способа разбиения промежутка  точками  , ни от выбора , то этот предел называют определенным интегралом от функции по промежутку , а саму функцию — интегрируемой на . Обозначают    .  

Из приведенного определения естественно следует геометрический смысл определенного интеграла: если , то   равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми . 

Формула Ньютона-Лейбница.

Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница =, здесь символ  означает, что из значения  при верхнем пределе b нужно вычесть значение при нижнем пределе a , — первообразная функция для . Таким образом, вычисление определенного интеграла сводится к нахождению первообразной, то есть неопределенного интеграла. 

Методы вычисления определенного интеграла.

Если — непрерывно дифференцируемая на отрезке  функция, , и , когда  изменяется на  , то, положив  , получим формулу замены переменной в определенном интеграле  .

Пусть  — непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям   . Эта формула применяется для тех же классов функций, что и при вычислении неопределенного интеграла.

 

 

Наверх

18. Применение определенного интеграла для площадей и длин дуг.

Вычисление площадей и длин дуг кривых в декартовых координатах.

Пусть на плоскости задана область, ограниченная снизу кривой  , заданной в декартовых координатах, сверху – кривой  , слева – прямой   (ее может и не быть, если  ), справа – прямой  . Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле   . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия. 

Пусть на отрезке  уравнением  задана плоская кривая. Ее длина вычисляется по формуле  

Вычисление площадей и длин дуг при параметрическом задании кривых.

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть   , при этом  , а сверху – кривой   . Тогда площадь такой плоской фигуры вычисляем по формуле . Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что  . 

Пусть кривая на плоскости задана параметрически   . Тогда длина этой кривой вычисляется по формуле  .

Вычисление площадей и длин дуг кривых в полярных координатах.

Когда кривая, ограничивающая область, задана в полярных координатах , то площадь этой области вычисляем по формуле  . Основная трудность в использовании этой формулы заключается в определении пределов интегрирования  . Здесь нужно понимать, что кривая  определена только, если . Поскольку в формуле присутствует , то она учтет и не существующую площадь, когда  . Решив уравнение , найдем пределы интегрирования. 

Если кривая, ограничивающая область, задана в полярных координатах  , то ее длина вычисляется по формуле . Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.

 

 

Наверх

19. Несобственные интегралы.

Интеграл как функция верхнего предела.

Для функции , интегрируемой для всех  , значение интеграла  зависит от значения верхнего предела ; можно рассмотреть функцию переменной : каждому значению ставится в соответствие число, равное значению интеграла  . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: ; функция определена в области интегрируемости подынтегральной функции . Если — первообразная для , то значение можно вычислить по формуле Ньютона—Лейбница: . Функцию можно исследовать, не вычисляя первообразной. Для интегрируемой при функции справедливы следующие утверждения:   непрерывна на промежутке , причем ; если при , то     монотонно возрастает на промежутке ; если непрерывна при , то дифференцируема на промежутке , причем . 

Несобственные интегралы по неограниченному промежутку.

Пусть функция  интегрируема для всех  и   . Если существует предел , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его  . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл для интегрируемой при  функции  и интеграл для функции , интегрируемой на . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится. 

Несобственные интегралы от неограниченных функций.

Пусть функция  интегрируема на любом отрезке, целиком содержащемся в промежутке, и бесконечно большая в точке . Если существует предел , то этот предел называют несобственным интегралом от неограниченной функции по и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл от интегрируемой на любом конечном отрезке, содержащемся в , бесконечно большой в точке  функции . Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится. 

Исследование несобственных интегралов на сходимость.

Вычисление несобственных интегралов сводится к вычислению первообразной, использованию формулы Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе достаточно сложен, и разумно приступать к ним, если есть уверенность, что интеграл сходится, то есть предел конечен. Поэтому, в конечном счете, самым важным в теории несобственных интегралов является исследование их на сходимость: если интеграл расходится, то его и вычислять не надо. Одним из главных инструментов исследования несобственных интегралов на сходимость являются теоремы сравнения.

Рассмотрим две неотрицательные функции  и , определенные при . Пусть  для всех  , начиная с некоторого числа . Тогда, если сходится интеграл от большей функции , то сходится и интеграл от меньшей, то есть. Если расходится интеграл от меньшей функции  ,то расходится и интеграл от большей — . 

Если   , то несобственные интегралы от этих функций или оба сходятся или оба расходятся. 

Аналогичные утверждения, которые называют признаками сравнения, имеют место и для интегралов по конечному промежутку от неограниченных функций.

 

 

Наверх

20.

Числовые ряды.

Числовой ряд. Рассмотрим произвольную числовую последовательность и формально составим сумму ее членов    Это выражение называют числовым рядом, или просто рядом. Члены последовательности называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда . Эта сумма называется n-ой частичной суммой. 

 

Сходимость числового ряда. Ряд    называют сходящимся, если существует и конечен предел последовательности     частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают   , . Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность  называется остатком ряда. Очевидно, что для сходящегося ряда    . Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то  (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться. 

 

 

Суммирование числовых рядов. Если возможно найти общий член последовательности    , то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.

 

 

Наверх

21. Сходимость знакоположительных рядов.

Теоремы сравнения.

1. Рассмотрим два числовых ряда с неотрицательными членами   и  , . Если при всех n, начиная с некоторого номера,  , то из сходимости ряда  следует сходимость ряда. Наоборот, из расходимости ряда следует расходимость ряда. 

2. Если для таких же двух рядов   , то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд   , который сходится при и расходится при , или геометрический ряд , который сходится при  и расходится при  .  

Признаки сходимости. Признаки сходимости Даламбера. Для ряда с положительными членами , вычислим   . Если , то ряд сходится, — расходится. При признак Даламбера ответа не дает: ряд может как сходиться, так и расходиться. 

Признак сходимости Коши. Для ряда с неотрицательными членами   , вычислим . Если   , то ряд сходится, — расходится. При    признак Коши ответа не дает: ряд может как сходиться, так и расходиться.

 

 

Наверх

22. Сходимость знакопеременных рядов.

Абсолютная и условная сходимость. Если в последовательности  бесконечно много положительных и отрицательных членов, то ряд называется знакопеременным. Ряд   называется знакочередующимся. Знакопеременный ряд   называется абсолютно сходящимся, если сходится ряд   . Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда   начинают с исследования на сходимость ряда из модулей  методами для рядов с неотрицательными членами. Если такой ряд сходится, то получен ответ: ряд сходится абсолютно. 

 

Исследование знакочередующихся рядов. Если ряд из модулей расходится, то для знакочередующегося ряда можно применить признак Лейбница: если последовательность   стремится к нулю, монотонно убывая,   , то ряд    сходится, по крайней мере, условно. Для знакочередующегося ряда очень просто оценивается остаток ряда: .

 

 

Наверх

23. Функциональные ряды, равномерная сходимость.

Функциональный ряд, его сходимость. Рассмотрим ряд,   , членами которого являются функции, определенные на промежутке   . При каждом фиксированном   имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда   также является функцией от х:   . По определению предела последовательности: если для   можно указать номер  ( что интересно, для каждого фиксированного   — свой номер, т.е.  ), такой, что для    выполняется неравенство  , то это и означает, что функциональный ряд сходится к функции. Множество , для которого это выполняется, называется областью сходимости функционального ряда. 

 

Равномерная сходимость функционального ряда. Пусть   , т.е. функциональный ряд сходится. Если для   можно указать номер  независимо от  , такой, что для выполняется неравенство  , то говорят, что функциональный ряд сходится равномерно на множестве .   

  

Исследование на равномерную сходимость. Признак Вейерштрасса равномерной сходимости функционального ряда: если существует сходящийся числовой ряд   с положительными членами, такой, что для всех  , начиная с некоторого номера и всех  выполняется неравенство , то функциональный ряд   сходится на равномерно. Числовой ряд   в этом случае называют мажорантой для функционального ряда.

 

 

Наверх

24. Ряд Тейлора.

Степенные ряды. Функциональный ряд     , где — числовая последовательность, называется степенным рядом. Степенной ряд сходится на интервале   с центром в точке   . Число  — радиус сходимости степенного ряда может быть вычислено по формулам , или     . Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда. 

 

Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция   определена в некоторой окрестности точки   и имеет в этой точке производные всех порядков. Ряд 

называется рядом Тейлора для функции    в точке . При такой ряд называют также рядом Маклорена:    . Функция  может быть разложена в степенной ряд на интервале , если существует степенной ряд, сходящийся к  на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки , то это ряд Тейлора. Пусть функция   бесконечно дифференцируема на интервале и все ее производные ограничены в совокупности на этом интервале, то есть существует число   , такое, что для всех    и для всех   справедливо неравенство . Тогда ряд Тейлора сходится к   для всех   . Приведем разложения в ряд Тейлора для основных элементарных функций. 

 

 

Наверх

25. Ряд Фурье.

Ряд Фурье, его сходимость. Пусть функция  абсолютно интегрируема на отрезке  , то есть существует   . Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье: . Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье: . Если функция  кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если   — сумма ряда Фурье, то для любого        . То есть, если   непрерывна в точке  , то   . Если в точке   у   разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке . 

  

Разложение в ряд Фурье на произвольном отрезке. Для кусочно-гладкой на отрезке  функции задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке  :   , .

 

 

Наверх

26. Сходимость ряда Фурье.

Сходимость ряда Фурье, явление Гиббса. Если функция  кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если — сумма ряда Фурье, то для любого  . То есть, если  непрерывна в точке  , то  . Если в точке  у     разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке  . В окрестности точек непрерывности функции   разность между значением функции в точке и значением частичной суммы ряда в этой точке стремится к нулю при  , что полностью соответствует теории, поскольку в этом случае   . В окрестности точек разрыва   частичные суммы ряда Фурье ведут себя иначе. Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Оно состоит в том, что для некоторых функций в точке ее скачка      существуют такие значения    , что

Это не противоречит теории, поскольку у Гиббса рассмотрен предел  , а в теории v     .  

Приближение функций, минимальное свойство коэффициентов Фурье. Функция , где    — произвольные числа, называется тригонометрическим многочленом. Тригонометрическим многочленом наилучшего приближения n-ой степени для функции     на отрезке   называется такой многочлен , среднеквадратичное отклонение  которого от функции  минимально:    . Для любой ограниченной интегрируемой на    функции частичная сумма   ее ряда Фурье является тригонометрическим многочленом наилучшего приближения n-ой степени. 

 

Зависимость скорости сходимости от гладкости функций. Скорость сходимости ряда Фурье функции зависит от ее гладкости (количества непрерывных производных). Если   непрерывно дифференцируема r раз на отрезке   , то справедливо неравенство , где  . Для среднеквадратичного отклонения справедлива оценка   , где  .

 

 

Наверх

27. Функции многих переменных.

Функция двух переменных. Переменная  (с областью изменения  ) называется функцией независимых переменных  в множестве  , если каждой паре их значений из   по некоторому правилу или закону ставится в соответствие одно определенное значение   из множества . Множество v область определения функции, множество   v область ее значений. Функциональная зависимость   от обозначается так:  и т.п. Выберем в пространстве систему координат  , изобразим на плоскости   множество  ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных. 

Линии и поверхности уровня. Линией уровня функции двух переменных   называется геометрическое место точек на плоскости   , в которых функция    принимает одно и то же значение. Линии уровня функции определяются уравнением  , где . Изучая линии уровня функции, можно исследовать характер ее изменения, не прибегая к пространственному графику. Поверхностью уровня функции трех переменных    называется геометрическое место точек в пространстве, в которых функция  принимает одно и то же значение. Уравнение поверхностей уровня имеет вид:  . Поскольку график функции трех переменных нам недоступен, поверхности уровня являются единственным средством изучения таких функций.  

  

Локальные экстремумы. Точка называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что  для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.

 

 

Наверх

28. Частные производные, градиент.

Частные производные. Пусть  — функция двух переменных, определенная в некоторой окрестности точки . Если существует конечный предел   , то говорят, что функция   имеет в точке частную производную по переменной   . Аналогично определяется частная производная по    . Обозначают:

 . 

Пусть — функция n переменных, определенная в области   n-мерного пространства. Частной производной функции по переменной  называется предел 

. 

Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.  

Производная по направлению. Если в n-мерном пространстве задан единичный вектор , то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению: . В частности, для функции трех переменных   ,  — направляющие косинусы вектора  . 

Градиент. Производная по направлению представляет собой скалярное произведение вектора   и вектора с координатами   , который называется градиентом функции    и обозначается    . Поскольку   , где   — угол между   и   , то вектор указывает направление скорейшего возрастания функции   , а его модуль равен производной по этому направлению. 

Полный дифференцал. Для приращения дифференцируемой функции   справедливо равенство    . Линейная по приращениям аргументов часть приращения функции называется полным дифференциалом функции и обозначается    . 

Производные и дифференциалы высших порядков. Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим производные второго порядка. Например, для функции двух переменных: . Если смешанные производные     и     непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например,     . Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных:    . Здесь учтено равенство смешанных производных второго порядка и принято    . При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения:   .

 

 

Наверх

29. Неявные функции.

Неявная функция одной переменной. Пусть в некоторой области   плоскости задана функция , и пусть линия уровня этой функции , определяемая уравнением   , является графиком некоторой функции   , определяемой уравнением    . В этом случае говорят, что функция    задана неявно уравнением   . Для существования неявной функции требуется выполнение следующих условий: функция   и ее частная производная по    непрерывны в     , . Тогда в некоторой окрестности точки   существует единственная непрерывная функция     , задаваемая уравнением   , так, что в этой окрестности   . 

  

Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение     задает неявно функцию   . Это же уравнение может задавать неявно функцию или      . 

 

Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение  : . Отсюда получим формулу для производной функции    , заданной неявно:   . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением   : , .

 

 

Наверх

30. Формула Тейлора для многих переменных.

Формулы Тейлора и Маклорена. Если функция   имеет в некоторой окрестности точки непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки из этой окрестности справедлива формула Тейлора n-го порядка:  , где ,

 ,

 

и т. д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2: . 

 

Аппроксимация функции многочленом. Выражение

называется многочленом Тейлора n-го порядка. Поскольку , то в окрестности точки функцию можно приближенно заменить, или, как говорят, аппроксимировать, ее многочленом Тейлора, т.е.  . Чем ближе точка  к точке , тем выше точность такой аппроксимации; кроме того, точность возрастает с ростом n. Это означает, что, чем больше непрерывных производных имеет функция  , тем точнее представляет ее многочлен Тейлора.

 

 

Наверх

31. Исследование на экстремум.

Локальные экстремумы. Точка   называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что   для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.  

 

Исследование на экстремум функции двух переменных. Обозначим через приращение функции   в точке  . Если — точка локального минимума функции  , то существует окрестность   , в которой   (обратное неравенство в случае максимума). Из формулы Тейлора первого порядка   следует, что приращение   дважды непрерывно дифференцируемой функции   может сохранять знак, если главная линейная часть приращения функции в точке экстремума (максимума или минимума) равна нулю, т.е. выполнено необходимое условие экстремума: если точка   — точка экстремума, то   . Такая точка называется стационарной точкой функции. Приращение функции в стационарной точке имеет вид . Обозначим . Справедливо следующее достаточное условие экстремума. Пусть функция    дважды непрерывно дифференцируема в окрестности точки   и  . Если   , то в точке  функция достигает экстремума. Если при этом , то этот экстремум v минимум, при — максимум. Если же    , то в точке   экстремума нет. Геометрически достаточное условие означает, что в окрестности экстремума график функции   близок к поверхности . Если    , то для определения знака приращения   необходимо изучить члены формулы Тейлора более высокого порядка.

 

 

Наверх

32. Условный экстремум.

Условные экстремумы. Пусть функция  определена в некоторой области  и в этой области задана кривая уравнением . Условным экстремумом функции двух переменных  называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить , то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной . 

 

Метод множителей Лагранжа. Если уравнение  не разрешимо ни относительно  , ни относительно , то рассматривают функцию Лагранжа. Необходимым условием существования условного экстремума функции  при условии  является равенство нулю всех частных производных функции Лагранжа:   . 

  

Наибольшее и наименьшее значение функции в области. Поскольку функция  , непрерывная в ограниченной замкнутой области достигает в ней своего наибольшего и наименьшего значений, задача об их нахождении разделяется на две части: найти экстремумы функции двух переменных внутри области, найти ее условные экстремумы на границе области, при условии, что граница задана уравнением .

 

 

Наверх

33. Двойной и тройной интегралы.

Двойной интеграл в декартовых координатах. Пусть   ограниченная замкнутая область плоскости с кусочно-гладкой границей и пусть функция определена и ограничена на  . Посредством сетки кусочно-гладких кривых разобьем на конечное число элементарных областей с площадями  (разбиение ). Пусть — наибольший из диаметров областей , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число    называется интегральной суммой и ставится в соответствие каждому разбиению и каждому выбору точек . Если существует    и он не зависит от выбора разбиения  и точек , то функция называется интегрируемой по Риману в области , а сам предел называется двойным интегралом от функции  по области и обозначается    или   . Двойной интеграл существует, если  непрерывна на . Допустимы точки разрыва первого рода, лежащие на конечном числе гладких кривых в . 

 

Свойства двойного интеграла. Свойства двойного интеграла аналогичны свойствам определенного интеграла: 

Линейность:  

. Аддитивность: 

, если S1 и S2 две области без общих внутренних точек. 

Если для каждой точки  выполнено неравенство  , то . 

Если  интегрируема на , то функция   также интегрируема, причем . 

Если  и  наименьшее и наибольшее значения функции в области, а ее  площадь, то . 

Теорема о среднем значении: если  непрерывна в связной области , то существует, по крайней мере, одна точка такая, что   . 

Вычисление двойного интеграла. 

Если  , где —    непрерывные на функции, то двойной интеграл может быть вычислен двумя последовательными интегрированиями: . Аналогично, если , то     . 

Тройной интеграл и его свойства. Пусть — ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция  определена и ограничена в  . Посредством сетки кусочно-гладких поверхностей разобьем на конечное число элементарных областей   с объемами  (разбиение). Пусть . наибольший из диаметров областей  , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число ставится в соответствие каждому разбиению  и каждому выбору точек и называется интегральной суммой. Если существует   и он не зависит от выбора разбиения и точек,  то функция называется интегрируемой по Риману в области  , а сам предел называется тройным интегралом от функции   по области  и обозначается  . Свойства тройных интегралов такие же, как и у двойных интегралов. 

Вычисление тройного интеграла в декартовых координатах. Пусть  является цилиндрическим телом, проекция которого на плоскость  есть область  и которое ограничено снизу поверхностью , а сверху v поверхностью , где   — непрерывные функции в . Тогда , то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области . Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.

 

 

Наверх

34.

Замена переменных в кратных интегралах.

Замена переменных в двойном интеграле. Пусть функции взаимно однозначно отображают открытое множество, содержащее область плоскости на открытое множество, содержащее область , и пусть является образом . Если и их частные производные непрерывны, а определитель   , то . Выражение  называется элементом площади в криволинейных координатах, функциональный определитель — якобианом. 

 

Вычисление площади.

Замена переменных в тройном интеграле. Пусть посредством функций производится взаимно однозначное отображение открытого множества, содержащего область пространства на открытое множество, содержащее область пространства и  есть образ . Если эти три функции непрерывны вместе со своими первыми частными производными в области и якобиан, то . Выражение  называется элементом объема в криволинейных координатах . 

 

Вычисление объема.

Двойной интеграл в полярных координатах. Введем на плоскости полярные координаты. Пусть — область, полученная взаимно однозначным отображением области плоскости , определяемым функциями . Тогда , а двойной интеграл в полярных координатах вычисляется по формуле: .Элемент площади в полярных координатах есть .

 

 

Наверх

35. Сферические и цилиндрические координаты.

Тройной интеграл в цилиндрических координатах. Введем в пространстве цилиндрические координаты. Для этого на плоскости используем полярные координаты, а третья координата произвольной точки остается . Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические:  . Тогда  и тройной интеграл в цилиндрических координатах вычисляется по формуле: . Элемент объема в цилиндрической системе координат есть  . 

  

Тройной интеграл в сферических координатах. Введем в пространстве сферическую систему координат. Для этого рассмотрим произвольную точку  в декартовой системе координат. Спроектируем ее на плоскость , получив точку  . Положение точки в пространстве будем характеризовать ее расстоянием от начала координат , углом между отрезком и положительной полуосью , углом между отрезком и положительной полуосью . Декартовы координаты точки выражаются через сферические по формулам: . В этом случае    . Тогда тройной интеграл в сферических координатах вычисляется по формуле: 

.

Элемент объема в сферической системе координат есть  .

 

 

Наверх

36. Поверхностный интеграл по площади поверхности.

Площадь гладкой поверхности. Рассмотрим кусок поверхности  , заданной уравнением . Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Разобьем поверхность сеткой гладких кривых на элементарные области ( разбиение ). Пусть   — наибольший из диаметров элементарных областей. Если независимо от разбиения  существует , то он и называется площадью данной поверхности. Пусть    однозначно проектируется на плоскость и  — эта проекция. Элементу площади области на плоскости  соответствует элемент площади поверхности , равный , где — угол между нормалью к поверхности и осью . Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла  по проекции поверхности на плоскость. Если поверхность задана уравнением , то     и площадь поверхности вычисляется по формуле   , здесь — проекция поверхности на плоскость . Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности. 

 

Поверхностный интеграл 1-го рода. Пусть некоторая функция определена и ограничена на гладкой поверхности . Выберем разбиение поверхности и точки на каждой элементарной области   и составим интегральную сумму . Если независимо от выбора разбиения и точек существует , то он называется поверхностным интегралом по площади поверхности (1-го рода) от функции и обозначается    . 

 

Свойства и вычисление поверхностного интеграла по площади поверхности. Если поверхность задана уравнением  и однозначно проектируется на плоскость , то поверхностный интеграл 1-го рода вычисляется по формуле . Нетрудно получить аналогичные формулы, если поверхность однозначно проектируется на другие координатные плоскости. Поскольку вычисление поверхностного интеграла сводится к двойному интегралу, то, естественно, все свойства поверхностного интеграла 1-го рода такие же, как и у двойного.

 

 

Наверх

37. Криволинейный интеграл по длине дуги.

Криволинейный интеграл 1-го рода. Пусть — отрезок кусочно-гладкой кривой с началом в точке и концом в точке и — ограниченная функция, определенная в некоторой области, содержащей кривую . Выберем на кривой произвольные точки , разбивая ее на элементарные отрезки (разбиение ), длина каждого  . Обозначим . Пусть  — произвольная точка на элементарном отрезке . Составим интегральную сумму . Если независимо от разбиения и выбора точек существует    , то он называется криволинейным интегралом по длине кривой (1-го рода) и обозначается  . Аналогично определяется криволинейный интеграл 1-го рода      от функции трех переменных   по отрезку пространственной кривой. 

 

Свойства и вычисление криволинейного интеграла по длине дуги. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой , то есть. Это единственное свойство, которое не совпадает с обычными свойствами интегралов, определеямых через предел интегральной суммы. Если — отрезок кусочно-гладкой кривой, заданной параметрически:

 , то криволинейный интеграл вычисляется по формуле:

. Если плоская кривая задана в явном виде, то криволинейный интеграл вычисляется по формуле: .

 

 

Наверх

38. Скалярное поле.

Скалярное поле. Если каждой точке пространства ставится в соответствие скалярная величина , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также

 или      . Поле может быть плоским, если   , центральным (сферическим), если   , цилиндрическим, если .

 

Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых   принимает постоянное значение. Их уравнение:  . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение: 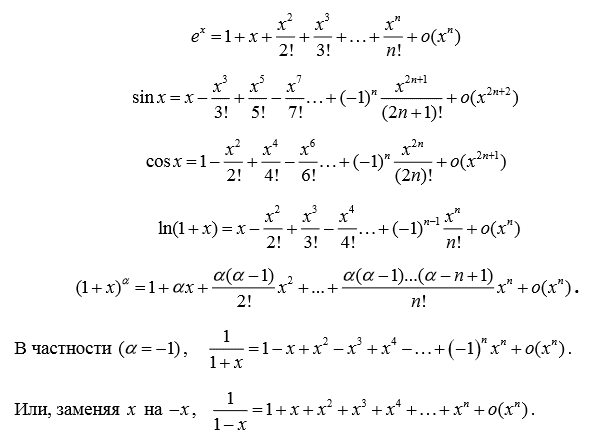  . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые. 

 

Производная по направлению и градиент скалярного поля. Пусть   — единичный вектор с координатами  ,  — скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле  . Производная по направлению представляет собой скалярное произведение вектора   и вектора с координатами  , который называется градиентом функции  и обозначается  . Поскольку  , где  — угол между   и  , то вектор  указывает   направление скорейшего возрастания поля , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента: 

 

 

Наверх

39. Векторное поле.

Векторное поле. Если каждой точке пространства ставится в соответствие вектор , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде: . Скалярные функции однозначно определяют векторное поле. Векторное поле может быть плоским, если , сферическим, когда , , цилиндрическим, когда , . 

 Векторные линии (линии тока). Для наглядного представления векторных полей используют векторные линии (линии тока). Это кривые, в каждой точке которых вектор является касательным вектором. Через каждую точку проходит одна линия тока. За исключением точек, где поле не определено или , линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид:

 

 

Наверх

40. Поток векторного поля.

Поток векторного поля. Рассмотрим кусок поверхности , заданной уравнением . Пусть выполняется условие  , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Выберем одну из сторон поверхности следующим образом: построим на поверхности достаточно малый замкнутый контур, на котором задано направление обхода. Построим вектор нормали в точке поверхности, лежащей внутри контура. Если из конца вектора нормали обход контура кажется происходящим против часовой стрелки, то будем называть сторону поверхности, обращенную к вектору нормали положительной стороной. Таким образом, будем рассматривать ориентированную двухстороннюю поверхность, а односторонние поверхности лист Мебиуса, бутылку Клейна оставим в покое. Потоком векторного поля   через ориентированную поверхность называется поверхностный интеграл по площади поверхности (1-го рода)  , где —     единичный вектор нормали, направленный в положительную сторону. Выбор положительной стороны обычно диктуется физическими условиями задачи. 

 

Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции , где  — компоненты векторного поля,  — направляющие косинусы вектора нормали.

 

 

Наверх

41. Формула Остроградского.

Поток векторного поля через замкнутую поверхность. Рассмотрим кусочно-гладкую двухстороннюю замкнутую ориентированную поверхность  . Поток векторного поля   через замкнутую поверхность является важной характеристикой поля и позволяет судить о наличии источников и стоков поля. При непосредственном вычислении потока через замкнутую поверхность приходится разбивать ее на части, однозначно проектируемые на координатные плоскости. 

Формула Остроградского. Пусть замкнутая поверхность ограничивает некоторый объем  . Тогда в декартовых координатах справедлива формула Остроградского: , где  — компоненты векторного поля. 

 

 

Дивергенция векторного поля. Дивергенцией   векторного поля  называется . Точка  находится внутри замкнутой поверхности , ограничивающей объем   , который при вычислении предела стягивается в эту точку.  является скалярной величиной и служит мерой источников поля. Если в некоторой области поля  , то источников поля в этой области нет. Такое поле называют соленоидальным. Используя формулу Остроградского, нетрудно получить выражение для вычисления дивергенции в декартовых координатах: . Из свойств частных производных следуют свойства дивергенции векторного поля: 

 

 

Наверх

42. Криволинейный интеграл в векторном поле.

Криволинейный интеграл в векторном поле. Пусть заданы некоторое векторное поле  и кривая АВ (А — начальная точка, В — конечная). Криволинейный интеграл в векторном поле     есть скаляр, полученный следующим образом: 

Разобьем кривую точками А=А0, А1, А2-Аn=В на n частей, приближенно изображаемых векторами  (разбиение ). 

Обозначим  . 

На границе или внутри каждой элементарной дуги Аi-1Ai выберем точку, которой соответствует радиус-вектор   и составим интегральную сумму   . 

Если существует     и он не зависит от разбиения  и выбора точек, то этот предел называется криволинейным интегралом в векторном поле. В декартовой системе координат:, где — компоненты векторного поля.

Если кривая задана в параметрической форме:

, то вычисление криволинейного интеграла сводится к определенному интегралу: 

. Используя определение и формулу для вычисления нетрудно получить свойства криволинейного интеграла: 

Подчеркнем, что, в отличие от криволинейного интеграла по длине дуги, криволинейный интеграл в векторном поле меняет знак при изменении направления интегрирования. 

Если   векторное поле, описывающее физическое силовое поле, то криволинейный интеграл выражает работу, которую совершает   сила при переносе материальной точки из пункта А в пункт В вдоль кривой АВ. 

 

Циркуляция векторного поля. Важной характеристикой векторного поля является циркуляция векторного поля, которая равна криволинейному интегралу по замкнутой кривой в области поля, или, как говорят, по замкнутому контуру:   . Циркуляция векторного поля является скалярной величиной и характеризует вихревые свойства поля. Если в некоторой области поля циркуляция равна нулю, то поле называют безвихревым.

 

 

Наверх

43. Формула Стокса.

Формула Стокса. Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности , край которой образуется кусочно-гладкой кривой . Выберем положительную сторону поверхности (из конца единичного вектора нормали      обход границы представляется против часовой стрелки). Для циркуляции векторного поля     вдоль контура границы имеет место формула Стокса: , где   — компоненты векторного поля,   — направляющие косинусы вектора нормали. 

  

Ротор векторного поля. Рассмотрим в пространстве замкнутый контур  с выбранным направлением обхода, лежащий в ориентированной плоскости на ее положительной стороне (из конца единичного вектора нормали   обход контура представляется против часовой стрелки). Ротором    (или вихрем) векторного поля в точке  называется вектор, проекция которого на направление вектора нормали есть    . Точка лежит  на плоскости внутри контура  , который стягивается в эту точку при вычислении предела. Поскольку ротор поля определяется через циркуляцию, то он тоже является мерой завихренности поля. Найдем компоненты ротора в декартовой системе координат, воспользовавшись формулой Стокса. Для этого выберем сначала координатную плоскость y0z с нормальным вектором   , затем x0z,     , затем x0y,   . Применяя каждый раз теорему о среднем для интеграла, получим:    

Теперь теорема Стокса может быть сформулирована следующим образом: циркуляция векторного поля вдоль контура равна потоку ротора поля через поверхность, натянутую на этот контур. Выражение для ротора поля проще запомнить, если записать его в виде определителя:. Используя свойства частных производных и определителей, получим следующие свойства ротора векторного поля:

 

 

 

Наверх

44. Потенциальное поле.

Потенциальное поле. Если векторное поле  , то оно называется потенциальным, а скалярное поле , соответственно, его потенциалом. Самым известным примером такого соответствия является электрическое поле, напряженность которого  , где — потенциал электрического поля. Минус в формуле связан с историческим выбором направления вектора напряженности от плюса к минусу, когда уже умели тереть шерсть об янтарь, но не знали, как это описывать математически. 

  

Условие потенциальности поля. Пусть задано скалярное поле  , причем данная функция дважды непрерывно дифференцируема. Напомним, что в этом случае смешанные частные производные второго порядка не зависят от порядка дифференцирования. Вычислим  . 

Нетрудно видеть, что при этих условиях получается тождественный ноль. То есть, если поле потенциальное, то его  . 

 

 

Вычисление потенциала векторного поля. Если мы убедились, что поле  является потенциальным, то есть его ротор равен нулю, то представляет интерес вычислить потенциал этого поля. Для этого рассмотрим криволинейный интеграл в данном векторном поле:  , где точки А и В — начальная и конечная точки кривой. Поскольку  , то скалярное произведение векторов     и      является полным дифференциалом функции  : . Поэтому из свойств криволинейного интеграла следует, что . Смысл полученной формулы состоит в том, что работа поля по перемещению материальной точки из А в В не зависит от пути интегрирования, а только от конечной и начальной точек, точнее, от разности потенциалов в этих точках. Понятие разности потенциалов хорошо известно из физики. Для вычисления потенциала поля в произвольной точке В выберем начальную точку А, от которой начнем отсчет (в физике часто это — бесконечно удаленная точка). Тогда . Поскольку интеграл не зависит от пути интегрирования, то выберем его так, как нам удобно: сначала параллельно оси 0х, потом параллельно 0у, наконец, параллельно 0z. Обозначая , получим: 

.

Здесь    — компоненты векторного поля    . Поскольку выбор начальной точки произволен, потенциал поля определяется с точностью до произвольной постоянной, которая определяется физическими соображениями.

Формула Тейлора с остаточным членом в форме Пеано

Допустим, мы знаем значение функции f в какой-то точке x0, а хотим узнать её значение в точке x. Если мы ничего знаем про функцию f дополнительно, дело это безнадёжное: f(x) может равняться чему угодно, даже если x близко к x0. Например, функция Дирихле принимает значения 0 и 1 в сколь угодно близких точках. Однако, если потребовать, чтобы f обладало какими-нибудь хорошими свойствами, задача становится не столь бессмысленной. Об этом мы и поговорим. Но сперва нужно ввести некоторые обозначения.

21.1o-символика

21.1.1Определение o-малого

Пусть функцию f дифференцируема в точке x0. Тогда, как мы знаем, справедливо утверждение о линейном приближении:

f(x)=f(x0)+f′(x0)(x−x0)+α(x−x0)⋅(x−x0),(21.1)

f(x)=f(x0)+f′(x0)(x−x0)++α(x−x0)⋅(x−x0),(21.1)

где α(x−x0)→0 при x→x0. Иными словами, выражение α(x−x0)⋅(x−x0) не просто маленькое при x близком к x0, а оно маленькое по сравнению с разностью x−x0.

В дальнейшем нам пригодится более компактное обозначение для функций, которые являются маленькими по сравнению с какими-то другими функциями.

Определение 1. Говорят, что функция f является o-маленьким (или o-малым) от функции g при x→x0 если f и g определены в некоторой проколотой окрестности точки x0, g в этой окрестности не обращается в ноль и

limx→x0f(x)g(x)=0.(21.2)

Неформально это означает, что f(x) становится во сколько угодно раз меньше g(x) при x→x0.

Пример 1. Функция x2 является o-маленьким от x при x→0, поскольку

limx→0x2x=limx→0x=0.

Пример 2. Функция sin(1/x) является o-маленьким от функции 1/x при x→0, поскольку

limx→0sin(1/x)1/x=limx→0xsin1x=0.

Мы воспользовались тем, что произведение ограниченной функции и стремящейся к нулю стремится к нулю.

Пример 3. Функция sin(x) не является o-маленьким от функции x при x→0, поскольку

limx→0sin(x)x=1≠0.

(Это первый замечательный предел. )

Пример 4. Функция sin(1/x) не является o-маленьким от функции x при x→0, поскольку предел

limx→0sin(1/x)x

не существует.

Вопрос 1. Является ли функция x2 o-маленьким от функции x+x2 при x→0?

  Да

Верный ответ. Действительно,

limx→0x2x+x2=limx→0x1+x=0.

  Нет.

Неверный ответ. А если посчитать предел, что получается?

21.1.2Свойства o-малого

Можно сформулировать и доказать много разных утверждений про свойства o-малых, следующих из определения и свойств пределов. Например:

Утверждение 1. Пусть f(x)=o(g(x)) и h(x)=o(g(x)). Тогда f(x)+h(x)=o(g(x)). Это можно записать короче так:

o(g(x))+o(g(x))=o(g(x)).

В этом равенстве o-малые есть и справа и слева — на самом деле, правильно было бы записать так:

o(g(x))+o(g(x))⊂o(g(x)),

то есть для любого способа выбрать конкретные функции на место o(g(x)) в левой части найдётся функция справа, которая будет o(g(x)).

Доказательство. Проверим, что f(x)+h(x)=o(g(x)). Действительно:

limx→x0f(x)+h(x)g(x)=limx→x0(f(x)g(x)+h(x)g(x))=0

по теореме о пределе суммы.∎

Утверждение 2. Пусть f(x)=o(g(x)) и c≠0. Тогда f(x)=o(cg(x)).

Доказательство. Действительно,

limx→x0f(x)cg(x)=1climx→x0f(x)g(x)=0.

∎

На семинаре будут обсуждаться и другие свойства такого типа. Для тренировки можете придумать как можно больше верных свойств o-малых и доказать их.

21.2Приближение функций

21.2.1Непрерывность и дифференцируемость

Итак, пусть мы знаем значение функции f в точке x0, а нас интересует значение f в точке x. Будем считать, что x близко к x0.

Если мы знаем, что f непрерывна, это означает, что limx→x0f(x)=f(x0), то есть значения в близких точках близки к значению f(x0). Значит можно записать:

f(x)≈f(x0).

Если вы ничего не знаете про моделирование погоды и хотите узнать, какую погоду ждать завтра, самый лучший ответ, который вы можете дать — примерно такую же, как сегодня.

Знак приближенного равенства не имеет строгого смысла и не может использоваться в доказательствах. Однако, мы можем использовать o-символику, чтобы сформулировать аккуратное утверждение про непрерывность:

f(x)=f(x0)+o(1),(21.3)

где o(1) — это функция, являющаяся o-маленьким от 1 при x→x0. По определению, o(1) — это такая функция, которая при делении на единицу стремится к нулю, а поскольку деление на единицу ничего не меняет — она сама стремится к нулю. Иными словами, равенство (21.3) — это просто другой способ сказать, что функция f непрерывна в точке x0.

В общем, если мы знаем, что функция f непрерывна, и больше ничего, то лучшее, что мы можем сделать — это приблизить её константой, функцией y=f(x0).

Пусть теперь мы знаем, что f не только непрерывна в x0, но и дифференцируема, и, более того, мы знаем её производную в этой точке. Тогда справедливо равенство (21.1), которое может может быть записано в виде:

f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0),(21.4)

f(x)=f(x0)+f′(x0)(x−x0)++o(x−x0),(21.4)

где o(x−x0) — это какая-то функция, являющаяся o-маленьким от (x−x0) при x→x0. Действительно, если поделить α(x−x0)⋅(x−x0) на (x−x0), получится α(x−x0), а про неё мы знаем, что она стремится к нулю при x→x0.

В приближении (21.4) мы заменяем функцию не на константу, как в (21.3), а на линейную функцию, и говорим, что разница между настоящей функцией и её линейным приближением будет не просто маленькой при x→x0 (это было верно и в (21.3)), но маленькой по сравнению с (x−x0). Иными словами, воспользовавшись дополнительной информацией (дифференцируемосью и знанием производной), мы получили лучшее приближение для функции.

Можем ли мы продолжить этот процесс? Оказывается, да.

21.2.2Многочлен Тейлора второй степени

Обозначим правые части равенств (21. 3) и (21.4) без o-малых через T0(x) и T1(x) соответственно: T0(x):=f(x0),T1(x):=f(x0)+f′(x0)(x−x0). Введённые нами функции T0 и T1 являются многочленами соответственно нулевой и первой степени. У T0 в точке x0 такое же значение, как у f, а у T1 не только такое же значение, но и такая же производная:

T1(x0)=f(x0),T′1(x0)=f′(x0).

Пусть теперь мы знаем, что функция f имеет не только первую, но и вторую производную в точке x0, и знаем эту производную. Хотим найти многочлен T2 второй степени, который бы имел в точке x0 такое же значение и такие же производные, как f, то есть хотим, чтобы выполнялись равенства

T2(x0)=f(x0),T′2(x0)=f′(x0),T′′2(x0)=f′′(x0).

T2(x0)=f(x0),T′2(x0)=f′(x0),T′′2(x0)=f′′(x0).

Как этого добиться? Пусть

T2(x)=f(x0)+f′(x0)(x−x0)+q⋅(x−x0)2,

где q — какая-то константа. Видно, что каким бы ни было q, T2(x0)=f(x0) и

T′2(x)=f′(x0)+2q⋅(x−x0),

и значит T′2(x0)=f′(x0). Таким образом, первые два условия выполняются автоматически. Осталось выбрать такое q, чтобы выполнялось и третье условие:

T′′2(x)=2q=f′′(x0).

Значит q=f′′(x0)/2. Таким образом,

T2(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2.

T2(x)=f(x0)+f′(x0)(x−x0)++f′′(x0)2(x−x0)2.

Пример 5. Пусть f(x)=2+lnx. Тогда f′(x)=1/x и f′′(x)=−1/x2. Пусть x0=1. Построим T0, T1 и T2:

T0(x)=f(1)=2T1(x)=f(1)+f′(1)⋅(x−1)=2+(x−1)T2(x)=f(1)+f′(1)⋅(x−1)+f′′(1)2⋅(x−1)2=2+1⋅(x−1)−12(x−1)2=2+(x−1)−(x−1)22.

T0(x)=f(1)=2T1(x)=f(1)+f′(1)⋅(x−1)=2+(x−1)T2(x)=f(1)+f′(1)⋅(x−1)++f′′(1)2⋅(x−1)2==2+1⋅(x−1)−12(x−1)2==2+(x−1)−(x−1)22.

Посмотрим на графики y=f(x) и y=T0(x), y=T1(x) и y=T2(x), см. рис. 21.1. График y=f(x) пересекается с горизонтальной прямой y=T0(x) в точке x=1 и касается прямой y=T1(x) в той же точке. Парабола y=T2(x) также касается графика y=f(x), причём ещё «плотнее», чем это делает y=T1(x) — в точках, близких к x0, она лучше приближает график нашей функции.

Рис. 21.1: Нулевое, первое и второе приближение логарифма

Построенные нами многочлены T0, T1 и T2 называются многочленами Тейлора. Как видно из построения и примера 5, многочлен Тейлора первой степени — это просто функция, задающая касательную, а многочлен Тейлора второй степени обобщает понятие касательной: вместо приближения графика прямой линией мы приближаем его параболой, и за счёт этого можем получить лучшую точность приближения.

21.2.3Тейлоровские многочлены в общем виде

Процесс построения многочленов Тейлора можно продолжать. Пусть функция f имеет n-ю производную в точке x0 (и, стало быть, все производные меньших порядков тоже).

Определение 2. Построим многочлен

Tn(x):=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2+f′′′(x0)3!(x−x0)3+…+f(n)(x0)n!(x−x0)n==n∑k=0f(k)(x0)k!(x−x0)k.

Tn(x):=f(x0)+f′(x0)(x−x0)++f′′(x0)2(x−x0)2++f′′′(x0)3!(x−x0)3+…++f(n)(x0)n!(x−x0)n==n∑k=0f(k)(x0)k!(x−x0)k.

где f(k) — это k-я производная функции f, нулевая производная — это сама функция, 0!=1.

Этот многочлен называется многочленом Тейлора степени n для функции f в окрестности точки x0.

Утверждение 3. Для всех k=0,…,n:

T(k)n(x0)=f(k)(x0).

Доказательство. Утверждение проверяется непосредственно дифференцированием. Поскольку при каждом дифференцировании степень монома xl уменьшается на единицу, при k-кратном дифференцировании все слагаемые степени меньше k превращаются в ноль. Все слагаемые степени больше k будут иметь вид C(x−x0)m для каких-то чисел C и m∈N. При подстановке x=x0 они обнулятся. Значит, останется только слагаемое степени k. В результате каждого дифференцирования степень уменьшается на единицу и сносится коэффициентом рядом с соответствующим слагаемым. После k дифференцирований коэффициент будет равен k! и он сократится с k! в знаменателе. Останется f(k)(x0), что и требовалось получить. ∎

21.2.4Остаточный член в форме Пеано

До сих пор мы просто формально строили какие-то многочлены, ничего не говоря о том, как он будет соотноситься с исходной функцией f, по которой он строился. Настало время это исправить.

При построении каждого следующего тейлоровского многочлена мы используем всё больше и больше информации про функцию f: значение, производную, вторую производную, третью производную и т.д. Разумно ожидать, что многочлены больших степеней будут приближать нашу функцию всё лучше и лучше. Есть разные способы это формализовать. Сейчас мы сформулируем один из них.

Теорема 1. (Формула Тейлора с остаточным членом в форме Пеано) Пусть f имеет n производных в точке x0 и Tn — многочлен Тейлора для функции f в окрестности точки x0. Тогда

f(x)=Tn(x)+o((x−x0)n),x→x0.(21.5)

f(x)=Tn(x)+o((x−x0)n),x→x0.(21.5)

Доказательство. Для n=1 формула Тейлора совпадает с (21. 4) и была доказана ранее. Пусть n>1.

Нам нужно доказать, что f(x)−Tn(x) является o((x−x0)n) при x→x0, то есть доказать, что предел

limx→x0f(x)−Tn(x)(x−x0)n(21.6)

равен нулю.

Найдём этот предел явно. Поскольку f(x0)=Tn(x0), он является неопределенностью 0/0. Заметим, что числитель и знаменатель дифференцируемы в окрестности точки x0: поскольку у функции f есть n производных в точке x0, это означает, что (n−1)-я производная определена в некоторой окрестности точки x0, иначе производную от неё нельзя было определить; но тогда и (n−2)-я производная существует в окрестности и т.д. до первой производной; Tn является многочленом и дифференцируем сколько угодно раз где угодно, равно как и (x−x0)n в знаменателе. Производная знаменателя не обнуляется при x≠x0. Значит, можем применить правило Лопиталя и рассмотреть новый предел:

limx→x0f′(x)−T′n(x)n(x−x0)n−1.

Поскольку f′(x0)=T′n(x0), это снова неопределенность 0/0. Если n>2, вторая производная функции f существует в окрестности x0 и мы можем снова применить правило Лопиталя. Получится такой предел:

limx→x0f′′(x)−T′′n(x)n(n−1)(x−x0)n−2.

Так мы можем продолжать до тех пор, пока в числителе не появится производная порядка (n−1):

limx→x0f(n−1)(x)−T(n−1)n(x)n!(x−x0).(21.7)

Дальше использовать правило Лопиталя нельзя: нам известно, что n-я производная функции f существует к точке x0, но не факт, что она существует в окрестности этой точки. Значит, условия теоремы о правиле Лопиталя могут не выполняться. Однако, это не страшно. Заметим, что

T(n−1)n(x)=f(n−1)(x0)+f(n)(x0)(x−x0).

Проверьте, что это так (в частности, факториалы сократятся). Тогда предел (21.7) записывается в виде:

limx→x0f(n−1)(x)−f(n−1)(x0)−f(n)(x0)(x−x0)n!(x−x0)==1n!limx→x0(f(n−1)(x)−f(n−1)(x0)x−x0−f(n)(x0)).

limx→x01n!(x−x0)(f(n−1)(x)−−f(n−1)(x0)−f(n)(x0)(x−x0))==1n!limx→x0(f(n−1)(x)−f(n−1)(x0)x−x0−−f(n)(x0)).

Предел первого слагаемоего — это просто определение производной функции функции f(n−1) в точке x0. (Нужно приглядется к пределу и увидеть. Пригляделись? Ага, это оно.) А поскольку производная от (n−1)-й производной — это n-я производная, предел первого слагаемого равен f(n)(x0), а весь предел — нулю.

Теперь применение правила Лопиталя на каждом шаге обосновано и доказано, что исходный предел (21.6) тоже равен нулю. Что и требовалось!∎

21.3Применение формулы Тейлора

21.3.1Вычисление пределов

Пример 6. Найдём предел

limx→1ln(x)−x+1(x−1)2.

Это неопределенность 0/0 и в принципе её можно было бы раскрыть с помощью правила Лопиталя, но мы сделаем иначе. Разложим функцию ln(x) в ряд Тейлора с остаточным членом в форме Пеано в окрестности точки 1 до членов порядка 2 (ср. с примером 5 — разница только в константе). Получим:

lnx=(x−1)−(x−1)22+o((x−1)2).

Подставим это выражение в наш предел. Имеем:

limx→1ln(x)−x+1(x−1)2=limx→1(x−1)−(x−1)22+o((x−1)2)−x+1(x−1)2==limx→1−(x−1)22+o((x−1)2)(x−1)2=limx→1(−12+o((x−1)2)(x−1)2).

limx→1ln(x)−x+1(x−1)2==limx→1(x−1)−(x−1)22+o((x−1)2)−x+1(x−1)2==limx→1−(x−1)22+o((x−1)2)(x−1)2==limx→1(−12+o((x−1)2)(x−1)2).

Но по определению o-маленького, второе слагаемое стремится к нулю. (Какая бы функция не была написана вместо o((x−1)2), если её поделить на (x−1)2, частное будет стремиться к нулю.) Значит, предел равен −1/2.

21.3.2Достаточное условие экстремума

Теорема 2. Пусть функция f определена в окрестности x0, дважды дифференцируема в x0 и f′(x0)=0. Тогда если f′′(x0)>0, то в точке x0 строгий локальный минимум, а если f′′(x0)<0, то строгий локальный максимум.

Доказательство. Разложим функцию f в ряд Тейлора в точке x0 до членов порядка 2. Имеем:

f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2+o((x−x0)2).

f(x)=f(x0)+f′(x0)(x−x0)++f′′(x0)2(x−x0)2++o((x−x0)2).

Заметим, что f′(x0)=0, и второе слагаемое в формуле обнуляется. Заменим o((x−x0)2) на β(x−x0)(x−x0)2, где β(x−x0)→0 при x→x0. (Наличие такого представления эквивалентно определению o-малого.) Получаем такую штуку:

f(x)=f(x0)+(f′′(x0)2+β(x−x0))(x−x0)2.

f(x)=f(x0)++(f′′(x0)2+β(x−x0))(x−x0)2.

Поскольку β(x−x0)→0 при x→x0, в достаточно маленькой окрестности x0 знак выражения (f′′(x0)/2+β(x−x0)) совпадает со знаком f′′(x0), а (x−x0)2>0 при x≠0. Таким образом, если f′′(x0)>0, то второе слагаемое положительно, а f(x)>f(x0), а если f′′(x0)<0, то отрицательно, и f(x)<f(x0). Это и есть определения минимума и максимума соответственно.∎

21.4Заключение

Формула Тейлора с остаточным членом в форме Пеано — пожалуй, самый важный факт дифференциального исчисления. Это своего рода микроскоп, с помощью которого можно изучать сколь угодно тонкие локальные свойства функций. Однако, теорема 1 не говорит ничего про какую-то конкретную точку x. Она говорит, что если x приближается к x0, то тейлоровские многочлены быстро приближаются к значениям функции. Но что если мы будем делать наоборот — зафиксируем x и будем увеличивать n? Будет ли значение тейлоровских многочленов в точке x всё лучшим и лучшим приближением к f(x)? Оказывается, далеко не всегда. Однако во многих случаях — особенно важных с практической точки зрения — будет. Об этом — в следующей лекции.

---

← Предыдущая глава Следующая глава →

Разложение функций в ряд — Энциклопедия по экономике

Задачу, поставленную в предыдущем параграфе, можно решить путем разложения стоящей под знаком интеграла функции в ряд Тейлора с последующим интегрированием этого  [c.46]
Интегральный метод основан на применении моделей, которые в отличие от моделей дифференцирования, рассмотренных в первой главе, учитывают погрешность, возникающую при разложении функции в ограниченный ряд. Величины погрешности приближенно распределяют поровну между факторами.  [c.51]

Идея приближенных вычислений состоит в том, что сложную функцию представляют рядом, в котором ограничиваются первыми членами разложения. В данном случае, считая поправки и случайные отклонения от средних значений, малыми по сравнению с X и Y, разложим функцию / в ряд Тейлора  [c.161]

Решение этой системы и будет являться начальным приближением параметров. Очевидно, для того чтобы данный метод работал , необходимо, чтобы эта система нелинейных уравнений решалась довольно легко, например аналитически. 9.6.4. Разложение в ряд Тейлора по независимым переменным. Основой итеративной минимизации суммы квадратов является разложение функции регрессии в ряд Тейлора до линейных членов по параметрам. Для нахождения грубого начального приближения иногда бывает полезна процедура аппроксимации регрессии путем разложения ее в ряд Тейлора по независимым переменным Хг. Будем для простоты считать  [c.315]

На практике часто встречается ситуация, когда априорно известен нелинейный характер зависимости между объясняемыми и объясняющими переменными. В этом случае функция/в уравнении y=f(a,x) нелинейна (а — вектор параметров функции, которые нам нужно оценить). Например, вид зависимости между ценой и количеством товара в той же модели спроса и предложения она не всегда предполагается линейной, как в нашем примере. Нелинейную функцию можно преобразовать в линейную, как это было сделано, например, логарифмированием с функцией Кобба-Дугласа. Однако не все функции поддаются такой непосредственной линеаризации. Любую дифференцируемую нужное число раз функцию можно разложить в функциональный ряд и затем оценить регрессию объясняемой переменной с членами этого ряда. Тем не менее такое разложение всегда осуществляется в окрестности определенной точки, и лишь в этой окрестности достаточно точно аппроксимирует оцениваемую функцию. В то же время оценить зависимость требуется обычно на более или менее значительном интервале, а не только в окрестности некоторой точки. При линеаризации функции или разложении её в ряд с целью оценки регрессии возникают и другие проблемы искажение отклонений е и нарушение их первоначальных свойств, статистическая зависимость членов ряда между собой. Например, если оценивается формула  [c.359]

Разложение функций в степенные ряды  [c.178]

Сложным источником дохода можно назвать источник, доход которого является некоторой функцией нескольких случайных величин. Риск получения дохода из такого источника может быть оценен, как указано в главе 4, на основе линеаризации функции случайных аргументов. Напомним, что числовые характеристики функции случайных аргументов определяют путем разложения в ряд Тейлора. Обычно используют линейные приближения характеристик. Линейные оценки для связанных случайных аргументов имеют вид  [c.123]

Поиск интегральной функции распределения путем разложения плотности распределения в ряд с последующим аналитическим интегрированием этого ряда.  [c.46]

Для доказательства эквивалентности мы пройдем два этапа. На первом этапе мы осуществим для каждой функции полезности в условиях определенности U = U x) разложение в ряд Тейлора в точке х = Е[х]. На втором этапе мы применим оператор математического ожидания к аппроксимированной функции и получим, таким образом, функцию ожидаемой полезности.  [c.87]

Сначала предположим, что функции /о и /а- непрерывно дифференцируемы в точке х , а само это решение находится внутри Vx. Заменим, пользуясь малостью б, функции /о и /а- линейной частью их разложения в ряд Тейлора  [c.330]

В общем случае функцию ср можно считать аналитической, т.е. допускающей разложение в ряд Тейлора в точке х = О  [c.220]

Допустим, произошло смещение центра группирования на величину Дг, тогда t = ta + At, t b=-tb+ ДЛ Используя разложение в ряд Тейлора функции Лапласа Ф(0, получим  [c.54]

Эмпирическая энтропия Я является функцией случайной величины d. Ее математическое ожидание и дисперсию определим с помощью разложения функции Я (d/ri) в ряд Тейлора в точке q = М(д) [29]  [c.114]

В примере была использована высокая процентная ставка для того, чтобы было заметнее различие между результатами применения формул простых и сложных процентов. Разложение показательной функции в степенной ряд  [c.162]

Задача содержит определенные трудности. Ведь искомая функция v (0, х) имеет два разрыва, в ее разложении в ряд Фурье коэффициенты убывают не очень быстро, и хорошее восстановление v (0, х) затруднено тем, что в г (Т, х) соответствующие гармоники уже теряются в ошибках 8. Замена искомой функции v (0, х) на и (х) имеет и положительные, и отрицательные следствия. Положительным является своеобразный эффект регуляризации так как мы ограничимся относительно небольшим числом вариаций функции и (х) на величины Su (я)К1 S, то получить очень уж негладкую функцию и (0, х) не удается. С другой стороны, эта замена затрудняет и получение разрывов в v (О, х) ведь это требует построения в и (х) каких-то аппроксимаций 8-функций.  [c.365]

С этой целью воспользуемся разложением функции регрессии / (X,- В) в ряд Тейлора в окрестности точки 0 — В, (где  [c.353]

Этими исследованиями показано, что затраты на производство и хранение хорошо соответствуют квадратичным функциям, которые в допустимых пределах аппроксимируют структуру фактических затрат. Для нахождения квадратичных коэффициентов можно использовать метод наименьших квадратов, разложение в ряд Тейлора и т. д.  [c.216]

С принципиальной точки зрения прогноз hn величины hn по значениям At, А 0 дается формулой (24), где коэффициенты а получаются из разложения функции П(А) (см. (21)-(23)) в ряд Фурье с учетом формулы (31 ) для коэффициентов од, входящих в определение функции (рп ( А).  [c.185]

Первые члены разложения /0 (м) в ряд по м есть —1 +20/3м3. Остальные члены являются локально второстепенными по сравнению с м3. Поэтому исследование функции /(м, е) можно заменить в первом приближении исследованием функции 20/Зм3 +ем. Она имеет две стационарные точки V— е/20, при е стационарных точек при е > 0. Следовательно, так же устроена функция/(м, е) в окрестности нуля.  [c.132]

Для упрощения задачи заменим функцию и(.) ее квадратичной аппроксимацией, то есть разложением в ряд Тейлора вплоть до членов только второго порядка в некоторой точке (например, х = г0). Тогда функция U(.) примет вид  [c.62]

Можно интерпретировать это как квадратичную аппроксимацию первоначальной элементарной функции полезности получаемую разложением в ряд Тейлора вплоть до членов второго порядка в некоторой точке  [c.270]

Разложение функции f в ряд Тэйлора в фактической точке X по направлению X (= -Б), если в нем оставить только члены 1-го порядка, имеет вид  [c.10]

Как один из методов диагностики пригодности кандидатов тестирование нуждается в выявлении качества выполнения возложенных на него селективных функций. В качестве признанных для оценки тестов выступает ряд показателей, которые характеризуют как критерии качества, или добротности. Разложенные по жизненному циклу тестов — конструированию, проведению и вынесению оценки, они могут дать возможность проследить, на каком этапе тест в большей степени приобретает или теряет смысл, над каким аспектом его внедрения в практику специалистам предстоит работать еще. 140  [c.140]

Это последнее слагаемое в разложении произвольной функции называют остатком ряда.  [c.137]

Аналогично можно получить разложения в степенные ряды многих других функций.  [c.138]

РИС. 3.3 представляет собой схематическое изображение соотношения между доходностью и ценой облигации. Кривая, известная как кривая цены-доходности облигации, нелинейна и имеет отрицательный наклон. Моделирование изменения цены в результате изменения доходности облигации может оказаться очень сложным. Тем не менее, исходя из нашего понимания разложения рядов Тейлора, мы должны быть способны приблизиться к функции «цена-доходность» на определенном этапе разложения рядов Тейлора. Можно, например, применить первую производную цены облигации по доходности, вторую, третью и т.д. Фактически мы увидим далее, что применение рядов Тейлора всего лишь первых двух порядков прекрасно позволяет оценить изменение в цене облигации при малом изменении доходности. Более того, если мы разделим разные элементы рядов Тейлора на цену облигации, то получим очень полезный результат, показывающий волатильность цены облигации.  [c.139]

Таблица разложений в степенной ряд некоторых функций  [c.178]

Вместе с тем методологам анализа, вероятно, хотелось, как и в бухгалтерии (имеется в виду двойная запись как метод учета), иметь нечто неотъемлемо свое — поэтому и была предпринята абсолютизация роли факторного анализа в общей методике аналитических процедур, произошло неестественное выпячивание методов факторных разложений. При этом не только заимствовали из статистики известные методы индексного анализа, но и взяли из математического анализа способы разложений функции в ряд Тейлора. Появились дифференциальный, логарифмический и интегральный методы факторного анализа, якобы более точные и объективные. Началась игра в цифирьки , которая продолжается и по сей день (см., например, книги Г. В. Савицкой). Зачем нужны расчеты ради расчетов, к чему нужна повышенная точность в исчислении влияния отдельных факторов, что делать с выделенным факторами, насколько эти факторы управляемы — эти и другие подобные вопросы, а их список несложно расширить, традиционно оставляются без внимания главное — сделать факторные разложения, создать видимость серьезности анализа.  [c.350]

Дифференцирование — построение факторной модели приращения функции путем разложение ее в ряд Тейлора. Приращение представляется в виде ДДх.) = Е[(Э/7Эх) Дг], здесь F(x) — приращение функции Т7аргументов х., / — номера аргументов функции, 3F/3x — частные производные функции по аргументам л , Ах — приращения аргументов, значком обозначено суммирование по всем аргументам. Например, если прирост производства обусловлен приростом производительности труда и численности работников, то можно построить модель В = Р х Аи + п х д/>, где Д — прирост объемов производства, Р — плановая производительность, п — плановая численность работников, ДР и Ди — прирост производительности и численности по сравнению с планом.  [c.71]

ТЕЙЛОР (Taylor) Брук (1685-1731) — английский математик, член Лондонского королевского общества. Получил общую формулу разложения функций в степенной ряд, положил начало математическому изучению задачи о колебаниях струны. Он автор работ о полете снарядов, взаимодействии магнитов, центре качания, перспективе и др. К концу жизни занимался вопросами философии.  [c.136]

По теореме о разложении аналитической функции в ряд Тейлора частные производные функции отклика по факторам равны по величине и знаку, соответствующим коэффициентам регрессии. Следовательно, если изменять факторы пропорционально их коэффициентам регрессии и в ту сторону, которую указывает знак коэффициента, то движение будет осуществляться по градиенту. Эффективность градиента существенно зависит от характера поверхности отклика. Поэтому он не инвариантен относительно всего, что формирует поверхность от выбора параметра оптимизации и от выбора интервалов варьирования факторов. Действи-  [c.234]

Возможность использования этой функции для установления приближенной формулы основана па теореме Тейлора о разложении любой дифференцируемой функции в ряд по степени аргумента1.  [c.35]

На практике величину e kt-°a[c.252]

Линеаризация функции случайных аргументов. В общем случае числовые характеристики произвольной функции случайных аргументов определяются путем разложения в ряд Тейлора. Обычно используют линейные приближения оценок числовых характеристик, при необходимости их можно уточнить, вычисляя члены ряда Тейлора высших порядков. Линейные оценки для независимых случайных аргументов имеют вид12  [c.46]

Для построения схем стохастической аппроксимации с повышенной скоростью сходимости значительный интерес представляет работа Стратоновича [260]. Здесь исследованы возможности построения итеративных алгоритмов для отыскания корня уравнения регрессии по наблюдениям за реализациями случайной величины при различных значениях параметра. Рассматривается разложение функции регрессии в ряд Тейлора. Процедура Роббинса — Монро соответствует в этой схеме случаю, когда в разложении Тейлора сохраняются лишь линейные члены. Если в этой схеме удерживать также члены более высокого порядка, можно получить итеративные алгоритмы, скорость сходимости которых выше, чем в процедуре Роббинса — Монро.  [c.368]

Учитывая формулы (В. 19) и (В. 20) и воспользовавшись формальным разложением функции / ( — гх) в ряд Тейлора около точки , получаек соотношение между г и  [c. 42]

Дело в том, что в (6.6) стоит знак приближенного равенства, так как математическое ожидание величины /Тсл вычислено не точно (нам неизвестна функция распределения срока службы Тсл), а приближенно, на основе первых трех членов разложения величины /Тсл в ряд Тейлора. Но и с учетом этой поправки ясно, что политика амортизации (6.7) Я = л(1-)-е2) значительно надежнее, чем обычно используемая политика (6.5) п = /МТсл.  [c.193]

Приемов факторного анализа много, однако верхом аналитического совершенства считался так называемый интегральный метод, с помощью которого, по мнению его сторонников, можно было рассчитать факторные разложения с более высокой точностью1. Этот метод был заимствован из математики, причем без какого-либо осмысления возможности и оправданности его приложения к экономике. В математическом анализе соответствующий метод (разложение в ряд Тейлора) используется в условиях диф-ференцируемости функции, описывающей изучаемую взаимосвязь, и бесконечно малого изменения признаков, чего в экономике не может быть в принципе, так как многие показатели изменяются дискретно. Однако если даже абстрагироваться от этих формальных требований, то без какой-либо натяжки можно утверждать, что интегральный метод — лишь один из возможных способов факторного разложения, он не хуже и не лучше других, поскольку любое подобное разложение исключительно условно по самой своей сути. Если же подойти к этому вопросу критически, то несложно показать, что все подобные методы (дифференциальный, интегральный, логарифмический и др.) скорее вредны, нежели полезны, поскольку за счет утяжеления (именно утяжеления, а не усложнения) счетных процедур создается видимость серьезности анализа. Любые разговоры о преимуществе одних методов факторного анализа над другими, выражающемся в большей точности разложения (а это основной аргумент апологетов интегрального метода), представляют собой не более чем голословные утверждения. Кроме того, даже на мгновение согласившись с этим абсурдным утверждением, все же нельзя получить более или менее вразумительный ответ на вполне резонный вопрос а зачем нужна эта точность в приложении к ретроспективному анализу Поезд-то уже ушел Если же попытаться применить интегральный метод в перспективном анализе, то и здесь он абсолютно бессмыслен, поскольку исходный материал в этом случае — исключительно приблизительные прогнозные значения показателей. Иными словами, в любом случае анализ с помощью интегрального метода — это также игра в цифирьки , а пресловутая точность метода — не более чем лозунговый блеф. Применять интегральный метод — все равно что строгать скальпелем кол для изгороди строгать-то можно, только вот зачем  [c.348]

СПЕКТРАЛЬНЫЙ АНАЛИЗ [spe tral analysis] — математико-статистичес-кий метод анализа временных рядов, при котором ряд рассматривается как сложная совокупность, смесь гармонических колебаний, накладывающихся друг на друга. При этом основное внимание уделяется частоте колебаний используется, в частности, аппарат тригонометрических функций, разложение рядов, анализ автокорреляций. С.а. применяется при изучении колебаний деловой активности, корректировке сезонных колебаний для более наглядного представления тренда.  [c.338]

ХФ (к — л) + дН (х — fi), где Ф — функция нормального распределения, а Я — функция распределения произвольного симметричного относительно нуля закона не очень подходит как из-за симметрии Я, так и из-за того, что асимптотика, в которой q и Я фиксированы, а объемы выборки п -> оо, не вполне адекватна статистической практике с ростом объема выборки мы узнаем FQ с возрастающей точностью и в принципе могли бы путем преобразования переменных усилить близость распределения к нормальному закону. Более адекватной моделью засорения является схема последовательности серий выборок растущего объема, в которой пропорция засорения q= yn 1/2 убывает с ростом п [149, 215 и 14, п. 6.1.11]. 7.2.4. Эв-регрессия (i-регрессия). Ниже, используя тот же методический прием, что и при введении эв-оценок [14, п. 10.4.6],. с помощью цепочки определений вводится эв-регрессия и специальная мера отклонения от нее. Далее показывается, что эв-регрессия обладает рядом свойств, похожих на свойства обычной мнк-регрессии. Это облегчает содержательную интерпретацию эв-регрессии и выбор подходящего для конкретного случая значения Я. В заключение приводится асимптотическое разложение для оценок параметров эв-регрессии.  [c.218]

Полиномы Тейлора функций двух переменных

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

10916

• Пол Сибургер
• Общественный колледж Монро 92\),

  \[P_2′(c) = f'(c) \quad \text{and} \quad P_2»(c) = f»(c) \nonumber\]

  1-й и 2-й Полиномы Тейлора -степени для функций двух переменных

  Полиномы Тейлора работают таким же образом для функций двух переменных. (Просто больше каждой производной!)

  Определение: полином Тейлора первой степени функции двух переменных \(f(x, y)\)

  Для функции двух переменных \(f(x, y)\), первые части которого существуют в точке \((a, b)\), 9{\text{st}}\)-степень полинома Тейлора от \(f\) для \((x, y)\) вблизи точки \((a, b)\):

  \[f ( х, у) \приблизительно L(x, y) = f (a, b) + f_x(a, b) (x — a) + f_y(a, b) (y — b)\]

  \(L (x, y)\) также называется линейной (или касательной плоскостью ) приближением \(f\) для \((x, y)\) вблизи точки \((a, b) \).

  Обратите внимание, что на самом деле это просто уравнение касательной плоскости функции \(f\).

  Также обратите внимание, что первые частные производные этой полиномиальной функции равны \(f_x\) и \(f_y\)! 92 \]

  Примечание. Поскольку обе смешанные части равны, они объединяются, образуя средний член. Первоначально было четыре слагаемых для второго парциала, все они делились на 2. 2\), поскольку парциальное берется по отношению к \(x\) дважды, а в термине с \(f_{xy}(a,b)\) у вас есть множители \((x-a)\) и \((y-b)\) (оба возведены в первую степень), поскольку частичное берется по \(х\) один раз и по \(у\) один раз. 9y + 1\) для \((x, y)\) вблизи точки \((1, 0)\)

   

  Решение

  а. Чтобы определить линейную аппроксимацию полинома Тейлора первой степени, \(L(x, y)\), мы сначала вычисляем частные производные \(f\).

  \[ f_x(x, y) = 2\cos 2x \quad \text{and} \quad f_y(x,y) = -\sin y \nonumber\]

  Затем вычисление этих партиалов и самой функции в точка \((0,0)\) имеем:

  \[ \begin{align*} f(0,0) &= \sin 2(0) + \cos 0 = 1 \\ f_x(0, 0) &= 2\cos 2(0) = 2 \\ f_y(0,0) &= -\sin 0 = 0 \end{align*} \nonumber\] 9{\text{st}}\)-полином Тейлора степени, \(L(x,y) = 1 + 2x\)

  Чтобы определить приближение полинома Тейлора второй степени (квадратичное), \(Q(x, y)\), нам нужны вторые части \(f\):

  \[ \begin{align*} f_{xx}(x,y) &= -4\sin 2x \\ f_{xy}( x,y) &= 0 \\ f_{yy}(x,y) &= -\cos y \end{align*}\]

  Оценка этих 2-х частей в точке \((0,0)\) :

  \[ \begin{align*} f_{xx}(0,0) &= -4\sin 2(0) = 0 \\ f_{xy}(0,0) &= 0 \\ f_{ уу}(0,0) &= -\cos 0 = -1 \end{align*}\] 92}{2}\)

  Полиномы Тейлора высшей степени функции двух переменных

  Чтобы вычислить полином Тейлора степени \(n\) для функций двух переменных выше второй степени, нам нужно решить шаблон, который позволяет всем частям многочлена быть равными частям функции, аппроксимируемой в точке \((a,b)\), до заданной степени. 0 \\ 92 \end{align*}\]

  Это уравнение совпадает с уравнением \ref{tp2} выше.

  Обратите внимание, что \(P_2(x,y)\) является более формальным обозначением полинома Тейлора второй степени \(Q(x,y)\).

  Упражнение \(\PageIndex{1}\): нахождение полинома Тейлора третьей степени для функции двух переменных и используйте эту новую формулу для вычисления полинома Тейлора третьей степени для одной из функций в примере \(\PageIndex{1}\) выше. Проверьте свой результат с помощью графического редактора трехмерных функций, такого как CalcPlot3D.

  Ответить

  Как вы только что обнаружили, единственными новыми комбинациями \(i\) и \(j\) будут:

  \[\begin{align*} i = 0, && j = 3 \\ i = 1, && j = 2 \\ i = 2, && j = 1 \\ i = 3, && j = 0 \end{ выровнять*}\]

  Обратите внимание, что эти пары включают все возможные комбинации \(i\) и \(j\), которые можно добавить к \(3\). То есть эти пары соответствуют всем возможным членам третьей степени, которые мы могли бы иметь для функции двух переменных \(x\) и \(y\), помня, что \(i\) представляет степень \(x\). 3\) соответственно. 9Полиномы Тейлора {\text{nd}}\)-степени этих функций в этих точках. Используйте 3D-график, такой как CalcPlot3D, чтобы убедиться, что каждое линейное приближение касается данной поверхности в данной точке и что каждое квадратичное приближение не только касается поверхности в данной точке, но также имеет ту же вогнутость, что и поверхность в этой точке. точка.

  1) \( f(x,y)=x\sqrt{y},\quad P(1,4)\)

  Ответ:

  \( L(x,y) = 2x+\frac{1}{4}y−1\) 9j \nonumber\]

  10) Определите новые члены, которые будут добавлены к \(P_3(x,y)\) (которое вы нашли в упражнении 13.7.1), чтобы сформировать \(P_4(x,y)\) и определите полином Тейлора четвертой степени для одной из рассмотренных нами функций и начертите его вместе с графиком поверхности соответствующей функции в 3D-графике, таком как CalcPlot3D, чтобы убедиться, что он продолжает лучше соответствовать поверхности.

  Авторы

  • Пол Сибургер (Общественный колледж Монро)
  • Упражнения 1-4 были адаптированы из задач, приведенных в разделе Касательные плоскости и дифференциалы из учебника OpenStax Calculus 3.

  ---

  1. Наверх

  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или страница

     Автор

     Пол Сибургер

     Лицензия

     CC BY-NC-SA

     Показать страницу TOC

     нет

  2. Теги

     1. расчет: да

  Откуда берутся сериалы Тейлора и почему мы о них узнаем?

  Серии Тейлора часто могут показаться немного загадочными, когда мы впервые узнаем о них. Формула ряда Тейлора функции f(x) вокруг точки x=a задается как

  , где ƒ(n)(a) обозначает n-ю производную функции f(x) при x=a. Чтобы вычислить ряд Тейлора, мы находим производные n и подставляем их в формулу.

  Но что такое ряд Тейлора на самом деле? Ряды Тейлора — невероятно важный инструмент для численной аппроксимации. В этом посте мы разберем мотивацию сериалов Тейлора и прольем свет на то, откуда они берутся.

  Отправная точка: линейные приближения

  Один из самых простых типов функций, которые мы можем иметь, — это линейные функции, имеющие форму y=mx+b. Линейные функции легко отображать в виде графиков и вычислять.

  Предположим, у нас есть сложная функция, такая как f(x)=cos(x), которую трудно точно вычислить без калькулятора. Предположим теперь, что мы хотели оценить значение cos(x) вблизи x=0. Один из способов сделать это — линейное приближение. То есть мы построим линейную функцию g(x)=mx+b, близкую к f(x)=cos(x) при x=0. Для этого мы должны подумать о том, какие значения b и m дают нам наилучшее приближение f(x)=cos(x).

  Итак, поскольку мы ищем приближение вблизи x=0, хорошей отправной точкой будет g(x)=f(x) при x=0. То есть, поскольку cos(0)=1, мы хотим, чтобы g(0)=m(0)+b = 1, и поэтому b=1. Чтобы выяснить, какое значение m работает лучше всего, мы хотим, чтобы g(x) касалась f(x) при x=0, поэтому наклон m должен быть равен f'(0) = -sin(0) = 0 Это дает нам г (х) = 1 в качестве нашего линейного приближения.

  Мы можем видеть f(x)=cos(x) как красную кривую ниже и g(x) = 1 как синюю кривую ниже.

  Из приведенного выше графика видно, что для x, близкого к нулю, g(x)=1 является разумным приближением cos(x). То есть cos(x) для очень малых значений x близок к 1. Но это приближение не очень хорошо для больших значений x.

  Как мы можем улучшить нашу аппроксимацию?

  Улучшение: квадратичные аппроксимации

  Линейная аппроксимация g(x) = 1 для f(x) = cos(x) не учитывала кривизну графика cos(x). Если бы мы хотели уловить кривизну в нашем приближении, но при этом сохранить простоту нашего приближения, правильно было бы аппроксимировать f(x) = cos(x) не линейной функцией, а полиномом.

  Начнем с попытки аппроксимировать f(x) = cos(x) вблизи x=0 с помощью квадратичного многочлена

  Что мы можем сделать здесь лучше всего? Ну, как и в линейном случае, мы по-прежнему хотим, чтобы g(0) = f(0). Поскольку g(0) = a и f(0) = cos(0) = 1, это дает нам, что a=1.

  Мы также хотим, чтобы первые производные g’(0) = f’(0) отображали наклон касательной к графику вблизи x=0. Это дает нам, что b = -sin(0) = 0, и поэтому b=0.

  Попробуем также убедиться, что вторые производные от g(x) и f(x) совпадают при x=0. Вторая производная определяет скорость изменения производной, и поэтому сопоставление вторых производных примерно даст нам, что графики f (x) = cos (x) и нашего приближения g (x) кривые с той же скоростью вокруг x =0.

  Поскольку вторая производная g(x) при x=0 равна g»(0)=2c, а вторая производная f(x) = cos(x) при x=0 равна f»(0) = -cos(0) = -1, это дает нам, что 2c=-1, и поэтому c = -1/2.

  В результате наша квадратичная аппроксимация:

  Если мы нарисуем f(x) = cos(x) красным цветом, а нашу аппроксимацию g(x) — синим, мы получим следующий график:

   

  Мы видим, что это наше квадратичное приближение действительно является лучшим приближением нашей исходной функции вблизи x=0

  Приближения высшего порядка

  Но нет причин останавливаться на достигнутом! Мы могли бы продолжить аппроксимацию нашей функции f(x) = cos(x) полиномами все более и более высоких степеней. Пусть g(x) равно следующему:

  С помощью этого уравнения давайте сопоставим значения первых n производных g(x) при x=0 с соответствующими производными f(x) при x=0.

  Чему равна m-я производная g(x) при x=0? Что ж, немного подумав, мы можем увидеть, что если m не больше n, то верно следующее равенство:

  Это говорит нам о том, что мы должны иметь:

  Записав иначе, мы имеем:

  На приведенном ниже графике мы видим, что f(x) = cos(x) обозначено красным цветом, а некоторые лучше и лучшие полиномиальные приближения, найденные таким образом:

  показаны синим, зеленым и фиолетовым соответственно.

  Если мы продолжим этот процесс до бесконечности, то получим приближение Тейлора: внести:

  Если мы переставим члены, мы увидим, что:

  Это дает нам формулу для ряда Тейлора около x = 0 (иногда также известного как ряд Маклорена) общей функции f(x).

  Общая формула ряда Тейлора

  Чтобы закончить это обсуждение, отметим, что иногда мы хотим аппроксимировать функцию f(x) вблизи точки x=a, где a не обязательно равно нулю. Затем нам нужно сместить все это обсуждение так, чтобы оно сосредоточилось вокруг x=a, а не x=0.

  Для этого мы сопоставляем производные нашей функции f(x) и нашего ряда Тейлора не при x=0, а при x=a. При этом мы обнаруживаем, что правильным приближением является наше исходное выражение ряда Тейлора из начала этого поста.

  Так и было! Мы начали с линейных приближений, перешли к полиномиальным приближениям и закончили рядами Тейлора, которые в каком-то смысле являются бесконечно хорошими полиномиальными приближениями.

  Всякий раз, когда мы хотим численно аппроксимировать сложную функцию, мы можем взять первые несколько членов разложения функции в ряд Тейлора, чтобы получить хорошее полиномиальное приближение. Чем больше терминов мы возьмем, тем лучшее приближение получим. Эта связь с полиномиальными приближениями — лишь одно из многих свойств рядов Тейлора, которые делают их таким полезным и мощным математическим инструментом!

  Расширения серии Taylor | Математика ДПФ

  Разложение непрерывной функции в ряд Тейлора представляет собой полиномиальная аппроксимация . Это приложение является производным приближение ряда Тейлора неформально, затем вводит остаточный член и формальная формулировка теоремы Тейлора. Наконец, основной результат о полноте полиномиальной аппроксимации: заявил.

  У нас есть функция, и мы хотим аппроксимировать ее, используя 9-й порядок0545 многочлен :

  где

  , ошибка аппроксимации, называется остаточный срок . Мы можем предположим и действительно , но следующий вывод без изменений обобщается на сложный случай.

  Наша задача — найти фиксированные константы чтобы получить наилучшее возможное приближение. Давайте действовать оптимистично, как если бы приближение будет совершенным, и предположим для всех ( ), учитывая правильные значения . Тогда в мы должны быть

  Это одна постоянная работа! Теперь давайте посмотрим на первый производная по , снова предполагая, что

  :

  Оценка этого дает

  Таким же образом находим

  
  

  куда обозначает th производную относительно , оценивается в . Решив приведенные выше соотношения для искомого константы

  
  

  Таким образом, определяя (как это всегда бывает), мы вывели следующее полиномиальное приближение:

  Это разложение в ряд Тейлора порядка точка . Его вывод был довольно прост. Трудная часть показывая, что ошибка аппроксимации (остаточный член

  ) равна мало в широком интервале значений. Другая «математическая работа» состоит в том, чтобы определить условия, при которых ошибка аппроксимации стремится к нулю для всех, поскольку порядок стремится к бесконечности. Здесь важно отметить, что сам ряд Тейлора прост для вывести.

  ---

  Повторим вывод предыдущего раздела, но на этот раз относитесь к термину ошибки более внимательно.

  Снова мы хотим аппроксимировать полиномом порядка :

  — «остаточный член», который мы больше не будем считать равным нуль.

  Наша задача найти чтобы свести к минимуму на некотором интервале, содержащем . Есть много «критерии оптимальности» мы могли выбирать. Тот, который выпадает естественно здесь называется приближение Паде . Паде аппроксимация устанавливает значение ошибки и ее первые производные равными ноль в одной выбранной точке, которую мы принимаем за . Так как все «степени свободы» в полиномиальных коэффициентах используется для установки производных равными нулю в одной точке, приближение назвал максимально плоским в этой точке. Другими словами, как , полиномиальная аппроксимация порядка приближается с ошибкой, пропорциональной .

  Приближение Паде встречается в других областях обработки сигналов. За Например, это то, в каком смысле оптимальны фильтры Баттерворта. [53]. (Их частотные характеристики максимально плоские в центре полосы пропускания.) Кроме того, интерполяционные фильтры Лагранжа (которые не рекурсивны, а фильтры Баттерворта рекурсивны), может быть максимально плоским на постоянном токе в частотной области [82,36].

  Установка в указанном выше полиномиальном приближении дает

  где мы использовали тот факт, что ошибка должна быть точно равна нулю в в приближении Паде.

  Дифференциация полиномиальной аппроксимации и настройки дает

  где мы использовали тот факт, что нам также нужен наклон погрешность равна нулю при .

  Таким же образом находим

  для

  и первый производные остаточного члена равны нулю. Решение этих соотношений для искомых констант дает разложение в ряд Тейлора порядка точки

  как и раньше, но теперь мы лучше понимаем оставшийся член.

  Из этого вывода видно, что ошибка аппроксимации (остаток срок) является наименьшим в окрестности . Все степени свободы в полиномиальных коэффициентах были посвящены минимизации аппроксимации ошибка и ее производные при . Как и следовало ожидать, приближение ошибка обычно ухудшается по мере удаления от 0.

  Для получения более равномерного приближения на некотором интервале в , могут использоваться другие виды критериев ошибки. Классически, эта тема получила название «экономизация серий» или просто полиномиальная аппроксимация при различных критериях ошибки. В Матлаб или Октава, функция polyfit(x,y,n) найдет коэффициенты многочлена степень n, которая соответствует данным y по точкам x в смысл наименьших квадратов. То есть сводит к минимуму

  где

  .

  ---

  Формальное утверждение теоремы Тейлора

  Пусть непрерывна на вещественном интервале, содержащем (и ), и разреши существуют в и быть непрерывным для все . Тогда мы имеем следующее разложение в ряд Тейлора:

  
  

  куда называется остаточным членом . Затем Тейлор теорема [63, с. 95-96] утверждает, что существует некоторая между и таким, что

  В частности, если

  в , то

  который обычно мал, когда близок к .

  Когда , ряд Тейлора сводится к тому, что называется Маклорена. серия [56, с. 96].

  ---

  Аппроксимационная теорема Вейерштрасса убеждает нас в том, что многочлен аппроксимация может быть сколь угодно близкой к любой непрерывной функции, поскольку полиномиальный порядок увеличивается.

  Пусть непрерывна на вещественном интервале . Тогда для любого , существует многочлен th-го порядка , где зависит от , так что

  для всех .

  Доказательство см., , например. , [63, стр. 146-148].

  Таким образом, любая непрерывная функция может быть сколь угодно хорошо аппроксимирована значит многочлен. Это не обязательно означает, что Тейлор разложение в ряд может быть использовано для нахождения такого многочлена, поскольку в в частности, функция должна быть дифференцируемой всех порядков через . Кроме того, могут быть точки даже в бесконечно дифференцируемые функции, относительно которых разложение Тейлора не будет дают хорошее приближение, как показано в следующем разделе. главное здесь то, что благодаря приближению Вейерштрасса теореме, мы знаем, что хорошие полиномиальные приближения существует для любая непрерывная функция.

  ---

  Рассмотрим перевернутый гауссовский импульс, ^{E. 1}

  , т. е. , является хорошо известной гауссовой «гауссовой кривой». Ясно, что производные всех порядков существуют для всех . Тем не менее, это легко проверить, что все производных равны нулю. (Это легче проверить, что все производные колоколообразной кривой равны нулю при .) Поэтому каждое разложение в ряд Маклорена конечного порядка является нулевой функцией, а приближение Вейерштрасса теорема не может быть выполнена этим рядом.

  Как упоминалось в §E.2, мерой «плоскостности» является число ведущих нулевых членов в разложении Тейлора функции (не считая первый (постоянный) член). Таким образом, по этому показателю колоколообразная кривая «бесконечно плоская» на бесконечности, или, что то же самое, бесконечно плоский при .

  Еще одно свойство в том, что у него есть бесконечное количество «нулей» в . Тот факт, что функция имеет бесконечное число нулей в можно проверить с помощью показывая

  для всех

  . Для , существование бесконечного количество нулей в легко показать, посмотрев на нули в , т.е. ,

  для любого целого числа. Таким образом, более быстрое, чем экспоненциальное, затухание Колоколообразная кривая Гаусса не может опережать множитель ни при каком конечный . Другими словами, экспоненциальный рост или спад происходит быстрее. чем полиномиальный рост или затухание. (Как упоминалось в §3.10, разложение экспоненциальной функции в ряд Тейлора равно

  — полином «бесконечного порядка».)

  Обратная функция, содержащая нуль бесконечного порядка в точке имеет то, что называется существенной сингулярностью в [15, с. 157], также называемая несъемный сингулярность . Таким образом, имеет существенное особенность в , и имеет один в .

  Удивительный результат теории комплексных переменных [15, с. 270] что вблизи существенной особой точки ( т. е. , может быть комплексное число), неравенство

  удовлетворяется в какой-то момент в каждой окрестности , однако маленький! Другими словами, функция приходит произвольно близко ко всем возможным значениям в любой окрестности существенного сингулярная точка. Этот результат также принадлежит Вейерштрассу. [15].

  Таким образом, разложение в ряд Тейлора относительно этой точки будет всегда дают постоянное приближение, когда функция аппроксимируется бесконечно плоской при . По этой причине полиномиальное аппроксимации часто применяются в ограниченном диапазоне , с добавлены ограничения для обеспечения переходов от одного интервала к следующий. Это приводит к общей теме шлиц [81]. В частности, кубических сплайнов аппроксимаций состоят из последовательных сегментов, каждый из которых является многочленом третьего порядка. В каждом сегменте доступны четыре степени свободы (четыре полиномиальные коэффициенты). Два из них обычно посвящены сопоставлению амплитуда и наклон полинома в одну сторону, а две другие используются для максимизации некоторой меры соответствия по сегменту. точки, в которых соединяются соседние полиномиальные отрезки, называются «узлов», и поиск оптимального местоположения узлов обычно является относительно дорогие итерационные вычисления.

  ---

  Дифференцируемость звуковых сигналов

  Как упоминалось в §3.6, каждый звуковой сигнал можно рассматривать как бесконечно дифференцируемый из-за конечной пропускной способности человеческого слух. То есть для любого звукового сигнала его Фурье преобразование задается

  Для существования преобразования Фурье достаточно, чтобы абсолютно интегрируемый, т. е. ,

  . Ясно, все аудио сигналы на практике абсолютно интегрируемы. Обратный Фурье преобразование затем задается

  Поскольку полоса слуха ограничена, скажем, кГц, звуки идентичен ограниченному сигналу

  где

  . Теперь взять производные по времени просто (см. также §C.1):

  
  

  Поскольку длина интеграла конечна, нет возможности что он может «взорваться» из-за взвешивания в частотной области, введенной дифференцированием во временной области.

  Основное свойство Фурье сигналов и их спектров состоит в том, что сигнал не может быть ограничен как по времени, так и по частоте. Таким образом, посредством концептуальной «фильтрации нижних частот» каждый звуковой сигнал отбрасываем все частоты выше кГц, мы неявно делаем каждый звук сигнал вечен! Другими словами, «идеальное фильтр нижних частот «звенит» вечно». Нас такие тонкости не касаются на практике, но они важны для полного понимания основополагающая теория. Поскольку в действительности можно сказать, что сигналы имеют истинное начало и конец, надо признать, что все сигналы у нас действительно работают на практике имеют бесконечную полосу пропускания. То есть, когда сигнал включено или выключено, есть призрачное событие, простирающееся до самого конца. бесконечная частота (при этом «спадает» с частотой и имеет конечная полная энергия). ^Е.2

  Таким образом, звуковые сигналы с точки зрения восприятия эквивалентны сигналам с ограниченным диапазоном частот. сигналы, а сигналы с ограниченной полосой пропускания бесконечно гладкие в смысле что производные всех порядков существуют во все моменты времени . Логарифмы и децибелы Одним из наиболее важных применений бесконечных рядов является возможность используя начальную часть ряда для $f$, чтобы аппроксимировать $f$. Мы видели, например, что, когда мы складываем первые $n$ членов чередующийся ряд с убывающими членами, что разница между это и истинное значение не больше размера следующего члена. А аналогичный результат верен для многих рядов Тейлора. 9{-3}$? Что, если интервал вместо $[1,3/2]$? (отвечать)

  Пример 11.11.3 Найдите первые три ненулевых члена ряда Тейлора для $\tan x$ на $[-\pi/4,\pi/4]$, и вычислить гарантированный член ошибки, как указано Теорема Тейлора. (Вы можете использовать Мудрец или аналогичная помощь.) (отвечать)

  Пример 11.11.4 Покажите, что $\cos x$ равно своему ряду Тейлора для всех $x$ показав, что предел члена ошибки равен нулю, когда $N$ приближается бесконечность.

  9x$ равен своему ряду Тейлора для всех $x$ показав, что предел члена ошибки равен нулю, когда $N$ приближается бесконечность.

  Серия Тейлора – Чтение Фейнмана

  Я отправился в поход (на этот раз к базовому лагерю Аннапурны) и поэтому оставил книги по математике и физике в покое на неделю или две. Когда я вернулся, я как будто все забыл, и я не мог повторить упражнения. Вернемся к основам комплексных чисел еще раз. Начнем с формулы Эйлера:

  e ^{i x} = cos(x) + i sin(x)

  формулы во всей математике», так что, наверное, неудивительно, что я нахожу это интригующим и даже трудным для понимания. Давайте посмотрим на это. Итак, у нас есть реальное (но иррациональное) число e . Само по себе это увлекательное число, потому что оно появляется в разных математических выражениях, которые, на первый взгляд, не имеют между собой ничего общего. Например, e можно определить как сумму бесконечного ряда e = 1/0! + 1/2! + + 1/3! + 1/4! + … и так далее (n! обозначает факториал n в этой формуле), но его можно также определить как то уникальное положительное вещественное число, для которого другими словами, как основание экспоненциальной функции, которая является собственной производной). И, наконец, что не менее важно, есть также некоторые выражения с ограничениями, которые можно использовать для определения е . Когда начать? Что еще более важно, какова связь между всеми этими выражениями и формулой Эйлера?

  Во-первых, следует отметить, что e ^{i x} — это не просто число: это комплексное число — в отличие от более простого выражения e ^x , которое обозначает вещественных чисел. экспоненциальная функция (в отличие от сложной экспоненциальной функции e ^z ). Кроме того, следует отметить, что e ^{i x} — это комплексное число на единичной окружности . Таким образом, используя полярные координаты, мы должны сказать, что e ^{i x}   является комплексным числом с модулем 1 (модуль представляет собой абсолютное значение комплексного числа (т.е. расстояние от 0 до точки, в которой мы находимся). смотрим) или, иначе, мы могли бы сказать, что это величина вектора, определяемого точкой, на которую мы смотрим) и аргумент x (аргумент представляет собой угол (выраженный в радианах) между положительной действительной осью и прямой от 0 до точки, на которую мы смотрим).

  Теперь самоочевидно, что cos(x) + i sin(x) представляет в точности то же самое: точку на единичной окружности, определяемую углом x. Но это не доказывает формулу Эйлера, а только иллюстрирует ее. Итак, давайте перейдем к тому или иному доказательству формулы, чтобы попытаться понять ее несколько лучше. Я обращусь к Википедии, чтобы доказать формулу Эйлера in extenso , но позвольте мне просто резюмировать ее. Статья в Википедии (как я ее сегодня просмотрел) дает три доказательства.

  Первое доказательство использует разложение в степенной ряд (да, действительно ряд Тейлора/Маклорена — об этом позже) для экспоненциальной функции: e ^{i x} = 1 + i x + ( i x) ² /2! + ( i x) ³ /3! +… и так далее. Затем мы заменяем, используя  i ² = -1, i ³ = – i и так далее, и поэтому, когда мы затем перестраиваем члены, мы находим ряд Маклорена для cos (x) и sin(x) действительно работает. Я вернусь к этим силовым сериям в другом посте.

  Второе доказательство использует одно из предельных определений для e ^x , но применяет его к комплексной экспоненциальной функции . Действительно, можно записать e ^z (где z = x + i y) как e ^z = lim(1 + z/n) ⁿ для n, стремящегося к бесконечности. Доказательство заменяет i x на z, а затем вычисляет предел для действительно очень большого (или бесконечного) n. Это доказательство менее очевидно, чем кажется, потому что здесь мы имеем дело со степенными рядами, и поэтому нужно учитывать вопросы сходимости и все такое.

  Третье доказательство также выглядит сложным, но на самом деле оно, вероятно, является наиболее интуитивным из трех приведенных доказательств, поскольку оно использует производное определение e . Чтобы быть более точным, он берет производную от обеих частей формулы Эйлера, используя выражение в полярных координатах для комплексных чисел. Действительно, e ^{i x} является комплексным числом и, следовательно, может быть записано как некоторое число z = r(cosθ+ i sinθ), и поэтому здесь нужно решить вопрос: что такое r и θ ? Нам нужно записать эти два значения как функцию x. Как мы это делаем? Ну… Если мы возьмем производную от обеих частей, мы получим d( E ^{I x} )/DX = IE ^{I x} = (cosθ+ I SINu / дх. Это просто цепное правило для деривативов, конечно. Теперь, записывая все это и приравнивая действительную и мнимую части в обеих частях выражения, получаем следующее: dr/dx = 0 и dθ/dx = 1. Кроме того, мы должны иметь, что для x = 0 e ^{я 0} = [ e ^я ] ⁰ = 1, поэтому мы имеем r(0) = 1 (модуль комплексного числа (1,0) равен единице) и θ(0) = 0 (аргумент (1,0) равен нулю ). Отсюда следует, что функции r и θ равны r = 1 и θ = x, что доказывает формулу.

  Хотя эти доказательства (относительно) просты для понимания, формула остается странной, о чем также свидетельствуют ее частные случаи, такие как e ^{i 0} = e ^{i 2π}

  7 – =  =

  7 и ^{i π}  = – e ^{– i π}  или, что то же самое, e ^{i π}  + 10 = 0, которая представляет собой самую простую математическую формулу, объединяющую величины , 1, i , e и π. Это удивительная формула, потому что у нас есть два иррациональных числа, 90 545 e 90 546 и π, которые имеют определения, которые не относятся друг к другу 90 545 вообще 90 546 (последний раз, когда я проверял, π все еще определялось как простое отношение окружности круга к его диаметру, в то время как различные определения числа e не имеют ничего общего с кругами), и поэтому мы объединяем эти два, казалось бы, несвязанных числа, также вставляя мнимую единицу i (используя i π как показатель степени для e ) и получаем минус 1 как результат ( e ^{i π}  = – 1). Удивительно, правда?

  […] Ну… я бы сказал, по крайней мере, столь же удивительно, как разложение функции Тейлором или Маклореном, но я приберегу свои мысли об этом для другого поста (даже если я использую результаты этих разложений в этой статье). почта). На мой взгляд, формула Эйлера показывает удивительная сила математической записи на самом деле — и творческий подход. В самом деле, давайте посмотрим, что мы делаем с комплексными числами: мы начинаем только с одного или двух определений, и вдруг начинают появляться всевозможные замечательные вещи. На самом деле это выглядит примерно так:

  Мы начинаем с этих знакомых координат x и y точек на плоскости. Теперь мы называем ось x вещественной осью, а затем, просто чтобы отличить их от действительных чисел, мы называем числа на оси y мнимых чисел. Опять же, это просто для того, чтобы отличить их от действительных чисел, потому что на самом деле мнимые числа вовсе не мнимые: они так же реальны, как и действительные числа, или, возможно, нам следует сказать, что действительные числа так же мнимы, как и мнимые числа. потому что, когда все сказано и сделано, настоящие числа также являются умственными конструкциями, не так ли? Мнимые числа просто лежат на другой линии, перпендикулярной нашей так называемой реальной линии, поэтому мы добавляем маленький символ 9.0545 и (так называемая мнимая единица), когда мы их записываем. Итак, мы пишем 1 i (или i tout court ), 2 i, 3 ​​ i и так далее, или i /2, или что-то еще (неважно, пишем ли мы i перед действительным числом). число или после — до тех пор, пока мы последовательны).

  Затем мы объединяем эти два числа — действительное и мнимое — чтобы образовать так называемое комплексное число, которое есть не что иное, как точка (x, y) на этой декартовой плоскости. Действительно, хотя комплексные числа несколько сложнее, чем числа, к которым мы привыкли в повседневной жизни, я бы сказал, что они не из этого мира: это просто точки в пространстве, и поэтому мы также можем представить их в виде векторов. («стрелки») от начала координат до (x, y).

  Но вот что мы делаем на самом деле: мы комбинируем действительные и мнимые числа, используя очень знакомый знак плюс (+), так что мы пишем z = x + i y. Теперь , — это то место, где начинается волшебство: мы не складываем здесь одни и те же вещи, как если бы мы считали яблоки или что-то в этом роде, или когда мы складываем целые, рациональные или действительные числа вообще. Нет, мы складываем здесь два разных вещей — действительные и мнимые числа — которые, по сути, мы не можем сложить. Ведь твоя мамочка говорила тебе, что нельзя сравнивать яблоки с апельсинами, не так ли? Ну… Это именно то, что мы делаем здесь на самом деле, и поэтому мы действительно будем разделять эти действительные и мнимые числа в наших вычислениях: мы будем складывать действительные части комплексных чисел только друг с другом, а их мнимые части также друг с другом Только.

  Сложение довольно простое: мы просто складываем два вектора. Умножение несколько сложнее, но (геометрически) также легко интерпретируется: произведение двух комплексных чисел представляет собой вектор, длина которого равна сумме длин двух векторов, которые мы умножаем (т. е. двух комплексных чисел, которые составляют произведение), а его угол с действительной осью равен сумме углов двух исходных векторов. Из этого определения следует многое, и все в равной степени удивительные, но один из этих удивительных фактов состоит в том, что I ² = -1, I ³ = — I , I ⁴ = 1, I 5 9067 =

  467. В самом деле: умножение комплексного числа z = x + i y = (x, y) на воображаемую единицу i равносильно повороту его на 90° (против часовой стрелки) вокруг начала координат. Итак, мы , а не   , определяя i ² как равное минус 1 (во многих учебниках это равенство трактуется как определение): оно просто является фактом, который мы можем вывести из более раннего определения сложный продукт. Сладко, не правда ли?

  Теперь у нас есть сложение и умножение. Конечно, мы хотим сделать гораздо больше. После определения сложения и умножения мы хотим сделать сложные степени, и поэтому здесь всплывает эта история с e .

  Сначала нам нужно напомнить себе о том простом факте, что число e — это просто действительное число: оно равно 2,71828182845

  35360287471 и так далее. Нам приходится писать «etcetera», потому что e — это иррациональное число, которое — какой бы термин «иррациональный» ни подразумевал в повседневном языке — просто означает, что e — это , а не — дробь любых целых чисел (таким образом, иррациональное означает «, а не рациональное»). e  также является трансцендентным  числом – словом, которое предполагает всевозможные мистические свойства, но которое в математике означает только то, что мы можем , а не записать его как корень некоторого многочлена (многочлена с рациональными коэффициентами) . Так что странная цифра. При этом это также так называемое « натуральное » основание экспоненциальной функции. А? Почему математики взяли такое странное число в качестве так называемого «натурального» основания? Они должны быть иррациональными, не так ли? Ну… Нет. Если мы возьмем e в качестве основы экспоненциальной функции e ^x (так что это действительное (но иррациональное) число e в степени x, где x — переменная, бегущая вдоль ось абсцисс: следовательно, здесь у нас есть функция, которая принимает значение из набора действительных чисел и дает какое-то другое действительное число), то здесь у нас есть функция, которая является собственной производной: d( e ^x )/dx = e ^x . Это также естественная основа для логарифмической функции, и, как упоминалось выше, она как бы «всплывает» — я бы даже сказал «естественно» — во многих других выражениях, таких как, например, расчет сложных процентов или общая экспоненциальная функция. функция a ^x = e ^{x lna} . Другими словами, это и функции exp(x) и ln(x) нужны нам для определения степеней действительных чисел вообще. Вот почему математики называют это «естественным».

  Хотя пример вычисления сложных процентов звучит не очень захватывающе, все эти формулы с и и экспоненциальными функциями и что у вас сделали  вдохновили всех этих математиков 18 ^-го -го века, таких как Эйлер, которые искали логическое определение сложных полномочий.

  Давайте еще раз сформулируем проблему: мы можем складывать и умножать комплексные числа, но вопрос в том, как делать комплексные степени. Пытаясь понять это, Эйлер, очевидно, хотел сохранить обычные свойства степеней, такие как ^x a ^y = a ^x+y и, по сути, это свойство так называемой «естественной» экспоненциальной функции, что d( e ^x )/dx = e ^x . Другими словами, мы также хотим, чтобы комплексная экспоненциальная функция была собственной производной, поэтому d( e ^z )/dz снова должно дать нам e ^z .

  Пока Эйлер думал об этом (и, конечно, о многих других вещах), он хорошо знал, что можно разложить e ^x в тот степенной ряд, о котором я упоминал выше: e ^x  = 1/0! + х/1! + (х) ² /2! + (х) ³ /3! +… и так далее. Поэтому Эйлер просто сел, заменил действительное число x мнимым числом i x и посмотрел на него: e ^{i x} = 1 + i x + ( i x) ^{7 2 2 /2! + ( i x) 3 /3! +… и так далее. Теперь , о чудо, ! Принимая во внимание, что I 2 = -1, I 3 = — I , I 4 = 1, I}

  5 9067 = I

  5 = I

  5 9067. действительно переставьте члены, и поэтому Эйлер обнаружил, что это уравнение принимает вид ! +…) + i (х – х ³ /3! + х ⁵ /5! -… ). Теперь эти два члена действительно соответствуют рядам Маклорена для функций косинуса и синуса соответственно, так что вот что у него было: e ^{i x} = cos(x) + i sin(x). Его формула : формула Эйлера!

  Оттуда был еще один шаг, и это должно было написать E ^Z = E ^{x+ I Y} AS E ⁶⁶⁶⁶⁷

  4444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. y , так что у нас есть определение комплексной степени: это произведение двух множителей — e ^x и e ^{i y} — оба из которых мы теперь эффективно определили. Обратите внимание, что множитель e ^x — это просто действительное число, даже если мы запишем его как e ^x : он действует как своего рода коэффициент масштабирования для e ^{i y} , который вы будем помнить (как мы уже указывали выше), это точка на единичной окружности. В более общем виде можно показать, что 90 545 e 90 546 90 666 x 90 667 является абсолютным значением 90 545 e 90 546 ^z  (или модуль, или длина, или величина вектора — какой бы термин вы ни предпочли: все они относятся к одному и тому же), а y — аргумент комплексного числа e ^z  (т. е. угол вектора e ^z с реальной осью). [И, да, для тех, кто еще сомневается: e ^z — это просто еще одно комплексное число и, следовательно, двумерный вектор, т.е. просто точка на декартовой плоскости, поэтому мы имеем функцию которое происходит из набора комплексных чисел здесь (он принимает z в качестве входных данных) и дает другое комплексное число.]

  Конечно, вы заметите, что здесь нет чего-то вроде z ^w , то есть комплексного основания (т.е. z) с комплексным показателем (т.е. w), или даже формулы для комплексных степеней действительных чисел в общем случае 90 164 , т. е. формула для 90 666 w 90 667 с любым действительным числом (то есть не только 90 161 e 90 164, но и 90 161 действительно любое 90 164 действительное число) и w комплексным показателем степени. Однако эту проблему можно легко решить, записав z и w в их так называемой полярной форме, поэтому мы запишем z как z = ¦z¦ E ^Iθ = ¦Z¦ (COSθ+ I SINθ) и W AS ¦W¦ E ^{Iσ 9067 = Z¦ Iσ 9067 = ¦ Iσ 9067 = ¦ Iσ 9067 = ¦ Iσ . может взять его дальше оттуда. [Обратите внимание, что ¦z¦ и ¦w¦представляют модуль (то есть длину) z и w соответственно, а углы θ и σ, очевидно, являются аргументами одних и тех же z и w соответственно.] Конечно, если z является действительное число (то есть, если y = 0), то угол θ, очевидно, будет равен нулю (т. е. угол действительной оси с самой собой), и поэтому z будет равен действительному числу (т. равен нулю), и тогда мы возвращаемся к случаю действительного основания и комплексного показателя. Другими словами, это охватывает в случае.}

  […] Ну… Легко? ХОРОШО. Я немного упрощаю здесь, так как мне нужно, чтобы длина этого поста была управляемой, но на самом деле это на самом деле — это вопрос использования этих общих свойств степеней (таких как e ^a+bi e ^c = e ^(a+c)+bi и на самом деле делает  все работает. ‘ числа x на оси x с так называемыми «мнимыми» числами на оси y. 🙂

  Post scriptum :

  Книга Пенроуза Дорога к реальности посвящена целой главе сложному возведению в степень (глава 5). Однако на самом деле разработка не так проста и однозначна. Первый шаг в этом процессе — взять целых степеней — и целых корней — комплексных чисел, так что z ⁿ для n = 0, ±1, ±2, ±3… и так далее (или z ^1/2 , z ^1/3 , z ^1/4 , если мы говорим о целых корнях). Это легко, потому что ее можно решить, используя старую формулу 9.0161 Абрахам де Муавр : (cosθ + sinθ) ⁿ  = cos(nθ) + i sin(nθ) (де Муавр написал это уже в 1707 году, более чем за 40 лет до того, как Эйлер занялся этим вопросом) . Однако перейти оттуда к полноценным комплексным степеням, к сожалению, не так просто, так как это требует обходного пути: нам нужно работать с обратной (комплексной) экспоненциальной функцией e ^z , т. е. сложный) натуральный логарифм.

  Это не так просто, как кажется. Действительно, пока определение комплексного логарифма так же просто, как и определение действительных логарифмов (lnz — это функция, для которой e ^lnz = z), сама функция немного более… ну… сложная, я бы сказал. Во-первых, это многозначная функция: если решение w = lnz записать в виде w = u+ i v, то очевидно, что e ^w будет равно e ^{u+ i v} = e ^u e ^{i v} and this complex number e ^w  can then be written in its polar form e ^w  = r e ^iθ  with r = e ^u  и v = θ + 2nπ. Конечно, ln(e ^{u+ i v} ) = u + i v, поэтому решение w будет иметь вид w = lnr + i(θ + 2nπ) с n = 0, ±1, ±2. , ±3 и так далее. Короче говоря, у нас есть бесконечное число решений для w  (по одному на каждое выбранное n), так что у нас действительно есть проблема многозначности. Мы не будем останавливаться на этом здесь (по крайней мере, не в этом посте), а просто отметим, что эта проблема связана со свойствами самой комплексной показательной функции e ^z . Действительно, комплексная экспоненциальная функция e ^z  имеет совсем другие свойства, чем действительная экспоненциальная функция e ^x . Во-первых, отметим, что в отличие от e ^x (которое, как мы знаем, идет от нуля на дальнем конце отрицательной стороны действительной оси до бесконечности, когда x увеличивается на положительной стороне), e ^z является периодической функцией – поэтому он колеблется и через некоторое время дает одни и те же значения — причем это «через некоторое время» является периодичностью функции. В самом деле, e ^z = e ^z +2π i и, следовательно, его период 2πi (обратите внимание, что этот период является мнимым числом, но, следовательно, это «реальный» период, если вы понимаете, о чем я). :-)). Кроме того, и это тоже очень сильно отличается от реальной экспоненциальной функции e ^x , e ^z  могут быть отрицательными (а также принимать любые другие комплексные значения). Например, e ^{i π} = -1, как мы уже отмечали выше.

  При этом проблема многозначности может быть решена посредством определения главного значения lnz, и это, таким образом, приводит нас к тому, что мы здесь хотим: последовательному определению комплексной степени комплексного основания (или, другими словами, определение истинной комплексной экспоненциальной (и логарифмической) функции). Тем, кто хотел бы увидеть подробности этого (т. е. моим воображаемым читателям :-)), я бы сказал, что подход Пенроуза к этому вопросу в вышеупомянутой главе 5 из Дорога к реальности довольно загадочна — предположительно, потому, что ему приходится держать свою книгу всего около 1000 страниц (не так много, чтобы объяснить все Законы Вселенной) и, следовательно, курс Брауна и Черчилля (или любой другой курс, посвященный со сложным анализом), вероятно, облегчает чтение.

  [Что касается проблемы многозначности, то, вероятно, следует также отметить следующее: при извлечении n ^th корня комплексного числа (т. е. z ^1/n при n = 2, 3 и т. д.) мы также получаем установить значений n c _k (с k = 0, 1, 2,… n-1), а не только одно значение. Однако, как только у нас есть одно из этих значений, у нас есть все они, поскольку мы можем записать эти c _k как c _k = r ^1/n e ^{i (θ/n+2kπ/ n)} , (с исходным комплексным числом z, равным z = r e ^{i θ} ), тогда мы могли бы также просто рассмотреть главное значение c ₀ и, таким образом, рассмотреть функцию как однозначный. Короче говоря, проблема многозначных функций возникает почти везде в комплексном пространстве, но на самом деле это не проблема. Фактически, мы сталкиваемся с проблемой многозначности, как только расширяем экспоненциальную функцию в пространстве действительных чисел, а также допускаем рациональные и действительные показатели вместо только положительных целых чисел. Например, 4 ^1/2 равно ±2, так что здесь тоже два результата и, следовательно, несколько значений. Другим примером может быть 4   корень из 16: у нас есть 90 161 четыре 90 164 4   корня из 16: +2, -2, а затем два комплексных корня +2  i  и -2  i  . Однако стандартная практика заключается в том, что мы принимаем во внимание только положительное значение, чтобы гарантировать «хорошее поведение» экспоненциальной функции. Действительно, стандартное определение вещественной экспоненциальной функции таково: b ^x = ( E ^LNB ) ^x = E ^LNB E ^x и SO, если x = 1/n, NASTIN корень в e ^x . Стандартная практика также ограничивает значение b положительным действительным числом (b > 0). Эти соглашения обеспечивают не только положительный результат, но и непрерывность функции и, следовательно, существование производной, которую мы затем можем использовать для других целей. Кстати, определение также показывает — еще раз — почему e — такое красивое (или «натуральное») число: мы можем использовать его для вычисления значения любой экспоненциальной функции (для любого действительного основания b > 0). Но мы уже упоминали об этом, и теперь действительно пора перестать писать. Думаю, суть ясна.]

  Серия Тейлора в точку. Разложение Тейлора

  Разложение функции в ряд Тейлора, Маклорена и Лорана на сайте для отработки практических навыков. Это разложение функции в ряд дает математикам представление об оценке приблизительного значения функции в некоторой точке области ее определения. Вычислить значение такой функции гораздо проще, чем использовать таблицу Бредиса, которая настолько устарела в век вычислительной техники. Разложить функцию в ряд Тейлора — значит вычислить коэффициенты перед линейными функциями этого ряда и правильно записать. Учащиеся путают эти два ряда, не понимая, что является общим случаем, а что частным случаем второго. x, Sin(x), Cos(x) и другие, это разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее распространенной задачей в TFKT, поскольку он представляет собой двусторонний бесконечный ряд. Это сумма двух строк. Предлагаем вам посмотреть пример декомпозиции прямо на сайте сайт, это очень легко сделать нажав на «Пример» с любым номером, а затем на кнопку «Решение». Именно с этим разложением функции в ряд и связан мажорантный ряд, ограничивающий исходную функцию в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторный анализ сравнивают с еще одной интересной дисциплиной в математике. Поскольку каждый термин необходимо исследовать, для этого процесса требуется много времени. Любой ряд Тейлора можно связать с рядом Маклорена, заменив x0 нулем, но для ряда Маклорена обратное представление ряда Тейлора иногда неочевидно. Как бы это не требовалось делать в чистом виде но интересно для общего саморазвития. Каждому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами, ряд того же типа Тейлора, но несколько отличающийся вычислением коэффициентов. Об области сходимости ряда Лорана мы поговорим чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапное разложение функции в ряд вряд ли может быть достигнуто только за счет приведения членов к общему знаменателю, так как функции в знаменателях нелинейны. Приближенный расчет значения функционала требует постановки задач. Подумайте о том, что когда аргументом ряда Тейлора является линейная величина, то разложение происходит в несколько шагов, но совсем другая картина, когда в качестве аргумента разлагаемой функции выступает сложная или нелинейная функция, тогда процесс представления такой функции в степенной ряд очевиден, т. к. таким образом легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, имеющей мало влияние на дальнейшие расчеты. Это относится и к серии Маклорена. когда необходимо вычислить функцию в нулевой точке. Однако сам ряд Лорана представлен здесь разложением на плоскости с мнимыми единицами. Также не без успеха правильное решение задач во время общего процесса. В математике такой подход не известен, но он объективно существует. В результате можно прийти к выводу о так называемых точечных подмножествах, а при разложении функции в ряд нужно применять известные для этого процесса методы, например применение теории производных. Еще раз убеждаемся в правоте учителя, сделавшего свои предположения о результатах поствычислительных расчетов. Отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса сайта, не забывайте вид исходной функции, потому что может получиться что изначально необходимо задать область определения функции, т. е. выписать и исключить из дальнейшего рассмотрения те точки, в которых функция не определена в области определения действительных чисел. Так сказать, это покажет вашу расторопность в решении проблемы. Построение ряда Маклорена с нулевым значением аргумента не будет исключением из сказанного. При этом процесс нахождения области определения функции никто не отменял, и к этому математическому действию нужно подойти со всей серьезностью. Если ряд Лорана содержит главную часть, то параметр «а» будем называть изолированной особой точкой, а ряд Лорана разложим по кольцу — это пересечение областей сходимости его частей, из которых соответствующие теорема будет следовать. Но не все так сложно, как может показаться на первый взгляд неопытному школьнику. Изучив только ряд Тейлора, можно легко понять ряд Лорана — обобщенный случай расширения пространства чисел. Любое разложение функции в ряд может быть выполнено только в точке области определения функции. Следует учитывать свойства таких функций, например периодичность или бесконечную дифференцируемость. Мы также предлагаем вам воспользоваться таблицей готовых разложений в ряды Тейлора элементарных функций, так как одна функция может быть представлена ​​до десятков степенных рядов, отличающихся друг от друга, в чем можно убедиться из использования нашего онлайн калькулятор. Онлайн-ряд Маклорена проще, чем когда-либо, определить, пользуетесь ли вы уникальной услугой сайта, вам просто нужно ввести правильно написанную функцию и вы получите представленный ответ в считанные секунды, он будет гарантированно точен и стандартен. письменная форма. Вы можете переписать результат сразу на чистую копию для сдачи учителю. Было бы правильно сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разлагается в ряд Лорана по всем таким кольцам. Важным моментом является не упускать из виду членов ряда Лорана, содержащих отрицательные степени. Сосредоточьтесь на этом как можно больше. Хорошо использовать теорему Лорана о разложении функции в ряд по целым степеням.

  «Найти разложение Маклорена f(x)» — именно так звучит задача по высшей математике, которую одни студенты могут выполнить, а другие не справляются с примерами. Существует несколько способов разложения ряда по степеням, здесь мы приведем способ разложения функций в ряд Маклорена. При разработке функции в ряду вам нужно хорошо уметь вычислять производные.

  Пример 4.7 Разложить функцию в ряд по степеням х

  Вычисления: Выполняем разложение функции по формуле Маклорена. Сначала разложим знаменатель функции в ряд
  
  Наконец, мы умножаем разложение на числитель.
  Первый член — это значение функции в нуле f (0) = 1/3.
  Найти производные функций первого и высших порядков f(x) и значение этих производных в точке x=0
  
  
  
  
  Далее по схеме изменения значения производных к 0 запишем формулу для n-й производной
  
  Итак, представим знаменатель в виде разложения в ряд Маклорена
  
  Умножаем на числитель и получаем искомое разложение функции в ряд по степеням х
  
  Как видите, здесь нет ничего сложного.
  Все ключевые моменты основаны на возможности вычисления производных и быстрого обобщения значения производной высших порядков в нуле. Следующие примеры помогут вам научиться быстро расширять функцию в ряд.

  Пример 4.10. Нахождение разложения Маклорена функции

  92)
  Расчеты: В такого рода примерах необходимо разложить дробь через сумму простых дробей.
  Как это сделать, мы сейчас показывать не будем, а с помощью неопределенных коэффициентов придем к сумме ех дробей.
  Далее запишем знаменатели в показательной форме
  
  Осталось разложить члены по формуле Маклорена. Суммируя члены с одинаковыми степенями «х», составим формулу общего члена разложения функции в ряд
  

  
  Последнюю часть перехода к ряду в начале реализовать сложно, так как трудно совмещать формулы парных и непарных индексов (степеней), но с практикой у вас это получится лучше.

  Пример 4.18 Найдите разложение Маклорена функции

  Вычисления: Найдите производную этой функции:
  
  Разложим функцию в ряд по одной из формул Макларена:
  
  Суммируем ряд почленно на основании что оба абсолютно совпадают. Почленно интегрируя весь ряд, получаем разложение функции в ряд по степеням x
  
  Между двумя последними строками разложения есть переход, который в начале займет у вас много времени. Обобщение формулы ряда дается не всем легко, поэтому не беспокойтесь о том, что вам не удастся получить красивую и компактную формулу.

  Пример 4.28 Находим разложение Маклорена функции:

  Запишем логарифм следующим образом
  
  С помощью формулы Маклорена разложим логарифм функции в ряд по степеням х
  
  Окончательное складывание на первый взгляд сложно, но при чередовании символов всегда будет получаться что-то похожее. Вводное занятие по теме планирования функций подряд завершено. Другие не менее интересные схемы декомпозиции будут подробно рассмотрены в следующих материалах.

  Студенты высшей математики должны знать, что сумма некоторого степенного ряда, принадлежащего интервалу сходимости данного нам ряда, оказывается непрерывной и бесконечно много раз дифференцированной функцией. Возникает вопрос: можно ли утверждать, что данная произвольная функция f(x) является суммой некоторого степенного ряда? То есть при каких условиях функцию f(x) можно изобразить степенным рядом? Важность этого вопроса состоит в том, что можно приближенно заменить функцию f(x) суммой первых членов степенного ряда, т. е. полиномом. Такая замена функции достаточно простым выражением – полиномом – удобна и при решении некоторых задач, а именно: при решении интегралов, при вычислении и т. д.

  Доказано, что для некоторой функции f(x), у которой можно вычислить производные до (n + 1)-го порядка, включая последний, в окрестности (α — R; x 0 + R) некоторой точки x = α формула:

  Эта формула названа в честь известного ученого Брука Тейлора. Ряд, который получается из предыдущего, называется рядом Маклорена:

  Правило, позволяющее разложить в ряд Маклорена:

  1. Определить производные первого, второго, третьего… порядков.
  2. Вычислить производные при x=0.
  3. Напишите ряд Маклорена для этой функции, а затем определите интервал ее сходимости.
  4. Определить интервал (-R;R), где остаток формулы Маклорена

  R n (x) -> 0 для n -> бесконечность. Если он существует, то функция f(x) в нем должна совпадать с суммой ряда Маклорена.

  Теперь рассмотрим серию Маклорена для отдельных функций.

  1. Итак, первым будет f(x) = e x. Конечно, по своим признакам такая функция имеет производные самого разного порядка, и f(k)(x) = e x, где k равно всему Подставим x = 0. Получим f(k)(0 ) = e 0 = 1, k = 1,2… Исходя из вышеизложенного, ряд e x будет выглядеть так:

  2. Ряд Маклорена для функции f(x) = sin x. Сразу уточним, что функция при всех неизвестных будет иметь производные, к тому же f»(x)=cos x=sin(x+n/2), f»»(x)=-sin x=sin(x+ 2*n/2)…, f (k) (x) = sin(x+k*n/2), где k равно любому натуральному числу, то есть после несложных вычислений можно прийти к выводу что ряд для f(x) = sin x будет иметь следующий вид:

  3. Теперь попробуем рассмотреть функцию f(x) = cos x Она имеет производные произвольного порядка при всех неизвестных, и |f (k) (x)|=|cos(x+k*n/2)|

  Итак, мы перечислили наиболее важные функции, которые можно разложить в ряд Маклорена, но для некоторых функций они дополнены рядами Тейлора. Сейчас мы их перечислим. Также стоит отметить, что ряды Тейлора и Маклорена являются важной частью практики решения рядов в высшей математике. Итак, серия Тейлор.

  1. Первой будет строка для f-ii f(x)=ln(1+x). Как и в предыдущих примерах, учитывая, что f (x) = ln (1 + x), мы можем добавить ряд, используя общую форму ряда Маклорена. однако для этой функции ряд Маклорена можно получить гораздо проще. После интегрирования некоторого геометрического ряда получим ряд для f(x) = ln(1 + x) такой выборки:

  2. И вторым, который будет завершающим в нашей статье, будет ряд для f(x) = arctg x. Для x, принадлежащего интервалу [-1; 1], допустимо расширение:

  Вот и все. В данной статье были рассмотрены наиболее часто используемые ряды Тейлора и Маклорена в высшей математике, в частности, в экономических и технических вузах.

  Если функция f(x) имеет на некотором интервале, содержащем точку a , производные всех порядков, то к ней можно применить формулу Тейлора:

  где рн — так называемый остаточный член или остаток ряда, его можно оценить по формуле Лагранжа:

  , где число х заключено между Х и а .

  Если для некоторого значения x r n ®0 при n ®¥, то в пределе формула Тейлора для этого значения превращается в сходящуюся формулу Ряд Тейлора :

  Таким образом, функция разложить в ряд Тейлора в рассматриваемой точке X , если:

  1) имеет производные всех порядков;

  2) построенный ряд сходится в этой точке.

  В a = 0 мы получаем ряд с именем около Маклорена :

  Пример 1 f(x)= 2 х .

  Решение . Найдем значения функции и ее производных при х = 0

  f(x) = 2 х , f( 0 ) = 2 0 =1;

  f¢(x) = 2 x ln2, f¢( 0 ) = 2 0 In2=In2;

  f¢¢(x) = 2 x ln 2 2, f¢¢( 0 ) = 2 0 журнал 2 2= журнал 2 2;

  f(n)(x) = 2 x ln n 2, f(n)( 0 ) = 2 0 ln n 2=ln n 2.

  Подставив полученные значения производных в формулу ряда Тейлора, получим:

  Радиус сходимости этого ряда равен бесконечности, поэтому это разложение справедливо для -¥x

  Пример 2 X +4) для функции f(x)= e x .

  Решение . Нахождение производных функции е х и их значений в точке х =-4.

  f(x) = e x , f( -4 ) = е -4 ;

  f¢(x) = e x , f¢( -4 ) = е -4 ;

  f¢¢(x) = e x , f¢¢( -4 ) = е -4 ;

  f(n)(x) = e x , f(n)( -4 ) = е -4 .

  Следовательно, искомый ряд Тейлора функции имеет вид:

  Это разложение справедливо и для -¥x

  Пример 3 . Разложим функцию f(x) =ln х в ряд по степеням ( X- 1),

  (т.е. в ряд Тейлора в окрестности точки X =1).

  Решение . Находим производные этой функции.

  Подставив эти значения в формулу, получим искомый ряд Тейлора:0032

  ½ X- 1½

  Ряд сходится, если ½ X- 1½xX=2 мы получаем знакопеременный ряд, удовлетворяющий условиям признака Лейбница. При X =0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуинтервал (0;2].

  Приведем полученные таким образом разложения в ряд Маклорена (т. е. в окрестности точки X = 0) для некоторых элементарных функций:

  (2) ,

  (3) ,

  ( последнее разложение называется биномиальным рядом )

  Пример 4 . Расширьте функцию до мощного ряда

  Решение . В разложении (1) заменим X на — X 2 , получим:

  Пример 5 . Расширьте функции серии Maclaurin

  Решение . Имеем

  Используя формулу (4), можем записать:

  подставляя вместо X в формулу -X , получаем:

  Отсюда находим:

  Раскрывая скобки, переставляя члены ряда и производя сокращение подобных членов, получаем

  Этот ряд сходится на интервале

  (-1;1), так как он получен из двух рядов, каждый из которых сходится на этом интервале.

  Комментарий .

  Формулы (1)-(5) можно также использовать для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням ( Га ). Для этого необходимо произвести такие тождественные преобразования над заданной функцией, чтобы получить одну из функций (1) — (5), в которой вместо X стоит k( Ha ) m, где k — постоянное число, m — целое положительное число. Часто бывает удобно заменить переменную t = Ha и разложить полученную функцию по t в ряд Маклорена.

  Этот метод иллюстрирует теорему единственности разложения функции в степенной ряд. Суть этой теоремы состоит в том, что в окрестности одной и той же точки нельзя получить два разных степенных ряда, которые сходились бы к одной и той же функции, как бы ни производилось ее разложение.

  Пример 6 . Разложим функцию в ряд Тейлора в окрестности точки X =3.

  Решение .