Двоичная арифметика : сложение, вычитание, умножение, деление
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной.
Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример: 1011,12 + 1010,112
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,12 + 1112 + 101,12
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,012 — 1001,12
Умножение и деление двоичных чисел
Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 1011110112 в десятичную систему счисления.
Поскольку 1010 = 10102, запишем
Полученные остатки, 10012 = 910, =1112 = 710, 112 = 310. Искомое число 1011110112 = 37910.
Назад: Представление данных и архитектура ЭВМ
Двоичная арифметика – примеры чисел
4.
5
Средняя оценка: 4.5
Всего получено оценок: 270.
Средняя оценка: 4.5
Всего получено оценок: 270.
Операции сложения, вычитания, умножения и деления в двоичной системе – это двоичная арифметика. Некоторые примеры двоичной арифметики рассмотрены в данной статье.
Двоичная арифметика
Все арифметические действия, которые применимы к двоичным числам, выполняются аналогично как в десятичной системе. Удобнее всего двоичные числа складывать, вычитать, умножать и делить столбиком.
Числа записываются друг под другом с учетом разрядов. При необходимости производится перенос в старший разряд или заем из старшего разряда.
При сложении двоичных чисел следует помнить, что в числовом двоичном ряду после 1 идет 10. Это означает, что 1 + 1 = 10, а 11 + 1= 100.
Изучению двоичной системы много времени посвятил В. Лейбниц. По его просьбе была отчеканена медаль в честь двоичной системы, на которой отображались простейшие арифметические действия с двоичными числами.
Сложение
Вычисление суммы двоичных чисел производится следующим образом: числа записываются в столбик. Затем производится поразрядное суммирование цифр, начиная с младшего разряда, как в десятичной системе. Если сумма цифр текущего разряда превышает его размер, то происходит перенос единицы в старший разряд.
Правила сложения двоичных чисел:
0 + 0 = 0
0 + 1 = 1
1 + 1 =10
Например, сумма двоичных чисел 1000111 + 110011 = 1111010
Первое слагаемое | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
Второе слагаемое | 1 | 1 | 0 | 0 | 1 | 1 | |
Сумма | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
На примере видно, как происходит перенос в старший разряд.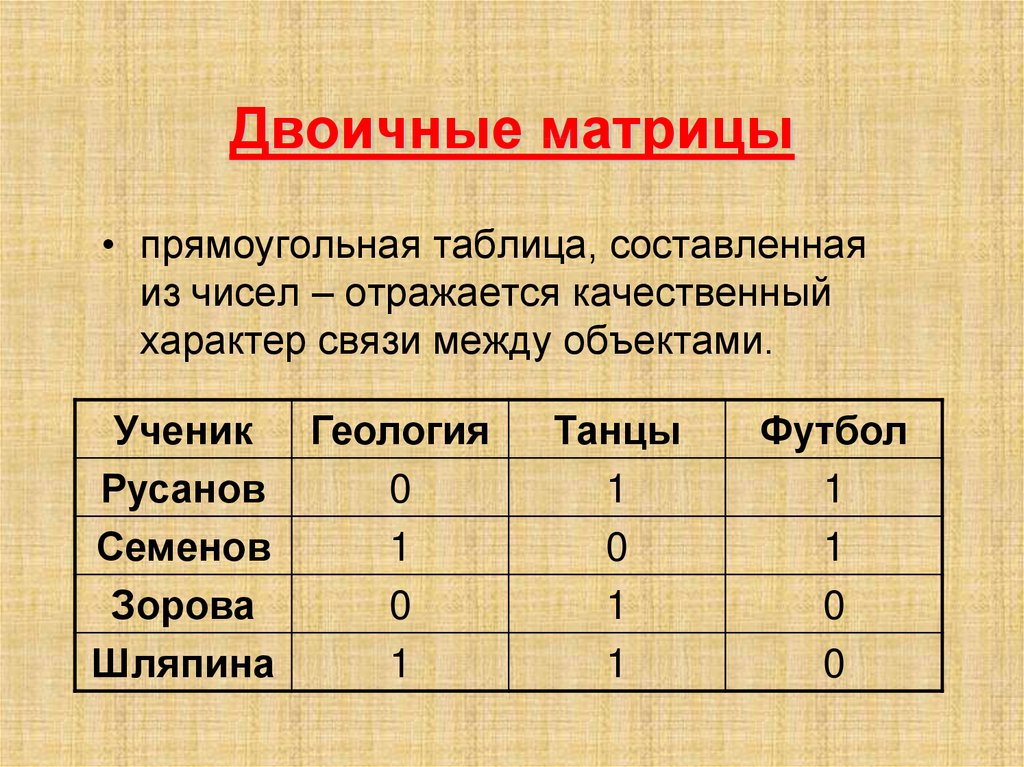
При сложении единиц самого младшего разряда получается 10. Ноль остается на своем месте, а единица переносится в старший разряд слева, где уже складываются две единицы. Получается 11. И снова, младшую единицу оставляют, а старшую переносят влево.
Вычитание
Действие разности следует также выполнять столбиком. Вычитание производится поразрядно. Если возникает ситуация, что приходится вычитать из нуля единицу, то происходит заем из старшего разряда.
Все как в десятичной системе. Только следует помнить, что в двоичной системе 10 – 1 = 1.
Например, разность чисел: 1000111 – 110011 = 10100
Уменьшаемое | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
Вычитаемое | 1 | 1 | 0 | 0 | 1 | 1 | |
Разность | 1 | 0 | 1 | 0 | 0 |
На примере видно, как производится заем в старшем разряде.
В пятом справа разряде производится вычитание 0 – 1. Здесь следует занять единицу из ближайшего старшего разряда слева.
Умножение
Умножать следует столбиком с учетом правил умножения:
0 * 0 = 0
0 * 1 = 0
1 * 1 = 1
Произведение выполняется также поразрядно, каждый разряд второго числа умножается на каждую цифру первого числа, результат суммируется
Произведение двоичных чисел 1101 * 11 = 100111
Первый множитель | 1 | 1 | 0 | 1 | ||
Второй множитель | 1 | 1 | ||||
1 | 1 | 0 | 1 | |||
1 | 1 | 0 | 1 | |||
Итог (произведение) | 1 | 0 | 0 | 1 | 1 | 1 |
Деление
Операция деления выполняется столбиком, аналогично как в десятичной системе счисления.
Всегда можно проверить результаты двоичной арифметики с помощью калькулятора. Считать можно и в двоичном формате. Электронный калькулятор в группе стандартных приложений операционной системы MS Windows имеет такой режим работы.
Рис. 3. Режим Программист электронного калькулятора ОС WindowsЧто мы узнали?
Над двоичными числами можно выполнять арифметические операции сложения, умножения, вычитания, деления. Удобнее всего это делать столбиком. Числа следует располагать с учетом разрядов и помнить об особенностях двоичной системы.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Алексей Беляев
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 270.
А какая ваша оценка?
Умножение двоичных чисел — Калькулятор двоичного произведения — Онлайн
Самый простой в мире калькулятор двоичного произведения для веб-разработчиков и программистов.
Просто вставьте свои двоичные числа в форму ниже, нажмите кнопку «Вычислить двоичный продукт», и вы получите все двоичные значения, перемноженные вместе. Нажмите кнопку, умножьте двоичный код. Никакой рекламы, ерунды или мусора.
Объявление : Мы только что запустили Online Fractal Tools — набор браузерных генераторов фракталов. Проверьте это!
(отменить)
Хотите добавить двоичные числа?
Используйте калькулятор двоичной суммы!
Хотите побитовые И двоичные числа?
Используйте побитовый И-калькулятор!
Хотите побитовое ИЛИ двоичных чисел?
Используйте калькулятор побитового ИЛИ!
Ищете дополнительные инструменты для веб-разработчиков? Попробуйте это!
Кодировщик URL
Декодер URL
Анализатор URL
Кодировщик HTML
Декодер HTML
Кодировщик Base64
Base64 Decoder
HTML Prettifier
HTML Minifier
JSON Prettifier
JSON Minifier
JSON Escaper
JSON Unescaper
JSON Validator
JS Prettifier
JS Minifier
JS Validator
CSS Prettify
CSS Minifier
XML Prettifier
XML Minifier
Преобразователь XML в JSON
Преобразователь JSON в XML
Преобразователь XML в CSV
CSV в XML преобразователь
XML в YAML Converter
YAML в XML Converter
YAML в TSV Converter
TSV TO YAML Converter
XML в TSV Converter
TSV TO TO TO XML
.
Конвертер JSON в CSVКонвертер CSV в JSON
Конвертер JSON в YAML
Конвертер YAML в JSON
Конвертер JSON в TSV
Конвертер TSV в JSON
Конвертер JSON в текст0003
CSV в YAML Converter
YAML в CSV Converter
TSV в CSV Converter
CSV в TSV Converter
CSV в текстовые столбцы. Преобразователь TSV
Преобразователь CSV
Преобразователь столбцов в строки CSV
Преобразователь строк в столбцы CSV
Преобразователь столбцов CSV
Экспортер столбцов CSV
Заменитель столбцов CSV
0003CSV Column Prepender
CSV Column Delesender
CSV -вставка CSV Delimiter Changer
TSV Transposer
COLLANS TOS TO ROWS COVERTER
TSV ROWS TS COLLANTS DALENTS 9000. TSV Column Exporter
TSV Column Replacer
TSV Column Prepender
TSV Column Appender
TSV Column Inserter
TSV Column Deleter
TSV DeLimiter Changer
DEDIMITED EXPORTORE
DELIMITED DELETER
DELIMITED COLMATER SPEANCER
ТЕКСПОСЕР
Текстовые столбцы в Rows Converter
Текстовые строки Texts Converter
Текстовый столбец Swapper
Текстовые строки для столбцов
Текстовый столбец.
Конвертер HTML в Markdown
Конвертер Markdown в HTML
Конвертер HTML в Jade
Конвертер Jade в HTML
Преобразователь BBCode в HTML
Преобразователь BBCode в Jade
Преобразователь BBCode в текст
Преобразователь HTML в текст
HTML Stripper
Преобразователь текста в HTML Entities
Преобразователь времени UNIX в время UTC
3
3
Преобразователь IP в двоичный
Преобразователь двоичного кода в IP
Преобразователь IP в десятичный
Преобразователь восьмеричного в IP
Преобразователь IP в восьмеричный
Преобразователь десятичного в IP
IP to Hex Converter
Hex to IP Converter
IP Address Sorter
MySQL Password Generator
MariaDB Password Generator
Postgres Password Generator
Bcrypt Password Generator
Bcrypt Password Checker
Scrypt Password Generator
Scrypt Средство проверки пароля
Кодер/декодер ROT13
Кодер/декодер ROT47
Кодер Punycode
Декодер Punycode
Base32 Encoder
Base32 Decoder
Base58 Encoder
Base58 Decoder
Ascii85 Encoder
Ascii85 Decoder
UTF8 Encoder
UTF8 Decoder
UTF16 Encoder
UTF16 Decoder
Uuencoder
Uudecoder
Morse Code Encoder
Декодер азбуки Морзе
Шифровщик XOR
Дешифратор XOR
Шифровщик AES
Дешифратор AES
Шифровщик RC4
RC4 Decryptor
DES Encryptor
DES DeCryptor
Triple DES Encryptor
Triple DES Decryptor
Calpulator
MASROLEHLOLEHLOLER.
Калькулятор хешей MD6
Калькулятор хэшей RipeMD128
Калькулятор хэшей RipeMD160
Калькулятор хэшей RipeMD256
Калькулятор хэшей RipeMD320
SHA1 Hash Calculator
SHA2 Hash Calculator
SHA224 Hash Calculator
SHA256 Hash Calculator
SHA384 Hash Calculator
SHA512 Hash Calculator
SHA3 Hash Calculator
CRC16 Hash Calculator
CRC32 Hash Calculator
Adler32 Hash Calculator
Калькулятор хэшей Whirlpool
Калькулятор всех хэшей
Конвертер секунд в H:M:S
Конвертер H:M:S в секунды
секунды до чтения от человека
двоичный в октальный преобразователь
Двоичный в десятичный преобразователь
Двоичный в шестнадцатеричный преобразователь
Октальный в двоичный преобразователь
Октальный в десятичный конвертер
Octal To Hex Converter
Прикал.
Преобразователь десятичного числа в восьмеричное
Преобразователь десятичного числа в шестнадцатеричное
Преобразователь шестнадцатеричного в двоичное
Преобразователь шестнадцатеричного в восьмеричное
Преобразователь шестнадцатеричного в десятичное
Десятичный в BCD -преобразователь
BCD в десятичный преобразователь
Октальный в BCD Converter
BCD в октальный преобразователь
HEX в BCD Converter
BCD в HEX -преобразователь
BBINAR TO GREAN TOVERTER
GRAY DOVERTE Восьмеричный преобразователь в серый
Преобразователь из серого в восьмеричный
Преобразователь из десятичного в серый
Преобразователь из серого в десятичный
Преобразователь из шестнадцатеричного в серый
Преобразователь из серого в шестнадцатеричный
Binary Sum Calculator
Binary Product Calculator
Binary Bitwise AND Calculator
Binary Bitwise NAND Calculator
Binary Bitwise OR Calculator
Binary Bitwise NOR Calculator
Binary Bitwise XOR Calculator
Binary Bitwise XNOR Calculator
Binary Bitwise NOT Calculator
Инвертор двоичных битов
Реверс двоичных битов
Вращатель двоичных чисел
Вращатель двоичных битов влево
Бинарный битовой ротатор справа
Номерной конвертер базового преобразователя
Римский в десятичный преобразователь
Десятичный в римский преобразователь
Числа до преобразователя слов
Слова для преобразователя чисел
Вверх
Круглые числа
UTF8.
Преобразователь Hex в UTF8
Преобразователь текста в коды ASCII
Преобразователь ASCII в текст
Преобразователь текста в двоичный код
Преобразователь двоичного кода в текст
Текст на восьмом преобразователе
Окта в текстовом преобразователе
Текст в Десятичный преобразователь
Десятичный в текстовый преобразователь
Текст в шестнадцатеричном преобразователе
Гекс в текстовый преобразователь
Текст в нижний перевод
Текст в верхний конвертер
Преобразователь текста в случайный регистр
Преобразователь текста в заголовки
Заглавные слова в тексте
Преобразователь регистра в тексте
Усечение строк текста
Обрезка строк текста
Пространства к вкладкам преобразователя
вкладкам в пространства преобразователя
Пространства в новые линии преобразователя
Новые линии в пространства преобразователь
Символ с акцентом.
Удаление обратной косой черты
Добавление обратной косой черты
Преобразование текста
Повторитель текста
Заменитель текста
Text Reverser
Text Rotate
Ротатор текста в левый
Ротатор текста вправо
Длина текста калькулятор
Сортер алфавитного текста
Numerer Text Sorter
Текст по длине сортировка
Текст из REGEX Generator Text Generator.
Текст по центру
Текст с выравниванием по правому краю
Текст с левой панелью
Текст с правой панелью
Выровнять текст по ширине
Средство форматирования текстовых столбцов
Извлечение соответствия регулярным выражениям
REGEX MATCH STACKER
Extractor Extractor
Extractor URL
Номер экстрактор
Слияние списка
Список Zipper
СПИСОК ПЕРЕДЕЛИЧЕСКИ
Извлечение диапазона строк
Сортировщик слов
Обертка слов
Разделитель слов
Добавление номеров строк
Добавление префиксов строк
Добавить линию суффиксы
Приложение префикс и суффикс
Найти самую длинную текстовую строку
Найти самую короткую текстовую строку
Длубленное снятие линии
Пустое средство для удаления линии
Stringizer
Letter Rampectiro Разделитель
Инвертор текстовой строки
Фильтр текстовой строки
Количество букв в текстовом счетчике
Количество слов в текстовом счетчике
Количество строк в текстовом счетчике
Number of Paragraphs in Text Counter
Letter Frequency Calculator
Word Frequency Calculator
Phrase Frequency Calculator
Text Statistics
Random Element Picker
Random JSON Generator
Random XML Generator
Random YAML Generator
Random Генератор CSV
Генератор случайных TSV
Генератор случайных паролей
Генератор случайных строк
Генератор случайных чисел
Random Fraction Generator
Random Bin Generator
Random Oct Generator
Random Dec Generator
Random Hex Generator
Random Byte Generator
Random IP Generator
Random MAC Generator
Random UUID Generator
Random GUID Generator
Генератор случайных дат
Генератор случайных значений времени
Генератор простых чисел
Генератор чисел Фибоначчи
Генератор числа Пи
E Digit Generator
Десятичный в научный преобразователь
Научный в десятичный преобразователь
JPG в PNG Converter
PNG в JPG Converter
GIF PNG Converter
GIF для JPG Converter
BMP TO PNG TO Converter
GIF -адрес JPG
BMP TO PNG
GIF — Преобразователь в JPG
Преобразователь изображения в Base64
Преобразователь файла в Base64
Преобразователь JSON в Base64
Преобразователь XML в Base64
Преобразователь Hex в RGB
RGB to Hex Converter
CMYK to RGB Converter
RGB to CMYK Converter
CMYK to Hex Converter
Hex to CMYK Converter
IDN Encoder
IDN Decoder
Miles to Kilometers Converter
Kilometers to Miles Converter
Конвертер градусов в градусы Цельсия
Конвертер градусов Фаренгейта в градусы
Конвертер градусов в радианы
Конвертер градусов в радианы
Конвертер фунтов в килограммы
Конвертер килограммов в фунты
Мой IP-адрес
Все инструменты
Совет для профессионалов: вы можете использовать аргумент запроса ?input=text для передачи текста в инструменты.
Методы двоичного умножения
[адсенс1]
Коммерческие приложения, такие как компьютеры, мобильные телефоны, высокоскоростные калькуляторы и некоторые процессоры общего назначения, требуют двоичных множителей.
По сравнению со сложением и вычитанием умножение — более сложный процесс. В процессе умножения число, которое нужно умножить на другое число, называется множимым, а умножаемое число называется множителем.
Схема
Двоичное умножение
Подобно умножению десятичных чисел, двоичное умножение следует тому же процессу для получения результата произведения двух двоичных чисел. Двоичное умножение намного проще, поскольку оно содержит только 0 и 1.
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Умножение двух двоичных чисел может быть выполнено с использованием двух распространенных методов, а именно сложения и сдвига частичного произведения, и с помощью параллельных умножителей.
Прежде чем обсуждать типы, давайте рассмотрим процесс умножения беззнаковых двоичных чисел. Рассмотрим два 4-битных двоичных числа как 1010 и 1011, а их умножение на эти два числа задается как
Из приведенного выше умножения частичные произведения генерируются для каждой цифры в множителе. Затем все эти частичные продукты складываются для получения конечной стоимости продукта. При умножении частичного произведения, когда бит множителя равен нулю, частичное произведение равно нулю, а когда бит множителя равно 1, результирующее частичное произведение является множимым.
Подобно десятичным числам, каждое последующее частичное произведение сдвигается на одну позицию влево относительно предыдущего частичного произведения перед суммированием всех частичных произведений.
Следовательно, это умножение использует n-сдвиги и добавляет для умножения n-битного двоичного числа. Комбинационная схема, реализованная для выполнения такого умножения, называется умножителем массива или комбинационным умножителем.
Наверх
[adsense2]
Цепь параллельного двоичного умножителя
Рассмотрим два беззнаковых 2-битных двоичных числа A и B, чтобы обобщить процесс умножения. Мультипликатор A равен A1A0, а множитель B равен B1B0. На рисунке ниже показан процесс умножения двух 2-битных двоичных чисел.
Этот процесс включает умножение двух цифр и сложение цифр с переносом или без переноса. После умножения каждого бита на множимое генерируются частичные произведения, а затем эти произведения складываются для получения общей суммы, которая представляет собой значение двоичного умножения.
Это умножение реализовано комбинационной схемой, так что умножение выполняется с помощью логических элементов И, тогда как сложение выполняется с использованием полусумматоров, как показано на рисунке.
Первое частичное произведение получается логическим элементом И, который представляет собой не что иное, как младший бит результата умножения. Поскольку второе частичное произведение сдвинуто влево, первое частичное второе слагаемое и второе частичное произведение первого слагаемого складываются с помощью полусумматора и производят выходную сумму вместе с переносом.
Это выполнение добавляется к следующему полусумматору в качестве входа, как показано на рисунке. Точно так же он производит результат умножения двух двоичных чисел, используя простую конфигурацию схемы. Умножение двух 2-битных чисел дает 4-битное двоичное число.
Рассмотрим умножение двух четырехбитных чисел без знака, в котором множимое A равно A3A2 A1A0, а множитель B равен B3B2B1B0. Частичные произведения производятся в зависимости от каждого бита множителя, умноженного на множимое.
Каждый частичный продукт состоит из четырех элементов продукта, которые сдвинуты влево относительно предыдущего частичного продукта, как показано на рисунке.
Все эти частичные произведения добавляются для получения 8-битного произведения.
Логическая схема для двоичного умножения 4×4 может быть реализована с использованием трех полных двоичных сумматоров вместе с вентилями И.
В приведенной выше операции первое частичное произведение получается путем умножения B0 на A3A2 A1A0, второе частичное произведение получается путем умножения B1 на A3A2 A1A0, аналогично для 3-го и 4-го частичных произведений. Таким образом, эти частичные произведения могут быть реализованы с помощью логических элементов И, как показано на рисунке.
Эти частичные произведения затем складываются с помощью 4-битного параллельного сумматора. Три старших бита первого частичного произведения с переносом (рассматриваемого как ноль) добавляются ко второму частичному члену в первом полном сумматоре.
Затем результат добавляется к следующему частичному произведению с переносом и продолжается до конечного частичного произведения, наконец, получается 8-битная сумма, которая указывает значение умножения двух двоичных чисел.
Наверх
Двоичный умножитель с использованием метода сдвига
В качестве альтернативы описанному выше автоматизированному методу можно реализовать ручное умножение с использованием n-битного сумматора, четырех регистров (A, B, C и Q) и логики сдвига и управления, как показано на рисунке ниже.
При этом 4-битный множитель сохраняется в регистре Q, 4-битное множимое сохраняется в регистре B, а регистр A первоначально очищается до нуля. Процесс умножения начинается с проверки младшего значащего бита B, является ли он 0 или 1.
Если B0 = 1, число в множимом (B) складывается с младшими битами регистра A и все биты регистров C, A и Q сдвигаются вправо на один бит.
Если бит B0 = 0, объединенные регистры C и Q сдвигаются вправо на один бит без выполнения сложения. Этот процесс повторяется n раз для n битовых чисел. Этот метод двоичного умножения называется параллельным умножением.
Рассмотрим рисунок ниже, на котором значения множителя и множимого указаны как 1011 и 1101, которые загружаются в регистры Q и A соответственно.