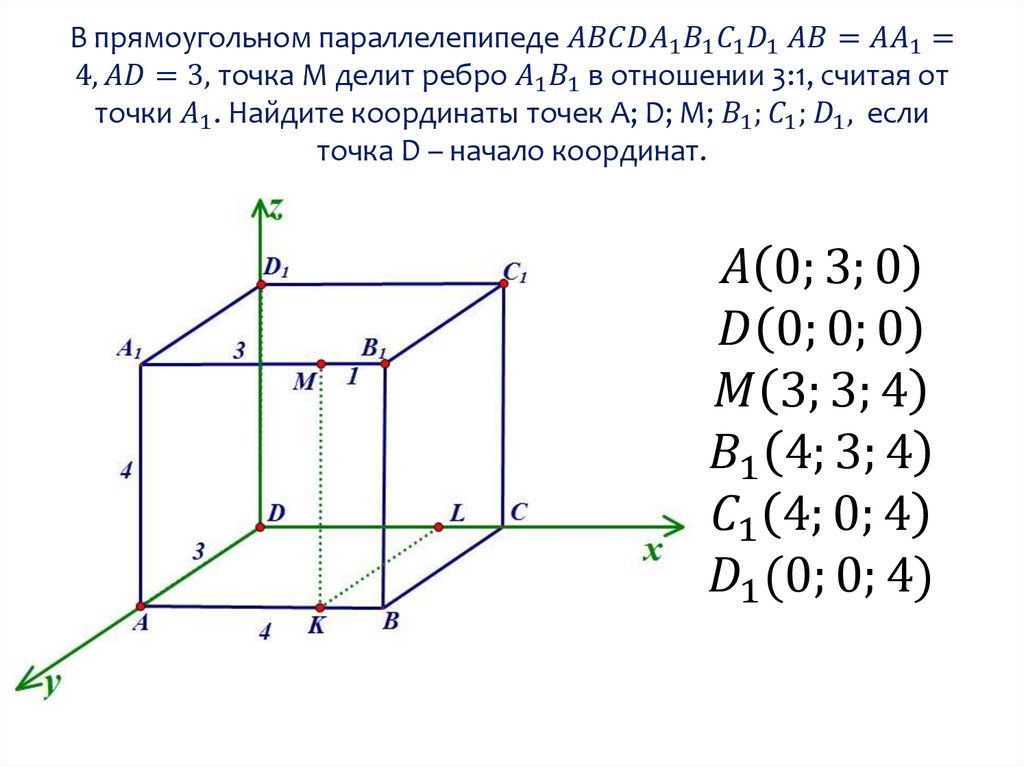
Решение высшей математики онлайн
‹— Назад
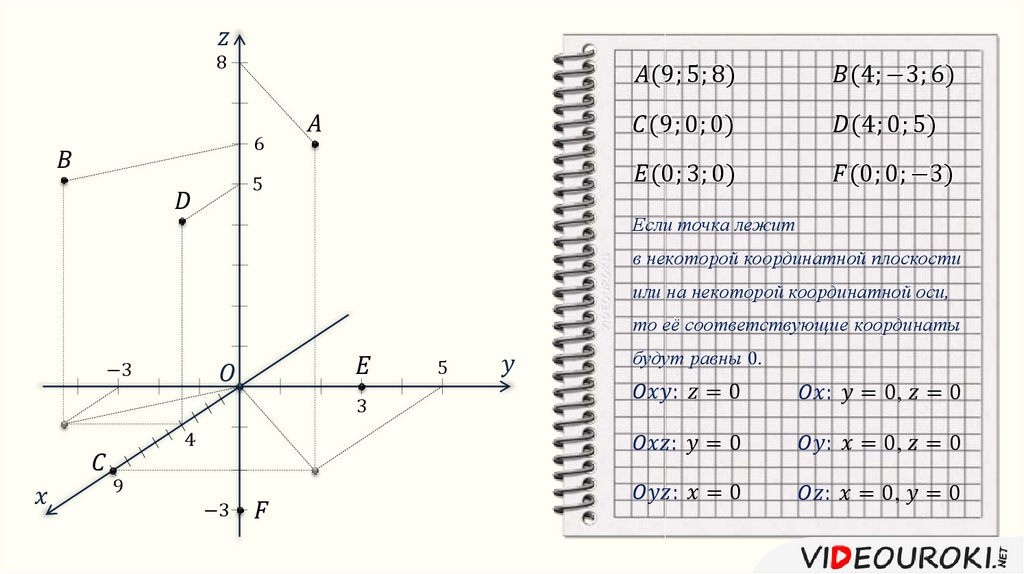
Рассмотрим случай трехмерного пространства (на плоскости все построения аналогичны). Фиксируем некоторую точку и возьмем произвольную точку . Радиус-вектором точки по отношению к точке называется вектор .
Если в пространстве выбран базис, то вектор раскладывается по этому базису. Таким образом точке можно сопоставить упорядоченную тройку чисел — координаты ее радиус-вектора.
Определение 10.17 Декартовой системой координат в пространстве называется совокупность точки и базиса.
Точка носит название начала координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат. Первая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Определение 10. 18 Координаты радиус-вектора точки по отношению к началу координат называются координатами точки в рассматриваемой системе координат.
18 Координаты радиус-вектора точки по отношению к началу координат называются координатами точки в рассматриваемой системе координат.
Первая координата называется абсциссой, вторая — ординатой, третья — аппликатой.
Аналогично определяются декартовы координаты на плоскости. Разумеется, точка на плоскости имеет только две координаты — абсциссу и ординату.
Координаты точки обычно пишут в скобках после буквы, обозначающей точку, например , .
Определение 10.19 Декартова система координат называется прямоугольной, если векторы базиса — единичные и попарно ортогональные (перпендикулярные) друг другу.
В дальнейшем мы будем использовать лишь декартову прямоугольную систему координат и для краткости будем называть ее просто «система координат».
Единичные попарно ортогональные векторы базиса принято, как правило, обозначать i, j, k.
Определение 10.20 Базис, образованный единичными попарно ортогональными векторами, называют ортонормированным.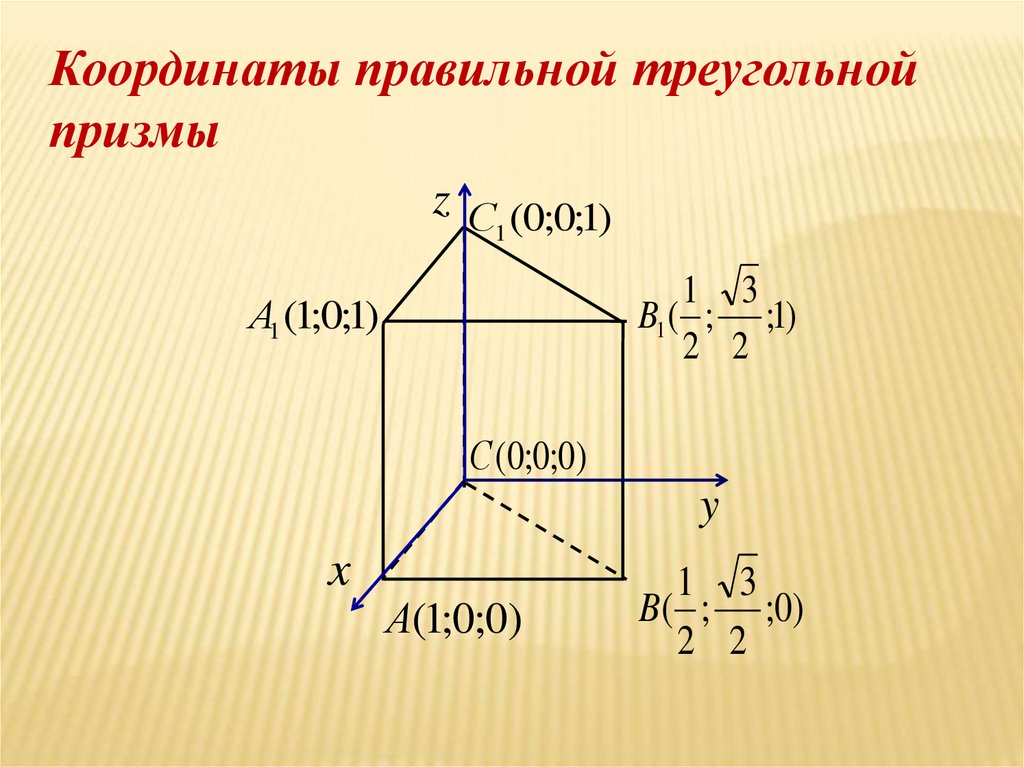
На рис. 10.15 показаны два способа изображения точки по ее координатам.
Рис.10.15.Построение точки
Так как точку пространства мы вынуждены изображать на плоскости, то, пока не указаны линии, связывающие изображение точки с осями координат, установить ее положение в пространстве невозможно! Это показывает рис. 10.16.
Рис.10.16.
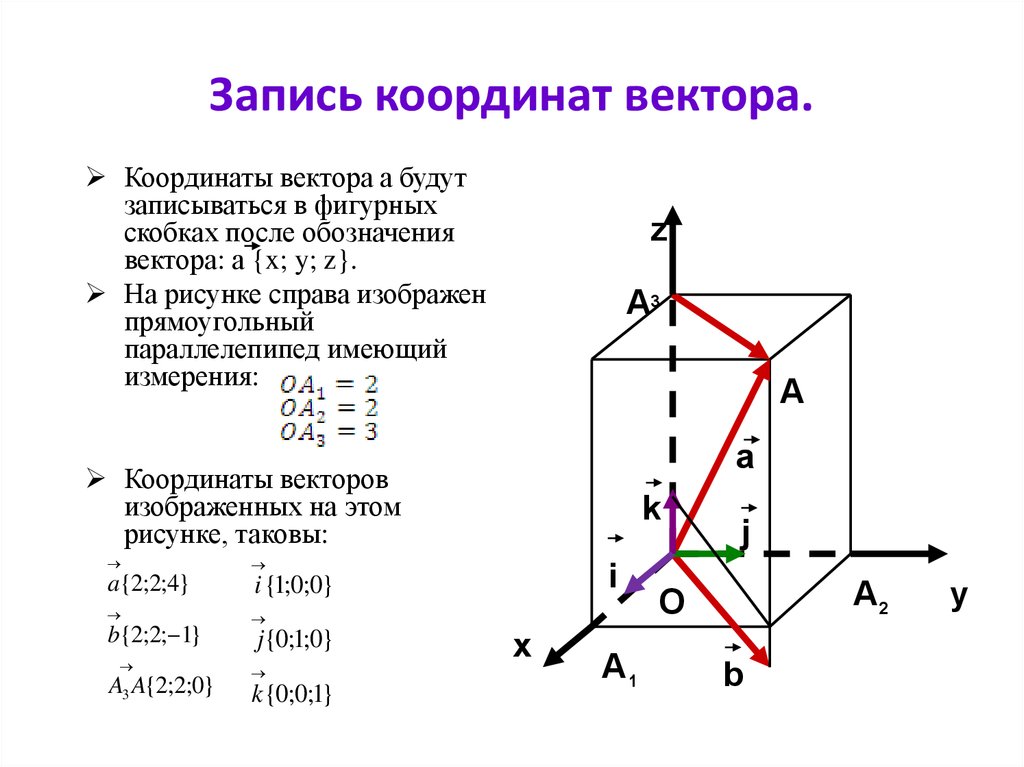
Зная координаты начала и координаты конца вектора, можно определить координаты самого вектора.
Предложение 10.12 Если точки заданы своими координатами , , то .
Доказательство. Очевидно соотношение (рис. 10.17),
Рис.10.17.Координаты вектора
откуда . Так как, по определению, координаты точки совпадают с координатами ее радиус-вектора, то , . В силу предложений 10.4, 10.5 получим .
Так как, по определению, координаты точки совпадают с координатами ее радиус-вектора, то , . В силу предложений 10.4, 10.5 получим .
Предложение 10.12 можно сформулировать так: чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Системы координат, проекции карт и преобразования—ArcGIS Pro
Данные, как правило, включают в себя массив чисел. Пространственные данные тоже, как правило, включают в себя массив чисел, но они также содержат в себе числовую информацию, которая позволяет вам расположить их где-то на поверхности Земли. Эти числа являются частью системы координат, которая обеспечивает фрейм привязки для ваших данных, чтобы находить объекты на земле, чтобы сопоставлять ваши данные с другими данными, чтобы выполнять пространственный анализ с высокой точностью и чтобы делать карты.
Пространственные данные тоже, как правило, включают в себя массив чисел, но они также содержат в себе числовую информацию, которая позволяет вам расположить их где-то на поверхности Земли. Эти числа являются частью системы координат, которая обеспечивает фрейм привязки для ваших данных, чтобы находить объекты на земле, чтобы сопоставлять ваши данные с другими данными, чтобы выполнять пространственный анализ с высокой точностью и чтобы делать карты.
Все пространственные данные создаются в каких-то системах координат независимо от того, идет ли речь о точках, линиях, полигонах, растрах или аннотациях. Сами координаты могут быть заданы различными способами – в десятичных градусах, футах, метрах или километрах; в действительности, в качестве системы координат может использоваться любая форма измерения. Определение этой системы измерений является первым шагом для выбора системы координат, которая будет отображать ваши данные в корректном положении в ArcGIS Pro относительно других ваших данных.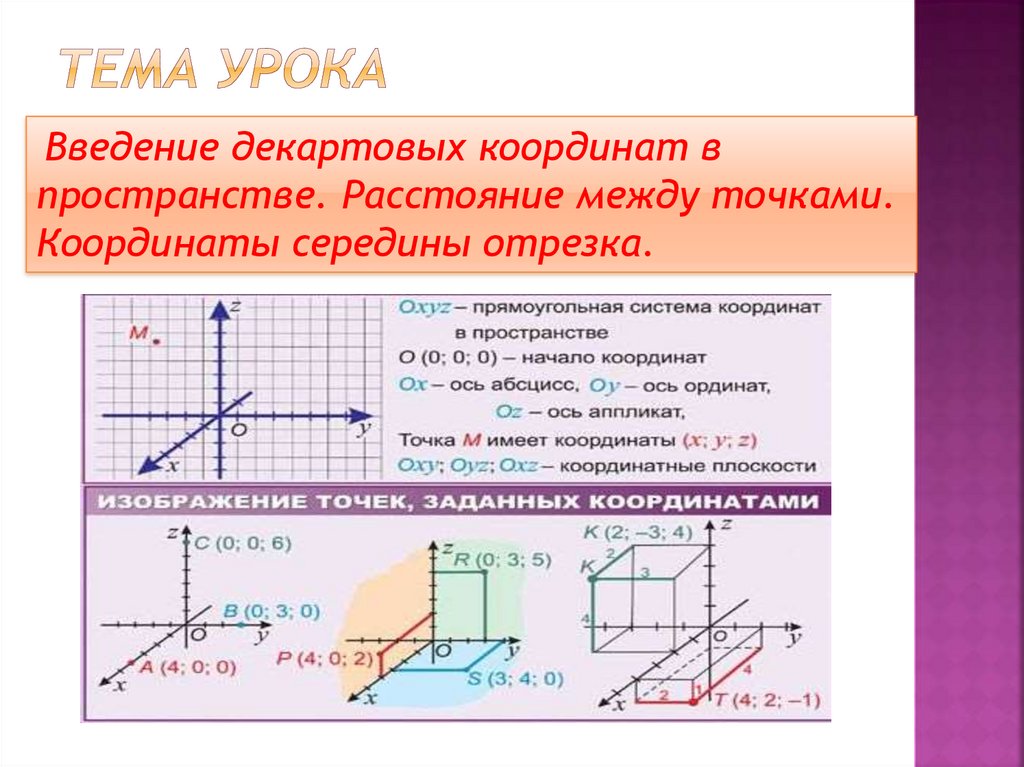
Системы координат
Данные заданы в горизонтальной и вертикальной системах координат. Горизонтальные системы координат отвечают за размещение объектов на поверхности Земли, а вертикальные определяют локализацию относительных высот и глубин объектов.
Горизонтальные системы координат
Существует три типа горизонтальных систем координат – географические, системы координат проекции и местные. Вы можете узнать, в какой системе координат находятся ваши данные, открыв свойства слоя.
Географические системы координат (GCS) основываются на трехмерной эллипсоидальной или сферической поверхности, а местоположения задаются угловыми измерениями, выраженными, как правило, в десятичных градусах, выражающие значения долготы (координаты x) и широты (координаты y). Местоположение данных может быть выражено положительными и отрицательными числами: положительными значениями х и у для районов севернее экватора и восточнее начального меридиана и отрицательными значениями х и у для районов к югу от экватора и западнее начального меридиана.
Загрузитьсписок поддерживаемых географических и вертикальных систем координат.
Системы координат проекции (СКП) — это плоские системы, в которых для координат используются линейные, а не угловые единицы. Система координат проекции основывается на географической системе координат и проекции карты. Проекция карты содержит математические вычисления, которые конвертируют угловые геодезические координаты GCS в декартовы координаты системы координат PCS на плоскости.
Загрузитьсписок поддерживаемых систем координат проекции.
Географическая система координат (слева), исчисляемая в угловых единицах, сравнивается с системой координат проекции (справа) в линейных единицах для того же местоположения в Атлантическом океане.
Локальная система координат использует условное начало координат (0, 0 или другое) в произвольном местоположении, которое может находиться в любой части земного шара. Местные системы координат часто используются для крупномасштабной картографии (небольшие участки земли). Условное начало координат может совпадать или не совпадать с известными реальными координатами, но для целей сбора данных для измерения направлений и расстояний скорее будет использоваться местная система координат, нежели глобальные координаты. В местных системах координат обычно в качестве единиц измерения используются метры или футы.
Условное начало координат может совпадать или не совпадать с известными реальными координатами, но для целей сбора данных для измерения направлений и расстояний скорее будет использоваться местная система координат, нежели глобальные координаты. В местных системах координат обычно в качестве единиц измерения используются метры или футы.
Вертикальные системы координат
Вертикальные системы координат бывают гравитационные и эллипсоидальные.
Чаще всего используются основанные на гравитации вертикальные системы координат. В них базовая поверхность задается вычислением высоты среднего уровня моря (или иногда получается из высоты одной точки.)
Высоты в эллипсоидальных системах координат отсчитываются от полученной математическими методами поверхности сферы или эллипсоида. Поскольку они вычисляются по математической модели, эллипсоидальные системы координат проще гравитационных вертикальных систем координат, но могут быть менее точными, особенно в случае крупных масштабов. К примеру, водоток на крупномасштабной карте может иметь другое направление при использовании эллипсоидальной системы координат. При работе с эллипсоидальной вертикальной системой координат необходимо убедиться в том, что она совпадает с географической системой координат. Например, если значение z задается в NAD 1983, географическая система координат или географическая система координат с системой координат проекции должна также задаваться в NAD 1983, а не в WGS 1984.
К примеру, водоток на крупномасштабной карте может иметь другое направление при использовании эллипсоидальной системы координат. При работе с эллипсоидальной вертикальной системой координат необходимо убедиться в том, что она совпадает с географической системой координат. Например, если значение z задается в NAD 1983, географическая система координат или географическая система координат с системой координат проекции должна также задаваться в NAD 1983, а не в WGS 1984.
Вертикальные системы координат содержат ссылку на z-координаты, являющиеся измерениями высот и глубин объектов. Вертикальные системы координат всегда выражены в линейных единицах измерения – в метрах или футах. С помощью вертикальной системы координат вы сможете улучшить точность задания местоположений объектов при анализе и редактировании. Вертикальные системы координат не применяются по умолчанию к новым картам и сценам — вам надо принудительно выбрать одну из них.
Вертикальные системы координат в глобальной сцене должны быть эллипсоидальными, за одним исключением. Они могут быть гравитационными, но только если полностью покрывают экстент всего мира. EGM2008 Geoid и EGM96 Geoid являются примерами глобальных вертикальных гравитационных систем координат.
Они могут быть гравитационными, но только если полностью покрывают экстент всего мира. EGM2008 Geoid и EGM96 Geoid являются примерами глобальных вертикальных гравитационных систем координат.
Внимание:
Помните, что эллипсоидальная вертикальная система координат не принимается во внимание при прорисовке. Это можно увидеть при вытягивании объектов.
Загрузитьсписок поддерживаемых географических и вертикальных систем координат.
Картографические проекции
Проекция — это способ отображения системы координат и своих данных на плоской поверхности, т.е. на листе бумаги или на экране. Для конвертации системы координат, используемой на не плоской поверхности Земли, в систему координат для плоской поверхности используются математические вычисления. Поскольку транспонировать не плоскую поверхность на плоскую без искажений невозможно, используются разные картографические проекции с разными свойствами. Некоторые сохраняют площадь, другие – углы. Некоторые сохраняют отдельные расстояния и направления. Ваш выбор картографической проекции должен быть сформирован экстентом, местоположением и свойствами, которые вы захотите сохранить для вашей системы координат проекции. На платформе ArcGIS существует приблизительно 6 тысяч систем координат, поэтому вы, вероятно, найдете подходящую для ваших данных. Если нет — вы можете создать пользовательскую систему координат проекции из более 100 проекций карты для отображения данных.
Ваш выбор картографической проекции должен быть сформирован экстентом, местоположением и свойствами, которые вы захотите сохранить для вашей системы координат проекции. На платформе ArcGIS существует приблизительно 6 тысяч систем координат, поэтому вы, вероятно, найдете подходящую для ваших данных. Если нет — вы можете создать пользовательскую систему координат проекции из более 100 проекций карты для отображения данных.
ArcGIS Pro проецирует данные на лету, поэтому любые данные, которые вы добавите в карту, примут систему координат, заданную для первого добавленного слоя. При условии, если система координат первого добавленного слоя будет определяться корректно, все другие данные с корректной системой координат будут перепроецироваться на лету в систему координат карты. Такой подход облегчает исследование и отображение данных, но он не должен использоваться для проведения анализов или редактирования, поскольку это может привести к неточностям из-за несопоставленных между разными слоями данных. При проецировании на лету данные прорисовываются медленнее. Если вы собираетесь проводить анализ или редактировать данные, сначала спроецируйте их в соответствующую систему координат, доступную для всех ваших слоев. Так будет создана новая версия ваших данных.
При проецировании на лету данные прорисовываются медленнее. Если вы собираетесь проводить анализ или редактировать данные, сначала спроецируйте их в соответствующую систему координат, доступную для всех ваших слоев. Так будет создана новая версия ваших данных.
См. список всех поддерживаемых в ArcGIS Pro картографических проекций.
Преобразования
Даже после того, как система координат задана, вы все равно можете захотеть использовать данные в другой системе координат. В таких случаях может оказаться полезной преобразование. Преобразование конвертирует данные между разными географическими или вертикальными системами координат. Если ваши данные не будут согласованы, то при проведении любых картографических действий или анализа вы будете сталкиваться с трудностями и неточностями.
Загрузитьсписок поддерживаемых географических и вертикальных преобразований.
Связанные разделы
Отзыв по этому разделу?
Место в космосе — Занятие
Quick Look
Уровень: 6 (6-9)
Необходимое время: 30 минут
(Плюс 15-20 минут, если учащиеся соберут свой собственный набор осей. )
)
Расходные материалы Стоимость/группа: 3,00 долл. США 04 Деятельность Зависимость:
Трехмерная система координат для карт галактик: новое измерение
предметных областей: Геометрия, наука и техника
Поделиться:
TE Информационный бюллетень
Краткое содержание
Студенческие группы используют «настоящую» трехмерную систему координат для построения точек в пространстве. Изготовленная из пробкового дерева или деревянных дюбелей, система имеет три оси под прямым углом и плоскость (плоскость XY), которая может скользить вверх и вниз по оси Z. Учащимся дается несколько координат и предлагается найти эти точки в пространстве. Затем они находят координаты восьми углов коробки/куба с заданными размерами. Инженерное подключение
Инженеры используют систему координат всякий раз, когда они создают инженерные чертежи объектов и конструкций, и декартова система координат, смоделированная в этой деятельности, используется чаще всего.
Цели обучения
После этого задания учащиеся должны уметь:
- Найдите точку в пространстве, зная ее координаты и начало координат.
- Описать положение данной точки в пространстве относительно некоторого начала координат с помощью координат.
Образовательные стандарты
Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.
Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются Сеть стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естественные науки или математика;
внутри типа по подтипу, затем по классам, и т.д. .
, естественные науки или математика;
внутри типа по подтипу, затем по классам, и т.д. .
Общие базовые государственные стандарты — математика
- Найдите и расположите целые числа и другие рациональные числа на горизонтальной или вертикальной числовой линейной диаграмме; найти и расположить пары целых чисел и других рациональных чисел на координатной плоскости.
(Оценка
6) Подробнее
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Решайте реальные и математические задачи, отображая точки во всех четырех квадрантах координатной плоскости.
 Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
(Оценка
6) Подробнее
Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
(Оценка
6) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
 (Оценка
7) Подробнее
(Оценка
7) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Создавайте формальные геометрические построения с помощью различных инструментов и методов (циркуль и линейка, струна, отражающие устройства, складывание бумаги, динамическое геометрическое программное обеспечение и т.
 д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
(Оценки
9-
12) Подробнее
д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
(Оценки
9-
12) ПодробнееСогласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
- Информационно-коммуникационные системы позволяют передавать информацию от человека к человеку, от человека к машине и от машины к человеку.
 (Оценки
6 —
8) Подробнее Посмотреть согласованную учебную программу
(Оценки
6 —
8) Подробнее Посмотреть согласованную учебную программуСогласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Использование символов, размеров и рисунков способствует четкому общению, предоставляя общий язык для выражения идей.
(Оценки
6 —
8) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
ГОСТ
Предложите выравнивание, не указанное вышеКакое альтернативное выравнивание вы предлагаете для этого контента?
Подписаться
Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!
PS: Мы никому не передаем личную информацию и электронные письма.
Список материалов
- 3-футовый штифт из пробкового дерева размером ¼ дюйма x ¼ дюйма или деревянный дюбель
- быстродействующий клей, такой как пистолет для горячего клея, резиновый клей или глиняный шарик размером с мяч для гольфа
- маркер
- линейка
- Канцелярский нож или ножницы
- Квадрат 1 дюйм x 1 дюйм из гофрированного картона, пенопласта или картона для плакатов
Рабочие листы и вложения
Рабочий лист 3D-координат (pdf)
Посетите [www.teachengineering.org/activities/view/duk_dimension_tech_act], чтобы распечатать или загрузить. Больше учебных программ, подобных этому
Высший элементарный урок
Трехмерная система координат для картирования галактик: следующее измерение
Учащиеся узнают о трехмерной декартовой системе координат и получают представление о размере нашей галактики (Млечный Путь) и расстоянии до ближайшей спиральной галактики (галактики Андромеды), используя трехмерную модель. Предоставляется рабочий лист ученика.
Предоставляется рабочий лист ученика.
Трехмерная система координат для карт галактик: новое измерение
Урок средней школы
Все о линейном программировании
Учащиеся узнают о линейном программировании (также называемом линейной оптимизацией) для решения задач инженерного проектирования. Они применяют эту информацию для решения двух практических задач инженерного проектирования, связанных с оптимизацией материалов и стоимости, путем построения графиков неравенств, определения координат и уравнений из …
Все о линейном программировании
Урок средней школы
Проекции и координаты: превращение трехмерной Земли в плоскость
Учащиеся узнают о проекциях и координатах в географических науках, которые помогают нам лучше понять природу Земли и то, как описать местоположение.
Проекции и координаты: превращение трехмерной Земли в плоскость
Урок средней школы
Координаты и декартова плоскость
Краткий обзор декартовой плоскости включает в себя то, как точки записываются в формате (x, y) и ориентированы по осям, а также какие направления являются положительными и отрицательными. Затем учащиеся узнают, что означает, что отношение является функцией, и как определить домен и диапазон набора точек данных.
Координаты и декартова плоскость
Предварительные знания
Минимальный предварительный опыт построения графиков в двух измерениях полезен, но не обязателен.
Введение/Мотивация
Содержимое раздела «Введение/мотивация» урока «Трехмерная система координат для картирования галактик: следующее измерение» также служит введением в это задание.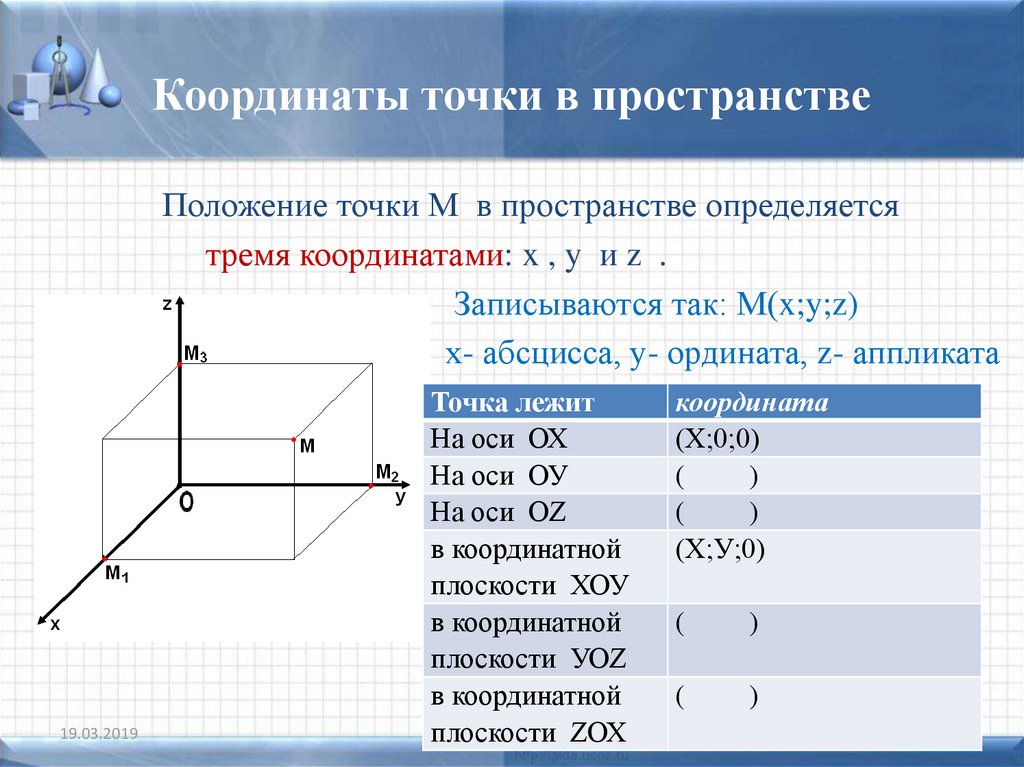
Процедура
Перед занятием
Соберите материалы и сделайте копии рабочего листа 3D-координат.
Выполните следующие действия, чтобы построить один набор осей для каждой группы. В качестве альтернативы, пусть группы сами построят оси.
- Разрежьте пробковое дерево на три сегмента по 1 футу каждый. (Вероятно, это займет дополнительные 15-20 минут.)
- С помощью клеевого пистолета (или другого клея или глины) склейте три детали вместе так, чтобы все три были перпендикулярны друг другу и встречались в одной точке. Это формирует три оси.
- С помощью линейки и маркера сделайте отметки через каждый дюйм по каждой из трех осей, удаляясь от исходной точки. Сделайте в общей сложности 10 меток на каждой оси. При желании пронумеруйте метки так, чтобы на каждой оси «1» была ближе всего к началу координат, а «10» — дальше всего от оси.
- С помощью канцелярского ножа или ножниц вырежьте из картона, пенопласта или картона для плакатов квадрат размером 1 фут x 1 фут.
 Сделайте небольшое отверстие в одном углу квадрата, примерно на полдюйма от краев. Сделайте отверстие достаточно большим, чтобы ось из пробкового дерева прошла через него.
Сделайте небольшое отверстие в одном углу квадрата, примерно на полдюйма от краев. Сделайте отверстие достаточно большим, чтобы ось из пробкового дерева прошла через него. - Эта доска из пеноматериала служит плоскостью XY. Сдвиньте его по одной из осей (ось Z) до упора вниз, пока он не ляжет на две другие оси. Отверстие, в котором ось Z проходит через плоскость XY, теперь находится в начале координат.
- С помощью линейки начертите на плоскости сетку размером 10 x 10 дюймов. Раздвигайте сетку через каждый дюйм, чтобы они совпадали с отметками на осях X и Y. Затем пометьте оси на плоскости «X» и «Y» и пронумеруйте от 1 до 10 (снова считая по мере удаления от исходной точки. Эти цифры должны совпадать с цифрами на осях X и Y бальсовых деревянных осей.
- Вы построили трехмерную систему координат с подвижной плоскостью XY. Чтобы найти точку, сначала найдите нужные координаты X и Y на плоскости XY (традиционный двухмерный график), а затем сдвиньте всю плоскость до указанной координаты Z.
Со студентами
- Разделите класс на группы по три ученика в каждой. Дайте каждой группе набор из трех осей.
- Раздайте рабочий лист, который поможет учащимся выполнить 3D-упражнение.
Словарь/Определения
ось: В математике линия, используемая в качестве ориентира для описания местоположения точки. Например, в декартовой системе координат ось представляет собой линию, отмеченную нулем в определенной точке. Затем местоположение объекта можно описать, измерив, насколько далеко (на линии) он находится от этого начала координат и в каком направлении. Во многих отношениях ось похожа на числовую прямую, которая бесконечно продолжается в обоих направлениях (положительном и отрицательном). Ось является одномерной.
Декартова система координат: прямоугольная система координат, разработанная знаменитым математиком Декартом. Он состоит из 2 или 3 осей (X, Y и Z), расположенных под прямым углом друг к другу и пересекающихся в заданном начале координат.
размерность: Мера особой степени. То, что мы видим вокруг себя, — это трехмерный мир, потому что предметы имеют три измерения: длину, ширину и высоту. Линия находится в одном измерении, площадь (например, прямоугольник, нарисованный на листе бумаги) — в двух измерениях, а прямоугольник (куб) — в трех измерениях.
график: визуальное представление математической функции или набора чисел. В предыдущем определении упорядоченной пары, если поверхность вашего стола представляет собой график, вы нанесли на график точку (2,3), то есть представили эти числа визуально (или графически).
упорядоченная пара: два числа, используемые для описания положения точки на плоскости относительно заданной опорной точки. Например, если вам сказали, что передний левый угол вашего стола является исходной точкой, и вы хотите найти точку, заданную упорядоченной парой (2, 3), и вы знаете, что используемая вами единица измерения — дюймы, вы начинаете с что передний левый угол вашего стола, сдвиньте на два дюйма вправо, а затем на 3 дюйма к задней части стола, и вы найдете эту точку.
origin : указанная опорная точка [(0,0,0) в большинстве систем координат]
плоскость: множество всех точек между двумя пересекающимися прямыми. Плоскость двухмерна, поэтому это плоская поверхность. Плоскую столешницу, например, можно представить как плоскость.
Оценка
Рабочий лист : Если учащиеся могут удовлетворительно заполнить Рабочий лист 3D-координат практически без помощи учителя или сверстников, то они демонстрируют хорошее понимание основ 3D-графики.
Вопросы безопасности
- Если учащиеся используют канцелярские ножи для резки картона или пенопластовой плиты, тщательно контролируйте их и следите за опасным использованием этих острых инструментов.
- Предупредите учащихся, что клеевые пистолеты и клей сильно нагреваются. Также будьте осторожны с другими клеями и соблюдайте инструкции по безопасности .
Расширения деятельности
Предложите учащимся найти точки для описания фигур, которые сложнее коробки.
Попробуйте нарисовать 3D-оси на листе бумаги. Затем попробуйте нарисовать куб в 3D, расположив точки на осях
.Измените плоскость с плоскости XY на плоскости XZ или YZ, сдвинув ее вниз по другой оси. Точки могут быть расположены таким же образом, и учащиеся узнают, что конкретные буквы и ориентация плоскостей произвольны.
Масштабирование активности
- Предложите менее продвинутым учащимся выполнить только двухмерную часть.
- Чтобы сэкономить время и деньги, создайте только один набор трехмерных осей и представьте упражнение в виде демонстрации класса вместо того, чтобы каждая группа имела свой собственный набор осей.
Авторские права
© 2013 Регенты Университета Колорадо; оригинал © Университет Дьюка, 2004 г.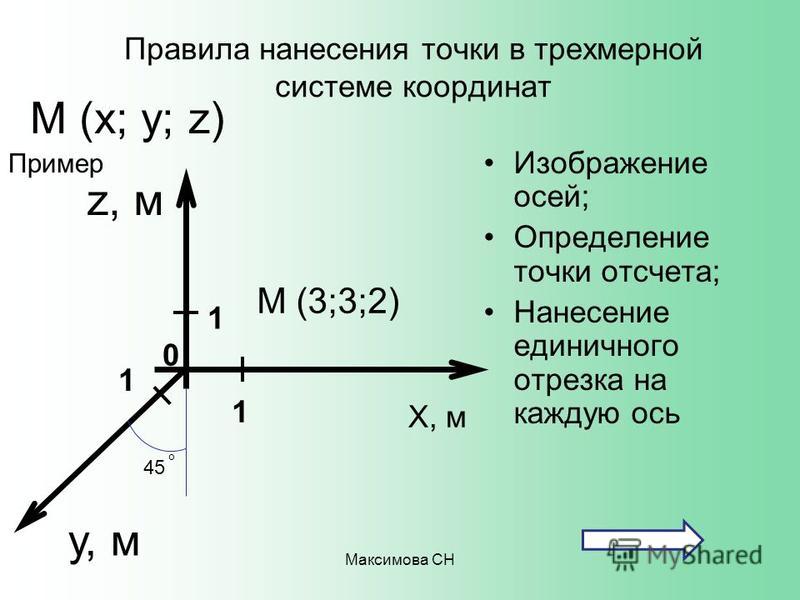
Авторы
Бен БернхэмПрограмма поддержки
Программа Techtronics, Инженерная школа Пратта, Университет ДьюкаБлагодарности
Этот контент был разработан в рамках программы MUSIC (Понимание математики через науку, интегрированную с учебной программой) Инженерной школы Пратта Университета Дьюка в рамках гранта Национального научного фонда GK-12 №. DGE 0338262. Однако это содержание не обязательно отражает политику NSF, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Последнее изменение: 15 февраля 2018 г.
Векторы в двух- и трехмерных декартовых координатах
Во введении к векторам мы обсуждали векторы без привязки к какой-либо системе координат.
Работая только с геометрическим определением величины и направления
векторов, мы смогли определить такие операции, как сложение, вычитание,
и умножение на скаляры. Мы также обсудили свойства этих операций.
Мы также обсудили свойства этих операций.
Часто система координат оказывается полезной, потому что проще управлять координатами вектора, чем непосредственно его величиной и направлением. Когда мы выражаем вектор в системе координат, мы идентифицируем вектор с помощью списка чисел, называемых координатами или компонентами, которые определяют геометрию вектора в терминах системы координат. Здесь мы обсудим стандартные декартовы системы координат на плоскости и в трехмерном пространстве.
Векторы на плоскости
Мы предполагаем, что вы знакомы со стандартной декартовой системой координат $(x,y)$ на плоскости. Каждая точка $\vc{p}$ на плоскости отождествляется со своими компонентами $x$ и $y$: $\vc{p} = (p_1,p_2)$.
Чтобы определить координаты вектора $\vc{a}$ на плоскости,
первый шаг — перевести вектор так, чтобы его хвост находился в начале координат
системы координат. Тогда голова вектора будет
в некоторой точке $(a_1,a_2)$ на плоскости. Мы называем $(a_1,a_2)$ координатами или компонентами вектора $\vc{a}$. 2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.
2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.
Приведенный ниже апплет, повторяющийся из введения вектора, позволяет исследовать взаимосвязь между компонентами вектора и его величиной.
Величина и направление вектора. Синяя стрелка обозначает вектор $\vc{a}$. Два определяющих свойства вектора, величина и направление, показаны красной полосой и зеленой стрелкой соответственно. Длина красной полосы — это величина $\|\vc{a}\|$ вектора $\vc{a}$. Зеленая стрелка всегда имеет длину единицу, но ее направление совпадает с направлением вектора $\vc{a}$. Единственным исключением является случай, когда $\vc{a}$ является нулевым вектором (единственным вектором с нулевой величиной), для которого направление не определено. Вы можете изменить любой конец $\vc{a}$, перетащив его мышью. Вы также можете переместить $\vc{a}$, перетащив середину вектора; однако изменение положения $\vc{a}$ таким образом не меняет вектор, так как его величина и направление остаются неизменными.
Дополнительная информация об апплете.
Векторные операции, которые мы определили во введении к векторам, легко выразить в терминах этих координат. Если $\vc{a}=(a_1,a_2)$ и $\vc{b}=(b_1,b_2)$, их сумма просто $\vc{a}+\vc{b}=(a_1+b_1,a_2+b_2)$, как показано на рисунке ниже. Также легко видеть, что $\vc{b}-\vc{a} = (b_1-a_1,b_2-a_2)$ и $\lambda \vc{a} = (\lambda a_1, \lambda a_2)$ для любого скаляра $\lambda$.
Приведенный ниже апплет, также повторяющийся из введения вектора, позволяет вам исследовать взаимосвязь между геометрическим определением сложения векторов и суммированием компонентов вектора.
Сумма двух векторов. Сумма $\vc{a}+\vc{b}$ вектора $\vc{a}$ (синяя стрелка) и вектора $\vc{b}$ (красная стрелка) показана зеленой стрелкой . Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$.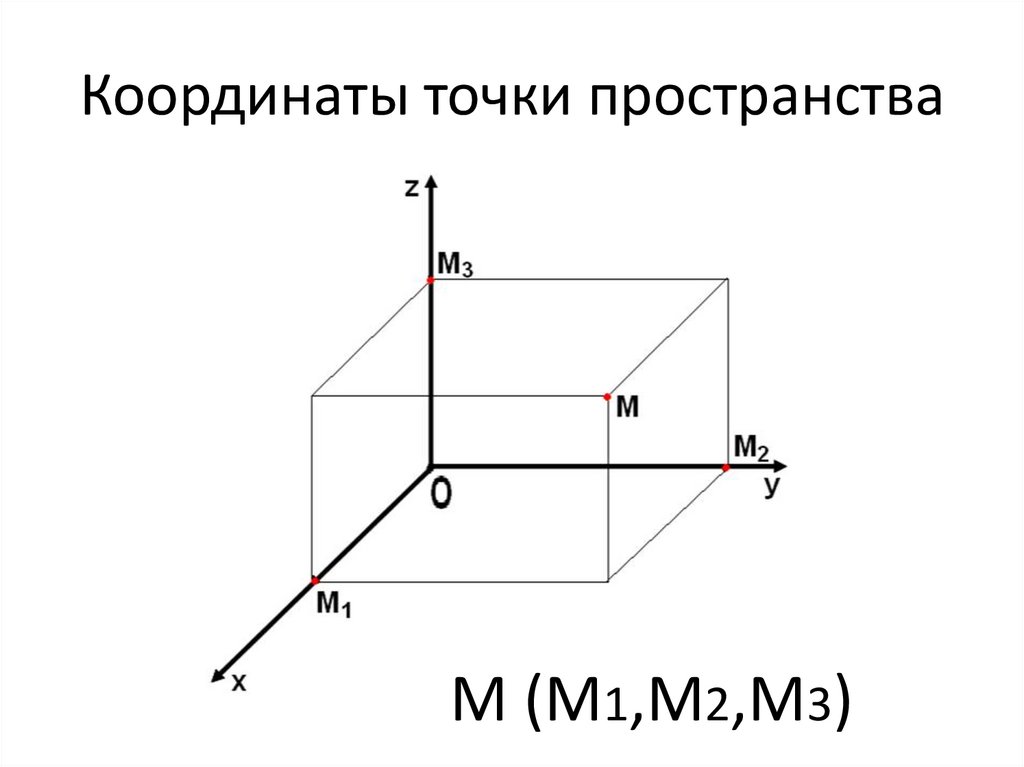 То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
Дополнительная информация об апплете.
Вы могли заметить, что мы используем одни и те же обозначения для обозначения точки и вектора. Мы не склонны подчеркивать какое-либо различие между точкой и вектором. Вы можете думать о точке как о представлении вектора, хвост которого зафиксирован в начале координат. Вам придется выяснить по контексту, думаем ли мы о векторе или нет. как с фиксированным хвостом в начале координат.
Другой способ обозначения векторов — стандартные единичные векторы
обозначаются $\vc{i}$ и $\vc{j}$. Единичный вектор — это вектор, длина которого равна единице.
Вектор $\vc{i}$ является единичным вектором в направлении положительной оси $x$. В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$.
Мы можем записать любой двумерный вектор в терминах этих единичных векторов как
$\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.
В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$.
Мы можем записать любой двумерный вектор в терминах этих единичных векторов как
$\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.
Векторы в трехмерном пространстве
В трехмерном пространстве существует стандартная декартова система координат $(x,y,z)$.
Начиная с точки, которую мы называем началом координат, построим три взаимно
перпендикулярные оси, которые мы называем осью $x$, осью $y$ и осью $z$.
Вот один из способов изобразить эти оси.
Встаньте в углу комнаты и посмотрите вниз, в точку, где стены соприкасаются с полом.
Затем пол и стена слева от вас пересекаются по линии, являющейся положительной осью $x$. Пол и стена справа от вас пересекаются по линии, являющейся положительной осью $y$. Стены пересекаются по вертикальной линии, являющейся положительной осью $z$.
Эти положительные оси изображены в приведенном ниже апплете и помечены как $x$, $y$ и $z$.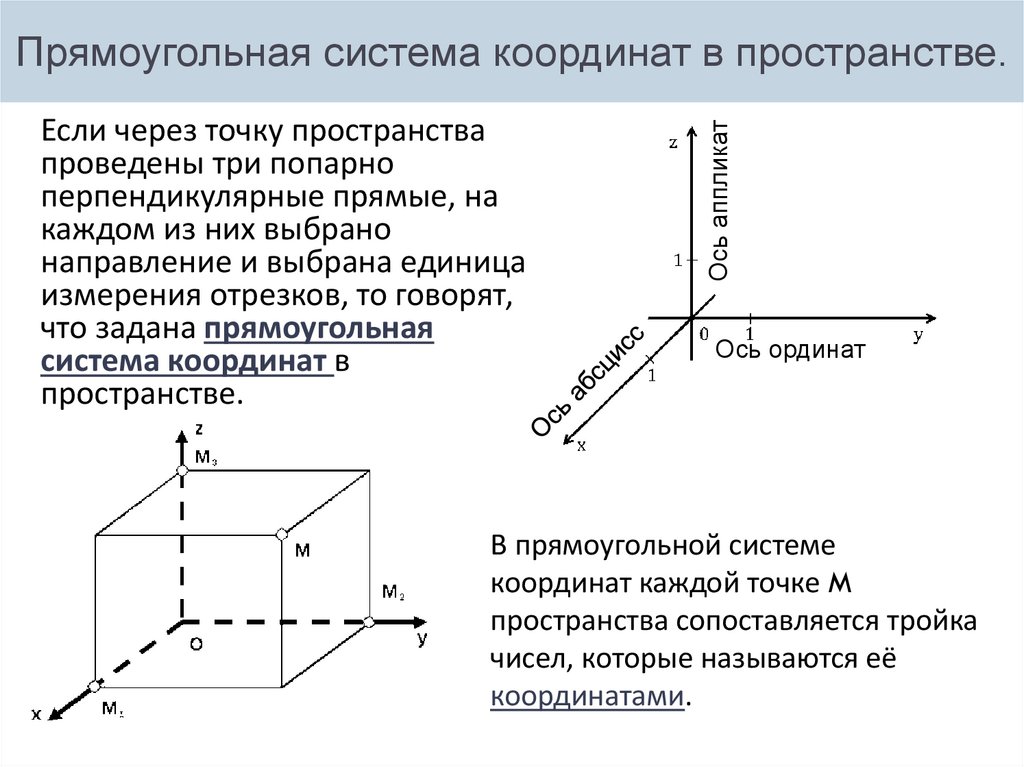 Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.
Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.
Загрузка апплета
Трехмерные декартовы оси координат. Представление трех осей трехмерной декартовой системы координат. Положительная ось $x$, положительная ось $y$ и положительная ось $z$ — это стороны, помеченные $x$, $y$ и $z$. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (немаркированная сторона) является отрицательной частью. Вы можете перетащить фигуру с помощью мыши, чтобы повернуть ее.
Дополнительная информация об апплете.
Мы установили относительное расположение положительных осей $x$, $y$ и $z$ чтобы сделать систему координат правой системой координат . Обратите внимание, что если согнуть пальцы правой руки от положительной оси $x$ к положительной оси $y$, большой палец правой руки будет указывать в направлении положительной оси $z$.
Если вы поменяли местами положительную ось $x$ и положительную ось $y$,
тогда у вас будет левосторонняя система координат. Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы.
Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.
Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы.
Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.
С помощью этих осей любой точке $\vc{p}$ в пространстве можно присвоить три координаты
$\vc{p}=(p_1,p_2,p_3)$. Например, учитывая приведенную выше аналогию с углом комнаты,
предположим, вы начинаете с угла комнаты и проходите четыре метра по оси $x$, затем поворачиваете налево и проходите три метра вглубь комнаты. Если ваш рост два метра, то ваша макушка находится в точке $(4,3,2)$. 93$ для обозначения того, что его можно описать тремя действительными координатами. Суммы, разности и скалярные умножения трехмерных векторов выполняются для каждого компонента. Если $\vc{a}=(a_1,a_2,a_3)$ и $\vc{b}=(b_1,b_2,b_3)$, то $\vc{a}+\vc{b}=(a_1+ b_1,a_2+b_2,a_3+b_3)$, $\vc{b}-\vc{a}=(b_1-a_1,b_2-a_2,b_3-a_3)$ и $\lambda\vc{a}= (\лямбда а_1, \лямбда а_2, \лямбда а_3)$.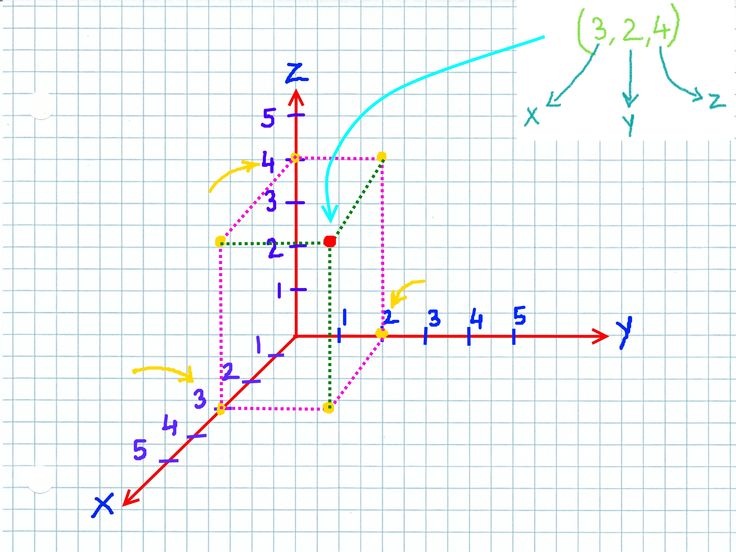
Загрузка апплета
Вектор в трехмерном пространстве. Представление вектора $\vc{a}=(a_1,a_2,a_3)$ в трехмерной декартовой системе координат. Вектор $\vc{a}$ изображается в виде зеленой стрелки с хвостом, закрепленным в начале координат. Вы можете перетащить мышкой кончик зеленой стрелки, чтобы изменить вектор. Чтобы показать трехмерную перспективу, розовый треугольник соединяет вектор с его проекцией $(a_1,a_2,0)$ на $xy$-плоскость (серая стрелка). Фиолетовые векторы показывают проекции $\vc{a}$ на каждую ось и представляют координаты $a_1$, $a_2$ и $a_3$. Вы также можете перетаскивать головки фиолетовых векторов, чтобы изменить только одну из координат вектора. Или перетащите вершину серого вектора в плоскости $xy$, чтобы изменить только координаты $x$ и $y$.
Дополнительная информация об апплете.
Как и в двух измерениях, мы также можем обозначать трехмерные векторы is в терминах стандартных единичных векторов $\vc{i}$, $\vc{j}$ и $\vc{k}$.
Эти векторы являются единичными векторами в положительных направлениях $x$, $y$ и $z$ соответственно. В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$.
Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме
$\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.
В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$.
Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме
$\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.
Загрузка апплета
Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях, $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный), представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.
Дополнительная информация об апплете.
Какова длина вектора $\vc{a}=(a_1,a_2,a_3)$? Мы можем разложить вектор на $(a_1,a_2,a_3) = (a_1,a_2,0)+(0,0,a_3)$, где два вектора
справа соответствуют двум зеленым сегментам линии
в вышеуказанном апплете. Эти два отрезка образуют прямоугольный треугольник,
гипотенуза — это вектор $\vc{a}$ (синий отрезок).