Построение онлайн интегральных кривых: Семейство кривых дифференциального уравнения · Как пользоваться Контрольная Работа РУ

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например,

уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.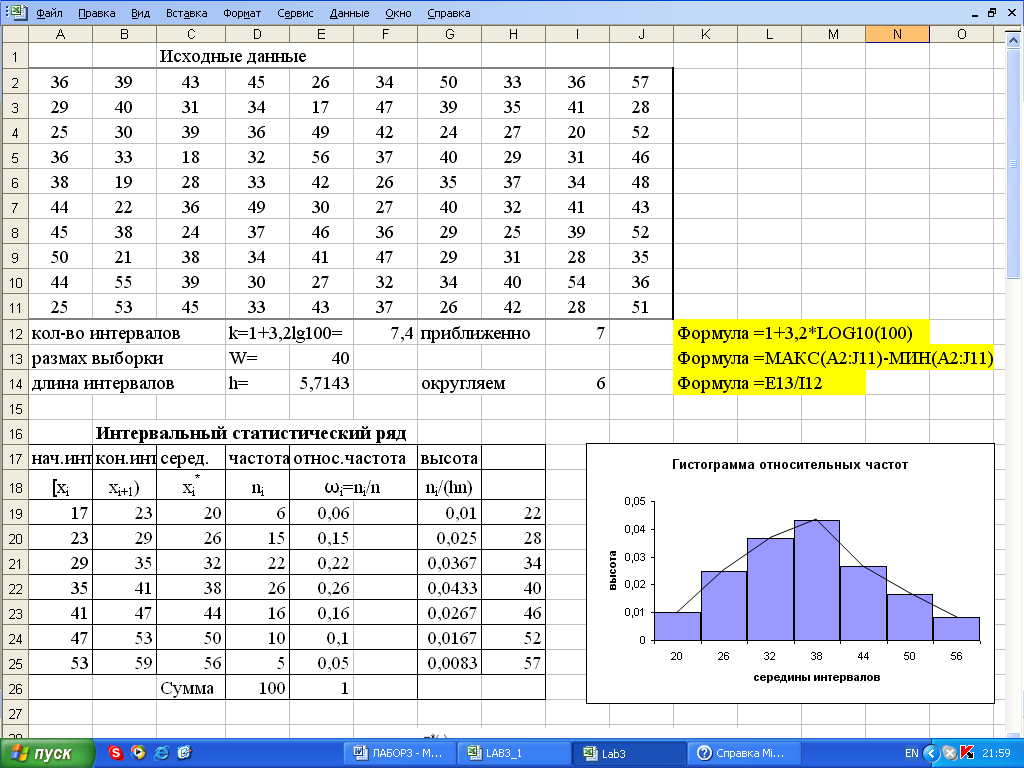

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Устойчивость положений равновесия

Важный вопрос, который можно задавать о дифференциальных уравнениях: насколько сильно поменяется решение, если мы чуть-чуть поменяем начальное условие? Для конечных промежутков времени на этот вопрос отвечает уравнение в вариациях (мы рассматривали его простейшую версию, когда обсуждали линейные уравнения первого порядка, см. параграф 9.1.1). Однако зачастую нас интересует, как устроено установившееся движение, то есть что происходит при t, стремящемся к бесконечности. Для анализа этого случая нужно ввести новые понятия. Чем мы и займёмся.

13.1Интуитивное представление об устойчивости

В принципе, можно сформулировать понятие устойчивости применительно к любому решению, но мы сосредоточимся на положениях равновесия.

Собственно, мы уже говорили о том, что положения равновесия (они же особые точки) дифференциального уравнения бывают устойчивыми или неустойчивыми, не вводя аккуратно соответствующие понятия. Напомним те примеры, для которых нам хватало интуиции, а потом сформулируем соответствующие определения аккуратно.

13.1.1Одномерное фазовое пространство

Рассмотрим уравнение

˙x=x2−1(13.1)

Его фазовый портрет состоит из пяти фазовых кривых: двух особых точек 1 и −1, двух лучей (−∞,−1) и (1,∞) и интервала (−1,1). Направления движения вдоль фазовых кривых определяются знаком правой части: от точки 1 и к точке −1, см. рис. 13.1 и 13.2.

Рис. 13.1: График правой части (сверху) и фазовые кривые (снизу) для уравнения (13.

1)

Рис. 13.2: Фазовые кривые (слева) и интегральные кривые (справа) для уравнения (13.1)

Точка −1 является устойчивым положением равновесия: если начальное условие немного «не попадёт» в эту точку или в какой-то момент чуть-чуть отклонится от него (например, в результате маленького случайного шока), то оно не только не уйдёт «далеко», но и наоборот будет стремиться к этому же положению равновесия в будущем.

А вот точка 1 совсем другая: если начальное условие отклоняется от него (даже совсем чуть-чуть), всё равно решение со временем уйдёт достаточно далеко либо в положительном направлении (уйдёт на бесконечность), либо в отрицательном (притянется к точке −1). Эта точка является неустойчивой.

13.1.2Двумерное фазовое пространство

Давайте вспомним, какие особые точки на плоскости нам встречались. В главе 10 мы построили полную классификацию невырожденных линейных особых точек.

Рис. 13.3: Линейные особые точки

Напомним также, как выглядят фазовые кривые математического маятника, см. рис. 13.4 (подробнее см. в параграфе 7.3).

Рис. 13.4: Фазовые кривые математического маятника

Здесь мы видим два типа особых точек: вблизи точки (0,0) фазовые кривые похожи на окружности (прямо как в линейном центре), а около точек (±π,0) — гиперболы (как в седловой особой точке).

Какие из особых точек, изображённых на рисунках 13.3 и 13.4, являются устойчивыми, а какие неустойчивыми? Проще всего разобраться с узлами и фокусами: это такие особые точки, что все траектории стремятся к ним либо в прямом времени (когда t→+∞), либо в обратном (t→−∞). Если все траектории стремятся к узлу (или фокусу) в прямом времени, то отклонившись немножко от этого положения равновесия мы со временем не только не уйдём от него далеко, но и будем неограниченно приближаться к нему. Мы уже раньше назвали такие особые точки устойчивым узлом и устойчивым фокусом (см. соответствующие картинки в нижнем ряду рис. 13.3) и было бы логично ожидать, что когда мы придумаем определение устойчивости, такие особые точки будут устойчивыми в соответствии с этим определением.

Наоборот, если все траектории стремятся к положению равновесию в обратном времени, то в прямом времени они уходят от него. В этом случае, если мы чуть-чуть «промахнёмся» мимо особой точки, то попадём на одну из таких убегающих траекторий и уйдём достаточно далеко от особой точки. Это соответствует неустойчивому фокусу и узлу (верхний ряд на рис. 13.3).

Посмотрим теперь на седло. Большинство траекторий седла имеют форму гипербол: они проходят вблизи седла, но со временем отдаляются от него, приближаясь к отталкивающему собственному направлению. Они не стремятся к седлу ни в прямом, ни в обратном времени. Однако, так ведут себя не все траектории: среди них есть так называемые сепаратрисы, проходящие вдоль собственных направлений и стремящиеся к седлу в прямом или обратном времени.

Точки (±π,0) на фазовом портрете маятника похожи на седла (хотя они не являются линейными особыми точками). Они соответствуют положениям равновесия, при которых маятник направлен вертикально вверх и неподвижен. Понятно, что такое положение равновесия трудно назвать устойчивым: малейшее отклонение маятника от вертикали скорее всего приведёт к тому, что он придёт в движение и через какое-то время уйдёт далеко от вертикального положения равновесия. Логично ожидать, что такие положения равновесия (и вообще любые седловые особые точки) будут неустойчивыми с точки зрения любого разумного определения устойчивости.

Наконец, рассмотрим особые точки типа «центр». Они похожи на положения равновесия (0,0) для математического маятника. При этом маятник направлен вертикально вниз и неподвижен. Небольшое отклонение маятника от такого положения приведёт к тому, что он начнёт колебаться — на фазовом портрете это соответствует замкнутой траектории, похожей на окружность. Чем меньше исходное отклонение, тем меньше амплитуда колебаний. Устойчиво ли такое положение равновесия? Вроде бы, да.

Итак, устойчивый узел, устойчивый фокус и центр устойчивы, неустойчивый узел, неустойчивый центр и седло — неустойчивы. Остаётся придумать математическое определение устойчивости, которое бы не противоречило нашей интуиции.

13.2Придумываем определение устойчивости

Рассмотрим дифференциальное уравнение

˙x=v(x).(13.2)

Пусть точка x∗ является положением равновесия, то есть v(x∗)=0. Пусть x=φ(t;x0) — решение этого уравнения с начальным условием φ(0;x0)=x0.

Упражнение 1. Придумайте определение устойчивости особой точки x∗.

Это упражнение очень полезно сделать перед чтением последующего текста: даже если ваши попытки окажутся неудачными, они помогут глубже понять правильное определение устойчивости. На лекциях в этом месте мы всегда играем в такую игру: аудитория пытается придумать определение, а потом мы обсуждаем, почему оно оказывается неправильным. Вот пара примеров таких попыток.

Определение 1. (Неверное.) Особая точка x∗ называется устойчивой, если для любого начального условия x0, достаточно близкого к x∗, соответствующая траектория стремится к особой точке x∗. Иными словами, существует такое ε>0, что для всякого начального условия x0∈Uε(x∗) (здесь как обычно Uε(x∗) — это ε-окрестность точки x∗) выполняется следующее: limt→+∞φ(t;x0)=x∗.

Вопрос 1. Почему это определение — не то, которое мы хотим?

  Узнать ответ

Верный ответ. Например, особая точка типа «центр» согласно такому определению является неустойчивой, а нам бы хотелось, чтобы она была устойчивой.

Определение 2. (Снова неверное.) Особая точка x∗ называется устойчивой, если для любого начального условия x0, достаточно близкого к x∗, соответствующая траектория не уходит от x∗ слишком далеко. Иными словами, существует такое ε>0, что для всякого начального условия x0∈Uε(x∗) выполняется следующее: ρ(φ(t,x0),x∗)≤M, где ρ(x,y) — расстояние (в какой-то метрике) между x и y, а M — какая-то константа.

Вопрос 2. Почему это определение тоже не подходит?

  Узнать ответ

Верный ответ. Рассмотрим уравнение на прямой ˙x=−x(x−1)(x+1). Точка 0 является особой, если x∈(0,1), то ˙x>0, а если x∈(−1,0), то ˙x<0. Отклонившись от точки 0 чуть-чуть мы начнём отклоняться от неё всё сильнее, однако не уйдём дальше точки 1 или −1, см. рис. 13.5. В то же время, сколь малым ни было бы наше отклонение от 0, траектория уйдёт от 0 достаточно далеко (на расстояние порядка 1). Поэтому точка 0 не должна быть устойчивой, а по предложенному определению была бы.

Рис. 13.5: Фазовые кривые (слева) и интегральные кривые (справа) для уравнения ˙x=−x(x−1)(x+1).

Определение 3. (Опять неверное!) Особая точка x∗ называется устойчивой, если существует такое ε>0, что любая траектория, стартующая в ε-окрестности точки x∗, не покидает эту окрестность. Иными словами, для всякого начального условия x0∈Uε(x∗) выполняется следующее: φ(t,x0)∈Uε(x∗).

Вопрос 3. Почему и это определение не подходит?

  Узнать ответ

Верный ответ. Рассмотрим особую точку типа «центр», но пусть фазовые кривые являются не окружностями, а вытянутыми по горизонтали эллипсами, см. рис. 13.6. Нарисуем какую-нибудь окрестность точки (0,0): для стандартной метрики она будет иметь форму круга. Траектории, стартующие вблизи верхней точки этого круга покидают эту окрестность из-за вытянутости эллипсов. Таким образом, данная особая точка была бы неустойчивой по нашему «определению», вопреки ранее принятым решениям.

Ну что же, дадим, наконец, и верное определение.

Определение 4. (Теперь верное.) Особая точка x∗ называется устойчивой по Ляпунову, если для всякого ε>0 найдётся такое δ>0, что для всякого начального условия x0∈Uδ(x∗), решение с этим начальным условием не покинет ε-окрестность точки x∗ (то есть для всякого t>0, φ(t,x0)∈Uε(x∗)).

Это определение похоже на определение предела: строго говоря, это определение равномерного предела семейства функций. Его можно понимать так: для всякой целевой окрестности можно выбрать окрестность поменьше, такую, что все траектории, стартующие в этой маленькой окрестности, не покинут целевую. Условие о том, что рассматриваются только значения t>0, очень важное — нас интересует, что происходит в прямом времени (при t→+∞), а не в обратном.

13.3Используем определение устойчивости по Ляпунову

Проверим, что для тех точек, которые мы обсуждали, определение устойчивости по Ляпунову согласуется с нашими интуитивными представлениями.

13.3.1Устойчивый узел

Сначала рассмотрим устойчивый линейный узел. Перейдём в нормализующие координаты (соответствующие собственному базису). Система примет вид

˙x=−λx˙y=−μy,

где λ>0 и μ>0. В любой момент времени обе координаты убывают по модулю, следовательно, убывает и расстояние до нуля. Значит в определении устойчивости для всякого ε можно положить δ=ε: любая траектория, стартующая в ε-окрестности нуля, не покидает эту ε-окрестность.

13.3.2Центры

Рассмотрим далее особую точку типа «центр». Её траекториями могут быть достаточно вытянутые эллипсы: точка, движущаяся вдоль такой траектории может как приближаться, так и удаляться от начала координат.

Тем не менее, особая точка является устойчивой по Ляпунову. Действительно, если нам дали черную окрестность, то красной окрестности будет недостаточно: существуют траектории, начинающиеся внутри красной окрестности, но покидающие чёрную. Зато фиолетовой окрестности нам хватит: выбирая любое начальное условие внутри фиолетового круга мы никогда не сможем выйти за черный круг. Можно аккуратно показать, что для любого чёрного круга найдётся свой фиолетовый.

13.3.3Седло

Рассмотрим теперь особую точку вида седло:

Сколь бы малую δ-окрестность мы бы ни выбрали, эту окрестность пересекают траектории из семейства гипербол, уходящие далеко от седла. Из этого следует, что седло является неустойчивым.

13.4Асимптотическая устойчивость

Когда мы обсуждали вопрос об «интуитивной» устойчивости линейных особых точек, у нас не возникло никаких сомнений по поводу узлов, фокусов и сёдел. С центрами всё не так однозначно. С одной стороны, траектории, близкие к особой точке, не уходят слишком далеко, и это вроде бы соответствует нашим представлениям об устойчивости и согласуется с определением устойчивости по Ляпунову. С другой стороны, нам может потребоваться более сильное условие: чтобы со временем траектория не просто не уходила далеко от особой точки, но и приближалась к ней. Это условие даёт нам определение асимптотической устойчивости.

Определение 5. Особая точка x∗ называется асимптотически устойчивой, если она устойчива по Ляпунову и существует такое δ>0, что для всякого начального условия x0∈Uδ(x∗) верно следующее: limt→+∞φ(t,x0)=x∗.

Заметим, что определение 5 очень похоже на неверное определение 1: разница состоит в том, что в определение асимптотической устойчивости явно входит требование устойчивости по Ляпунову. Может быть, достаточно только условия на предел? Оказывается, нет: можно построить пример системы, у которой имеется такая особая точка, что любая траектория, стартующая вблизи этой точки, возвращается к ней, но при этом может уйти достаточно далеко — и таким образом особая точка не является устойчивой по Ляпунову.

Упражнение 2. Рассмотрим дифференциальное уравнение, в полярных координатах задающееся следующим образом:

˙φ=sin(φ)+1,˙r=r(1−r).

1. Построить фазовый портрет в координатах (r,φ) и (x,y).
2. Что можно сказать о поведении решений при t→+∞?
3. Является ли положение равновесия (r=1,φ=0) асимптотически устойчивым?
4. Устойчивым по Ляпунову?

13.5Теорема об устойчивости по первому приближению

Доказывать устойчивость особой точки, пользуясь только определением, обычно не очень просто. К счастью, существует теорема, которая сильно упрощает решение задач такого типа.

Теорема 1. (Ляпунова, об устойчивости по первому приближению.)

Для особой точки x∗ системы дифференциальных уравнений (13.2) рассмотрим матрицу Якоби:

A=∂v∂x∣∣∣x=x∗.

Пусть собственные значения матрицы A равны λ1,…,λn.

1. Если все собственные значения имеют отрицательные вещественные части, то есть для всех i=1,…,n, Re(λi)<0 то особая точка асимптотически устойчива.
2. Если хотя бы одно собственное значение имеет положительную вещественную часть, то есть найдётся такое i, что Re(λi)>0, то особая точка не является устойчивой по Ляпунову.

Между двумя утверждениями теоремы есть «зазор»: бывают такие особые точки, про устойчивость которых теорема не говорит ничего.

Вопрос 4. Что вы можете сказать о собственных значениях особых точек, для которых теорема об устойчивости не говорит ничего?

  Узнать ответ

Верный ответ. Это особые точки, у которых есть собственные значения, лежащие на мнимой оси, то есть имеющие нулевую вещественную часть, а также, быть может, есть какое-то количество собственных значений с отрицательной вещественной частью.

Полное доказательство этой теоремы довольно сложное и мы не будем здесь его приводить. Рассмотрим лишь случай линейных уравнений; после этого поверить в общий случай можно будет легко, зная, что поведение нелинейных уравнений похоже на поведение соответствующих линейных.

Доказательство. (Набросок доказательства для линейных уравнений)

Начнём со второй части. Если есть хотя бы одно собственное значение λj с положительной вещественной частью, ему соответствует некоторый собственный вектор v и у уравнения есть решение вида ceλjtv. Если Reλj>0, экспонента возрастает при t→+∞, и существует далеко уходящее решение со сколь угодно близким к началу координат начальным условием (параметр c можно делать сколь угодно маленьким). Значит, особая точка не является устойчивой по Ляпунову.

Докажем теперь первую часть. Если все собственные числа имеют отрицательную вещественную часть, и матрица диагонализируема, вдоль всех направлений идёт приближение к нулю, и особая точка асимптотически устойчива.

Доказательство для жордановой клетки более сложное. Рассмотрим уравнение x=Jλx, где Jλ — жорданова клетка с собственным значением λ, причём Reλ<0. Рассмотрим для простоты случай вещественного λ, то есть λ<0. (Случай комплексного λ рассматривается аналогично, но с некоторыми техническими усложнениями.)

Идея состоит в том, чтобы доказать, что траектория, войдя в произвольный круг радиуса ε, никогда из него не выйдет. Чтобы это утверждение стало верным, нужно выбрать правильную систему координат. (В исходной системе координат вместо кругов нужно брать эллипсы.)

Заметим, что выбором координат можно единички в жордановой форме заменить на произвольное число μ. Действительно, рассмотрим такую диагональную матрицу перехода:

C=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝100⋯00μ0⋯000μ2⋯0⋮⋮⋮⋱⋮000⋯μn−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠

Прямое вычисление показывает, что

C−1JλC=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝λμ0⋯000λμ⋯0000λ⋯00⋮⋮⋮⋱⋮⋮000⋯λμ000⋯0λ⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠

В дальнейшем мы будем работать в новой системе координат. Число μ подберем позднее.

Теперь рассмотрим функцию ρ(x)=∥x∥2=x21+…+x2n. Мы хотим доказать, что Lvρ(x)<0 для всех x≠0, то есть производная вдоль векторного поля от функции ρ везде отрицательна (кроме нуля). Это будет означать, что в любой момент времени расстояние до начала координат уменьшается. Имеем:

Lvρ=n∑k=1∂ρ∂xkvk=n−1∑k=12xk(λxk+μxk+1)+2λx2n=λn∑k=1x2k+μn−1∑k=1xkxk+1.

Первое слагаемое является отрицательным, поскольку λ<0. Мы хотим подобрать такое маленькое μ, чтобы второе слагаемое по модулю было меньше первого. Это всегда можно сделать, поскольку

xkxk+1≤12(x2k+x2k+1)<n∑k=1x2k

Выбирая μ=1nλ, получаем требуемое.∎

---

← Предыдущая глава Следующая глава →

обыкновенных дифференциальных уравнений — Нахождение интегральных кривых векторного поля $x\partial y- y\partial x$

Задавать вопрос

спросил 4 года 9 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 2к раз 92}=-x$

и его решение представляет собой линейную комбинацию $sin$ и $cos$, но этот доклад слишком абстрактен для меня, я бы хотел, чтобы кто-нибудь дал мне точное решение этой задачи. 2=K$$

$\endgroup$

Некоторые интегральные кривые с новой рамкой

1 Введение

Дифференциальная геометрия использует технику исчисления для понимания форм и их свойств. Теория кривых является важным подразделом дифференциальной геометрии в смысле форм. Поскольку общие типы кривых необходимы для понимания, чтобы выйти за рамки этой теории, исследователи работают в этой области в течение длительного времени.

Пока мы изучаем теорию кривых, каркасы кривых необходимы для исследования их характеристик. Для пространственной кривой α в трехмерном евклидовом пространстве Е3 , адаптированные кадры представляют собой набор троек {v1,v2,v3} , где ви образуют ортонормированный базис Е3 такой, что v1 касается α и v2, v3 выбраны разрешительно на плоскости, которая нормальна к v1 . Несколько примеров адаптированных фреймов уже были импутированы. Наиболее известной и используемой является рама Френе, которая представляет собой подвижную рамку. Хотя это хорошо заявлено, в случае, когда вторая производная кривой равна нулю, она не определена, и ее вращение вокруг касательной к общей кривой позвоночника часто приводит к нежелательному искривлению в дизайне движения или моделировании поверхности сдвига. Подвижная система отсчета, которая не вращается вокруг мгновенной касательной к кривой позвоночника, называется вращающейся минимизирующей системой отсчета (RMF). RMF определяется непрерывно для любой регулярной кривой позвоночника. Благодаря свойству минимальной крутки и устойчивому поведению при наличии точек перегиба RMF предпочтительнее системы Френе во многих приложениях в компьютерной графике [1]. Несмотря на свою предпочтительность, RMF сложно вычислить. Кроме того, альтернативный фрейм, который называется фреймом Бишопа, определен Р. Л. Бишопом [2]. Каркас Бишопа представляет собой параллельный транспортный кадр. Параллельная транспортная система отсчета — это альтернативный подход к определению движущейся системы отсчета, который хорошо определен, даже если кривая имеет нулевую вторую производную [3].

Недавно Деде [4] определил новый фрейм, который называется фреймом кривой Френе. Этот новый кадр легко вычисляется с точки зрения использования перекрестного произведения первой и высшей производных кривой для вычисления вектора бинормалей кривой. Преимущество этого фрейма в том, что он уменьшает количество особых точек, где они не могут быть определены в фрейме Френе. Кроме того, это уменьшает нежелательное вращение вокруг касательного вектора кривой. Кроме того, Деде и соавт. В [5] указан q-репер вдоль пространственной кривой, но этот репер не инвариантен относительно евклидова вращения.

Ассоциированные кривые изучались преимущественно многими исследователями. Ассоциированная кривая состоит из другой кривой, и ее поведение можно исследовать с помощью связи между основной кривой и связанной с ней кривой. Некоторыми иллюстрациями этих кривых являются сопряжения эвольвента-эволюция, сопряжения Бертрана, пары Мангейма, сферические изображения и интегральные кривые.

В [6] Чой и Ким ввели ассоциированные кривые кривой Френе, которые они назвали главной (бинормальной) кривой направления и главной (бинормальной) кривой донора. Они дали взаимосвязь между направленными кривыми и главной кривой. В [7] Масит и Дюльдюл определили новые ассоциированные кривые, которые являются кривой W-направления и W-спрямляющей кривой с помощью вектора Дарбу кривой Френе, кривой V-направления, которая связана с кривой, лежащей на ориентированной поверхности в Е3 . Более того, Körpinar et al. изучал ассоциированные кривые с репером Бишопа в Е3 [8]. Ассоциированные кривые согласно каркасу Бишопа типа 2 были даны Йылмазом в [9]. ].

Интегральные кривые представляют интерес, поскольку они касаются в каждой точке векторного поля, которое используется для формирования кривой. Интегральная кривая — это параметрическая кривая, изображающая частное решение дифференциального уравнения или системы уравнений. В случае X векторное поле и α(t) параметрическая кривая, α(t) является интегральной кривой X , если это решение дифференциального уравнения α′(t)=X(α(t)). В литературе имеются различные исследования по этому вопросу (см. [6–10]).

С точки зрения дифференциальной геометрии спираль — это кривая, касательный вектор которой образует постоянный угол с фиксированным направлением, называемым осью спирали. Известный результат, указанный Ланкре в 1802 г. (см. [11]), состоит в том, что необходимым и достаточным условием того, чтобы кривая была общей спиралью, является соотношение (гармоническая кривизна) τκ постоянна, где κ и т обозначают кривизну и кручение кривой соответственно. Если оба κ и т являются ненулевыми константами, то кривая называется круговой спиралью. Спираль была обобщенной, которую Хейден назвал «обобщенной спиралью» [12]. Баррос определил общую спираль в форме трехмерного реального пространства, используя понятие векторного поля Киллинга вдоль кривой, и доказал теорему Ланкре для общих спиралей в этой пространственной форме [13]. В литературе можно найти множество исследований о спиралях [14–18].

В этой статье мы изучаем некоторые новые интегральные кривые, которые являются ассоциированными кривыми. Построим их по новому реперу полиномиальной пространственной кривой. Мы задаем их свойства с помощью аппарата Френе и нового репера и кривизны. Мы также характеризуем их в терминах пар Бертрана, пар Мангейма, пар эвольвента-эволюта и кривых Сальковского.

2 Предварительные занятия

Пусть α(t) быть регулярной пространственной кривой и невырожденным условием α′×α″≠0 . Тогда три ортогональных векторных поля, которые называются кадром Френе, определяются как

(2.1) t=α′∥α′∥,n=b×t,b=α′×α″∥α′×α″∥,

, где t — тангенс, н является главной нормой и б бинормальное векторное поле. Известные формулы Френе имеют вид

(2.2) t′n′b′=∥α′(t)∥0κ0−κ0τ0−τ0tnb,

где кривизна κ и кручение т кривой составляют (см. [19–21])

(2.3) κ=∥α′×α″∥∥α′∥3 и τ=det(α′,α″,α′″)∥α′×α″∥2.

Новый кадр, который называется Flc-кадр (фрейм, похожий на кривую Френе), определен Деде в [4]. Концепция Flc-фрейма приведена ниже.

Пусть α(t) — полиномиальная пространственная кривая степени n (а именно, α кривая в пространстве с полиномиальными компонентами). Мы предполагаем, что α(t) является регулярным и α′(t)≠0. Векторные поля Flc-фрейма следующие:

(2.4) t=α′∥α′∥,D1=α′×α(n)∥α′×α(n)∥,D2=D1×t,

, где t — единичный касательный вектор, Д1 является бинормальным вектором и Д2 — главный нормальноподобный вектор. Здесь штрих ′ указывает на производную по т и (н) является n -й производной.

Кривизны Flc-рамки d1 , d2 и d3 даны

(2,5) d1=〈t′,D2〉v,d2=〈t′,D1〉vandd3=〈D′2,D1〉v,

, где v=∥α′∥.

Также формулы типа Френе выражаются в [4] как

(2.6) t’D2’D2’=v0d1d2-d10d3-d2-d30tD2D1.

Отношения между кривой Френе и аппаратом кривой Френе следующие:

(2.7) d1=κcosθ,d2=−κsinθ,d3=dθ+τ

и

(2.8) D2=cosθn+sinθb, D1=−sinθn+cosθb,

, где θ угол между главным вектором нормали н и главный нормальный вектор Д2 .

Кроме того, Hacısalihoğlu [26] дал пары эвольвента-эволюта кривой как: если касательные векторы двух кривых ортогональны (а именно, 〈Т,Т*〉=0 , где Т и Т* являются касательными векторами кривых), то они называются эвольвентно-эвольвентными кривыми.

3 Новые интегральные кривые

В этом разделе мы определяем несколько новых интегральных кривых, которые называются «направленными кривыми». Затем мы даем аппарат Френе этих кривых с помощью нового репера и кривизны.

Теперь мы сформулируем теоремы, касающиеся обоих D2 — кривая направления и Д1 — кривая направления.

Теперь давайте переформулируем векторные поля Френе D2 — кривая направления β и D1 — кривая направления λ . Используя уравнения (3.2) и (3.5) и связь между аппаратом Френе и новыми векторными полями, существующими в уравнении. (2.8), имеем

(3.7) tλ=cosθn+sinθb,nλ=−d1d12+d32t−d3sinθd12+d32n+d3cosθd12+d32b,bλ=d3d12+d32t−d1sinθd12+d32n+d1cosθd12+d32b

и

tβ=−sinθn+cosθb,nβ=−d2d22+d32t−d3cosθd22+d32n−d3sinθd22+d32b,bβ=d3d22+d32t−d2cosθd22+d32n−d2sinθd22+d32b.

Рисунок 1

Кривая α .

Рисунок 2

Д ₁ — кривая направления α .

Рисунок 3

Д ₂ — кривая направления α .

Каталожные номера

[1] Венпин Ван , Берт Юттлер , Даю Чжэн , и Ян Лю , Вычисление кадров, минимизирующих вращение, ‎ACM Trans. График 27 (2008), вып. 1, ст. 2, 10.1145/1330511.1330513.Поиск в Google Scholar

[2] Ричард Л. Бишоп , Существует более одного способа обрамления кривой, амер. Мат. Ежемесячно 82 (1975), вып. 3, 246–251.10.1080/00029890.1975.11993807Поиск в Google Scholar

[3] Эндрю Дж. Хэнсон и Хуэй Ма , Параллельный транспортный подход к построению кривых, Тех. Республика, Университет Индианы, Блумингтон, Индиана, 1995. Поиск в Google Scholar

[4] Мустафа Деде , Новое представление трубчатых поверхностей, Houston J. Math. 45 (2019), вып. 3, 707–720. Поиск в Google Scholar

[5] Мустафа Деде , Джумали Экичи , и Али Гёргюлю , Направленный q-кадр вдоль пространственной кривой, IJARCSSE 5 (2015), нет. 12, 775–780. Поиск в Google Scholar

[6] Джин Хо Чой и Янг Хо Ким , Ассоциированные кривые кривой Френе и их приложения, Appl. Мат. вычисл. 218 (2012), вып. 18, 9116–9124.10.1016/j.amc.2012.02.064Поиск в Google Scholar

[7] Несибе Масит и Мустафа Дюльдюл , Некоторые новые связанные кривые кривой Френе в E3 и E4 , Турецкий J. Math. 38 (2014), 1023–1037.10.3906/mat-1401-85Поиск в Google Scholar

[8] Талат Кёрпинар , Мухаммед Т. Сарыайдын , и Эсин Турхан , Ассоциированные кривые в соответствии с репером Бишопа в евклидовом трехмерном пространстве, Adv. Модель. Оптим. 15 (2013), вып. 3, 713–717. Поиск в Google Scholar

[9] Суха Йылмаз , Характеристики некоторых ассоциированных и специальных кривых для репера Бишопа типа 2 в E3 , Университет Кыркларели J. Eng. науч. 1 (2015), 66–77. Поиск в Google Scholar

[10] Джон М. Ли , Введение в гладкие многообразия – Интегральные кривые и потоки, Тексты для выпускников по математике, Нью-Йорк, 2003 г., стр. 205–248.10.1007/9.78-0-387-21752-9Поиск в Google Scholar

[11] Дирк Дж. Струик , Лекции по классической дифференциальной геометрии, Дувр, Нью-Йорк, 1988. Поиск в Google Scholar

[12] Х. А. Хайден , Об общей спирали в римановом n-пространстве, Proc. Лондонская математика. соц. 32 (1931), вып. 2, 37–45. Поиск в Google Scholar

[13] Мануэль Баррос , Общие спирали и теорема Ланкре, Proc. Являюсь. Мат. соц. 125 (1997), вып. 5, 1503–1509.10.1090/S0002-9939-97-03692-7Поиск в Google Scholar

[14] Мануэль Баррос , Анхель Феррандес , Паскуаль Лукас , и Мигель А. Мероно , Общие спирали в трехмерных лоренцевских пространственных формах, Rocky Mountain J. Math. 31 (2001), вып. 2, 373–388.10.1216/rmjm/1020171565Поиск в Google Scholar

[15] Четин Камчи , Казым Иларслан , Левент Кула , и Х. Хилми Хаджисалихоглу , Гармонические кривизны и обобщенные спирали в En , Chaos Solitons Fractals 40 (2009), вып. 5, 2590–2596.10.1016/j.chaos.2007.11.001Поиск в Google Scholar

[16] Надя Шуайеб , Ален Гориели , и Джон Х. Мэддокс , Helices, PNAS 103 (2006), вып. 25, 9398–9403.10.1073/pnas.0508370103Поиск в Google Scholar пабмед ПабМед Центральный

[17] Унвер Чифтчи , Обобщение теоремы Ланкре, J. Geom. физ. 59 (2009), вып. 12, 1597–1603.10.1016/j.geomphys.2009.07.016Поиск в Google Scholar

[18] Эртугрул Оздамар и Х. Хилми Хаджисалихоглу , Характеристика наклонных кривых в евклидовом n-пространстве, Comm. Фак. науч. ун-т Анкара, Сер A1 24 (1975), 15–23.10.1501/Commua1_0000000262Поиск в Google Scholar

[19] Альфред Грей , Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica, 2-е изд., CRC Press, Бока-Ратон, Флорида, 1993. Поиск в Google Scholar

[20] Вольфганг Кюнель , Дифференциальная геометрия кривых-поверхностей-многообразий, 2-е изд., AMS, Providence, 2006. Поиск в Google Scholar

[21] Джон Опря , Дифференциальная геометрия и ее приложения, 2-е изд., The Math. доц. Америки, Вашингтон, 2006 г. Поиск в Google Scholar

[22] Хуили Лю и Фань Ван , партнерские кривые Мангейма в трехмерном пространстве, J. Geom. 88 (2008), 120–126.10.1007/s00022-007-1949-0Поиск в Google Scholar

[23] Хуан Монтерде , Новый взгляд на кривые Сальковского: семейство кривых с постоянной кривизной и непостоянным кручением, Comput. Помощник геом. Design 26 (2009), 271–278.