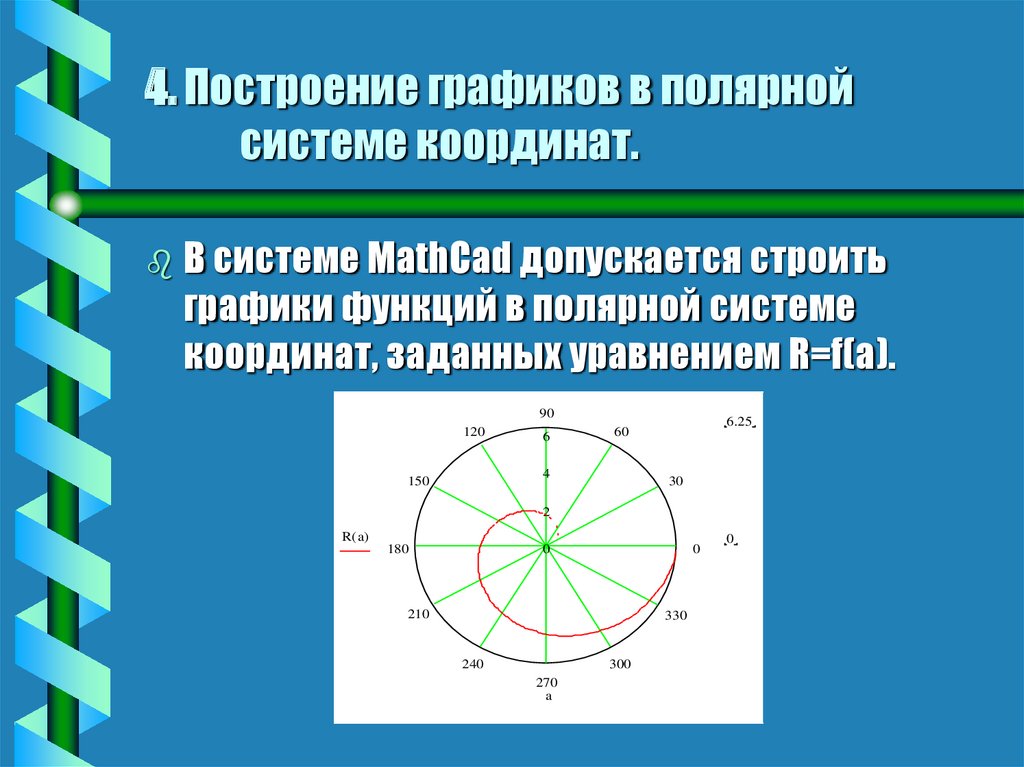
Построение графиков функций в полярной системе координат — Энциклопедия современных знаний
Рисунок 19
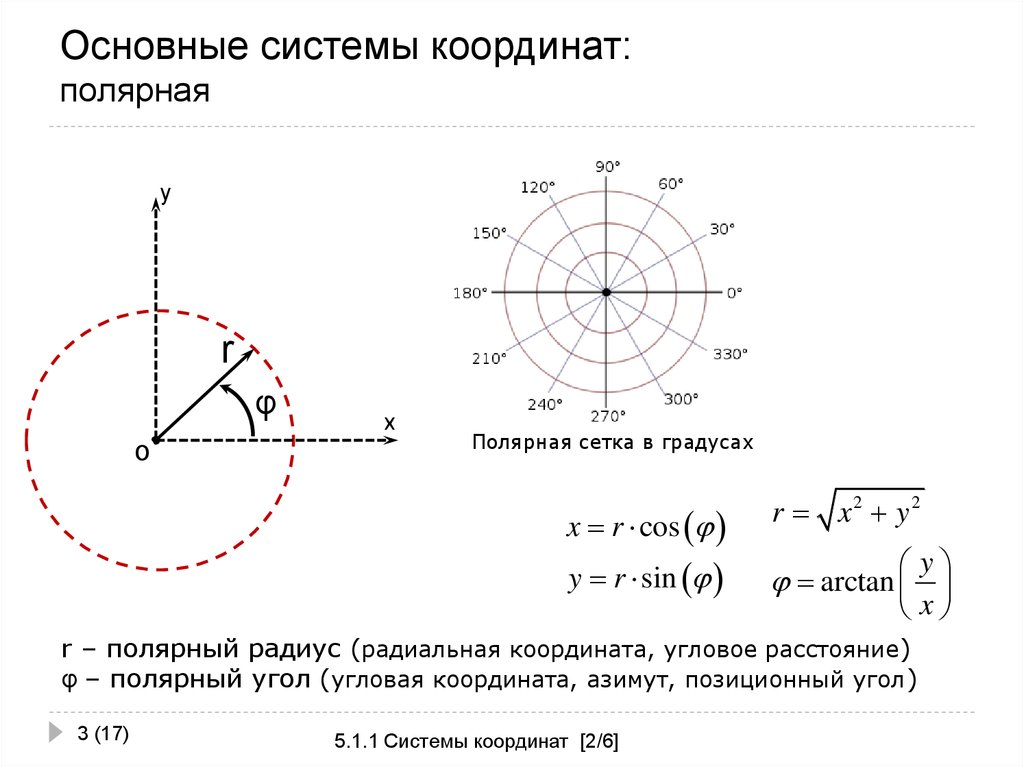
Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой , называемой полярной осью.
Положение точки M в полярной системе координат определяется расстоянием r (полярным радиусом) от точки M до полюса и углом j (полярным углом) между полярной осью и вектором . (рисунок 19).
Полярный радиус и полярный угол составляют полярные координаты точки M , что записывается в виде M(r,j). Полярный угол измеряется в радианах и отсчитывается от полярной оси:
— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Связь между декартовыми и полярными координатами
Пару полярных координат r и j можно перевести в Декартовы координаты x и y по следующим фомулам:
Обратно, полярный радиус r можно найти, зная декартовы координаты x и y , по теореме Пифагора (см. Рис. ??):
,
а полярный угол j в диапазоне [0, 2p), находится при помощи обратной (к тангенсу) тригонометрической функции арктангенс:
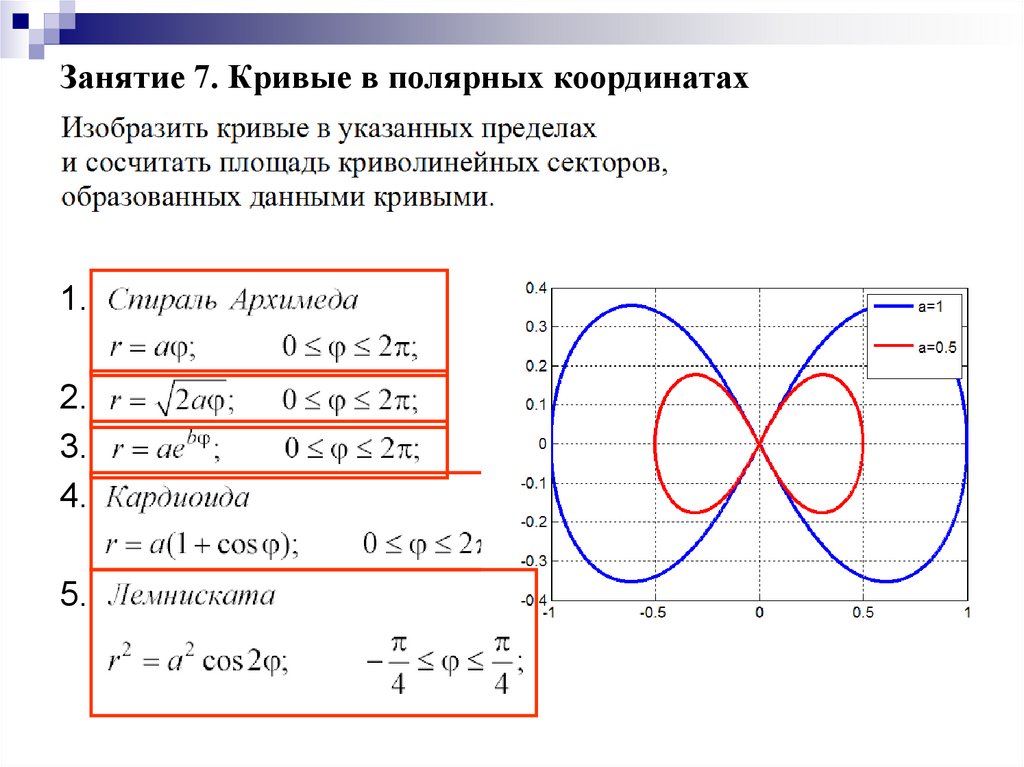
Пример № 2. Построить график функции r(j) = 2.
1. Задаём значения j в градусах в диапазоне [0, 2p] с шагом в 5 градусов с использованием автозаполнения (см. Приложение 1).
2. Перевести j из градусов в радианы с использованием функции РАДИАНЫ (см. Приложение 2).
3. Рассчитать значения r(jрад).
4. По значениям jрад и r(jрад) рассчитать декартовы координаты x и y.
5. По рассчитанным значениям x и y построить график, выбрав тип диаграммы Точечная.
Рисунок 20. Результаты расчёта
Рисунок 21. График функции r(j) = 2
Задание № 4
С помощью пакета Microsoft Excel построить график функций, приведенные в Приложении 5 соответственно варианту.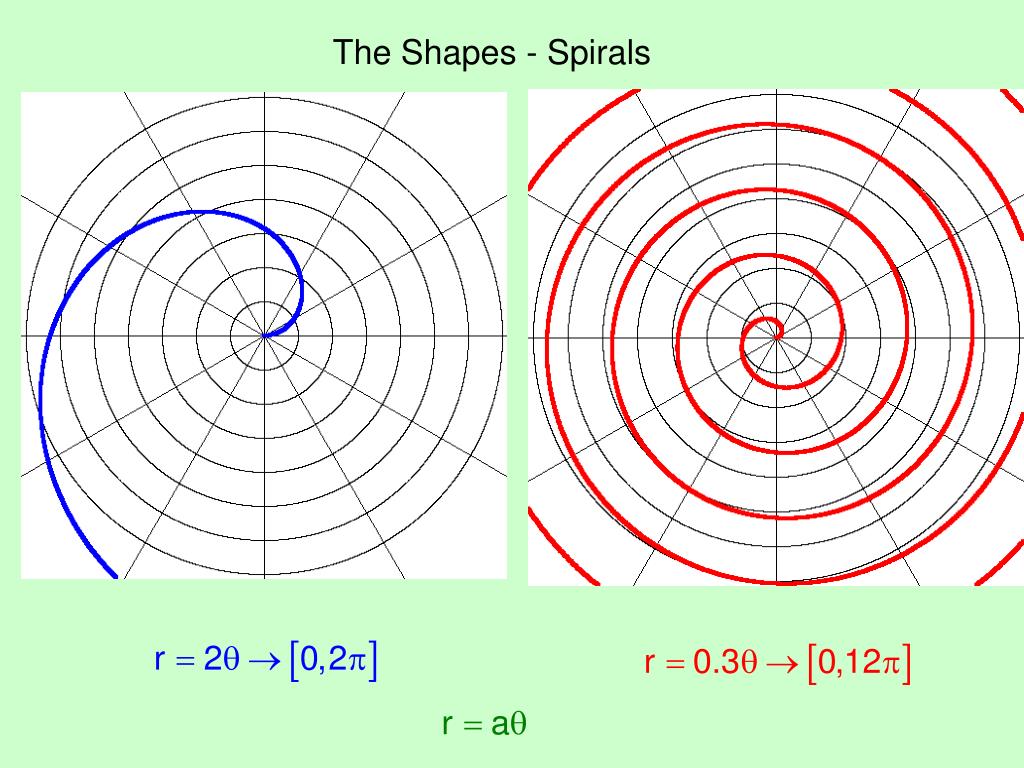 Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести расчётные формулы и результаты расчёта,
d. График построенной функции,
e. Указать полярные координаты точки графика, заданной преподавателем.
Построение графиков функций с использованием логарифмической шкалы.
| расстояния |
Шкала называетсялогарифмической,если метками шкалы являются числа, а расстояния между метками –пропорциональны логарифму отношения величин отмеченных на концах этого отрезка (в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах ). Ни нуль, ни отрицательные числа не могут быть показаны на логарифмической шкале (см. рисунок 22)
Рисунок 22
Логарифмическая шкала исключительно удобна для отображения очень больших диапазонов значений величин.
Пример № 3. Построить график функции . в диапазоне значений [-5, 5] и определить по графику значение функции для х = -3.6 и х = 4.
1. Задаём значения х в диапазоне [-5, 5] с шагом 0.5 с использованием автозаполнения (см. Приложение 1).
2. По заданным х рассчитываем значения функции у.
3. Строим график функции, используя тип диаграммы «точечная» и замечаем, например,что значение функции при отрицательных х очень близко к 0, так что определить его из графика не представляется возможным
Рисунок 23
4. Выделяем ось у.
5. Делаем щелчок правой кнопкой мыши и в раскрывшемся контекстном меню выбираем «формат оси» (см. рисунок 12)
6. В окне «формат оси» помечаем галочкой логарифмическую шкалу.
7. Добавить основные и промежуточные линии сетки.
Результаты представлены на Рисунке 24
Рисунок 24
Из рисунка определяем, что для х = -3.6 значение примерно равно 0.02, а для х = 4 .
6.1.Задание № 5.Построить график функций в диапазоне значений [-10, 10] с шагом 0. 5 . Уметь из графика определять значение функции для указанного (преподавателем) аргумента. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
5 . Уметь из графика определять значение функции для указанного (преподавателем) аргумента. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести графики без использования логарифмической шкалы,
d. Привести графики с использованием логарифмической шкалы,
e. Сравнить результаты.
Математика Без Ху%!ни. Полярные координаты. Построение графика функции.
Похожие статьи.
Построение графика функции, имеющей разрыв
Построение графика функции по заданным параметрам
Построение графиков функций.
Основные принципы построения и использования автоматизированных информационных систем во внешнеэкономической деятельности
Построение графиков функций онлайн
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики
и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн.
| Оператор | Значение |
|---|---|
-
|
вычитание |
*
|
умножение |
/
|
деление |
^n
|
возведение в степень: x^n — x в степени n |
^(1/n)
|
корень степени n: x^(1/n) |
()
|
скобки |
| |
|
скобки модуля: |x| |
Список функций
| Имя | Описание | |
|---|---|---|
log2(x)
|
логарифм по основанию 2 от x | |
lg(x) или log10(x)
|
логарифм по основанию 10 от x | |
log(x;b)
|
логарифм x по основанию b log(x;3) | |
ln(x)
|
натуральный логарифм (логарифм по основанию e (2. x x
|
экспонента от х (e в степени x) |
sqrt(x)
|
квадратный корень из x | |
sign(x)
|
функция знака: -1 если x<0, 1 если x>0 и 0 если x=0 | |
| Тригонометрические функции | ||
sin(x)
|
синус х | |
cos(x)
|
косинус х | |
tan(x)
|
тангенс х | |
ctg(x) или
cot(x)
|
котангенс х | |
arcsin(x) или
asin(x)
|
арксинус х | |
arccos(x) или
acos(x)
|
арккосинус х | |
arctg(x) или
atan(x)
|
арктангенс х | |
arcctg(x) или
acot(x)
|
арккотангенс х | |
sinh(x) или
sh(x)
|
гиперболический синус х | |
cosh(x) или
|
гиперболический косинус х | |
tanh(x) или
th(x)
|
гиперболический тангенс х | |
coth(x) или
cth(x)
|
гиперболический котангенс х | |
asinh(x)
|
гиперболический арксинус х | |
acosh(x)
|
гиперболический арккосинус х | |
atanh(x)
|
гиперболический арктангенс х | |
acoth(x)
|
гиперболический арккотангенс х | |
Встроенные константы
| Имя | Описание |
|---|---|
|
Пи = 3,14.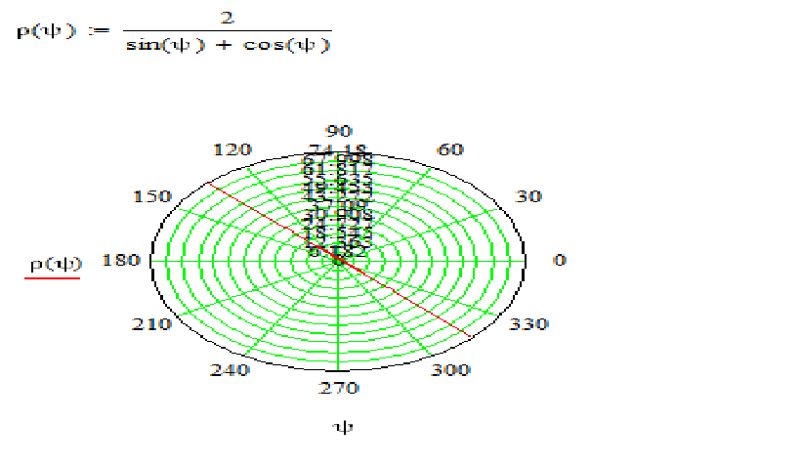 .. ..
|
e
|
e = 2,71828… число Эйлера |
10.3: Полярные координаты — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50235
- OpenStax
- OpenStax
Цели обучения
- Нанесение точек с использованием полярных координат.
- Преобразовать полярные координаты в прямоугольные.
- Преобразовать прямоугольные координаты в полярные.
- Преобразование уравнений между полярной и прямоугольной формами.
- Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.
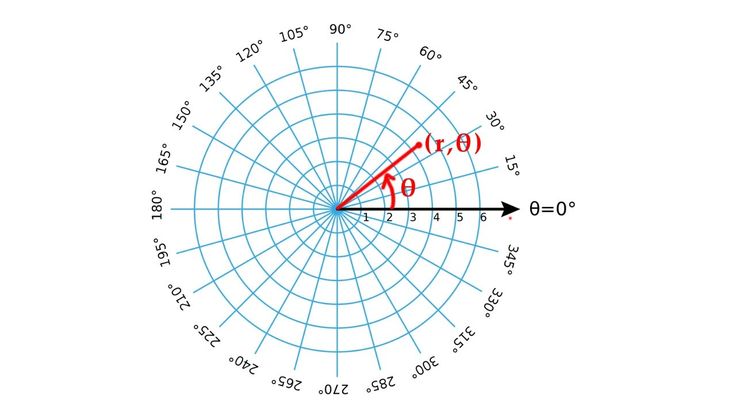
На расстоянии \(12\) километров от порта парусник попадает в непогоду и сбивается с курса ветром силой \(16\) узлов (см. рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Рисунок \(\PageIndex{1}\)
Нанесение точек с использованием полярных координат у)\) в
декартовой координатной плоскости . Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные \((r,\theta)\) и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.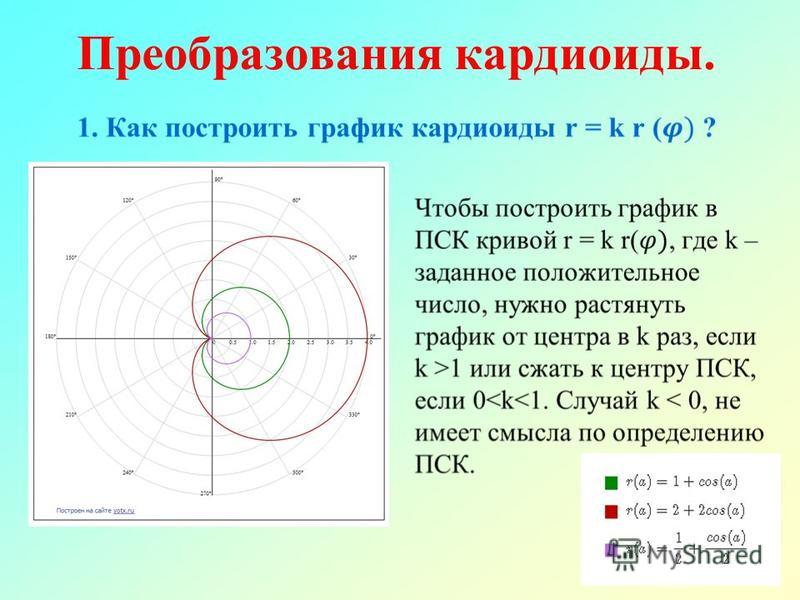
Полярная сетка масштабируется как единичный круг с положительной осью \(x\) — , которая теперь рассматривается как полярная ось, а начало координат — как полюс. Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса. Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\)
Пример \(\PageIndex{1}\): Нанесение точки на полярную сетку
Нанесение точки \(\left(3, \dfrac{\pi}{2}\right)\) на полярной сетке.
Решение
Угол \(\dfrac{\pi}{2}\) находится путем протягивания против часовой стрелки \(90°\) от полярной оси. Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\)
Упражнение \(\PageIndex{1}\)
Постройте точку \(\left(2, \dfrac{\pi}{3 }\right)\) в полярной сетке.
- Ответить
Рисунок \(\PageIndex{4}\)
Пример \(\PageIndex{2}\): Нанесение точки в полярной системе координат с отрицательной составляющей
Нанесение точки \(\left(−2, \dfrac{\pi}{6}\right) \) на полярной сетке.
Решение
Мы знаем, что \(\dfrac{\pi}{6}\) находится в первом квадранте. Однако \(r=−2\). Мы можем построить точку с отрицательным значением \(r\) двумя способами:
- Нанести точку \(\left(2,\dfrac{\pi}{6}\right)\), перемещая dfrac{\pi}{6}\) в направлении против часовой стрелки и продолжение направленного отрезка \(2\) единиц в первый квадрант.
 Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант;
Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант; - Переместите \(\dfrac{\pi}{6}\) в направлении против часовой стрелки и нарисуйте направленный отрезок от полюса \(2\) единиц в отрицательном направлении в третий квадрант.
См. рисунок \(\PageIndex{5a}\). Сравните это с графиком полярной координаты \((2,π6)\), показанным на рисунке \(\PageIndex{5b}\).
Рисунок \(\PageIndex{5}\)
Упражнение \(\PageIndex{2}\)
Постройте точки \(\left(3,−\dfrac{\pi}{ 6}\справа)\) и \(\слева(2,\dfrac{9\pi}{4}\right)\) на той же полярной сетке.
- Ответить
Рисунок \(\PageIndex{6}\)
Преобразование полярных координат в прямоугольные
Когда задан набор полярных координат , нам может потребоваться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными \(x\), \(y\), \(r\) и \(\theta\).
Для этого мы можем вспомнить отношения, существующие между переменными \(x\), \(y\), \(r\) и \(\theta\).
\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \ sin \theta\)
Если опустить перпендикуляр из точки плоскости на ось x-, получится прямоугольный треугольник, как показано на рисунке \(\PageIndex{7}\). Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.
Рисунок \(\PageIndex{7}\)
ПРЕОБРАЗОВАНИЕ ПОЛЯРНЫХ КООРДИНАТ В ПРЯМОУГОЛЬНЫЕ
Преобразование полярных координат \((r, \theta)\) в прямоугольные координаты \((x, y)\) , пусть
\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]
\[\sin \theta=\dfrac{y}{r}\rightarrow y =r \sin\theta\]
Как: данные полярные координаты преобразовать в прямоугольные координаты.

- Учитывая полярную координату \((r,\theta)\, запишите \(x=r \cos \theta\) и \(y=r \sin \theta\).
- Оценить \(\cos \theta\) и \(\sin \theta\).
- Умножьте \(\sin\theta\) на \(r\), чтобы найти \(y\) — координату прямоугольной формы.
Пример \(\PageIndex{3A}\): запись полярных координат в виде прямоугольных координат
Запись полярных координат \(\left(3,\dfrac{\pi}{2}\right)\) в виде прямоугольных координат.
Решение
Используйте эквивалентные соотношения.
\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y& = 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]
Прямоугольные координаты \((0,3)\). См. рисунок \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\)
Пример \(\PageIndex{3B}\): запись полярных координат в виде прямоугольных координат
Запишите полярные координаты \((−2,0)\) в виде прямоугольных координат.
Решение
См. рисунок \(\PageIndex{9}\). Записав полярные координаты в виде прямоугольника, мы имеем
\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]
Прямоугольные координаты также равны \((−2,0)\).
Рисунок \(\PageIndex{9}\)
Упражнение \(\PageIndex{3}\)
Запишите полярные координаты \(\left(−1,\dfrac{2\pi}{3}\right)\) в виде прямоугольных координат.
- Ответить
\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)
Преобразование прямоугольных координат в полярные координаты
Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 92\)
\(\tan \theta=\dfrac{y}{x}\)
Рисунок \(\PageIndex{10}\)
Пример \(\PageIndex{4} \): запись прямоугольных координат в виде полярных координат
Преобразование прямоугольных координат \((3,3)\) в полярные координаты.
Решение
Мы видим, что исходная точка \((3,3)\) находится в первом квадранте. Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это дает
92}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]Итак, \(r=3\ sqrt{2}\) и \(\theta=\dfrac{\pi}{4}\), что дает нам полярную точку \((3\sqrt{2},\dfrac{\pi}{4})\ ). См. рисунок \(\PageIndex{11}\).
Рисунок \(\PageIndex{11}\)
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) и \(\left(3\sqrt{2},−\dfrac{ 7\pi}{4}\right)\) будет совпадать с исходным решением \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) указывает на движение против часовой стрелки на \(\pi\), что прямо противоположно \(\ dfrac{\pi}{4}\). Радиус выражается как \(−3\sqrt{2}\).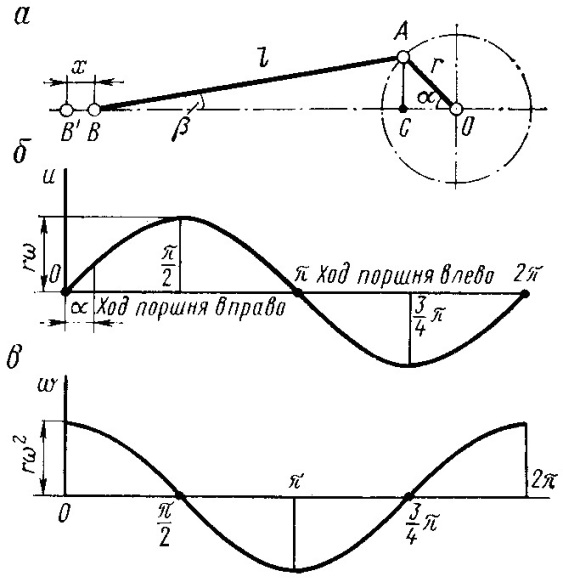 Однако угол \(\dfrac{5\pi}{4}\) расположен в третьем квадранте, и, поскольку \(r\) отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант . Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Однако угол \(\dfrac{5\pi}{4}\) расположен в третьем квадранте, и, поскольку \(r\) отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант . Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Преобразование уравнений между полярной и прямоугольной формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.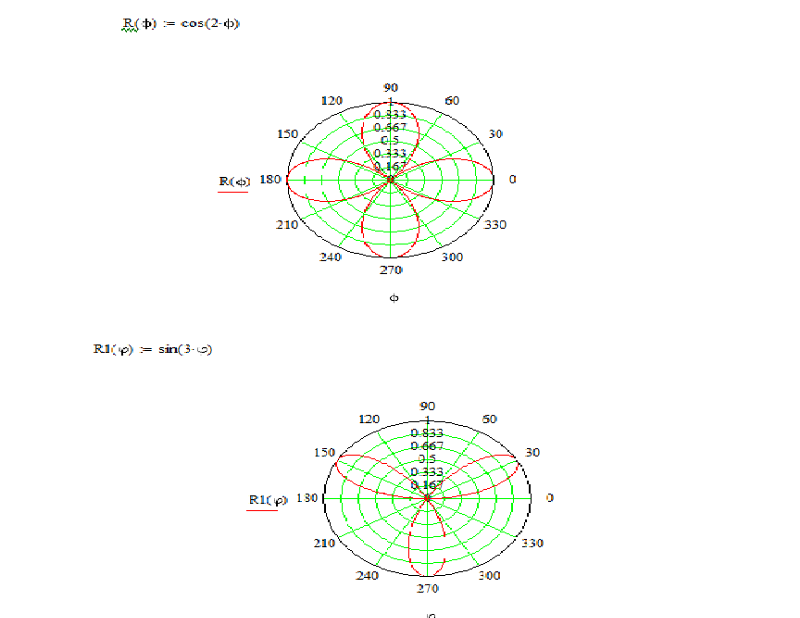
Как: Имея уравнение в полярной форме, начертите его с помощью графического калькулятора
- Измените РЕЖИМ на POL , представляя полярную форму.
- Нажмите кнопку Y= , чтобы вызвать экран, позволяющий ввести шесть уравнений: \(r_1\), \(r_2\),…, \(r_6\).
- Введите полярное уравнение, установите его равным \(r\).
- Нажмите ГРАФИК .
Пример \(\PageIndex{5A}\): запись декартова уравнения в полярной форме 92=6y\) (b) полярная форма \(r=6 \sin \theta\)
Декартово или прямоугольное уравнение наносится на прямоугольную сетку, а полярное уравнение наносится на полярную сетку. Ясно, что графики идентичны.
Упражнение \(\PageIndex{4A}\):
Переписывание декартова уравнения в полярной форме
Перепишите декартово уравнение \(y=3x+2\) как полярное уравнение.
- Ответить
Мы будем использовать соотношения \(x=r \cos \theta\) и \(y=r \sin \theta\).
 92\) в полярной форме.
92\) в полярной форме.- Ответить
\(r=\sqrt{3}\)
Идентификация и построение полярных уравнений путем преобразования в прямоугольные уравнения
Мы научились преобразовывать прямоугольные координаты в полярные координаты и увидели, что точки действительно совпадают. Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Пример \(\PageIndex{6A}\): построение графика полярного уравнения путем преобразования в прямоугольное уравнение
Преобразование полярного уравнения \(r=2 \sec \theta\) в прямоугольное уравнение и построение соответствующего ему графика .
Решение
Преобразование
\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \ theta &=2 \\ x &=2 \end{align*}\]
Обратите внимание, что уравнение \(r=2 \sec \theta\), нарисованное на полярной сетке, явно совпадает с вертикальной линией \( x=2\), нарисованный на прямоугольной сетке (см.
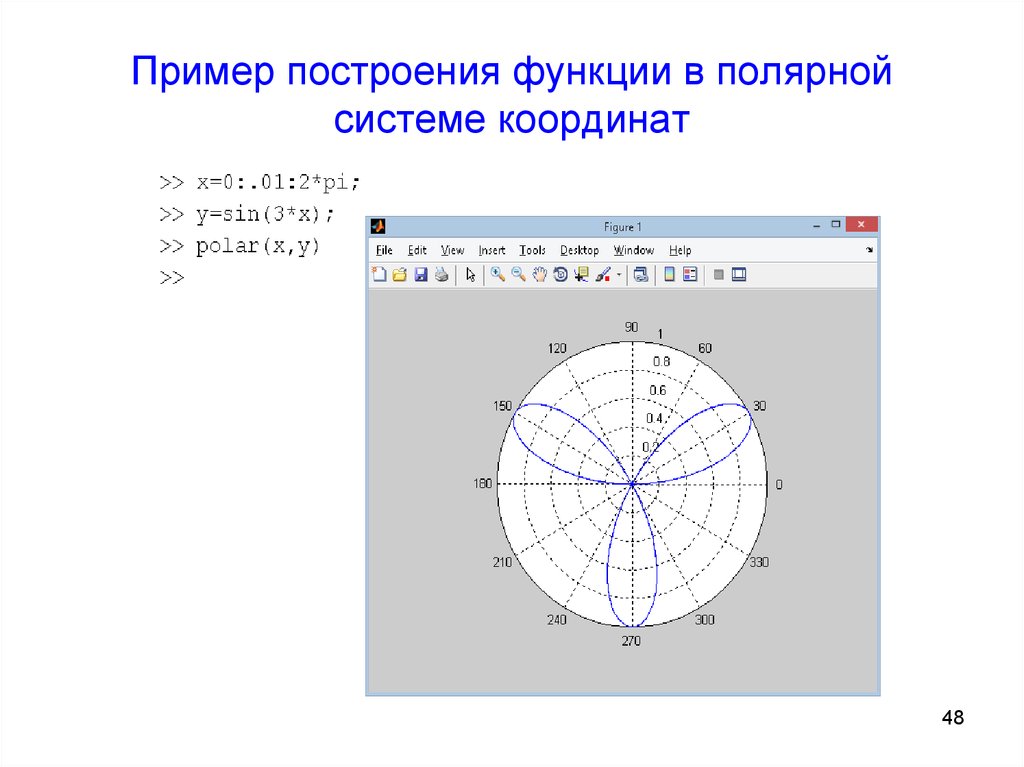 рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме.
рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме.Рисунок \(\PageIndex{14}\): (a) Полярная сетка (b) Прямоугольная система координат
Аналогичное обсуждение показало бы, что график функции \(r=2 \csc \theta\) будет горизонтальной линией \(y=2\). На самом деле \(r=c\csc\theta\) является стандартной формой горизонтальной линии в полярной форме, соответствующей прямоугольной форме \(y=c\).
Пример \(\PageIndex{6B}\): переписывание полярного уравнения в декартовой форме 92 \end{align*}\]
Когда все наше уравнение было изменено с \(r\) и \(\theta\) на \(x\) и \(y\), мы можем остановиться, если нас не попросят решить для \(у\) или упростить. См. рисунок \(\PageIndex{15}\).
Рисунок \(\PageIndex{15}\)
График в форме песочных часов называется гиперболой .
 2}. \конец{массив}\) 9{\frac{2}{3}}\)
2}. \конец{массив}\) 9{\frac{2}{3}}\)СМИ
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с полярными координатами.
- Введение в полярные координаты
- Сравнение полярных и прямоугольных координат
Ключевые уравнения
Формулы преобразования \(\cos\theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\)
\(\sin\theta=\dfrac{y}{r} \rightarrow y=r \sin\theta\) 92\)
\(\тангенс\тета=\dfrac{y}{x}\)
Основные понятия
- Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или источника.
- Чтобы нанести точку в виде \((r,\theta)\), \(\theta>0\), переместитесь против часовой стрелки от полярной оси на угол \(\theta\), а затем продлите направленный отрезок от полюса на длину \(r\) в направлении \(\theta\).
 2}\). См. пример \(\PageIndex{5}\).
2}\). См. пример \(\PageIndex{5}\). - Преобразование уравнений между полярной и прямоугольной формами означает выполнение соответствующих замен на основе доступных формул вместе с алгебраическими манипуляциями. См. Пример \(\PageIndex{6}\), Пример \(\PageIndex{7}\) и Пример \(\PageIndex{8}\).
- Использование соответствующих замен позволяет переписать полярное уравнение как уравнение прямоугольной формы, а затем изобразить его на прямоугольной плоскости. См. Пример \(\PageIndex{9}\), Пример \(\PageIndex{10}\) и Пример \(\PageIndex{11}\).
Эта страница под названием 10.3: Polar Coordinates распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- полярные координаты
- полярная сетка
- прямоугольные координаты
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus - источник[1]-math-2682
Как отобразить полярные оси в Matplotlib
Обзор
Matplotlib предоставляет модуль и функции для построения координат по полярным осям. Точка в полярных координатах представляется как (r, θ\thetaθ). Пара имеет расстояние и угол — rrr для радиуса или расстояния от начала координат и тета — θ\thetaθ для угла, под которым r должен быть измерен от начала координат. Модуль pyplot в matplotlib предоставляет функцию полярный для построения полярного графика.
Scope
- В этой статье мы обсуждаем полярные оси в matplotlib.
- Нам нужны две переменные для построения данных в полярной системе координат (r,θθ) (расстояние от начала координат и угол от оси).
- Затем мы обсудим применение полярных координат.
- Мы также обсудим построение полярных координат и несколько примеров.
Введение
Полярная система координат отображает на графике угловые данные, т. е. периодические функции. Точка в полярной системе координат представляется как (r,θr,\thetar,θ), где r — расстояние от начала координат, а тета — угол от оси. matplotlib.pyplot.polar() используется для построения кривой на полярных осях.
Когда использовать полярные координаты
Двумя наиболее популярными способами нанесения точек на график являются прямоугольная система координат и полярная система координат. Полярные координаты лучше всего использовать при рассмотрении периодических функций. Полярные координаты точек описывают их положение с точки зрения расстояния от начала координат и фиксированного направления (угла).
Было бы непрактично использовать прямоугольную систему координат, когда мы имеем дело с широтой и долготой. Предположим, мы указываем местоположение сферического объекта. В этом случае мы используем полярные координаты, потому что они будут определять местоположение с большей точностью, расстояние от центра сферического объекта и угол от осей.
Точно так же в GPS концепция полярных координат используется для определения местоположения человека в реальном времени. Более того, многие физические системы, например те, которые касаются тел, движущихся вокруг центральной точки, или явлений, исходящих из центральной точки, проще и нагляднее моделировать с использованием полярных координат.
Угловые данные
Для построения полярных координат в полярной системе координат нам нужны две вещи: rrr и θ\thetaθ, где rrr — расстояние от начала координат до точки, а θ\thetaθ — угол проекции точки к оси x.
Пример: построение угловых данных в полярной системе координат
На приведенном выше графике полярная система координат выглядит следующим образом: углы — это ось x, а расстояние от начала координат до окружности равно ось Y. Как мы видим, в системе координат есть маркер. Это полярная координата, где r=8 и тета=45°.
Как построить полярные оси в Matplotlib
Как это работает?
Прежде чем отображать полярные координаты на графике, мы должны изменить систему координат с прямоугольной на полярную, что можно сделать с помощью функции matplotlib.
 pyplot.axes(projection =), где мы должны передать значение «полярный» в поле проекция параметров.
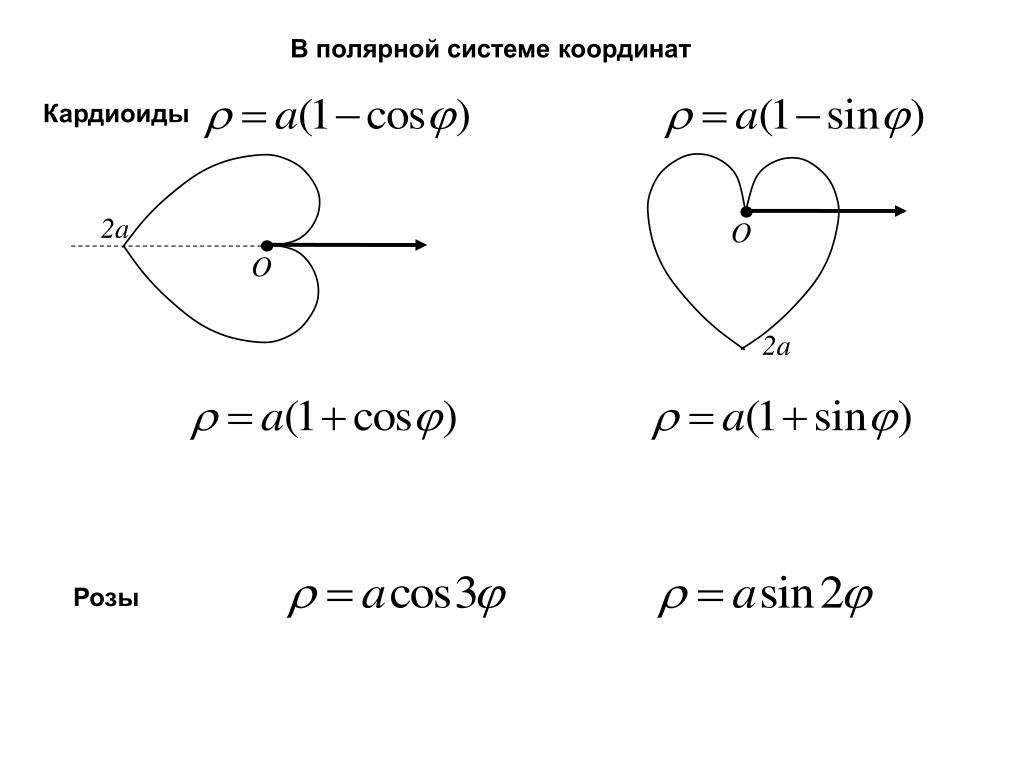
Модули pyplot функции matplotlib.pyplot.polar() используются для построения полярных координат. Эта функция отображает различные фигуры, такие как круги, эллипсы, кардиоиды и архимедовы спирали. Для отображения полярных координат на графике требуется как минимум два параметра, т. е. r и тета.
pyplot.axes(projection =), где мы должны передать значение «полярный» в поле проекция параметров.
Модули pyplot функции matplotlib.pyplot.polar() используются для построения полярных координат. Эта функция отображает различные фигуры, такие как круги, эллипсы, кардиоиды и архимедовы спирали. Для отображения полярных координат на графике требуется как минимум два параметра, т. е. r и тета.Синтаксис и параметры
Синтаксис функции построения полярных координат:
matplotlib.pyplot.polar(*args, **kwargs)
Параметры функции,
- тета: Угол, на который наносим точку.
- r: Расстояние между исходной точкой и точкой.
- kwargs: Аргумент ключевого слова для изменения визуальных свойств точек, таких как маркер, цвет, размер, ширина и т. д.
Как отображать данные в полярной системе координат
Ниже представлена реализация построения точек на полярных осях в matplotlib.
# Импорт необходимых модулей импортировать matplotlib.pyplot как plt импортировать numpy как np # Создание новой фигуры и настройка разрешения рис = plt.figure (dpi = 200) # Изменяем систему координат с масштабной на полярную топор = fig.add_subplot (проекция = 'полярный') # Генерация точек данных осей X и Y г=[8,8,8,8,8,8,8,8,8] тета = np.deg2rad (np.arange (45,406,45)) # построение полярных координат в системе plt.polar(тета,r,маркер='o') # Установка предела оси топор.set_ylim (0,10) # Отображение графика plt.plot()
Вывод:
Объяснение кода:
- Импорт необходимых модулей.
- Создание новой фигуры и настройка разрешения с помощью функции matplotlib.pyplot.figure(dpi=).
- Добавление подграфиков к созданной фигуре и установка системы координат на полярную путем установки значения проекции параметра на «полярную».
- Затем сгенерируйте r и тета и сохраните их в списке.
- Построение точки в полярной системе координат с помощью функции matplotlib.pyplot.polar().
- Затем установите диапазон делений по оси Y с помощью функции .add_subplot().set_ylim.
- Отображение графика с помощью функции matplotlib.pyplot.show().
Общие примеры
Полярные проекции
Полярные проекции — это некоторые графики, которые можно построить на примере полярной системы координат, окружности, эллипса или архимедовой спирали.
Пример 1: Рисование круга в полярной системе координат
Для рисования круга в полярной системе координат нам нужен радиус и список углов от 0 до 2π в очень коротком интервале.
# Импорт необходимых модулей импортировать matplotlib.pyplot как plt импортировать numpy как np # Создание новой фигуры и установка разрешения рис = plt.figure (dpi = 200) # Добавление подзаголовка к фигуре топор = fig.add_subplot (проекция = 'полярный') # Установка диапазона тика топор.
 set_ylim (0,5)
# Радиус и углы для построения окружности
радиус= 4
тета = np.arange (0,2 * np.pi, 0,01)
# Построение полярных координат
для я в тета:
plt.polar(i,радиус,'k.')
# Отображение графика
plt.show()
92)}}r=(asinθ)2+(bcosθ)2)a∗b
set_ylim (0,5)
# Радиус и углы для построения окружности
радиус= 4
тета = np.arange (0,2 * np.pi, 0,01)
# Построение полярных координат
для я в тета:
plt.polar(i,радиус,'k.')
# Отображение графика
plt.show()
92)}}r=(asinθ)2+(bcosθ)2)a∗b Где,
a = длина большой полуоси b = длина малой полуоси
импортировать numpy как np импортировать matplotlib.pyplot как plt импортировать математику # Создание новой фигуры и установка разрешения рис = plt.figure (dpi = 200) # Добавление подзаголовка к фигуре топор = fig.add_subplot (проекция = 'полярный') # полумажор а = 4 # малые полуоси б = 3 тета = np.arange (0, (2 * np.pi), 0,01) # построение эллипса для я в тета: r = (a*b)/math.sqrt((a*np.sin(i))**2 + (b*np.cos(i))**2) plt.polar(i, r, 'r.') # отображаем полярный график plt.show()Вывод:
Полигоны
Пример: Реализация полигона в matplotlib
# Импорт необходимых модулей импортировать matplotlib.
