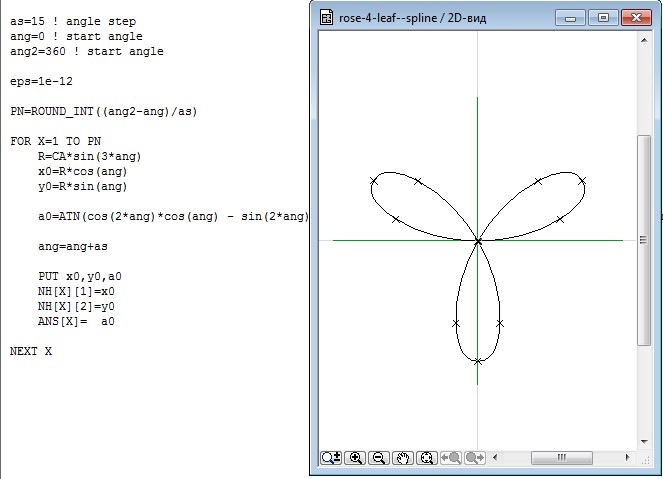
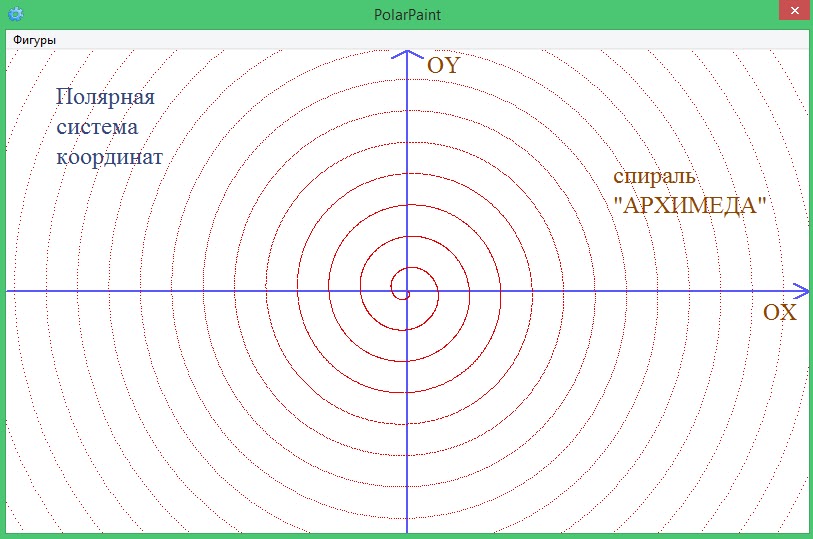
Построение графика функции в полярных координатах: Построить график в полярных координатах на плоскости

Построение графиков в полярных координатах

Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) и вставить в появившиеся шаблоны имена переменных и функций, которые будут нарисованы в полярной системе координат: угол (нижний шаблон) и радиус-вектор (левый шаблон). Аналогично построению графика в декартовых координатах по осям могут быть отложены два вектора элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции.

Пример 4.

График функции в полярных координатах можно построить также с помощью преобразований полярных координат в декартовые.

В примере 5 построен график кардиоиды в полярных координатах, уравнение которого задано в виде . Уравнения для и – обычное преобразование полярных координат в прямоугольные (декартовые).

Пример 5.

3 . Размещение нескольких графиков на чертеже.

График может содержать несколько выражений по оси ординат в зависимости от одного выражения по оси абсцисс или несколько значений по оси ординат, согласованных с соответствующими выражениями по оси абсцисс. Чтобы представить графически несколько выражений по оси ординат относительно одного выражения по оси абсцисс, необходимо ввести первое выражение для оси ординат, сопровождаемое запятой. Непосредственно под первым выражением появится пустое поле (шаблон). В появившемся месте ввода записывается имя второй функции, сопровождаемое другой запятой и т.д. Все выражение должно использовать одну и ту же переменную.

Пример 6.

Чтобы построить несколько независимых кривых на одном чертеже, введите два или более выражения, отделяемых запятыми на оси абсцисс, и то же самое число выражений на оси ординат. MathCAD согласует выражения попарно: первое выражение оси абсцисс с первым выражением оси ординат, второе со вторым и т.

д. Можно построить до 16 функций на оси ординат в зависимости от одного аргумента на оси абсцисс. Если для каждой кривой используется свой аргумент, то можно отобразить только до 10 графиков.

П ример 7.

Все графики на чертеже совместно используют одни границы на осях. Для каждой оси все выражения и границы должны иметь совместимые размерности.

Изменение размеров графика.

Чтобы изменить размеры графика, необходимо:

1. Заключить его в выделяющий прямоугольник с помощью щелчка мыши.

2. Переместить указатель мыши к левому нижнему краю выделяющего прямоугольника. Указатель превратится в двойную стрелку.

3. Переместить указатель при нажатой кнопке мыши, растягивая графическую область в желаемом направлении.

4. По достижении желаемого размера отпустить кнопку мыши.

Для отмены выделения щелкните мышью вне графической области.

4. Форматирование двумерных графиков.

При двойном щелчке мышью в области графика (либо выборе в контекстном меню команды Format) открывается окно форматирования графика.

На вкладке Trace (Трасировки) предоставляется возможность задать следующие параметры:

• Legend Label (Легенда) – текст легенды, описывающий ряд данных.

• Symbol (Символ) – значок, отмечающий выделенную точку:

• solid – сплошная;

• dot – мелкий пунктир;

• dadot – штрих-пунктир;

• dash – крупный пунктир.

• Color (Цвет) цвет линии и точек данных,

• Weight (Толщина) – толщина линии и точек данных,

• Type (Тип) – тип представления ряда данных:

• line – линия;

• point – точка;

• bar – столбик гистограммы;

• solidbar – закрашенный столбик;

• step – ступенька;

• stem – палочка с кружочком;

• draw – рисованная линия;

• error – позволяет отложить на графике вычисленную ошибку.

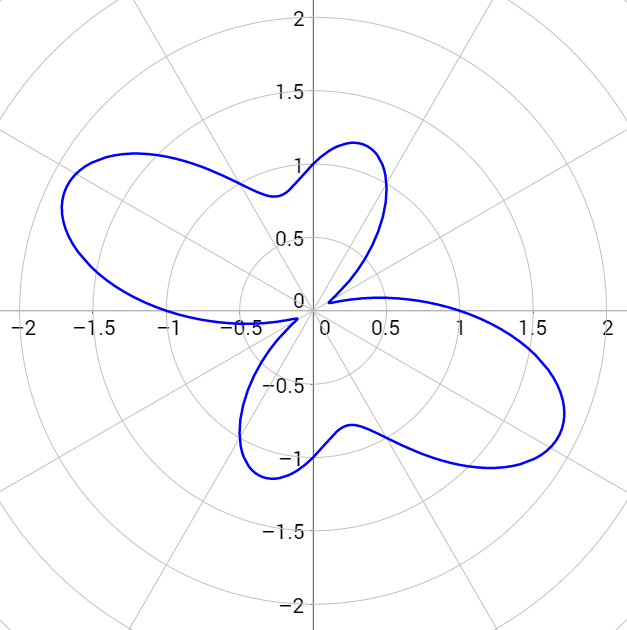
Сохранение установок по умолчанию.

На вкладке Defaults (По умолчанию)

диалога Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) находятся два элемента управления:

• кнопка Change to Defaults (Вернуть установки по умолчанию) позволяет изменить все установки выделенного графика на установки по умолчанию, принятые для текущего документа;

• — флажок проверки Use for Defaults (Использовать для установок по умолчанию) фиксирует установками по умолчанию для данного документа установки выбранного графика.

Создание заголовка графика.

Чтобы создать заголовок графика, необходимо:

1. Дважды щелкнуть мышью в области графика.

2. В диалоге Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) перейти на вкладку Labels (Метки).

3. В поле Title (Заголовок) ввести текст заголовка.

4. Установить флажок проверки Show Title (Показать заголовок).

5. Выбрать переключатель Above (Сверху) или Below (Снизу), чтобы заголовок появился сверху или снизу графика.

6. Нажать кнопку ОК.

Форматирование осей графиков.

Возможности форматирования координатных осей графиков включают в себя управление их внешним видом, диапазоном, шкалой, нумерацией и отображением некоторых значений на осях при помощи маркеров.

Построение графика функции, заданной в полярной системе координат. — Информатика, информационные технологии

Создайте в новом проекте форму «График функции в полярной системе координат»

1.Условие:

Построить график функции, заданной в полярной системе координат.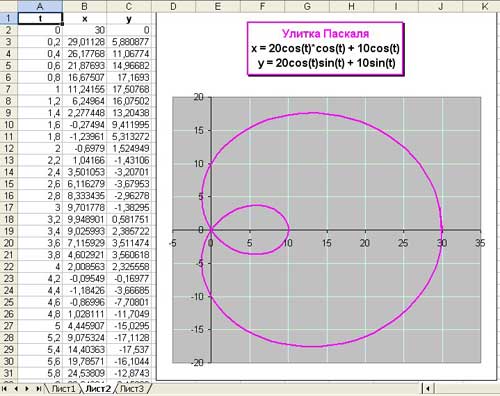

R=10*(1+cos(t)), где t € [0; 2?] шаг изменения t h=0.01

2.Программа:

Результат;

Сохранитепроект в папкеЛабораторная работа 11/Задание 3.

Задание 4

Построение графиков функций

Создайте в новом проекте форму «Построение графиков функций»

Создаваемое приложение должно состоять из таблицы для задания списка точек графика функции и графического поля для рисования графика. При этом любое изменение данных в таблице должно вызывать обновление графика.

Описание работы

Программа будет состоять из одной формы, на которой необходимо разместить:

Элемент	Caption	Name	Другие свойства
Форма	Построение графика функции	ChartForm
Таблица для ввода координат точек		StringGrid	Options – qoEditing – True ColCount.RowCount – 3
Панель для расположения диаграммы	отсутствует	PanelChart
Компонент TPaintBox для отображенияграфика функции		PaintBox
Метка	График функции	Label1
Метка	Исходные точки	Label2
Панель для отображения ошибок ввода данных	отсутствует	PanelStatus
Кнопка	Выход	ButtonExit	Можно добавить свойство ModalResult — mrOk

Таблица для ввода координат точек должна автоматически изменять размер в соответствии с количеством уже введенных точек функции. Как это сделать, описано в предыдущих лабораторных работах.

После ввода данных необходимо сформировать два массива введенных координат X и Y, отсортировать их по оси X, после чего необходимо перерисовать окно с графиком.

Замечание

При необходимости перерисовки компонента в ответ на какое-то событие, например, нажатие кнопки, сразу не рисуйте, а вызовите метод Invalidate и создайте обработчик события OnPaint визуального компонента, например, формы или TPaintBox.

Рассмотрим, как Windows отображает все свои окна.

Окнами в общем случае являются кнопки, строки ввода, списки и т.д. Они могут находиться друг в друге, например, кнопки в диалоговом окне или окна внутри многодокументного интерфейса. Каждое окно при этом имеет специальную главную управляющую процедуру, которая обрабатывает поступающие от системы сообщения. Некоторые из этих сообщений Delphi преобразует в события, которые можно затем обрабатывать в программе.

Windows сама никогда не хранит изображения окон, поэтому одним из сообщений является команда о необходимости отображения содержимого окна на экране.

В нашей программе сразу же после ввода координат точек мы не должны вызывать процедуру рисования. При этом мы должны указать Windows, что как только появится свободное процессорное время, система должна послать сообщение о необходимости реального отображения окна. При таком подходе, если окно приложения будет временно закрыто другим окном и опять станет видимым, система автоматически пошлет сообщение о необходимости восстановления графического изображения в окне.

В Delphi для указания, что необходимо перерисовать любой элемент управления, нужно вызвать его метод Invalidate.

Для изображения произвольной графики в Delphi обычно используется компонент TPaintBox, находящийся на закладке System палитры компонентов. Этот компонент имеет событие OnPaint, для которого мы и должны создать обработчик для рисования графика.

Для прорисовки произвольных изображения используется класс TCanvas(холст), а также методы, позволяющие рисовать графические примитивы (краткое описание свойств и методов объектов для рисования графики приведено выше).

Для упрощения алгоритма рисования графика будем считать, что обе координаты всех точек попадают в интервал
[-10, 10]’. Процедура рисования графика при этом распадается на две части:

-рисование осей координат с засечками и подписями

-и собственно изображение графика.

Теперь рассмотрим вопрос автоматического изменения положения и размеров визуальных компонентов при изменении формы. Для этого у компонентов имеются такие свойства, как Align и Anchors. Собственно, свойство Align является подмножеством возможностей свойства Anchors. Свойство Anchors имеет 4 логических подсвойства:

-akLefn,

-akTop,

-akRight,

-akBotton

Например, если свойство akRight установлено в True, то правая сторона элемента будет находиться на одинаковом расстоянии от правой стороны содержащей его формы при изменении пользователем ее размера, иначе правая сторона элемента будет находиться на одинаковом расстоянии от левой стороны. При изменении свойства Align на самом деле изменяется свойство Anchors, которое впоследствии и учитывается при изменении размеров.

Замечание
По возможности делайте любое окно растягиваемым, но при этом не забывайте отслеживать, чтобы внутренности окна изменялись при изменении его размеров. Для этого используйте свойства Аlign и Anchors.

Поэкспериментируйте приведенными свойствами и добейтесь, чтобы в нашем приложении график растягивался в размерах при увеличении размеров формы, но в то же время таблица оставалась с правой стороны формы, a кнопка выхода в правом нижнем.Обратите внимание, что процедура рисования графика должна учитывать изменяющийся размер элемента TPaintBox.

Программа:

Результат

На рис. приведен внешний вид запущенного приложения после того, как окно растянуто.

Сохранитепроект в папкеЛабораторная работа 11/Задание 4.

Вопросы и задания для самостоятельной работы

1. Как Windows перерисовывает свои окна?

2. Как заставить Windows перерисовать какое-то окно?

3. Для чего используются свойства визуальных компонентов Align и Anchors?

4. Поместите на форму компоненты для выбора стиля изображения на графике введенных точек (кружочки, квадратики или «не изображать»), толщины и цвета линий. При этом график должен автоматически перерисовываться при изменении этих параметров.

5. Добавьте кнопку для генерации случайного набора точек.

Статьи к прочтению:

• Построение графиков и диаграмм
• Построение и работа импульсного кольца.

14 вопросов которые нужно задать до свадьбы? Сатья дас. Карпаты. 3.08.2017

Похожие статьи:

• Построение графика функции с двумя и более условиями. 3 страница

  2. Найти с помощью инструмента Подбор параметра корни кубического уравнения с одной переменной согласно своему варианту. Вариант 1. Вариант 2. Вариант 3….

• Построение графика функции с двумя и более условиями. 4 страница

  б) Дважды щелкнув имя поля в верхней части окна. в) Щелкнув в столбце в конце строки Поле и из раскрывающегося списка выберать нужное поле. В строке…

Как строить полярные функции и кривые

Учитесь на знаниях сообщества. Эксперты добавляют свои идеи в эту совместную статью на основе ИИ, и вы тоже можете.

Это новый тип статьи, которую мы начали с помощью ИИ, и эксперты продвигают ее вперед, делясь своими мыслями непосредственно в каждом разделе.

Если вы хотите внести свой вклад, запросите приглашение, поставив лайк или ответив на эту статью. Узнать больше

— Команда LinkedIn

Последнее обновление: 2 апреля 2023 г.

Полярные координаты — это способ представления точек на плоскости с использованием углов и расстояний от фиксированного начала координат.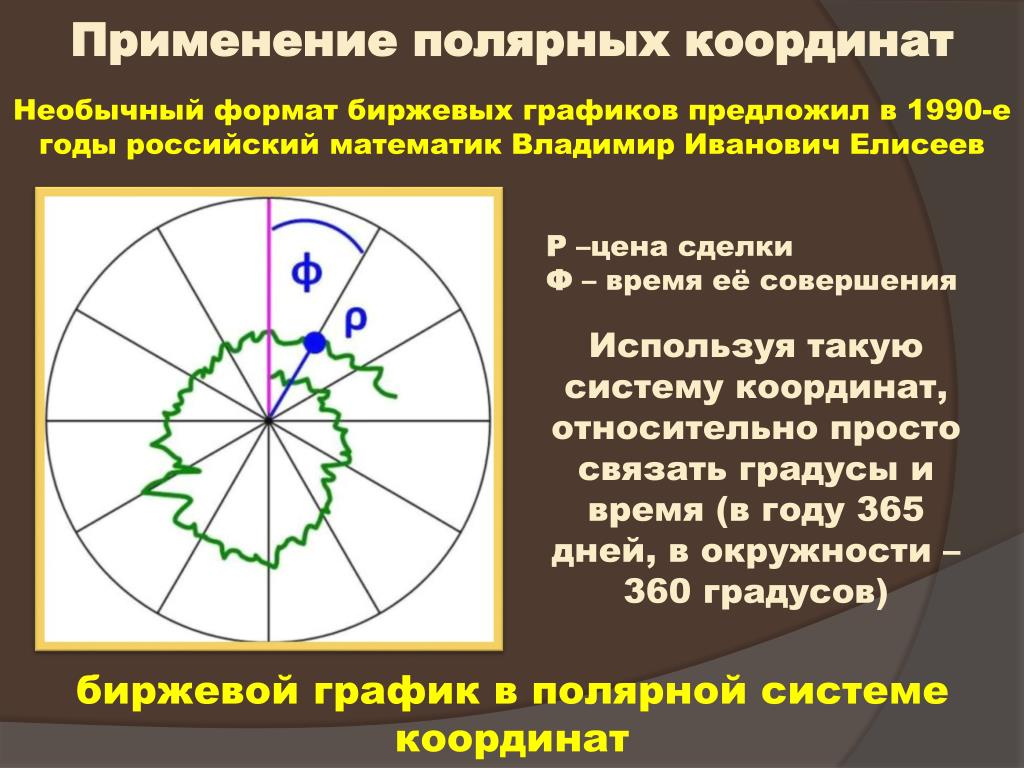 Они могут быть полезны для построения графиков функций и кривых, имеющих круглую, радиальную или спиральную форму или зависящих от направления точки. В этой статье вы узнаете, как строить функции и кривые в полярных координатах, используя некоторые основные формулы и инструменты.

Полярные и декартовы координаты

Наиболее распространенным способом определения местоположения точек на плоскости являются декартовы координаты, основанные на двух перпендикулярных осях: оси x (горизонтальная) и оси y (вертикальная). ). Точка в декартовых координатах задается парой чисел (x, y), которые указывают, насколько далеко точка находится от начала координат по каждой оси. Например, точка (3, 4) находится на 3 единицы вправо и на 4 единицы вверх от начала координат.

Полярные координаты, с другой стороны, основаны на угле и радиусе. Угол, обычно обозначаемый тета (θ), измеряется от положительной оси x против часовой стрелки. Радиус, обычно обозначаемый r, представляет собой расстояние от начала координат до точки.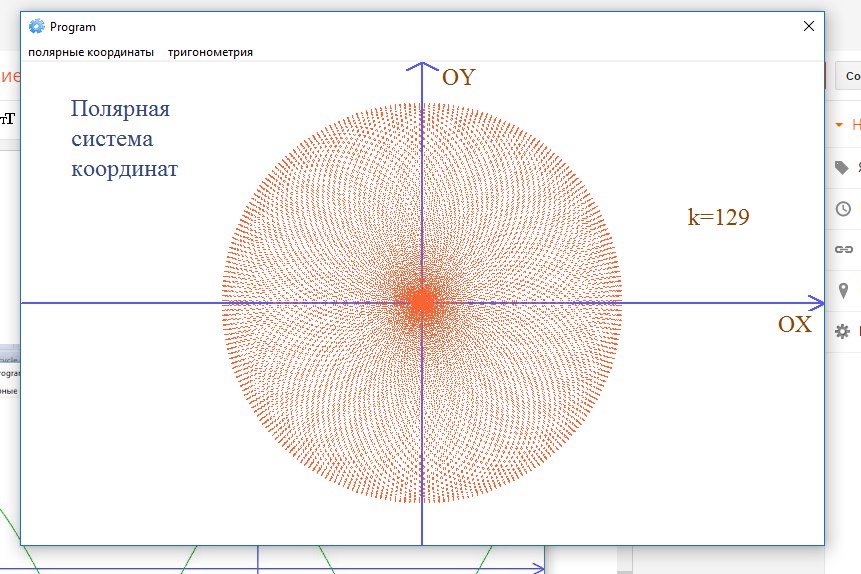 Точка в полярных координатах задается парой чисел (r, θ), которые указывают, как далеко и в каком направлении находится точка от начала координат. Например, точка (5, π/4) находится на расстоянии 5 единиц от начала координат и под углом 45 градусов к положительной оси x. 9-1 (4/3) = 0,927 радиан или 53,13 градуса

Итак, полярные координаты (3, 4) равны (5, 0,927) или (5, 53,13°).

Построение полярных функций

Полярная функция — это функция, связывающая радиус r с углом θ. Например, r = 2 + cos θ — это полярная функция, описывающая кардиоиду, кривую в форме сердца. Чтобы построить полярную функцию, вы можете использовать графический калькулятор, онлайн-инструмент или программу, поддерживающую полярные графики. Кроме того, вы можете преобразовать полярную функцию в декартову функцию, используя приведенные выше формулы, и нанести ее на обычную плоскость xy. 92 — 2x — 2 = 0

Это декартова функция, которую можно изобразить на плоскости xy стандартными методами.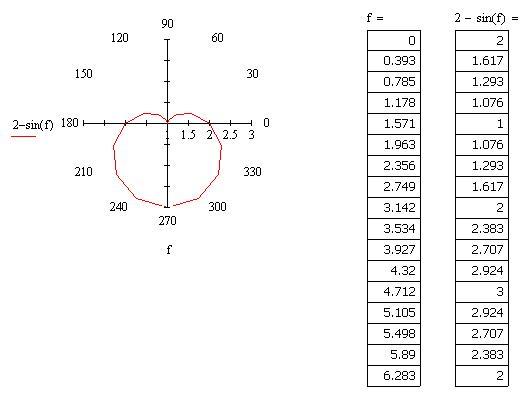

Построение полярных кривых

Полярная кривая — это кривая, которая определяется набором точек в полярных координатах. Например, окружность с радиусом 3 и центром в точке (0, π/2) представляет собой полярную кривую, которую можно представить уравнением r = 3 sin θ. Чтобы построить полярную кривую, вы можете использовать те же методы, что и для построения полярных функций, или вы можете использовать таблицу значений, чтобы найти соответствующие декартовы точки и нанести их на плоскость xy.

Например, чтобы построить круг r = 3 sin θ, вы можете использовать следующую таблицу значений:

θ | р | х | у

0 | 0 | 0 | 0

π/6 | 1,5 | 1.3 | 0,75

π/4 | 2.1 | 1,5 | 1,5

π/3 | 2,6 | 1,5 | 2,25

π/2 | 3 | 0 | 3

… | … | … | …

Затем вы можете нанести точки (x, y) на плоскость xy и соединить их плавной кривой, чтобы получить круг.

Советы и рекомендации

Построение функций и кривых в полярных координатах можно упростить и сделать более точным с помощью следующих советов и рекомендаций: использование радианов вместо градусов; полярная сетка вместо обычной сетки; использование преимуществ симметрии и периодичности; и использование калькулятора или программного обеспечения для упрощения расчетов и преобразований. Радианы более удобны для вычислений и преобразований, тогда как полярная сетка состоит из концентрических окружностей и радиальных линий, которые делят плоскость на сектора. Кроме того, симметрия и периодичность могут уменьшить объем необходимой работы, такой как построение точек для θ в [0, π] и их отражение по оси x. Наконец, калькулятор или программа могут обрабатывать комплексные числа и тригонометрические функции для упрощения вычислений и преобразований.

Вот что еще нужно учитывать

Здесь можно поделиться примерами, историями или идеями, которые не вписываются ни в один из предыдущих разделов. Что бы вы еще хотели добавить?

Оцените эту статью

Мы создали эту статью с помощью ИИ. Что вы думаете об этом?

Спасибо за ваш отзыв

Ваш отзыв является частным. Поставьте лайк или отреагируйте, чтобы перенести разговор в свою сеть.

• Как вы включаете независимость от разрешения в свой рабочий процесс 2D-графики и передовые методы?

  6 апр.

  2023 г.

• Каковы преимущества и недостатки использования полярных координат для круглых форм?

  4 апр. 2023 г.

• Каковы некоторые рекомендации по организации и именованию смарт-объектов и смарт-фильтров в ваших проектах?

  4 апр. 2023 г.

• Как импортировать многоуровневые файлы из разных программных приложений без потери качества или совместимости?

  3 апр.

  
  2023 г.

• Каковы некоторые рекомендации и советы по работе с примитивами и путями в 2D-графике?

  2 апр. 2023 г.

• Как вы используете методы дизеринга и сглаживания в пиксель-арте?

  30 марта 2023 г.

• Какие советы и рекомендации по использованию инструмента «Перо» для рисования плавных кривых и форм в Photoshop?

  29 марта 2023 г.

  

• Как вы обновляете и актуализируете свою 2D-карту?

  29 марта, 2023 г.

• Как экспортировать и оптимизировать векторную графику для разных платформ и форматов?

  28 марта 2023 г.

• Как вы используете текстовые эффекты и анимацию для улучшения 2D-графики без ущерба для читаемости?

  28 марта 2023 г.

  

Cartesian & Polar Function Grapher

Самый продвинутый в мире Cartesian и полярный Function Grapher для рисования графика функций, способный анимирует процесс полярной графики наиболее подходящим образом. Он показывает, как полярный график функции строится постепенно в своей области определения. Вы также можете построить график заданной функции в декартовой системе координат , сняв флажок Polar .

Устройство для построения графиков полярных функций — это калькулятор для построения графиков функций , который рисует график функции в заданной области в полярной системе координат. Такой график называется полярным графиком или полярной кривой данной функции.

Процесс построения графика в полярной системе координат и его визуализация с использованием функционального графического калькулятора принципиально отличается от построения графика в декартовой системе координат . Это связано с тем, что полярный граф необходимо рисовать постепенно, чтобы можно было визуализировать, как полярный граф конструируется в своей области.

Этот функциональный граф , использующий самые сложные декартовы и полярные системы координат , является единственным известным графическим инструментом, который может отображать неперпендикулярную декартову систему координат , а также помогает правильно визуализировать полярную кривую постепенно становится сконструировал с помощью анимации полярной графики . Таким образом, вы можете посмотреть, как шаг за шагом рисуются все ваши крутые полярные графики .

Вы можете использовать эту чрезвычайно полезную функцию, нажав ► в нижней части графического калькулятора функций (если он скрыт, сначала нажмите кнопку Animate ).

Запускает анимацию процесса построения полярных графиков функции в фокусе . График рисуется постепенно от начального значения θ₁ до конечного значения θ₂ радиальной оси . Анимированный полярный график показывает вращения угловых осей ( радиальных осей ) и радиальных расстояний .

Затем вы можете нажать ‖ до приостановить анимацию или нажать Готово до остановить ее. Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите Кнопка Animate в верхней части полярного графа.

Вы также можете изменить скорость анимации полярной графики с помощью ползунка , предоставленного

Этот бесплатный онлайн-калькулятор полярной функции также рисует полярных графиков с 1 полярной осью .

Советы: по мере ввода:

• ..t заменяется на θ . ( Вы также можете использовать x или t. Они заменяются внутри на θ ).
• пи заменяется на π .
• inf ( бесконечность ) заменяется на ∞ .

Для построения графика кусочно-определенных функций введите каждую часть с соответствующим подинтервалом в виде одиночной функции .

Самый быстрый способ ввести dom=(0, 2π) или dom=(-∞, ∞) — полностью удалить домен, включая дом = .

МышьМатикс! Вы можете использовать мышь, чтобы Повернуть оси , Переместить и Изменить масштаб

В дополнение к вводу данных — сначала нажав кнопку шестеренки — вы можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивный функциональный граф , как описано ниже.

• Щелкните по оси (или рядом с ней) и переместите мышь. это будет повернуть ось . графики перерисовываются в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось.
• Перетащите мышь на переместите систему координат вместе с графиками.
• Дважды щелкните холст, чтобы переместить исходную точку туда, где был сделан щелчок.
• Удерживая клавишу Alt, щелкните по оси до изменить масштаб (увеличение в одном направлении) ; в точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.

Анимация вращения оси: Икс у ► ⬛

сообщение

 

f(x) =

?

f( ) =

 

⌨

4 Десятичные разряды

Graph FinenessBest (медленно)+2+1Normal-1-2Fast (низко)

Label Axes ось x: ось y: Повернуть оси Ось x°: Ось Y°:

⚙

РезультатыСкрыть

Наложение Прозрачный 92-4)

Другие графики

√(4sin(2x)) √(4cos(2x))

Функции — Полярный

Линии

2csc(θ) 2сек(θ) 1/(sin(θ) — cos(θ))

Круги

1 2 6sin(θ) 8cos(θ)

Спирали

θ θ/5 дом=(0, 10π) √(θ) дом=(0, 10π) 1/θ дом=(0, 10π)

Розы

4sin(3θ) 4sin(2θ) 4sin(5θ) 4sin(4θ)

Эллипсы

1/(1-.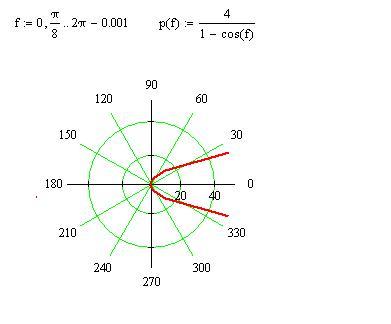 8cos(θ)) 1/(1-0,8sin(θ)) 1/(1+.8cos(θ)) 1/(1+.8sin(θ))

Параболы

1/(1-sin(θ)) 1/(1+cos(θ)) 1/(1+sin(θ)) 1/(1-cos(θ))

Гипербола

1/(1+2cos(θ)) 4/(1+2sin(θ)) 1/(1-2cos(θ)) 4/(1-2sin(θ)) 95 дом = (0, 12π)

РАД Полярный

🔍+ 1 🔍−

время построения графика (с)

Калькулятор загружается.
Пожалуйста, подождите….

Сделайте это прозрачным

Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осей

заголовок

…

Медленный Быстрый

Показать угловые оси Сделанный

Отключить программную клавиатуру

Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.

Этот интерактивный графомер полярных функций был разработан для построения графиков, и, в частности, для демонстрации с помощью анимации того, как график функции создается в полярной системе координат . Полярные кривые могут быть очень сложными и иметь много петель. Все остальные полярные графы

(до этого графического калькулятора полярных функций — недавно некоторые другие графографы в партнерстве с Google и Microsoft начали следовать этому правилу)

отображают полярный график функции, не показывая, где начинается или заканчивается кривая, а также прослеживаются ли петли, если таковые имеются, и как. Этот уникальный калькулятор графических функций в полярных координатах предлагает правильный способ построения графических функций в полярных системах координат . А именно, он начинает строить график с начального значения угловой координаты θ₁ и постепенно показывает процесс построения графика до конечного значения θ₂, показывая, повторяются ли петли или какая-либо часть кривой. Более того, этот графограф полярных функций позволяет изменять скорость процесса построения полярных графиков.

Легко использовать декартовых или графических функций полярных функций ; введите функцию в любое поле выражения , например, f(x) или r(θ) . График функций отображается при вводе (по умолчанию) в выбранной системе координат . (Не беспокойтесь о том, какую переменную вы используете, функция графического редактора автоматически изменяет переменные в соответствии с выбранными система координат.)

• В график два или более функции в одной и той же декартовой или полярной системе координат Панель с несколькими графиками состоит из панелей выражений , которые можно добавлять или удалять по желанию, нажимая + или × . на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
• Для удобства графопостроитель полярных функций или графопостроитель декартовых функций добавляет подходящий интервал, dom = (0, 2π) или dom = (-∞, ∞), соответственно, к функциональным выражениям и графикам на указанных домен. При желании можно изменить конечные точки . Конечные точки должны быть конечными для построения полярного графика. Устройство графического отображения полярных функций автоматически изменяет бесконечности, если таковые имеются, на конечные значения.
• Полярные диаграммы или декартовы диаграммы отображаются сразу же после ввода. Вы можете анимировать процесс построения полярного графика, как описано выше.
• Можно установить тонкость декартовой или полярной кривых , выбрав нужный параметр в раскрывающемся списке Graph Fineness . Как правило, чем выше точность, тем больше времени требуется графическому редактору функций для построения графиков функций.
• Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графиком функций . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
• Чтобы оценить функцию , введите число или числовое (постоянное) выражение в соответствующем поле; функциональный граф отображает рассчитанные значения функции с количеством знаков после запятой, которое можно указать с помощью предоставленного ползунка.

Интересные кривые : Нарисуйте любое из выражений в разделе Интересные графики , а также отобразите несколько классных полярных графиков , выбрав его. Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness как «+1» или выше.

Вы можете установить следующие параметры, нажав кнопку ⚙ (шестеренка) в правом верхнем углу графического холста.

• Измените толщину графиков с помощью предоставленного ползунка.
• Выберите режим угла ( радиан — по умолчанию , градусов или градусов ).
• Если вы отмените выбор График при вводе параметра , вам придется нажать График выбранных выражений , который затем появится в нижней части калькулятора, чтобы обновлять графики всякий раз, когда вы вносите какие-либо изменения в выражения или координаты. плоскость (т. е. переместить начало координат, повернуть оси и т. д.).
• При необходимости отобразите элементы управления в верхней части графического редактора функций , которые позволяют запускать/приостанавливать и останавливать вращение любой или всех осей.