Пирамида с вырезом в трех проекциях: Построить три проекции пирамиды с вырезом | Интерактивное сообщество — Решение задач по инженерной графике

Чертеж пирамиды с вырезом

Содержание

1. 6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды
2. Упражнение
3. 6.2. Призма. Развертка призмы
4. Упражнение
5. 6.3. Взаимное пересечение многогранников
6. Упражнение
7. Упражнение
8. 6.4. Задачи для самостоятельной работы

Графическая работа 2.

1 Нарисуйте три проекции геометрического тела (пирамиды) с вырезом или через призматическое окно.
2. делать профильные надрезы.

Смотрите обучающее видео: “Пирамида с отверстием” на нашем канале YouTube → ДЛЯ СТУДЕНТОВ

♦ Чертеж на формате A3.

♦ Программное обеспечение: Компас (.cdw)

ПОДПИСЫВАЙТЕСЬ и смотрите видеоуроки на нашем канале ДЛЯ СТУДЕНТА

Возможно изготовление подобных работ в других вариантах по запросу, пожалуйста, напишите нам:

На рисунке 37 показано построение пирамиды с углублением (в результате того, что пирамида сечется несколькими выступающими плоскостями). В этом случае выемка образована тремя плоскостями: горизонтальной (горизонтальная плоскость) – Q, фронтальной выступающей плоскостью – R и профильной плоскостью – H.

Горизонтальная плоскость Q пересекает боковую поверхность пирамиды по пятиугольнику 1 11 12 4 13, грани которого параллельны граням основания пирамиды, в пределах выемки имеет ломаную линию 2 1 6 5 4 3. Выступающая торцевая плоскость R пересекает боковую поверхность пирамиды по ломаной линии 3 8 9 10 2. Профильная плоскость H пересекает боковую поверхность пирамиды по ломаной линии 6 7 5 внутри выемки. Полученные точки соединяем по видимости в заданном порядке (так, чтобы две точки принадлежали одной секущей плоскости и одной пирамидальной стенке).

|	следующая лекция ==>
Пересечение многогранников плоскостью	|	Поперечное сечение цилиндра через плоскость

Дата добавления: 2014-01-20 ; Дисплеи: 2080 ; Нарушение авторских прав? ;

Нам важны ваши отзывы! Был ли опубликованный материал полезен? Да | Нет

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранник – это твердое тело, ограниченное плоскими многоугольниками, называемыми гранями.

Грани образуются путем их пересечения.
Грани образуют вершины путем пересечения.
Рассмотрим два основных типа многогранников:

Пирамида – это многогранник, боковые стенки которого являются треугольниками, а основание – правильным многоугольником.

Упражнение

Дана пирамида, основание которой параллельно π1. Основанием является определенный треугольник.

S – вершина пирамиды (рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды с прямой линией

Нам нужно построить точки пересечения прямой m в общем положении с поверхностью пирамиды.

1. Проведите вспомогательную секущую плоскость σ∈m и σ⊥π2 через прямую.
2. Постройте сечение ∆ (123) пирамидальной поверхности плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскости общего положения (боковые стенки пирамиды) и плоскости частичного положения (σ-плоскость).

Примечание. В случае круто наклоненных ребер (близких к вертикальным), построение недостающей проекции точки на ребре по одной заданной проекции следует выполнять путем пропорционального деления отрезка.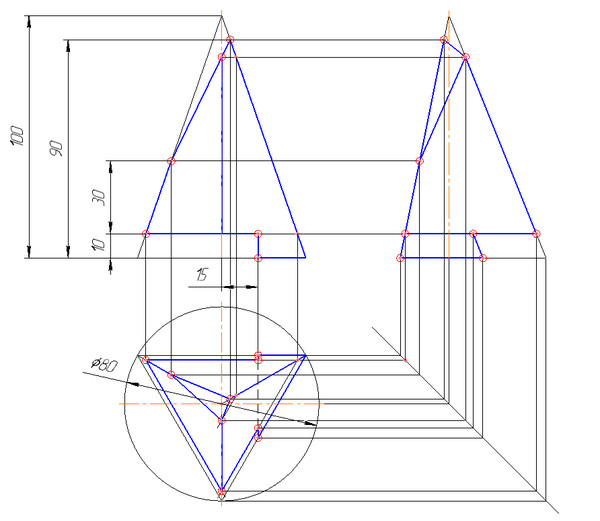

1. Найдите точки M и N, принадлежащие прямой m на отрезке.
2. Определите видимость линии m.

Открытый многогранник – это фигура, полученная путем последовательного совмещения граней многогранника с плоскостью.

Развертка всегда строится внешней (лицевой) стороной к наблюдателю.

Для построения развертки пирамиды необходимо определить истинные значения всех ребер пирамиды и построить стены пирамиды в виде треугольников, последовательно приложенных друг к другу.

Основание может быть прикреплено к любой грани, например, AC (рис. 6.2).

Рисунок 6.2 – Построение пирамиды развертки

В упражнении истинные значения граней определяются вращением. Для построения линии отрезка на развёртке построим суперлинейные точки , суперлинейные точки , суперлинейные точки , проводя горизонтальные линии (траектории движения точек 1, 2, 3) до пересечения с соответствующими реальными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – это многогранник, боковые стенки которого являются параллелограммами, а основания – многоугольниками, лежащими в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны проективной плоскости π1.

Требуется построить точки пересечения прямой m с поверхностью призмы (рисунок 6.3).

Рисунок 6.3 – Построение точек “встречи” прямой линии с поверхностью наклонной призмы

1. Проведите вспомогательную плоскость σ∈m и σ⊥π2 через прямую.
2. Постройте сечение поверхности призмы плоскостью σ →(∆(123)).
3. Найдите точки K и L прямой m на отрезке.
4. Определите видимость линии m. Если ребро AB на π2 видно, то K на π2 видно, ребро BC невидимо, следовательно, L невидимо.

Рассмотрим перекошенную призму. Пусть основание призмы параллельно π1, а ребра параллельны π2.

Построим нормальное сечение, то есть сечение через плоскость σ, перпендикулярную ребрам призмы (рис. 6.4).

Этот участок развивается по прямой линии. Боковые края перпендикулярны линии сечения.

Рисунок 6.4 – Чертеж сечения призмы.
Чертежный заказ :

1. Найдем истинное значение отрезка – (102030), для чего повернем отрезок (123) вокруг оси n⊥π2, (можно ввести DPP π3//σ).
2. Проведите горизонтальную линию на свободном пространстве пластины. Нанесите на него несколько интервалов:
   /10-20/; /20-30/; /30-10/.

1. Проведите через точки ребра, перпендикулярные этой линии: 10; 20; 30 и измерьте расстояния от нормального сечения (на π2) вверх и вниз до верхней и нижней ножек, положив их на края.

6.3. Взаимное пересечение многогранников

При пересечении многогранников получается ломаная линия.

Существует два возможных случая пересечения многогранников (рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины многогранников – это точки пересечения ребер одного многогранника с гранями другого многогранника.

Сегменты полилинии – это линии пересечения ребер.

Для решения задачи нам необходимо найти вершины полилинии, то есть точки пересечения всех ребер, участвующих в пересечении.

Соедините разорванные точки.

Упражнение

Постройте линии пересечения призмы и пирамиды (рис. 6.6).

Рисунок 6.6: Построение линий пересечения призмы и пирамиды
Решение

1. Найдите π2 проекции точек пересечения ребра пирамиды с выступающими стенками призмы (точки 12 и 22). Найдите их горизонтальные проекции.
2. Постройте точки пересечения ребер призмы с боковыми гранями пирамиды (точки 32 и 42), для чего используем вспомогательную плоскость τ⊥π2.
3. Точки 3, 2, 4, 1 в π1 соединены отрезками прямых. Сегменты 11-31, 11-21, 11-41 невидимы. Получаем замкнутую линию пересечения между пирамидой и призмой.

Упражнение

Постройте три проекции пирамиды с углублением и разверткой (рис. 6.7).

1. Используя две проекции, постройте третью;
2. Используя все три проекции, постройте проекции линии пересечения вдавливания призмы и пирамиды;
3. Покажите невидимые места линий пересечения и места расположения граней многогранников пунктирной линией;
4. Постройте развертку пирамиды с помощью чертежа линии пересечения.

Рисунок 6.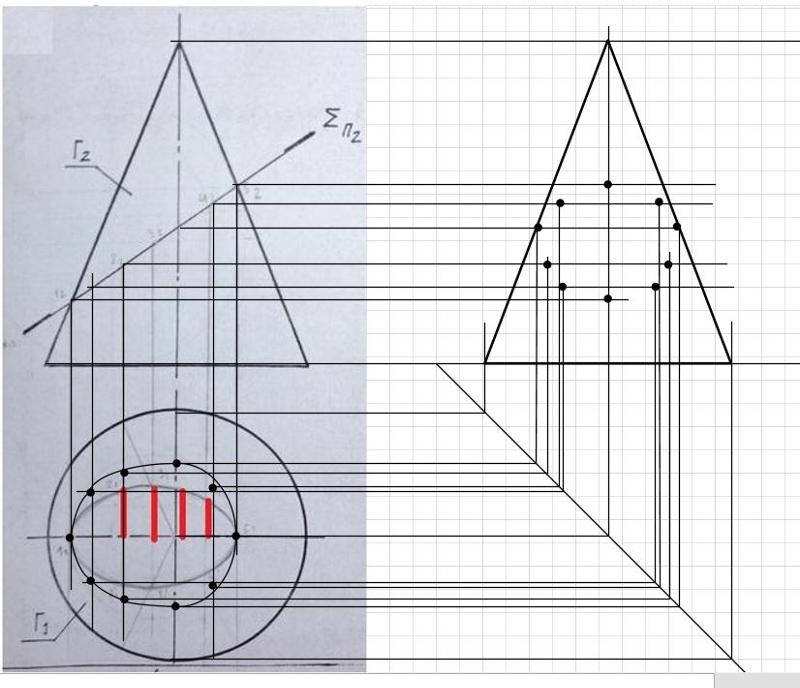 7: Чертежные проекции пирамиды с вырезом и разверткой
Решение

1. Проведите граничные линии призмы на всех проекциях.
2. Представьте плоскость σ⊥π2, σ//π1:

• σ//ABC – это основание пирамиды;
• σ пересекает сечение пирамиды, подобное ΔA1B1C1.

Этот участок пересекается:

– с ребром D в двух точках 1 и 4;

– с ребром Е в двух точках 2 и 5.

Соедините найденные точки: 1-2-3-1; 4-6-5-7-4 и определить видимость.

Конструкция развертки была рассмотрена ранее.

6.4. Задачи для самостоятельной работы

1-4 Начертите линию пересечения граней. Покажите видимость (рис. 6.8-6.11).

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

“>

Начертательная геометрия | Лекция 6. Многогранники

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р.

/ак.ч.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра.
Ребра, пересекаясь, образуют вершины.
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой  параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Решение

1.  

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂ .
2. Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции  необходимо выполнять при помощи пропорционального деления отрезка.

3. В сечении находим точки M и N принадлежащие прямой m.
4. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6. 2).

Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline{1},\overline{2},\overline{3}, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π

1.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

Порядок построения:

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения:

1.  

1. Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

3. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1.  

1. Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
3. Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение:

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость σ⊥π₂, σ//π₁:

• σ//АВС – основанию пирамиды;
• σ пересекает пирамиду ’ сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Грань D₂E₂∩S₂B₂ =6₂.

Ребро F₂∩S₂B₂ =7₂.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты.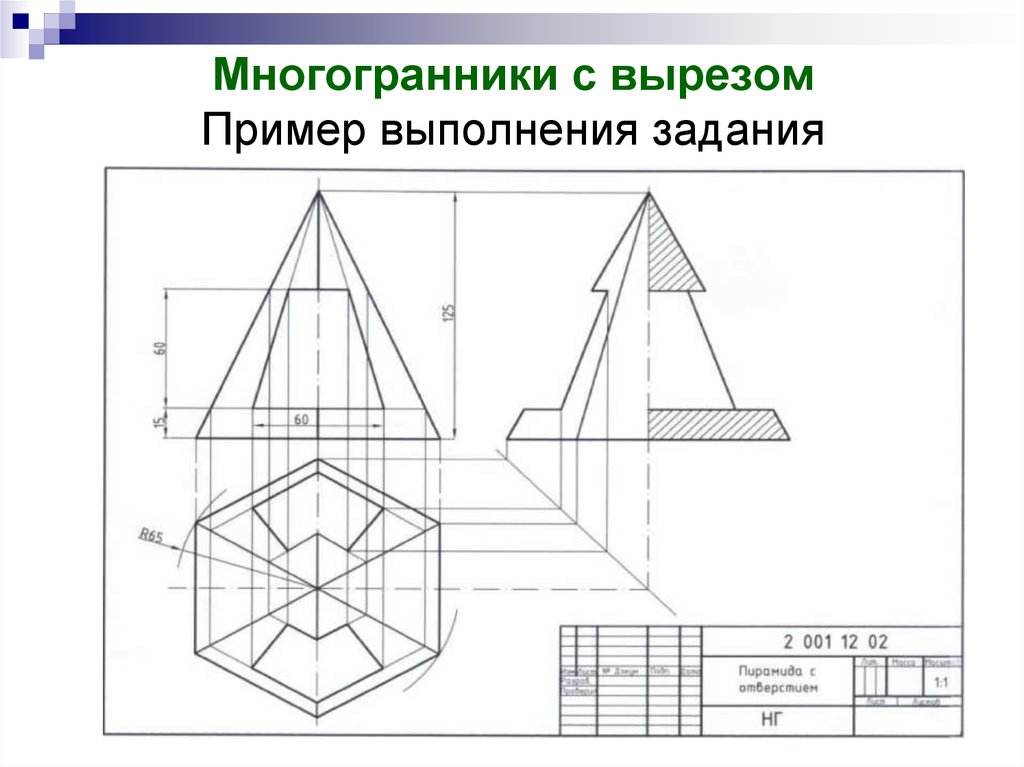 Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

Фруста | ClipArt ETC

Галерея Frusta ClipArt предлагает 48 иллюстраций частей твердого тела, обычно конуса или пирамиды, которые находятся между двумя параллельными плоскостями, пересекающими твердое тело.

Конус, срезанный плоскостью

Иллюстрация прямого круглого конуса, срезанного плоскостью, параллельной основанию. Нижняя часть…

Конус, срезанный плоскостью

Иллюстрация прямого круглого конуса, срезанного плоскостью, параллельной основанию. Верхняя часть…

Усеченный конус

Иллюстрация усеченного прямого кругового конуса со скрытыми ребрами. Когда конус разрезается…

Усеченный конус

Иллюстрация усеченного прямого кругового конуса. Когда конус разрезается плоскостью, параллельной основанию,…

Усеченная пирамида десятиугольной формы

Иллюстрация десятиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Верхняя секция…

Усеченная десятиугольная пирамида

Иллюстрация полой десятиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная пирамида десятиугольной формы

Иллюстрация десятиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Верхняя секция…

Усеченная пирамида десятиугольной формы

Иллюстрация полой семиугольной/семиугольной пирамиды, которая была разрезана плоскостью, параллельной…

Усеченная пирамида

Если пирамиду разрезать в плане параллельно основанию так, чтобы образовались две части, то нижняя часть называется…

Усеченная пирамида

Усеченная часть пирамиды – это часть пирамиды, заключенная между основанием и сечением, параллельным…

Усеченная треугольная пирамида

Усеченная треугольная пирамида эквивалентна сумме трех пирамид, общая высота которых…

Шестиугольная пирамида, разрезанная плоскостью

Иллюстрация правильной шестиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Нижний…

Усеченная шестиугольная пирамида

Иллюстрация правильной шестиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная шестиугольная пирамида

Иллюстрация правильной шестиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная шестиугольная пирамида

Иллюстрация правильной шестиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная многоугольная пирамида

Иллюстрация полой многоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Восьмиугольная пирамида, разрезанная плоскостью

Иллюстрация правильной восьмиугольной пирамиды со скрытыми ребрами, которая была разрезана плоскостью, параллельной…

Восьмиугольная пирамида, разрезанная плоскостью

Иллюстрация правильной восьмиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Нижний…

Усеченная восьмиугольная пирамида

Иллюстрация полой восьмиугольной пирамиды, разрезаемой плоскостью, параллельной основанию. Топ…

Усеченная пятиугольная пирамида

Иллюстрация правильной пятиугольной пирамиды, разрезаемой плоскостью, параллельной основанию. Топ…

Усеченная пятиугольная пирамида

Иллюстрация полой пятиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная пятиугольная пирамида

Иллюстрация правильной пятиугольной пирамиды, высота которой намного больше длины ребер основания,…

Усеченная пятиугольная пирамида

Иллюстрация правильной пятиугольной пирамиды, высота которой меньше длин ребер основания,…

Усеченная пятиугольная пирамида

Иллюстрация полой пятиугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная пирамида

Усеченная пирамида — это часть пирамиды, заключенная между основанием и секцией, параллельной…

Усеченная пирамида для объема

Объем усеченной пирамиды любой пирамиды равен сумме объемов трех пирамид, чьи…

Усеченная пирамида

Иллюстрация пирамиды с вершиной, срезанной плоскостью, параллельной основанию. Оставшаяся часть…

Прямоугольная пирамида, разрезанная плоскостью

Иллюстрация правильной прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Нижний…

Прямоугольная пирамида, разрезанная плоскостью

Иллюстрация правильной прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Прямоугольная пирамида, разрезанная плоскостью

Иллюстрация правильной прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Прямоугольная пирамида, разрезанная плоскостью

Иллюстрация правильной прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Нижний…

Усеченная прямоугольная пирамида

Иллюстрация прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная прямоугольная пирамида

Иллюстрация прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию. Топ…

Усеченная прямоугольная пирамида

Иллюстрация прямоугольной полой пирамиды, разрезанной плоскостью, параллельной основанию.…

Усеченная прямоугольная пирамида

Иллюстрация прямоугольной полой прямоугольной пирамиды, разрезанной плоскостью, параллельной основанию.…

Правая шестиугольная пирамида со стороной основания 20 мм и высотой оси 40 мм опирается на одну из его треугольное лицо на земле.

20kviews

Правая шестигранная пирамида с основанием 20 мм и высотой оси 40 мм опирается одной из своих треугольных граней на землю. 90$ в ПО. Нарисуйте его проекции, считая вершину ближе к ВП.

технический чертеж

ДОБАВИТЬ КОММЕНТАРИЙ Изменить

1 Ответ

3

2,6KViews

РАБОТА ДАННЫЕ

КРЕМА ОСА = 20 ММ

Длина оси = 40 мм

. основания, содержащегося в покоящейся треугольной грани, наклонено на 45° с вершиной VP

ближе к VP.

Этап 1

1. Нарисуйте линию XY.

2. Пирамида опирается на ХП, поэтому на ТВ будет виден шестиугольник, а на FV треугольник.

3. Нарисуйте TV в виде шестиугольника с двумя сторонами, перпендикулярными VP (линия XY).

4. Назовите шестиугольник 1 2 3 4 5 6.

5. Возьмите проекции всех угловых точек в FV.

6. Укомплектуйте FV, взяв длину оси 40 мм.

7. Назовите FV как 1’ 2’ 3’ 4’ 5’ 6’ в основании и точке вершины как O’.

Этап 2

1. Так как одна из треугольных граней лежит на земле (HP), считайте, что треугольная грань O’4’5’ пирамиды лежит на HP.

2. Итак, сначала отметьте точку 4’5’ на удобном расстоянии по линии XY.

3. Используя компас, отметьте точки O’ и 1’2’, которые указывают на вершину O’, и завершите FV на 2-м этапе.

4. Возьмите проекции всех 7 точек 1’2’3’4’5’6’ и O’ на TV.

5. Возьмите горизонтальные проекции точек основания и вершины шестиугольных пирамид вправо.

6. Отметьте точки пересечения 1, 2, 3..12 и вершину O.

7. Наклонные края O4 и O5 не видны на ТВ, поэтому нарисуйте эти две линии пунктиром.

8. Нарисуйте оставшиеся линии как непрерывные сплошные линии, так как они видны на экране телевизора.

Этап 3

1. Теперь на третьем этапе ребро основания (4 5) треугольной грани О 4 5 наклонено к ВП под углом 45°.