Основание системы счисления определение: 1. Дать определение системы счисления. Назвать и охарактеризовать свойства системы счисления. 2. Какие символы используются…

Системы счисления

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЭКОНОМИКИ И УПРАВЛЕНИЯ

Кафедра Экономической Информатики

Лабораторный практикум

Для студентов всех специальностей дневной формы обучения

Новосибирск 2007

Введение

Лабораторный практикум по теме «Системы счисления» предназначен для проведения практических занятий с целью получения основных понятий о том, как происходят вычислительные операции в ЭВМ.

В лабораторном практикуме содержатся основные определения о системах счисления, их видах и назначениях. Разбирается, как образуются целые числа в позиционных системах счисления. Приведены таблицы соответствия между числами в различных позиционных системах счисления. Даны правила перевода между системами счисления.

Показано, как происходят операции сложения, вычитания, умножения и деления в позиционных системах счисления.

После разбора каждой темы студентам предлагается выполнить самостоятельную работу по вариантам (вариант соответствует номеру компьютера).

Защита лабораторной работы выполняется в виде индивидуального задания и ответа на контрольные вопросы.

Для ответов на контрольные вопросы необходимо прочитать соответствующую литературу.

Самостоятельные и индивидуальные работы выполняются аналогично разобранным примерам, т.е. содержат схемы перевода, вычислений и проверку¹.

Индивидуальные задания оформляются средствами текстового процессора Word и содержат титульный лист, текст задания и решение.

Система счисления–это знаковая система, в которой числа записываются по определенным правилам, с помощью символов некоторого алфавита.

Символы алфавита, который используется для записи чисел, называются цифрами.

Системы счисления разделяются на две большие группы:

• позиционные

• непозиционные

1. Непозиционные системы счисления

Самой распространенной из непозиционных систем счислении является римская. Мы пользуемся ею для обозначения юбилейных дат, для нумерации страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д.

В этой системе в качестве цифр используются некоторые буквы. В настоящее время римские цифры выглядят так:

I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000

Значение цифры не зависит от ее положения в числе. Например, в числе XXX цифра X встречается трижды, и в каждом случае обозначает 10. Само число XXX означает 30.

Величина числа в римской системе счисления определяется как сумма или разность чисел.

Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.

Например, 1998 = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1 + 1 = M CM XC V I I I

Подряд одна и та же цифра ставится не более 3-х раз. Например, если число 80 = LXXX, то 90 записывается как XC, а не LXXXX.

2. Позиционные системы счисления

Позиционные системы счисления используются для счета.

В позиционных системах счисления величина числа зависит от позиции цифры в числе. Например, в десятичной системе счисления числа 58 и 85 не равны, хотя содержат одни и те же цифры.

Любая позиционная система счисления характеризуется своим основанием.

основание позиционной системы счисления – это количество различных знаков или символов, которые используются для изображения цифр в данной системе счисления.

Основание системы счисления 10 2 8 16

Цифры, используемые в системе счисления 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F

В принципе основанием системы счисления может быть любое натуральное число – два, три, четыре. Следовательно, возможно бесчисленное множество позиционных систем счисления: двоичная, троичная, четверичная и т.д.

Закономерность построения позиционных чисел имеет математическое представление.

Введем обозначения:

q – основание системы счисления;

a_i – любая цифра из множества цифр, принятых в данной системе счисления;

i – индекс, который обозначает номер разряда, занимаемого цифрой в числе,

где a_i удовлетворяет неравенству

и принимает в этом диапазоне только целые значения.

Позицию для целых чисел обозначим номерами 1,2,…, n, а позиции в правильных дробях – номерами -1, -2,…, -m.

Тогда любое число А в произвольной позиционной системе счисления с основанием q можно записать следующим образом:

A_n = a_n-1q ^n-1 + a_n-2 q ^n-2 + … + a₁q ¹ + a₀q ⁰ + a _-1q ^-1 + … + a _{– m}q ^-m , (1)

где qⁱ называется позиционным значением или весом i – го разряда.

Для десятичной системы счисления понятие веса разряда соответствует названиям позиций – единицы, десятки, сотни, десятые доли, сотые доли и т.д.

ПРИМЕР:

Для десятичной системы счисления

Разряды 3 2 1 0

Число 2 1 2 4₁₀ = 2 х 10³ + 1 х 10² + 2 х 10¹ + 4 х 10⁰

Для двоичной системы счисления

Разряды 3 2 1 0 -1

Число 1 0 0 1, 1 ₂ = 1 х 2³ + 0 х 2² + 0 х 2¹ + 1 х 2 ⁰ + 1 х 2^-1

Для восьмеричной системы счисления

Разряды 3 2 1 0 -1 -2

Число 3 0 5 2, 4 1 ₈ = 3 х 8³ + 0 х 8² + 5 х 8¹ + 2 х 8 ⁰ + 4 х 8^-1 +1 х 8^-2

Системы счисления | Практическая информатика

Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.

В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы:

I 	V 	X 	L	C	D 	M
1 	5 	10 	50	100	500 	1000

Например, VI = 5 + 1 = 6, а IX = 10 — 1 = 9.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе — шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим — десятки. Следы вавилонской системы сохранились до наших дней в способах измерения и записи величин углов и промежутков времени.

Однако наибольшую ценность для нас имеет индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.

Для того чтобы лучше понять различие позиционной и непозиционной систем счисления, рассмотрим пример сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Большая цифра соответствует большему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.

Далее мы будем рассматривать только позиционные системы счисления.

Основание системы счисления, в которой записано число, обычно обозначается нижним индексом.

Например, 555₇ — число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы — это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x=a_n*pⁿ+a_n-1*p^n-1+ a₁*p¹+a₀*p⁰, где a_n…a₀ — цифры в представлении данного числа. Так, например,

103510=1*103+0*102+3*101+5*100;
10102 = 1*23+0*22+1*21+0*20 = 10.

Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины. Однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.

Для того чтобы нормально оперировать с числами, записанными в таких нетрадиционных системах, важно понимать, что принципиально они ничем не отличаются от привычной нам десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.

Почему же мы не пользуемся другими системами счисления? В основном потому, что в повседневной жизни мы привыкли пользоваться десятичной системой счисления, и нам не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать над числами, записанными в двоичном виде, довольно просто.

Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.

База | Определение, примеры и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.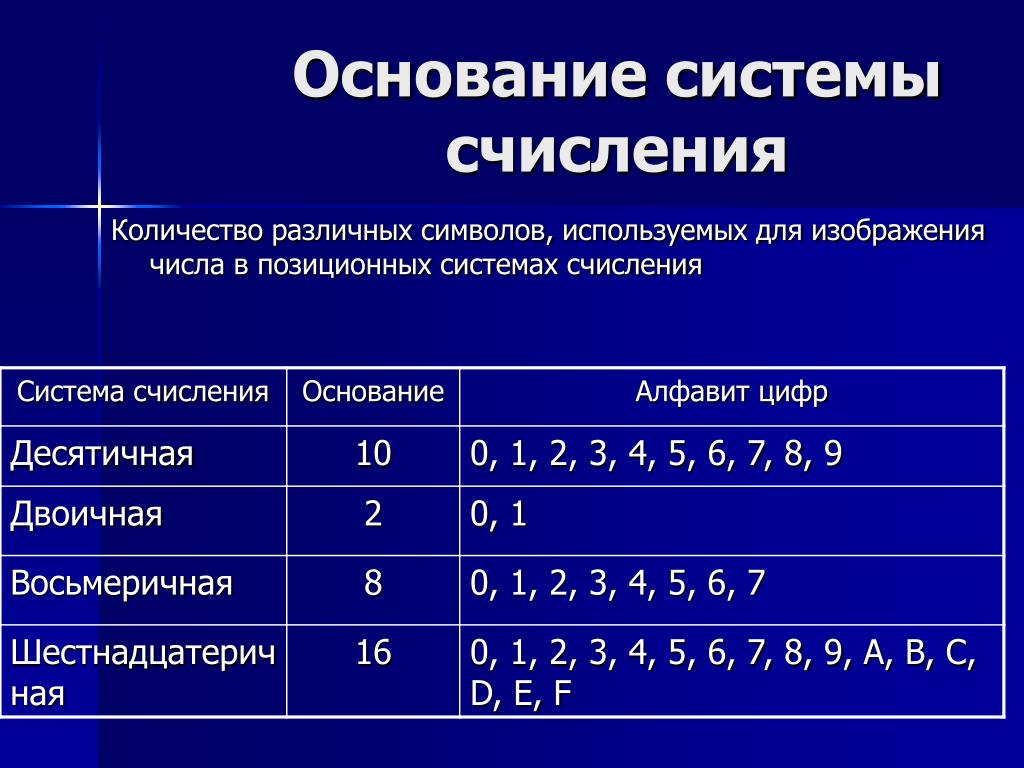
• Britannica Beyond
  Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Факты и сопутствующий контент

Основание (математика) — Простая английская Википедия, бесплатная энциклопедия

Из Простая английская Википедия, бесплатная энциклопедия

В математике основание или основание счисления — это количество различных цифр или комбинация цифр и букв которые система счета использует для представления чисел.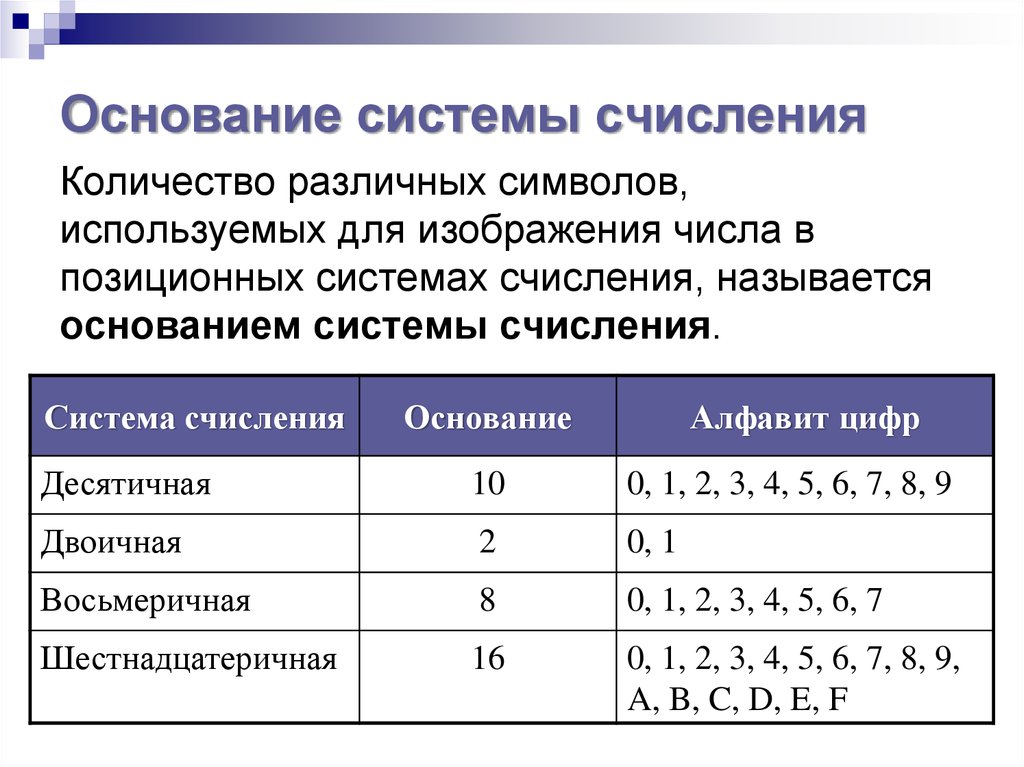 Например, наиболее распространенной системой, используемой сегодня, является десятичная система. Поскольку «dec» означает 10, в нем используются 10 цифр от 0 до 9.. Большинство людей думают, что мы чаще всего используем основание 10, потому что у нас 10 пальцев.

Основание обычно представляет собой целое число больше 1, хотя математически возможны и нецелочисленные основания. Основание числа может быть написано рядом с числом: например, 238{\displaystyle 23_{8}} означает 23 по основанию 8 (что равно 19 по основанию 10).

В компьютерах часто используются разные базы. Двоичный (с основанием 2) используется, потому что на самом простом уровне компьютеры могут работать только с 0 и 1. Шестнадцатеричный формат (с основанием 16) используется из-за того, как компьютеры группируют двоичные числа. Каждые четыре двоичных разряда превращаются в один шестнадцатеричный разряд при переходе между ними. Поскольку в шестнадцатеричном формате более 10 цифр, шесть цифр после 9показаны как A, B, C, D, E и F.