Основание числа: Урок 8. представление чисел в позиционных системах счисления - Информатика

Содержание

Как определить основание числа в информатике

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

Подробная инструкция, как быстро научиться считать в двоичной и шестнадцатеричной системах приведена на сайте https://itvdn.com/ru/blog/article/binary-hexadecimal-system.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд – это позиция цифры в числе. Разрядность числа – количество цифр, из которых состоит число (например, 264 – трехразрядное число, 00010101 – восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 – это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101

2 = 1358.

Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 10000002

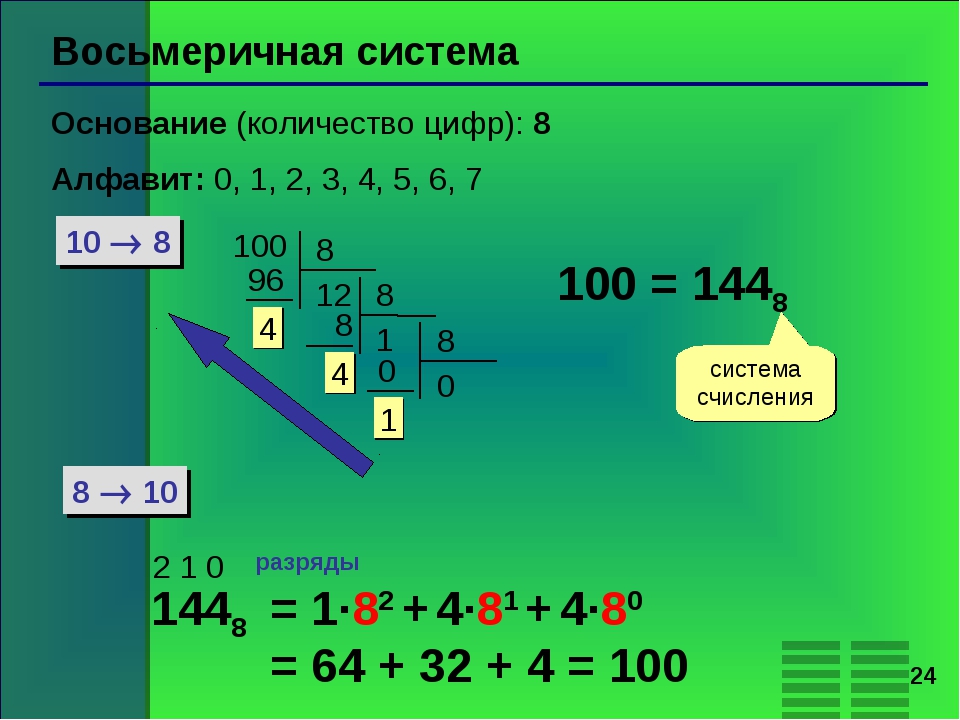
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

6728 = 6 * 8 2 + 7 * 8 1 + 2 * 8 0 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8 2 + 0 * 8 1 + 0 * 8 0 = 6410

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи – это FF.

FF = 15 * 161 + 15 * 160 = 240 + 15 = 255

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее

5 ответов 5

Это ж всё брутфорс, это ж несерьезно 🙂

На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.

Это означает, что

3x 5 + 5x 4 + 2x 2 + x – 118920 = 0

Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂

Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона.

Решаем, и получаем:

x = 8

Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 – 4.865i) 🙂

1) если нужно проверить может ли быть такое число a в данной системе счисления с основанием b, проверьте что все цифры a меньше основания b

т.е. 2358 не может являться числом в 4-ной СС

2)если вы перевели число a из десятичной СС в p-ичную, то для того, чтобы проверить, верно ли вы это сделали, просто переведите ее обратно в десятичную, и проверьте, получится ли то же число а.

Для того чтобы перевести число из p-ичной СС в десятичную, умножьте первую справа цифру на 1, вторую справа на p, третью на p², и т.д. умножая на степени p, а потом найдите сумму всего этого

1.3. СИСТЕМЫ СЧИСЛЕНИЯ. — Основы информатики

1.3.1.ПОНЯТИЕ СИСТЕМЫ СЧИСЛЕНИЯ.

Все фантастические возможности вычислительной техники (ВТ) реализуются путем создания разнообразных комбинаций сигналов высокого и низкого уровней, которые условились называть «единицами» и «нулями».

Система счисления(СС) — это система записи чисел с помощью определенного набора цифр.CС называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе. Десятичная СС является позиционной: 999.Римская СС является непозиционной. Значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.Количество различных цифр, употребляемых в позиционной СС, называется основанием СС.

Развернутая форма числа — это запись, которая представляют собой сумму произведений цифр числа на значение позиций.

Например: 8527=8*10³+5*10²+2*10¹+7*10⁰

Развернутая форма записи чисел произвольной системы счисления имеет вид

, где

X — число;
a — основа системыисчисления;
i — индекс;
m — количество разрядов числа дробной части;
n — количество разрядов числа целой части.

Например: 327.46 n=3, m=2, q=10

Если основание используемой СС больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение.

Например: если 10=А, а 11=В, то число 7А.5В₁₂можно расписать так:

7А.5В₁₂= В·12^-2+ 5 ·2^-1+А ·12⁰+ 7 ·12¹.

В шестнадцатеричной СС основа — это цифры 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 с соответствующими обозначениями 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Примеры чисел: 17D.ECH, F12AH.

ДвоичнаяСС— это система, в которой для записи чисел используются две цифры 0 и 1. Основанием двоичной системы счисления является число 2.

Двоичный код числа — запись этого числа в двоичной системе счисления. Например,

0=0₂
1=1₂
2=10₂
3=11₂…
7=111₂
120=1111000₂.

В ВТ применяют позиционные СС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную. Для обозначения используемой СС число снабжают верхним или нижним индексом, в котором записывают основание СС. Другой способ – использование латинских букв после записи числа:

D – десятичная СС
В – двоичная СС
О – восьмеричная СС
Н – 16-ричная СС.

Несмотря на то, что 10-тичная СС имеет широкое распространение, цифровые ЭВМ строятся на двоичных элементах, т.к. реализовать элементы с 10 четко различимыми состояниями сложно. Историческое развитие ВТ сложилось таким образом, что ЭВМ строятся на базе двоичных цифровых устройств: триггеров, регистров, счетчиков, логических элементов и т.д.

16-ричная и 8-ричная СС используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов – команд, данных, адресов и операндов.

Задача перевода из одной СС в другую часто встречается при программировании, особенно, на языке Ассемблера. Например, при определении адреса ячейки памяти. Отдельные стандартные процедуры языков программирования Паскаль, Бейсик, Си, HTML требуют задания параметров в 16-ричной СС. Для непосредственного редактирования данных, записанных на жесткий диск, также необходимо умение работать с 16-ричными числами. Отыскать неисправность в ЭВМ невозможно без представлений о двоичной СС.

В таблице приведены некоторые числа, представленные в различных СС.

Двоичные числа	Восьмеричные числа	Десятичные числа	Шестнадцатеричные числа
0	0	0	0
1	1	1	1
10	2	2	2
11	3	3	3
100	4	4	4
101	5	5	5
110	6	6	6
111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

1.

3.2. ПЕРЕВОД ЧИСЕЛ ИЗ ПРОИЗВОЛЬНОЙ СС В ДЕСЯТИЧНУЮ И ОБРАТНО.

Перевод чисел из произвольной системы в десятичную. Для перевода числа из любой позиционной СС в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂=1*2³+1*2²+0*2¹+1*2⁰=13₁₀

17D.ECH=12·16^-2 + 14·16^-1 +13·16⁰ + 7·16¹ + 1·16²=381.921875

Перевод чисел из десятичной СС в заданную.

1) Для преобразования целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание СС, пока не получат нуль. Числа, которые возникают как остаток от деления на основание СС, представляют собой последовательную запись разрядов числа в выбранной СС от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

Например:

Читая остатки от деления снизу вверх, получим 111011011.

Проверка:

1*2⁸+1*2⁷+1*2⁶+0*2⁵+1*2⁴+1*2³+0*2²+1*2¹+1*2⁰=1+2+8+16+64+128+256=475₁₀.

2) Для преобразования десятичных дробей десятичной СС в число любой СС последовательно выполняют умножение на основание системы счисления , пока дробная часть произведения не станет равной нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например: перевести число 0.375 ₁₀в двоичную СС.

Полученный результат — 0.011₂.

Необходимо отметить, что не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части, округляя последний разряд.

1.3.3. ПЕРЕВОД МЕЖДУ ОСНОВАНИЯМИ, СОСТАВЛЯЮЩИМИ СТЕПЕНЬ 2.

Для того, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

Например:

1234.777₈= 001 010 011 100.111 111 111₂= 1 010 011 100.111 111 111₂

1234567₈= 001 010 011 100 101 110 111₂= 1 010 011 100 101 110 111₂

Обратный перевод: каждая триада двоичных цифр заменяется восьмеричной цифрой, при этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Например:

1100111₂= 001 100 111₂= 147₈

11.1001₂= 011.100 100₂= 3.44₈

110.0111₂= 110.011 100₂= 6.34₈

При переводах между двоичной и шестнадцатеричной СС используются четверки цифр. При необходимости выравнивание выполняется до длины двоичного числа, кратной четырем.

Например:

1234.AB77₁₆= 0001 0010 0011 0100.1010 1011 0111 0111₂=1 0010 0011 0100.1010 1011 0111 0111₂

CE4567₁₆= 1100 1110 0100 0101 0110 0111₂

0.1234AA₁₆= 0.0001 0010 0011 0100 1010 1010₂

1100111₂= 0110 0111₂= 67₁₆

11.1001₂= 0011.1001₂= 3.9₁₆

110.0111001₂= 0110.0111 0010₂= 65.72₁₆

При переходе из восьмеричного счисления в шестнадцатеричное счисление и обратно используется вспомогательный двоичный код числа.

Например:

1234567₈= 001 010 011 100 101 110 111₂= 0101 0011 1001 0111 0111₂= 53977₁₆

0. 12034₈= 0.001 010 000 011 100₂= 0.0010 1000 0011 1000₂= 0.2838₁₆

120.34₈= 001 010 000. 011 100₂= 0101 0000.0111 0000₂= 50.7₁₆

1234.AB77₁₆= 0001 0010 0011 0100.1010 1011 0111 0111₂=

= 001 001 000 110 100.101 010 110 111 011 100₂= 11064.526734₈

CE4567₁₆= 1100 1110 0100 0101 0110 0111₂= 110 011 100 100 010 101 100 111₂= 63442547₈

0.1234AA₁₆=0.0001 0010 0011 0100 1010 1010₂=0.000 100 100 011 010 010 101 010₂=0.04432252₈

1.6. Перевод чисел из одной системы счисления в другую

Как мы уже отмечали, человек привык работать в десятичной системе счисления, а ЭВМ ориентирована на двоичную систему. Поэтому общение человека с машиной невозможно без создания простых и надёжных алгоритмов перевода чисел из одной системы в другую и наоборот. Итак, как осуществить перевод чисел из десятичной системы в двоичную?

Допустим, надо перевести число 11 в двоичную систему счисления. Разделим 11 на 2. Получим частное 5 и остаток 1. Следовательно, в двоичной записи числа 11 последняя цифра равна 1. Для нахождения второй цифры разделим найденное нами частное 5 снова на 2. Получим частное 2 и остаток 1. Следовательно, вторая цифра с конца в двоичной записи числа 11 тоже равна 1. Частное 2 снова делим на 2. Получим 1 и 0 в остатке. Полученная 1 и есть первая цифра в двоичной записи числа 11. Остаток от последнего деления 0 — вторая цифра.

Если необходимо преобразовать нецелое число — десятичную дробь, то производим следующие действия:

1. Целую часть числа преобразовываем в двоичную систему способом, описанным выше.

2. Дробную часть необходимо преобразовывать умножением на основание системы, в которую мы переводим число.

В результате умножения дробной части — числа 0,7 на основание системы — число 2 получим 1,4. Целую часть данного числа (цифру 1) выделяем, а дробную часть — число 0,4 снова умножаем на 2.

Очевидно, что процесс перевода числа 0,7 может продолжаться бесконечно. Действительно, за шесть шагов мы можем получить число 0,101100, а за семь шагов получили бы 0,1011001, которое является более точным представлением числа 0,7 в двоичной системе. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа. В результате перевода получим ответ:

49,710 = 110001,1011002

Для перевода десятичных чисел в другие позиционные системы счисления пользуются теми же правилами, лишь меняется лишь основание системы, в которую надо перевести числа.

Большие числа в двоичной системе счисления имеют очень громоздкие записи. Конечно, можно перевести число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоёмки. На помощь приходят системы, родственные двоичной — восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме.

Системами счисления родственными двоичной считаются такие системы, основания которых являются значением степени числа 2.

Например, четверичная, восьмеричная и шестнадцатеричная системы счисления являются системами, родственными двоичной.

Для перевода чисел из двоичной системы счисления в системы, родственные двоичной, необходимо выполнить следующие действия:

1.Разбить число на некоторое количество разрядов, равное степени числа 2 основания системы, в которую переводим.

2.Если в старших и младших разрядах после разбиения не хватает знаков, то добавить их нулями.

3.По таблице определить значение пары, триады, тетрады и т.п. разрядов, записанных в двоичной системе счисления, соответственно значению в той системе, в которую переводим.

Например, дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в восьмеричную систему счисления разобьём число на триады (т.к. основание числа 2 равно 3), начиная от запятой, вправо и влево: 1.111.010.111.010,011.1 . Разбиение показано точками. В старшей и младшей триадах не хватает разрядов. Дополним их нулями: 001.111.010.111.010,011.100. По таблице определим восьмеричные цифры, соответствующие триадам. Получается восьмеричное число 17272,34.

Рассмотрим ещё один пример: дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в шестнадцатеричную систему счисления разобьём число на тетрады (т.к. основание числа 2 равно 4): 1.1110.1011.1010,0111. В старшей тетраде не хватает разрядов. Дополним их нулями: 0001.1110.1011.1010,0111. По таблице определим шестнадцатеричные знаки, соответствующие тетрадам. Получается шестнадцатеричное число 1EBA,7.

Пусть дано то же число. Для перевода его в четверичную систему счисления разобьём число на пары (т.к. основание числа 2 равно 2): 1.11.10.10.11.10.10,01.11. В старшей паре не хватает одного разряда. Дополним его нулём: 01.11.10.10.11.10.10,01.11. Определим четверичные цифры, соответствующие парам. Получается четверичное число 1322322,13.

Как осуществить обратный перевод?

Пусть дано число 73,62 , записанное в восьмеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру числа запишем в виде триады из 0 и 1, соответствующей значению восьмеричной цифры в двоичной системе счисления: 111.011,110.010.

Следовательно, 73,628 = 111011,1100102

Рассмотрим ещё один пример: дано число 7В3,Е6, записанное в шестнадцатеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру шестнадцатеричного числа запишем в виде тетрады из 0 и 1,соответствующей значению знака в двоичной системе счисления: 0111. 1011.0011,1110.0110.

7В3,Е1616 = 11110110011,11100112

Перевод чисел из р-ичной позиционной системы счисления в десятичную.

Все позиционные системы счисления, о которых мы говорили выше, строятся по одному общему принципу. Выбирается некоторое число р — основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, т.е. произвольное число в системе счисления с основанием р имеет вид:

Функция LOG — Служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции LOG в Microsoft Excel.

Описание

Возвращает логарифм числа по заданному основанию.

Синтаксис

LOG(число;[основание])

Аргументы функции LOG описаны ниже.

Число Обязательный. Положительное вещественное число, для которого вычисляется логарифм.
Основание Необязательный. Основание логарифма. Если аргумент «основание» опущен, предполагается, что он равен 10.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=LOG(10)	Логарифм числа 10. Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10.	1
=LOG(8; 2)	Логарифм числа 8 по основанию 2. Результат (3) — степень, в которую необходимо возвести основание, чтобы получить число 8.	3
=LOG(86; 2,7182818)	Логарифм числа 86 по основанию e (приблизительно 2,718). Результат (4,454) — степень, в которую необходимо возвести основание, чтобы получить число 86.	4,4543473

Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников

Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.

Целые числа (int)

Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:

x + y	Сложение
x — y	Вычитание
x * y	Умножение
x / y	Деление
x // y	Получение целой части от деления
x % y	Остаток от деления
-x	Смена знака числа
abs(x)	Модуль числа
divmod(x, y)	Пара (x // y, x % y)
x ** y	Возведение в степень
pow(x, y[, z])	x^y по модулю (если модуль задан)

Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти). yПобитовое исключающее илиx & yПобитовое иx << nБитовый сдвиг влевоx >> yБитовый сдвиг вправо~xИнверсия битов

Дополнительные методы

int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.

>>> n = -37
>>> bin(n)
'-0b100101'
>>> n.bit_length()
6

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

>>> (1024).to_bytes(2, byteorder='big')
b'\x04\x00'
>>> (1024).to_bytes(10, byteorder='big')
b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00'
>>> (-1024).to_bytes(10, byteorder='big', signed=True)
b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00'
>>> x = 1000
>>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little')
b'\xe8\x03'

classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.

>>> int.from_bytes(b'\x00\x10', byteorder='big')
16
>>> int.from_bytes(b'\x00\x10', byteorder='little')
4096
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
-1024
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
64512
>>> int.from_bytes([255, 0, 0], byteorder='big')
16711680

Системы счисления

Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:

int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
bin(x) — преобразование целого числа в двоичную строку.
hex(х) — преобразование целого числа в шестнадцатеричную строку.
oct(х) — преобразование целого числа в восьмеричную строку.

Примеры:

>>> a = int('19') # Переводим строку в число
>>> b = int('19.5')  # Строка не является целым числом
Traceback (most recent call last):
  File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5)  # Применённая к числу с плавающей точкой, отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011  # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19

Вещественные числа (float)

Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:

>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

>>> a = 3 ** 1000
>>> a + 0.1
Traceback (most recent call last):
  File "", line 1, in
OverflowError: int too large to convert to float

Простенькие примеры работы с числами:

>>> c = 150
>>> d = 12.9
>>> c + d
162.9
>>> p = abs(d - c)  # Модуль числа
>>> print(p)
137.1
>>> round(p)  # Округление
137

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float. hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

>>> (10.5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5

Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.

Модуль math предоставляет более сложные математические функции.

>>> import math
>>> math.pi
3.141592653589793
>>> math.sqrt(85)
9.219544457292887

Модуль random реализует генератор случайных чисел и функции случайного выбора.

>>> import random
>>> random.random()
0.15651968855132303

Комплексные числа (complex)

В Python встроены также и комплексные числа:

>>> x = complex(1, 2)
>>> print(x)
(1+2j)
>>> y = complex(3, 4)
>>> print(y)
(3+4j)
>>> z = x + y
>>> print(x)
(1+2j)
>>> print(z)
(4+6j)
>>> z = x * y
>>> print(z)
(-5+10j)
>>> z = x / y
>>> print(z)
(0.44+0.08j)
>>> print(x.conjugate())  # Сопряжённое число
(1-2j)
>>> print(x.imag)  # Мнимая часть
2.0
>>> print(x.real)  # Действительная часть
1.0
>>> print(x > y)  # Комплексные числа нельзя сравнить
Traceback (most recent call last):
  File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y)  # Но можно проверить на равенство
False
>>> abs(3 + 4j)  # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2)  # Возведение в степень
(-7+24j)

Для работы с комплексными числами используется также модуль cmath.

Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно максимально возможное основание системы счисления?

СИСТЕМА СЧИСЛЕНИЯ
Вариант №1 Вариант №2 Вариант №3 Вариант №4
В1Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1.

Чему равно максимально возможное основание системы счисления?
Запись числа 280 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления. Запись числа 381 в системе счисления с основанием N содержит 3 цифры и оканчивается на 3. Чему равно максимально возможное основание системы счисления? Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
В2Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 348 оканчивается на 20.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 84 оканчивается на 14. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 61 оканчивается на 15.
В3 Запись числа 30 в некоторой системе счисления выглядит так: 110q. Найдите основание системы счисления q. Запись числа 23 в некоторой системе счисления выглядит так: 212q. Найдите основание системы счисления q.
Запись числа 2B16 в некоторой системе счисления выглядит так: 111q. Найдите основание системы счисления q.
Запись числа 2105 в некоторой системе счисления выглядит так: 313q. Найдите основание системы счисления q.
В4Чему равно число Х, если выполнено равенство
25х+172х=135х 25х+183х=126х 14х+262х=136х 242х+163х=224х
В5 Найти значение выражения и записать в двоичной системе счисления
1216+118*104 1016+128*114 1116+108*124 1016*114+128
В6Решите уравнение. Ответ дайте в восьмеричной системе счисления
11002+102*Х=1010102 11012+102*Х=1010112 10012+102*Х=1011018 11112+102*Х=1010112
В7Переведите число
249 из 12-ричной в 5-ричную с/с 249 из 13-ричной в 6-ричную с/с 315 из 11-ричной в 7-ричную с/с 183 из 15-ричной в 9-ричную с/с

Приложенные файлы

82236447
Размер файла: 15 kB Загрузок: 4

целые, вещественные, комплексные — Питошка

Числа в Python 3: целые, вещественные, комплексные. yПобитовое исключающее илиx & yПобитовое иx << nБитовый сдвиг влевоx >> yБитовый сдвиг вправо~xИнверсия битов

Дополнительные методы

>>> n = -37
>>> bin(n)
'-0b100101'
>>> n.bit_length()
6

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

>>> (1024).to_bytes(2, byteorder='big')
b'\x04\x00'
>>> (1024).to_bytes(10, byteorder='big')
b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00'
>>> (-1024).to_bytes(10, byteorder='big', signed=True)
b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00'
>>> x = 1000
>>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little')
b'\xe8\x03'

classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.

>>> int.from_bytes(b'\x00\x10', byteorder='big')
16
>>> int.from_bytes(b'\x00\x10', byteorder='little')
4096
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
-1024
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
64512
>>> int.from_bytes([255, 0, 0], byteorder='big')
16711680

Системы счисления

int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
bin(x) — преобразование целого числа в двоичную строку.
hex(х) — преобразование целого числа в шестнадцатеричную строку.
oct(х) — преобразование целого числа в восьмеричную строку.

Примеры:

>>> a = int('19') # Переводим строку в число
>>> b = int('19.5')  # Строка не является целым числом
Traceback (most recent call last):
  File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5)  # Применённая к числу с плавающей точкой, отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011  # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19

Вещественные числа (float)

>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

>>> a = 3 ** 1000
>>> a + 0.1
Traceback (most recent call last):
  File "", line 1, in
OverflowError: int too large to convert to float

Простенькие примеры работы с числами:

>>> c = 150
>>> d = 12.9
>>> c + d
162.9
>>> p = abs(d - c)  # Модуль числа
>>> print(p)
137.1
>>> round(p)  # Округление
137

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float.hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

>>> (10.5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5

Модуль math предоставляет более сложные математические функции.

>>> import math
>>> math.pi
3.141592653589793
>>> math.sqrt(85)
9.219544457292887

Модуль random реализует генератор случайных чисел и функции случайного выбора.

>>> import random
>>> random.random()
0.15651968855132303

Комплексные числа (complex)

В Python встроены также и комплексные числа:

>>> x = complex(1, 2)
>>> print(x)
(1+2j)
>>> y = complex(3, 4)
>>> print(y)
(3+4j)
>>> z = x + y
>>> print(x)
(1+2j)
>>> print(z)
(4+6j)
>>> z = x * y
>>> print(z)
(-5+10j)
>>> z = x / y
>>> print(z)
(0.44+0.08j)
>>> print(x.conjugate())  # Сопряжённое число
(1-2j)
>>> print(x.imag)  # Мнимая часть
2.0
>>> print(x.real)  # Действительная часть
1.0
>>> print(x > y)  # Комплексные числа нельзя сравнить
Traceback (most recent call last):
  File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y)  # Но можно проверить на равенство
False
>>> abs(3 + 4j)  # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2)  # Возведение в степень
(-7+24j)

Также для работы с комплексными числами используется также модуль cmath.

Number Base | Блестящая вики по математике и науке

Для целых чисел:

Для преобразования десятичной системы в другую систему счисления выполните следующие шаги:

Разделите десятичное число, которое нужно преобразовать, на новое основание и запишите остаток.
Разделите частное, полученное в предыдущем делении, на новое основание и запишите остаток.
Повторяйте шаг 2, пока частное не станет равным 0.
Теперь, когда частное станет 0, запишите полученные остатки справа налево в том порядке, в котором они были получены; если вы получите 1 как остаток от первого деления, 3 от второго деления и 6 от третьего деления, запишите его как 631.

Преобразовать 271027_ {10} 2710 в базу 8.
Используя шаги, изученные выше, мы имеем следующее:
разделив 27 на 8, мы получим остаток 3 и частное 3,
разделив 3 на 8, мы получим остаток 3 и частное 0.
Следовательно, его эквивалентное восьмеричное представление 33833_8338. □ _ \ квадрат □

Для чисел с плавающей запятой:

Предположим, что у нас есть положительное целое число cncn − 1 ⋯ c3c2c1c0.c − 1c − 2 ⋯ c − m‾ \ overline {c_nc_ {n-1} \ cdots c_3c_2c_1c_0.c _ {- 1} c _ {- 2} \ cdots c _ {- m}} cn cn − 1 ⋯ c3 c2 c1 c0 .c − 1 c − 2 ⋯ c − m в десятичной системе счисления с nnn цифрами перед десятичной точкой и mmm цифрами после. Затем можно отдельно преобразовать целую и дробную части, а затем сложить.

Целая часть может быть преобразована, как в приведенном выше примере, поэтому теперь нам нужно преобразовать дробную часть. То есть 0.c − 1c − 2 ⋯ c − m0.c _ {- 1} c _ {- 2} \ cdots c _ {- m} 0.c − 1 c − 2 ⋯ c − m в десятичной системе счисления. необходимо преобразовать в базовый bbb.Это можно сделать, выполнив следующие действия:

Умножьте десятичную дробную часть на bbb.
Обратите внимание на целую часть полученного числа.
Теперь снова возьмем дробную часть предыдущего полученного числа как новую дробную часть. Если он равен нулю, то все готово. Если нет, то мы повторим вышеуказанные шаги.
Все указанные целые части записываются слева направо в том порядке, в котором они были получены, с предшествующей десятичной точкой.

Это наглядно можно понять на примере:

Преобразовать 987.11111111111… 987.11111111111 \ ldots 987.11111111111… в основе восьмеричного числа.
Во-первых, целая часть 987987987 будет равна 173317331733 в восьмеричной системе счисления согласно вышеупомянутой теории.
Теперь возьмем дробную часть 0.111111111111… 0.111111111111 \ ldots0.111111111111….
Умножая на 8, получаем 0,888888888888888888… 0,888888888888888888 \ ldots0,888888888888888888….
Теперь целая часть равна нулю, а новая дробная часть — 0,888888888888… 0.888888888888 \ ldots0.888888888888….
Снова умножая эту новую дробную часть на 8, мы получаем 7.1111111111111… 7.1111111111111 \ ldots7.1111111111111….
Теперь целая часть равна 7, а новая дробная часть — 0,111111111… 0,111111111 \ ldots0,111111111….
Здесь мы видим, что у нас снова 0,111111111… 0,111111111 \ ldots0.111111111…, поэтому цифры будут повторяться.
Следовательно, восьмеричное представление 0,11111111111… 0,11111111111 \ ldots0,11111111111… равно 0,070707070707… 0.070707070707 \ ldots0.070707070707….
Таким образом, новое число будет 1733.07070707… 1733.07070707 \ ldots1733.07070707… в восьмеричной системе счисления. □ _ \ квадрат □

Узнайте о системе счисления

Мы привыкли записывать числа в десятичной системе счисления, используя символы для 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Например, 75 означает 7 десятков и пять единиц. Однако числа можно записывать любым числом. база.

Если мы используем базу 8 вместо десяти, то 75 будет записано как 113 что обозначает один шестьдесят четыре (8 ²), один восемь (8 ¹) и 3 единицы (вместо сотен, десятков и единицы измерения).

Base 2 особенно полезен, так как требует только двух символов, для нуля и единицы, и именно так числа представлены в компьютеры.

Так же, как и в десятичной системе счисления, столбцы представляют степени 10 и имеют «разрядное значение» 1, 10, 10 ², 10 ³ и т. д. (чтение справа налево), поэтому в базе 2 столбцы представляют степени 2. Следовательно, число 1001011 означает (чтение справа слева):

1 шт. (2 ⁰), 1 два (2 ¹), без четверок (2 ²), 1 восьмерка (2 ³), без шестнадцати (2 ⁴), нет тридцать два (2 ⁵), 1 шестьдесят четыре (2 ⁶).

Число 1001011 в базе 2 совпадает с числом 75 в основание десять.

В качестве другого примера мы используем символы 0, 1, 2, 3 и 4 для представляют числа в базе 5. Столбцы в базе 5 имеют место значение ‘1, 5, 25, 125, 625 и т. д. чтение справа налево. В число 75 по основанию десять совпадает с числом 300 по основанию пять, то есть 3 двадцати пяти, без пятерок и без единиц.

Число 4102 в основании 5 означает 2 единицы, без пятерок, 1 двадцать пять и четыреста двадцать пять, всего 527 по основанию десять.

Записав число 75 в основание шесть, мы получим 203, что представляет 2 тридцать шестерок, без шестерок и 3 шт.

Мы видели, что 75 (base10), 1001011 (base 2), 300 (base 5), 113 (основание 8) и 203 (основание 6) представляют одно и то же число.

Точно так же мы можем написать 75 в любой базе, которую мы выберем, и мы можем запишите все числа в любую базу.

Для записи чисел от 0 до 1 мы используем отрицательные степени база. Например, в базе 2 мы используем половинки, четверти, восьмые, шестнадцатые и т. д. вместо десятых, сотых, тысячных и т. д.{-2} $. Эквивалент в базе 10 равен $ 2 + 1 + {1 \ over 2} + {1 \ over 4} $, то есть 3,75 по основанию 10.

Номерные базы | Математика | Вычислительная техника

Существует более простое объяснение основ счисления, наряду с интерактивными страницами. на двоичных, двоичных дробях, нормализованных двоичных числах с плавающей запятой и шестнадцатеричный в Интерактивный раздел . Также существует система счисления Abacus , которую вы можете использовать для экспериментов с различными основами счисления, и вы можете смотрите видеоролики по номерным базам на YouTube-канале AdvancedICT . Для большинства курсов по компьютерным наукам GCSE требуется преобразование между основами счисления.

Что такое основание счисления?

Немецкий математик Леопольд Кронекер однажды сказал, что «Бог дал нам целые числа, а все остальное — дело рук человека». Я думаю, что он имел в виду, что числа существуют, но мы можем выбирать их по-разному и делать с ними разные вещи. Не вдаваясь в философские размышления, полезно помнить, что часто то, что мы думаем о числах, на самом деле являются символами, представляющими число — точно так же, как вы пишете свое имя, это не вы, и вы все тот же человек, если набираете ваше имя, напишите его другим цветом или используйте другой алфавит.

Числовые базы — это разные способы написания и использования одного и того же числа. Для нашей арифметики мы используем систему, называемую десятичной системой, или динарией, но оснований счисления почти столько же, сколько и чисел. Многие думают, что мы используем основание 10, потому что у нас есть 10 пальцев, по которым мы можем считать. Компьютеры и другие электронные устройства могут надежно использовать только электрический ток или его отсутствие для счета (например, имея два пальца), и поэтому они, как правило, используют основание 2 (двоичное) для внутренних целей.

Важно помнить, что числовые базы — это просто разные способы записи чисел — точно так же, как римские цифры или счетные таблицы, — но в остальном числа ведут себя как обычно. Это не означает, что их арифметика принципиально отличается — на самом деле, поведение основ счисления полностью согласовано.

Как они работают?

Вы познакомитесь с идеей базы 10 и заголовками столбцов, о которых вы говорили в начальной школе — единицы, десятки, сотни, тысячи и т. Д.- точно так же работают и другие числовые базы. У них есть столбцы с заголовками, которые используются для представления чисел, а разные цифры размещаются в разных местах, начиная с правого.

Заголовки столбцов для общих оснований и общего основания x показаны в таблице ниже:

Заголовки столбцов								Номер База
128	64	32	16	8	4	2	1	2 (двоичный)
и т. п.	262144	32768	4096	512	64	8	1	8 (восьмеричный)
	и т. Д.	100000	10000	1000	100	10	1	10 (денар.)
		и т. Д.	65536	4096	256	16	1	16 (шестнадцатеричный)
и т. Д.	Х ⁶	Х ⁵	Х ⁴	Х ³	Х ²	Х ¹	Х ⁰	Х

Основание обычно записывается как нижний индекс после числа, поэтому вы можете сказать, что 111 ₂ — это 7 в двоичной системе, а не сто одиннадцать.

Вы можете работать с любой системой счисления (кроме 1, что на самом деле не имеет смысла), и некоторые языки программирования, такие как Lisp, позволяют вам это делать.Однако в вычислениях вы обычно сталкиваетесь только со следующими четырьмя базами, и вы уже знаете базу 10. Эти общие базы также имеют имена собственные, указанные в скобках:

с основанием 2 (двоичный)
основание 8 (восьмеричное)
по основанию 10 (денар)
с основанием 16 (шестнадцатеричный)

Самая большая цифра, которая может быть в любом столбце, — это на единицу меньше номера основания. Таким образом, для двоичного кода (основание 2) это 1, затем 7 для восьмеричного (основание 8), 9 для денарного (основание 10) и т.д.

Однако после основания 10 у нас заканчиваются цифры для представления чисел, поэтому мы должны использовать буквы, где A = 10, B = 11, C = 12 и т. Д. Таким образом, последовательность для чисел, записанных в шестнадцатеричном формате, равна 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, за которыми следуют 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F и т. Д.

Когда мы пишем число по основанию 10, мы знаем его значение, потому что умножаем отдельные цифры на соответствующие им заголовки столбцов. Например, когда мы видим 123, даже если мы не думаем об этом, мы вычисляем 1 x 100 + 2 x 10 + 3 x 1, чтобы получить сто двадцать три.Остальные числовые базы работают точно так же.

Вы можете использовать эту информацию, чтобы преобразовать числа из других оснований в основание 10, например:

32	16	8	4	2	1
		1	0	1	1 ₂	= 8 + 2 + 1 = 11 ₁₀

32768	512	64	8	1
	1	2	3	4 ₈	= 1 x 512 + 2 x 64 + 3 x 8 + 4 x 1 ₁₀ = 512 + 128 + 24 + 4 ₁₀ = 668 ₁₀

Двоичный (База 2)

В наши дни вы, вероятно, не часто сталкиваетесь с двоичными файлами, но полезно понимать, что именно так компьютеры работают внутри, чтобы вы могли понять такие концепции, как параллельная передача.Тот факт, что компьютеры используют двоичный код, является причиной того, что все кратно 2 — почему компьютеры поставляются с 8 МБ, 16 МБ, 32 МБ, 64 МБ и т. Д. Памяти, а не 10, 20, 30 Мб и т. Д., А также почему их 1024 байт в килобайте (1024 = 2 ¹⁰), а не 1000 байт.

Его основное использование, вероятно, заключается в сочетании с методами поразрядной логики, показанными на предыдущей странице, для объединения и разделения значений, хранящихся в одном байте (или слове).

Есть еще несколько терминов, относящихся к двоичным файлам, которые вам нужно знать.Во-первых, бит , — это двоичная цифра , , то есть единственное вхождение 0 или 1. Это наименьшая единица хранения, которую вы можете иметь внутри компьютера. Группы из 8 бит называются байтом . Байт может использоваться для представления числа, цвета или символа (например, с использованием ASCII). Вы также можете услышать термин полубайт , что составляет 4 бита. Наконец, слово — это наибольшее количество бит, которое процессор может обработать за один раз — например, когда мы говорим, что новые компьютеры имеют 64-битные процессоры, мы имеем в виду, что длина слова составляет 64 бита или 8 байтов. .

Наибольшее значение, которое вы можете сохранить, используя определенное количество битов, можно определить довольно легко. Используя n бит, наибольшее значение, которое вы можете сохранить, составляет 2 ⁿ — 1 , а количество различных значений, которые вы можете сохранить, составляет 2 ⁿ (от 1 до 2 ⁿ — 1 , а затем и 0). Таким образом, используя 8 бит, наибольшее число, которое вы можете сохранить, будет 2 ⁸ — 1 = 255, а количество возможных значений — 2 ⁸ = 256 (т.е.е. 0 — 255). Таким образом, 32-разрядный компьютер может обрабатывать значения до 4 194 967 296 за один такт — очевидно, он может справиться с большими числами, но сначала необходимо их разделить.

Восьмеричный (база 8)

Я никогда не встречал ничего, что использует восьмеричное! Я думаю, что он, вероятно, включен в спецификации экзамена по чисто академическим причинам и потому, что его легко преобразовать в двоичный (см. Ниже).

Шестнадцатеричный (основание 16)

Шестнадцатеричный формат до сих пор используется довольно часто, особенно для таких вещей, как цвета в HTML или языках программирования.Это также весьма полезно, потому что представления больших чисел относительно компактны, но легко конвертируются в двоичные, чтобы вы могли видеть битовые шаблоны.

Биты перестановочные

Вы, несомненно, заметили, что с числами с основанием 10 вы можете перемещать цифры влево или вправо на одно место, умножая или деля число на 10. Тот же трюк работает с разными основами чисел — вы просто умножаете и делите на основание число (например, умножьте на 2 в двоичном формате, чтобы сдвинуть биты влево на одно место).

Это может быть полезно для таких вещей, как создание шестнадцатеричных значений цвета (например, для веб-страниц). В 24-битной системе (такой как HTML) цвета представлены 24-битными числами от 000000 до FFFFFF (каждая шестнадцатеричная цифра соответствует 4 битам — см. Ниже). 24 бита состоят из 8 бит, каждый для количества красного, зеленого и синего цвета.

Итак, каждый компонент представлен 8 битами, то есть числом от 0 до 255. Если вы знаете, сколько красного, зеленого и синего вы хотите, как вы объедините их, чтобы найти полный цвет? Для HTML правильный порядок битов — RRGGBB (r = красный, g = зеленый, b = синий), поэтому нам нужно «сдвинуть» значения зеленого и красного компонентов, а затем сложить все три компонента вместе. .

Мы можем оставить синее значение как есть, но нам нужно переместить значение зеленого в два места. Чтобы переместиться на одно место в шестнадцатеричном формате, мы умножаем его на 16, поэтому, чтобы переместиться на два места, просто сделайте это дважды — 16 x 16 = 256 — так что умножьте зеленое значение на 256. Для красного значения нам нужно переместить четыре позиции — 16 x 16 x 16 x 16 = 65 536 — поэтому мы умножаем значение красного компонента на 65 536.

Очевидно, что если бы вы просто пытались определить цвет самостоятельно, вам не нужно было бы выполнять эти шаги, но если бы вы создали программу, подобную моему цветовому микшеру, то вы бы сделали это именно так.

Преобразование между базами

Вы можете преобразовать восьмеричное в двоичное и наоборот, сгруппировав эти двоичные цифры (или биты) в тройки, а затем преобразовав их в их двоичные эквиваленты. Например:

Что такое 101100 ₂ в восьмеричном формате?

101 ₂ = 5 ₁₀

100 ₂ = 4 ₁₀

Просто объедините две цифры:
101100 ₂ = 54 ₈

То же самое можно сделать и для шестнадцатеричного числа, только биты должны быть сгруппированы по четверкам, т. е.грамм.

Что такое 10110110 ₂ в шестнадцатеричной системе счисления?

1011 ₂ = 11 ₁₀ = B ₁₆

0110 ₂ = 6 ₁₀

Просто объедините два результата:
10110110 ₂ = B6 ₁₆

Наконец, шутка о цифрах! Почему программисты путают Рождество с Хэллоуином? Потому что 31 OCT = 25 DEC!

Искусство решения проблем

Чтобы понять понятие базовых чисел , мы рассмотрим нашу собственную систему счисления.Мы используем десятичную систему счисления или десятичную систему счисления. Чтобы объяснить, что это означает, рассмотрим число 2746. Это число можно переписать как

. Обратите внимание, что каждое число в 2746 на самом деле является просто заполнителем, который показывает, сколько всего существует в определенной степени 10. Первая цифра слева от десятичного разряда (напомним, что десятичный разряд находится справа от 6, т.е. 2746.0) говорит нам, что есть шесть, вторая цифра говорит нам, что есть четыре, третья цифра говорит нам, что есть семь, а четвертая цифра говорит нам, что есть два.

Base-10 использует цифры 0-9. Обычно основание или основание , основание числа обозначается как нижний индекс, записанный в правом конце числа (например, в нашем примере выше, 10 — это основание системы счисления).

Основной номер Темы

История

Base-10 — очевидная система счета, потому что у людей 10 пальцев. Исторически сложилось так, что разные общества использовали другие системы. Известно, что вавилонские культуры использовали основание 60; вот почему мы говорим, что в круге 360 градусов, и (проверьте факты) почему мы считаем 60 минут в час и 60 секунд в минуте (они могли использовать это, потому что у него так много кратных, 12 в на самом деле, нам бы не нужны дроби).Римская система, в которой вообще не было никакой базовой системы, использовала определенные буквы для обозначения определенных значений (например, I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000). Представьте, как сложно было бы умножить LXV на MDII! Вот почему введение арабской системы счисления с основанием 10 произвело революцию в математике и естественных науках в Европе.

Примеры задач

Новичок

Вычислить как число в десятичной системе.
- Решение: необходимо переписать в десятичной системе счисления (основание 10) перед вычислением квадратного корня.Для этого умножьте и сложите Таким образом, ответ будет 7.

Найдите число с основанием 2, которое эквивалентно

Средний

2003 AIME I Проблема 13
Задача 3 канадской олимпиады по математике
Предположим, что это неизвестный многочлен неизвестной степени с неотрицательными целыми коэффициентами. Ваша цель — определить этот многочлен. У вас есть доступ к оракулу, который, учитывая целое число, выдает значение полинома at.Однако оракул взимает плату за каждое такое вычисление, поэтому вы хотите минимизировать количество вычислений, которые вы просите оракула выполнить. Покажите, что можно однозначно определить многочлен только после двух консультаций с оракулом. (UIUC POW)

Ресурсы

Книги

Классы

См. Также

Что такое система счисления по основанию 10?

Если вы когда-либо считали от 0 до 9, значит, вы использовали base-10, даже не зная, что это такое.Проще говоря, счисление по основанию 10 — это способ присвоения числовым значениям разрядных значений. Иногда ее называют десятичной системой, потому что значение цифры в числе определяется ее положением относительно десятичной точки.

Силы 10

В системе base-10 каждая цифра числа может иметь целочисленное значение от 0 до 9 (10 вариантов) в зависимости от ее положения. Места или позиции чисел основаны на степени 10. Каждая числовая позиция в 10 раз больше значения справа от нее, отсюда и термин основание-10.Превышение числа 9 в позиции инициирует отсчет в следующей наивысшей позиции.

Цифры больше 1 появляются слева от десятичной точки и имеют следующие разрядные значения:

Единицы
Десятки
сот
тыс.
Десятки тысяч
Сотен тысяч и т. Д.

Справа от десятичной точки отображаются значения, составляющие долю или меньше 1:

Десятые
сотых
тысячных
Десятитысячные
Стотысячных и т. Д.

Каждое действительное число может быть выражено в десятичной системе счисления.Каждое рациональное число, знаменатель которого состоит только из 2 и / или 5 в качестве простых множителей, можно записать как десятичную дробь. Такая дробь имеет конечное десятичное разложение. Иррациональные числа могут быть выражены как уникальные десятичные числа, в которых последовательность не повторяется и не заканчивается, например π. Начальные нули не влияют на число, хотя конечные нули могут иметь значение при измерениях.

Использование Base-10

Давайте посмотрим на пример большого числа и воспользуемся основанием 10 для определения разрядного значения каждой цифры.Например, если использовать целое число 987 654 125, положение каждой цифры будет следующим:

9 имеет номинальную стоимость
0
8 имеет значение 80 000
7 имеет значение 7000
6 имеет значение 600
5 имеет значение 50
4 имеет значение 4
1 имеет значение 1/10
2 имеет значение 2/100
5 имеет значение 5/1000-е

Происхождение Base-10

База-10 используется в большинстве современных цивилизаций и была наиболее распространенной системой для древних цивилизаций, скорее всего, потому, что у людей 10 пальцев.Египетские иероглифы, датируемые 3000 годом до нашей эры. показать свидетельство десятичной системы. Эта система была передана Греции, хотя греки и римляне также обычно использовали base-5. Десятичные дроби впервые стали использоваться в Китае в I веке до нашей эры.

Некоторые другие цивилизации использовали другие системы счисления. Например, майя использовали основание 20, возможно, из-за счета пальцев рук и ног. В калифорнийском языке юки используется основание 8 (восьмеричное), где считаются промежутки между пальцами, а не цифры.

Другие системы счисления

Базовые вычисления основаны на двоичной системе счисления или системе счисления с основанием 2, в которой всего две цифры: 0 и 1. Программисты и математики также используют систему счисления с основанием 16 или шестнадцатеричную систему, которая, как вы, вероятно, догадались, имеет 16 различных цифровых символов. . Компьютеры также используют основание 10 для выполнения арифметических операций. Это важно, поскольку позволяет производить точные вычисления, что невозможно при использовании дробных двоичных представлений.

Преобразователь базы

— двоичный, десятичный, шестнадцатеричный, восьмеричный

Базовые числа

Основание (основание) — это количество уникальных цифр и букв для представления числа.Базы счисления в основном до 36, поскольку есть 10 цифр (от 0 до 9) и 26 букв английского алфавита (от A до Z), но может быть намного больше баз счисления, если включено больше букв и символов.

Самая распространенная основа — это десятичная система счисления (основание 10), в которой используются только цифры от 0 до 9. Мы используем десятичные числа в повседневной жизни для представления любых чисел. Двоичное (основание-2), восьмеричное (основание-8) и шестнадцатеричное (основание-16) в основном используются в вычислениях.

Как преобразуются основные числа?

Чтобы преобразовать базовое число в другое базовое число, хотя существуют некоторые методы прямого преобразования между двоичными, восьмеричными и шестнадцатеричными числами, обычно вам необходимо сначала преобразовать базовое число в десятичное число, а затем преобразовать это десятичное число в другое базовое число. номер.

Для преобразования десятичного числа в другое базовое число:

Чтобы преобразовать десятичное число в другое базовое число, десятичное число многократно делится на новое базовое число, а остаток берется до тех пор, пока частное не станет равным нулю. Первый остаток будет самой младшей цифрой (крайняя правая цифра), а последний остаток будет самой старшей цифрой (крайняя левая цифра).

Например, это шаги для преобразования десятичного числа « 50 » в основание 6:

1) 50/6

2) Частное (8), остаток (2)

3) 8/6

4) Частное (1), остаток (2)

5) 1/8

6) Частное (0), остаток (1)

7) Обратить остатки от младших к старшим разрядам 1, 2, 2

, что делает десятичную дробь 50 равной 122 по основанию 6.

Чтобы преобразовать базовое число в десятичное:

Чтобы преобразовать базовое число в эквивалентное десятичное число, умножьте цифру основного числа на степень расположения цифры основного числа и просуммируйте все множители. Степень начинается с 0 и увеличивается на единицу, когда вы идете влево на каждую цифру основного числа.

Например, это шаги для преобразования числа с основанием 6 « 122 » в десятичное:

1) (1 * 6 ²) + (2 * 6 ¹) + (2 * 6 ⁰)

2) 36 + 12 + 2

3) 50

, что делает число 122 с основанием 6 равным 50 в десятичной форме.

Чтобы преобразовать базовое число в другое базовое число:

Чтобы преобразовать базовое число в другое базовое число, сначала преобразуйте базовое число в десятичное число, а затем преобразуйте десятичное число в новое базовое число.

Есть несколько быстрых клавиш для преобразования двоичных, восьмеричных и шестнадцатеричных чисел. Для них, пожалуйста, посетите соответствующие конвертеры, перечисленные ниже, чтобы получить инструкции.

Числа в других базах

Подсчет чисел с основанием, отличным от десяти

Обычно мы используем арабские числа, которые являются основанием 10 или десятичный.Компьютеры используют двоичный файл, который является базовым 2. Эта страница имеет дело с числами в других базах. Введите число, чтобы преобразовать его на другую базу или считайте в базе.

Как работают числа в других базах

В арабских числах (десятичных или с основанием 10) 10 цифр: 0,1,2,3,4,5,6,7,8,9. Вам нужно по одной цифре, чтобы сосчитать до 9, но две цифры — десять, и три цифры — сто, то есть десять умножить на десять.В двоичном формате с основанием 2 вам нужны две цифры для двух, так как у вас есть только две цифры, 0 и 1. База 5 состоит из пяти цифр, а число пять становится 10. Для основания 16 вам понадобится шестнадцать цифр, а цифр всего десять. Итак, мы используем буквы A, B, C, D, E, F. Они представляют собой десятичные числа 10, 11, 12, 13, 14. и 15. Посмотрите на таблицу ниже и найдите образец для этих оснований.

1111 9016 1 711111121 D211

База 10	База 2	База 3	База 4	База 5	База 8	База 16
1	1	1	1	1
2	10	2	2	2	2	2
3	11	10	3 901 3 901
4	100	11	10	4	4	4
5	101	12	11	10	10	10		110	20	12	11	6	6
7	111	21	13	12	7
8	1000	22	20	13	10	8
9	1001	100	21	11
10	1010	101	22	20	12	A
11	1011	102	23	13 12	23	21 12		1100	110	30	22	14	C
13	1101	111	31	23	15	15	112	32	24	16	E
15	1111	120	33	30	17	F
16	10000	121	100	31	20	10
17	10001	901 901		901 901	901 901 11
18	10010	200	102	33	22	12
19	10011	201	103 34	20	10100	202	110	40	24	14

Все эти базы позиционные, как арабские числа (основание 10).

Как определить основание числа в информатике

5 ответов 5

1.3. СИСТЕМЫ СЧИСЛЕНИЯ. — Основы информатики

1.

1.3.3. ПЕРЕВОД МЕЖДУ ОСНОВАНИЯМИ, СОСТАВЛЯЮЩИМИ СТЕПЕНЬ 2.

1.6. Перевод чисел из одной системы счисления в другую

Функция LOG — Служба поддержки Office

Описание

Синтаксис

Пример

Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников

Целые числа (int)

Дополнительные методы

Системы счисления

Вещественные числа (float)

Дополнительные методы

Комплексные числа (complex)

Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно максимально возможное основание системы счисления?

целые, вещественные, комплексные — Питошка

Number Base | Блестящая вики по математике и науке

Узнайте о системе счисления

Номерные базы | Математика | Вычислительная техника

Что такое основание счисления?

Как они работают?

Двоичный (База 2)

Восьмеричный (база 8)

Шестнадцатеричный (основание 16)

Биты перестановочные

Преобразование между базами

Искусство решения проблем

Основной номер Темы

История

Примеры задач

Новичок

Средний

Ресурсы

Книги

Классы

См. Также

Что такое система счисления по основанию 10?

Силы 10

Использование Base-10

0

Происхождение Base-10

Другие системы счисления

— двоичный, десятичный, шестнадцатеричный, восьмеричный

Числа в других базах

Подсчет чисел с основанием, отличным от десяти

Как работают числа в других базах

Добавить комментарий Отменить ответ