Определение натуральной величины отрезка прямой общего положения – Определение натуральной величины отрезка

Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Содержание

1. Метод прямоугольного треугольника
2. Способ параллельного переноса
3. Поворот вокруг оси

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

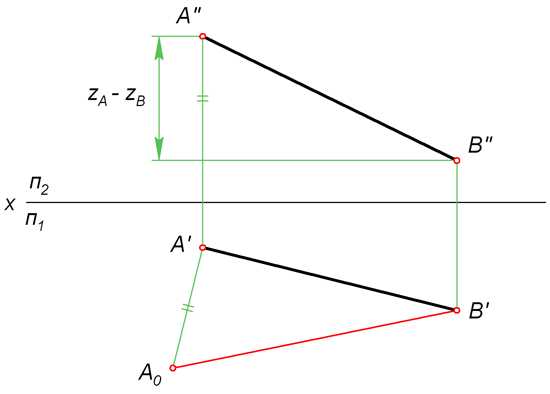
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A₀A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A

0 равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A₀ = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу A₀B’ треугольника A₀A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Пример построения

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»₁ и F»₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Пример построения

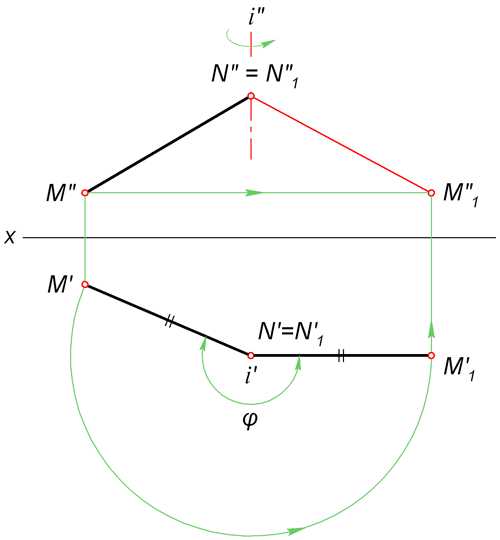
Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.

По линиям связи находим точку M»₁. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»₁ и M»₁ искомым отрезком. На рисунке он выделен красным цветом.

Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.

ngeometry.ru

10.Определение натуральной величины прямой общего положения( 2 способа)

а) модель б) эпюр

Рисунок 32. Определение натуральной величины отрезка и угла его к фронтальной плоскости.

12. Определение расстояния от точки до прямой. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ

Для того чтобы определить расстояние от точки до прямой, необходимо из точки опустить на прямую перпендикуляр. Прямого решения эта задача не имеет, так как прямой угол между прямыми общего положения будет проецироваться с искажением.

Проведем через точку М плоскость , перпендикулярную прямой 1 (рис.10.4). Зададим эту плоскость двумя пересекающимися прямыми — горизонталью и фронталью. В этом случае горизонтальная проекция горизонтали будет перпендикулярна горизонтальной проекции прямой

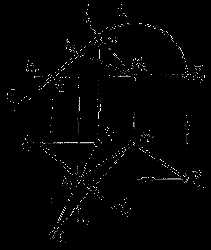1. Фронтальная проекция фронтали — перпендикулярна фронтальной проекции прямой 1. Рис. 10.4.

Построим точку встречи прямой 1 с плоскостью , l = К. Так как прямая 1 перпендикулярна плоскости , следовательно, она перпендикулярна любой прямой, принадлежащей плоскости , в том числе — и прямой МК, т.е. прямая МК перпендикулярна прямой 1.

Отрезок МК спроецировался с искажением. Его натуральную величину найдем способом вращения вокруг фронтально проецирующей прямой, проходящей через точку М. M₁K₁ = MK .

Решение задачи методом проецирования на дополнительнуюплокость приведено на рис.10.5 в следующем разделе. M₅K₅ = MK .

13.Взаимное положение прямой и плоскости.

Прямая линия, параллельная плоскости

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии:прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскостии не принадлежит этой плоскости.

Задача. Дано: проекции плоскости общего положения ABC и прямой общего положения а.

Требуется оценить их взаимное положение (рис.5.20).Гайки навинчиваются на резьбовой конец болта, при этом соединяемые детали зажимаются между гайкой и головкой болта. Рисунок плоскостями гипсовой головы в двух поворотах Это задание отчасти напоминает предыдущее, но теперь мы пользуемся плоскостями произвольной формы и ориентации. Суть задания заключается в том чтобы выразить конкретную форму через минимальное количество плоскостей но с максимальным сходством. Пропуск или ошибка хотя бы в одном из размеров делают чертеж непригодным к использованию. Последовательность нанесения размеров

	а) модель Выполнение графических работ Проекции плоских углов			б) эпюр
Рисунок 5.20. Прямая параллельная плоскости

Для этого через прямую а проведем вспомогательную секущую плоскость  — в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей   и АВС- прямую п (DF). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а₁ и со следом плоскости . Проекция прямой п₂  параллельна а₂, п₃  параллельна а₃, следовательно, прямая а параллельна плоскости AВС.

 

Прямая линия, пересекающая плоскость

Нахождение точки пересечения прямой линии и плоскости – основная задача начертательной геометрии.

Задача. Дано: плоскость AВС и прямая а.

Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.

Для решения задачи:

Через горизонтальную проекцию прямой а₁ проведем вспомогательную горизонтально проецирующую плоскость  (таким образом а).

Горизонтальный след плоскости ₁ пересекает проекцию плоскости A₁В₁С₁ в точках D₁ и F₁, которые определяют положение горизонтальной проекции п₁— линии пересечения плоскостей  и AВС. Для нахождения фронтальной  и профильной проекции пспроецируем точки D и F на фронтальную  и профильную плоскости проекций.

На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает  проекции а в точке К, которая и является  проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К₁.

Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.

	а) модель			б) эпюр
Рисунок 5.21. Нахождение точки пересечения прямой и плоскости

Таким образом алгоритм решения задачи состоит из следующей последовательности действий (рис.5.21):

1. Построение вспомогательной секущей плоскости  ( горизонтально – проецирующая плоскость ), которую проводят через прямую аа;

2. Построение линии пересечения вспомогательной плоскости  и заданной плоскости  п;

3. Определение искомой точки К, как точки пересечения двух прямых, заданной — а и полученной в результате пересечения плоскостей – п Ка  п. В качестве вспомогательной плоскости  рекомендуется брать одну из проецирующих плоскостей.

4. Определение видимости прямой а относительно плоскости 

Прямая линия перпендикулярная плоскости.

Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n₁ h₁. Аналогично для фронтали – f  n  f₂  n₂.

Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.

Доказательство следует из теоремы  о проецировании прямого угла.

Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.5.22).

Задача. Дано: плоскость ВСD и точка А.

Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.

В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А₁ прямую n₁перпендикулярно горизонтальной проекции горизонтали h₁, а на фронтальной плоскости проекций через точку А₂ прямую n₂перпендикулярно фронтальной проекции фронтали f₂, согласно выше сказанному полученная прямая n будет перпендикулярна плоскостиВСD.

studfiles.net

§ 5. Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций

Построение проекций отрезка прямой общего и частного положения позволяет решать не только позиционные задачи (расположение относительно плоскостей проекций), но и метрические – определение длины отрезка и углов наклона к плоскостям проекций. Но эта задача может быть решена только в случае, если отрезок параллелен или перпендикулярен к одной или нескольким плоскостям. Рассмотрим способ решения такой задачи для отрезка общего положения.

Пусть дан отрезок АВ общего положения относительно плоскостей ₁ и ₂. АВ’В – прямоугольный треугольник (рис. 3.10), в котором катет АВ’ = А₁В₁ (проекции отрезка АВ на плоскость ₁), а катет ВВ’ равен z – разности расстояний точек А и В до плоскости ₁. Угол  в прямоугольном треугольнике АВ’В определяет угол наклона прямой АВ к плоскости ₁.

Рассмотрим треугольник ВА’А (рис. 3.11), где катет ВА’ равен проекции А₂В₂ (ВА’ = А₂В₂), а второй катет АА’ равен  y – разности расстояний точек А и В от плоскости  ₂. Угол в прямоугольном треугольнике ВАА’ определяет угол наклона прямой АВ к плоскости₂.

Таким образом, натуральная длина отрезка прямой общего положения определяется гипотенузой прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй катет – алгебраической разности расстояний от концов отрезка до одной из плоскостей проекций.

Рис. 3.10	Рис. 3.11

 

§ 6. Определение натуральной величины отрезка прямой общего положения

Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника.

Рассмотрим последовательность этого положения (табл. 3.4).

Таблица 3.4

Вербальная форма	Графическая форма
Определить на комплексном чертеже Аz, Bz, Ay, By:  z – разность расстояний от точек А и В до плоскости 1;  y – разность расстояний от точек А и В до плоскости 2
а) либо перпендикуляр к А2В2 через точку В2 или А2; б) либо перпендикуляр к А1В1 через точку В1 или А1

или от точки B1 отложить  z
4. Соединить A2 и В’2; A1 и В’1
5. Обозначить натуральную величину отрезка АВ (гипотенузу треугольника): |АВ| = А1В’1 = А2В’2

 –угол наклона отрезка АВ к плоскости 1; –угол наклона отрезка АВ к плоскости 2

При решении подобной задачи находить натуральную величину отрезка можно только один раз (либо на  ₁, либо на  ₂). Если требуется определить углы наклона прямой к плоскостям проекций, то данное построение выполняется дважды – на фронтальной и горизонтальной проекциях отрезка.

studfiles.net

1.6. Определение натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций способом прямоугольного треугольника

Натуральная величина отрезка прямой определяется как гипотенуза прямоугольного треугольника, один катет которого равен проекции отрезка на заданную плоскость проекций, а другой равен разности расстояний от концов отрезка до этой же плоскости. Угол наклона прямой к плоскости проекций равен углу между натуральной величиной прямой и ее проекцией на эту плоскость (рис. 1.12).

Пример 2. Определить натуральную величину отрезка АВ и угол наклона его к горизонтальной плоскости проекций П₁ (рис. 1.13). АВ  П₁,П₂; АВ? ₁?

Рис. 1.12 Рис. 1.13

Анимации\Рис. 1.12, 1.13.exe

1.7. Деление отрезка в пропорциональном отношении

Если точка, принадлежащая отрезку, делит этот отрезок в каком-то отношении, то проекции этого отрезка делятся проекциями этой точки в том же отношении.

Пример 3. Разделить отрезок АВ в отношении АС:СВ2:1 (рис. 1.14).

Решение можно производить на любой проекции. Из любого конца отрезка АВ под произвольным углом к проекции прямой проводят луч произвольной длины, на нем откладывают 3 равных между собой произвольных отрезка. Конечную точку В₀ соединяют с точкой В₁, определяют точку С₀, которая делит отрезок А₁В₀ в отношении 2:1. Проводят отрезок С₀С₁ параллельно В₀В₁. Точка с₁ делит горизонтальную проекцию отрезка А₁В₁ в отношении 2:1. С₂ определяют по линиям связи.

1.8. Следы прямой

Следами прямой называются точки пересечения прямой с плоскостями проекций (рис. 1.15). Прямая общего положения имеет три следа, уровня – 2, проецирующая -1.

М— горизонтальный след;

М₁ — горизонтальная проекция горизонтального следа;

М₂ — фронтальная проекция горизонтального следа;

N – фронтальный след;

N₁ — горизонтальная проекция фронтального следа;

N₂ — фронтальная проекция фронтального следа.

Одноименные проекции следов совпадают с самими

следами.

Рис. 1.14 Рис. 1.15 Анимации\Рис.1.15.exe

Для построения горизонтального следа прямой фронтальную проекцию прямой А₂В₂ продолжают до пересечения с осью Ох и получают фронтальную проекцию горизонтального следа М₂. Так как точка М принадлежит прямой АВ, то ее горизонтальная проекция М₁ находится на горизонтальной проекции прямой А₁В₁ и лежит на одной линии связи с проекцией М₂. Для построения фронтального следа прямой его горизонтальную проекцию А₁В₁ продолжают до пересечения с осью Ох и получают горизонтальную проекцию фронтального следа N₁. Фронтальную проекцию фронтального следа N₂ прямой находят по линии связи на ее фронтальной проекции.

1.9. Взаимное расположение прямых

Прямые в пространстве могут быть параллельны, пересекаться или скрещиваться.

Если прямые параллельны, то их одноименные проекции на чертеже параллельны (рис. 1.16). Если прямые пересекаются, то на чертеже проекции их точки пересечения лежат на одной линии связи

(рис. 1.17).

Рис. 1.16 Рис. 1.17

Если прямые не пересекаются и не параллельны, то они скрещиваются. У скрещивающихся прямых на одной из проекций совпадают проекции двух точек, поэтому одна из совпадающих точек становится закрытой. Такие точки еще называют конкурирующими (рис. 1.18).

1 и 2 (1₂=2₂)— фронтально–конкурирующие точки;

3 и 4 (3₁=4₁)— горизонтально–конкурирующие точки.

Рис. 1.18 Анимации\Рис. 1.18.exe

Из двух горизонтально-конкурирующих точек на чертеже видимой будет та, фронтальная проекция которой расположена выше;

из двух фронтально-конкурирующих точек видимой будет та, горизонтальная проекция которой будет ниже.

Точки 2 и 3 – закрытые, 1 и 4 – открытые.

studfiles.net

3 Преобразования чертежа

Основные понятия преобразования чертежа

1 Задачей, решаемой преобразованиями чертежа, является задача на …

+определение натуральной величины углов

построение развертки поверхности

построение параллельных прямой и плоскости

построение точки, принадлежащей плоскости

2 Способом преобразования чертежа, при котором геометрический объект в пространстве перемещается называется способ …

+вращения вокруг проецирующей прямой

замены плоскостей проекций

параллельного проецирования

дополнительного проецирования

3 Задачей, решаемой преобразованиями чертежа, является …

+определение натуральной величины плоской фигуры

построение нормалей

построение разверток поверхностей

построение прямой пересечения двух плоскостей

Способ начертательной геометрии, относящийся к преобразованию чертежа основных видов, называется способом…

+плоскопараллельного перемещения

вспомогательных плоскостей частного положения

триангуляции

прямоугольного треугольника

4 Задачей, решаемой преобразованиями чертежа, является …

+определение натуральной величины отрезка прямой

построение параллельных плоскостей

построение нормали к поверхности

построение точки, принадлежащей плоскости

12 Задача, решаемая преобразованиями чертежа, является задача на …

+определение натуральной величины плоской фигуры

построение развертки поверхности

построение параллельных прямой и плоскости

построение точки, принадлежащей плоскости

11 Задача, решаемая заменой плоскостей проекций, является задача на …

+определение натуральной величины углов

построение развертки поверхности

построение параллельных прямой и плоскости

построение точки, принадлежащей плоскости

10 Задача, решаемая двойным преобразованием чертежа, является задача на …

+определение натуральной величины плоской фигуры

построение развертки поверхности

построение параллельных прямой и плоскости

построение точки, принадлежащей плоскости

9 Задача, решаемая простым преобразованием чертежа, является задача на …

+определение натуральной величины отрезка прямой

построение развертки поверхности

построение параллельных прямой и плоскости

построение точки, принадлежащей плоскости

8 Способ замены плоскостей проекций заключается в последовательной замене основной плоскости проекции на новую, обозначаемую …

+П₅

П₁

П₂

П¢

Способ замены плоскостей проекций

Натуральная величина отрезка AB(обозначенаA₄B₄) построена правильно на рисунке …

+Б

A

В

Г

Способ замены плоскостей проекций заключается в последовательной замене основной плоскости проекции на новую, обозначаемую …

+П₄

П₁

П₂

П¢

Способ преобразования чертежа, при котором геометрический объект в пространстве остается неподвижным, называется способом …

+замены плоскостей проекций

вращения вокруг проецирующей прямой

плоско-параллельного перемещения

вращения вокруг прямой уровня

Натуральная величина отрезка АВ(обозначенаА₄В₄)неверно построенана _____ рисунке(ах).

+трех

двух

одном

четырех

Натуральная величина отрезка CD (обозначенаC₄D₄) построена правильно на рисунке …

+Б

А

В

Г

Натуральная величина отрезка EF (обозначенаE₄F₄) построена правильно на рисунке …

+А

Б

В

Г

1. Способами начертательной геометрии, относящиеся к преобразованию чертежа основных видов, являются …

1. способ замены плоскостей проекций +

2. способ вспомогательных плоскостей частного положения

3. способ вращения вокруг проецирующих прямых +

4. способ триангуляции

2. Задачей, решаемой преобразованиями чертежа, является задача на …

1. определение расстояния от точки до плоскости +

2. построение развертки поверхности

3. построение параллельных прямой и плоскости

4. построение точки, принадлежащей плоскости

3. Натуральная величина отрезка AB (обозначенаA₄B₄) построена правильно на _____ рисунке(ах).

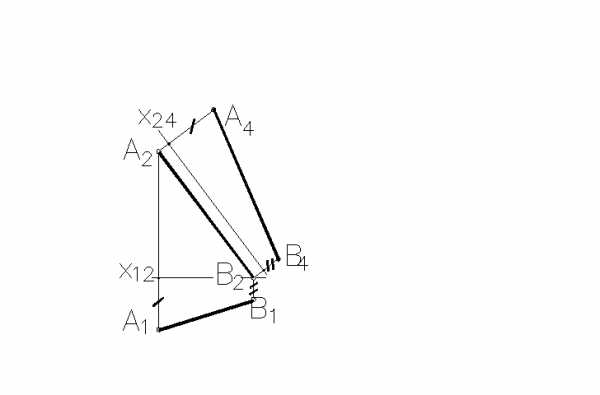
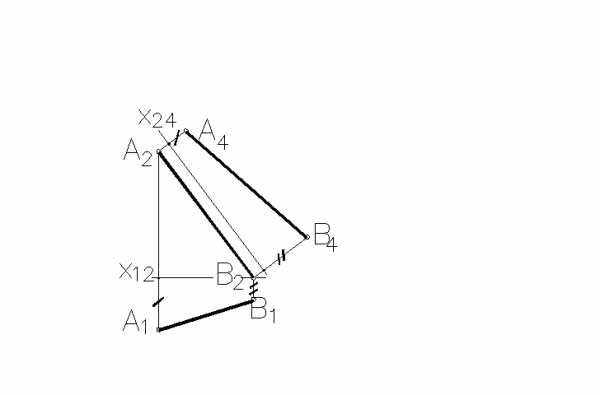
1 2

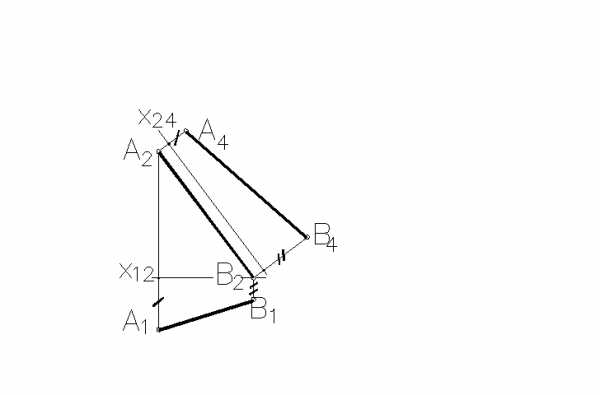
3 4

1 трех

2 двух

3 одном +

4 четырех

4. Построение натуральной величины отрезка прямой общего положения выполняется способами …

1. замены плоскостей проекций +

2. конкурирующих точек

3. вращения вокруг проецирующей прямой +

4. триангуляции

5. Преобразование отрезка прямой общего положения в отрезок прямой частного положения выполняется способами …

1. замены плоскостей проекций +

2. плоскопараллельного перемещения +

3. эксцентрических сфер

4. концентрических сфер

6. Преобразование плоскости общего положения в плоскость частного положения выполняется способами …

5. замены плоскостей проекций +

6. плоскопараллельного перемещения +

7. эксцентрических сфер

8. концентрических сфер

7 Виды преобразований применяемых в начертательной геометрии …

а) простые и двойные +

б) множественные и нелинейные

в) многозначные и кубические

г) квадратичные и топологические

6 Определение натуральной величины отрезка прямой общего положения выполняется _____ преобразованием.

а) простым +

б) двойным

в) многозначным

г) квадратичным

5 На рисунке показано преобразование прямой общего положения в проецирующую прямую, выполненное способом …

а) замены плоскостей проекций +

б) вращения вокруг проецирующей прямой

в) плоскопараллельного перемещения

г) вращения вокруг прямой уровня

Решение задач на преобразование плоскости

Установите правильную последовательность действий при решении задачи нахождения натуральной величины треугольника ABCспособом замены плоскостей проекции.

Построить проекции горизонтали принадлежащей плоскости треугольника ABC

Перпендикулярно горизонтальной проекции горизонтали провести первую новую ось чертежа х₁₄и построить новые проекции вершин треугольника A₄,B₄,C₄ наП₄

Параллельно полученной новой проекции треугольника A₄B₄C₄(прямой) провести вторую новую ось чертежах₄₅и построить новые проекции вершин треугольника A₅,B₅,C₅ наП₅

Соединить полученные новые проекции точек A₅,B₅,C₅ и получить натуральную величину треугольникаABC–D(A₅B₅C₅)

Установите правильную последовательность действий при решении задачи нахождения натуральной величины треугольника ABCспособом замены плоскостей проекции.

Построить проекции фронтали, принадлежащей плоскости треугольника ABC

Перпендикулярно фронтальной проекции фронтали провести первую новую ось чертежа х₂₄и построить новые проекции вершин треугольника A₄,B₄,C₄ наП₄

Параллельно полученной новой проекции треугольника A₄B₄C₄(прямой) провести вторую новую ось чертежах₄₅и построить новые проекции вершин треугольника A₅,B₅,C₅ наП₅

Соединим полученные новые проекции точек A₅,B₅,C₅ и получим искомую натуральную величину — треугольникA₅B₅C₅

Установите правильную последовательность действий при решении задачи нахождения натуральной величины треугольника ABCспособом замены плоскостей проекции.

Проведите новую ось чертежа х₁₄ параллельно горизонтальной проекции треугольника A₁B₁C₁

Строим новые проекции вершин треугольника A₄,B₄,C₄

Соединяем полученные новые проекции точек A₄,B₄,C₄ и получаем искомую натуральную величину — треугольникA₄B₄C₄

Установите правильную последовательность действий при решении задачи нахождения натуральной величины треугольника ABCспособом замены плоскостей проекции.

Провести новую ось чертежа х₂₄ параллельно фронтальной проекции треугольника

A₂B₂C₂

Построить новые проекции вершин треугольника A₄,B₄,C₄

Соединить полученные новые проекции точек A₄,B₄,C₄ и получим искомую натуральную величину — треугольникA₄B₄C₄

Установите правильную последовательность действий при решении задачи нахождения натуральной величины треугольника ABCспособом замены плоскостей проекции.

Провести новую ось чертежа х₃₄ параллельно профильной проекции треугольника A₃B₃C₃

Построить новые проекции вершин треугольника A₄,B₄,C₄

Соединить полученные новые проекции точек A₄,B₄,C₄ и получим искомую натуральную величину — треугольникA₄B₄C₄

Установите правильную последовательность действий при решении задачи нахождения натуральной величины треугольника ABCспособом замены плоскостей проекции.

Построить проекции профильной прямой уровня, принадлежащей плоскости треугольника ABC

Перпендикулярно профильной проекции профильной прямой уровня провести первую новую ось чертежа х₃₄и построить новые проекции вершин треугольника A₄,B₄,C₄ наП₄

Параллельно полученной новой проекции треугольника A₄B₄C₄(прямой) провести вторую новую ось чертежах₄₅и построить новые проекции вершин треугольника A₅,B₅,C₅ наП₅

Соединим полученные новые проекции точек A₅,B₅,C₅ и получим искомую натуральную величину — треугольникA₅B₅C₅

4 Натуральная величина отрезка AB (обозначенаA₄B₄) построена правильно на рисунке ___.

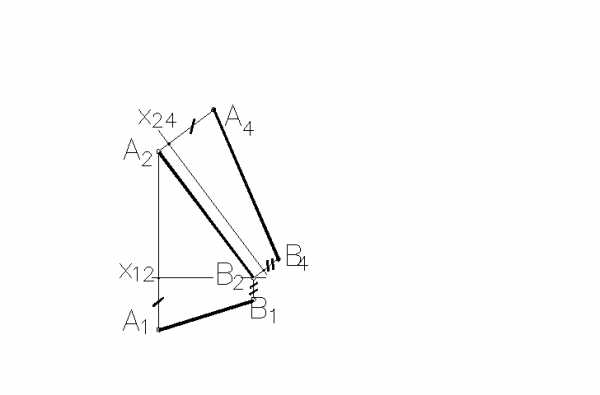
1 2

3 4

+1

2

3

4

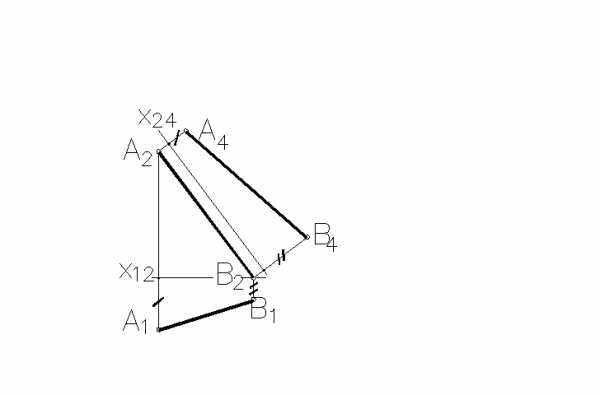
3 Натуральная величина отрезка AB (обозначенаA₄B₄) построена правильно на рисунке ___.

+Б

А

В

Г

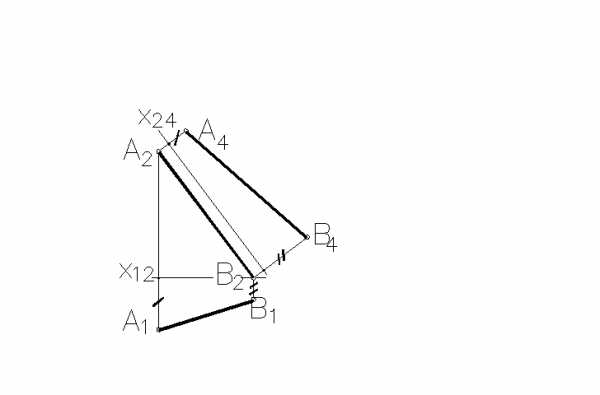
2 Натуральная величина отрезка AB (обозначенаA₄B₄) построенанеправильнона рисунке (ах)___.

+трех

двух

одном

четырех

1 На рисунке показано решение задачи нахождения натуральной величины треугольника АВС способом …

а) замены плоскостей проекций +

б) вращения вокруг проецирующей прямой

в) плоскопараллельного перемещения

г) вращения вокруг прямой уровня

studfiles.net

§ 3. Прямые частного положения

Прямые частного положения – это прямые, которые либо параллельны (табл. 3.1), либо перпендикулярны одной из плоскостей проекций (табл. 3.2).

Прямые уровня

Всякую линию, параллельную плоскости проекций, называют линией уровня. В начертательной геометрии различают три основные линии уровня: горизонталь, фронталь и профильную линии (табл. 3.1).

Таблица 3.1

Прямые уровня

Определение	Наглядное изображение	Комплексный чертеж
Горизонталью называют всякую линию, параллельную горизонтальной плоскости p1: A2B2   || Оx; A3B3i || y. A1B1 – натуральная величина отрезка, b – угол наклона к 2

Фронталью называют линию, параллельную фронтальной плоскости 2: A1B1i  || Оx; A2B2 – натуральная величина; А3B3 i || z; –угол наклона к 1
Профильной линией называют линию, параллельную профильной плоскости  3; A2B2i || z; A1B1i|| y; A3B3 – натуральная величина отрезка, –угол наклона к 1; –угол наклона к  2

Проецирующие прямые

Проецирующими прямыми называют прямые, расположенные перпендикулярно к плоскостям проекций ₁, ₂, ₃. Различают три основные проецирующие прямые: горизонтальную, фронтальную и профильную.

Если прямая перпендикулярна какой-либо из плоскостей проекций, то на эту плоскость она проецируется в виде точки. Две другие ее проекции параллельны осям и равны натуральной величине отрезка (табл. 3.2).

Таблица 3.2

Проецирующие прямые

Определение	Наглядное изображение	Комплексный чертеж
Горизонтально проецирующей прямой называют прямую, перпендикулярную к плоскости 1; A2B2 – натуральная величина AB, в плоскости 1 отрезок АВ проецируется в точку А1 В1

Фронтально проецирующей прямой называют прямую, перпендикулярную к плоскости 2; AB || 1 и AB 2, А1В1 – натуральная величина АВ, в плоскости 2 отрезок проецируется в точку А2В2
Профильно проецирующей прямой называют прямую, перпендикулярную к плоскости 3; AB || 1 и AB || 2, А1В1 и А2В2 – натуральные величины отрезка АВ, А3В3 проецируется на 3 в точку

При сравнительном анализе изображений прямых частного положения на комплексном чертеже (табл. 3.1 и 3.2) следует:

1. Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции обязательно параллельны осям проекций.

2. Проекция прямой уровня, к той плоскости, которой она параллельна, составляет с осями проекций углы, равные углам наклона линии уровня с плоскостями проекций.

3. Если прямая перпендикулярна плоскости проекций, то ее проекцией на эту плоскость является точка, а вторая проекция располагается перпендикулярно осям проекций.

§ 4. Построение третьей проекции отрезка по двум заданным

В нашем примере мы будем рассматривать построение прямой общего положения в первой четверти (табл. 3.3).

Таблица 3.3

Вербальная форма	Графическая форма
1. Прямая AB задана двумя проекциями А1В1 и А2В2. Необходимо построить третью проекцию А3В3
2. Построить третью проекцию точки А – А3:
а) на оси z и y отложить координаты точки А: Az и Aу	a)
б) построить Ау для профильной проекции	б)

в) построить перпендикуляры из Аz и Ay. Обозначить полученную профильную проекцию точки А3	в)
3. Построить третью проекцию точки В3:
а) на осях z и y отложить координаты точки В: Вz и Ву	а)
б) построить Ву для профильной проекции точки В	б)

в) построить перпендикуляры: ВzВ3  z. ВyВ3  y. Обозначить профильную проекцию точки В3	в)
4. Соединить полученные проекции А3 и В3 – это и будет проекция отрезка АВ на плоскость  3

 

Задача № 1

При решении задач использовать алгоритм построения третьей проекции прямой по двум заданным (табл. 3.3).

1. По двум заданным проекциям построить третью на рис. 3.1–3.9:

Рис. 3.1.	Рис. 3.2.	Рис. 3.3.
Рис. 3.4.	Рис. 3.5.	Рис. 3.6.
Рис. 3.7.	Рис. 3.8.	Рис. 3.9.

 

Задача № 2

Определить, на каком из комплексных чертежей данная прямая является натуральной величиной отрезка. Где можно определить углы наклона прямой к плоскостям проекций (рис. 3.1–рис. 3.9)?

studfiles.net

Определение натуральной величины отрезка прямой общего положения способом прямоугольного треугольника.

Натуральная величина (н.в.) отрезка АВ прямой общего положения является гипотенузой прямоугольного треугольника АВК. В этом треугольнике катет АК параллелен плоскости проекций π1 и равен горизонтальной проекции отрезка A’B’. Катет BK равен разности расстояний точек A и B от плоскости π1.

В общем случае для определения натуральной величины отрезка прямой необходимо построить гипотенузу прямоугольного треугольника, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, другим катетом — отрезок, равный по величине алгебраической разности координат Z (Y) крайних точек отрезка.

Из прямоугольного треугольника находят угол α — угол наклона прямой к горизонтальной плоскости проекций.

 

Разрезы простые и сложные. Обозначение разрезов.

Разрез – изображение предмета, мысленно рассеченного одной (или несколькими) секущими плоскостями. В зависимости от положения секущей плоскости относительно плоскости проекций разрезы называют горизонтальными, вертикальными и наклонными. Горизонтальный разрез имеет секущую плоскость, параллельную горизонтальной плоскости проекций. Вертикальный разрез имеет секущую плоскость, горизонтальной плоскости проекций. Наклонный разрез имеет секущую плоскость, не параллельную и не горизонтальной плоскости проекций. Когда секущая плоскость совпадает с плоскостью симметрии предмета в целом, то положение секущей плоскости не обозначают и разрез надписью не сопровождают. Разрез обозначается, если секущая плоскость не является плоскостью симметрии предмета (А – А).

Местные разрезы.Разрез, служащий для выяснения устройства предмета лишь в отдельном, ограниченном месте, называют местным. Местный разрез выделяют на виде сплошной волнистой линией или сплошной тонкой линией с изломом. Она не должна совпадать с какими-либо другими линиями изображения.

Сложные разрезы: ломаные и ступенчатые.В зависимости от числа секущих плоскостей разрезы разделяют на простые – при одной секущей плоскости и сложные – при нескольких секущих плоскостях. Сложные разрезы называют ступенчатыми, если секущие плоскости параллельны, и ломаными, если секущие плоскости пересекаются.

Образование цилиндрической поверхности. Сечения цилиндрической поверхности плоскостями.

В некоторой плоскости α рассмотрим окружность w(O,R) с центром в точке O и радиусом R. Через каждую точку окружности проведём прямую перпендикулярную плоскости α.

Цилиндрической поверхностью называется фигура образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.

 



infopedia.su