Норма фробениуса не является операторной. Норма матрицы
» Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц
Если все миноры матрицы A порядка k равны нулю, то все миноры порядка k+1, если такие существуют, тоже равны нулю.
Рангом матрицы A называется наибольший из порядков миноров матрицы A , отличных от нуля.
Максимум ранг может быть равен минимальному числу из количества строк или столбцов матрицы, т.е. если матрица имеет размер 4х5, то максимум ранг будет 4.
Минимум ранг матрицы равен 1, если только вы не имеете дело с нулевой матрицей, там всегда ранг равен нулю.
Ранг невырожденной квадратной матрицы порядка n равен n, так как ее определитель является минором порядка n и у невырожденной матрицы отличен от нуля.
При транспонировании матрицы ее ранг не меняется.
Пусть ранг матрицы равен . Тогда любой минор порядка , отличный от нуля, называется базисным минором .
Пример. Дана матрица А.
Определитель матрицы равен нулю.
Минор второго порядка . Следовательно, r(A)=2 и минор базисный.
Базисным минором является также минор .
Минор , т.к. =0, поэтому не будет базисным.
Задание : самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
При элементарных преобразованиях ранг матрицы не меняется.
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
Пусть требуется вычислить ранг матрицы размеров m x n .
В результате расчетов матрица А1 имеет вид
Если все строки, начиная с третьей, нулевые, то , так как минор . Иначе перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д.
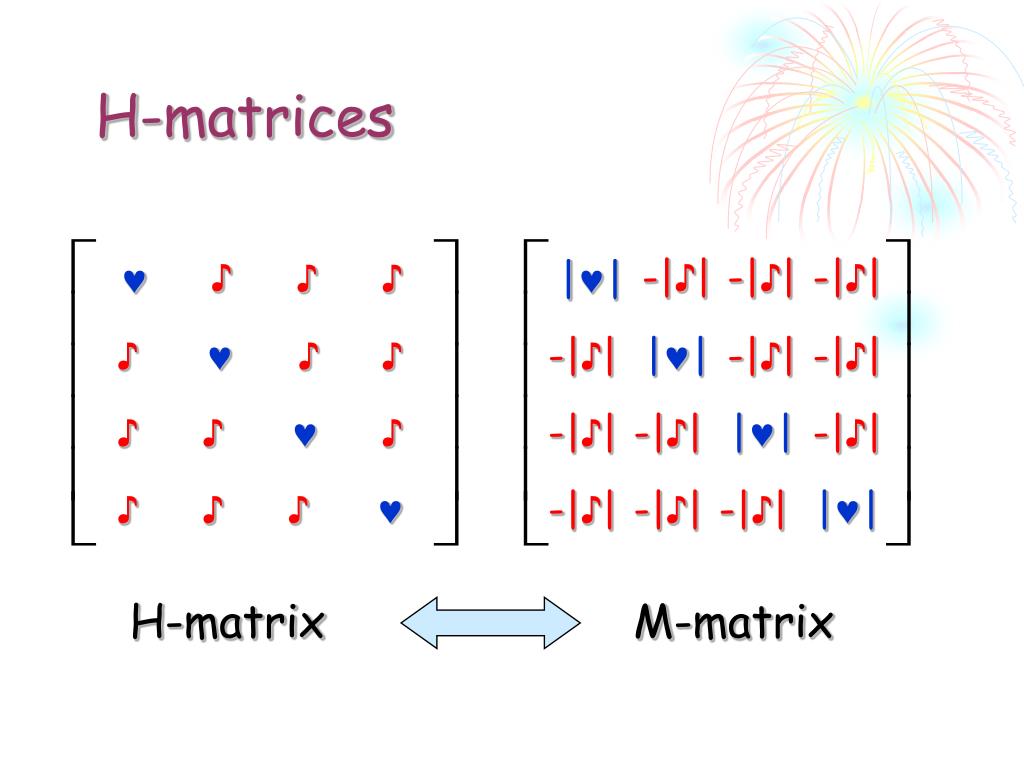Ранг такой матрицы равен . Следовательно, Rang(A)=r.В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
В лабораторно-практической работе рассмотрим пример нахождения ранга матрицы.
АЛГОРИТМ НАХОЖДЕНИЯ НОРМЫ МАТРИЦЫ .
Выделяют всего три нормы матрицы.
Первая норма матрицы = максимальному из чисел, полученных при сложении всех элементов каждого столбца, взятых по модулю.
Пример: пусть дана матрица А размера 3х2 (рис.10). В первом столбце стоят элементы: 8, 3, 8. Все элементы положительные.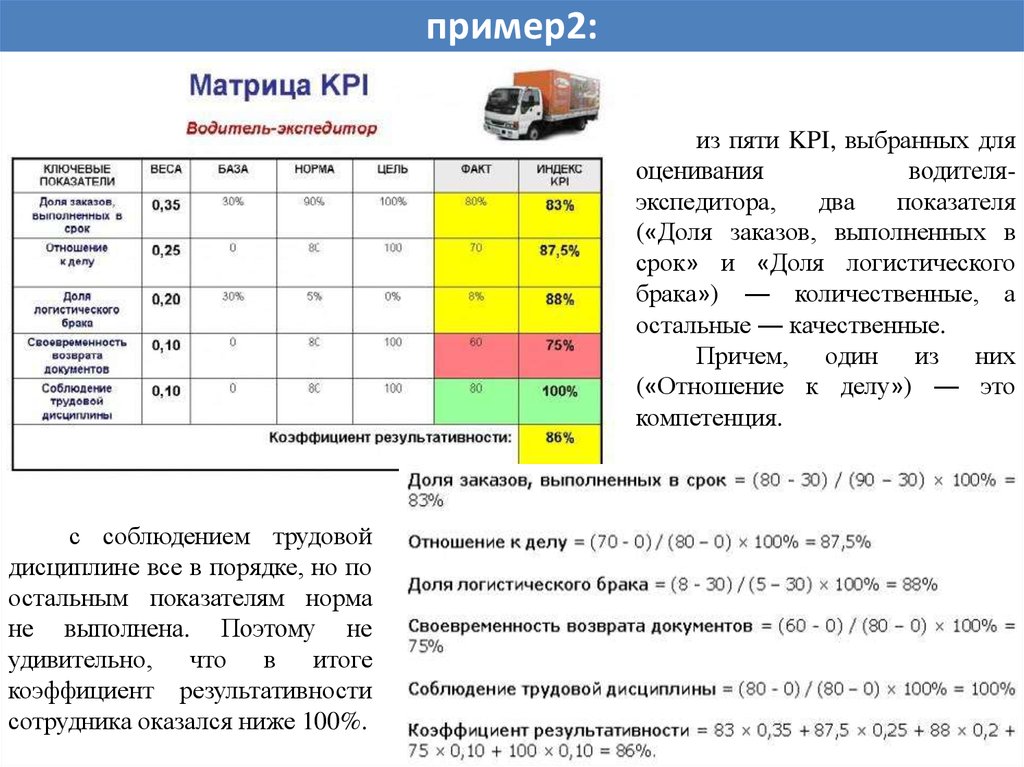
Найдем их сумму: 8+3+8=19. Во втором столбце стоят элементы: 8, -2, -8. Два элемента — отрицательные, поэтому при сложении этих чисел, необходимо подставлять модуль этих чисел (т.е. без знаков «минус»). Найдем их сумму: 8+2+8=18. Максимальное из этих двух чисел — это 19. Значит первая норма матрицы равна 19.
Рисунок 10.
Вторая норма матрицы
В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень.
Третья норма матрицы представляет из себя максимальное из чисел, полученных при сложении всех элементов каждой строки, взятых по модулю.
В нашем примере: в первой строке стоят элементы: 8, 8.
Все элементы положительные. Найдем их сумму: 8+8=16. В второй строке стоят элементы: 3, -2. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 3+2=5. В третьей строке стоят элементы 8, и -8. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 8+8=16. Максимальное из этих трех чисел — это 16. Значит третья норма матрицы равна 16.
Составитель: Салий Н.А.
Энциклопедичный YouTube
Субтитры
Определение
Пусть K — основное поле (обычно K = R или K = C ) и — линейное пространство всех матриц с m строками и n столбцами, состоящих из элементов K . На пространстве матриц задана норма, если каждой матрице ставится в соответствие неотрицательное действительное число ‖ A ‖ {\displaystyle \|A\|} , называемое ее нормой, так, что
В случае квадратных матриц (то есть m = n ), матрицы можно перемножать не выходя из пространства, и потому нормы в этих пространствах обычно также удовлетворяют свойству субмультипликативности
Субмультипликативность может выполняться также и для норм неквадратных матриц, но определённых сразу для нескольких нужных размеров.
{n},\ x\neq 0\right\}.\end{aligned}}}
При условии согласованного задания норм на пространствах векторов, такая норма является субмультипликативной (см. ).
Примеры операторных норм
Свойства спектральной нормы:
- Спектральная норма оператора равна максимальному сингулярному числу этого оператора.
- Спектральная норма нормального оператора равна абсолютному значению максимального по модулю собственного значения этого оператора.
- Спектральная норма не изменяется при умножении матрицы на ортогональную (унитарную) матрицу.
Неоператорные нормы матриц
Существуют нормы матриц, не являющиеся операторными. Понятие неоператорных норм матриц ввел Ю. И. Любич и исследовал Г. Р. Белицкий.
Пример неоператорной нормы
Например, рассмотрим две различные операторные нормы
‖
A
‖
1
{\displaystyle \|A\|_{1}}
и
‖
A
‖
2
{\displaystyle \|A\|_{2}}
, например строчную и столбцовую нормы. Образуем новую норму
‖
A
‖
=
m
a
x
(‖
A
‖
1
,
‖
A
‖
2)
{\displaystyle \|A\|=max(\|A\|_{1},\|A\|_{2})}
.
{m\times n}}
верно двойное неравенство.
Нормой матрицы назовем поставленное в соответствие этой матрице вещественное число ||A|| такое, что которое как вещественное число ставится в соответствие каждой матрице из n-мерного пространства и удовлетворяет 4 аксиомам:
1. ||A||³0 и ||A||=0, только если A – нулевая матрица;
2. ||αA||=|α|·||A||, где a R;
3. ||A+B||£||A||+||B||;
4. ||A·B||£||A||·||B||. (свойство мультипликативности)
Норма матриц может быть введена различными способами. Матрицу A можно рассматривать как
Эта норма называется евклидовой нормой матрицы.
Если для любой квадратной матрицы A и любого вектора x, размерность которого равна порядку матрицы, выполняется неравенство ||Ax||£||A||·||x||,
то говорят, что норма матрицы A согласована с нормой вектора. Заметим, что слева в последнем условии стоит норма вектора (Ax – вектор).
С заданной векторной нормой согласованы различные матричные нормы.
Выберем среди них наименьшую. Таковой будет
Эта матричная норма- подчиненная заданной векторной норме. Существование максимума в этом выражении следует из непрерывности нормы, ибо всегда существует вектор x -> ||x||=1 и ||Ax||=||A||.
Покажем, xто норма N(A) не подчинена ни одной векторной норме. Нормы матрицы, подчиненные ранее введенным векторным нормам, выражаются следующим образом:
1. ||A|| ¥ = |a ij | (норма-максимум)
2. ||A|| 1 = |a ij | (норма-сумма)
3. ||A|| 2 = , (спектральная норма)
где s 1- наибольшое собств значение симметричной матрицы A¢A, являющейся произведением транспонированной и исходной матриц. Т к матрица A¢A симметричная, то все ее собственные значения вещественны и положительны. Число l -собств значение, а ненулевой вектор x – собственный вектор матрицы A(если они связаны между собой соотношением Ax=lx). Если же матрица A сама является симметричной, A¢ = A, то A¢A = A 2 и тогда s 1 = , где — наибольшее по модулю собственное значение матрицы A.
Следовательно, в этом случае мы имеем = .
Собственные числа матрицы не превышают любой из ее согласованных норм. Нормируя определяющее собственные числа соотношение, получим ||λx||=||Ax||, |λ|·||x||=||Ax||£||A||·||x||, |λ|£||A||
Поскольку справедливо ||A|| 2 £||A|| e , где евклидова норма вычисляется просто, в оценках вместо спектральной нормы можно использовать евклидову норму матрицы.
30.Обусловленность систем уравнений. Коэффициент обусловленности .
Степень обусловленности — влияние решения на исходные данные. Ax = b : вектору b соответствует решение x . Пусть b изменится на величину . Тогда вектору b+ будет соответствовать новое решение x+ : A(x+ ) = b+ . Так как система линейна, то Ax + A = b+ , тогда A = ; = ; = ; b = Ax ; = тогда ; * , где — относительная погрешность возмущения решения, – коэффициент обусловленности cond(A) (во сколько раз может возрасти погрешность решения), – относительное возмущение вектора b .
cond(A) = ; cond(A)* Свойства коэффициента: зависит от выбора нормы матрицы; cond( = cond(A) ; умножение матрицы на число не влияет на коэффициент обусловленности. Чем больше коэффициент, тем сильнее сказывается на решении СЛАУ ошибка в исходных данных. Число обусловленности не может быть меньше 1.
31. Метод прогонки для решения систем линейных алгебраических уравнений.
Часто возникает необходимость в решении систем, матрицы которых, являясь слабозаполненными, т.е. содержащими много ненулевых элементов. Матрицы таких систем обычно имеют определенную структуру, среди которых выделяют системы с матрицами ленточной структуры, т.е. в них ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами метод Гаусса можно трансформировать в более эффективные методы. Рассмотрим наиболее простой случай ленточных систем, к которым, как мы увидим впоследствии, сводится решение задач дискретизации краевых задач для дифференциальных уравнений методами конечных разностей, конечных элементов и др.
Трёх диагональной матрицей называется такая матрица, у которой ненулевые элементы стоят только на главной диагонали и соседних с ней:
У трёх диагональной матрицы ненулевых элементов всего (3n-2).
Переобозначим коэффициенты матрицы:
Тогда в покомпонентной записи систему можно представить в виде:
A i * x i-1 + b i * x i + c i * x i+1 = d i, i=1, 2,…, n; (7)
a 1 =0, c n =0. (8)
Структура системы предполагает взаимосвязь только между соседними неизвестными:
x i =x i * x i +1 +h i (9)
x i -1 =x i -1* x i + h i -1 и подставим в (7):
A i (x i-1* x i + h i-1)+ b i * x i + c i * x i+1 = d i
(a i * x i-1 + b i)x i = –c i * x i+1 +d i –a i * h i-1
Сравнивая полученное выражение с представлением (7), получаем:
Формулы (10) представляют рекуррентные соотношения для вычисления коэффициентов прогонки. Они требуют задания начальных значений. В соответствии с первым условием (8) для i =1 имеем a 1 =0, а значит
Далее вычисляются и сохраняются остальные прогоночные коэффициенты по формулам (10) для i=2,3,…, n, причем при i=n, с учетом второго условия (8), получаем x n =0.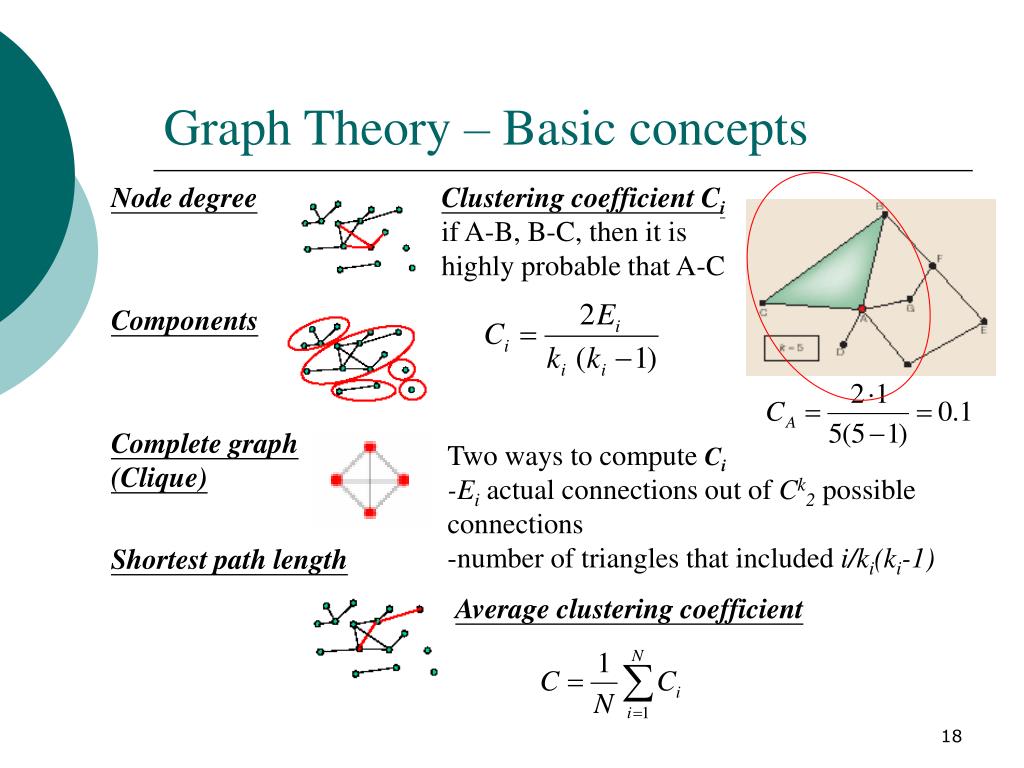
Следовательно, в соответствии с формулой (9) x n = h n .
После чего по формуле (9) последовательно находятся неизвестные x n -1 , x n -2 , …, x 1 . Этот этап расчета называется обратным ходом, в то время как вычисление прогоночных коэффициентов называется прямым ходом прогонки.
Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при большой размерности систем не должно быть быстрого роста погрешностей округления. Будем называть прогонку корректной , если знаменатель прогоночных коэффициентов (10) не обращается в ноль, и устойчивой , если ½x i ½
Теорема. Пусть коэффициенты a i и c i уравнения (7) при i=2,3,…, n-1 отличны от нуля и пусть
½b i ½>½a i ½+½c i ½ при i=1, 2,…, n. (11)
Тогда прогонка, определяемая формулами (10), (9) корректна и устойчива.
3.5.2. Нормы векторов и матриц
Пусть — вектор-столбец, . Приведем некоторые известные нормы векторов:
1.
— эклидова норма вектора;
2. — так называемая —Норма, или Норма Гильберта-Шмидта (при совпадает с эвклидовой нормой, а при совпадает с так называемой 1-нормой).
3. — Чебышевская норма.
Все эти нормы в эквивалентны: сходимость в одной из этих норм влечет за собой сходимость в другой (следствие конечности ).
Перейдем к понятию Матричной нормы. Пусть — множество квадратных вещественных матриц порядка . Пусть каждой матрице поставлено в соответствие число . Это число называется Нормой матрицы A, если выполняются следующие аксиомы:
1. ;
2. ;
3. — неравенство треугольника;
4. — кольцевое свойство.
Определение 1. Норма называется Мультипликативной, если выполняются все четыре аксиомы, и Аддитивной, если выполняются только первые три аксиомы.
Определение 2. Если матричная норма удовлетворяет условию
, где , | (1) |
То такая норма называется Согласованной с нормой вектора.
Большинство используемых в числовом анализе матричных норм согласованы с той или иной векторной нормой.
Определим некоторые наиболее употребительные на практике матричные нормы.
—
— Евклидова норма или норма Фробениуса (Norm(A,‘Fro’) — в MATLAB).
—
— Спектральная норма (Norm(A)=Norm(A,2) в MATLAB),
Где — собственные значения симметричной матрицы (сингулярные числа матрицы А). Обе указанные нормы согласованы с эвклидовой нормой вектора .
—
— Столбцовая норма (Norm(A,1)). (Согласована с векторной нормой ).
—
— строчная норма (Norm(A,Inf)). (Согласована с ).
Замечание. Из всех приведенных матричных норм, согласованных с евклидовой нормой вектора, спектральная норма принимает минимальное значение.
Определение 3. Число (вообще говоря, комплексное) называется Собственным значением матрицы А, соответствующим собственному вектору X, если выполняется условие:
. | (20) |
Определение 4. Множество всех собственных чисел матрицы А , записанных с учетом их кратности, называется Спектром матрицы А и обозначается S(A).
Определение 5. Спектральным радиусом r(A) квадратной матрицы А называется максимальное по модулю собственное значение матрицы A.
Система (20) эквивалентна следующей однородной системе уравнений:
. | (21) |
Как известно из курса линейной алгебры, система (21) имеет нетривиальные решения тогда и только тогда, когда
. | (22) |
Уравнение (22) — алгебраическое уравнение N-ой степени относительно . Все его корни – собственные значения матрицы А.
Определение 6. Сингулярным числом матрицы А называется собственное значение матрицы .
Определение 7. Матрица А называется положительно (неотрицательно) определенной (пишут: или ), если соответствующая квадратичная форма
.
Простейшие следствия из определений.
Следствие 1. (Критерий Сильвестра). все ведущие угловые миноры матрицы А положительны. доказывается в курсе линейной алгебры
Следствие 2. , причем .
следует из критерия Сильвестра.
Следствие 3. все собственные значения . (Для ).
Пусть — собственное значение, соответствующее собственному вектору V. По условию
.
Следствие 4. Пусть А – вещественная матрица матрица .
Имеем: {по свойству скалярного произведения}.
Следствие 5. Сингулярные числа вещественной матрицы А – неотрицательны.
Следует из С.3 и С.4.
Следствие 6. Пусть А – вещественная и симметрическая матрица .
Имеем: .
Следствие 7. Если А – невырожденная матрица собственные значения матриц А и A-1 взаимообратны.
Пусть результат.
| < Предыдущая | Следующая > |
|---|
Норму Фробениуса можно представить себе как взятие столбцов матрицы, наложение их друг на друга для создания вектора размера \(m \times n \text{,}\) и затем взятие векторной 2-нормы результата.
Домашнее задание 1.3.3.1.
Разбиение \(m \times n \) матрицы \(A \) по столбцам:
\begin{уравнение*} A = \left( \begin{массив}{c | c | c} a_0 \amp \cdots \amp a_{n-1} \end{массив} \right). \end{уравнение*}
Покажи, что 92 } \конец{массив} \end{уравнение*}
Домашнее задание 1.3.3.2.
Докажите, что норма Фробениуса является нормой.
Решение
Установить, что эта функция положительно определена и однородна, несложно. Чтобы показать, что неравенство треугольника выполняется, полезно понять, что если \(A = \left( \begin{array}{c | c | c | c} a_0 \amp a_1 \amp \cdots \amp a_{n-1} \end{array} \right) \) then
\begin{equation*}
\начать{массив}{л}
\| А \|_F \\
~~~=~~~~ \lt \mbox{ определение} \gt \\
\sqrt{
\sum_{i=0}^{m-1} \sum_{j=0}^{n-1}
\vert \alpha_{i,j} \vert^2
} \\
~~~=~~~~ \lt \mbox{ коммутативность сложения} \gt \\
\sqrt{
\sum_{j=0}^{n-1} \sum_{i=0}^{m-1}
\vert \alpha_{i,j} \vert^2
} \\
~~~=~~~~ \lt \mbox{ определение векторной 2-нормы } \gt \\
\sqrt{
\sum_{j=0}^{n-1} \| a_j \|_2^2
} \\
~~~=~~~~ \lt \mbox{ определение векторной 2-нормы } \gt \\
\sqrt{
\влево\|
\влево(\начать{массив}{с}
а_0 \\
а_1 \\
\vdots\\
а_{n-1}
\конец{массив}
\Правильно)
\право\|_2^2
}.
Т
\left( \begin{массив}{c| c | c | c}
\overline \alpha_{0,0} \amp \overline \alpha_{1,0} \amp \cdots \amp
\overline \alpha_{m-1,0} \\ \hline
\overline \alpha_{0, 1} \amp \overline \alpha_{1, 1} \amp \cdots \amp
\overline \alpha_{m-1, 1} \\ \hline
\vdots \amp \vdots \amp \amp \vdots \\ \vdots \\\hline
\overline \alpha_{0, n-1} \amp \overline \alpha_{1, n-1} \amp \cdots \amp
\overline \alpha_{m-1, n-1} \
\конец{массив} \справа),
\end{уравнение*} 9Н =
\overline \alpha \text{.}\)
(Если вы рассматриваете скаляр как матрицу, а затем транспонируете ее по эрмитовому методу, вы получаете матрицу с единственным элементом \(\overline \alpha \text{.}\))
Без паники! . Хотя работа со скалярами, векторами и матрицами с комплексными значениями поначалу может показаться немного пугающей, вскоре вы заметите, что на самом деле это ненамного сложнее, чем работа с их аналогами с действительными значениями.
Домашнее задание 1.3.3.4.
Пусть \(A \in \C^{m \times k} \) и \(B \in \C^{k
\times n} \text{.
H \text{.}\) 9Н \|_F
\конец{массив}
\end{equation*}
Точно так же другие нормы матрицы могут быть созданы из векторных норм, рассматривая матрицу как вектор. Оказывается, кроме нормы Фробениуса, на практике они не представляют особого интереса. Пример можно найти в разделе Домашнее задание 1.6.1.6.
матриц — В чем разница между нормой Фробениуса и 2-нормой матрицы?
спросил
Изменено 1 год, 2 месяца назад
Просмотрено 92к раз
$\begingroup$
Если задана матрица, всегда ли норма Фробениуса этой матрицы равна ее 2-норме, или существуют определенные матрицы, для которых эти два метода норм дадут разные результаты?
Если они идентичны, то я полагаю, единственная разница между ними заключается в методе расчета, а?
- матрицы
- нормированные пространства
- матричные нормы
$\endgroup$
4
$\begingroup$
Существует три важных типа матричных норм.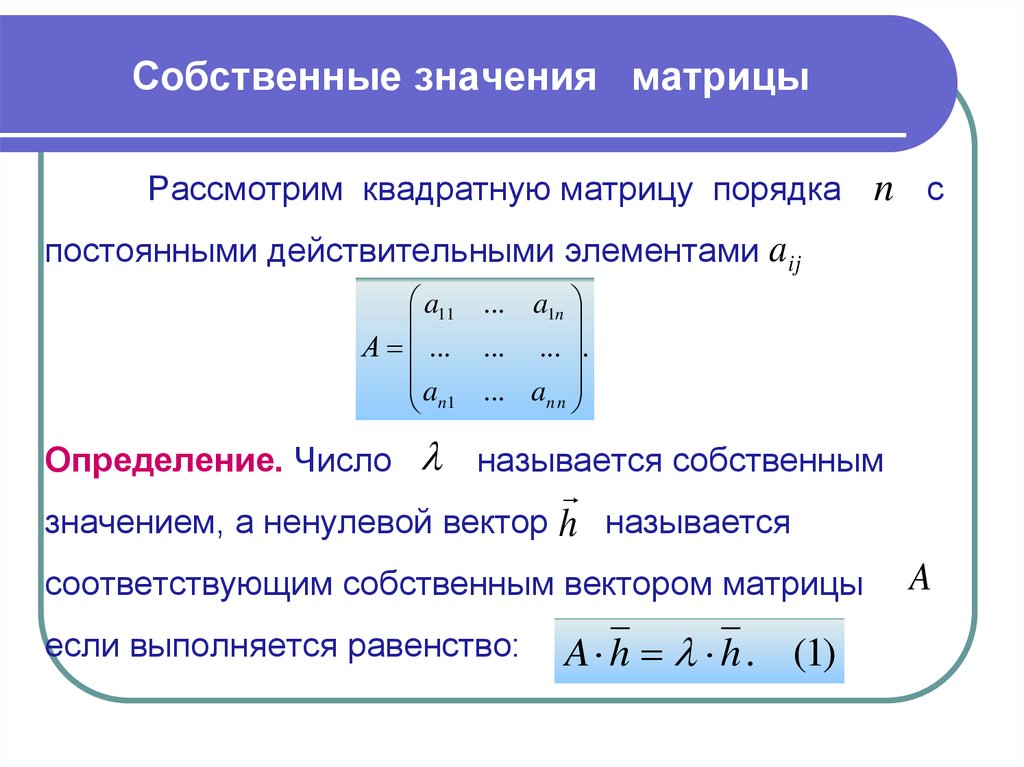
Для некоторой матрицы $A$
Индуцированная норма, измеряющая максимум $\frac{\|Ax\|}{\|x\|}$ для любого $x \neq 0$ (или, что то же самое, , максимум $\|Ax\|$ при $\|x\|=1$).
Поэлементная норма, аналогичная развертыванию $A$ в длинный вектор с последующим вычислением его векторной нормы.
Норма Шаттена, измеряющая векторную норму сингулярных значений $A$.
Итак, отвечая на ваш вопрос:
Итак, если под «2-нормой» вы подразумеваете поэлементную или норму Шаттена, то они идентичны норме Фробениуса. Если вы имеете в виду индуцированную 2-норму, вы получите спектральную 2-норму, которая является $\le$ нормой Фробениуса. (должно быть меньше или равно)
Насколько я понимаю, если не уточнять, о каком типе идет речь, обычно подразумевается индуцированная норма. Например, в Matlab норма (A, 2) дает вам индуцированную 2-норму, которую они просто называют 2-нормой. Таким образом, в этом смысле ответ на ваш вопрос заключается в том, что (индуцированная) матричная 2-норма $\le$, чем норма Фробениуса, и они равны только тогда, когда все собственные значения матрицы имеют одинаковую величину.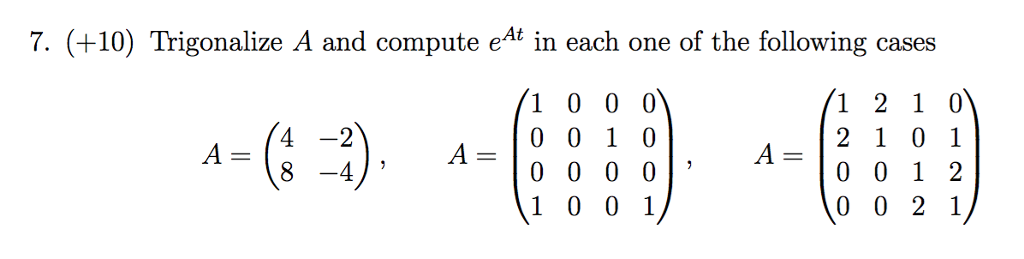
$\endgroup$
$\begingroup$ 92}$$
(r — ранг A).
Вот его 2D-версия: $x$ — это любой вектор на единичной окружности. $Ax$ — деформация всех этих векторов. Длина красной линии — это 2-норма (наибольшая сингулярная величина). А длина зеленой линии – это норма Форбениуса (диагональ).
$\endgroup$
1
$\begingroup$
Все определения см. в Википедии. Возьмите эту матрицу:
$$ \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix} $$
Его фробениусова норма равна $\sqrt{10}$, но собственные значения равны $3,1$, поэтому, если матрица симметрична, ее $2$-норма равна спектральному радиусу, т. е. $3$. Норма Фробениуса всегда не меньше спектрального радиуса. Норма Фробениуса не превышает $\sqrt{r}$ спектрального радиуса, и это, вероятно, мало (см.