Операторы отношения и их функции MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1615 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы
Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?
Операторы отношения служат для сравнения двух величин, векторов или матриц. Все операторы отношения имеют два операнда, например х и у, и записываются, как показано в табл. 8.2.
Таблица 8.2. Операторы и функции отношения
| Функция | Название | Оператор | Пример |
| Eq | Равно | = = | x = = y |
| Ne | He равно | ~ = | x ~ = y |
| Lt | Меньше чем | < | x<y |
| Gt | Больше чем | > | x>y |
| Le | Меньше или равно | <= | x<=y |
| Ge | Больше или равно | >= | x>=y |
Данные операторы
выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают
значение 1 (True), если элементы идентичны, и значение 0 (False) в противном
случае. Если операнды — действительные числа, то применение операторов отношения
тривиально:
Если операнды — действительные числа, то применение операторов отношения
тривиально:
» eq(2.2)
ans =
1
» 2==2
ans =
1
» ne(l,2)
ans =
1
» 2 ~- 2
ans =
0
» 5 > 3
ans =
1
» le(5.3)
ans =
0
Следует отметить,
что операторы <, <=, > и >= при комплексных операндах используют
для сравнения только действительные части операндов — мнимые отбрасываются.
» (2+3i)>-(2+i)
ans=
1
» (2+3i)>(2+i)
ans=
0
» abs(2+3i)>abs(2+i)
ans =
1
» (2+3i)—(2+i)
ans =
0
» (2+3i)-(2+i)
ans =
1
Если один из операндов — скаляр, происходит сравнение всех элементов второго операнда-массива со значением этого скаляра:
M=
-1 0
1 2
» М>=0
ans =
0 1
1 1
В общем случае операторы отношения сравнивают два массива одного размера и выдают результат в виде массива того же размера:
»
М>[0 1;.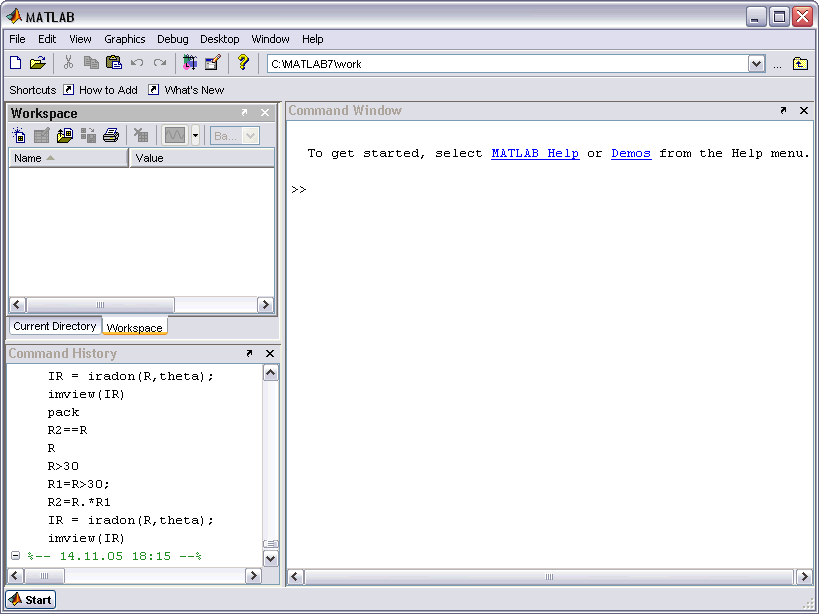 1 0]
1 0]
ans
=
0 0
0 1
Таким образом, спектр применения операторов отношения в системе MATLAB шире, чем в обычных языках программирования, поскольку операндами являются не только числа, но и векторы, матрицы и массивы. Возможно применение операторов отношения и к символьным выражениям:
» ‘b’>’а’
ans =
1
» ‘abc’= =’abc’
ans =
1 1 1
» ‘cba'<‘abc’
ans =
0 0 1
В этом случае
символы, входящие в выражения, представляются своими ASCII-кодами. Строки воспринимаются
как векторы, содержащие значения кодов. Все это надо учитывать при использовании
управляющих структур языка программирования, в которых широко применяются операторы
отношения.
Строки воспринимаются
как векторы, содержащие значения кодов. Все это надо учитывать при использовании
управляющих структур языка программирования, в которых широко применяются операторы
отношения.
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8241 0
Визуализация и графические средства MatLab
9746 0
Техническая документация по системе MatLab
6266 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2298 s
О программных ошибках на примере MATLAB и SimInTech / Хабр
Сила — в правде. На уровне программирования она выражается в том, что одни и те же программы при одних и тех же начальных условиях обязаны выдавать истинную правду, т. е. одинаковые результаты. И даже разные программы, реализующие одну и ту же задачу, должны вести себя одинаково. Действительно, было бы странно, если бы два калькулятора выдавали отличающиеся результаты на одной и той же операции. Или, по-другому, все это своего рода «программистская аксиома».
е. одинаковые результаты. И даже разные программы, реализующие одну и ту же задачу, должны вести себя одинаково. Действительно, было бы странно, если бы два калькулятора выдавали отличающиеся результаты на одной и той же операции. Или, по-другому, все это своего рода «программистская аксиома».
И, вроде бы все так, да не всегда. Критично ли наличие ошибок в программах? Странный вопрос — конечно, критично. Но, тем не менее, найдутся и те, кто скажет – не беда. И даст этому свое объяснение. Здесь, правда, можно вспомнить, как фирма Intel объясняла несущественность ошибки деления с плавающей точкой в процессоре Pentium (подробнее см. [1]). Но общественность и пользователи объяснили Intel, что она не права. И, понеся большие репутационные и финансовые потери, ей пришлось с этим согласиться и исправить положение.
Далее, обсуждая конкретные программы, мы столкнемся с тем, что нужно считать ошибками. Отличие от ситуации с Intel только в том, что необходимо будет конкретизировать, кто ошибается и ошибается ли и где источник ошибок. Но то, что идет явно не по плану, подтверждают результаты нашего тестирования. Просто ситуация несколько сложнее проблемы одной операции деления FDIV.
Но то, что идет явно не по плану, подтверждают результаты нашего тестирования. Просто ситуация несколько сложнее проблемы одной операции деления FDIV.
Итак. Выберем для экспериментов три среды: две известные – это MATLAB, SimInTech и одну, известную больше по статьям вашего покорного слуги, — среду параллельного автоматного программирования ВКПа. Для первых двух можно скачать ограниченные версии. Их возможностей вполне будет достаточно для наших примеров. Ну, а в отношении третьей — придется довериться автору.
Соберем в рамках упомянутых сред простую схему, состоящую из трех блоков — генератора синусоидального сигнала, интегратора и блока отображения. На рис. 1, 2, 3 представлены как подобные решения, так и результаты их работы. И пока ни что не вызывает беспокойства.
Рис.1. Интегрирование синусоидального сигнала в MATLAB Рис.2. Интегрирование синусоидального сигнала в SimInTech Рис. 3. Интегрирование синусоидального сигнала в ВКПаДля пущей уверенности мы собрали еще одну аналогичную схему, заменив только синусоидальный генератор на генератор импульсных сигналов. Но это в целом ситуацию не изменило. Хотя, что там греха таить, основная цель всех этих экспериментов была все же проверить «честность» блока интегрирования среды ВКПа и, если необходимо, доработать его функциональность.
Но это в целом ситуацию не изменило. Хотя, что там греха таить, основная цель всех этих экспериментов была все же проверить «честность» блока интегрирования среды ВКПа и, если необходимо, доработать его функциональность.
Далее в рамках тестирования ВКПа на примерах все более сложных задач мы создали схемы аттракторов, описанных в статье на Хабре [2]. Это аттракторы Лоренца, Ресслера, Рикитаки и Нозе-Гувера. В статье они представлены схемами в МАТЛАБ. Аналогичные схемы мы собрали для SymInTech и ВКПа. Сравнительные результаты их тестирования оказались столь любопытны, что заслуживают того, чтобы с ними был ознакомлен и Хабр.
При этом отличия в результатах тестирования аттракторов Лоренца проявились в наибольшей степени. Они приведены для МАТЛАБ на рис. 4, для SymInTech — на рис. 5 и для ВКПа на рис. 6. Глядя на результаты можно лишь сказать, что они похожи и не более того. Поэтому, анализируя их, надо бы признать, что они фактически опровергают сформулированную нами ранее «программистскую аксиому». С таким положением мириться нельзя и это, безусловно, требует своего разбирательства и поиска причин случившегося.
С таким положением мириться нельзя и это, безусловно, требует своего разбирательства и поиска причин случившегося.
Рис. 5. Тестирование аттрактора Лоренца в SymInTechРис. 6. Тестирование аттрактора Лоренца в ВКПа
Почему сертифицированный SimInTech выдает результаты, которые отличаются от, наверное, столь же сертифицированного пакета MATLAB? Может, можно все списать на хаос, который моделируют аттракторы? Однако, повторный перезапуск программ свидетельствует о его отсутствии.
Но автора обеспокоило совсем другое — достаточно сильное на фоне остальных программ отличие результатов, показанных ВКПа. Отметим также, что перезапуск ВКПа порождал близкие, но все же отличающиеся результаты. Т.е. в какой-то мере они больше отвечали поставленной цели – моделированию хаоса. Но причины этого достаточно понятны. К хаосу они имеют мало отношения и это мы объясним позже.
И тут пришло время вспомнить про параллелизм. Уравнения каждого из аттракторов представляют собой систему из нескольких параллельных дифференциальных уравнений. Но только у ВКПа можно выбрать один из двух режимов работы: использовать при расчетах теневую память (это стандартный режим, обеспечивающий параллельные свойства среды [3]) или работать в обычном режиме. Напомним, что в режиме теневой памяти измененные на текущем такте данные помещаются в буфер, чтобы, когда выполнятся все действия, стать новыми значениями. В обычном режиме данные обновляются ровно в моменты их изменений.
Но только у ВКПа можно выбрать один из двух режимов работы: использовать при расчетах теневую память (это стандартный режим, обеспечивающий параллельные свойства среды [3]) или работать в обычном режиме. Напомним, что в режиме теневой памяти измененные на текущем такте данные помещаются в буфер, чтобы, когда выполнятся все действия, стать новыми значениями. В обычном режиме данные обновляются ровно в моменты их изменений.
После изменения режима расчета в ВКПа были получили графики, представленные на рис. 7. Сам режим работы при этом определяется состоянием переключателем shadow mode of variables (см. рис. 7), т.е. код вычислительных процессов ни как не затрагивается. Как можно видеть, полученные графики в большей степени походят на результаты конкурентов, чем на свой, но полученный в теневом режиме работы среды. Из этого следует, что два других пакета, решая поставленную задачу, скорее всего, вычисления выполняют строго последовательно, искажая тем самым «правду».
С подобной проблемой параллельных расчетов автору уже приходилось сталкиваться. Тогда участником экспериментов был пакет LabVIEW и решалась проблема моделирования адаптивного ПИД-регулятора (об этом см. статью на Хабре [4]). Значения данных, рассчитанных пакетом, полностью совпадали со значениями, полученными в ВКПа, но были сдвинуты по времени. Это говорило о последовательной работе созданных моделей объекта и регулятора. Доказано это было, как и выше, путем изменения режима работы среды.
Разные же результатов у ВКПа от запуска к запуску объясняются принципом работы ядра среды. Если первые два рассчитывают работу приложения, то ВКПа ее именно моделирует. Это происходит в дискретном времени, длительность такта которого «плавающая». Эту разницу соответственно и «ловит» блок интегрирования. Отсюда и некий «хаос» в поведении аттрактора в ВКПа. Но, еще раз, он вполне объясним и потому даже ожидаем.
Основное вывод, который следует сделать, сводится к тому, что современное программирование, как ни крути, а «антипараллельно».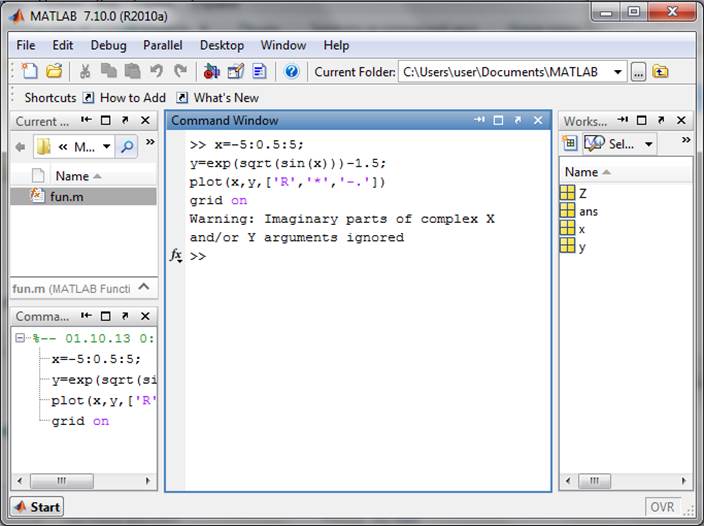 А потому в его рамках сложно в полной мере доверяться даже достаточно известным программным пакетам. Но самое опасное в том, что они используются огромным числом специалистов, не подозревающих о тех последствиях, которые могут произойти, если им доверяться всецело и безоглядно.
А потому в его рамках сложно в полной мере доверяться даже достаточно известным программным пакетам. Но самое опасное в том, что они используются огромным числом специалистов, не подозревающих о тех последствиях, которые могут произойти, если им доверяться всецело и безоглядно.
В их оправдание можно лишь сказать, что ни MATLAB ни SimInTech лишь отчасти виноваты в том, что не учитывают параллельные свойства реальных систем. Они просто следуют тенденциям и понятиям современного программирования. А те «сертификации», которые они успешно проходят, похоже, столь же «антипараллельны», как и само современное программирование.
По-хорошему теперь нужно ждать разъяснений по поводу разницы в результатах «обычных» прогонов, а также по поводу учета параллелизма, как программных, так и вполне реальных систем. Это особенно важно, т.к. в перечень решаемых пакетами задач входят те, которые весьма критичны к ошибкам. Вдруг, не дай Бог, что-то не так взлетит, не туда попадет, внезапно откажет или не вовремя утонет? Такой хаос нам не нужен!
Приложение
Схемы аттрактора Лоренца в MATLAB, SymInTech, ВКПа
Схемы остальных аттрактор аналогичны и результаты их тестирования достаточно похожи друг на друга. Даже в обоих режимах работы ВКПа.
Даже в обоих режимах работы ВКПа.
Литература
Ошибка Pentium FDIV
Генераторы хаоса на ПЛИС
Автоматное программирование: определение, модель, реализация
Параллелизм, корутины, событийные автоматы,… живая математика
Оператор MATLAB — Javatpoint
следующий → ← предыдущая Оператор — это символ, который указывает компилятору выполнять различные числовые или логические операции. MATLAB предназначен для работы в основном с целыми матрицами и массивами. Поэтому функции в MATLAB работают как со скалярными, так и с нескалярными данными. MATLAB имеет несколько типов операторов, символов и специальных символов для работы с переменными, функциями и арифметическими операциями. Арифметические операторы MATLAB Арифметические операторы помогают выполнять простые арифметические операции, такие как сложение, вычитание, умножение, деление и возведение в степень.
Арифметические операторы и массивы За исключением некоторых матричных операторов, арифметические операторы MATLAB работают с соответствующими функциями массивов одинаковой размерности. В этом примере используется скалярное расширение для вычисления произведения скалярного операнда и матрицы. А = магия (3) А = 8 1 6 3 5 7 4 9 2 3 * А ответ= 24 3 18 9 15 21 12 27 6 Реляционные операторы MATLABРеляционные операторы выполняют операции сравнения значений.
Реляционные операторы и массивы Реляционные операторы MATLAB сравнивают соответствующие компоненты массивов одинаковой размерности. А = [2 7 6; 9 0 5; 3 0,5 6]; В = [8 7 0; 3 2 5; 4 -1 7]; А == Б ответ = 0 1 0 0 0 1 0 0 0 Для векторов и прямоугольных массивов оба операнда должны иметь одинаковый размер, если только один из них не является скаляром. В этом случае, когда один операнд является скаляром, а другой — нет, MATLAB проверяет скаляр относительно каждого элемента другого операнда. Места, где конкретное отношение истинно, получают логическую 1. Места, где отношение ложно, получают логический 0. Логические операторы MATLABЛогические операторы выполняют логические операции и выводят результат в логическом состоянии true или false с использованием чисел 1 и 0 соответственно. MATLAB предлагает три типа логических операторов и функций:
Значения, возвращаемые логическими операторами и функциями MATLAB, за исключением побитовых функций, имеют логический тип и подходят для использования с логическим индексированием. Элементарные операторы и функцииСледующие логические операторы и функции выполняют поэлементные логические операции со своими входными данными для создания выходного массива одинакового размера. Примеры показаны в следующей таблице с использованием векторных входных данных A и B, где А = [0 1 1 0 1];
Для операторов и функций, которые принимают два операнда массива (&, | и xor), оба массива должны иметь одинаковые размеры, причем все измерения должны быть одного размера. Единственным исключением является случай, когда один операнд является скаляром, а другой — нет. Примечание. MATLAB преобразует любые конечные ненулевые математические значения, используемые в качестве входных данных для логических выражений, в логическую 1 или истину. Побитовый операторСледующие функции выполняют побитовые логические операции над входными неотрицательными целыми числами. Входные данные могут быть скалярными или массивами. Если в массивах, эти операции создают выходной массив одинакового размера. Примеры, представленные в следующей таблице, используют скалярные входы A и B, где А = 28; % двоичный 11100
Операторы короткого замыканияСледующие операторы выполняют операции И и ИЛИ над логическими выражениями, включая скалярные значения. Это операторы короткого замыкания в том смысле, что они вычисляют свой второй операнд только тогда, когда первый операнд не полностью определяет вывод.
Специальные символы MATLABСпециальные символы выполняют определенные задачи в зависимости от их поведения и положения, в котором они используются.
Специальные символы форматирования строк и символов MATLAB Некоторые специальные символы можно использовать только в тексте символа или строки.
Следующая темаФорматирование текста ← предыдущая следующий → |
Функция Strcmp в MatLab
В следующей статье объясняется, как использовать функцию strcmp в MATLAB® для сравнения двух строк, массивов ячеек из символьных векторов, символьных векторов или массивов из символьных строк.
Функция strcmp широко используется и входит в стандартные библиотеки всех популярных в мире языков программирования, а режим ее выполнения одинаков для всех них.
Эта статья содержит практические примеры и снимки экрана, показывающие, как можно использовать эту функцию с различными типами входных аргументов. Мы также покажем вам некоторые из наиболее распространенных ошибок, генерируемых этой функцией, соответствующие сообщения об ошибках и способы их решения, чтобы упростить программирование.
Синтаксис
l = strcmp(s1, s2)
Описание и примеры
Функция strcmp() сравнивает две строки символов «s1» и «s2» и возвращает логический результат в «L», true ( 1) если «s1» и «s2» совпадают или false (0), если строки «s1» и «s2» разные. При использовании этой функции порядок ввода не влияет на результат сравнения.
Входные параметры, которые принимает эта функция, могут быть символьными строками, массивами ячеек из символьных векторов, символьными векторами или массивами символьных строк, и это поддерживает международные наборы символов. Если и «s1», и «s2» являются массивами строк или массивами ячеек из символьных векторов, то «s1» и «s2» должны иметь одинаковый или совместимый размер, если только один из них не является скаляром. Если s1 и s2 — массивы символов с несколькими строками, то «s1» и «s2» могут иметь разное количество строк.
Как сравнить две чистые строки символов.
В следующем примере показан простейший способ использования этой функции, когда входными аргументами являются два строковых скаляра. Как показано ниже, в первом случае строки одинаковы, поэтому функция strcmp возвращает логическую «1» в «L». Строки символов во втором случае отличаются, и функция strcmp возвращает логический «0» в «L».
Как показано ниже, в первом случае строки одинаковы, поэтому функция strcmp возвращает логическую «1» в «L». Строки символов во втором случае отличаются, и функция strcmp возвращает логический «0» в «L».
L = strcmp («Эквивалентно», «Эквивалентно»)
L = strcmp («Не эквивалентно», «Эквивалентно»)
Если «s1» и «s2» равны, функция strcmp() возвращает логическую 1 в «L», а если «s1» и «s2» не равны, она возвращает логический 0 в «L».
Как сравнить два строковых скаляра.
Далее мы рассмотрим, как вызывать функцию strcmp(), посылая в качестве входных аргументов символьные скаляры вместо простых строк. Для этого мы создаем векторы «s1» и «s2». То же самое относится к массивам векторов символов или массивам строк.
s1 = «Эквивалент»;
s2 = «Эквивалент»;
L = strcmp(s1, s2)
В результате будет возвращена логическая 1.
Как использовать функцию strcmp для поиска строки символов в массиве строк.
Также можно найти строку символов, содержащуюся в «s1», в массиве ячеек из символьных векторов или массивов строк, используя функцию strcmp.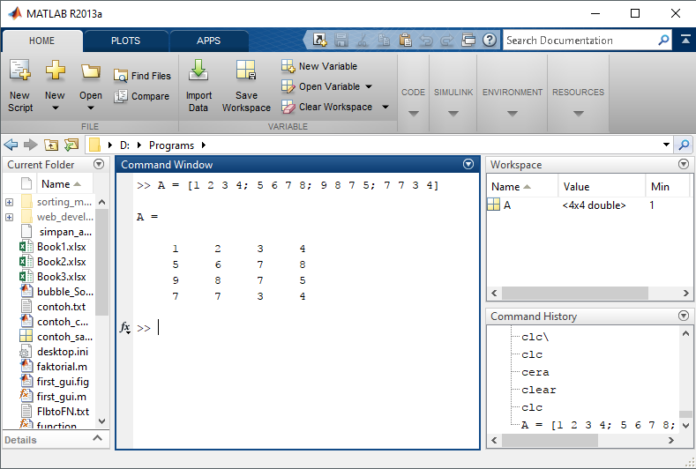 Это сравнивает строку, содержащуюся в «s1», с каждым из элементов в «s2».
Это сравнивает строку, содержащуюся в «s1», с каждым из элементов в «s2».
s1 = ‘Эквивалент’;
s2 = {‘Эквивалентно’, ‘Не эквивалентно’, ‘Не эквивалентно’;
‘Эквивалентный’, ‘Неэквивалентный’, ‘Эквивалентный’;
‘Эквивалентно’, ‘Не эквивалентно’, ‘Эквивалентно’};
Lc = strcmp(s1, s2)
В результате функция strcmp вернет массив «Lc» логических элементов истинного (1) или ложного (0) в порядке и размере «s2».
Lc=
1 0 0
1 0 1
1 0 1
Что произойдет, если мы захотим сравнить две строки символов с массивом?
В приведенном выше примере функция strcmp() была отправлена с одним скаляром в качестве входного аргумента в «s1», чтобы найти совпадающую строку в «s2». В этом примере «s1» отправляется с двумя строками, поэтому правило совместимого размера массива не выполняется.
s1 = {‘Эквивалентно’, ‘Не эквивалентно’};
s2 = {‘Эквивалентно’, ‘Не эквивалентно’, ‘Не эквивалентно’;
‘Эквивалентно’, ‘Не эквивалентно’, ‘Эквивалентно’;
‘Эквивалентно’, ‘Не эквивалентно’, ‘Эквивалентно’};
Lc = strcmp(s1, s2)
В этом случае функция strcmp() вернет следующее сообщение об ошибке:
«Ошибка при использовании strcmp Входные данные должны быть одного размера, иначе любой из них может быть скалярным».
Как использовать функцию strcmp() для сравнения двух массивов ячеек символьных векторов.
В этом примере показано, как можно использовать функцию strcmp для сравнения двух массивов ячеек из символьных векторов.
s1 = {‘Эквивалент’, ‘Эквивалент’; ‘Эквивалент’, ‘Эквивалент’};
s2 = {‘Эквивалент’, ‘Эквивалент’; ‘Не эквивалентно’, ‘Не эквивалентно’};
lc = strcmp(s1,s2)
В результате будет возвращен логический массив того же размера и порядка, что и «s1» или «s2».
lc=
1 1
0 0
Кроме того, в этом случае входные параметры должны быть массивами ячеек из символьных векторов одинакового размера; в противном случае функция strcmp() возвращает следующее сообщение об ошибке:
«Ошибка при использовании strcmp. Входные данные должны быть одного размера, иначе любой из них может быть скалярным».
Как сравнить два массива строк с помощью функции strcmp.
Теперь мы увидим, как сравнивать массивы строк с помощью функции strcmp. Для этого создадим массивы «s1» и «s2» с элементами 3×3.
s1 = [«Равно», «Не эквивалентно», «Эквивалентно»];
s2 = [«Равно», «Эквивалентно», «Эквивалентно»];
Lc = strcmp(s1,s2)
В результате будет возвращен логический массив того же размера и порядка, что и «s1» или «s2».
Lc=
1 0 1
Как сравнить две строки символов с помощью операторов отношения в MATLAB.
Операторы также могут использоваться для выполнения операций над строками. Правила размера и совместимости для массивов такие же, как и для strcmp.
Далее мы покажем вам еще один способ сравнения строк символов — использование оператора отношения «==». Синтаксис следующий:
L = s1==s2.
s1 = [«Равно», «Не эквивалентно», «Эквивалентно»];
s2 = [«Равно», «Эквивалентно», «Эквивалентно»];
Lc = s1==s2
Вывод:
В этой статье объясняется, как использовать основные функции MATLAB для сравнения строк с помощью функции strcmp().

 Для векторов и прямоугольных массивов оба операнда должны быть одинакового размера, если только один из них не является скаляром. Если один операнд является скаляром, а другой нет, MATLAB применяет скаляр к каждому элементу другого операнда, это свойство называется скалярным расширением.
Для векторов и прямоугольных массивов оба операнда должны быть одинакового размера, если только один из них не является скаляром. Если один операнд является скаляром, а другой нет, MATLAB применяет скаляр к каждому элементу другого операнда, это свойство называется скалярным расширением. Реляционные операторы всегда работают поэлементно. В этом примере результирующая матрица присутствует, где элемент A равен соответствующей части B.
Реляционные операторы всегда работают поэлементно. В этом примере результирующая матрица присутствует, где элемент A равен соответствующей части B.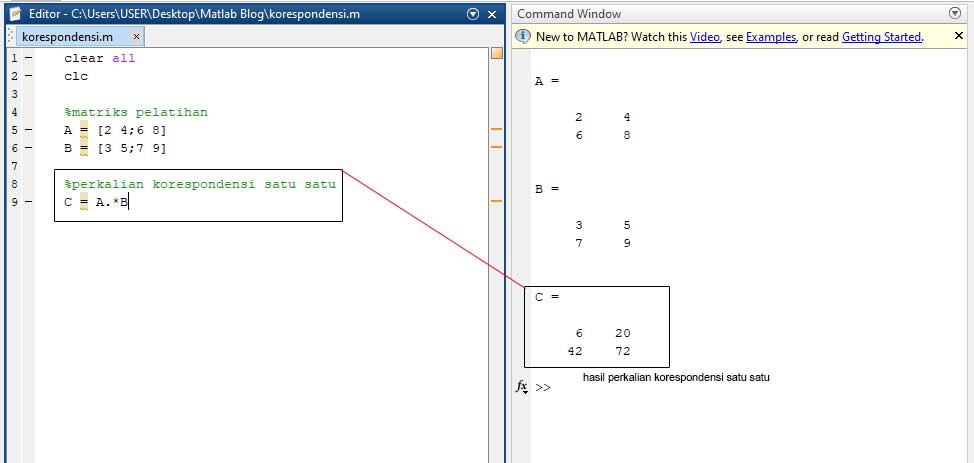
 Эти специальные символы используются для вставки новой строки или возврата каретки, указания путей к папкам.
Эти специальные символы используются для вставки новой строки или возврата каретки, указания путей к папкам. m
m