Наибольший общий делитель (НОД): определение, примеры и свойства
Эта статья посвящена такому вопросу, как нахождение наибольшего общего делителя. Сначала мы объясним, что это такое, и приведем несколько примеров, введем определения наибольшего общего делителя 2, 3 и более чисел, после чего остановимся на общих свойствах данного понятия и докажем их.
Что такое общие делители
Чтобы понять, что из себя представляет наибольший общий делитель, сначала сформулируем, что вообще такое общий делитель для целых чисел.
В статье о кратных и делителях мы говорили, что у целого числа всегда есть несколько делителей. Здесь же нас интересуют делители сразу некоторого количества целых чисел, особенно общие (одинаковые) для всех. Запишем основное определение.
Определение 1Общим делителем нескольких целых чисел будет такое число, которое может быть делителем каждого числа из указанного множества.
Пример 1Вот примеры такого делителя: тройка будет общим делителем для чисел -12 и 9, поскольку верны равенства 9=3·3 и −12=3·(−4). У чисел 3 и -12 есть и другие общие делители, такие, как 1, −1 и −3. Возьмем другой пример. У четырех целых чисел 3, −11, −8 и 19 будет два общих делителя: 1 и -1.
У чисел 3 и -12 есть и другие общие делители, такие, как 1, −1 и −3. Возьмем другой пример. У четырех целых чисел 3, −11, −8 и 19 будет два общих делителя: 1 и -1.
Зная свойства делимости, мы можем утверждать, что любое целое число можно разделить на единицу и минус единицу, значит, у любого набора целых чисел уже будет как минимум два общих делителя.
Также отметим, что если у нас есть общий для нескольких чисел делитель b, то те же числа можно разделить и на противоположное число, то есть на -b. В принципе, мы можем взять лишь положительные делители, тогда все общие делители также будут больше 0. Такой подход также можно использовать, однако совсем игнорировать отрицательные числа не следует.
Что такое наибольший общий делитель (НОД)
Согласно свойствам делимости, если b является делителем целого числа a, которое не равно 0, то модуль числа b не может быть больше, чем модуль a, следовательно, любое число, не равное 0, имеет конечное число делителей. Значит, число общих делителей нескольких целых чисел, хотя бы одно из которых отличается от нуля, также будет конечным, и из всего их множества мы всегда можем выделить самое большое число (ранее мы уже говорили о понятии наибольшего и наименьшего целого числа, советуем вам повторить данный материал).
В дальнейших рассуждениях мы будем считать, что хотя бы одно из множества чисел, для которых нужно найти наибольший общий делитель, будет отлично от 0. Если они все равны 0, то их делителем может быть любое целое число, а поскольку их бесконечно много, выбрать наибольшее мы не сможем. Иначе говоря, найти наибольший общий делитель для множества чисел, равных 0, нельзя.
Переходим к формулировке основного определения.
Определение 2Наибольшим общим делителем нескольких чисел является самое большое целое число, которое делит все эти числа.
На письме наибольший общий делитель чаще всего обозначается аббревиатурой НОД. Для двух чисел его можно записать как НОД (a, b).
Пример 2Какой можно привести пример НОД для двух целых чисел? Например, для 6 и -15 это будет 3. Обоснуем это. Сначала запишем все делители шести: ±6, ±3, ±1, а потом все делители пятнадцати: ±15, ±5, ±3 и ±1. После этого мы выбираем общие: это −3, −1, 1 и 3. Из них надо выбрать самое большое число.
Для трех и более чисел определение наибольшего общего делителя будет почти таким же.
Определение 3Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Для чисел a1, a2, …, an делитель удобно обозначать как НОД (a1, a2, …, an). Само значение делителя записывается как НОД (a1, a2, …, an) =b.
Пример 3Приведем примеры наибольшего общего делителя нескольких целых чисел: 12, -8, 52, 16. Он будет равен четырем, значит, мы можем записать, что НОД (12, -8, 52, 16) =4.
Проверить правильность данного утверждения можно с помощью записи всех делителей этих чисел и последующего выбора наибольшего из них.
На практике часто встречаются случаи, когда наибольший общий делитель равен одному из чисел. Это происходит тогда, когда на данное число можно разделить все остальные числа (в первом пункте статьи мы привели доказательство этого утверждения).
Пример 4Так, наибольший общий делитель чисел 60, 15 и -45 равен 15, поскольку пятнадцать делится не только на 60 и -45, но и на само себя, и большего делителя для всех этих чисел не существует.
Особый случай составляют взаимно простые числа. Они представляют собой целые числа с наибольшим общим делителем, равным 1.
Основные свойства НОД и алгоритм Евклида
У наибольшего общего делителя есть некоторые характерные свойства. Сформулируем их в виде теорем и докажем каждое из них.
Отметим, что данные свойства сформулированы для целых чисел больше нуля, а делители мы рассмотрим только положительные.
Определение 4Числа a и b имеют наибольший общий делитель, равный НОД для b и a, то есть НОД (a, b)=НОД (b, a). Перемена мест чисел не влияет на конечный результат.
Данное свойство следует из самого определения НОД и не нуждается в доказательствах.
Определение 5Если число a можно разделить на число b, то множество общих делителей этих двух чисел будет аналогично множеству делителей числа b, то есть НОД (a, b)=b.
Докажем это утверждение.
Доказательство 1Если у чисел a и b есть общие делители, то на них можно разделить любое из них. В то же время если a будет кратным b, то любой делитель b будет делителем и для a, поскольку у делимости есть такое свойство, как транзитивность. Значит, любой делитель b будет общим для чисел a и b. Это доказывает, что если мы можем разделить a на b, то множество всех делителей обоих чисел совпадет с множеством делителей одного числа b. А поскольку наибольший делитель любого числа есть само это число, то наибольший общий делитель чисел a и b будет также равен b, т.е. НОД (a, b)=b. Если a=b, то НОД (a, b)=НОД (a, a)=НОД (b, b) =a=b, например, НОД (132, 132) =132.
В то же время если a будет кратным b, то любой делитель b будет делителем и для a, поскольку у делимости есть такое свойство, как транзитивность. Значит, любой делитель b будет общим для чисел a и b. Это доказывает, что если мы можем разделить a на b, то множество всех делителей обоих чисел совпадет с множеством делителей одного числа b. А поскольку наибольший делитель любого числа есть само это число, то наибольший общий делитель чисел a и b будет также равен b, т.е. НОД (a, b)=b. Если a=b, то НОД (a, b)=НОД (a, a)=НОД (b, b) =a=b, например, НОД (132, 132) =132.
Используя это свойство, мы можем найти наибольший общий делитель двух чисел, если одно из них можно разделить на другое. Такой делитель равен одному из этих двух чисел, на которое можно разделить второе число. К примеру, НОД (8, 24) =8, так как 24 есть число, кратное восьми.
Определение 6Если верно равенство a=b·q+c (здесь все переменные являются целыми числами), то все общие делители двух чисел a и b будут такими же, как и у чисел b и c, то есть НОД (a, b)=НОД (b, c).
Попробуем доказать данное свойство. У нас изначально есть равенство a=b·q+c, и любой общий делитель a и b будет делить и c, что объясняется соответствующим свойством делимости. Поэтому любой общий делитель b и c будет делить a. Значит, множество общих делителей a и b совпадет с множеством делителей b и c, в том числе и наибольшие из них, значит, равенство НОД (a, b)=НОД (b, c) справедливо.
Следующее свойство получило название алгоритма Евклида. С его помощью можно вычислить наибольший общий делитель двух чисел, а также доказать другие свойства НОД.
Перед тем, как сформулировать свойство, советуем вам повторить теорему, которую мы доказывали в статье о делении с остатком. Согласно ей, делимое число a можно представить в виде b·q+r, причем b здесь является делителем, q – некоторым целым числом (его также называют неполным частным), а r – остатком, который удовлетворяет условию 0≤r≤b.
Допустим, у нас есть два целых числа больше 0, для которых будут справедливы следующие равенства:
a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1
Эти равенства заканчиваются тогда, когда rk+1становится равен 0.
В первую очередь нам надо доказать, что rk– это общий делитель чисел a и b, а после этого – то, что rk является не просто делителем, а именно наибольшим общим делителем двух данных чисел.
Просмотрим список равенств, приведенный выше, снизу вверх. Согласно последнему равенству,
rk−1 можно разделить на rk. Исходя из этого факта, а также предыдущего доказанного свойства наибольшего общего делителя, можно утверждать, что rk−2 можно разделить на rk, так как
rk−1 делится на rk и rkделится на rk.
Третье снизу равенство позволяет нам сделать вывод, что rk−3 можно разделить на rk, и т.д. Второе снизу – что b делится на rk, а первое – что a делится на rk. Из всего этого заключаем, что rk

Теперь докажем, что rk=НОД (a, b). Что для этого нужно сделать? Показать, что любой общий делитель a и b будет делить rk. Обозначим его r0.
Просмотрим тот же список равенств, но уже сверху вниз. Исходя из предыдущего свойства, можно заключить, что r1 делится на r0, значит, согласно второму равенству r2 делится на r0. Идем по всем равенствам вниз и из последнего делаем вывод, что rk делится на r0. Следовательно, rk=НОД (a, b).
Рассмотрев данное свойство, заключаем, что множество общих делителей a и b аналогично множеству делителей НОД этих чисел. Это утверждение, которое является следствием из алгоритма Евклида, позволит нам вычислить все общие делители двух заданных чисел.
Перейдем к другим свойствам.
Определение 8Если a и b являются целыми числами, не равными 0, то должны существовать два других целых числа u0 и v0, при которых будет справедливым равенство НОД (a, b) =a·u0+b·v0.
Равенство, приведенное в формулировке свойства, является линейным представлением наибольшего общего делителя a и b. Оно носит название соотношения Безу, а числа u0 и v0 называются коэффициентами Безу.
Оно носит название соотношения Безу, а числа u0 и v0 называются коэффициентами Безу.
Докажем данное свойство. Запишем последовательность равенств по алгоритму Евклида:
a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1
Первое равенство говорит нам о том, что r1=a−b·q1. Обозначим 1=s1 и −q1=t1 и перепишем данное равенство в виде r1=s1·a+t1·b. Здесь числа s1 и t1 будут целыми. Второе равенство позволяет сделать вывод, что r2=b−r1·q2=b−(s1·a+t1·b) ·q2=−s1·q2·a+(1−t1·q2) ·b. Обозначим −s1·q2=s2 и 1−t1·q2=t2 и перепишем равенство как r2=s2·a+t2·b, где s2 и t2 также будут целыми. Это объясняется тем, что сумма целых чисел, их произведение и разность также представляют собой целые числа. Точно таким же образом получаем из третьего равенства r3=s3·a+t3·b, из следующего r4=s4·a+t4·b и т.д. В конце заключаем, что rk=sk·a+tk·b при целых sk и tk. Поскольку rk=НОД (a, b), обозначим sk=u0 и tk=v0, В итоге мы можем получить линейное представление НОД в требуемом виде: НОД (a, b) =a·u0+b·v0.
НОД (m·a, m·b) =m·НОД(a, b) при любом натуральном значении m.
Доказательство 4Обосновать это свойство можно так. Умножим на число m обе стороны каждого равенства в алгоритме Евклида и получим, что НОД (m·a, m·b) =m·rk, а rk – это НОД (a, b). Значит, НОД (m·a, m·b) =m·НОД(a, b). Именно это свойство наибольшего общего делителя используется при нахождении НОД методом разложения на простые множители.
Определение 10Если у чисел a и b есть общий делитель p, то НОД (a:p, b:p)=НОД(a, b):p. В случае, когда p=НОД (a, b) получим НОД (a:НОД(a, b), b:НОД (a, b)=1, следовательно, числа a:НОД(a, b) и b:НОД (a, b) являются взаимно простыми.
Поскольку a=p·(a:p) и b=p·(b:p), то, основываясь на предыдущем свойстве, можно создать равенства вида НОД(a, b)=НОД(p·(a:p), p·(b:p))=p·НОД(a:p, b:p), среди которых и будет доказательство данного свойства. Это утверждение мы используем, когда приводим обыкновенные дроби к несократимому виду.
Определение 11Наибольшим общим делителем a1, a2, …, ak будет число dk, которое можно найти, последовательно вычисляя НОД (a1, a2)=d2, НОД (d2, a3) =d3, НОД (d3, a4) =d4, …, НОД (dk-1, ak) =dk.
Это свойство полезно при нахождении наибольшего общего делителя трех и более чисел. С помощью него можно свести это действие к операциям с двумя числами. Его основой является следствие из алгоритма Евклида: если множество общих делителей a1, a2 и a3 совпадает с множеством d2 и a3, то оно совпадет и с делителями d3. Делители чисел a1, a2, a3 и a4 совпадут с делителями d3, значит, они совпадут и с делителями d4, и т.д. В конце мы получим, что общие делители чисел a1, a2, …, akсовпадут с делителями dk, а поскольку наибольшим делителем числа dkбудет само это число, то НОД (a1, a2, …, ak) =dk.
Это все, что мы хотели бы рассказать о свойствах наибольшего общего делителя.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Наибольший Общий Делитель
Давайте вспомним, что означают эти буквы: аббревиатура «НОД» расшифровывается как «Наибольший Общий Делитель».
Делитель – это число, на которое другое число делится без остатка.
Обычно необходимо найти НОД для двух чисел. Иногда эту задачу усложняют и ищут НОД для трех, четырех и более чисел.
Например:
Два числа: 9 и 12
Три числа: 9, 12 и 24
Дадим определение:
Наибольший Общий Делитель (НОД) – это такое наибольшее число, на которое исследуемые числа делятся без остатка.
Найдем НОД для чисел 9 и 12
Запишем все делители этих чисел:
12 – ( 1, 2, 3, 4, 6, 12)
9 – ( 1, 3, 9)
Сравним оба ряда. В обоих рядах наибольшим одинаковым числом является 3. Это число и будет НОД для этой пары чисел. Оба этих числа делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Таким образом, НОД (12 и 9) = 3
Зачем нужен НОД?
Например, чтобы упростить большую дробь.
Вот числа 9 и 12. Наибольший Общий Делитель для них будет число 3.
Если у нас будет дробь 9/12, то её можно упростить, разделив числитель и знаменатель на НОД, т.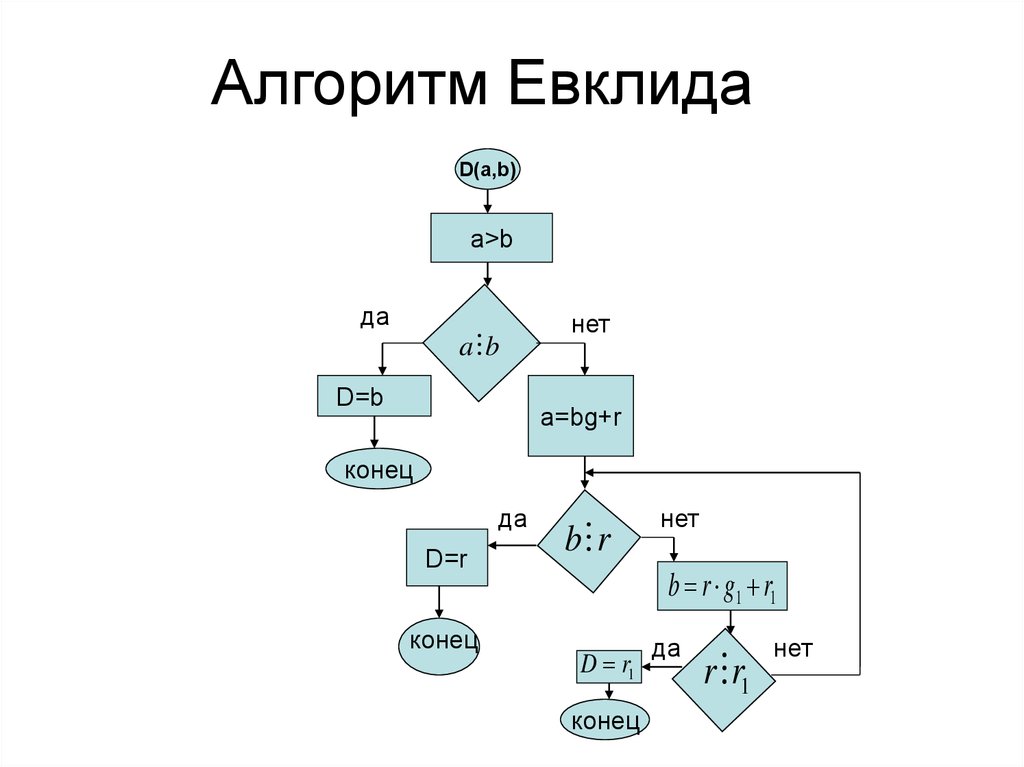 е. на 3, получим:
е. на 3, получим:
9/12 = (9 ∶ 3)/(12 ∶ 3) = 3/4
Согласитесь, что с дробью 3/4 гораздо удобнее проводить дальнейшие вычисления, чем с 9/12 .
Чтобы найти НОД двух чисел, существует несколько способов.
Один мы рассмотрели выше, когда нашли НОД для пары чисел 12 и 9.
Рассмотрим теперь другой, самый наглядный способ. Он подходит для нахождения НОД любых чисел (и маленьких, и больших).
Например, найти НОД для чисел 24 и 18.
Решение:
Разложим эти два числа на простые множители:
24 I 2 18 I 2
12 I 2 9 I 3
6 I 2 3 I 3
3 I 3 1 I
1 I
Итак, получаем разложения:
24 = 2 · 2 · 2 · 3
18 = 2 · 3 · 3
Теперь ищем в этих разложениях одинаковые пары чисел, подчеркнем эти пары:
24 = 2 · 2 · 2 · 3
18 = 2 · 3 · 3
Получили две пары: (2 и 2) и (3 и 3). Остальные числа в рядах не имеют совпадений.
Получаем, что общими множителями чисел 24 и 18 являются числа 2 и 3.
Чтобы получить НОД этих чисел, мы перемножим эти числа и получим:
2 · 3 = 6
Получаем: НОД (24 и 18) = 6
Именно на это число мы можем разделить 24 и 18 без остатка:
24 : 6 = 4
18 : 6 = 3
Это число является их делителем. И именно это число будет их наибольшим делителем, т.е. НОДом.
Теперь возьмем числа побольше.
Например,
Найти НОД для чисел 72 и 128.
Решение:
Разложим эти два числа на простые множители:
128 I 2 72 I 2
64 I 2 36 I 2
32 I 2 18 I 2
16 I 2 9 I 3
8 I 2 3 I 3
4 I 2 1 I
2 I 2
1 I
Итак, получаем разложения:
128 = 2 · 2 · 2 · 2 · 2 · 2 · 2
72 = 2 · 2 · 2 · 3 · 3
Теперь ищем в этих разложениях одинаковые пары чисел, выделим эти пары подчеркиванием:
128 = 2 · 2 · 2 · 2 · 2 · 2 · 2
72 = 2 · 2 · 2 · 3 · 3
Получили три пары: (2 и 2), (2 и 2) и (2 и 2). Остальные числа в рядах не имеют совпадений.
Остальные числа в рядах не имеют совпадений.
Получаем, что общими множителями чисел 128 и 72 являются числа 2, 2 и 2.
Чтобы получить НОД этих чисел, мы перемножим эти числа и получим:
2 · 2 · 2 = 8
Получаем: НОД (128 и 72) = 8
Именно на это число делятся исследуемые числа без остатка:
128 : 8 = 16
72 : 8 = 9
И именно это число будет их наибольшим делителем, т.е. НОДом.
Немного усложним задачу и найдем НОД для трех чисел.
Например,
Найти НОД для чисел 36, 24 и 18.
Решение:
Разложим эти три числа на простые множители:
24 I 2 18 I 2 36 I 2
12 I 2 9 I 3 18 I 2
6 I 2 3 I 3 9 I 3
3 I 3 1 I 3 I 3
1 I 1 I
Итак, получаем разложения:
24 = 2 · 2 · 2 · 3
18 = 2 · 3 · 3
36 = 2 · 2 · 3 · 3
Теперь ищем в этих разложениях одинаковые тройки чисел, выделим эти тройки подчеркиванием:
24 = 2 · 2 · 2 · 3
18 = 2 · 3 · 3
36 = 2 · 2 · 3 · 3
Получили две тройки: (2, 2 и 2) и (3, 3 и 3). Остальные числа в рядах не имеют совпадений.
Остальные числа в рядах не имеют совпадений.
Получаем, что общими множителями чисел 36, 24 и 18 являются числа 2 и 3.
Чтобы получить НОД этих чисел, мы перемножим эти числа и получим:
2 · 3 = 6
Получаем: НОД (36, 24 и 18) = 6
Именно на это число мы можем разделить 36, 24 и 18 без остатка:
24 : 6 = 4
18 : 6 = 3
36 : 6 = 6
Это число является их делителем. И именно это число будет их наибольшим делителем, т.е. НОДом.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Наибольший общий делитель (НОД) – определение, примеры и свойства. Зачем вводить понятия «Наибольший общий делитель (НОД)» и «Наименьшее общее кратное (НОК)» чисел в школьный курс математики
Решим задачу. У нас есть два типа печенья. Одни шоколадные, а другие простые. Шоколадных 48 штук, а простых 36. Необходимо составить из этого печенья максимально возможное число подарков, при этом надо использовать их все.
Для начала выпишем все делители каждого из этих двух чисел, так как оба эти числа должны делиться на количество подарков.
Получаем,
- 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
- 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Найдем среди делителей общие, которые есть как у первого, так и у второго числа.
Общими делителями будут: 1, 2, 3, 4, 6, 12.
Наибольшим из всех общих делителей является число 12. Это число называют наибольшим общим делителем чисел 36 и 48.
Исходя из полученного результата, можем заключить, что из всего печенья можно составить 12 подарков. В одном таком подарке будет 4 шоколадных печенья и 3 обычных печенья.
Определение наибольшего общего делителя
- Наибольшее натуральное число, на которое делятся без остатка два числа a и b, называют наибольшим общим делителем этих чисел.
Иногда для сокращения записи используют аббревиатуру НОД.
Некоторые пары чисел имеют в качестве наибольшего общего делителя единицу. Такие числа называют взаимно простыми числами. Например, числа 24 и 35. Имеют НОД =1.
Такие числа называют взаимно простыми числами. Например, числа 24 и 35. Имеют НОД =1.
Как найти наибольший общий делитель
Для того чтобы найти наибольший общий делитель не обязательно выписывать все делители данных чисел.
Можно поступить иначе. Сначала разложить на простые множители оба числа.
- 48 = 2*2*2*2*3,
- 36 = 2*2*3*3.
Теперь из множителей, которые входят в разложение первого числа, вычеркнем все те, которые не входят в разложение второго числа. В нашем случае это две двойки.
- 48 = 2*2*2*2*3 ,
- 36 = 2*2*3 *3.
Останутся множители 2, 2 и 3. Их произведение равно 12. Это число и будет являться наибольшим общим делителем чисел 48 и 36.
Это правило можно распространить на случай с тремя, четырьмя и т.д. числами.
Общая схема нахождения наибольшего общего делителя
- 1. Разложить числа на простые множители.
- 2. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.

- 3. Посчитать произведение оставшихся множителей.
Нахождение наибольшего общего делителя трех и большего количества чисел может быть сведено к последовательному нахождению НОД двух чисел. Мы об этом упоминали, при изучении свойств НОД. Там мы сформулировали и доказали теорему: наибольший общий делитель нескольких чисел a 1 , a 2 , …, a k равен числу d k , которое находится при последовательном вычислении НОД(a 1 , a 2)=d 2 , НОД(d 2 , a 3)=d 3 , НОД(d 3 , a 4)=d 4 , …,НОД(d k-1 , a k)=d k .
Давайте разберемся, как выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.
Пример.
Найдите наибольший общий делитель четырех чисел 78 , 294 , 570 и 36 .
Решение.
В этом примере a 1 =78 , a 2 =294 , a 3 =570 , a 4 =36 .
Сначала по алгоритму Евклида определим наибольший общий делитель d 2 двух первых чисел 78 и 294 . При делении получаем равенства 294=78·3+60 ; 78=60·1+18 ;60=18·3+6 и 18=6·3 . Таким образом, d 2 =НОД(78, 294)=6 .
При делении получаем равенства 294=78·3+60 ; 78=60·1+18 ;60=18·3+6 и 18=6·3 . Таким образом, d 2 =НОД(78, 294)=6 .
Теперь вычислим d 3 =НОД(d 2 , a 3)=НОД(6, 570) . Опять применим алгоритм Евклида:570=6·95 , следовательно, d 3 =НОД(6, 570)=6 .
Осталось вычислить d 4 =НОД(d 3 , a 4)=НОД(6, 36) . Так как 36 делится на 6 , тоd 4 =НОД(6, 36)=6 .
Таким образом, наибольший общий делитель четырех данных чисел равен d 4 =6 , то есть,НОД(78, 294, 570, 36)=6 .
Ответ:
НОД(78, 294, 570, 36)=6 .
Разложение чисел на простые множители также позволяет вычислять НОД трех и большего количества чисел. В этом случае наибольший общий делитель находится как произведение всех общих простых множителей данных чисел.
Пример.
Вычислите НОД чисел из предыдущего примера, используя их разложения на простые множители.
Решение.
Разложим числа 78 , 294 , 570 и 36 на простые множители, получаем 78=2·3·13 ,294=2·3·7·7 , 570=2·3·5·19 , 36=2·2·3·3 . Общими простыми множителями всех данных четырех чисел являются числа 2 и 3 . Следовательно, НОД(78, 294, 570, 36)=2·3=6 .
Общими простыми множителями всех данных четырех чисел являются числа 2 и 3 . Следовательно, НОД(78, 294, 570, 36)=2·3=6 .
Ответ:
НОД(78, 294, 570, 36)=6 .
К началу страницы
Нахождение НОД отрицательных чисел
Если одно, несколько или все числа, наибольший делитель которых нужно найти, являются отрицательными числами, то их НОД равен наибольшему общему делителю модулей этих чисел. Это связано с тем, что противоположные числа a и −a имеют одинаковые делители, о чем мы говорили при изучении свойств делимости.
Пример.
Найдите НОД отрицательных целых чисел −231 и −140 .
Решение.
Модуль числа −231 равен 231 , а модуль числа −140 равен 140 , иНОД(−231, −140)=НОД(231, 140) . Алгоритм Евклида дает нам следующие равенства:231=140·1+91 ; 140=91·1+49 ; 91=49·1+42 ; 49=42·1+7 и 42=7·6 . Следовательно,НОД(231, 140)=7 . Тогда искомый наибольший общий делитель отрицательных чисел−231 и −140 равен 7 .
Следовательно,НОД(231, 140)=7 . Тогда искомый наибольший общий делитель отрицательных чисел−231 и −140 равен 7 .
Ответ:
НОД(−231, −140)=7 .
Пример.
Определите НОД трех чисел −585 , 81 и −189 .
Решение.
При нахождении наибольшего общего делителя отрицательные числа можно заменить их абсолютными величинами, то есть, НОД(−585, 81, −189)=НОД(585, 81, 189) . Разложения чисел 585 , 81 и 189 на простые множители имеют соответственно вид585=3·3·5·13 , 81=3·3·3·3 и 189=3·3·3·7 . Общими простыми множителями этих трех чисел являются 3 и 3 . Тогда НОД(585, 81, 189)=3·3=9 , следовательно,НОД(−585, 81, −189)=9 .
Ответ:
НОД(−585, 81, −189)=9 .
35. Корені многочлена. Теорема Безу. (33 и выше)
36. Кратні корені, критерій кратності кореня.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Например :
Число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
Число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа . Делитель натурального числа a — это такое натуральное число, которое делит данное число a без остатка. Натуральное число, которое имеет более двух делителей, называется составным . Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12.
Общий делитель двух данных чисел a и b — это число, на которое делятся без остатка оба данных числа a и b . Общий делитель нескольких чисел (НОД) — это число, служащее делителем для каждого из них.
Кратко наибольший общий делитель чисел a и b записывают так:
Пример : НОД (12; 36) = 12.
Делители чисел в записи решения обозначают большой буквой «Д».
Пример:
НОД (7; 9) = 1
Числа 7 и 9 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми чи слами .
Взаимно простые числа — это натуральные числа, которые имеют только один общий делитель — число 1. Их НОД равен 1.
Наибольший общий делитель (НОД), свойства.
- Основное свойство: наибольший общий делитель m и n делится на любой общий делитель этих чисел. Пример : для чисел 12 и 18 наибольший общий делитель равен 6; он делится на все общие делители этих чисел: 1, 2, 3, 6.
- Следствие 1: множество общих делителей m и n совпадает с множеством делителей НОД(m , n ).
- Следствие 2: множество общих кратных m и n совпадает с множеством кратных НОК (m , n ).
Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.
- Наибольший общий делитель чисел m и n может быть определён как наименьший положительный элемент множества всех их линейных комбинаций:
и поэтому представим в виде линейной комбинации чисел m и n :
Это соотношение называется соотношением Безу , а коэффициенты u и v — коэффициентами Безу . Коэффициенты Безу эффективно вычисляются расширенным алгоритмом Евклида. Это утверждение обобщается на наборы натуральных чисел — его смысл в том, что подгруппа группы , порождённая набором , — циклическая и порождается одним элементом: НОД (a 1 , a 2 , … , a n ).
Коэффициенты Безу эффективно вычисляются расширенным алгоритмом Евклида. Это утверждение обобщается на наборы натуральных чисел — его смысл в том, что подгруппа группы , порождённая набором , — циклическая и порождается одним элементом: НОД (a 1 , a 2 , … , a n ).
Вычисление наибольшего общего делителя (НОД).
Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм . Кроме того, значение НОД (m ,n ) можно легко вычислить, если известно каноническое разложение чисел m и n на простые множители:
где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД (m ,n ) и НОК (m ,n ) выражаются формулами:
Если чисел более двух: , их НОД находится по следующему алгоритму:
— это и есть искомый НОД.
Также, для того, чтобы найти наибольший общий делитель , можно разложить каждое из заданных чисел на простые множители . Потом выписать отдельно только те множители, которые входят во все заданные числа. Потом перемножаем между собой выписанные числа — результат перемножения и есть наибольший общий делитель.
Потом выписать отдельно только те множители, которые входят во все заданные числа. Потом перемножаем между собой выписанные числа — результат перемножения и есть наибольший общий делитель.
Разберем пошагово вычисление наибольшего общего делителя:
1. Разложить делители чисел на простые множители:
Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных. Поясним сразу на примере. Разложим на простые множители числа 28 и 64.
2. Подчёркиваем одинаковые простые множители в обоих числах:
28 = 2 . 2 . 7
64 = 2 . 2 . 2 . 2 . 2 . 2
3. Находим произведение одинаковых простых множителей и записываем ответ:
НОД (28; 64) = 2 . 2 = 4
Ответ: НОД (28; 64) = 4
Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».
Первый способ записи НОД:
Найти НОД 48 и 36.
НОД (48; 36) = 2 . 2 . 3 = 12
Второй способ записи НОД:
Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.
Д (10) = {1, 2, 5, 10}
Д (15) = {1, 3, 5, 15}
Д (10, 15) = {1, 5}
Наибольший общий делитель
Определение 2
Если натуральное число a делится на натуральное число $b$, то $b$ называют делителем числа $a$, а число $a$ называют кратным числа $b$.
Пусть $a$ и $b$-натуральные числа. Число $c$ называют общим делителем и для $a$ и для $b$.
Множество общих делителей чисел $a$ и $b$ конечно, так как ни один из этих делителей не может быть больше, чем $a$. Значит,среди этих делителей есть наибольший, который называют наибольшим общим делителем чисел $a$ и $b$ и для его обозначения используют записи:
$НОД \ (a;b) \ или \ D \ (a;b)$
Чтобы найти наибольший общий делитель двух, чисел необходимо:
- Найти произведение чисел, найденных на шаге 2. Полученное число и будет искомым наибольшим общим делителем.

Пример 1
Найти НОД чисел $121$ и $132.$
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Выбрать числа, которые входят в разложение этих чисел
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=2\cdot 11=22$
Пример 2
Найти НОД одночленов $63$ и $81$.
Будем находить согласно представленному алгоритму. Для этого:
Разложим числа на простые множители
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Выбираем числа, которые входят в разложение этих чисел
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Найдем произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=3\cdot 3=9$
Найти НОД двух чисел можно и по-другому, используя множество делителей чисел.
Пример 3
Найти НОД чисел $48$ и $60$.
Решение:
Найдем множество делителей числа $48$: $\left\{{\rm 1,2,3.4.6,8,12,16,24,48}\right\}$
Теперь найдем множество делителей числа $60$:$\ \left\{{\rm 1,2,3,4,5,6,10,12,15,20,30,60}\right\}$
Найдем пересечение этих множеств: $\left\{{\rm 1,2,3,4,6,12}\right\}$- данное множество будет определять множество общих делителей чисел $48$ и $60$. Наибольший элемент в данном множестве будет число $12$. Значит наибольший общий делитель чисел $48$ и $60$ будет $12$.
Определение НОК
Определение 3
Общим кратным натуральных чисел $a$ и $b$ называется натуральное число, которое кратно и $a$ и $b$.
Общими кратными чисел называются числа которые делятся на исходные без остатка.Например для чисел $25$ и $50$ общими кратными будут числа $50,100,150,200$ и т.д
Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК$(a;b)$ или K$(a;b).$
Чтобы найти НОК двух чисел, необходимо:
- Разложить числа на простые множители
- Выписать множители, входящие в состав первого числа и добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Пример 4
Найти НОК чисел $99$ и $77$.
Будем находить согласно представленному алгоритму. Для этого
Разложить числа на простые множители
$99=3\cdot 3\cdot 11$
Выписать множители, входящие в состав первого
добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наименьшим общим кратным
$НОК=3\cdot 3\cdot 11\cdot 7=693$
Составление списков делителей чисел часто очень трудоемкое занятие. Существует способ нахождение НОД, называемый алгоритмом Евклида.
Утверждения, на которых основан алгоритм Евклида:
Если $a$ и $b$ —натуральные числа, причем $a\vdots b$, то $D(a;b)=b$
Если $a$ и $b$ —натуральные числа, такие что $b
Пользуясь $D(a;b)= D(a-b;b)$, можно последовательно уменьшать рассматриваемые числа до тех пор, пока не дойдем до такой пары чисел, что одно из них делится на другое. Тогда меньшее из этих чисел и будет искомым наибольшим общим делителем для чисел $a$ и $b$.
Свойства НОД и НОК
- Любое общее кратное чисел $a$ и $b$ делится на K$(a;b)$
- Если $a\vdots b$ , то К$(a;b)=a$
Если К$(a;b)=k$ и $m$-натуральное число, то К$(am;bm)=km$
Если $d$-общий делитель для $a$ и $b$,то К($\frac{a}{d};\frac{b}{d}$)=$\ \frac{k}{d}$
Если $a\vdots c$ и $b\vdots c$ ,то $\frac{ab}{c}$ — общее кратное чисел $a$ и $b$
Для любых натуральных чисел $a$ и $b$ выполняется равенство
$D(a;b)\cdot К(a;b)=ab$
Любой общийй делитель чисел $a$ и $b$ является делителем числа $D(a;b)$
Эта статья посвящена такому вопросу, как нахождение наибольшего общего делителя. Сначала мы объясним, что это такое, и приведем несколько примеров, введем определения наибольшего общего делителя 2 , 3 и более чисел, после чего остановимся на общих свойствах данного понятия и докажем их.
Yandex.RTB R-A-339285-1
Что такое общие делители
Чтобы понять, что из себя представляет наибольший общий делитель, сначала сформулируем, что вообще такое общий делитель для целых чисел.
В статье о кратных и делителях мы говорили, что у целого числа всегда есть несколько делителей. Здесь же нас интересуют делители сразу некоторого количества целых чисел, особенно общие (одинаковые) для всех. Запишем основное определение.
Определение 1
Общим делителем нескольких целых чисел будет такое число, которое может быть делителем каждого числа из указанного множества.
Пример 1
Вот примеры такого делителя: тройка будет общим делителем для чисел — 12 и 9 , поскольку верны равенства 9 = 3 · 3 и − 12 = 3 · (− 4) . У чисел 3 и — 12 есть и другие общие делители, такие, как 1 , − 1 и − 3 . Возьмем другой пример. У четырех целых чисел 3 , − 11 , − 8 и 19 будет два общих делителя: 1 и — 1 .
Зная свойства делимости, мы можем утверждать, что любое целое число можно разделить на единицу и минус единицу, значит, у любого набора целых чисел уже будет как минимум два общих делителя.
Также отметим, что если у нас есть общий для нескольких чисел делитель b , то те же числа можно разделить и на противоположное число, то есть на — b . В принципе, мы можем взять лишь положительные делители, тогда все общие делители также будут больше 0 . Такой подход также можно использовать, однако совсем игнорировать отрицательные числа не следует.
В принципе, мы можем взять лишь положительные делители, тогда все общие делители также будут больше 0 . Такой подход также можно использовать, однако совсем игнорировать отрицательные числа не следует.
Что такое наибольший общий делитель (НОД)
Согласно свойствам делимости, если b является делителем целого числа a , которое не равно 0, то модуль числа b не может быть больше, чем модуль a , следовательно, любое число, не равное 0 , имеет конечное число делителей. Значит, число общих делителей нескольких целых чисел, хотя бы одно из которых отличается от нуля, также будет конечным, и из всего их множества мы всегда можем выделить самое большое число (ранее мы уже говорили о понятии наибольшего и наименьшего целого числа, советуем вам повторить данный материал).
В дальнейших рассуждениях мы будем считать, что хотя бы одно из множества чисел, для которых нужно найти наибольший общий делитель, будет отлично от 0 . Если они все равны 0 , то их делителем может быть любое целое число, а поскольку их бесконечно много, выбрать наибольшее мы не сможем. Иначе говоря, найти наибольший общий делитель для множества чисел, равных 0 , нельзя.
Иначе говоря, найти наибольший общий делитель для множества чисел, равных 0 , нельзя.
Переходим к формулировке основного определения.
Определение 2
Наибольшим общим делителем нескольких чисел является самое большое целое число, которое делит все эти числа.
На письме наибольший общий делитель чаще всего обозначается аббревиатурой НОД. Для двух чисел его можно записать как НОД (a , b) .
Пример 2
Какой можно привести пример НОД для двух целых чисел? Например, для 6 и — 15 это будет 3 . Обоснуем это. Сначала запишем все делители шести: ± 6 , ± 3 , ± 1 , а потом все делители пятнадцати: ± 15 , ± 5 , ± 3 и ± 1 . После этого мы выбираем общие: это − 3 , − 1 , 1 и 3 . Из них надо выбрать самое большое число. Это и будет 3 .
Для трех и более чисел определение наибольшего общего делителя будет почти таким же.
Определение 3
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Для чисел a 1 , a 2 , … , a n делитель удобно обозначать как НОД (a 1 , a 2 , … , a n) . Само значение делителя записывается как НОД (a 1 , a 2 , … , a n) = b .
Пример 3
Приведем примеры наибольшего общего делителя нескольких целых чисел: 12 , — 8 , 52 , 16 . Он будет равен четырем, значит, мы можем записать, что НОД (12 , — 8 , 52 , 16) = 4 .
Проверить правильность данного утверждения можно с помощью записи всех делителей этих чисел и последующего выбора наибольшего из них.
На практике часто встречаются случаи, когда наибольший общий делитель равен одному из чисел. Это происходит тогда, когда на данное число можно разделить все остальные числа (в первом пункте статьи мы привели доказательство этого утверждения).
Пример 4
Так, наибольший общий делитель чисел 60 , 15 и — 45 равен 15 , поскольку пятнадцать делится не только на 60 и — 45 , но и на само себя, и большего делителя для всех этих чисел не существует.
Особый случай составляют взаимно простые числа. Они представляют собой целые числа с наибольшим общим делителем, равным 1 .
Они представляют собой целые числа с наибольшим общим делителем, равным 1 .
Основные свойства НОД и алгоритм Евклида
У наибольшего общего делителя есть некоторые характерные свойства. Сформулируем их в виде теорем и докажем каждое из них.
Отметим, что данные свойства сформулированы для целых чисел больше нуля, а делители мы рассмотрим только положительные.
Определение 4
Числа a и b имеют наибольший общий делитель, равный НОД для b и a , то есть НОД (a , b) = НОД (b , a) . Перемена мест чисел не влияет на конечный результат.
Данное свойство следует из самого определения НОД и не нуждается в доказательствах.
Определение 5
Если число a можно разделить на число b , то множество общих делителей этих двух чисел будет аналогично множеству делителей числа b , то есть НОД (a , b) = b .
Докажем это утверждение.
Доказательство 1
Если у чисел a и b есть общие делители, то на них можно разделить любое из них. В то же время если a будет кратным b, то любой делитель b будет делителем и для a , поскольку у делимости есть такое свойство, как транзитивность. Значит, любой делитель b будет общим для чисел a и b . Это доказывает, что если мы можем разделить a на b , то множество всех делителей обоих чисел совпадет с множеством делителей одного числа b . А поскольку наибольший делитель любого числа есть само это число, то наибольший общий делитель чисел a и b будет также равен b , т.е. НОД (a , b) = b . Если a = b , то НОД (a , b) = НОД (a , a) = НОД (b , b) = a = b , например, НОД (132 , 132) = 132 .
Значит, любой делитель b будет общим для чисел a и b . Это доказывает, что если мы можем разделить a на b , то множество всех делителей обоих чисел совпадет с множеством делителей одного числа b . А поскольку наибольший делитель любого числа есть само это число, то наибольший общий делитель чисел a и b будет также равен b , т.е. НОД (a , b) = b . Если a = b , то НОД (a , b) = НОД (a , a) = НОД (b , b) = a = b , например, НОД (132 , 132) = 132 .
Используя это свойство, мы можем найти наибольший общий делитель двух чисел, если одно из них можно разделить на другое. Такой делитель равен одному из этих двух чисел, на которое можно разделить второе число. К примеру, НОД (8 , 24) = 8 , так как 24 есть число, кратное восьми.
Определение 6 Доказательство 2
Попробуем доказать данное свойство. У нас изначально есть равенство a = b · q + c , и любой общий делитель a и b будет делить и c , что объясняется соответствующим свойством делимости. Поэтому любой общий делитель b и c будет делить a . Значит, множество общих делителей a и b совпадет с множеством делителей b и c , в том числе и наибольшие из них, значит, равенство НОД (a , b) = НОД (b , c) справедливо.
Значит, множество общих делителей a и b совпадет с множеством делителей b и c , в том числе и наибольшие из них, значит, равенство НОД (a , b) = НОД (b , c) справедливо.
Определение 7
Следующее свойство получило название алгоритма Евклида. С его помощью можно вычислить наибольший общий делитель двух чисел, а также доказать другие свойства НОД.
Перед тем, как сформулировать свойство, советуем вам повторить теорему, которую мы доказывали в статье о делении с остатком. Согласно ей, делимое число a можно представить в виде b · q + r , причем b здесь является делителем, q – некоторым целым числом (его также называют неполным частным), а r – остатком, который удовлетворяет условию 0 ≤ r ≤ b .
Допустим, у нас есть два целых числа больше 0 , для которых будут справедливы следующие равенства:
a = b · q 1 + r 1 , 0
Эти равенства заканчиваются тогда, когда r k + 1 становится равен 0 . Это случится обязательно, поскольку последовательность b > r 1 > r 2 > r 3 , … представляет собой ряд убывающих целых чисел, который может включать в себя только конечное их количество. Значит, r k является наибольшим общим делителем a и b , то есть, r k = НОД (a , b) .
Значит, r k является наибольшим общим делителем a и b , то есть, r k = НОД (a , b) .
В первую очередь нам надо доказать, что r k – это общий делитель чисел a и b , а после этого – то, что r k является не просто делителем, а именно наибольшим общим делителем двух данных чисел.
Просмотрим список равенств, приведенный выше, снизу вверх. Согласно последнему равенству,
r k − 1 можно разделить на r k . Исходя из этого факта, а также предыдущего доказанного свойства наибольшего общего делителя, можно утверждать, что r k − 2 можно разделить на r k , так как
r k − 1 делится на r k и r k делится на r k .
Третье снизу равенство позволяет нам сделать вывод, что r k − 3 можно разделить на r k , и т.д. Второе снизу – что b делится на r k , а первое – что a делится на r k . Из всего этого заключаем, что r k – общий делитель a и b .
Теперь докажем, что r k = НОД (a , b) . Что для этого нужно сделать? Показать, что любой общий делитель a и b будет делить r k . Обозначим его r 0 .
Просмотрим тот же список равенств, но уже сверху вниз. Исходя из предыдущего свойства, можно заключить, что r 1 делится на r 0 , значит, согласно второму равенству r 2 делится на r 0 . Идем по всем равенствам вниз и из последнего делаем вывод, что r k делится на r 0 . Следовательно, r k = НОД (a , b) .
Рассмотрев данное свойство, заключаем, что множество общих делителей a и b аналогично множеству делителей НОД этих чисел. Это утверждение, которое является следствием из алгоритма Евклида, позволит нам вычислить все общие делители двух заданных чисел.
Перейдем к другим свойствам.
Определение 8
Если a и b являются целыми числами, не равными 0 , то должны существовать два других целых числа u 0 и v 0 , при которых будет справедливым равенство НОД (a , b) = a · u 0 + b · v 0 .
Равенство, приведенное в формулировке свойства, является линейным представлением наибольшего общего делителя a и b . Оно носит название соотношения Безу, а числа u 0 и v 0 называются коэффициентами Безу.
Доказательство 3
Докажем данное свойство. Запишем последовательность равенств по алгоритму Евклида:
a = b · q 1 + r 1 , 0
Первое равенство говорит нам о том, что r 1 = a − b · q 1 . Обозначим 1 = s 1 и − q 1 = t 1 и перепишем данное равенство в виде r 1 = s 1 · a + t 1 · b . Здесь числа s 1 и t 1 будут целыми. Второе равенство позволяет сделать вывод, что r 2 = b − r 1 · q 2 = b − (s 1 · a + t 1 · b) · q 2 = − s 1 · q 2 · a + (1 − t 1 · q 2) · b . Обозначим − s 1 · q 2 = s 2 и 1 − t 1 · q 2 = t 2 и перепишем равенство как r 2 = s 2 · a + t 2 · b , где s 2 и t 2 также будут целыми. Это объясняется тем, что сумма целых чисел, их произведение и разность также представляют собой целые числа. Точно таким же образом получаем из третьего равенства r 3 = s 3 · a + t 3 · b , из следующего r 4 = s 4 · a + t 4 · b и т.д. В конце заключаем, что r k = s k · a + t k ·b при целых s k и t k . Поскольку r k = НОД (a , b) , обозначим s k = u 0 и t k = v 0 , В итоге мы можем получить линейное представление НОД в требуемом виде: НОД (a , b) = a · u 0 + b · v 0 .
Определение 9
НОД (m · a , m · b) = m · НОД (a , b) при любом натуральном значении m .
Доказательство 4
Обосновать это свойство можно так. Умножим на число m обе стороны каждого равенства в алгоритме Евклида и получим, что НОД (m · a , m · b) = m · r k , а r k – это НОД (a , b) . Значит, НОД (m · a , m · b) = m ·НОД (a , b) . Именно это свойство наибольшего общего делителя используется при нахождении НОД методом разложения на простые множители.
Определение 10
Если у чисел a и b есть общий делитель p , то НОД (a: p , b: p) = НОД (a , b) : p . В случае, когда p = НОД (a , b) получим НОД (a: НОД (a , b) , b: НОД (a , b) = 1 , следовательно, числа a: НОД (a , b) и b: НОД (a , b) являются взаимно простыми.
Поскольку a = p · (a: p) и b = p · (b: p) , то, основываясь на предыдущем свойстве, можно создать равенства вида НОД (a , b) = НОД (p · (a: p) , p · (b: p)) = p ·НОД (a: p , b: p) , среди которых и будет доказательство данного свойства. Это утверждение мы используем, когда приводим обыкновенные дроби к несократимому виду.
Определение 11
Наибольшим общим делителем a 1 , a 2 , … , a k будет число d k , которое можно найти, последовательно вычисляя НОД (a 1 , a 2) = d 2 , НОД (d 2 , a 3) = d 3 , НОД (d 3 , a 4) = d 4 , … , НОД (d k — 1 , a k) = d k .
Это свойство полезно при нахождении наибольшего общего делителя трех и более чисел. С помощью него можно свести это действие к операциям с двумя числами. Его основой является следствие из алгоритма Евклида: если множество общих делителей a 1 , a 2 и a 3 совпадает с множеством d 2 и a 3 , то оно совпадет и с делителями d 3 . Делители чисел a 1 , a 2 , a 3 и a 4 совпадут с делителями d 3 , значит, они совпадут и с делителями d 4 , и т.д. В конце мы получим, что общие делители чисел a 1 , a 2 , … , a k совпадут с делителями d k , а поскольку наибольшим делителем числа d k будет само это число, то НОД (a 1 , a 2 , … , a k) = d k .
Это все, что мы хотели бы рассказать о свойствах наибольшего общего делителя.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
НОД и НОК
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
Теперь выпишем кратные обоих чисел:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
Показать решение
Задание 2. Найдите НОК чисел 12 и 16
Решение:
Показать решение
Задание 3. Найдите НОД чисел 40 и 32
Решение:
Показать решение
Задание 4. Найдите НОК чисел 40 и 32
Найдите НОК чисел 40 и 32
Решение:
Показать решение
Задание 5. Найдите НОД чисел 54 и 86
Решение:
Показать решение
Задание 6. Найдите НОК чисел 54 и 86
Решение:
Показать решение
Задание 7. Найдите НОД чисел 98 и 35
Решение:
Показать решение
Задание 8. Найдите НОК чисел 98 и 35
Решение:
Показать решение
Задание 9. Найдите НОД чисел 112 и 82
Решение:
Показать решение
Задание 10. Найдите НОК чисел 112 и 82
Решение:
Показать решение
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
Показать решение
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
Показать решение
Задание 13. Найдите НОД чисел 18, 48, 96
Решение:
Показать решение
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
Показать решение
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
Показать решение
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Чему равен нод двух чисел.
 Умножение
УмножениеСейчас и в дальнейшем мы будем подразумевать, что хотя бы одно из данных чисел отлично от нуля. Если все данные числа равны нулю, то их общим делителем является любое целое число, а так как целых чисел бесконечно много, то мы не можем говорить о наибольшем из них. Следовательно, нельзя говорить о наибольшем общем делителе чисел, каждое из которых равно нулю.
Теперь мы можем дать определение наибольшего общего делителя двух чисел.
Определение.
Наибольший общий делитель двух целых чисел – это наибольшее целое число, делящее два данных целых числа.
Для краткой записи наибольшего общего делителя часто используют аббревиатуру НОД – Наибольший Общий Делитель. Также наибольший общий делитель двух чисел a и b часто обозначают как НОД(a, b) .
Приведем пример наибольшего общего делителя (НОД) двух целых чисел. Наибольший общий делитель чисел 6
и −15
равен 3
. Обоснуем это. Запишем все делители числа шесть: ±6
, ±3
, ±1
, а делителями числа −15
являются числа ±15
, ±5
, ±3
и ±1
. Теперь можно найти все общие делители чисел 6
и −15
, это числа −3
, −1
, 1
и 3
. Так как −3
Теперь можно найти все общие делители чисел 6
и −15
, это числа −3
, −1
, 1
и 3
. Так как −3
Определение наибольшего общего делителя трех и большего количества целых чисел аналогично определению НОД двух чисел.
Определение.
Наибольший общий делитель трех и большего количества целых чисел – это наибольшее целое число, делящее одновременно все данные числа.
Наибольший общий делитель n целых чисел a 1 , a 2 , …, a n мы будем обозначать как НОД(a 1 , a 2 , …, a n) . Если найдено значение b наибольшего общего делителя этих чисел, то можно записать НОД(a 1 , a 2 , …, a n)=b .
В качестве примера приведем НОД четырех целых чисел −8 , 52 , 16 и −12 , он равен 4 , то есть, НОД(−8, 52, 16, −12)=4 . Это можно проверить, записав все делители данных чисел, выбрав из них общие и определив наибольший общий делитель.
Отметим, что наибольший общий делитель целых чисел может быть равен одному из этих чисел. Это утверждение справедливо в том случае, если все данные числа делятся на одно из них (доказательство приведено в следующем пункте этой статьи). Например, НОД(15, 60, −45)=15
. Это действительно так, так как 15
делит и число 15
, и число 60
, и число −45
, и не существует общего делителя чисел 15
, 60
и −45
, который превосходит 15
.
Например, НОД(15, 60, −45)=15
. Это действительно так, так как 15
делит и число 15
, и число 60
, и число −45
, и не существует общего делителя чисел 15
, 60
и −45
, который превосходит 15
.
Особый интерес представляют так называемые взаимно простые числа , — такие целые числа, наибольший общий делитель которых равен единице.
Свойства наибольшего общего делителя, алгоритм Евклида
Наибольший общий делитель обладает рядом характерных результатов, иными словами, рядом свойств. Сейчас мы перечислим основные свойства наибольшего общего делителя (НОД) , формулировать их мы будем в виде теорем и сразу приводить доказательства.
Все свойства наибольшего общего делителя мы будем формулировать для положительных целых чисел, при этом будем рассматривать лишь положительные делители этих чисел.
Наибольший общий делитель чисел a и b равен наибольшему общему делителю чисел b и a , то есть, НОД(a, b)=НОД(a, b) .
Это свойство НОД напрямую следует из определения наибольшего общего делителя.
Если a делится на b , то множество общих делителей чисел a и b совпадает со множеством делителей числа b , в частности, НОД(a, b)=b .
Доказательство.
Любой общий делитель чисел a и b является делителем каждого из этих чисел, в том числе и числа b . С другой стороны, так как a кратно b , то любой делитель числа b является делителем и числа a в силу того, что делимость обладает свойством транзитивности, следовательно, любой делитель числа b является общим делителем чисел a и b . Этим доказано, что если a делится на b , то совокупность делителей чисел a и b совпадает с совокупностью делителей одного числа b . А так как наибольшим делителем числа b является само число b , то наибольший общий делитель чисел a и b также равен b , то есть, НОД(a, b)=b .
В частности, если числа a и b равны, то НОД(a, b)=НОД(a, a)=НОД(b, b)=a=b . К примеру, НОД(132, 132)=132 .
Доказанное свойство наибольшего делителя позволяет нам находить НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число. Например, НОД(8, 24)=8
, так как 24
кратно восьми.
При этом НОД равен одному из этих чисел, на которое делится другое число. Например, НОД(8, 24)=8
, так как 24
кратно восьми.
Если a=b·q+c , где a , b , c и q – целые числа, то множество общих делителей чисел a и b совпадает со множеством общих делителей чисел b и c , в частности, НОД(a, b)=НОД(b, c) .
Обоснуем это свойство НОД.
Так как имеет место равенство a=b·q+c , то всякий общий делитель чисел a и b делит также и c (это следует из свойств делимости). По этой же причине, всякий общий делитель чисел b и c делит a . Поэтому совокупность общих делителей чисел a и b совпадает с совокупностью общих делителей чисел b и c . В частности, должны совпадать и наибольшие из этих общих делителей, то есть, должно быть справедливо следующее равенство НОД(a, b)=НОД(b, c) .
Сейчас мы сформулируем и докажем теорему, которая представляет собой алгоритм Евклида . Алгоритм Евклида позволяет находить НОД двух чисел (смотрите нахождение НОД по алгоритму Евклида). Более того алгоритм Евклида позволит нам доказать приведенные ниже свойства наибольшего общего делителя.
Более того алгоритм Евклида позволит нам доказать приведенные ниже свойства наибольшего общего делителя.
Прежде чем дать формулировку теоремы, рекомендуем освежить в памяти теорему из раздела теории , которая утверждает, что делимое a может быть представлено в виде b·q+r , где b – делитель, q – некоторое целое число, называемое неполным частным, а r – целое число, удовлетворяющее условию , называемое остатком.
Итак, пусть для двух ненулевых целых положительных чисел a
и b
справедлив ряд равенств
заканчивающийся, когда r k+1 =0
(что неизбежно, так как b>r 1 >r 2 >r 3 , …
— ряд убывающих целых чисел, и этот ряд не может содержать более чем конечное число положительных чисел), тогда r k
– это наибольший общий делитель чисел a
и b
, то есть, r k =НОД(a, b)
.
Доказательство.
Докажем сначала, что r k является общим делителем чисел a и b , после чего покажем, что r k не просто делитель, а наибольший общий делитель чисел a и b .
Будем двигаться по записанным равенствам снизу вверх. Из последнего равенства можно сказать, что r k−1
делится на r k
. Учитывая этот факт, а также предыдущее свойство НОД, предпоследнее равенство r k−2 =r k−1 ·q k +r k
позволяет утверждать, что r k−2
делится на r k
, так как и r k−1
делится на r k
и r k
делится на r k
. По аналогии из третьего снизу равенства заключаем, что r k−3
делится на r k
. И так далее. Из второго равенства получаем, что b
делится на r k
, а из первого равенства получаем, что a
делится на r k
. Следовательно, r k
является общим делителем чисел a
и b
.
Из последнего равенства можно сказать, что r k−1
делится на r k
. Учитывая этот факт, а также предыдущее свойство НОД, предпоследнее равенство r k−2 =r k−1 ·q k +r k
позволяет утверждать, что r k−2
делится на r k
, так как и r k−1
делится на r k
и r k
делится на r k
. По аналогии из третьего снизу равенства заключаем, что r k−3
делится на r k
. И так далее. Из второго равенства получаем, что b
делится на r k
, а из первого равенства получаем, что a
делится на r k
. Следовательно, r k
является общим делителем чисел a
и b
.
Осталось доказать, что r k =НОД(a, b) . Для достаточно показать, что любой общий делитель чисел a и b (обозначим его r 0 ) делит r k .
Будем двигаться по исходным равенствам сверху вниз. В силу предыдущего свойства из первого равенства следует, что r 1 делится на r 0 . Тогда из второго равенства получаем, что r 2 делится на r 0 . И так далее. Из последнего равенства получаем, что r k делится на r 0 . Таким образом, r k =НОД(a, b) .
Из рассмотренного свойства наибольшего общего делителя следует, что множество общих делителей чисел a
и b
совпадает с множеством делителей наибольшего общего делителя этих чисел. Это следствие из алгоритма Евклида позволяет найти все общие делители двух чисел как делители НОД этих чисел.
Это следствие из алгоритма Евклида позволяет найти все общие делители двух чисел как делители НОД этих чисел.
Пусть a и b – целые числа, одновременно не равные нулю, тогда существуют такие целые числа u 0 и v 0 , то справедливо равенство НОД(a, b)=a·u 0 +b·v 0 . Последнее равенство представляет собой линейное представление наибольшего общего делителя чисел a и b , это равенство называют соотношением Безу, а числа u 0 и v 0 – коэффициентами Безу.
Доказательство.
По алгоритму Евклида мы можем записать следующие равенства
Из первого равенства имеем r 1 =a−b·q 1
, и, обозначив 1=s 1
и −q 1 =t 1
, это равенство примет вид r 1 =s 1 ·a+t 1 ·b
, причем числа s 1
и t 1
— целые. Тогда из второго равенства получим r 2 =b−r 1 ·q 2 =
b−(s 1 ·a+t 1 ·b)·q 2 =−s 1 ·q 2 ·a+(1−t 1 ·q 2)·b
. Обозначив −s 1 ·q 2 =s 2
и 1−t 1 ·q 2 =t 2
, последнее равенство можно записать в виде r 2 =s 2 ·a+t 2 ·b
, причем s 2
и t 2
– целые числа (так как сумма, разность и произведение целых чисел является целым числом). Аналогично из третьего равенства получим r 3 =s 3 ·a+t 3 ·b
, из четвертого r 4 =s 4 ·a+t 4 ·b
, и так далее. Наконец, r k =s k ·a+t k ·b
, где s k
и t k
— целые. Так как r k =НОД(a, b)
, и, обозначив s k =u 0
и t k =v 0
, получим линейное представление НОД требуемого вида: НОД(a, b)=a·u 0 +b·v 0
.
Аналогично из третьего равенства получим r 3 =s 3 ·a+t 3 ·b
, из четвертого r 4 =s 4 ·a+t 4 ·b
, и так далее. Наконец, r k =s k ·a+t k ·b
, где s k
и t k
— целые. Так как r k =НОД(a, b)
, и, обозначив s k =u 0
и t k =v 0
, получим линейное представление НОД требуемого вида: НОД(a, b)=a·u 0 +b·v 0
.
Если m – любое натуральное число, то НОД(m·a, m·b)=m·НОД(a, b) .
Обоснование этого свойства наибольшего общего делителя таково. Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД(m·a, m·b)=m·r k , а r k – это НОД(a, b) . Следовательно, НОД(m·a, m·b)=m·НОД(a, b) .
На этом свойстве наибольшего общего делителя основан способ нахождения НОД с помощью разложения на простые множители .
Пусть p – любой общий делитель чисел a и b , тогда НОД(a:p, b:p)=НОД(a, b):p , в частности, если p=НОД(a, b) имеем НОД(a:НОД(a, b), b:НОД(a, b))=1 , то есть, числа a:НОД(a, b) и b:НОД(a, b) — взаимно простые.
Так как a=p·(a:p)
и b=p·(b:p)
, и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД(a, b)=НОД(p·(a:p), p·(b:p))=
p·НОД(a:p, b:p)
, откуда и следует доказываемое равенство.
Только что доказанное свойство наибольшего общего делителя лежит в основе .
Сейчас озвучим свойство НОД, которое сводит задачу нахождения наибольшего общего делителя трех и большего количества чисел к последовательному отысканию НОД двух чисел.
Наибольший общий делитель чисел a 1 , a 2 , …, a k равен числу d k , которое находится при последовательном вычислении НОД(a 1 , a 2)=d 2 , НОД(d 2 , a 3)=d 3 , НОД(d 3 , a 4)=d 4 , …, НОД(d k-1 , a k)=d k .
Доказательство базируется на следствии из алгоритма Евклида. Общие делители чисел a 1
и a 2
совпадают с делителями d 2
. Тогда общие делители чисел a 1
, a 2
и a 3
совпадают с общими делителями чисел d 2
и a 3
, следовательно, совпадают с делителями d 3
. Общие делители чисел a 1
, a 2
, a 3
и a 4
совпадают с общими делителями d 3
и a 4
, следовательно, совпадают с делителями d 4
. И так далее. Наконец, общие делители чисел a 1 , a 2 , …, a k
совпадают с делителями d k
. А так как наибольшим делителем числа d k
является само число d k
, то НОД(a 1 , a 2 , …, a k)=d k
.
На этом закончим обзор основных свойств наибольшего общего делителя.
Список литературы.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
- Виноградов И.М. Основы теории чисел.
- Михелович Ш.Х. Теория чисел.
- Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.
Наибольший общий делитель
Определение 2
Если натуральное число a делится на натуральное число $b$, то $b$ называют делителем числа $a$, а число $a$ называют кратным числа $b$.
Пусть $a$ и $b$-натуральные числа. Число $c$ называют общим делителем и для $a$ и для $b$.
Множество общих делителей чисел $a$ и $b$ конечно, так как ни один из этих делителей не может быть больше, чем $a$. Значит,среди этих делителей есть наибольший, который называют наибольшим общим делителем чисел $a$ и $b$ и для его обозначения используют записи:
$НОД \ (a;b) \ или \ D \ (a;b)$
Чтобы найти наибольший общий делитель двух, чисел необходимо:
- Найти произведение чисел, найденных на шаге 2.
 Полученное число и будет искомым наибольшим общим делителем.
Полученное число и будет искомым наибольшим общим делителем.
Пример 1
Найти НОД чисел $121$ и $132.$
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Выбрать числа, которые входят в разложение этих чисел
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=2\cdot 11=22$
Пример 2
Найти НОД одночленов $63$ и $81$.
Будем находить согласно представленному алгоритму. Для этого:
Разложим числа на простые множители
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Выбираем числа, которые входят в разложение этих чисел
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Найдем произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=3\cdot 3=9$
Найти НОД двух чисел можно и по-другому, используя множество делителей чисел.
Пример 3
Найти НОД чисел $48$ и $60$.
Решение:
Найдем множество делителей числа $48$: $\left\{{\rm 1,2,3.4.6,8,12,16,24,48}\right\}$
Теперь найдем множество делителей числа $60$:$\ \left\{{\rm 1,2,3,4,5,6,10,12,15,20,30,60}\right\}$
Найдем пересечение этих множеств: $\left\{{\rm 1,2,3,4,6,12}\right\}$- данное множество будет определять множество общих делителей чисел $48$ и $60$. Наибольший элемент в данном множестве будет число $12$. Значит наибольший общий делитель чисел $48$ и $60$ будет $12$.
Определение НОК
Определение 3
Общим кратным натуральных чисел $a$ и $b$ называется натуральное число, которое кратно и $a$ и $b$.
Общими кратными чисел называются числа которые делятся на исходные без остатка.Например для чисел $25$ и $50$ общими кратными будут числа $50,100,150,200$ и т.д
Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК$(a;b)$ или K$(a;b).$
Чтобы найти НОК двух чисел, необходимо:
- Разложить числа на простые множители
- Выписать множители, входящие в состав первого числа и добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Пример 4
Найти НОК чисел $99$ и $77$.
Будем находить согласно представленному алгоритму. Для этого
Разложить числа на простые множители
$99=3\cdot 3\cdot 11$
Выписать множители, входящие в состав первого
добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наименьшим общим кратным
$НОК=3\cdot 3\cdot 11\cdot 7=693$
Составление списков делителей чисел часто очень трудоемкое занятие. Существует способ нахождение НОД, называемый алгоритмом Евклида.
Утверждения, на которых основан алгоритм Евклида:
Если $a$ и $b$ —натуральные числа, причем $a\vdots b$, то $D(a;b)=b$
Если $a$ и $b$ —натуральные числа, такие что $b
Пользуясь $D(a;b)= D(a-b;b)$, можно последовательно уменьшать рассматриваемые числа до тех пор, пока не дойдем до такой пары чисел, что одно из них делится на другое. Тогда меньшее из этих чисел и будет искомым наибольшим общим делителем для чисел $a$ и $b$.
Свойства НОД и НОК
- Любое общее кратное чисел $a$ и $b$ делится на K$(a;b)$
- Если $a\vdots b$ , то К$(a;b)=a$
Если К$(a;b)=k$ и $m$-натуральное число, то К$(am;bm)=km$
Если $d$-общий делитель для $a$ и $b$,то К($\frac{a}{d};\frac{b}{d}$)=$\ \frac{k}{d}$
Если $a\vdots c$ и $b\vdots c$ ,то $\frac{ab}{c}$ — общее кратное чисел $a$ и $b$
Для любых натуральных чисел $a$ и $b$ выполняется равенство
$D(a;b)\cdot К(a;b)=ab$
Любой общийй делитель чисел $a$ и $b$ является делителем числа $D(a;b)$
Решим задачу. У нас есть два типа печенья. Одни шоколадные, а другие простые. Шоколадных 48 штук, а простых 36. Необходимо составить из этого печенья максимально возможное число подарков, при этом надо использовать их все.
Для начала выпишем все делители каждого из этих двух чисел, так как оба эти числа должны делиться на количество подарков.
Получаем,
- 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
- 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.

Найдем среди делителей общие, которые есть как у первого, так и у второго числа.
Общими делителями будут: 1, 2, 3, 4, 6, 12.
Наибольшим из всех общих делителей является число 12. Это число называют наибольшим общим делителем чисел 36 и 48.
Исходя из полученного результата, можем заключить, что из всего печенья можно составить 12 подарков. В одном таком подарке будет 4 шоколадных печенья и 3 обычных печенья.
Определение наибольшего общего делителя
- Наибольшее натуральное число, на которое делятся без остатка два числа a и b, называют наибольшим общим делителем этих чисел.
Иногда для сокращения записи используют аббревиатуру НОД.
Некоторые пары чисел имеют в качестве наибольшего общего делителя единицу. Такие числа называют взаимно простыми числами. Например, числа 24 и 35. Имеют НОД =1.
Как найти наибольший общий делитель
Для того чтобы найти наибольший общий делитель не обязательно выписывать все делители данных чисел.
Можно поступить иначе. Сначала разложить на простые множители оба числа.
- 48 = 2*2*2*2*3,
- 36 = 2*2*3*3.
Теперь из множителей, которые входят в разложение первого числа, вычеркнем все те, которые не входят в разложение второго числа. В нашем случае это две двойки.
- 48 = 2*2*2*2*3 ,
- 36 = 2*2*3 *3.
Останутся множители 2, 2 и 3. Их произведение равно 12. Это число и будет являться наибольшим общим делителем чисел 48 и 36.
Это правило можно распространить на случай с тремя, четырьмя и т.д. числами.
Общая схема нахождения наибольшего общего делителя
- 1. Разложить числа на простые множители.
- 2. Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.
- 3. Посчитать произведение оставшихся множителей.
Одной из задач, вызывающих проблему у современных школьников, привыкших к месту и не к месту использовать калькуляторы, встроенные в гаджеты, является нахождение наибольшего общего делителя (НОД) двух и более чисел.
Невозможно решить никакую математическую задачу, если неизвестно, о чём собственно спрашивают. Для этого нужно знать, что означает то или иное выражение , используемое в математике.
Необходимо знать:
- Если некое число можно использовать для подсчёта различных предметов, например, девять столбов, шестнадцать домов, то оно является натуральным. Самым маленьким из них будет единица.
- Когда натуральное число делится на другое натуральное число, то говорят, что меньшее число — это делитель большего.
- Если два и более различных числа делятся на некое число без остатка, то говорят, что последнее будет их общим делителем (ОД).
- Самый большой из ОД именуется наибольшим общим делителем (НОД).
- В таком случае, когда у числа есть только два натуральных делителя (оно само и единичка), оно называется простым. Самое маленькое среди них — двойка, к тому же она и единственное чётное в их ряду.
- В случае если у двух чисел максимальным общим делителем является единица, то они будут взаимно простыми.

- Число, у которого больше чем два делителя, именуется составным.
- Процесс когда находятся все простые множители, которые при умножении между собой дадут в произведении начальное значение в математике называют разложением на простые множители. Причём одинаковые множители в разложении могут встречаться неоднократно.
В математике приняты следующие записи:
- Делители Д (45) = (1;3;5;9;45).
- ОД (8;18) = (1;2).
- НОД (8;18) = 2.
Различные способы найти НОД
Проще всего ответить на вопрос как найти НОД в том случае, когда меньшее число является делителем большего. Оно и будет в подобном случае наибольшим общим делителем.
Например, НОД (15;45) = 15, НОД (48;24) = 24.
Но такие случаи в математике являются весьма редкими, поэтому для того, чтобы находить НОД используются более сложные приёмы, хотя проверять этот вариант перед началом работы все же весьма рекомендуется.
Способ разложения на простые сомножители
Если необходимо найти НОД двух или более различных чисел , достаточно разложить каждое из них на простые сомножители, а затем произвести процесс умножения тех из них, которые имеются в каждом из чисел.
Пример 1
Рассмотрим, как находить НОД 36 и 90:
- 36 = 1*2*2*3*3;
- 90 = 1*2*3*3*5;
НОД (36;90) = 1*2*3*3 = 18.
Теперь посмотрим как находить то же самое в случае трёх чисел , возьмём для примера 54; 162; 42.
Как разложить 36 мы уже знаем, разберёмся с остальными:
- 162 = 1*2*3*3*3*3;
- 42 = 1*2*3*7;
Таким образом, НОД (36;162;42) = 1*2*3 = 6.
Следует заметить, что единицу в разложении писать совершенно необязательно.
Рассмотрим способ, как просто раскладывать на простые множители , для этого слева запишем необходимую нам цифру, а справа станем писать простые делители.
Разделять колонки можно, как знаком деления, так и простой вертикальной чертой.
- 36 / 2 продолжим наш процесс деления;
- 18 / 2 далее;
- 9 / 3 и ещё раз;
- 3 / 3 сейчас совсем элементарно;
- 1 — результат готов.
Искомое 36 = 2*2*3*3.
Евклидов способ
Этот вариант известен человечеству ещё со времён древнегреческой цивилизации, он во многом проще, и приписывается великому математику Евклиду, хотя весьма похожие алгоритмы применялись и ранее. Этот способ заключается в использовании следующего алгоритма , мы делим большее число с остатком на меньшее. Затем наш делитель делим на остаток и продолжаем так действовать по кругу пока не произойдёт деление нацело. Последнее значение и окажется искомым наибольшим общим делителем.
Этот способ заключается в использовании следующего алгоритма , мы делим большее число с остатком на меньшее. Затем наш делитель делим на остаток и продолжаем так действовать по кругу пока не произойдёт деление нацело. Последнее значение и окажется искомым наибольшим общим делителем.
Приведём пример использования данного алгоритма :
попробуем выяснить какой НОД у 816 и 252:
- 816 / 252 = 3 и остаток 60. Сейчас 252 разделим на 60;
- 252 / 60 = 4 в остатке на этот раз окажется 12. Продолжим наш круговой процесс, разделим шестьдесят на двенадцать;
- 60 / 12 = 5. Поскольку на сей раз никакого остатка мы не получили, то у нас готов результат, двенадцать будет искомым для нас значением.
Итак, по завершении нашего процесса мы получили НОД (816;252) = 12.
Действия при необходимости определения НОД если задано более двух значений
Мы уже разобрались, что делать в случае, когда имеется два различных числа, теперь научимся действовать, если их имеется 3 и более .
При всей кажущейся сложности, данная задача проблем у нас уже не вызовет. Сейчас мы выбираем два любые числа и определяем искомое для них значение. Следующим шагом отыскиваем НОД у полученного результата и третьего из заданных значений. Затем снова действуем по уже известному нам принципу для четвёртого пятого и так далее.
Заключение
Итак, при кажущейся большой сложности поставленной перед нами изначально задачи, на самом деле все просто, главное уметь выполнять безошибочно процесс делений и придерживаться любого из двух описанных выше алгоритмов.
Хотя оба способа и являются вполне приемлемыми, в общеобразовательной школе гораздо чаще применяется первый способ . Это связано с тем, что разложение на простые множители понадобится при изучении следующей учебной темы — определение наибольшего общего кратного (НОК). Но все же стоит ещё раз заметить — применение алгоритма Евклида ни в коей мере не может считаться ошибочным.
Видео
С помощью видео вы сможете узнать, как найти наибольший общий делитель.
Не получили ответ на свой вопрос? Предложите авторам тему.
Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найти НОД и НОК
Найдено НОД и НОК: 5806
Как пользоваться калькулятором
- Введите числа в поле для ввода
- В случае ввода некорректных символов поле для ввода будет подсвечено красным
- нажмите кнопку «Найти НОД и НОК»
Как вводить числа
- Числа вводятся через пробел, точку или запятую
- Длина вводимых чисел не ограничена , так что найти НОД и НОК длинных чисел не составит никакого труда
Что такое НОД и НОК?
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД .
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК .
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.
Пример: определить, делится ли на 2 число 34938 .
Решение: смотрим на последнюю цифру: 8 — значит число делится на два.
2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.
Пример: определить, делится ли число 34938 на 5.
Решение: смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.
4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36) :
- Раскладываем оба числа на множители: 28 = 1·2·2·7 , 36 = 1·2·2·3·3
- Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.
- Вычисляем произведение этих множителей: 1·2·2 = 4 — это и есть наибольший общий делитель чисел 28 и 36.
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
- Находим произведение чисел 28 и 36: 28·36 = 1008
- НОД(28, 36), как уже известно, равен 4
- НОК(28, 36) = 1008 / 4 = 252 .

Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c) .
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример: найти НОД и НОК для чисел 12, 32 и 36.
- Cперва разложим числа на множители: 12 = 1·2·2·3 , 32 = 1·2·2·2·2·2 , 36 = 1·2·2·3·3 .
- Найдём обшие множители: 1, 2 и 2 .
- Их произведение даст НОД: 1·2·2 = 4
- Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96 .
- Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3 , 36 = 1·2·2·3·3 , НОД = 1·2·2·3 = 12 .

- НОК(12, 32, 36) = 96·36 / 12 = 288 .
Как находить наибольший общий делитель (НОД) двух чисел. Как находить наибольший общий делитель
Автор Historian Просмотров 110 Опубликовано
Аналогично, их можно найти и по другим ценам: 100 и 40. 100 и 40. После разложения из первого удаляются еще пять. Распространение дает 20. Это самый большой раздел после валидации.
Содержание
- Как находить наибольший общий делитель (НОД) двух чисел
- Общие понятия и определения
- Различные способы найти НОД
- Способ разложения на простые сомножители
- Евклидов способ
- Действия при необходимости определения НОД если задано более двух значений
- Понятие наибольшего общего делителя
- Способы нахождения наибольшего общего делителя
- 1. Разложение на множители
- 2. Алгоритм Евклида
- Свойства наибольшего общего делителя
- Как найти наибольший общий делитель для двух чисел
- Общие сведения
- Признаки делимости
- Разложение на простые элементы
- Примеры решения
Как находить наибольший общий делитель (НОД) двух чисел
Одна из проблемных задач современных школьников, которые привыкли пользоваться встроенными в свои устройства калькуляторами, — найти наибольшее общее делимое двух или более чисел.
Невозможно решить математическую задачу, если не знать, что представляет собой настоящий вопрос. Для этого необходимо знать выражения, используемые в математике.
Общие понятия и определения
Необходимо знать:.
- Если некое число можно использовать для подсчёта различных предметов, например, девять столбов, шестнадцать домов, то оно является натуральным. Самым маленьким из них будет единица.
- Когда натуральное число делится на другое натуральное число, то говорят, что меньшее число — это делитель большего.
- Если два и более различных числа делятся на некое число без остатка, то говорят, что последнее будет их общим делителем (ОД).
- Самый большой из ОД именуется наибольшим общим делителем (НОД).
- В таком случае, когда у числа есть только два натуральных делителя (оно само и единичка), оно называется простым. Самое маленькое среди них — двойка, к тому же она и единственное чётное в их ряду.
- В случае если у двух чисел максимальным общим делителем является единица, то они будут взаимно простыми.

- Число, у которого больше чем два делителя, именуется составным.
- Процесс когда находятся все простые множители, которые при умножении между собой дадут в произведении начальное значение в математике называют разложением на простые множители. Причём одинаковые множители в разложении могут встречаться неоднократно.
В математике принята следующая символика
Различные способы найти НОД
Самый простой способ ответить на этот вопрос — если наименьшее число является делителем многих. В этом случае он является наибольшим общим делителем.
Например, nod (15; 45) = 15, nod (48; 24) = 24.
В математике такие случаи очень редки, поэтому существуют более сложные способы поиска узлов, но перед началом работы неплохо бы проверить.
Способ разложения на простые сомножители
Если вам нужно найти два или более различных чисел, достаточно разделить каждое из них на первый множитель и выполнить процесс умножения на коэффициенты каждого числа.
Рассмотрим, как найти узлы 36 и 90:.
Теперь посмотрим, как то же самое можно найти в случае трех чисел: 162. 162; 42.
Поскольку мы уже знаем, как свернуть 36, давайте разберемся с остальным: с
Следовательно, nod (36; 162; 42) = 1*2*3 = 6.
Обратите внимание, что необязательно писать в расширениях.
Давайте посмотрим, как просто проанализировать первый фактор. Напишите искомое число в левой части и первый делитель в правой части.
Колонки могут быть разделены либо знаком деления, либо простой вертикальной линией.
- 36 / 2 продолжим наш процесс деления;
- 18 / 2 далее;
- 9 / 3 и ещё раз;
- 3 / 3 сейчас совсем элементарно;
- 1 — результат готов.
Евклидов способ
Этот вариант известен человечеству по древнегреческой культуре, он гораздо проще и приписывается великому математику Евклиду, но подобные алгоритмы использовались и ранее. Метод заключается в делении большего числа на меньшее по следующему алгоритму Затем делитель делится с остатком делимого и так продолжается до тех пор, пока не будет разделено все число. Окончательное значение будет наибольшим общим делителем.
Окончательное значение будет наибольшим общим делителем.
Следуйте примеру использования этого алгоритма.
Найдем узлы 816 и 252.
- 816 / 252 = 3 и остаток 60. Сейчас 252 разделим на 60;
- 252 / 60 = 4 в остатке на этот раз окажется 12. Продолжим наш круговой процесс, разделим шестьдесят на двенадцать;
- 60 / 12 = 5. Поскольку на сей раз никакого остатка мы не получили, то у нас готов результат, двенадцать будет искомым для нас значением.
Таким образом, в конце процесса мы получили нод (816; 252) = 12.
Действия при необходимости определения НОД если задано более двух значений
Вы узнали, что делать, когда есть два разных числа. Теперь вам нужно знать, что делать, если чисел три или больше.
Несмотря на кажущуюся сложность, эта проблема не вызывает у нас никаких затруднений. Следующий шаг — выбрать два числа и определить цену, которую вы ищете. Следующий шаг — кивнуть этот результат и найти третье из заданных значений. Затем мы снова действуем в соответствии с четвертым известным авторитетом.
Как и в случае с НОД, поиск ННК может осуществляться тремя способами, аналогичными предыдущим. Каждый из них может быть использован в зависимости от состояния и легкости проблемы.
Понятие наибольшего общего делителя
Во-первых, поймите, что такое общий делитель. Существует множество делителей для целых чисел. И сейчас нас особенно интересует, как одновременно иметь дело со многими целочисленными делителями.
Делители натуральных чисел — это целые натуральные числа, на которые число делится без остатка. Если натуральное число имеет три или более делителей, оно называется комплексным числом.
Общие делители многих целых чисел — это числа, которые могут быть делителями каждого числа в сумме. Например, числа 12 и 8 имеют общие делители 4 и 1. Чтобы проверить это, напишите верные уравнения: 8 = 4 * 2 и 12 = 3 * 4.
Каждое число может делиться само на себя на 1. Поэтому каждое множество целых чисел имеет по крайней мере два общих делителя.
Наибольший общий делитель двух чисел A и B — это наибольшее число, на которое можно разделить несимметричные числа a и b. Это можно записать с помощью аббревиатуры nod. Для двух чисел можно написать: nod(a, b).
Например, для 4 и 16 кивком будет 4.
- Зафиксируем все делители четырех: 4, 2, 1.
- А теперь все делители шестнадцати: 16, 8, 4 и 1.
- Выбираем общие: это 4, 2, 1. Самое большое общее число: 4. Вот и ответ.
Наибольший общий делитель трех или более чисел — это наибольшее целое число, которое одновременно делит все эти числа.
Найдем наибольший общий делитель множества целых чисел 10, 6, 44 и 18. Оно будет равно 3. Ответ можно записать так: nod(12, 6, 42, 18) = 3. Чтобы проверить точность ответа, напишите все делители и выберите наибольший из них.
Первое взаимнооднозначное число является натуральным числом и имеет только один общий делитель — 1. Их кивок — 1.
Другой пример. Вычислите узлы 28 и 64.
- Распишем простые множители для каждого числа и подчеркнем одинаковые
Вы можете искать узелки в колонках, как указано выше или как показано на рисунке.
Способы нахождения наибольшего общего делителя
Существует два способа найти наибольший общий делитель. Рассмотрите оба варианта, чтобы выбрать наилучшее действие при решении проблемы.
1. Разложение на множители
Чтобы найти множество чисел, просто разделите числа на первый множитель и умножьте на общий множитель всех чисел.
Пример 1. Найдите НОД (84, 90).
- Разложим числа 84 и 90 на простые множители:
Пример 2. Найдите НОД (15, 28).
- Разложим 15 и 28 на простые множители:
Пример 3. Найдите узлы 24 и 18.
- Разложим оба числа на простые множители:
Онлайн-курсы по математике для детей могут улучшить их оценки и помочь им подготовиться к тестам, IEP и экзаменам.
2. Алгоритм Евклида
Метод Евклида помогает находить узлы через последовательные деления. Сначала посмотрите, как он работает с двумя числами, а затем примените его к трем и более.
Алгоритм Евклида заключается в следующем: если два или более чисел делятся на минимум, то наименьшее число является наибольшим общим делителем. С помощью метода Евклида легко найти больший общий делитель, используя этот тип.
С помощью метода Евклида легко найти больший общий делитель, используя этот тип.
nod: тип nod(a, b) = nod(b, c), где c делится на b.
Пример 1. Найдите узлы 24 и 8.
Поскольку 24 делится на 8 и 8, общий делитель этих чисел, 8, уменьшается на 8. Этот делитель максимален, потому что 8 не может быть разделено ни на какое число, большее самого себя. Таким образом, nod(24, 8) = 8.
В других случаях для нахождения наибольшего общественного делителя двух чисел выполните следующую последовательность действий.
- Большее число поделить на меньшее.
- Меньшее число поделить на остаток, который получается после деления.
- Первый остаток поделить на второй остаток.
- Второй остаток поделить на третий и т. д.
- Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.
Пример 2. Найдите наибольший общий делитель чисел 140 и 96.
- 140 : 96 = 1 (остаток 44)
- 96 : 44 = 2 (остаток 8)
- 44 : 8 = 5 (остаток 4)
- 8 : 4 = 2
Последний делитель равен 4 — это означает: nod(140, 96) = 4.
Пошаговое деление можно описать в столбцах.
Чтобы найти наибольший общий делитель трех или более чисел, делайте это в следующем порядке.
- Найти наибольший общий делитель любых двух чисел из данных.
- Найти НОД найденного делителя и третьего числа.
- Найти НОД последнего найденного делителя и четвёртого числа и т. д.
Свойства наибольшего общего делителя
Наибольшие общие делители обладают определенными свойствами. Мы описываем их в форме теории и приводим непосредственные доказательства.
Примечание: Все свойства NOD сформулированы для положительных целых чисел и учитывают только делители больше нуля.
Свойство 1. Наибольший общий делитель A и B равен наибольшему общему делителю B и A, т.е. NOD(A, B) = NOD(B, A). Изменения в цифрах не влияют на конечный результат.
Доказывать это свойство не имеет смысла, так как оно вытекает непосредственно из определения самого узла.
Неподвижный 2. Если A делится на B, то NOD(A, B) = B, так как все общие делители A и B совпадают с множеством делителей B.
Доказательство.
Каждый общий делитель чисел A и B является делителем каждого из этих чисел, содержащих B. Поскольку A кратно B, то по свойству деления каждый делитель B также является делителем A. Каждый делитель B оказывается общим делителем A и B.
Таким образом, когда A делится на B, все делители A и B равны одному целому делителю B. Кроме того, поскольку наибольшим разбиением B является сам B, наибольший общий делитель A и B равен B, то есть NOD(A, B) = B.
В частности, если a = b, то nod(a, b) = nod(a, a) = nod(b, b) = a = b.
Доказанное свойство больших делителей можно использовать для нахождения двух чисел при делении одного на другое. В этом случае кивок равен одному из этих чисел, а второе делится.
Неподвижно 3. a = bq + c, где a, b, c и q — целые числа, тогда все общие делители чисел a и b равны всем общим делителям чисел b и c. Применимо равенство nod(a, b) = nod(b, c).
Доказательство.
Поскольку существует равенство A = BQ + C, то каждый общий делитель A и B делит C по свойству деления. По той же причине каждый общий делитель B и C делит A. Поэтому каждый общий делитель A и B совпадает с каждым общим делителем B и C.
По той же причине каждый общий делитель B и C делит A. Поэтому каждый общий делитель A и B совпадает с каждым общим делителем B и C.
Поэтому максимумы этих общих делителей совпадают и равенство и nod(a, b) = nod(b, c) можно считать верным.
Неподвижный 4. nod(mb) = m * nod(a, b), если m — натуральное число.
Доказательство.
Умножая каждое равенство алгоритма Евклида на m и в обе стороны, его узел (MM, MB) = MR, где R — узел (a, b). Это свойство наибольшего общего делителя используется для нахождения нода путем рассмотрения первого числа.
Свойство 5. p с общими делителями чисел a и b и nod(a:p, b:p) = nod(a, b):p. То есть, если p = nod(a, b), то nod(a:nod(a, b), b:nod(a, b)) = 1, то есть числа a:nod(a, b) и B:nod(a, b) изначально взаимно однозначны.
Для предыдущего состояния, где a = p (a:p) и b = p (b:p), и для предыдущего состояния можно написать цепочку уравнений, например, nod(a, b) = nod(p(a:p)), p(b:p)) = p * nod(a:p, b:p).
Знакомство с темой наибольшего общего делителя начинается в первом классе в теории и практически подкрепляется оценками. В этой статье вы узнали все основные определения, качества, признаки и методы кивания.
В этой статье вы узнали все основные определения, качества, признаки и методы кивания.
Чтобы лучше понять, как найти два числа, достаточно заменить заданную переменную на первое число, например, 12 или 9. Другими словами, наименьшие делители 12 и 9 — это те, для которых решение может быть найдено без разрыва из.
Как найти наибольший общий делитель для двух чисел
При решении математических задач в начальной школе может возникнуть необходимость найти наибольший общий делитель или кивок на аббревиатуру. Однако не все студенты знают правильный алгоритм этого закона и путают его с НОК (наименьшее общее кратное). Чтобы избежать подобных ошибок, математики разработали универсальный алгоритм для различения и нахождения цен.
При решении математических задач в начальной школе может возникнуть необходимость найти наибольший общий делитель или кивок на аббревиатуру. Однако не все студенты знают правильный алгоритм этого закона и путают его с НОК (наименьшее общее кратное). Чтобы избежать подобных ошибок, математики разработали универсальный алгоритм для различения и нахождения цен.
Чтобы избежать подобных ошибок, математики разработали универсальный алгоритм для различения и нахождения цен.
Общие сведения
Перед началом обучения эксперты рекомендуют написать список основных знаний, необходимых для нахождения наибольшего общего делителя и меньшего общего кратного. Он состоит из следующих элементов.
- Определения величин.
- Признаки делимости чисел.
- Разложение на простые элементы или множители.
- Алгоритмы или методики нахождения.
НОД — это максимальное значение, на которое делятся два или более чисел. NOC — это параметр, описывающий наименьший общий делитель. Чтобы понять разницу между этими терминами, необходимо проанализировать акт деления двух чисел.
Первый элемент — делитель. Это означает, что делитель делится на определенный элемент (делимое). Результатом является коэффициент. Математики называют последнее квантом двух или более величин. Затем необходимо проанализировать точки делителей.
Признаки делимости
В математике есть два понятия: числа и цифры. Основное отличие заключается в том, что комбинация цифр приводит к цифре. Кроме того, каждое значение состоит из чисел (единиц, десятков, тысяч и тысяч). Эти числа читаются слева направо. Так, 657 состоит из единиц (7), десятков (5) и сотен (6). Стоит поискать их комбинацию. Операция выглядит следующим образом: 7 + 50 + 600 = 657.
Точка деления — это критерий, с помощью которого число может быть разделено на требуемое значение без остатка. Включены следующие правила.
- R (любое действительное число).
- Последняя цифра — четная, т. е. 24/2 — делится, т. к. 4 — четное.
- Сумма цифр, составляющих число, возможно разделить на 3. Пример: 36/3==12.
- Последние 2 цифры можно разделить на 4, т. е. 844/4==211.
- Последний разряд эквивалентен одному из двух значений (0 или 5), 810/5==162.
- Для числа 6 одновременно выполняются второй и третий пункт.
 Пример: 96/6= и =16.
Пример: 96/6= и =16. - 7: расчет по формуле a*b*c*d+e/7, где e — разряд единиц, а все остальные (слева направо) — десятки, сотни, тысячи и десятки тысяч. Правило справедливо и для величин с разным количеством разрядов. Пример: 861/7==123.
- Деление на 8 осуществляется по второму и четвертому признакам одновременно, т. е. 184/8= и =23.
- Сумму разрядов можно разделить на 9. Пример: 108/9==12.
- Последняя цифра эквивалентна 0, т. е. 140/10==14.
- 2 разряда равны между собой (11, 22, 33 и т. д. ) или величина, образованная разрядами сотен и десятков без единиц, делится на 11 (121=).
Однако признаков деления недостаточно, чтобы перейти к соответствующему алгоритму. Следующим шагом является разбиение числа на простые элементы натурального типа.
Разложение на простые элементы
Основные элементы — это числа, делящиеся на единицу или один эквивалент, т.е. 7/1 и 7/7. Снизить цену ключевых элементов — найти набор чисел, произведение которых будет соответствовать искомой цене. Например, 30 = 3*5*2. математики разработали специальные алгоритмы для выполнения этого действия.
Например, 30 = 3*5*2. математики разработали специальные алгоритмы для выполнения этого действия.
Примеры решения
Одна из трудностей заключается в следующем: найти наибольший общий делитель чисел 32, 66 и 84. Для ее решения могут быть использованы методы. Оптимальным является умножение.
Не рекомендуется решать евклидовым методом, так как это усложняет расчет. Фундаментальным принципом в физико-математических дисциплинах является оптимизация вычислений. Это означает, что вам необходимо найти метод с наименьшим количеством преобразований и вычислений.
В следующей задаче необходимо найти узлы 66, 121, 77 и 110. В этом случае также рекомендуется разделить все четыре числа на первый коэффициент. Поиск решений осуществляется с помощью этой методологии.
Глядя на эти два примера, можно сделать вывод, что найти кивок довольно просто. Далее необходимо найти 22 и 32 НОК. Это делается с помощью данной методологии.
Другой тип задачи — одновременное нахождение НОД и НОК для чисел 45, 85, 94 и 96. Решения могут принимать следующие формы
Решения могут принимать следующие формы
- 45=5*3*3.
- 85=17*5.
- 94=2*47.
- 96=2*2*3*2*2*2.
- НОД=1 (нет общих множителей, кроме единицы).
- НОК=5*3*3*17*2*47*2*2*2*2*2=1150560.
В математике есть и более сложные задачи. Одно из них утверждается следующим образом: два числа равны 9, первое число — 90, которое больше второго. Необходимо найти значение интеграла, наиболее близкое ко второму. Задача решается следующим алгоритмом
Поскольку ближайшее целое число равно 81, задача решается методом подбора.
Поэтому поиск ноды — очень простой процесс, если иметь базовые знания по алгоритму.
НОД (наибольший общий делитель) — Как найти НОД? Примеры
Наибольший общий делитель (НОД) относится к наибольшему положительному целому числу, которое является общим делителем для данного набора положительных целых чисел. Его также называют наивысшим общим фактором (HCF) или наибольшим общим фактором (GCF). В этом уроке мы подробно научимся находить наибольший общий делитель.
| 1. | Что такое наибольший общий делитель? |
| 2. | Как найти наибольший общий делитель? |
| 3. | Нахождение наибольшего общего делителя методом НОК |
| 4. | Алгоритм Евклида для наибольшего общего делителя |
| 5. | Часто задаваемые вопросы о наибольшем общем делителе |
Что такое наибольший общий делитель?
Для набора целых положительных чисел (a, b) наибольший общий делитель определяется как наибольшее положительное число, являющееся общим множителем обоих целых положительных чисел (a, b). НОД любых двух чисел никогда не бывает отрицательным или равным 0, поскольку наименьшее положительное целое число, общее для любых двух чисел, всегда равно 1. Есть два способа определить наибольший общий делитель двух чисел:
- Путем нахождения общих делителей
- По алгоритму Евклида
Как найти наибольший общий делитель?
Для набора из двух натуральных чисел (a, b) мы используем приведенные ниже шаги, чтобы найти наибольший общий делитель:
- Шаг 1: Запишите делители натурального числа «a».

- Шаг 2: Напишите делители натурального числа «b».
- Шаг 3: Запишите общие делители чисел «а» и «б».
- Шаг 4: Теперь найдите делитель, который является наибольшим из «a» и «b».
Пример: Найдите наибольший общий делитель чисел 13 и 48.
Решение: Мы используем следующие шаги для определения наибольшего общего делителя (13, 48).
Делители 13 равны 1 и 13.
Делителями числа 48 являются 1, 2, 3, 4, 6, 8, 12, 16, 24 и 48.
Общий делитель чисел 13 и 48 равен 1,
Наибольший общий делитель чисел 13 и 48 равен 1,
Таким образом, НОД(13, 48) = 1,
Нахождение наибольшего общего делителя методом НОК
Согласно методу НОК для наибольшего общего делителя НОД двух натуральных чисел (a, b) можно рассчитать по следующей формуле: метод НОК:
- Шаг 1: Найдите произведение a и b.

- Шаг 2: Найдите наименьшее общее кратное (НОК) чисел a и b.
- Шаг 3: Разделите значения, полученные на шаге 1 и шаге 2.
- Шаг 4: Полученное значение после деления является наибольшим общим делителем (a, b).
Пример: Найдите наибольший общий делитель 15 и 70 с помощью метода НОК.
Решение: Наибольший общий делитель 15 и 70 можно вычислить как:
- Произведение 15 и 70 задается как 15 × 70
- LCM (15, 70) равен 210.
- НОД (15, 20) = (15 × 70)/ 210 = 5.
∴ Наибольший общий делитель числа (15, 70) равен 5.
Алгоритм Евклида для наибольшего общего делителя
В соответствии с алгоритмом Евклида для наибольшего общего делителя НОД двух натуральных чисел (a, b) можно рассчитать как:
- Если a = 0, то НОД (a, b) = b как НОД (0, б) = б.
- Если b = 0, то НОД (a, b) = a, поскольку НОД (a, 0) = a.

- Если и a≠0, и b≠0, мы записываем «a» в форме остатка в частном (a = b×q + r), где q — частное, а r — остаток, и a>b.
- Найдите НОД (b, r) как НОД (b, r) = НОД (a, b)
- Мы повторяем этот процесс, пока не получим в остатке 0.
Пример: Найдите НОД чисел 12 и 10, используя алгоритм Евклида.
Решение: НОД чисел 12 и 10 можно найти, выполнив следующие шаги:
а = 12 и б = 10
а≠0 и б≠0
В форме остатка в частном мы можем записать 12 = 10 × 1 + 2
.
Таким образом, НОД (10, 2) должен быть найден, как НОД (12, 10) = НОД (10, 2)
Теперь a = 10 и b = 2
а≠0 и б≠0
В форме остатка в частном мы можем записать 10 = 2 × 5 + 0
.
Таким образом, НОД (2,0) должен быть найден как НОД (10, 2) = НОД (2, 0)
Теперь a = 2 и b = 0
а≠0 и b=0
Таким образом, НОД (2,0) = 2
НОД (12, 10) = НОД (10, 2) = НОД (2, 0) = 2
Таким образом, НОД 12 и 10 равен 2.
Алгоритм Евклида очень полезен для нахождения НОД больших чисел, так как в нем мы можем легко разбить числа на меньшие, чтобы найти наибольший общий делитель.
Темы, относящиеся к наибольшему общему делителю
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о наибольшем общем делителе (НОД) и связанных с ним темах.
- Общий знаменатель
- Каков наименьший общий знаменатель чисел 8 и 9??
- Калькулятор числителя и знаменателя
- Калькулятор общего знаменателя
- Рабочие листы наименьшего общего знаменателя
- Рационализация знаменателя
Примеры на наибольший общий делитель
Пример 1: Определить наибольший общий делитель чисел 12 и 26.
Решение: Наибольший общий делитель чисел 12 и 26 можно вычислить как:
Делители 12 равны 1, 2, 3, 4, 6 и 12.
Делители 26 равны 1, 2, 13 и 26.Общие делители 12 и 26 равны 1 и 2.
.
∴ Наибольший общий делитель числа (12, 26) равен 2,Пример 2. Используя метод НОК, определите значение наибольшего общего делителя чисел 20 и 65.
Решение: Мы можем вычислить значение наибольшего общего делителя чисел 20 и 65, используя следующие шаги:
- Произведение 20 и 65 задается как 20 × 65
- LCM (20, 65) равен 260.
- НОД (20, 65) = (20 × 65)/ 260 = 5.
∴ Наибольший общий делитель числа (20, 65) равен 5.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по наибольшему общему делителю
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о наибольшем общем делителе
Что означает наибольший общий делитель?
Наибольший общий делитель любых двух натуральных чисел (a, b) — это наибольший делитель, общий для целых чисел a и b. Он также известен как наивысший общий множитель или наибольший общий множитель.
Он также известен как наивысший общий множитель или наибольший общий множитель.
Как найти наибольший общий делитель двух чисел?
Наибольший общий делитель двух чисел можно определить, выполнив следующие шаги:
- Шаг 1: Найдите делители натурального числа «a».
- Шаг 2: Найдите делители натурального числа «b».
- Шаг 3: Найдите делители, общие для «a» и «b».
- Шаг 4: Найдите делитель, который является наибольшим из всех общих делителей чисел «a» и «b».
Что такое метод НОК для наибольшего общего делителя?
Мы можем определить значение наибольшего общего делителя, используя метод НОК. Согласно методу НОК, мы можем получить НОД любых двух положительных целых чисел, найдя произведение обоих чисел и наименьшее общее кратное обоих чисел. Метод НОК для получения наибольшего общего делителя задается как НОД (a, b) = (a × b)/ НОК (a, b).
Как найти наибольший общий делитель с помощью метода НОК?
Мы можем найти НОД (a, b), используя метод LCM, выполнив следующие шаги:
- Шаг 1: Определите произведение a и b.

- Шаг 2: Теперь найдите наименьшее общее кратное (НОК) чисел a и b.
- Шаг 3: разделите значения, полученные на шаге 1 и шаге 2.
- Шаг 4: Полученное значение после деления является наибольшим общим делителем (a, b).
Может ли наибольший общий делитель быть отрицательным?
Нет, наибольший общий делитель не может быть отрицательным, поскольку он представляет собой наибольший общий делитель двух положительных целых чисел. Наименьшее значение НОД может быть равно 1 и не меньше его. Это доказывает, что НОД не может иметь отрицательное значение.
GCD и HCF — одно и то же?
Да, GCD и HCF одинаковы. В любом случае значение GCD, HCF можно определить, проверив общие делители или множители, а затем найдя наибольший делитель обоих чисел.
Наибольший общий делитель | Brilliant Math & Science Wiki
Содержание
- Вычисление наибольшего общего делителя
- Алгоритм Евклида и многое другое.

- Приложения НОД
- Решение проблем
НОД нескольких чисел можно вычислить, просто перечислив множители каждого числа и определив наибольший общий множитель. Хотя на практике это ужасно неэффективно, в особо мелких случаях это можно сделать вручную. Процесс можно разделить с помощью метода пар множителей: если определен множитель aaa числа nnn, то частное na\frac{n}{a}an также обязательно является множителем. Например, поскольку 2 является множителем 24, 242=12\frac{24}{2} = 12224=12 также является множителем.
Найдите наибольший общий делитель чисел 30,36,30,36,30,36 и 24,24,24.
Делители каждого числа равны
30:1,2,3,5,6,10,15,3036:1,2,3,4,6,9,12,18,3624:1,2,4,6,12,24 \begin{выровнено} 30: &1, 2, 3, 5, 6, 10, 15, 30\ 36: &1, 2, 3, 4, 6, 9, 12, 18, 36\ 24: &1, 2, 4, 6, 12, 24 \end{выровнено} 30:36:24:1,2,3,5,6,10,15,301,2,3,4,6,9,12,18,361,2,4,6,12,24
Наибольшее число, встречающееся в каждом списке, — 6, 6, 6, поэтому это наибольший общий делитель: 9.
0003
НОД(30,36,24)=6. □ \gcd(30,36,24)=6.\ _\squaregcd(30,36,24)=6. □
Когда числа велики, список факторов может быть чрезмерно длинным, что делает описанный выше метод очень сложным. Несколько более эффективный метод состоит в том, чтобы сначала вычислить простую факторизацию каждого числа в наборе. Полученный НОД является произведением простых чисел, которые появляются в каждой факторизации, до наименьшего показателя степени, наблюдаемой в факторизациях. На словах это сбивает с толку, поэтому давайте посмотрим на пример: 9{\ мин (\ альфа_к, \ бета_к)} . gcd(a,b)=p1min(α1,β1)p2min(α2,β2)…pkmin(αk,βk).
Аналогичная формула применима для нахождения НОД нескольких целых чисел путем взятия наименьшего показателя степени для каждого простого числа.
Три золотые монеты весом 780 г, 840 г и 960 г разрезаны на мелкие кусочки одинакового веса. Если для перевозки одного куска золота требуется 2 человека, то какое наименьшее количество людей потребуется для перевозки всех этих кусков?
Хотя метод простой факторизации часто является наиболее практичным для выполнения вручную, иногда определение простой факторизации очень сложно, и в этом случае возникает необходимость в альтернативном подходе. Как правило, в этих случаях используются алгоритмы, описанные в следующем разделе.
Как правило, в этих случаях используются алгоритмы, описанные в следующем разделе.
Поскольку с большими числами трудно работать вручную, существует ряд алгоритмов, используемых для упрощения задачи до управляемого уровня. Поскольку НОД обладает тем свойством, что
НОД(a,b,c)=gcd(gcd(a,b),c)\text{gcd}(a, b, c) = \text{gcd}(\text {gcd}(a,b), c)gcd(a,b,c)=gcd(gcd(a,b),c)
НОД можно вычислить «по два за раз», например если бы мы хотели найти НОД чисел 20, 28 и 24, мы могли бы сначала найти НОД чисел 202020 и 282828 (что равно 4), а затем НОД чисел 4 и 24 (что также равно 4). В результате почти все алгоритмы ориентированы на простейший случай определения НОД двух чисел.
Алгоритм Евклида основан на следующем ключевом наблюдении: если ddd делит aaa и ddd делит bbb, то ddd также делит a−ba — ba−b (например, с помощью модульной арифметики). Это означает, что НОД aaa и bbb такой же, как НОД a-ba — ba-b и bbb, что является прогрессом, так как это делает числа меньше.
В результате мы можем повторить этот процесс, чтобы сформировать алгоритм:
- Если a=ba = ba=b, стоп — НОД aaa и aaa, конечно же, aaa. В противном случае перейдите к шагу 2.
- Если a>ba > ba>b, замените aaa на a-ba — ba-b и вернитесь к шагу 1.
- Если b>ab > ab>a, замените bbb на b-ab — ab-a и вернитесь к шагу 1.
Определите наибольший общий делитель чисел 84 и 132.
Следуем нашему алгоритму:
- aaa равно 84, а bbb равно 132. Поскольку b>ab > ab>a, мы заменяем bbb на b−a=132−84=48b — a = 132 — 84 = 48b−a=132−84=48.
- aaa равно 84, а bbb равно 48. Поскольку a>ba > ba>b, мы заменяем aaa на a−b=84−48=36a — b = 84 — 48 = 36a−b=84−48=36.
- aaa равно 36, а bbb равно 48. Поскольку b>ab > ab>a, мы заменяем bbb на b−a=12b — a = 12b−a=12.
- aaa равно 36, а bbb равно 12. Поскольку a>ba > ba>b, мы заменяем aaa на a−b=24a — b = 24a−b=24.
- aaa равно 24, а bbb равно 12.
Поскольку a>ba > ba>b, мы заменяем aaa на a−b=12a – b = 12a−b=12.
- aaa равно 12, а bbb равно 12. Поскольку a=ba = ba=b, НОД равен 12.
Поскольку числа с каждой точкой становятся меньше, этот алгоритм в конечном итоге завершится и выдаст НОД. На практике это можно сделать довольно эффективно, как описано на главной вики-странице — вы, возможно, заметили, например, что как только мы доберемся до 36 и 12, мы можем «пропустить» шаг a=24a = 24a=24. Алгоритм Евклида особенно полезен вручную, так как часто НОД становится «очевидным» при проверке, когда числа становятся достаточно низкими (например, вы могли заметить при a = 36, b = 12, a = 36, b = 12, a = 36). ,b=12 шаг, что НОД равен 12, так как 36=12⋅336 = 12 \cdot 336=12⋅3).
Кроме того, существует немного более сложный алгоритм, называемый Алгоритм Штейна , который основан на том же наблюдении, но дополнительно проверяет четность обоих чисел:
- Если a=ba = ba=b, стоп — НОД числа ааа и ааа это, конечно, ааа.
 В противном случае перейдите к шагу 2.
В противном случае перейдите к шагу 2. - Если aaa и bbb оба четные, замените aaa на a2\frac{a}{2}2a, bbb на b2\frac{b}{2}2b и увеличьте значение счетчика.
- Если aaa четное, а bbb нечетное, замените aaa на a2\frac{a}{2}2a.
- Если aaa нечетно, а bbb четно, заменить bbb на b2\frac{b}{2}2b.
- Если aaa и bbb оба нечетны, замените aaa на a-ba — ba-b (точно так же, как в приведенном выше алгоритме Евклида).
Это несколько более эффективно для компьютеров, поскольку деление на 2 выполняется очень быстро из-за использования двоичных чисел. Также более естественно делать это вручную; по сути, если вы заметили «очевидные» общие множители в любой точке алгоритма Евклида (здесь «очевидный» общий множитель равен 2, но это могут быть и другие, используя правила делимости).
НОД используется для ряда простых и сложных приложений. Фактически, вы, вероятно, неявно вычисляли НОД, не распознавая его при упрощении дробей: сокращение дроби — это вопрос деления и числителя, и знаменателя на их НОД.
Что такое 246642 \frac{246}{642}642246 в наименьшем выражении?
Любым из вышеперечисленных методов мы вычисляем наибольший общий делитель чисел 246246246 и 642642642, равный 6.6.6. Разделите верх и низ на 6 66, чтобы получить 41107\frac{41}{107}10741. Эта дробь действительно является наименьшей (как мы и ожидали), потому что единственное положительное целое число, которое делит и 41 4141, и 107 107 107, равно 1.1.1. □_\квадрат□
Пары целых чисел, такие как 414141 и 107,107,107, НОД которых равен 1·11, называются взаимно простыми и полезны по ряду причин, таких как тождество Безу.
НОД также используется в расширенном алгоритме Евклида для вычисления модульных инверсий, которые чрезвычайно важны в схемах шифрования, таких как RSA. Кроме того, это очень важно при рассмотрении порядка элемента, особенно в теореме Лагранжа, особенно применительно к модулярной арифметике. Это делает его частой темой на соревнованиях и олимпиадах. 9{2015}\text{gcd} \left(x,2015\right),x=1∑2015gcd(x,2015),
где gcd(a,b)\text{gcd}(a,b)gcd(a,b) — функция наибольшего общего делителя.
9{2015}\text{gcd} \left(x,2015\right),x=1∑2015gcd(x,2015),
где gcd(a,b)\text{gcd}(a,b)gcd(a,b) — функция наибольшего общего делителя.
Найдите максимально возможное значение наибольшего общего делителя чисел 5n+65n+65n+6 и 8n+78n+78n+7, где nnn — произвольное натуральное число.
Сколько существует упорядоченных пар целых чисел (a,b) (a,b) (a,b), таких что 100≤a≤1000,100≤b≤1000 100 \leq a \leq 1000, 100 \leq b \leq 1000 100≤a≤1000,100≤b≤1000 и
ab=1221? \frac{a}{b} = \frac{12}{21}? ба=2112?
Детали и предположения:
- Для упорядоченной пары целых чисел (a,b)(a,b)(a,b) порядок целых чисел имеет значение. Упорядоченная пара (1,2)(1,2)(1,2) отличается от упорядоченной пары (2,1)(2,1)(2,1).
Цитировать как: Наибольший общий делитель. Brilliant.org . Извлекаются из https://brilliant.org/wiki/greatest-common-divisor/
Наибольший общий делитель — Citizendium
Из Citizendium
Перейти к навигацииПерейти к поиску
| | Основной артикул | Обсуждение | Статьи по теме [?] | Библиография [?] | Внешние ссылки [?] | Версия для цитирования [?] | Учебники [?] |
| |||||||||||
Эта редактируемая основная статья находится в разработке и подлежит отказу от ответственности . [изменить введение] | |||||||||||||||||||
Наибольший общий делитель (часто сокращается до НОД или НОД , иногда также называется наибольший общий делитель ) двух или более натуральных чисел это наибольшее число, на которое оба (или все) числа делятся без остатка. Поскольку 1 делит все числа, и поскольку делитель числа не может быть больше этого числа, наибольшим общим делителем некоторых чисел является число между 1 и наименьшим из чисел включительно, и поэтому его можно определить (по крайней мере, в принципе ) путем проверки конечного числа чисел.
Числа, у которых наибольший общий делитель равен 1, называются взаимно простыми . Если (для трех и более чисел) любые два из них взаимно просты, они называются попарно взаимно простыми .
Наибольший общий делитель двух чисел a и b обычно записывается как gcd( a , b ) или, если не следует ожидать путаницы, просто как ( a , b ).
Содержимое
- 1 Нахождение наибольшего общего делителя
- 2 примера
- 3 приложения
- 4 Обобщения
- 5 формул
Нахождение наибольшего общего делителя
Теоретически важный метод нахождения наибольшего общего делителя использует разложение на простые множители: Каждый простой делитель общего делителя должен быть простым делителем всех чисел. Таким образом, наибольший общий делитель является произведением всех общих простых множителей. взятые в наибольшей степени, общей для всех чисел. Однако, поскольку первичная факторизация неэффективна, это наиболее практично для небольших чисел (или для чисел, факторизация которых уже известна). Это выражение произведения показывает, что наибольший общий делитель можно охарактеризовать следующим свойством: НОД является общим делителем, и каждый общий делитель делит его нацело.
К счастью, алгоритм Евклида предоставляет эффективные средства для вычисления наибольшего общего делителя. Это также показывает, что наибольший общий делитель может быть выражен
в виде целочисленной линейной комбинации чисел ( a , b ) = ra + sb (с целыми числами r и s ).
Поскольку каждая такая линейная комбинация делится на все делители, общие для a и b , это, в свою очередь, показывает, что это наименьшая положительная линейная комбинация,
и поэтому (на языке теории колец)
идеал, порожденный a и b , является главным идеалом, порожденным ( a , b ).
Это также показывает, что наибольший общий делитель может быть выражен
в виде целочисленной линейной комбинации чисел ( a , b ) = ra + sb (с целыми числами r и s ).
Поскольку каждая такая линейная комбинация делится на все делители, общие для a и b , это, в свою очередь, показывает, что это наименьшая положительная линейная комбинация,
и поэтому (на языке теории колец)
идеал, порожденный a и b , является главным идеалом, порожденным ( a , b ).
Примеры
Например,
- (4,9) = 1, (4,6) = 2 и (4,12) = 4, потому что
- делители 4 равны 1 ,2,4; делители 9 равны 1 ,3,9; и единственный общий делитель и НОД 1 ;
- делители 4 на 1, 2 ,4; делители 6 равны 1, 2 ,3,6; общие делители равны 1 и 2 , а НОД равен 2 ;
- делители 4 равны 1,2, 4 ; делители 12 равны 1,2,3, 4 ,6,12; общие делители равны 1,2, 4 , а НОД равен 4 .

- (72,108) = 36, потому что
- простые факторизации 72 = 2 • 2 • 2 • 3 • 3 и 108 = 2 • 2 • 3 • 3 • 3 обладают Amploy Amber
9 2 2 2 2 2 3 2 2 2 2 . 3 • 3 = 36. - 6, 10 и 15 — Относительно Prime , но не Пари Относительно PRIM = 1, но (6,10) = 2, (6,15) = 3, (10,15) = 5, как видно либо
- из простых факторизаций 6 = 2 • 3, 10 = 2 • 5, 15 = 3 • 5, в которых ни одно простое число не встречается во всех трех произведениях, или
- из списков делителей: 1,2,3,6 на 6, 1,2,5,10 на 10 и 1,3,5,15 на 15.
- 7, 9 , и 10 являются относительно простыми , но не попарно относительно простыми, потому что
- gcd(4,9,10) = 1, но (4,10) = 2, хотя две пары (4 ,9) = (9,10) = 1 взаимно просты.

- gcd(4,9,10) = 1, но (4,10) = 2, хотя две пары (4 ,9) = (9,10) = 1 взаимно просты.
- 7, 9, 10 являются попарно взаимно простыми , а значит, и взаимно простыми
- , потому что (7,9) = (7,10) = (9,10) = (7 ,9,10) = 1.
См. также Учебник.
Приложения
В элементарной арифметике для упрощения выражений используется наибольший общий делитель. за счет уменьшения размера задействованных чисел, например, учитывая некоторую дробь p / q , затем p /( p , q ) / q /( p , q ) является его сокращенным представлением. Например:
- Сокращенная форма 9/12 равна 3/4, потому что (9,12) = 3.
Аналогичным образом уравнения можно упростить:
- The quadratic equation 9 x 2 + 12 x = 0 is equivalent to 3 x 2 + 4 x = 0.
Moreover, the gcd can be used to calculate наименьшее общее кратное: лкм( a , b ) = ab / gcd ( a , b ):
- lcm(9,12) = 9•12 / gcd(9,12) = 108/3 = 36
Обобщения
Понятие делимости можно обобщить на контекст колец, однако идея наибольшего общего делителя не всегда применима.
 {\ min (a (p), b) (р))}}
{\ min (a (p), b) (р))}}Наибольший общий делитель
Наибольшее число, которое делится точно на два или более чисел.
Это «величайшая» вещь для упрощения дробей!Начнем с примера…
Наибольший общий делитель чисел 12 и 16
- Найти все делителей каждого числа,
- Обведите Общие факторы,
- Выберите Наибольшее из этих
Итак… что такое «Фактор»?
Факторы — это числа, которые мы можем перемножить, чтобы получить другое число:
Число может иметь много делителей:
Коэффициенты 12 равны 1, 2, 3, 4, 6 и 12 …
… потому что 2 × 6 = 12, или 4 × 3 = 12, или 1 × 12 = 12,
(Прочитайте, как найти все делители числа. В нашем случае нам не нужны отрицательные.)
Что такое «Общий фактор»?
Допустим, мы вычислили множители двух чисел:
.
Пример: Коэффициенты 12 и 30
Коэффициенты 12 составляют 1, 2, 3, 4, 6 и 12 Факторы 30: 1, 2, 3, 5, 6, 10, 15 и 30 Тогда общие факторы — это те, которые встречаются в обоих списки:
- Обратите внимание, что 1, 2, 3 и 6 присутствуют в обоих списках?
- Итак, общие делители 12 и 30 равны: 1, 2, 3 и 6
Это обычный множитель , когда он представляет собой множитель двух (или более) чисел.
Вот еще один пример с тремя числами:
Пример: Общие делители 15, 30 и 105
Делители 15 равны 1, 3, 5, и 15 Факторы 30: 1, 2, 3, 5, 6, 10, 15 и 30 Коэффициенты 105 равны 1, 3, 5, 7, 15, 21, 35 и 105 Общие для всех трех чисел множители 1, 3, 5 и 15
Другими словами, общие делители чисел 15, 30 и 105 равны 1, 3, 5 и 15
Что такое «Наибольший общий делитель»?
Это просто наибольших общих множителей.

В нашем предыдущем примере наибольший из общих делителей равен 15, поэтому наибольший общий делитель чисел 15, 30 и 105 равен 15
«Наибольший общий делитель» — это наибольший из общих делителей (двух или более чисел)
Почему это полезно?
Одна из самых полезных вещей, когда мы хотим упростить дробь:
Пример: Как упростить
12 30 ?Ранее мы обнаружили, что общие делители чисел 12 и 30 равны 1, 2, 3 и 6, поэтому наибольший общий делитель числа равен 6 .
Таким образом, самое большое число, на которое мы можем разделить как 12, так и 30, равно 6 9.0514, вот так:
÷ 6 12 30 = 2 5 ÷ 6 Наибольший общий делитель чисел 12 и 30 равен 6 .

И так 12 30 можно упростить до 2 5
Нахождение наибольшего общего делителя
Вот три способа:
1. Мы можем:
- найти все множителей обоих чисел (используйте Калькулятор всех множителей),
- затем найдите те, которые являются общими для обоих, и
- , затем выберите самый большой .
Пример:
Две цифры Факторы Общие факторы Наибольший
Общий множительПример упрощенный
Дробь9 и 12 9 : 1, 3, 9
12 : 1, 2, 3, 4, 6, 121, 3 3 9 12 = 3 4 И другой пример:
Две цифры Факторы Общие факторы Наибольший
Общий множительПример упрощенный
Дробь6 и 18 6 : 1, 2, 3, 6
18 : 1, 2, 3, 6, 9, 181, 2, 3, 6 6 6 18 = 1 3 2 .
 Или мы можем найти простые множители и объединить общие вместе:
Или мы можем найти простые множители и объединить общие вместе:Два числа Думая… Наибольший
Общий множительПример упрощенный
Дробь24 и 108 2 × 2 × 2 × 3 = 24, и
2 × 2 × 3 × 3 × 3 = 1082 × 2 × 3 = 12 24 108 = 2 9 3. Или иногда мы можем просто поиграть с с факторами, пока не обнаружим:
Два числа Думая… Наибольший
Общий множительПример упрощенный
Дробь9 и 12 3 × 3 = 9 и 3 × 4 = 12 3 9 12 = 3 4 Но в этом случае мы должны проверить, что мы нашли наибольший общий делитель.

Калькулятор наибольшего общего множителя
Хорошо, есть также действительно простой метод: мы можем использовать Калькулятор наибольшего общего фактора, чтобы найти его автоматически.
Другие названия
«Наибольший общий делитель» часто сокращается до « GCF «, а также известен как:
- «Наибольший общий делитель (НОД)», или
- «Наивысший общий множитель (HCF)»
Нахождение наибольшего общего делителя с помощью метода списка
Другой способ определить НОД: наибольший общий делитель двух чисел — это наибольший делитель, общий для обоих чисел.
Два приведенных выше определения означают одно и то же.
Не смущайтесь, если встретите другие названия наибольшего общего делителя. Все они имеют одинаковое значение. Альтернативные названия GCF:
- Наибольший общий делитель, сокращенно НОД
- Наибольший общий делитель, сокращенно HCF
Прежде чем продолжить, убедитесь, что вы знаете, как найти все делители число.
 В противном случае, пожалуйста, просмотрите мой короткий урок о том, как найти все делители числа с помощью метода радуги.
В противном случае, пожалуйста, просмотрите мой короткий урок о том, как найти все делители числа с помощью метода радуги.Шаг 1: Перечислите или напишите ВСЕ множители каждого числа.
Шаг 2: Определите общие факторы. Вы можете сделать это, обведя каждый общий фактор или нарисовав отрезок между ними. Это действительно зависит от вас, как вы хотите отметить общие факторы, чтобы они выделялись.
Шаг 3: После определения общих факторов выберите число, имеющее наибольшее значение. По сути, это число будет Наибольшим общим фактором (GCF).
Примеры нахождения наибольших общих делителей
ПРИМЕЧАНИЕ. Я решил сосредоточиться на нахождении НОД двух чисел, потому что это наиболее распространенные проблемы, с которыми вы столкнетесь при изучении НОД.
Пример 1 : Найдите наибольший общий делитель чисел 12 и 18.
Эта задача проста, потому что в ней используются относительно простые числа.
 Вы должны быть в состоянии найти все делители 12 и 18, используя метод радуги. В качестве альтернативы я перечислил все множители чисел от 1 до 100, чтобы вы могли использовать их по своему усмотрению.
Вы должны быть в состоянии найти все делители 12 и 18, используя метод радуги. В качестве альтернативы я перечислил все множители чисел от 1 до 100, чтобы вы могли использовать их по своему усмотрению.Итак, вот все делители числа 12 и 18.
Факторы числа 12 : 1, 2, 3, 4, 6, 12
Факторы числа 18 : 1, 2, 3, 6, 9 , 18
Перечислив все факторы каждого числа, мы теперь определяем общие факторы. Как вы можете видеть ниже, общими делителями чисел 12 и 18 являются 1, 2, 3 и 6. Обратите внимание, что я обозначил общие делители, заключив их в «прямоугольник».
Так что же такое GCF? Очевидно, что GCF является одним из общих факторов. Общий множитель, который имеет наибольшее значение, на самом деле является Наибольшим общим множителем. Следовательно, GCF 12 и 18 равен 6. Вот и все!
Пример 2 : Найдите наибольший общий делитель чисел 64 и 96.
Во многих случаях в математике по мере увеличения числа возрастает и уровень сложности задачи.
 Да, это верно и при нахождении GCF двух больших чисел. Однако концепция или процедура никогда не меняются.
Да, это верно и при нахождении GCF двух больших чисел. Однако концепция или процедура никогда не меняются.Итак, приступим. Найдем полные делители 64 и 96.
◉ Полные делители числа 64 равны 1, 2, 4, 8, 16, 32 и 64.
◉ Полные делители числа 96 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 и 96.
Ниже приведены списки факторов в вертикальном формате.
Следующим шагом является сравнение списков факторов. Затем нарисуйте фигуру так, чтобы общий множитель находился внутри каждой фигуры. Здесь можно творить! Обратите внимание, что на иллюстрации ниже у нас есть шесть (6) общих делителей, которые равны 1, 2, 4, 8, 16 и 32. , наибольший общий делитель 64 и 96 — это просто 32.
Пример 3 : Определите наибольший общий делитель чисел 42 и 126.
Легко торопиться с решением математической задачи, потому что вы уже знакомы с этапами ее решения. Однако рекомендуется сделать паузу или сделать шаг назад и посмотреть на проблему с более широкой точки зрения, прежде чем углубляться в процесс решения самой проблемы.

Причина в том, что процедура, которую вы уже знаете, может быть не самой эффективной по времени, потому что может быть лучший способ, то есть более короткое решение.
Давайте подойдем к этому так. Если 42 может делить 126 без остатка, то это означает, что 42 является делителем 126. Мало того, что 42 является общим делителем 42 и 126, но это также общий делитель, который имеет наибольшее значение.
Если подумать, общий делитель не может быть больше 42, потому что он не может быть больше меньшего числа из данных двух чисел.
Значит, 42 делят 126 поровну? Ответ — да! Следовательно, наибольший общий делитель (НОД) 42 и 126 равен просто 42. Готово!
Пример 4 : Чему равен GCF 71 и 223 ?
Как и в случае с , пример #3 , не торопитесь применять шаги, которые вы уже знаете. Я не могу переоценить важность практики сдержанности при решении математических задач в целом. Отступить назад, чтобы увидеть общую картину, чрезвычайно важно, потому что это позволит вам выработать стратегию и, следовательно, разработать жизнеспособный подход к проблеме.

Итак, теперь, если вы внимательно изучите два числа — 71 и 223, — вы легко поймете, что оба они являются простыми числами. Помните, что простое число имеет ровно два делителя , которые равны 1 и самому себе. Другими словами, мы можем сказать, что простое число делится только на 1 и само на себя.
Перечисление множителей 71 и 223:
Множителей 71: 1, 71
Множителей 223: 1, 223
Мы можем заключить, что, поскольку 1 является ТОЛЬКО общим множителем, отсюда следует, что 1 также должен быть наибольшим общим делителем по умолчанию. Таким образом, {\rm{gcf}}\left( {71,223} \right) = 1.
Пример 5 : Каков GCF 72 и 84?
Во-первых, мы знаем, что оба числа не простые, на самом деле оба числа четные. Это означает, что они имеют общие делители, отличные от 1. Во-вторых, также очевидно, что меньшее число 72 не может разделить без остатка большее число 84. Это позволяет нам заключить, что меньшее из двух чисел, 72, , а НЕ самое большое.
 тоже общий фактор.
тоже общий фактор.Что ж, остается только один вариант — продолжить пошаговую процедуру нахождения НГК двух чисел, описанную в первой части этого урока.
Перечисляя все множители каждого числа, мы имеем:
множители 72 : 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
множители 84 : 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
При сравнении списков множителей общие множители 72 и 84 равны 1, 2, 3 , 4, 6 и 12.
Судя по диаграмме, 12 — наибольший общий делитель 72 и 84. Готово!
Вас также может заинтересовать:
Использование простой факторизации для поиска НОК
Поиск НОК с помощью метода списка
Использование простой факторизации для поиска НОК
Наибольший общий делитель — это наибольшее число или выражение, являющееся множителем двух или более чисел или выражений.
Произношение: /greɪt.
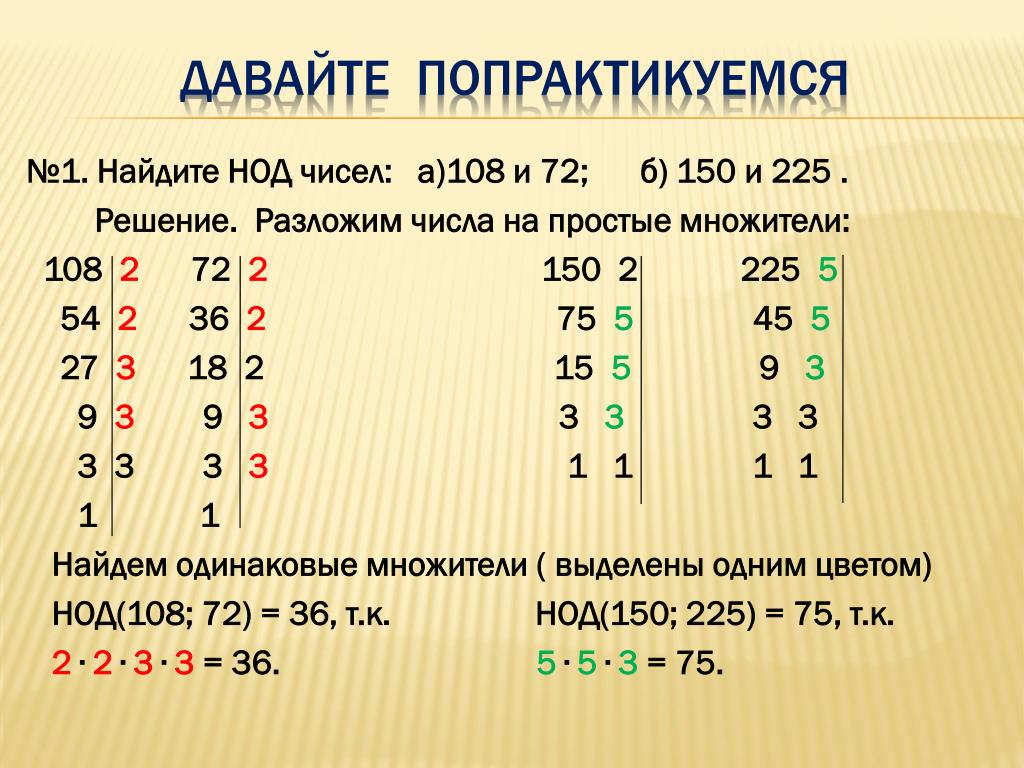 est ˈkɒm.ən ˈfæk.tər/ Объяснить
est ˈkɒm.ən ˈfæk.tər/ Объяснить Наибольший общий множитель — это наибольшее число или выражение это фактор двух или более чисел или выражений. Величайший общий множитель также можно назвать наибольший общий делитель. В британском английском самый большой общий делитель называется наивысший общий делитель а наибольший общий делитель называется наибольший общий делитель. сокращения для этих терминов:
Term Abbreviation greatest common factor gcf greatest common divisor gcd highest common factor hcf highest common divisor hcd Таблица 1: Сокращения Наибольший общий делитель 8 и 12 это 4. Наибольший общий множитель ( х 91 551 + 3)( 91 550 х 91 551 — 2) и (2 x — 6)( x — 2) ( х — 2).

Как найти наибольший общий делитель с помощью Факторизация простых чисел
Чтобы найти наибольший общий делитель чисел или выражений, нужно выполнить два шага:
- Найти все главные факторы каждого из чисел или выражений.
- Определите все простые множители, общие для всех чисел или выражений.
Пример: Найдите наибольший общий делитель 60 и 70.
- Разложение числа 60 на простые множители равно 2 · 2 · 3 · 5. Простая факторизация числа 70 2 · 5 · 7.
- Общие делители равны 2 и 5. Наибольший общий множитель 2 · 5 = 10.
Проверка понимания
Для каждого шага найдите ответ, затем нажмите Нажмите, чтобы ответить.
- Каков наибольший общий делитель чисел 12 и
6?
- Каковы простые делители числа 12?
Нажмите, чтобы ответить Простые множители числа 12 равны 2, 2 и 3. Это также может быть
написано 2 2 · 3 = 12.
Это также может быть
написано 2 2 · 3 = 12. - Каковы простые делители числа 6?
Нажмите, чтобы ответить Простые множители числа 6 равны 2 и 3. Это также может быть написано 2 · 3 = 6. - Какие простые делители
общий
на 6 и 12?
Нажмите, чтобы ответить Общие простые делители 6 а 12 это 2 и 3. - Перемножьте простые множители, чтобы получить наибольший общий множитель.
Нажмите, чтобы ответить 2 · 3 = 6. Наибольшее общий делитель 6 и 12 равен 6.
- Каковы простые делители числа 12?
- Каков наибольший общий делитель 12 и
6?
- Каковы простые делители числа 12?
Нажмите, чтобы ответить Простые множители числа 12 равны 2, 2 и 3. Это также может быть написано 2 2 · 3 = 12. - Каковы простые делители числа 6?
Нажмите, чтобы ответить Простые множители числа 6 равны 2 и 3. Это также может быть
написано 2 · 3 = 6.
Это также может быть
написано 2 · 3 = 6. - Какие простые делители
общий
на 6 и 12?
Нажмите, чтобы ответить Общие простые делители 6 а 12 это 2 и 3. - Перемножьте простые множители, чтобы получить наибольший общий множитель.
Нажмите, чтобы ответить 2 · 3 = 6. наибольший общий делитель 6 и 12 это 6.
- Каковы простые делители числа 12?
- Какой наибольший общий делитель чисел 9 и 12?
- Каковы простые делители числа 9?
Нажмите, чтобы ответить Простые множители числа 93 и 3. Это может также можно записать 3 2 = 9. - Каковы простые делители числа 12?
Нажмите, чтобы ответить Простые множители числа 12 2, 2 и 3. Это также можно записать 2 2 · 3 = 12. - Какие простые делители
общий
на 9 и 12?
Нажмите, чтобы ответить Общий делитель 9 и 12 это 3.
- Поскольку существует только один общий простой делитель, наибольший общий делитель является простым делителем.
Нажмите, чтобы ответить Наибольший общий делитель 9 а 12 это 3.
Как использовать алгоритм Евклида для нахождения наибольших общих делителей
Алгоритм Евклида — это быстрый метод нахождение наибольшего общего делителя двух чисел. Он основан на факте что наибольший общий делитель двух чисел равен наибольшему общий множитель каждого числа и их разность. Например, используйте 51 и 85. gcf(51,85) = 17. Теперь вычтем 51. из 85. 85 — 51 = 34. gcf(85,34) = 17 и gcf(51,34) = 17.
Алгоритм Евклида использует этот факт для нахождения наибольшего общего делителя. Найти наибольший общий множитель с использованием алгоритма Евклида:
Итерация Первая
НомерВторая
НомерРазница Обсуждение 0 1 8 1
8
217 217 — 124 = 93 Начиная со 193 а 124 меньшее из трех чисел, используйте их для следующего шага. 
2 124 93 124 — 93 = 31 Так как 93 и 31 являются меньшее из трех чисел, используйте их для следующего шага. 3 93 31 93 — 31 = 62 Так как 62 и 31 являются меньшее из трех чисел, используйте их для следующего шага. 4 62 31 62 — 31 = 31 Так как 31 и 31 являются меньшее из трех чисел, используйте их для следующего шага. 5 31 31 31 — 31 = 0 Поскольку разность равна нулю, наибольший общий делитель 217 и 124 это 31. Таблица 2 Каталожные номера
- МакАдамс, Дэвид Э.. Словарь всех математических слов, наибольший общий делитель . Издание 2-го класса 20150108-4799968. стр. 87. Life is a Story Problem LLC. 8 января 2015. Купить книгу
Дополнительная информация
- МакАдамс, Дэвид Э.
 . Общий . allmathwords.org. ООО «Жизнь — это проблема истории». 12.03.2009. https://www.allmathwords.org/en/c/common.html.
. Общий . allmathwords.org. ООО «Жизнь — это проблема истории». 12.03.2009. https://www.allmathwords.org/en/c/common.html. - Евклид Александрийский. Элементы . Университет Кларка. 06.09.2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.
Цитируйте эту статью как:
МакАдамс, Дэвид Э. Наибольший общий делитель . 21.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/g/greatestcommonfactor.html.Авторы изображений
- Все изображения и манипуляции сделаны Дэвидом МакАдамсом, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.
История изменений
21.04.2019: Уравнения и выражения обновлены до нового формата.
- Каковы простые делители числа 9?
- 6, 10 и 15 — Относительно Prime , но не Пари Относительно PRIM = 1, но (6,10) = 2, (6,15) = 3, (10,15) = 5, как видно либо
- простые факторизации 72 = 2 • 2 • 2 • 3 • 3 и 108 = 2 • 2 • 3 • 3 • 3 обладают Amploy Amber