Список вопросов average [python, numpy, average, netcdf4, r]
Усреднение нескольких файлов netCDF4 с помощью python
Я немного разбираюсь в netCDF в Python, поэтому, пожалуйста, извините за этот нубский вопрос. У меня есть папка, заполненная примерно 3650 файлами netCDF4. Один файл в день в течение десятилетия. нилы называются yyyymmdd.nc (например, 20100101,…
57 просмотров
python numpy average netcdf4
schedule 18.08.2022
Средние восьмичасовые значения в R studio
Я хочу получить восьмичасовые (столбец Time) средние значения максимальных значений столбца O. Важно, чтобы столбец времени отображал каждый час одного дня. Кроме того, набор данных содержит следующие столбцы: (место) несколько мест, (дата) 365…
25 просмотров
r average
schedule
 09.2022
09.2022Вычислить средние значения в панельных данных R
Я новичок в R. У меня несбалансированные панельные данные. BvD_ID_Number — это идентификационный номер для каждой фирмы, TotalAsset — это значение общих активов из балансовых отчетов за каждый период времени (год). Вот обзор ( panel_overview ). Я…
47 просмотров
r average panel panel-data
schedule 29.05.2022
С# написание функции для расчета среднего возраста, которая принимает массив объектов в качестве параметра
Мне нужно создать функцию для расчета среднего возраста класса из 50 учеников, вот мой код public class Student { public int[] age = new int[10]; Student() { age[0] = 17; age[1] = 19;…
818 просмотров
arrays class c# average integer
schedule 11. 07.2022
07.2022
MySQL, используя где во вновь созданном столбце
Итак, я думаю, что это довольно просто, но я что-то напутал. у меня есть запрос SELECT AVG(price), food_type FROM instructor GROUP BY food_type Что производит это: Price | food_type | 2.25 | Drink | 1.50 | Candy | 3 | Soup…
52 просмотров
mysql sql average where-clause having-clause
schedule 20.08.2022
Этот код получает количество идентификаторов, которые появляются для каждого месяца в году. WITH t1 as (SELECT * FROM daily WHERE EVENT_DATE BETWEEN DATE ‘2019-01-01’ and DATE ‘2019-12-31’), SELECT ID, COUNT(ID) AS monthly_count,…
18 просмотров
sql oracle datetime count average
schedule 23. 09.2022
09.2022
Как вычислить среднее значение столбца массива, используя только положительные записи в Python?
import numpy as np A = np.random.rand(3,3) A[1,0] = -666 A[0,1] = -666 A[2,2] = -666 У меня есть матрица, все элементы которой положительные, за исключением того, что -666 представляет отсутствующее значение или выброс. Как я могу вычислить…
31 просмотров
numpy average numpy-ndarray
schedule 14.06.2022
Power BI в среднем за неделю
Мне нужно рассчитать средний объем клиентов в неделю. Мои меры настроены как: Total Volume = COUNT ( Table[LoadNumber] ) Total Weeks = DISTINCTCOUNT ( Table[Weeks] ) Average Volume = DIVIDE ( [Total Volume], [Total Weeks] ) Однако не у всех…
1824 просмотров
powerbi dax average
schedule 28.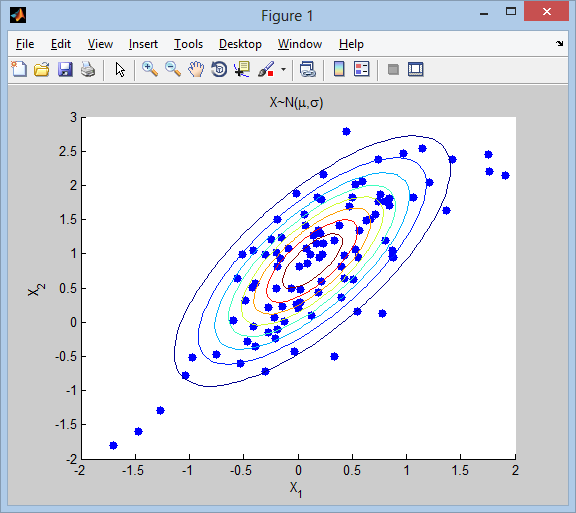 05.2022
05.2022
Мне нужно найти среднее значение всех записей (Qty), которые связаны с номерами поставщиков (SNo), если есть хотя бы одна запись
Мне нужно найти среднее значение всех записей (Qty), которые связаны с номерами поставщиков (SNo) как S1, S2 и т. д. даже если есть хотя бы одна запись, соответствующая условию этот запрос выбирает только одну запись и условие проверки запроса,…
32 просмотров
sql group-by average having
schedule 19.06.2022
Используя Excel, как вы вычисляете среднее количество одинаковых чисел в столбце?
Например: [Столбец A] 1,1,2,2,3,3,3 = среднее значение 2,3 [Столбец B] 2,2,3,3,4,4 = среднее значение равно 2 (каждое число появляется 2 раза) [Столбец C] 2,2,2,3,3,3,4,4,4 = среднее значение равно 3 (каждое число встречается 3 раза)
50 просмотров
excel average excel-formula
schedule 06.
Как рассчитать среднее количество чатов в день в таблице LEFT JOIN в Snowflake SQL?
Как в диктовке Snowflake SQL усреднить количество видеочатов в день, используя поле из таблицы, которое я оставил присоединенным ко всему запросу? Я думаю, что мне нужно выполнить функцию СУММ, чтобы подсчитать количество видеочатов, а затем…
38 просмотров
sql date snowflake-cloud-data-platform average sum
schedule 05.08.2022
Проверьте закон больших чисел в MATLAB
Проблема: если бросается большое количество правильных N -гранных игральных костей, среднее значение смоделированных бросков, вероятно, будет близко к среднему значению 1,2,… N т.е. ожидаемое значение одного кубика. Например, ожидаемое значение…
874 просмотров
random matlab average
schedule 20. 04.2022
04.2022
Замените среднее значение предыдущего и следующего доступных значений поля для значений NA в кадре данных
Пример набора данных из доступного гораздо большего набора данных имеет следующий формат: Station <-c(«A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A»,»A») Parameter <-c(2,3,NA,4,4,9,NA,NA,10,15,NA,NA,NA,18,20) Par_Count…
41 просмотров
r average na na.approx
schedule 16.08.2022
С# datatable с использованием вычислений для вычисления среднего значения в диапазоне строк
Я пытаюсь использовать .Compute для таблицы данных, при этом он вычисляет только среднее значение для набора строк. Я просмотрел документы Microsoft и некоторое время искал и не могу найти, где фильтр работает против структуры данных. Ищу что-то…
460 просмотров
datatable c# average
schedule 24. 05.2022
05.2022
Вычислить среднее значение для сгруппированного поля с помощью С# LINQ
Кто-то может помочь мне рассчитать среднее значение с помощью С# Linq для следующих данных: Year city1 city2 value 2016 CIT01 CIT01 578 2016 CIT01 CIT02 1067 2016 CIT01 CIT03 17 2016 CIT02 CIT01 1105 2016…
1213 просмотров
c# linq average
schedule 24.05.2022
Есть ли способ контролировать начальную точку и диапазон средней функции с помощью ячейки
У меня есть некоторые числовые данные в столбце, я хочу, чтобы «пользователь» мог выбрать начальную ячейку и последнюю ячейку или диапазон среднего значения. Я попытался использовать комбинацию средней функции и функции выбора. Я также пытался…
23 просмотров
excel average excel-formula
schedule 18.
Как усреднить группу данных по дням в R, а затем извлечь данные за определенный диапазон дат
Я относительно новичок в R, у меня есть большой набор данных, который дает несколько значений данных за этот день. Поэтому для упрощения мне нужно получить среднее значение за каждый день в одной таблице, отображающей день и среднее значение….
174 просмотров
r mean average date-range time-series
schedule 16.05.2022
Расчет скользящей средней
Я изо всех сил пытаюсь реализовать формулу скользящего среднего в своей функции. Мне потребовалось довольно много времени, чтобы понять, где сейчас находится код. Есть ли библиотека, которую я мог бы взять? Вход: ma([2,3,4,3,2,6,9,3,2,1],…
811 просмотров
python data-science average moving-average
schedule 12. 09.2022
09.2022
Как рассчитать среднесуточные значения из набора данных с почасовыми значениями в JavaScript
У меня есть такой набор данных: var ds = [ {time: «t1», parameter_q: «value1»}, {time: «t2», parameter_q: «value2»}, {time: «t3», parameter_q: «value3»}, …. ]; Набор данных содержит почасовые значения, а формат даты/времени — дд/мм/гггг…
884 просмотров
javascript average
schedule 16.08.2022
Как получить 2-ю формулу СРЗНАЧЕСЛИМН для поглощения, если 1-я формула СРЗНАЧЕСЛИМН не работает (Google Таблицы)? (Используйте ЕСЛИОШИБКА или СУММПРОИЗВ ??)
Я пытаюсь получить AVERAGEIF выполнение нескольких условий (с другого листа: SHEET1 ). Если условия не выполняются, я хочу, чтобы вступила в силу другая AVERAGEIFS формула. Не знаю, как объединить эти два аргумента. Они работают нормально…
44 просмотров
google-sheets average excel-formula
schedule 29. 04.2022
04.2022
Ответы на тесты Интуит «Моделирование систем»
Помощь с дистанционным обучением
Получи бесплатный расчет за 15 минут
Введите контактный e-mail:
Введите номер телефона
Что требуется сделать?
Каким способом с Вами связаться?:
Телефон
Напишем вам на вашу почту
Перезвоним вам для уточнения деталей
Перезвоним вам для уточнения деталей
или напишите нам прямо сейчас
Написать в WhatsApp
Какое значение принимает логарифмическая функция правдоподобия при найденной оценке параметра того или иного вероятностного распределения случайных величин?
- минимальное
- (Правильный ответ) максимальное
- среднее значение
- нулевое значение
Что необходимо рассчитывать для определения площади эллипса методом Монте — Карло?
- периметр квадрата, в который вписывается данный эллипса
- площадь треугольника, который вписывается в данный эллипс
- (Правильный ответ) площадь прямоугольника, в который вписывается данный эллипс
- периметр круга, в который вписывается данный эллипс
Для чего применяется метод максимального правдоподобия?
- для ковариационной оценки параметров вероятностных распределений
- для интервальной оценки параметров вероятностных распределений
- для дисперсионной оценки параметров вероятностных распределений
- (Правильный ответ) для точечной оценки параметров вероятностных распределений
Чему равно математическое ожидание равномерно распределенных случайных величин из интервала от нуля до единицы?
- 1
- 0
- 1/4
- 1/3
- (Правильный ответ) 1/2
Чему равен параметр функции распределения экспоненциально распределенных случайных величин, если их математическое ожидание равно двум?
- 1
- 4/2
- 3/2
- (Правильный ответ) 1/2
Какая функция системы MATLAB применяется для определения влия-ния факторов на изучаемую величину в двухфакторном дисперсионном анализе?
- (Правильный ответ) finv
- find
- factor
- feval
Каковы составляющие градиента при использовании линейной регрессионной модели в каждой точке факторного пространства?
- кодированные значения факторов в каждой точке факторного пространства
- числовые значения функции отклика для кодированных факторов
- числовые значения функции отклика в каждой точке факторного пространства
- значения уровней факторов
- (Правильный ответ) числовые коэффициенты регрессионной модели в каждой точке факторного пространства
Какая функция системы MATLAB может быть использована для определения оценки вектора параметров линейной модели наблюдений неполного ранга?
- exp
- (Правильный ответ) eye
- step
- find
- eig
В каком случае логарифмическая функция правдоподобия будет иметь максимум?
- (Правильный ответ) если в точке экстремума вторая производная функции будет отрица-тельной
- (Правильный ответ) если вблизи экстремума все значения функции будут меньше, чем в точке экстремума
- если вблизи точки экстремума все значения функции будут больше, чем в точке экстремума
- если в точке экстремума вторая производная функции будет положительной
С помощью какой функции системы MATLAB осуществляется переход от матрицы коэффициентов дискретной системы управления к матрице коэффициентов непрерывной системы?
- loglog
- lcm
- (Правильный ответ) logm
- log
Сколько специальных свойств имеет матрица Мура — Пенроуза?
- одно
- два
- (Правильный ответ) четыре
- три
- пять
Какое основное свойство обобщенной обратной матрицы ?
- (Правильный ответ)
- , где матрица S произвольного ранга
Какая функция системы MATLAB применяется для построения переходной функции дискретной системы управления?
- impulse
- (Правильный ответ) step
- stem
- plot
Какую размерность имеет дисперсия экспоненциально распределенной случайной величины между требованиями Пуассоновского потока?
- секунда в минус первой степени
- секунда
- (Правильный ответ) секунда в квадрате
- безразмерная величина
Вероятности состояний многофазной системы массового обслуживания являются
- распределенными по нормальному закону
- (Правильный ответ) в каждый момент времени являются независимыми
- (Правильный ответ) несовместными
- строго зависимыми между собой
- детерминированными
Чему будет пропорциональна интенсивность обслуживания требований при расчете вероятности k-го состояния (m ? k ? K) системы массового обслуживания типа M/M/m/K/M?
- она будет пропорциональна интенсивности обслуживания одного прибора
- она будет пропорциональна интенсивности входного потока требований
- (Правильный ответ) она будет пропорциональна количеству приборов обслуживания системы
- она будет пропорциональна числу источников нагрузки
Каковы пределы области определения логарифмической функции правдоподобия относительно оценки параметра биномиального распределения случайных величин?
- от 0 до 100
- от минус бесконечности до плюс бесконечности
- от нуля до плюс бесконечности
- (Правильный ответ) от 0 до 1
- от 0 до 10
Чему будет пропорциональна интенсивность обслуживания требований при расчете вероятности k-го состояния (0 < k ? m) системы массового обслуживания типа M/M/m?
- (Правильный ответ) она будет пропорциональна номеру состояния
- она будет обратно пропорциональна номеру состояния
- она будет пропорциональна количеству поступающих требований в систему
- она будет пропорциональна количеству требований, получивших отказ в обслуживании
Какая матрица системы MATLAB может быть использования для формирования матрицы коэффициентов дискретной системы управления?
- expinv
- (Правильный ответ) expm
- exр
- expfit
Что означает линейная зависимость столбцов матрицы произвольного ранга?
- (Правильный ответ) если хотя бы один из столбцов матрицы получен в результате умножения на постоянное число любого другого столбца
- если хотя бы один из столбцов матрицы получен в результате возведения в квадрат любого другого
- если хотя бы один из столбцов матрицы получен в результате сложения всех элементов любого другого столбца с постоянным числом
- если хотя бы один из столбцов матрицы получен в результате возведения в куб любого другого
Чему равно математическое ожидание равномерно распределенных случайных величин из интервала от -1 до +1?
- 1
- 1/2
- 1/3
- (Правильный ответ) 0
- 1/4
Чему будет пропорциональна возможная длина очереди при расчете вероятности k-го состояния (m ? k ? K) системы массового обслуживания типа M/M/m/K/M?
- она будет пропорциональна сумме числа требований, находящихся в системе, и общего числа обслуживающих приборов
- она будет пропорциональна разности между числом источников нагрузки и общим числом обслуживающих приборов
- она будет пропорциональна числу источников нагрузки
- (Правильный ответ) она будет пропорциональна разности между числом требований, находящихся в системе, и общим числом обслуживающих приборов
С помощью какой функции системы MATLAB рассчитывается исправленное стандартное отклонение выборки случайных чисел?
- (Правильный ответ) std
- var
- cov
- mean
Что называется факторным пространством?
- пространство, одной из координат которого является время
- (Правильный ответ) пространство, координатами которого являются значения факторов
- пространство, одной из координат которого является наблюдаемое значение функции отклика
- (Правильный ответ) пространство, в котором строится поверхность отклика
Какое распределение случайной величины применяется для расчета определенных интегралов с помощью метода Монте — Карло ?
- (Правильный ответ) равномерное
- экспоненциальное
- гамма-распределение
- нормальное
В каких пределах изменяется функция распределения случайных величин, распределенных по закону Эрланга 4-го порядка с параметром равным 2?
- (Правильный ответ) от 0 до +1
- от 1 до 2
- от -2 до +2
Как рассчитывается нормировочное условие для системы массового обслуживания типа M/M/m/K/M?
- суммируются все вероятности состояний для всех моментов времени
- рассчитывается произведение несовместных вероятностей
- (Правильный ответ) суммируются все вероятности состояний для одного из выбранного моментов времени
- рассчитывается произведение стационарных вероятностей всех состояний системы
Многофазная система массового обслуживания применяется в том случае, когда
- (Правильный ответ) требования обслуживаются в системе последовательно
- время обслуживания требований зависит от их количества
- необходимо повторное обслуживание
- требования обслуживаются параллельно расположенными приборами обслуживания
Какой тип модуляции обычно применяется при дискретизации непрерывной системы управления?
- кодово-импульсная
- (Правильный ответ) амплитудно-импульсная
- широтно-импульсная
- фазоимпульсная
Чему будет равна функция плотности равномерно распределенная случайная величина Х из интервала от -1 до +1?
- линейной функцией от Х
- 0
- (Правильный ответ) 1/2
- 2
Что необходимо сначала выполнить для регрессионной идентификации линейных непрерывных систем управления?
- получить дискретную передаточную функцию
- получить передаточную функцию непрерывной системы управления
- получить переходную функцию непрерывной системы управления
- (Правильный ответ) получить соответствующую дискретную во времени модель управления
На каком методе в основном базируется регрессионный анализ?
- (Правильный ответ) на методе наименьших квадратов
- на методе статистических испытаний
- на методе наибольших квадратов
- на методе интервальных оценок вероятности события
Какая функция системы MATLAB обычно используется при выборе степени аппроксимирующего полинома?
- pink
- pcg
- pie
- (Правильный ответ) psi
Стандартное отклонение — это такая характеристика входного потока требований системы типа M/M/m, которая определяет собой
- минус корень квадратный из дисперсии
- (Правильный ответ) плюс корень квадратный из дисперсии
- (Правильный ответ) меру отклонения от математического ожидания числа требований в потоке
- ковариационное отношение
В каком квадранте декартовой системы координат располагается логарифмическая функция правдоподобия относительно оценки параметра меньше единицы экспоненциального распределения случайных величин?
- в третьем
- в первом
- (Правильный ответ) в четвертом
- во втором
Для чего применяют исправленную выборочную дисперсию?
- чтобы упростить расчеты
- (Правильный ответ) чтобы получить несмещенную оценку истинной дисперсии
- чтобы упростить расчет стандартного отклонения
- чтобы получить смещенную оценку истинной дисперсии
Для чего выполняют центрирование нормально распределенных слу-чайных величин при интервальной оценке их математического ожидания?
- чтобы получить отсортированную выборку случайных чисел
- (Правильный ответ) чтобы пользоваться таблицами критических точек соответствующего распределения
- (Правильный ответ) чтобы преобразовать их к стандартному нормальному закону
- чтобы облегчить дальнейшие вычисления
В каком квадранте декартовой системы координат располагается логарифмическая функция правдоподобия относительно оценки параметра биномиального распределения случайных величин?
- в первом
- во втором
- (Правильный ответ) в четвертом
- в третьем
Что необходимо знать для определения функции максимального правдоподобия случайной дискретной величины?
- (Правильный ответ) аналитическое выражение распределения вероятностей случайной величины
- уравнение правдоподобия
- среднее арифметическое выборки случайных величин
- дисперсию выборки случайных величин
Какая арифметическая операция используется в методе Фибонначи генерирования целых псевдослучайных чисел?
- (Правильный ответ) вычитание
- деление
- умножение
- сложение
Сколько имеет степеней свободы выборочная дисперсия внутри серий по уровням фактора при однофакторном эксперименте?
- равно числу дублирующих опытов
- (Правильный ответ) на единицу меньше чем число экспериментов
- на единицу больше чем число экспериментов
- одну
Чему равен ранг обобщенной обратной матрицы?
- равен числу неизвестных параметров линейной модели наблюдений
- (Правильный ответ) равен числу линейно независимых столбцов матрицы регрессоров
- равен числу, на единицу меньшего числа неизвестных параметров линейной модели наблюдений
- (Правильный ответ) равен числу линейно независимых строк матрицы регрессоров
- равен нулю
Как называют обобщенную обратную матрицу?
- сингулярной обратной матрицей
- разреженной матрицей
- (Правильный ответ) g-обратной матрицей
- вырожденной матрицей
При расчете вероятности k-го состояния (m ? k ? K) системы массового обслуживания типа M/M/m/K с ограниченным временем ожидания возможная длина очереди
- равна нулю
- всегда равна общему числу приборов обслуживания
- (Правильный ответ) пропорциональна разности между номером состояния и общим числом обслуживающих приборов
- равна произведению числа нетерпеливых требований, ушедших из очереди, на общее число приборов обслуживания
Какие операторы и блоки системы GPSS/PC обеспечивают обслуживание по заданному вероятностному закону?
- table и tabulate
- (Правильный ответ) function и advance
- table и generate
- initial и seize
В каком случае фактор будет оказывать существенное влияние на изучаемую величину?
- когда будет значимой остаточная дисперсия
- когда будет незначимой факторная дисперсия
- (Правильный ответ) когда различие между факторной и остаточной дисперсиями будет значимым
- когда различие между факторной и остаточной дисперсиями будет незначимым
Область определения функции распределения экспоненциально распределенных случайных величин заключена в пределах
- от минус бесконечности до плюс бесконечности
- (Правильный ответ) от нуля до плюс бесконечности
- от нуля до единицы
- от минус бесконечности до нуля
Какой в общем случае является таблица наблюдений однофакторного эксперимента при дисперсионном анализе?
- квадратной
- (Правильный ответ) прямоугольной
- треугольной
- в виде одной строки и нескольких столбцов
Что лежит в основе метода крутого восхождения при поиске экстремума функции отклика?
- (Правильный ответ) метод градиентного спуска
- метод циклического покоординатного спуска
- метод покоординатного спуска
- метод ветвей и границ
В каких пределах может изменяться коэффициент доверия?
- может быть любым неотрицательным числом
- от 0 до 100
- от 0 до 10
- (Правильный ответ) от 0 до 1
Какой должна быть стратегия планирования эксперимента при поиске оптимальных условий?
- должна обеспечить поиск по линейному критерию
- должна максимизировать число опытов
- (Правильный ответ) должна минимизировать число опытов
- должна минимизировать число значимых факторов
Чему равно математическое ожидание экспоненциально распределенных случайных величин, если параметр функции распределения равен одной второй?
- (Правильный ответ) 4/2
- 3/2
- 1/2
- 1
Если случайные величины распределены по закону Эрланга 4-го порядка с параметром равным 1, то чему будет равно математическое ожидание случайных величин?
- 1
- (Правильный ответ) 4 или 5
- 3 или 4
- 2 или 3
Какая функция системы MATLAB применяется для генерирования псевдослучайных чисел по методу Лемера?
- (Правильный ответ) mod
- mean
- mesh
- magic
Что необходимо предпринять в случае неполного ранга матрицы регрессоров при регрессионной идентификации дискретной системы управления?
- (Правильный ответ) необходимо использовать матрицу Мура — Пенроуза
- необходимо из матрицы регрессоров удалить линейно зависимые столбцы
- (Правильный ответ) необходимо использовать псевдообратную матрицу
- необходимо из матрицы регрессоров удалить линейно зависимые строки
Выборка случайных чисел с экспоненциальным распределением может быть определена
- (Правильный ответ) с помощью равномерно распределенных чисел из интервала от нуля до единицы
- (Правильный ответ) с помощью равномерно распределенных чисел
- с помощью нормально распределенных случайных чисел
- с помощью биномиально распределенных случайных чисел
Чему равняется число необходимых данных для проведения двухфакторного дисперсионного анализа?
- (Правильный ответ) произведению числа уровней данных факторов
- сумме числа уровней данных факторов
- разнице между большим числом уровней факторов и меньшим числом
- (Правильный ответ) числу всех комбинаций уровней факторов
Какая функция системы MATLAB применяется для определения исправленной выборочной дисперсии выборки случайных чисел?
- vpa
- (Правильный ответ) var
- (Правильный ответ) cov
- damp
Какая функция системы MATLAB применяется для определения среднего значения выборки случайных чисел?
- mesh
- magic
- mod
- (Правильный ответ) mean
Что необходимо определить при расчете площади заданной плоской фигуры методом Монте — Карло?
- (Правильный ответ) площадь прямоугольника или квадрата
- (Правильный ответ) площадь фигуры, в которую вписывают заданную фигуру
- периметр заданной плоской фигуры
- площадь фигуры Лиссажу
Какими должны быть входные величины для корректного применения метода регрессионного анализа?
- должны быть зависимыми между собой
- должны быть коррелированными между собой
- (Правильный ответ) должны быть некоррелированными между собой
- (Правильный ответ) должны измеряться с более высокой точностью по сравнению с выходными переменными
Входной поток требований будет обладать свойством стационарности, если
- (Правильный ответ) они поступают по простейшему пуассоновскому закону
- вероятность поступления заданного числа требований не зависит от длины временного интервала, но зависит от того, где именно на оси времени этот интервал расположен
- в каждый момент времени требования являются независимыми
- (Правильный ответ) вероятность поступления заданного числа требований зависит от длины временного интервала и не зависит от того, где именно на оси времени этот интервал расположен
Какие операторы или функции системы MATLAB могут использоваться для расчета площади круга методом Монте — Карло?
- (Правильный ответ) for или while
- exprnd
- (Правильный ответ) rand
- randn
Что представляет собой оценка наблюдения функции отклика в заданной точке факторного пространства?
- средняя величина разности между ее максимальным и минимальным значениями
- (Правильный ответ) среднее арифметическое ее значений
- среднее геометрическое ее значений
- среднее квадратическое ее значений
Если случайные величины распределены по закону Эрланга 4-го порядка с параметром равным 1, то чему будет равна дисперсия случайных величин?
- (Правильный ответ) 4 или 5
- 1
- 2 или 3
- 3 или 4
Как вычисляется оценка градиента в каждой точке факторного пространства при движении к максимуму функции отклика?
- по результатам оценки среднего значения функции отклика
- по результатам оценки стандартного отклонения значений факторов относительно заданной точки факторного пространства
- по результатам оценки дисперсии значений факторов относительно заданной точки факторного пространства
- (Правильный ответ) по результатам эксперимента
Какая функция системы MATLAB может быть применена для определения исправленного среднего квадратического отклонения выборки случайных чисел?
- svds
- svd
- (Правильный ответ) std
- (Правильный ответ) var
Какая функция системы MATLAB используется при расчете квантилей при интервальной оценке математического ожидания нормально распределенной случайной величины с неизвестной дисперсией?
- chi2inv
- (Правильный ответ) tinv
- expinv
- norminv
Какая матричная операция используется при формировании информационной матрицы при регрессионной идентификации непрерывной системы управления?
- (Правильный ответ) операция транспонирования
- операция псевдообращения
- операция приведения к нижней треугольной матрице
- операция приведения к верхней треугольной матрице
- операция триангуляции
Как можно определить размерность вектора наблюдений Y в системе MATLAB?
- size(Y, 2)
- (Правильный ответ) size(Y, 1)
- (Правильный ответ) length(Y)
- schur(Y)
Какая из перечисленных функций системы MATLAB может быть использована при расчете обобщенной обратной матрицы?
- size
- length
- (Правильный ответ) zeros
- (Правильный ответ) inv
- range
Что необходимо для построения регрессионной модели по данным пассивного эксперимента?
- (Правильный ответ) чтобы дисперсии выходных случайных величин были однородными
- чтобы дисперсии выходных случайных величин были неоднородными
- (Правильный ответ) чтобы дисперсии выходных случайных величин были примерно равными между собой
- чтобы дисперсии выходных случайных величин были существенно различными
Из каких чисел должны состоять случайные последовательности, полученные с помощью программных методов?
- (Правильный ответ) из статистически независимых
- (Правильный ответ) из равномерно распределенных
- из простых чисел
- из нормально распределенных
Нормальный закон распределения случайных величин характеризуется следующими параметрами:
- (Правильный ответ) математическим ожиданием и средним квадратическим отклонением
- средним значением функции распределения и средним значением нормированной корреляционной функции
- коэффициентами ковариации и корреляции
- (Правильный ответ) математическим ожиданием и стандартным отклонением
- величиной три-сигма и максимальным значением функции плотности
Что необходимо определить при расчете заданного объема тела методом Монте — Карло?
- площадь поверхности заданного тела
- (Правильный ответ) объем тела, в который помещают заданное тело, объем которого необходимо рассчитать
- тройной интеграл по поверхности заданного тела
- (Правильный ответ) объем многомерного параллелепипеда
Что выступают в качестве аргументов оценки параметра вероятностного распределения случайной дискретной величины?
- дисперсия и стандартное отклонение выборки случайных величин
- (Правильный ответ) значения выборки случайных величин
- (Правильный ответ) частоты появления случайных величин
- значения коэффициентов заданного распределения вероятностей случайных величин
Какие методы получили наибольшее распространение при поиске экстремума функции отклика?
- метод золотого сечения
- метод покоординатного спуска
- (Правильный ответ) градиентные
- (Правильный ответ) метод Бокса и Уильсона
- прямые методы поиска
Помощь с дистанционным обучением
Получи бесплатный расчет за 15 минут
Введите контактный e-mail:
Введите номер телефона
Что требуется сделать?
Каким способом с Вами связаться?:
Телефон
Напишем вам на вашу почту
Перезвоним вам для уточнения деталей
Перезвоним вам для уточнения деталей
или напишите нам прямо сейчас
Написать в WhatsApp
Модуль statistics в Python, статистика в математике.
Модуль statistics предоставляет функции для вычисления математической статистики числовых (вещественных) данных.
Модуль не предназначен для того, чтобы конкурировать со сторонними библиотеками, такими как NumPy, SciPy, или проприетарными полнофункциональными статистическими пакетами, предназначенными для профессиональных статистиков, таких как Minitab, SAS и Matlab.
Модуль statistics нацелен на уровень графических и научных калькуляторов.
Функции модуля statistics поддерживают типы Python int, float, Decimal и Fraction, если явно не указано иное. Поведение с другими типами (будь то в числовой башне или нет) в настоящее время не поддерживается.
Последовательности с элементами разных типов также не поддерживаются и зависят от реализации. Если входные данные состоят из смешанных типов, то можно использовать встроенную функцию map() для обеспечения согласованного результата, например: map(float, input_data).
Примечание. Функции не требуют сортировки данных. Для удобства чтения в большинстве примеров показаны отсортированные последовательности.
Модуль statistics определяет одно исключение:
statistics.StatisticsError:Исключение statistics.StatisticsError представляет собой подкласс исключения ValueError для исключений, связанных с модулем статистики.
Функция mean() и fmean() модуля statistics в Python, среднее арифметическое.
Функции mean() и fmean() модуля statistics рассчитывают и возвращают примерное среднее арифметическое данных data. Функция statistics.fmean() работает быстрее, чем функция statistics.mean() и всегда возвращает float.
Функция geometric_mean() модуля statistics в Python, среднее геометрическое.
Функция geometric_mean() модуля statistics преобразует элементы последовательности data в числа с плавающей запятой float и вычисляет и возвращает среднее геометрическое этой последовательности.
Функция harmonic_mean() модуля statistics в Python, среднее гармоническое.
Функция harmonic_mean() модуля statistics возвращает **среднее гармоническое значение** числовой последовательности.
Функция median() модуля statistics в Python, медиана последовательности.
Функция median() модуля statistics возвращает медиану (среднее значение) числовой последовательности data, используя общий метод “среднее из двух средних”.
Функция median_low() модуля statistics в Python, наименьшее среднее значение.
Функция median_low() модуля statistics возвращает наименьшее среднее значение числовых данных data (наименьшую медиану).
Функция median_high() модуля statistics в Python, наибольшее среднее значение.
Функция median_high() модуля statistics возвращает наибольшее среднее значение числовых данных data (наибольшую медиану).
Функция median_grouped() модуля statistics в Python, медиана непрерывных данных.
Функция median_grouped() модуля statistics возвращает медиану сгруппированных непрерывных данных, рассчитанную как 50-й процентиль, при помощи интерполяции.
Функция mode() модуля statistics в Python, распространенный элемент.
Функция mode() модуля statistics возвращает единственный наиболее распространенный элемент данных data из дискретных или номинальных данных.
Функция multimode() модуля statistics в Python, часто встречающиеся элементы.
Функция multimode() модуля statistics возвращает список наиболее часто встречающихся значений элементов в последовательности data в том порядке, в котором они были обнаружены.
Функция pstdev() модуля statistics в Python, стандартное отклонение.
Функция pstdev() модуля statistics возвращает стандартное отклонение числовой последовательности data (квадратный корень из дисперсии генеральной совокупности).
Функция pvariance() модуля statistics в Python, дисперсия элементов.
Функция pvariance() модуля statistics возвращает дисперсию элементов непустой числовой последовательности или итерации.
Функция stdev() модуля statistics в Python, выборочное отклонение.

Функция stdev() модуля statistics возвращает стандартное отклонение выборки из элементов числовой последовательности data (квадратный корень из дисперсии выборки).
Функция variance() модуля statistics в Python, выборочная дисперсия.
Функция variance() модуля statistics возвращает дисперсию выборки из элементов числовой последовательности data. Возвращаемое значение представляет собой итерацию по крайней мере двух действительных чисел.
Функция quantiles() модуля statistics в Python, интервалы равной вероятности.
Функция quantiles() модуля statistics делит числовую последовательность с данными data на n непрерывных интервалов с равной вероятностью. Возвращает список из n — 1 элементов отсечения, разделяющих эти интервалы.
Класс NormalDist() модуля statistics в Python, распределение случайной величины.
NormalDist — это инструмент для создания нормальных распределений случайной величины и управления ими. Это класс, который рассматривает среднее значение и стандартное отклонение измерений данных][statistics. pstdev] как единое целое.
pstdev] как единое целое.
Функция covariance() модуля statistics в Python ковариация данных.
Функция covariance() модуля statistics возвращает выборку ковариации двух входных данных x и y. Ковариация — это мера совместной изменчивости двух входных данных.
Функция correlation() модуля statistics в Python, корреляция Пирсона.
Функция correlation() модуля statistics возвращает коэффициент корреляции Пирсона для двух последовательностей входных данных.
Функция linear_regression() модуля statistics в Python, линейная регрессия.
Функция linear_regression() модуля statistics возвращает наклон и точку пересечения аргументов простой линейной регрессии, оцененные с помощью обычного метода наименьших квадратов.
Расчет средневзвешенного значения в Excel
39050 08.01.2018 Скачать пример
Основная идея
Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:
Оценки по различным предметам у наших кандидатов следующие:
Свободное место, допустим, только одно, и наша задача — выбрать достойного.
Первое, что обычно приходит в голову — это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ (AVERAGE).
На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется «Программирование», а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.
Средневзвешенное — это среднее с учетом различной ценности (веса, важности) каждого из элементов.
В бизнесе средневзвешенное часто используется в таких задачах, как:
- оценка портфеля акций, когда у каждой из них своя ценность/рисковость
- оценка прогресса по проекту, когда у задач не равный вес и важность
- оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
- и т.
 д.
д.
Расчет средневзвешенного формулами
Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:
Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах — оценки абитурента и вес каждого предмета — а затем суммирует все полученные произведения. Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость.
Так что берем Машу, а Иван пусть поступает в институт физкультуры ;)
Расчет средневзвешенного в сводной таблице
Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:
Предположим, что у нас есть вот такая таблица с данными по продажам:
Обратите внимание, что я преобразовал ее в «умную» таблицу с помощью команды Главная — Форматировать как таблицу (Home — Format as Table) и дал ей на вкладке Конструктор (Design) имя Data.
Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:
=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33
То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.
Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду Итоги по (Summarize Values By):
В этом списке есть среднее, но нет средневзвешенного :(
Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:
Теперь можно рядом закинуть в область значений стоимость и количество — и мы получим почти то, что требуется:
Останется поделить одно на другое, но сделать это, вроде бы, простое математическое действие внутри сводной не так просто. Придется либо добавлять в сводную вычисляемое поле (вкладка Анализ — Поля, элементы, наборы — Вычисляемое поле), либо считать обычной формулой в соседних ячейках или привлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA), о которой я уже писал. А если завтра изменятся размеры сводной (ассортимент товаров), то все эти формулы придется вручную корректировать.
Придется либо добавлять в сводную вычисляемое поле (вкладка Анализ — Поля, элементы, наборы — Вычисляемое поле), либо считать обычной формулой в соседних ячейках или привлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA), о которой я уже писал. А если завтра изменятся размеры сводной (ассортимент товаров), то все эти формулы придется вручную корректировать.
В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.
Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX
Если у вас Excel 2013-2016, то в него встроен супермощный инструмент для анализа данных — надстройка Power Pivot, по сравнению с которой сводные таблицы с их возможностями — как счеты против калькулятора. Если у вас Excel 2010, то эту надстройку можно совершенно бесплатно скачать с сайта Microsoft и тоже себе установить. С помощью Power Pivot расчет средневзвешенного (и других невозможных в обычных сводных штук) очень сильно упрощается.
1. Для начала, загрузим нашу таблицу в Power Pivot. Это можно сделать на вкладке Power Pivot кнопкой Добавить в модель данных (Add to Data Model). Откроется окно Power Pivot и в нем появится наша таблица.
2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:
Несколько нюансов по формуле:
- В Power Pivot есть свой встроенный язык с набором функций, инструментов и определенным синтаксисом, который называется DAX. Так что можно сказать, что эта формула — на языке DAX.
- Здесь WA — это название вычисляемого поля (в Power Pivot они еще называются меры), которое вы придумываете сами (я называл WA, имея ввиду Weighted Average — «средневзвешенное» по-английски).
- Обратите внимание, что после WA идет не равно, как в обычном Excel, а двоеточие и равно.
- При вводе формулы будут выпадать подсказки — используйте их.

- После завершения ввода формулы нужно нажать Enter, как и в обычном Excel.
3. Теперь строим сводную. Для этого в окне Power Pivot выберите на вкладке Главная — Сводная таблица (Home — Pivot Table). Вы автоматически вернетесь в окно Excel и увидите привычный интерфейс построения сводной таблицы и список полей на панели справа. Осталось закинуть поле Наименование в область строк, а нашу созданную формулой меру WA в область значений — и задача решена:
Вот так — красиво и изящно.
Общая мораль: если вы много и часто работаете со сводными таблицами и вам их возможности «тесноваты» — копайте в сторону Power Pivot и DAX — и будет вам счастье!
Ссылки по теме
- Что умеет функция СУММПРОИЗВ на самом деле
- Зачем нужна функция ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ
- Настройка вычислений в сводных таблицах
Среднее значение в MATLAB (средняя функция)
В этой статье о MATLAB мы покажем вам, как реализовать функцию mean() для нахождения средних значений вектора, строк или столбцов матрицы или всех ее элементов.
Mean() обеспечивает большую гибкость как при вводе, так и при выводе, а также в режимах использования, поскольку позволяет указывать тип выходных данных, опускать значения NaN и легко работать с любым измерением в двумерных или многомерных массивах.
Далее мы рассмотрим полное описание этой функции, ее синтаксис, входные аргументы, ее выходные данные и ее управляющие флаги. Затем мы рассмотрим несколько практических примеров с фрагментами кода и изображениями, показывающими различные способы вызова mean() в разных измерениях.
MATLAB mean() Функция Syntax m = среднее ( ___, outtype )
m = среднее ( ___, nanflag )
MATLAB mean() Описание функции
Функция MATLAB mean() возвращает в «m» среднее значение, полученное из элементов вектора или из определенных элементов входной матрицы «а». Если входным аргументом этой функции является вектор, она возвращает в «m» скаляр со средним значением «a». В случаях, когда «a» является массивом, функция mean() предоставляет возможность использования флага «all», чтобы получить среднее значение всех элементов или среднее значение по строкам или столбцам и в измерениях, которые мы указываем при вызове функции с параметром входы «dim» и «vecdim».
Гибкость этой функции также позволяет нам использовать ввод «outtype», чтобы указать тип данных, которые должны иметь скалярный или векторный вывод, а также ввод «nanflag», чтобы мы могли опускать значения NaN. Ниже вы можете увидеть список со всеми входными аргументами и флагами управления этой функции, а также их соответствующим значением и использованием.
a: Входной вектор или матрица: это двумерный или многомерный вектор или матрица, из которых мы хотим получить средние значения.
«все» : Флаг «все»: когда мы вызываем функцию с этим флагом, mean() возвращает скаляр со средним значением всех элементов массива. Этот флаг представляет собой строку символов, поэтому он должен быть заключен в одинарные кавычки.
Dim: Он устанавливает размер матрицы, с которой мы собираемся работать. Когда мы вызываем эту функцию для получения средних значений строк, результатом является вектор-столбец, где каждый элемент является средним значением соответствующей строки 9. 0003
0003
| Размер =1 | и | и | А | ||
| и | и | А | |||
| а = | и | и | А | Ввод | Матрица |
| и | и | А | |||
| и | и | А | |||
| м = | м | м | М | Выход | Вектор |
Когда мы получаем средние значения столбца (dim = 2), результатом является вектор-строка со средними значениями каждого столбца, как показано на следующем рисунке:
| Dim =2 | и | и | А | м | |
| и | и | А | м | ||
| а = | и | и | и | м = | м |
| и | и | и | м | ||
| и | и | и | м | ||
| Матрица ввода | Выход | вектор |
Vecdim: Это вектор измерений. Каждый элемент этого массива указывает измерение так же, как «dim», если входной массив многомерный. Эти значения должны быть явно заключены в квадратные скобки и разделены запятыми или неявно представлены в виде вектора.
Каждый элемент этого массива указывает измерение так же, как «dim», если входной массив многомерный. Эти значения должны быть явно заключены в квадратные скобки и разделены запятыми или неявно представлены в виде вектора.
outtype: Указывает, какой тип данных будет выводиться.
Nanflag: Пропустить или включить результаты NaN в выходные аргументы.
Как получить среднее значение вектора с помощью функции среднего значения MATLAB
В этом примере мы будем использовать функцию mean() для нахождения среднего значения вектора. Для этого мы создаем вектор «a» из десяти элементов со значениями от 1 до 10 и вызываем функцию mean(), передавая этот вектор в качестве входного аргумента, как показано в следующем фрагменте:
a = [ 1, 4, 5, 9, 2, 3, 3, 4, 9, 10];
m = среднее ( a )
Как мы видим в командной консоли MATLAB на следующем рисунке, mean() в «m» возвращает скаляр со средним значением из элементов вектора «a».
Как получить среднее значение всех элементов массива с помощью ввода «все» функции MATLAB Mean()
Теперь давайте посмотрим, как мы можем использовать флаг «все», чтобы найти среднее значение все элементы массива. Для этого мы создаем матрицу «а» с элементами 4 х 4 и отправляем ее в качестве входного аргумента функции mean() вместе с флагом «все», разделенным запятыми.
а = [ 1, 4, 5, 9; 2, 3, 1, 4;
9, 10, 33, 14; 66, 20, 36, 7];
m = среднее ( a, ‘все’
)
Таким образом, функция mean() с флагом «все» возвращает скаляр со средним значением, полученным в результате вычисления всех значений, содержащихся в массиве «а».
Как получить среднее значение каждой строки, используя «тусклые» входные данные функции MATLAB Mean()
В этом примере мы покажем вам, как найти среднее значение каждой строки матрицы, используя «тусклые» входные данные этой функции. функция. В этом случае мы найдем среднее значение строк матрицы, которую мы использовали в предыдущем примере. Для этого мы отправляем матрицу в качестве входного аргумента через запятую. Значение входа «dim», которое в данном случае имеет размерность 2. Далее мы увидим фрагмент кода для этой цели.
Для этого мы отправляем матрицу в качестве входного аргумента через запятую. Значение входа «dim», которое в данном случае имеет размерность 2. Далее мы увидим фрагмент кода для этой цели.
а = [ 1, 4, 5, 9; 2, 3, 1, 4;
9, 10, 33, 14; 66, 20, 36, 7];
m = среднее ( a, 2 )
Как показано на изображении ниже, mean() возвращает вектор-столбец, где каждый элемент является средним значением каждой строки матрицы «a».
Как получить среднее значение каждого столбца, используя ввод «dim» функции MATLAB Mean()
Чтобы получить среднее значение каждого столбца матрицы «a», мы используем тот же метод вызова, что и в предыдущем примере, но указываем размер 1 на входе «dim», как показано ниже.
а = [ 1, 4, 5, 9; 2, 3, 1, 4;
9, 10, 33, 14; 66, 20, 36, 7];
m = среднее ( a, 1 )
Как показано на изображении ниже, mean() возвращает вектор-строку, где каждый элемент является средним значением каждой строки матрицы «a».
Заключение
Нахождение средних значений является первым шагом в любом статистическом расчете. В этой статье Matlab мы показали вам, как использовать функцию для нахождения средних значений вектора или матрицы в любом измерении. Мы также подробно описали отдельные входные аргументы для этой функции и показали различные возможные применения на практических примерах с фрагментами кода и изображениями.
Обновление с Matlab — документация sidpy 0.10
Крис Р. Смит
Вот несколько индивидуальных переводов многих популярных функций в Matlab и Python, которые должны упростить переход с Matlab на Python
Системные функции
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
адрес пути | sys.path.append | Добавить в путь |
Файловый ввод/вывод
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
dlmread | либо чтение и разбор, либо skimage. | Чтение файла числовых данных с разделителями ASCII в матрицу |
имрид | pyplot.imread | чтение файла изображения; N — количество используемых файлов |
Тип данных
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
инт | numpy.int | Преобразование данных в целое число со знаком |
двойной | numpy.float | Преобразовать данные в двойные |
реальный | numpy.real | Вернуть действительную часть комплексного числа |
изображение | numpy.imag | Возврат мнимой части комплексного числа |
Математика
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
кв | math. | Квадратный корень |
math.erf или scipy.special.erf | Функция ошибки | |
атан2 | math.erf или numpy.atan2 | Четырехквадрантный арктангенс |
абс | абс или numpy.abs | Абсолютное значение |
эксп | exp или numpy.exp | Экспоненциальная функция |
грех | грех или numpy.sin | Синусоидальная функция |
Создание массива
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
нули | число.нули | Создать массив нулей |
сетка | numpy. | Создание сетки координат в 2 или 3 измерениях |
ndgrid | numpy.mgrid или numpy.ogrid | Прямоугольная сетка в пространстве N-D |
Дополнительные функции
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
перестановка | numpy.transpose | Изменение размеров N-мерного массива |
уголок | numpy.угол | Фазовые углы для элементов сложной решетки |
макс. | numpy.max | Возвращает максимальный элемент массива |
мин | число.мин | Возвращает минимальный элемент массива |
изменение формы | numpy. | Изменить форму массива |
среднее | numpy.mean | Взять среднее значение по указанному размеру |
размер | числовой размер | получить общее количество записей в массиве |
Cell2mat | numpy.vstack([numpy.hstack(cell) для ячейки в ячейках]) | преобразует структуру данных из ячейки в мат; объединяет несколько массивов разного размера в один массив |
репмат | numpy.плитка | Повторные копии массива |
развернуть | нп.развернуть | Сдвинуть фазу массива таким образом, чтобы не было скачков более чем на желаемый угол (значение пи по умолчанию) |
Индексация массива
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
найти | numpy. | Найти все индексы матрицы, для которых верно логическое утверждение |
иснан | numpy.isnan | проверяет каждую запись массива на наличие NaN |
инф | numpy.isinf | проверяет каждую запись массива на наличие Inf |
ишар | numpy.ischar | проверяет каждую запись массива на наличие символа |
Дополнительные функции
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
fft2 | число.fft.fft2 | 2D быстрое преобразование Фурье |
левое смещение | число.fft.fftshift | смещение нулевой составляющей в центр спектра |
переключение | число. | обратная передача |
ефф2 | число.fft.fifft2 | обратное 2d фт |
интерп2 | scipy.interpolate.RectBivariateSpline или scipy.interpolate.interp2 | Интерполяция для двумерных данных с координатной сеткой в формате meshgrid |
имшоупара | skimage.measure.structural_similarity | Сравнить различия между 2 изображениями |
imregconfig | Создает конфигурации для выполнения регистрации изображений на основе интенсивности | |
имрегистр | Регистрация изображений на основе интенсивности | |
имрегтформ | skimage.feature.register_translation или skimage.transform.estimate_transform | Оценка геометрического преобразования для выравнивания двух изображений |
деформация | skimage. | Применение геометрического преобразования к изображению |
imref2d | Привязка двухмерного изображения к координатам xy | |
корр2 | scipy.signal.correlate2d | 2d коэффициент корреляции |
оптимсет | Создание опций оптимизации редактирования для перехода к fminbnd, fminsearch, fzero или lsqnonneg | |
лсккривфит | scipy.optimize.curve_fit | Решение нелинейных задач подбора кривой |
Фастика | sklearn.decomposition.FastICA | быстрый алгоритм с фиксированной точкой для анализа независимых компонентов и поиска проекций |
kmeans | sklearn.cluster.Kmeans | kmeans кластеризация |
fsolve | scipy. | Поиск корня. В Scipy нет метода изгиба доверенной области, который работает точно так же, как fsolve в Matlab. Метод «Андерсона» во многих случаях воспроизводит результаты. Для других проблем, возможно, потребуется изучить другие методы. |
Основные чертежи
Функция Matlab | Эквивалент Python | Описание |
|---|---|---|
цифра | matplotlib.pyplot.figure | Создать новый объект фигуры |
clf | рис.clf | четкая фигура; не требуется в Python, так как каждая фигура будет уникальным объектом |
участок | фигура.подзаголовки или фигура.добавить_подзаговор | 1-й создает набор подграфиков на рисунке, 2-й создает один подграфик и добавляет его к рисунку |
участок | фигура. | Добавить линейный график к текущему рисунку |
Название | объект.название | Название участка; лучше определить при создании объекта, если возможно |
xметка | метка оси.x | Метка для оси X графика |
ярлык | axes.ylabel | Метка для оси Y графика |
изображенияc | pyplot.imshow или pyplot.matshow | Масштабирование данных изображения до полного диапазона цветовой карты и отображения |
ось | оси.ось | Свойства оси |
серфинг | axes3d.plot_surface или axes3d.plot_trisurf | Постройте трехмерную поверхность, необходимо использовать mpl_toolkits.mplot3d и Axes3d; который вы используете, зависит от формата данных |
затемнение | Устанавливается при создании графика в качестве аргумента | |
вид | axes3d. | Изменение угла обзора для 3D-графика |
карта цветов | plot.colormap | Установить цветовую карту; лучше сделать это при создании графика, если возможно |
цветная полоса | фигура.add_colorbar(оси) | Добавить цветную полосу к выбранным осям |
Создание инновационной модели интеллектуальной обработки финансовой информации предприятия на основе технологии Интернета вещей
- Список журналов
- Компьютер Intel Neurosci
- v.2022; 2022
- PMC
89 Компьютер Intel Neurosci.
 2022 г.; 2022: 7153260.
2022 г.; 2022: 7153260.Опубликовано онлайн 2022 мая 6. DOI: 10.1155/2022/7153260
Авторская информация Примечания к заявлению об обращении к информации и получению лицензии
- . Технология обеспечивает условия для систематизации финансовых данных предприятия и интеллектуализации управления финансами. В этом исследовании алгоритм метода опорных векторов (SVM) и генетический алгоритм (GA) объединены для получения инновационной модели интеллектуальной обработки финансовой информации предприятия на основе алгоритма оптимизации GA-SVM. В качестве влияющих факторов выбраны девять факторов, влияющих на обработку финансовой информации предприятия с 2010 по 2018 год, и в соответствии с идеей и методом моделирования данных с помощью MATLAB проводится имитационный эксперимент модели интеллектуальной обработки финансовой информации предприятия. Результаты показывают, что средняя приспособленность GA-SVM близка к наилучшей приспособленности, что указывает на то, что каждый индивидуум в популяции близок к оптимальному решению.
 RMSE GA-SVM составляет 0,35%, а полученная среднеквадратическая ошибка больше этого значения, что показывает, что эффект применения GA-SVM значительно лучше, чем у SVM с использованием метода перекрестной проверки, и он более подходит для точного предсказания. В то же время это также отражает надежность оптимизации параметров SVM с помощью GA. Алгоритм может быть лучше применен при интеллектуальной обработке финансовой информации предприятия и может предоставить предприятиям определенную справку в управлении финансами на основе Интернета вещей.
RMSE GA-SVM составляет 0,35%, а полученная среднеквадратическая ошибка больше этого значения, что показывает, что эффект применения GA-SVM значительно лучше, чем у SVM с использованием метода перекрестной проверки, и он более подходит для точного предсказания. В то же время это также отражает надежность оптимизации параметров SVM с помощью GA. Алгоритм может быть лучше применен при интеллектуальной обработке финансовой информации предприятия и может предоставить предприятиям определенную справку в управлении финансами на основе Интернета вещей.С тенденцией развития рыночной экономики Китая в полном разгаре технология Интернета вещей быстро развивалась и стала одной из ключевых технологий, применяемых различными предприятиями [1]. Развитие предприятий неотделимо от передовых технологий, особенно финансового управления предприятиями [2]. В эпоху Интернета вещей управление финансовой информацией предприятия стало ключом к развитию предприятия. Предприятия должны обновить традиционные концепции и в полной мере использовать передовые технологии Интернета вещей, чтобы эффективно завершить управление финансами [3].
 Интернет вещей – это система, основанная на сети Интернет, реализующая связь между вещами и реализующая мониторинг в любое время посредством современных технологий радиочастотной идентификации, инфракрасной индукции и беспроводной связи [4]. Технология Интернета вещей широко используется в основных отраслях промышленности, что позволяет эффективно контролировать финансовую информацию предприятия, осуществлять весь процесс управления финансовой информацией предприятия, делать обработку финансовой информации предприятия более эффективной, своевременной и надежной и, наконец, повышать эффективность финансовой деятельности предприятия. управление [5].
Интернет вещей – это система, основанная на сети Интернет, реализующая связь между вещами и реализующая мониторинг в любое время посредством современных технологий радиочастотной идентификации, инфракрасной индукции и беспроводной связи [4]. Технология Интернета вещей широко используется в основных отраслях промышленности, что позволяет эффективно контролировать финансовую информацию предприятия, осуществлять весь процесс управления финансовой информацией предприятия, делать обработку финансовой информации предприятия более эффективной, своевременной и надежной и, наконец, повышать эффективность финансовой деятельности предприятия. управление [5].Для инновационной модели интеллектуальной обработки финансовой информации предприятия это исследование объединяет связанные технологии генетического алгоритма (ГА) и машины опорных векторов (SVM), вводит генетический алгоритм GA в параметры SVM машины опорных векторов и строит инновационная модель интеллектуальной обработки финансовой информации предприятия в соответствии с идеей и методом моделирования данных.
 Наконец, MATLAB используется для имитационного эксперимента.
Наконец, MATLAB используется для имитационного эксперимента.В этом исследовании в основном используется сочетание методов исследования и экспериментов по моделированию, в качестве направления используется идея системной инженерии и теории сложности, извлекаются данные, влияющие на обработку финансовой информации предприятия с 2010 по 2018 год, применяется метод нормализованных данных и строится инновационная модель интеллектуальной обработки финансовой информации предприятия в соответствии с идеей и методом моделирования данных. Цель состоит в том, чтобы повысить скорость работы модели и обеспечить точность системы.
Содержание исследования в этой статье в основном состоит из четырех частей. Вторая часть — это исследовательский статус генетического алгоритма (GA-SVM) для оптимизации машины опорных векторов в стране и за рубежом. Третья часть в основном знакомит с алгоритмом исследования. В первом разделе описывается разработка алгоритма GA-SVM, а во втором разделе обсуждается реализация алгоритма GA-SVM.
 Четвертая часть предварительно обрабатывает влияющие факторы, эмпирически анализирует алгоритм GA-SVM и сравнивает результаты с традиционным алгоритмом SVM. Результаты показывают, что эффект применения GA-SVM значительно лучше, чем у SVM с использованием метода перекрестной проверки, и он больше подходит для точного прогнозирования.
Четвертая часть предварительно обрабатывает влияющие факторы, эмпирически анализирует алгоритм GA-SVM и сравнивает результаты с традиционным алгоритмом SVM. Результаты показывают, что эффект применения GA-SVM значительно лучше, чем у SVM с использованием метода перекрестной проверки, и он больше подходит для точного прогнозирования.В последние годы технология Интернета вещей все чаще применяется для обработки финансовой информации предприятий, и исследователи в стране и за рубежом также проводят углубленные исследования этой технологии. Лутра и др. использовали серый реляционный анализ (GRA) и процесс аналитической иерархии (AHP) для анализа проблем, с которыми сталкивается внедрение и распространение Интернета вещей в Индии, чтобы помочь специалистам-практикам и лицам, принимающим решения, устранить препятствия на пути успешного внедрения и продвижения Интернет вещей [6]. Ван Р и другие разработали новый режим финансирования залога запасов в соответствии со специальными функциями технологии Интернета вещей и бизнес-процессом режима финансирования запасов.
 Результаты показывают, что разрыв в стоимости потерь от риска, вызванный различными событиями потерь в Интернете вещей в сочетании с режимом залогового финансирования финансовых запасов в цепочке поставок, велик, среди которых потери от внешнего мошенничества являются самыми большими. Наконец, установлено, что режим финансирования цепочки поставок, основанный на технологии Интернета вещей, эффективно снижает операционный риск [7]. Лопес Б.С. и другие проанализировали влияние искусственного интеллекта и технологий Интернета вещей на изменение системы управления бизнес-процессами. Интернет вещей позволяет доставлять информацию, улучшать контроль и автоматизацию, а также предоставляет возможности для оптимизации операционных расходов вашей компании [8]. Вэнь С. и другие используют технологию распределенной поисковой системы для настройки поискового робота для получения необходимых данных о банковских картах и транзакциях из разнородных данных из множества источников в финансовой индустрии Интернета вещей, разработки соответствующего искрового параллельного алгоритма для предварительной обработки данных и установления инвертированная таблица и вторичный индексный документ, который обеспечивает источник данных для платформы анализа больших данных.
Результаты показывают, что разрыв в стоимости потерь от риска, вызванный различными событиями потерь в Интернете вещей в сочетании с режимом залогового финансирования финансовых запасов в цепочке поставок, велик, среди которых потери от внешнего мошенничества являются самыми большими. Наконец, установлено, что режим финансирования цепочки поставок, основанный на технологии Интернета вещей, эффективно снижает операционный риск [7]. Лопес Б.С. и другие проанализировали влияние искусственного интеллекта и технологий Интернета вещей на изменение системы управления бизнес-процессами. Интернет вещей позволяет доставлять информацию, улучшать контроль и автоматизацию, а также предоставляет возможности для оптимизации операционных расходов вашей компании [8]. Вэнь С. и другие используют технологию распределенной поисковой системы для настройки поискового робота для получения необходимых данных о банковских картах и транзакциях из разнородных данных из множества источников в финансовой индустрии Интернета вещей, разработки соответствующего искрового параллельного алгоритма для предварительной обработки данных и установления инвертированная таблица и вторичный индексный документ, который обеспечивает источник данных для платформы анализа больших данных. Результаты показывают, что этот метод может значительно снизить вероятность того, что банки формулируют первую и вторую нормы ошибок, и эффективно снизить потери, вызванные ненадлежащим кредитным регулированием, при оценке кредитного риска финансового финансирования Интернета вещей [9].].
Результаты показывают, что этот метод может значительно снизить вероятность того, что банки формулируют первую и вторую нормы ошибок, и эффективно снизить потери, вызванные ненадлежащим кредитным регулированием, при оценке кредитного риска финансового финансирования Интернета вещей [9].].Генетический алгоритм опорных векторов (GA-SVM) был высоко оценен многими специалистами. Дайма А. и соавт. предложил систему поиска изображений на основе контента, основанную на алгоритме машины генетических опорных векторов (GA-SVM). Пользователи извлекают изображения, отправляя изображения запросов, извлекают визуальные признаки для получения изображений запросов и реализуют их в среде MATLAB для проверки превосходства производительности [10]. Ян и др. использовал GA-SVM для анализа неисправности системы мониторинга качества воды по растворенному кислороду. Результаты показывают, что оптимизированные значения штрафного коэффициента и параметров после итерации составляют 2,1649.и 5,3312 соответственно, а GA-SVM имеет хорошую точность [11].
 Инь и др. предложил метод обнаружения символов на основе GA-SVM для решения этой проблемы с разных сторон и преобразовал процесс декодирования символов в процесс численных вычислений. Результаты показывают, что по сравнению с традиционным методом вычисления пороговых символов декодирования, GA-SVM улучшает показатели частоты ошибок по битам (BER) CBWCS, упрощает процесс обнаружения символов и устраняет процесс идентификации канала и вычисления порога [12]. Жая и др. предложил гибридный метод, сочетающий генетический алгоритм (ГА) и машину опорных векторов (SVM). Генетический алгоритм используется для определения ключевых факторов, а машина опорных векторов используется для вычисления функции пригодности генетического алгоритма. Используя данные опроса China Aviation Industry Corporation (AVIC), экспериментально анализируется эффективность предлагаемого гибридного метода. Экспериментальные результаты показывают, что метод гибридной генетической машины опорных векторов, предложенный в этой статье, может быть использован в качестве альтернативы исследованию ключевых факторов [13].
Инь и др. предложил метод обнаружения символов на основе GA-SVM для решения этой проблемы с разных сторон и преобразовал процесс декодирования символов в процесс численных вычислений. Результаты показывают, что по сравнению с традиционным методом вычисления пороговых символов декодирования, GA-SVM улучшает показатели частоты ошибок по битам (BER) CBWCS, упрощает процесс обнаружения символов и устраняет процесс идентификации канала и вычисления порога [12]. Жая и др. предложил гибридный метод, сочетающий генетический алгоритм (ГА) и машину опорных векторов (SVM). Генетический алгоритм используется для определения ключевых факторов, а машина опорных векторов используется для вычисления функции пригодности генетического алгоритма. Используя данные опроса China Aviation Industry Corporation (AVIC), экспериментально анализируется эффективность предлагаемого гибридного метода. Экспериментальные результаты показывают, что метод гибридной генетической машины опорных векторов, предложенный в этой статье, может быть использован в качестве альтернативы исследованию ключевых факторов [13]. Благодаря исследованиям отечественных и зарубежных ученых по генетическому алгоритму и машине опорных векторов можно увидеть, что метод исследования сочетания генетического алгоритма и машины опорных переменных является основным направлением исследований в будущем. Поэтому в этом исследовании в основном обсуждается создание инновационной модели интеллектуальной обработки финансовой информации предприятия, используется алгоритм модели GA-SVM для оценки обработки финансовой информации предприятия и используется программное обеспечение MATLAB для моделирования и проверки алгоритма.
Благодаря исследованиям отечественных и зарубежных ученых по генетическому алгоритму и машине опорных векторов можно увидеть, что метод исследования сочетания генетического алгоритма и машины опорных переменных является основным направлением исследований в будущем. Поэтому в этом исследовании в основном обсуждается создание инновационной модели интеллектуальной обработки финансовой информации предприятия, используется алгоритм модели GA-SVM для оценки обработки финансовой информации предприятия и используется программное обеспечение MATLAB для моделирования и проверки алгоритма.3.1. Алгоритм оптимизации GA-SVM
Метод опорных векторов может найти наилучшую схему между способностью к обучению и сложностью в соответствии с моделью с ограниченной выборочной информацией, чтобы получить минимальный доверительный диапазон и эмпирический риск и получить лучшую способность к обобщению и статистический закон, когда статистические выборки являются неполными [14]. Машина опорных векторов (SVM) представляет собой модель классификации с двумя классами.
 Его базовой моделью является линейный классификатор с наибольшим интервалом, определенным в пространстве признаков. Машина опорных векторов также включает метод ядра, что делает его по существу нелинейным классификатором. Стратегия обучения машины опорных векторов — это максимизация интервала, которую можно формализовать как задачу решения выпуклого квадратичного программирования, что также эквивалентно минимизации регуляризованной функции потерь шарнира. Алгоритм обучения машины опорных векторов представляет собой алгоритм оптимизации для решения выпукло-квадратичного программирования. Обучение SVM необходимо для обучения оптимизации квадратичного программирования. Если объем данных большой, это вызовет очень большой объем вычислений SVM [15]. Если обучающие данные просто сократить, это не только окажет большое влияние на точность и обучающий эффект классификатора, но и повлияет на выбор параметров. Выбор индекса функции ядра и штрафной функции также влияет на точность прогнозирования и классификацию модели.
Его базовой моделью является линейный классификатор с наибольшим интервалом, определенным в пространстве признаков. Машина опорных векторов также включает метод ядра, что делает его по существу нелинейным классификатором. Стратегия обучения машины опорных векторов — это максимизация интервала, которую можно формализовать как задачу решения выпуклого квадратичного программирования, что также эквивалентно минимизации регуляризованной функции потерь шарнира. Алгоритм обучения машины опорных векторов представляет собой алгоритм оптимизации для решения выпукло-квадратичного программирования. Обучение SVM необходимо для обучения оптимизации квадратичного программирования. Если объем данных большой, это вызовет очень большой объем вычислений SVM [15]. Если обучающие данные просто сократить, это не только окажет большое влияние на точность и обучающий эффект классификатора, но и повлияет на выбор параметров. Выбор индекса функции ядра и штрафной функции также влияет на точность прогнозирования и классификацию модели. Как правило, показатели параметров постоянно подбираются искусственно и путем повторных экспериментов, но человеческий опыт обуславливает определенную субъективность эксперимента и большие временные затраты. Традиционный процесс проектирования машины опорных векторов [16] показан на рис.
Как правило, показатели параметров постоянно подбираются искусственно и путем повторных экспериментов, но человеческий опыт обуславливает определенную субъективность эксперимента и большие временные затраты. Традиционный процесс проектирования машины опорных векторов [16] показан на рис.Открыть в отдельном окне
Традиционный процесс проектирования SVM.
В этом исследовании выбор параметров и функция ядра SVM оптимизированы с помощью GA. Потенциальный параллелизм и глобальная оптимальность ГА недоступны в традиционных алгоритмах. Этапы реализации ГА показаны в [17]. В этом исследовании используются преимущества ГА, предлагается улучшенный метод алгоритма SVM и устанавливается новая модель алгоритма GA-SVM. Функция ядра GA-SVM принимает радиальную базисную функцию, параметры модели глобально оптимизируются и генетически кодируются методом кодирования вещественных чисел, а окончательные параметры модели GA-SVM принимают найденный оптимальный параметр ядра и штрафной параметр C [18].
 ].
].Открыть в отдельном окне
Этапы реализации генетического алгоритма.
Конкретные идеи построения модели GA-SVM заключаются в следующем: во-первых, закодировать параметры модели SVM. Процесс нахождения оптимального параметра ядра и штрафного параметра C представляет собой задачу непрерывной оптимизации сложных параметров. В этом исследовании используется метод кодирования действительных чисел, чтобы избежать повторного кодирования и декодирования в процессе работы. Он также может решить проблему ограниченной длины двоичного кодирования, чтобы повысить точность и производительность генетического алгоритма. Если параметр штрафа C достаточно велик, это приведет к «переобучению» алгоритма модели. В настоящее время модель SVM относит все обучающие выборки к категориям с большим размером выборки.
SVM, основанный на принципе минимизации структурного риска и статистической теории, выбран в качестве нового метода машинного обучения для эффективной регрессии и классификации нелинейных и линейных данных.
 Алгоритм SVM включает в себя линейные и нелинейные алгоритмы. Когда данные в наборе данных являются линейно разделимыми или приблизительно линейно разделимыми, он максимизирует линейный классификатор через жесткий интервал или мягкий интервал. Когда набор данных имеет нелинейную структуру, нелинейный SVM изучается путем максимизации мягкого интервала и использования метода ядра. Например, для двумерной плоскости
Алгоритм SVM включает в себя линейные и нелинейные алгоритмы. Когда данные в наборе данных являются линейно разделимыми или приблизительно линейно разделимыми, он максимизирует линейный классификатор через жесткий интервал или мягкий интервал. Когда набор данных имеет нелинейную структуру, нелинейный SVM изучается путем максимизации мягкого интервала и использования метода ядра. Например, для двумерной плоскостиT=x1,y1,x2,y2,…,xN,yN.
(1)
в (1), x I ∈ R N , Y I {+1, 1, I {+1, 1, I . 1,2,…, N and x i represent eigenvectors, y i is the class mark of x i , and ( x я , у i ) представляет точки выборки. Таким образом, он распространяется на n-мерную гиперплоскость, где B представляет собой скаляр, а W представляет вектор весов.
 Подстраивая скаляр и весовой вектор, SVM ищет гиперплоскость на стороне наибольшего ребра следующим образом:
Подстраивая скаляр и весовой вектор, SVM ищет гиперплоскость на стороне наибольшего ребра следующим образом:h2:W·X+b≥1,yi=+1,h3:W·X+b≤1, уи=-1.
(2)
Выборка, удовлетворяющая приведенной выше формуле на гиперплоскости H 1 или H 2 , является опорным вектором. Необходимо максимизировать расстояние и поддерживать гиперплоскость, чтобы ее можно было оптимизировать дважды, следующим образом:
minW,b12W2,
(3)
yiW·xi+b≥1, i=1,2,…,N.
(4)
Оптимальные решения W ∗ и b ∗ можно получить из (4)
W*·x+b*=0.
(5)
Разделить решающую функцию следующим образом:
fx=signW*·x+b*.
(6)
Если набор данных решения не является линейно разделимым, возможны два случая: линейная аппроксимация отделимости и нелинейная. Когда данные линейно разделимы, релаксационная переменная ξ i необходимо ввести, чтобы он достиг «сепарабельного» состояния, и представление квадратичной оптимизации выглядит следующим образом: )
yiW·xi+b≥1−ξ, i=1,2,…,N.

(8)
Среди них ξ i ≥ 0, i =1,2,…, N . Получено оптимальное решение. Гиперплоскость разделения и решающая функция разделения показаны в следующих уравнениях:
W*·x+b*=0,
(9)
fx=signW*·x+b*.
(10)
Для нелинейного набора данных его необходимо преобразовать в линейную задачу в многомерном пространстве признаков для решения. Функция ядра используется для замены экземпляра внутреннего продукта в нелинейной классификации, функция ядра K ( x , z ) = ϕ ( x ) · ϕ ( z ). Соответственно, полученный нелинейный SVM показан в следующем уравнении:
fx=sign∑i=1Nαi∗yiKx,xi+b∗.
(11)
Радиальная базисная функция ядра (RBF) показана в следующем уравнении:
Kx,x′=expx−x′22σ2.
(12)
В (12), K ( x , x ′) представляет собой радиальную базисную функцию ядра, x и x ′ представляют собой две тренировочные точки, а
03 σ функция ядра, то есть ширина в направлении функции, среднеквадратичное отклонение функции Гаусса и σ значение прямо пропорционально ширине функции.
Благодаря экспериментальной проверке функции ядра RBF видно, что значение σ имеет тесную корреляцию с ‖ x − x ‖ 2 . Если минимальное расстояние между обучающими выборками намного больше, чем σ , σ ⟶0. Если минимальное расстояние между обучающими выборками много меньше значения σ , то σ ⟶ ∞ . Это исследование определяет пространство поиска для значения σ со значением интервала [min(‖ x − x j ‖ 2 ∙ × 10 −2 ), max − x j ‖ 2 × 10 −2 )] и дополнительно сокращает диапазон поиска в этом интервале для более точного определения диапазона.
Штрафной коэффициент C в основном используется для ограничения фактора Лагранжа A. Когда значение штрафного коэффициента C достигает определенного значения, ограничение на и не удастся.
1 C1 i =1,2,……, l что если C ≥ 0, сначала выбрать достаточно большое C, а затем применить SVM-модель этого значения для решения a i ( i =1,2,……, n ), где n представляет количество обучающих выборок. В это время, если C 1 = MAX ( A I ) и C 1 < C , затем верхняя граница C . 1 , что указывает на то, что a i все еще ограничено значением C. В настоящее время следует выбрать большую емкость C для поддержки обучения модели SVM до тех пор, пока C не станет намного больше С 1 . В это время сложность SVM в подпространстве данных станет наибольшей, а ее обобщающая способность и эмпирический риск не изменятся. В данном исследовании предлагается новый метод поиска c-интервала. Видно из 0 ≤ a l , a i ∗ 3 0 1
В это время сложность SVM в подпространстве данных станет наибольшей, а ее обобщающая способность и эмпирический риск не изменятся. В данном исследовании предлагается новый метод поиска c-интервала. Видно из 0 ≤ a l , a i ∗ 3 0 1 Следовательно, интервал поиска C может быть подтвержден, и интервал равен (0, C 1 ).
Следовательно, интервал поиска C может быть подтвержден, и интервал равен (0, C 1 ).Затем разрабатывается фитнес-функция генетического алгоритма. В соответствии с экспериментальным объектом данного исследования предлагается следующая функция генетической пригодности:
Fσ,C=1Error.
(13)
В (13) ошибка представляет собой частоту ошибочной классификации обучающей выборки модели SVM. Чем выше ошибка классификации модели SVM на тестовой выборке, тем меньше параметр приспособленности хромосом. Далее идет генетическая операция, которая включает в себя операцию отбора, операцию скрещивания и операцию мутации. Сортировка особей в популяции операции отбора осуществляется по приспособленности, а затем по выбранной вероятности P i особей рассчитывается, как показано в следующем уравнении:
Pi=r×1−ri−1.
(14)
В (14) r представляет вероятность выбора первого индивидуума, а i представляет порядковый номер сортировки индивидуума.
 Вероятность отбора не имеет ничего общего со значением пригодности, а только с ранжированием особей в популяции. Перекрестная операция — это перекрестный режим работы, который в основном применяет режим линейной комбинации. Если х 1 и х 2 хромосом перекрещиваются, это выражается в следующей формуле:
Вероятность отбора не имеет ничего общего со значением пригодности, а только с ранжированием особей в популяции. Перекрестная операция — это перекрестный режим работы, который в основном применяет режим линейной комбинации. Если х 1 и х 2 хромосом перекрещиваются, это выражается в следующей формуле:x1=ax1+1−ax2,x2=ax2+1−ax2.
(15)
В (15) a представляет собой случайное число и [0,1]. Операция мутации заключается в случайном выборе одного из битов мутации j в мутировавшей хромосоме и преобразовании бита мутации j в случайное число U ( a i , 9 ).0030 б и ). a i представляет собой верхний предел бита вариации, а b i представляет нижний предел бита вариации, как показано в следующем уравнении:
xj=Uai,bj, i=j,xi,i≠j.
(16)
3.
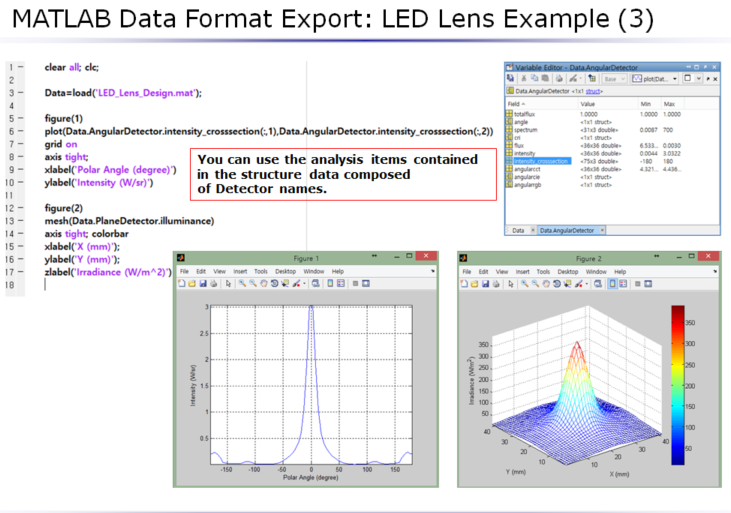 2. Построение модели интеллектуальной обработки финансовой информации предприятия
2. Построение модели интеллектуальной обработки финансовой информации предприятияПосле разработки алгоритма GA-SVM в этом исследовании предлагается модель интеллектуальной обработки финансовой информации предприятия на основе алгоритма GA-SVM. Конкретные этапы реализации показаны на . Во-первых, регрессионная модель опорного вектора предназначена для определения значений параметров ядра и штрафных коэффициентов. Определяется индивидуальная длина ГА, m хромосом генерируются случайным образом путем кодирования действительных чисел, и формируется начальная популяция P ( t ) генетического алгоритма. В соответствии с последовательностью генов выберите стратегию отбора для объединения факторов. Программа SVM используется для подсчета особей в исходной популяции, определения прогнозируемого значения, проверки его соответствия выборке, расчета коэффициента ошибочной классификации тестовой выборки и, наконец, вычисления индивидуальной приспособленности хромосом F ( σ , C ).
 Повторите операцию м раз, чтобы вычислить значение пригодности каждого индивидуума в исходной популяции. Для получения популяции следующего поколения реализованы операторы скрещивания, мутации и отбора. Выбирается оптимальный индивидуум и выполняется поиск по сетке рядом с оптимальным индивидуумом для поиска оптимальной комбинации параметров. В соответствии с режимом критерия того, заканчивается ли итерация или нет, если нет, продолжайте итерацию и возвращайтесь к пересчету индивидуального значения пригодности хромосомы до тех пор, пока не будут выполнены условия. Тогда решение инверсии параметров представляет собой оптимальную особь в популяции. Оптимальная комбинация параметров, то есть параметры ядра и параметры штрафа, вводится в машинную программу регрессии опорных векторов, и создается модель для прогнозирования и анализа данных в выборке.
Повторите операцию м раз, чтобы вычислить значение пригодности каждого индивидуума в исходной популяции. Для получения популяции следующего поколения реализованы операторы скрещивания, мутации и отбора. Выбирается оптимальный индивидуум и выполняется поиск по сетке рядом с оптимальным индивидуумом для поиска оптимальной комбинации параметров. В соответствии с режимом критерия того, заканчивается ли итерация или нет, если нет, продолжайте итерацию и возвращайтесь к пересчету индивидуального значения пригодности хромосомы до тех пор, пока не будут выполнены условия. Тогда решение инверсии параметров представляет собой оптимальную особь в популяции. Оптимальная комбинация параметров, то есть параметры ядра и параметры штрафа, вводится в машинную программу регрессии опорных векторов, и создается модель для прогнозирования и анализа данных в выборке.Открыть в отдельном окне
Этапы реализации алгоритма GA-SVM.
Производительность SVM определяется рациональностью выбора параметров.
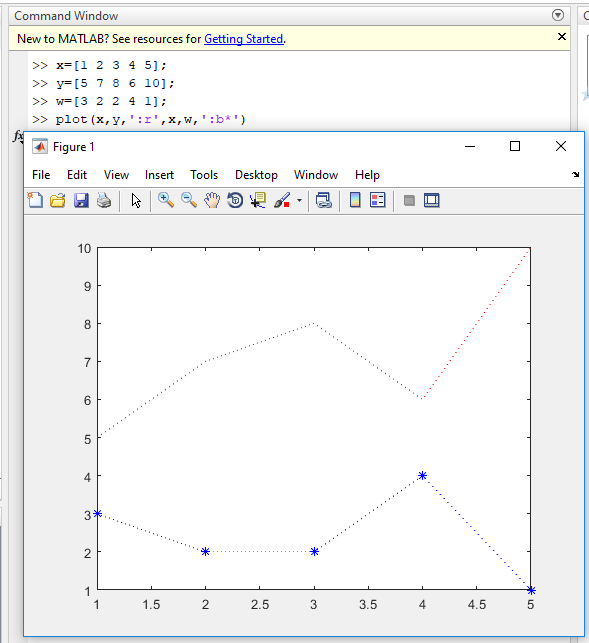 В настоящее время традиционный метод подбора параметров имеет большие недостатки, и человеческий фактор приведет к неточности выбора параметров. Использование алгоритма кроссовера для выбора параметров часто сопровождается огромным объемом вычислений, а его алгоритм громоздок. Генетический алгоритм обладает сильным поиском и надежной производительностью и играет большую роль в глобальной оптимизации, что делает адаптивность генетического алгоритма очень сильной и широко используется в различных областях.
В настоящее время традиционный метод подбора параметров имеет большие недостатки, и человеческий фактор приведет к неточности выбора параметров. Использование алгоритма кроссовера для выбора параметров часто сопровождается огромным объемом вычислений, а его алгоритм громоздок. Генетический алгоритм обладает сильным поиском и надежной производительностью и играет большую роль в глобальной оптимизации, что делает адаптивность генетического алгоритма очень сильной и широко используется в различных областях.После определения базовых данных необходимо предварительно обработать данные, чтобы повысить точность модели и уменьшить ошибку прогноза, ускорить обучение сети и избежать переобучения. Нормализация данных — основная работа предварительной обработки. Эта операция предназначена для управления данными в определенном диапазоне с использованием определенной функции или метода, например преобразования всех данных в 0 ~ 1. Эта операция в основном предназначена для устранения различий между обучающими данными.
 В MATLAB существуют следующие методы нормализации: во-первых, postmnmx, premnmx, mapminmax, tramnmx и scaleforsvm; второй, трастд, постстд, предстд. Третий — программирование в MATLAB. Существует два алгоритма программирования, а именно метод максимума и минимума и метод средней дисперсии [19].]. Для измерения ошибки в данных в этом исследовании используется метод анализа среднеквадратичной ошибки и относительной ошибки, где RMSE представляет собой среднеквадратичную ошибку, а RE представляет собой относительную ошибку [20].
В MATLAB существуют следующие методы нормализации: во-первых, postmnmx, premnmx, mapminmax, tramnmx и scaleforsvm; второй, трастд, постстд, предстд. Третий — программирование в MATLAB. Существует два алгоритма программирования, а именно метод максимума и минимума и метод средней дисперсии [19].]. Для измерения ошибки в данных в этом исследовании используется метод анализа среднеквадратичной ошибки и относительной ошибки, где RMSE представляет собой среднеквадратичную ошибку, а RE представляет собой относительную ошибку [20].Путем предварительной обработки влияющих факторов алгоритм GA-SVM эмпирически анализируется и сравнивается с традиционным алгоритмом SVM. Результаты показывают, что эффект применения GA-SVM явно лучше, чем SVM с перекрестной проверкой, и он больше подходит для точного прогнозирования.
В данном исследовании используются финансовые данные 132 предприятий региона за 2019 г., исключая 30 аномальных данных, а количество эффективных выборок данных составляет 102.
 В качестве влияющих факторов выбраны следующие факторы, в том числе скорость оборачиваемости дебиторской задолженности, коэффициент общей задолженности, рентабельность чистых активов, коэффициент быстрой ликвидности, коэффициент текущей ликвидности, коэффициент затрат на прибыль, коэффициент оборотного капитала и совокупных активов, коэффициент прибыли основного бизнеса, общий коэффициент оборачиваемости активов и т. д., а также данные, влияющие на обработку финансовой информации предприятия с 2010 по 2018 г. [21, 22].
В качестве влияющих факторов выбраны следующие факторы, в том числе скорость оборачиваемости дебиторской задолженности, коэффициент общей задолженности, рентабельность чистых активов, коэффициент быстрой ликвидности, коэффициент текущей ликвидности, коэффициент затрат на прибыль, коэффициент оборотного капитала и совокупных активов, коэффициент прибыли основного бизнеса, общий коэффициент оборачиваемости активов и т. д., а также данные, влияющие на обработку финансовой информации предприятия с 2010 по 2018 г. [21, 22].Сначала анализируются результаты и ошибки нейросетевого прогноза BP. Видно, что ошибки составляют менее 10 %, что соответствует требованиям прогнозирования, как показано в [23, 24]. При анализе модели прогнозирования SVM первые восемь факторов влияния используются в качестве входного вектора, а девятый фактор влияния используется в качестве выходного вектора для создания модели SVM, а тест моделирования выполняется в MATLAB [9,25]. ]. Радиальная функция ядра Гаусса выбрана в качестве функции ядра, предсказанной в этом исследовании, а параметры SVM выбраны путем перекрестной проверки.
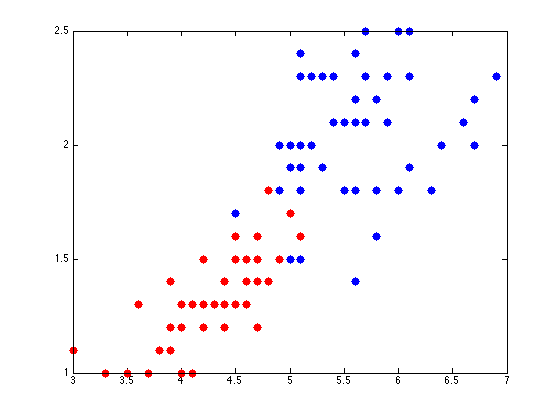 Параметры σ =0,02, г =0,105, C = 256 Результаты прогноза показаны на .
Параметры σ =0,02, г =0,105, C = 256 Результаты прогноза показаны на .Открыть в отдельном окне
Результаты прогнозирования и анализ ошибок нейросети BP и SVM. (а) Нейронная сеть BP. (b) Машина опорных векторов.
показывает результаты предсказания SVM. Далее этот метод будет сравниваться с моделью прогнозирования GA-SVM. Для выбора прогнозных данных модели GA-SVM в качестве обучающих выборок выбраны данные с 2010 по 2014 год, а данные с 2015 по 2019 год.выбираются в качестве тестовых образцов для получения пригодности параметров оптимизации ГА, как показано на рис.
Открыть в отдельном окне
Фитнес-кривая оптимизации генетического алгоритма.
Данные за период с 2010 по 2014 год выбраны в качестве обучающей выборки, а данные за период с 2015 по 2019 год выбраны в качестве тестовой выборки для получения соответствия параметров оптимизации ГА, как показано на рис. Как видно из , средняя приспособленность очень близка к наилучшей приспособленности, что свидетельствует о хороших результатах.
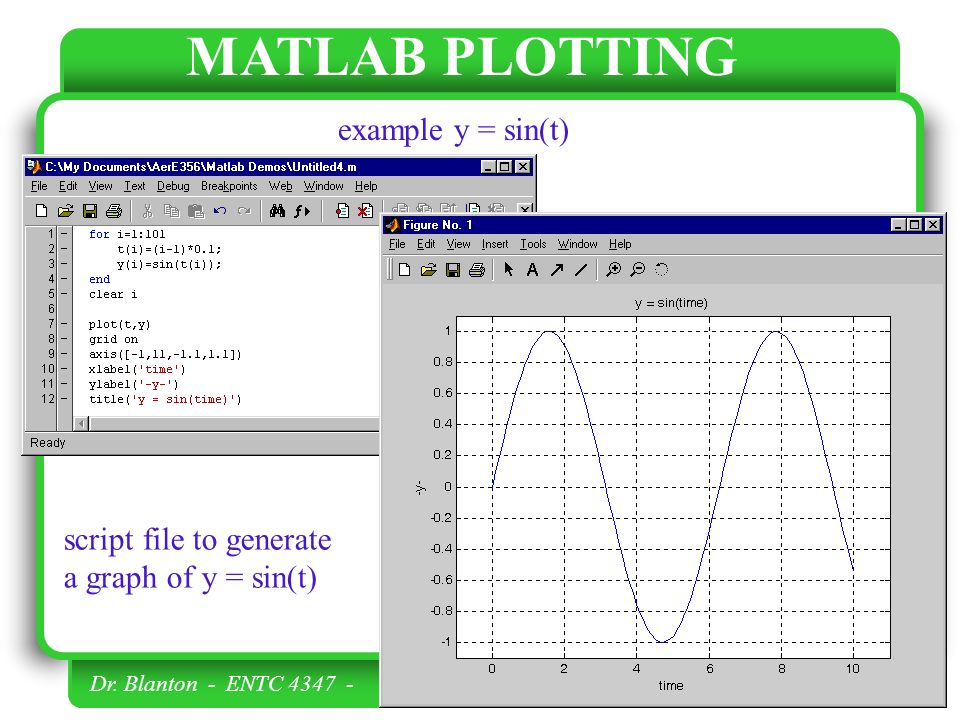 Сравнивая результаты прогнозирования модели SVM и модели GA-SVM, значение подгонки выбирает данные с 2010 по 2014 год, а значение прогноза выбирает данные с 2015 по 2019 год.. Результаты показывают, что ошибки прогнозирования модели SVM и модели GA-SVM очень малы, менее 1%, что соответствует требованиям прогнозирования. Результаты прогнозирования модели SVM и модели GA-SVM лучше, чем у нейронной сети BP.
Сравнивая результаты прогнозирования модели SVM и модели GA-SVM, значение подгонки выбирает данные с 2010 по 2014 год, а значение прогноза выбирает данные с 2015 по 2019 год.. Результаты показывают, что ошибки прогнозирования модели SVM и модели GA-SVM очень малы, менее 1%, что соответствует требованиям прогнозирования. Результаты прогнозирования модели SVM и модели GA-SVM лучше, чем у нейронной сети BP.СКО GA-SVM составляет 0,35, а среднеквадратическая ошибка больше этого значения, что показывает, что эффект применения GA-SVM явно лучше, чем у SVM с методом перекрестной проверки, и он более подходит для предсказания точности. В то же время это также свидетельствует о том, что генетический алгоритм надежен для оптимизации параметров машины опорных векторов. Сравнение ошибок между моделью SVM и моделью GA-SVM показано на рис.
Открыть в отдельном окне
Сравнение влияния ошибок между GA-SVM и SVM.
Для дальнейшей проверки эффективности модели в программу вводится фактор fat_ 1, FAT_ 2 и FAT_ 3, вычисляется функциональная связь между финансовой безопасностью и различными факторами, определяется оптимальное количество узлов, дерево структурная диаграмма, диаграмма эволюции вариации и диаграмма изменения вероятности кроссовера, а также диаграмма оптимизации подгонки отдельного алгоритма получаются в процессе расчета для моделирования и эмпирического анализа.
 После моделирования программы получается динамическая тенденция изменения уровней, узлов и согласия дерева структуры, как показано на рис.
После моделирования программы получается динамическая тенденция изменения уровней, узлов и согласия дерева структуры, как показано на рис.Открыть в отдельном окне
Связь степени подгонки с узлами и слоями дерева.
Как видно из , с развитием генетической алгебры качество подгонки будет продолжать улучшаться. Однако через 34 поколения эффективность эволюции стала оставаться неизменной, и фиксировалась текущая оптимальная особь, включающая количество узлов индивидуальной структуры и глубину дерева. FAT всех выборок данных_ 1, FAT_ 2, FAT_ Значение 3 вводится в оптимальный структурный расчет для обеспечения соблюдения финансовых стандартов предприятия и подгонки теоретических значений, как показано на рис.
Открыть в отдельном окне
Таблица эффектов подгонки обучающего образца.
Как видно из , модель оценки, предложенная в данном исследовании, отражает взлеты и падения в процессе обработки финансовых данных. Используя модель для проверки выборочных данных, точность модели составляет 87,51%.
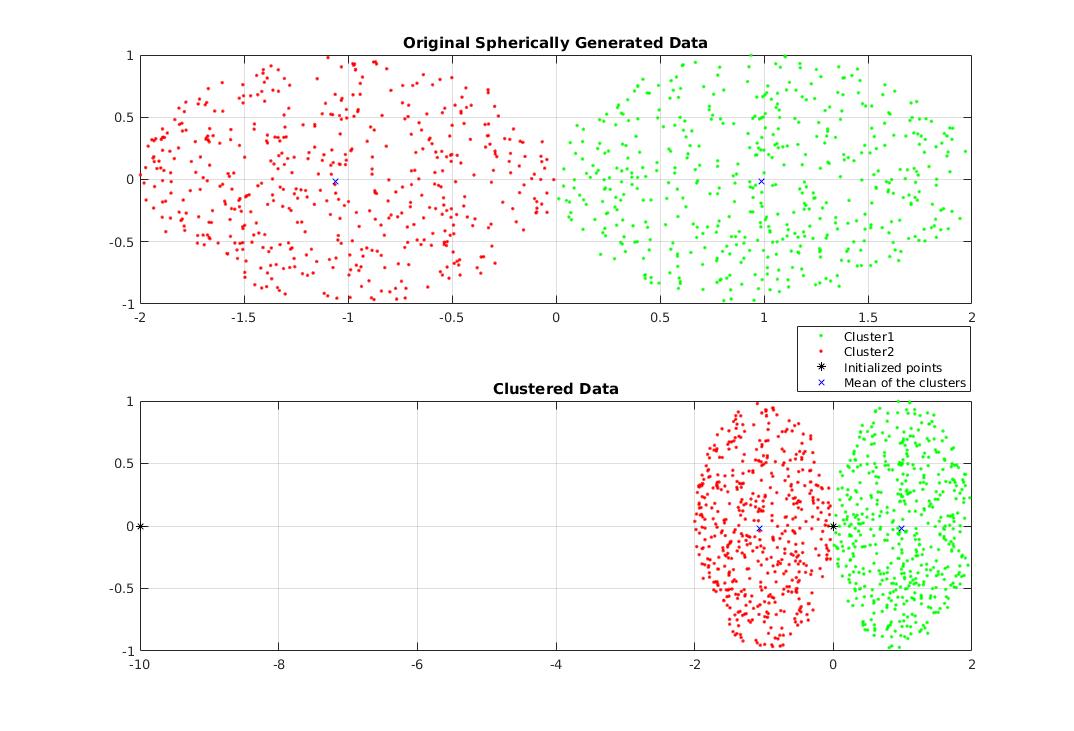 Экспериментальные результаты хорошо согласуются с финансовыми данными.
Экспериментальные результаты хорошо согласуются с финансовыми данными.Путем сравнения результатов прогнозирования модели SVM и модели GA-SVM значение подбора выбирает данные с 2010 по 2014 год, а значение прогноза выбирает данные с 2015 по 2019 год.. Результаты показывают, что ошибки прогнозирования модели SVM и модели GA-SVM очень малы, менее 1%, что соответствует требованиям прогнозирования. Результаты прогнозирования модели GA-BP и модели SVM-BP лучше, чем у модели SVM-BP. Это показывает, что алгоритм имеет широкое практическое применение на предприятиях.
В этой статье модель алгоритма оптимизации GA-SVM на основе Интернета вещей создана для управления финансовой информацией предприятия, а эксперимент по моделированию проводится на платформе MATLAB. Результаты показывают, что радиальная функция ядра Гаусса выбрана в качестве функции ядра, предсказанной в этой статье, а параметры SVM выбраны путем перекрестной проверки. Параметры = 0,02, g =0,105, C = 256.
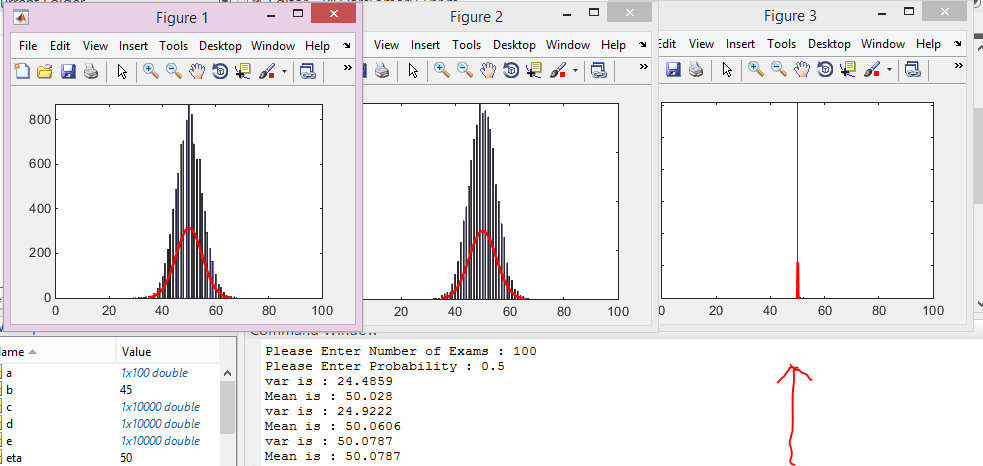 Для отбора прогностических данных модели GA-SVM в качестве обучающей выборки выбраны данные с 2010 по 2019 год, а в качестве тестовой — данные с 2011 по 2015 год. Значение средней приспособленности GA-SVM близко к наилучшей приспособленности, что указывает на то, что каждый индивидуум в популяции близок к оптимальному решению, что отражает хороший эффект алгоритма. RMSE GA-SVM составляет 364,062, а полученная среднеквадратическая ошибка больше этого значения, что показывает, что эффект применения GA-SVM значительно лучше, чем у SVM с использованием метода перекрестной проверки, и он больше подходит для точное предсказание. В то же время это также отражает надежность оптимизации параметров SVM с помощью GA. Это исследование также имеет некоторые недостатки. Из-за множества факторов, влияющих на управление финансами предприятия, в данном исследовании выбраны только некоторые из них. В дальнейших исследованиях мы уделим больше внимания выбору влияющих факторов модели.
Для отбора прогностических данных модели GA-SVM в качестве обучающей выборки выбраны данные с 2010 по 2019 год, а в качестве тестовой — данные с 2011 по 2015 год. Значение средней приспособленности GA-SVM близко к наилучшей приспособленности, что указывает на то, что каждый индивидуум в популяции близок к оптимальному решению, что отражает хороший эффект алгоритма. RMSE GA-SVM составляет 364,062, а полученная среднеквадратическая ошибка больше этого значения, что показывает, что эффект применения GA-SVM значительно лучше, чем у SVM с использованием метода перекрестной проверки, и он больше подходит для точное предсказание. В то же время это также отражает надежность оптимизации параметров SVM с помощью GA. Это исследование также имеет некоторые недостатки. Из-за множества факторов, влияющих на управление финансами предприятия, в данном исследовании выбраны только некоторые из них. В дальнейших исследованиях мы уделим больше внимания выбору влияющих факторов модели.Данные, использованные для подтверждения результатов этого исследования, можно получить у соответствующего автора по запросу.

Автор заявляет об отсутствии конфликта интересов.
1. Тан С.-П., Хуан Т.С.-К., Ван С.-Т. Влияние внедрения Интернета вещей на производительность компании. Телематика и информатика . 2018;35(7):2038–2053. doi: 10.1016/j.tele.2018.07.007. [CrossRef] [Google Scholar]
2. Цао Ю. Исследование применения технологий Интернета вещей в финансовом лизинге интеллектуальных производственных предприятий. Международный журнал передовых производственных технологий . 2020;107(4):1061–1070. doi: 10.1007/s00170-019-04370-1. [CrossRef] [Google Scholar]
3. Компелла С., Кам С. Специальный выпуск о возрасте информации. Журнал связи и сетей . 2019;21(3):201–203. doi: 10.1109/jcn.2019.100012. [CrossRef] [Google Scholar]
4. Ким М., Джо В., Ким Дж., Шон Т. Визуализация для Интернета вещей: случаи энергосистемы и финансовой сети. Мультимедийные инструменты и приложения . 2018;78(3):3241–3265. doi: 10.1007/s11042-018-6730-x.
 [CrossRef] [Google Scholar]
[CrossRef] [Google Scholar]5. Zhang X., Wang Y. Исследование модели финансирования счетов с предоплатой на основе встроенной системы и Интернета вещей. Микропроцессоры и микросистемы . 2021;82(VI) doi: 10.1016/j.micpro.2021.103935.103935 [CrossRef] [Google Scholar]
6. Лутра С., Гарг Д., Мангла С. К., Сингх Бервал Ю. П. Анализ проблем Интернета вещей (IoT). ) принятие и распространение: индийский контекст. Информатика Procedia . 2018; 125:733–739. doi: 10.1016/j.procs.2017.12.094. [CrossRef] [Google Scholar]
7. Ван Р., Ю С., Ван Дж. Построение режима управления финансовыми рисками цепочки поставок на основе Интернета вещей. Доступ IEEE . 2019;7(99):323–332. doi: 10.1109/access.2019.2932475. [CrossRef] [Google Scholar]
8. Лопес Б. С., Алькайде А. В. Блокчейн, искусственный интеллект, интернет вещей для улучшения управления, финансового управления и контроля над кризисом: тематическое исследование COVID-19. Социально-экономические проблемы .
 2020;4(2):78–89. doi: 10.21272/sec.4(2).78-89.2020. [CrossRef] [Google Scholar]
2020;4(2):78–89. doi: 10.21272/sec.4(2).78-89.2020. [CrossRef] [Google Scholar]9. Вэнь С., Ян Дж., Ган Л., Пан Ю. Интернет вещей на основе больших данных для оценки кредитоспособности и раннего предупреждения в финансах. Компьютерные системы будущего поколения . 2021; 124(4) doi: 10.1016/j.future.2021.06.003. [CrossRef] [Google Scholar]
10. Дайма А., Шривастава А., Саксена А. К., Манория М. Метод опорных векторов (линейное ядро) и интерактивный метод поиска изображений контента на основе генетического алгоритма. Конспект лекций по сетям и системам . 2018;34:151–159. doi: 10.1007/978-981-10-8198-9_16. [CrossRef] [Google Scholar]
11. Ян П., Ли З., Ли З., Ю Ю., Ши Дж., Сун М. Исследования по диагностике неисправностей датчика растворенного кислорода на основе GA-SVM. Математические биологические науки и инженерия . 2021;18(1):386–399. doi: 10.3934/mbe.2021021. [PubMed] [CrossRef] [Google Scholar]
12. Инь Х.-П., Жэнь Х.
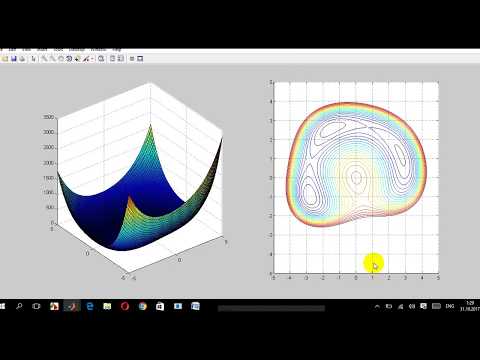 -П. Прямое декодирование символов с использованием GA-SVM в хаотической системе беспроводной связи основной полосы частот. Журнал Института Франклина . 2021;358(12):6348–6367. doi: 10.1016/j.jfranklin.2021.06.012. [CrossRef] [Google Scholar]
-П. Прямое декодирование символов с использованием GA-SVM в хаотической системе беспроводной связи основной полосы частот. Журнал Института Франклина . 2021;358(12):6348–6367. doi: 10.1016/j.jfranklin.2021.06.012. [CrossRef] [Google Scholar]13. Чжай Л., Цинь Дж., Ю Л. Гибридизация методов опорных векторов в генетический алгоритм для исследования ключевых факторов при оценке основных компетенций авиационных производственных предприятий. Филомат . 2016;30(15):4191–4198. doi: 10.2298/fil1615191z. [CrossRef] [Google Scholar]
14. Gholipour M., Toroghi Haghighat A., Meybodi M.R. Предотвращение перегрузок Hop-by-Hop в беспроводных сенсорных сетях на основе генетической машины опорных векторов. Нейрокомпьютинг . 2016; 223:63–76. [Google Scholar]
15. Zhu F., Wei J. Алгоритм локализации в беспроводных сенсорных сетях на основе усовершенствованной машины опорных векторов. Журнал наноэлектроники и оптоэлектроники . 2017;12(5):452–459.
 doi: 10.1166/jno.2017.2049. [CrossRef] [Google Scholar]
doi: 10.1166/jno.2017.2049. [CrossRef] [Google Scholar]16. Сюй Дж., Тан В., Ли Т. Прогнозирование обледенения лопастей вентилятора с помощью оптимизации роя частиц и алгоритма опорных векторов. Компьютеры и электротехника . 2020;87(1) doi: 10.1016/j.compeleceng.2020.106751.106751 [CrossRef] [Google Scholar]
17. Паниккат П., Саркар П. К., Кришнасвами С. Метод решения некорректной обратной задачи нейтрона развертывание спектра с использованием генетического алгоритма поиска в итерациях Монте-Карло. Европейский физический журнал плюс . 2021;136(4):1–18. doi: 10.1140/epjp/s13360-021-01437-5. [CrossRef] [Google Scholar]
18. Кумар П. Б., Пархи Д. Р. Интеллектуальная гибридизация метода регрессии с генетическим алгоритмом для навигации гуманоидов в сложных средах. Роботика . 2020;38(4):565–581. doi: 10.1017/s026357471
69. [CrossRef] [Google Scholar]
19. Gedong J., Ping X., Jun Y., Xuesong M., Lei M. Моделирование тепловой ошибки с грязной и маленькой обучающей выборкой для моторизованного шпинделя прецизионного расточной машины.
 Международный журнал передовых производственных технологий . 2017;93(1-4):571–586. [Google Scholar]
Международный журнал передовых производственных технологий . 2017;93(1-4):571–586. [Google Scholar]20. Jing M., Long C., Ke-Li C., Be-sheng H. Качественный и количественный анализ фальсификации янтаря с помощью спектроскопии в ближней инфракрасной области на основе метода опорных векторов. Журнал китайских медицинских материалов . 2017;40(1):32–37. [Google Scholar]
21. Клеофас-Санчес Л., Санчес Дж. С., Гарсия В., Вальдовинос Р. М. Ассоциативное обучение в несбалансированной среде: эмпирическое исследование. Экспертные системы с приложениями . 2016;54:387–397. doi: 10.1016/j.eswa.2015.10.001. [CrossRef] [Google Scholar]
22. Prenat G., Jabeur K., Vanhauwaert P., Di Pendi G. Сверхбыстрая и высоконадежная SOT-MRAM: от замены кэша до нормально выключенных вычислений. Транзакции IEEE в многомасштабных вычислительных системах . 2017;2(1):49–60. [Google Scholar]
23. Зеленков Ю., Федорова Е., Чекризов Д. Метод двухступенчатой классификации на основе генетического алгоритма для прогнозирования банкротства.
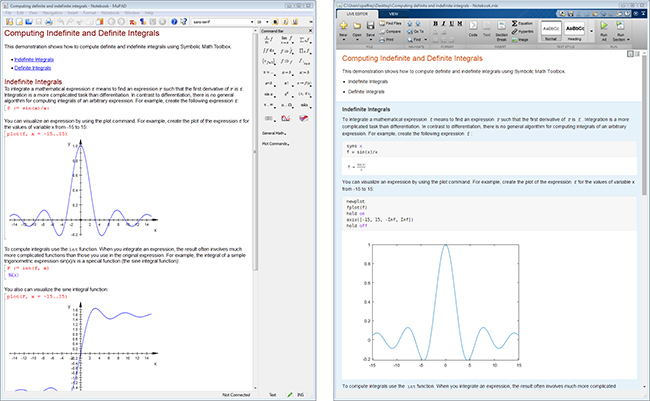
- . Технология обеспечивает условия для систематизации финансовых данных предприятия и интеллектуализации управления финансами. В этом исследовании алгоритм метода опорных векторов (SVM) и генетический алгоритм (GA) объединены для получения инновационной модели интеллектуальной обработки финансовой информации предприятия на основе алгоритма оптимизации GA-SVM. В качестве влияющих факторов выбраны девять факторов, влияющих на обработку финансовой информации предприятия с 2010 по 2018 год, и в соответствии с идеей и методом моделирования данных с помощью MATLAB проводится имитационный эксперимент модели интеллектуальной обработки финансовой информации предприятия. Результаты показывают, что средняя приспособленность GA-SVM близка к наилучшей приспособленности, что указывает на то, что каждый индивидуум в популяции близок к оптимальному решению.
 io.imread
io.imread sqrt или numpy.sqrt
sqrt или numpy.sqrt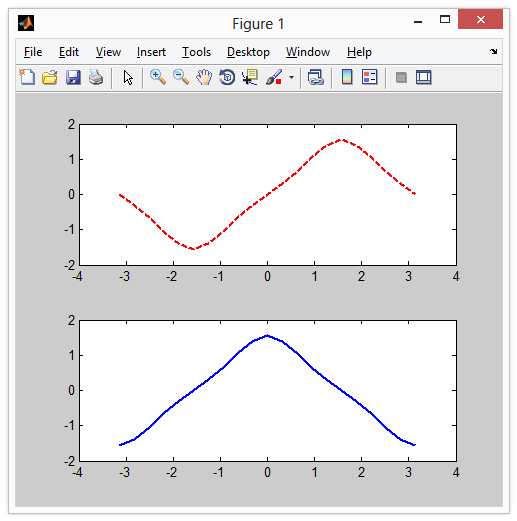 где
где fft.ifftshift
fft.ifftshift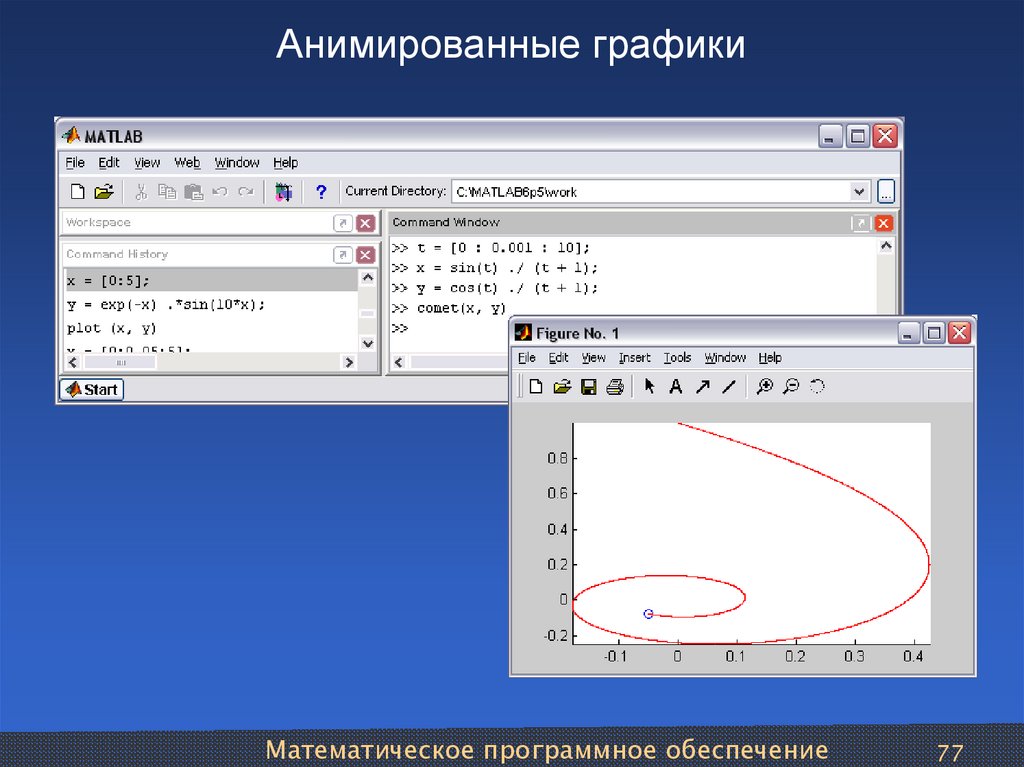 transform.warp
transform.warp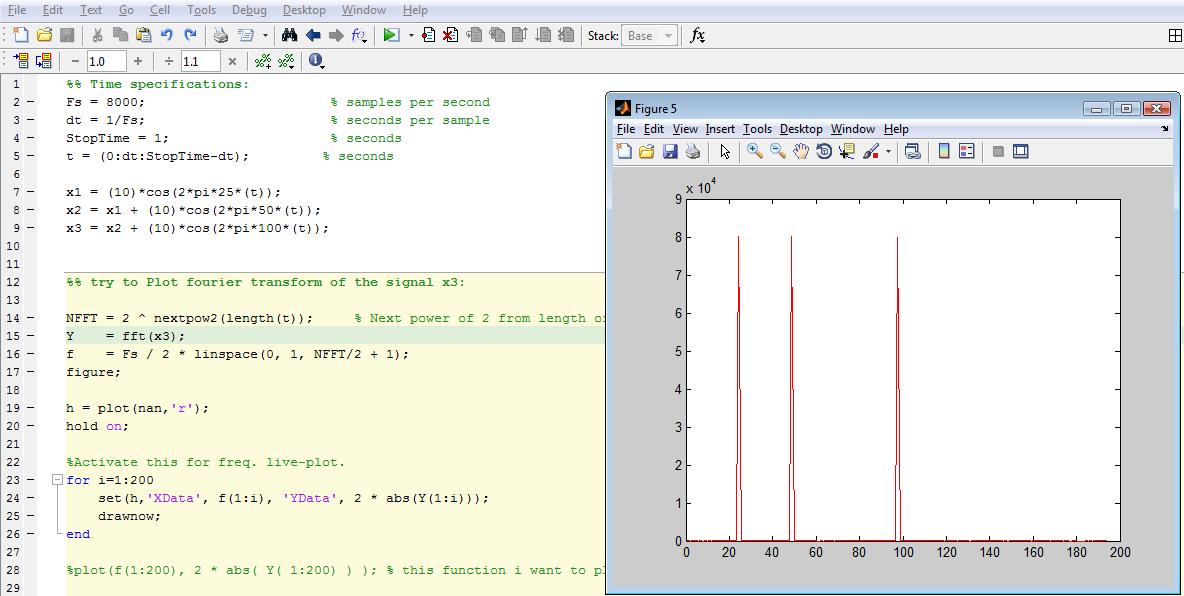 optimize.root(func, x0, method=’anderson’)
optimize.root(func, x0, method=’anderson’) график или осей.график
график или осей.график view_init
view_init