Метод наименьших квадратов matlab: Аппроксимация в Matlab — CodeTown.ru

1.9. Реализация метода наименьших квадратов в пакете matlab

Метод наименьших квадратов реализован в подавляющем большинстве современных математических и прикладных вычислительных пакетов программ. Например, в пакете математического программного обеспечения MATLAB при решении задачи идентификации методом МНК для линейной по параметрам полиномиальной модели используется функция polyfit:

Эта функция отыскивает коэффициенты полинома порядка m, доставляющие минимум критерия метода МНК, когда исходная выборка задана векторами u и х. Результирующий вектор p размерности m + 1 содержит оптимальные коэффициенты полинома в порядке убывания степеней его членов:

.

Функция polyval служит для пересчета полиномиальной модели с заданными коэффициентами:

Вектор x составлен из значений полиномиальной модели МНК с коэффициентами α, соответствующих вектору значений независимой переменной

u.

Покажем применение метода МНК для задачи восстановления зависимости по выборке . Выборочные значения функции содержат нормально распределенную случайную ошибку со стандартным отклонением 0.1. Оператор поиска коэффициентов полиномиальной модели имеет вид

>> α = polyfit(1:10,(1:10) + normrnd(0,0.1,1,10),1)

α =

0.9931 0.0612

>>

Полином с найденными коэффициентами в выборочных точках рассчитывается следующим образом:

>> polyval(α,1:10)

ans =

Columns 1 through 10

1.0542 2.0473 3.0404 4.0335 5.0266 6.0196 7.0127 8.0058 8.9989 9.9919

>>

Приведенный пример наглядно иллюстрирует простоту программной реализации метода наименьших квадратов в пакете MATLAB.

Метод стохастической аппроксимации был разработан в 1951 г. для определения единственного корня уравнения в случае, когда значение этой функции измеряется с некоторой случайной ошибкой:

.

(1.66)

Алгоритмы, реализующие метод, получили название алгоритмов Робинса–Монро. Затем подобные алгоритмы были использованы для отыскания экстремума унимодальной функции , также включающей случайный шум согласно уравнению (1.66). Алгоритмы такого типа называют алгоритмами Кифера–Волфовитца. А. Дворецким была сформулирована и доказана теорема, которая дала наиболее слабые условия сходимости для любых типов алгоритмов стохастической аппроксимации. Пользуясь результатами этой теоремы, можно построить различные алгоритмы идентификации параметров модели.

Получим простейший алгоритм стохастической аппроксимации на примере решения задачи по отысканию оценки истинного значения величины X на основе ее n измерений: x_i, i = 1, 2, …, n. Пусть , где – некоторая случайная помеха с нулевым средним и конечной дисперсией: , . Из математической статистики известно, что наилучшей оценкой X будет среднее арифметическое ее n измерений:

.

(1.67)

Согласно закону больших чисел Колмогорова можно записать

.

(1.68)

Получим рекуррентную формулу для вычисления по среднему значению выборки после n измерений и поступившему новому измерению . По формуле (1.67) для n + 1 измерений имеем:

.

(1. 69)

Подставляя выражение (1.67) в (1.69), получим:

.

(1.70)

Последнее равенство преобразуем к виду:

.

(1.71)

Это рекуррентное выражение и есть алгоритм стохастической аппроксимации для определения оценки параметра x по его зашумленным наблюдениям. При этом новая оценка равна сумме старой оценки и корректирующего члена с некоторым весовым коэффициентом . С ростом n эти весовые коэффициенты образуют убывающую последовательность

,

(1. 72)

которая обладает еще двумя важнейшими асимптотическими свойствами:

,	(1.73)
.	(1.74)

Эти свойства можно объяснить следующим образом. Вес корректирующего члена, т. е. его влияние на оценку, будет уменьшаться в соответствии с условием (1.72), поскольку закон больших чисел гарантирует, что при этой процедуре оценка стремится к истинному значению параметра с увеличением числа итераций. Однако коррекция должна производиться вне зависимости от того, сколько итераций уже было сделано с начала процедуры оценивания, что и отражается условием (1.73), в котором сумма корректирующей последовательности расходится, значит эффект от корректирующего члена никогда не будет равен нулю. Свойство (1.74) является необходимым для сходимости общей процедуры стохастической аппроксимации, поскольку при большом числе итераций оно влечет за собой уменьшение влияния индивидуальных ошибок.

Кроме последовательности вида этим условиям удовлетворяют и многие другие последовательности, например , где q > 1/2. Таким образом, любой рекуррентный алгоритм вида (1.71) или в более общем случае вида , где последовательность весовых коэффициентов при корректирующем члене удовлетворяет условиям (1.72)–(1.74), согласно теореме Дворецкого является алгоритмом стохастической аппроксимации (типа Робинса–Монро) и обеспечивает сходимость оценок к истинным параметрам по вероятности.

В качестве примера рассмотрим алгоритм стохастической аппроксимации для оценивания параметров линейной регрессии. При этом последовательность весовых коэффициентов, удовлетворяющих условиям (1.72)–(1.74), выберем в виде ряда , где . Корректирующий член или невязку в общей рекуррентной формуле можно определить, используя скалярный квадратичный показатель качества идентификации:

,

(1. 75)

откуда невязку можно получить, продифференцировав этот показатель по :

.

(1.76)

Окончательно имеем следующий рекуррентный алгоритм стохастической аппроксимации для оценивания параметров линейной регрессии:

.

(1.77)

Важным достоинством алгоритмов стохастической аппроксимации является то, что для их применения не требуется никаких специальных знаний о вероятностном распределении или каких-либо статистических характеристиках ошибки измерения. Исключение составляет информация о том, что ошибки измерения образуют последовательность независимых случайных величин с нулевым средним (для несмещенности оценок) и ограниченной дисперсией.

Заметим, что на практике обеспечение этих условий обычно не вызывает затруднений. Кроме того, алгоритмы стохастической аппроксимации очень просты при вычислениях. Однако при этом они не обладают какими-либо оптимальными свойствами и непригодны для отыскания глобального экстремума многоэкстремальных функций, а также очень медленно сходятся к истинному значению параметра. Это связано с тем, что основное внимание в этих алгоритмах согласно теореме Дворецкого уделяется самому факту сходимости, а не скорости этой сходимости.

Эта проблема была разрешена во многих алгоритмах, ускоряющих процедуру сходимости по сравнению с обычным алгоритмом стохастической аппроксимации. Одним из наиболее удачных и эффективных является алгоритм, в котором коэффициенты остаются постоянными до тех пор, пока корректирующий член сохраняет свой знак, и только после изменения знака этого члена берется следующий элемент последовательности. Дж. Саридисом было доказано, что такая схема обеспечивает сходимость по вероятности и значительно ускоряет скорость сходимости.

НОУ ИНТУИТ | Лекция | Статистическая обработка данных в системе MATLAB

< Лекция 8 || Лекция 3: 123

Аннотация: Система MATLAB – одна из старейших, тщательно проработанных и проверенных временем систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Это нашло отражение в названии системы MATrix Laboratory – матричная лаборатория. Применение матриц, как основных объектов системы, способствует уменьшению числа циклов, которые очень распространены при выполнении матричных вычислений на обычных языках программирования высокого уровня, и облегчению реализации параллельных вычислений .

Ключевые слова: расширяемость, Си, Toolbox, интеграция, моделирование, math, операции, инвертирование, вычисление, вывод, алгебраические, предметной области, язык программирования, входной, запись, представление, операторы, вектор, аргумент, матрица, пробел, пользователь, выражение, enter, координаты, график, метода наименьших квадратов, значение, функция, полином, интерполяция, интервал, property, editor, tools, аппроксимация

intuit.ru/2010/edi»>Важным достоинством системы являются ее открытость и расширяемость. Большинство команд и функций системы реализованы в виде m-файлов текстового формата (с расширением m.)и файлов на языке Си, причем все файлы доступны для модификации. Пользователю дана возможность создать не только отдельные файлы, но и библиотеки файлов для реализации специфических задач. Такие файлы можно готовить как в простом и удобном редакторе m-файлов системы MATLAB, так и в любом другом текстовом редакторе. Более того, такие файлы можно перенести с помощью буфера в командную строку MATLAB и тут же исполнить.

Легкость модификации системы и возможность ее адаптации к решению специфических задач науки и техники привели к созданию десятков пакетов прикладных программ (Toolbox), намного расширивших сферы применения системы.

Новые свойства системе MATLAB придала ее интеграция с программной системой Simulink, созданной для моделирования блочно-заданных динамических систем и устройств. Базируясь на принципах визуально-ориентированного программирования, Simulink, позволяет выполнять моделирование сложных устройств с высокой степенью достоверности и прекрасными средствами представления результатов. Помимо естественной интеграции с пакетами расширения Symbolic Math и Simulink, MATLAB интегрируется с десятками мощных пакетов расширения.

Система MATLAB выполняет сложные и трудоемкие операции над векторами и матрицами даже в режиме прямых вычислений, без какого либо программирования. Ею можно пользоваться как калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями, могут использоваться такие сложные операции, как инвертирование матрицы, вычисление ее собственных значений и принадлежащих им векторов, решение систем линейных уравнений, вывод графиков двухмерных и трехмерных функций и многое другое.

В базовый набор слов системы входят спецзнаки, знаки арифметических и логических операций, арифметические, алгебраические, тригонометрические и некоторые специальные функции. Словом MATLAB предоставляет пользователям обширный набор готовых средств.

Дополнительный уровень развития системы образуют ее пакеты расширения. Они позволяют быстро ориентировать систему на решение задач в той или иной предметной области: в специальных разделах математики, физики, астрономии, проектировании и.т.д. Благодаря этому MATLAB обеспечивает высочайший уровень адаптации к решению задач конечного пользователя [3,4].

Система MATLAB может решать множество задач без программирования в командном режиме. Однако система изначально создавалась одновременно и как мощный, ориентированный на технические вычисления, язык программирования высокого уровня.

Система MATLAB имеет входной язык. Запись программ в системе традиционна и потому привычна для большинства пользователей компьютеров. К тому же система дает возможность редактировать программы с помощью любого, привычного для пользователя текстового редактора. Имеет она и собственный редактор с отладчиком.

Система MATLAB состоит из многих тысяч файлов, находящихся в множестве папок. Полезно иметь представление о содержании основных папок, поскольку это позволяет быстро оценить возможности системы – например, узнать какие операторы функции или графические команды входят в систему.

Система MATLAB создана таким образом, что любые вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. Можно почти мгновенно задать и вывести графики различных функций – от простой синусоиды до сложной трехмерной фигуры.

В большинстве математических систем вычисление или , где – вектор, сопровождалось бы выдачей ошибки, поскольку функции и должны иметь аргумент в виде скалярной величины. Однако MATLAB – матричная система, а вектор является разновидностью матрицы с размером или . Поэтому в нашем случае результат вычисления будет вектором того же размера, что и аргумент , но элементы возвращаемого вектора будут синусами или экспонентами от элементов вектора .

Матрица задается в виде векторов, представляющих ее строки и заключенных в квадратные скобки. Для разделения элементов векторов используются пробел или запятая, а для отделения одного вектора от другого – точка с запятой.

Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал вопрос – получил ответ». Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его в командной строке и завершает ввод нажатием клавиши ENTER.

Дальше >>

< Лекция 8 || Лекция 3: 123

Регрессия наименьших квадратов в программировании MATLAB

Программное обеспечение MATLAB Curve Fitting Toolbox™ использует метод наименьших квадратов при подборе данных. Подгонка требует параметрической модели, которая связывает данные ответа с данными предиктора с одним или несколькими коэффициентами. Результатом процесса подгонки является аппроксимация коэффициентов модели.

Чтобы получить оценки коэффициентов, метод наименьших квадратов уменьшает суммарный квадрат невязок. Остаток для i-й точки данных ri описывается как разница между наблюдаемым значением отклика yi и подобранным значением отклика ŷi и отображается как ошибка, связанная с данными.

Суммарный квадрат невязок определяется как

, где n — количество точек данных, содержащихся в подборе, а S — оценка ошибки суммы квадратов. Поддерживаемые типы аппроксимации методом наименьших квадратов включают:

•   Линейный метод наименьших квадратов
•   Взвешенный линейный метод наименьших квадратов
•   Надежный метод наименьших квадратов
•   Нелинейный метод наименьших квадратов 2

Линейный метод наименьших квадратов

Программное обеспечение MATLAB Curve Fitting Toolbox использует линейный метод наименьших квадратов, чтобы подогнать линейную модель к данным. Линейная модель описывается как уравнение, линейное относительно коэффициентов. Например, многочлены линейны, а гауссианы нелинейны. Чтобы показать линейный процесс подбора методом наименьших квадратов, предположим, что у пользователя есть n точек данных, которые можно смоделировать с помощью полинома первой степени.

Взвешенный метод наименьших квадратов

Обычно предполагается, что данные ответов имеют одинаковое качество и, следовательно, имеют постоянную дисперсию. Если это предположение нарушается. Взвешенная регрессия наименьших квадратов уменьшает оценку ошибки.

Надежный метод наименьших квадратов

Обычно предполагается, что ошибки отклика подчиняются нормальному распределению и что экстремальные значения встречаются редко. Тем не менее, экстремальные значения, называемые выбросами, все же встречаются.

Нелинейный метод наименьших квадратов

Программное обеспечение MATLAB Curve Fitting Toolbox использует нелинейный метод наименьших квадратов, чтобы подогнать нелинейную модель к данным. Нелинейная модель описывается как уравнение, нелинейное по коэффициентам, или как комбинация линейного и нелинейного по коэффициентам. Например, гауссианы, отношения полиномов и степенные функции нелинейны.

Matlabsolutions.com обеспечивает гарантированное удовлетворение обязательством выполнить работу в срок. В сочетании с нашей тщательной рабочей этикой и обширным опытом работы в домене мы являемся идеальным партнером для всех ваших потребностей в домашней работе / задании. Мы обязуемся обеспечить поддержку 24 часа в сутки, 7 дней в неделю, чтобы развеять все ваши академические сомнения. Мы состоит из более чем 300 уважаемых Matlab и других экспертов, которые были отобраны после обширных исследований и проверки качества.

Matlabsolutions.com уделяет пристальное внимание каждому заказу Matlab с методическим подходом к решению. Наша сеть не ограничивается США, Великобританией и Австралией, а распространяется на такие страны, как Сингапур, Канада и ОАЭ. Наши справочные услуги по заданиям Matlab включают в себя задания по обработке изображений, задания по электротехнике, помощь в выполнении домашних заданий по Matlab, помощь в исследовательской работе по Matlab, помощь по Matlab Simulink. Выполняйте свою работу по лучшей цене в отрасли.

Наши услуги

Справка по назначению Matlab

Справка по моделированию Matlab

Справка по проектам Matlab

Справка по домашнему заданию Matlab

Исследовательская справка по Matlab

R Помощь по программированию

Справка по программированию на Python

Справка по назначению CNN

[PDF] Метод наименьших квадратов для моделирования: набор инструментов Matlab

• Идентификатор корпуса: 13293070

  title={Всеобщий подход наименьших квадратов к моделированию: набор инструментов Matlab},
  автор = {Дагмар Бедн {\ 'a} rov {\ 'a}},
  год = {2010}
} 

• D. Bednárová
• Опубликовано в 2010 г.
• Математика

В этой статье рассматривается математический метод, известный как метод полных наименьших квадратов или ортогональная регрессия или метод ошибок в переменных. Указанный метод может быть использован для моделирования статических, а также динамических процессов. Широкая область других приложений находится в обработке сигналов и изображений. Мы также представляем набор инструментов Matlab, который может решать основные проблемы, связанные с полным методом наименьших квадратов в моделировании. Приведено также несколько иллюстративных примеров. В этой статье мы представляем общее наименьшее… 

actamont.tuke.sk

Наборы инструментов и программ для идентификации, моделирования, симуляции и управления системами дробного порядка

Доступные в настоящее время программные наборы и программные комплексы для решения задач идентификации, моделирования, симуляции и управления системами дробного порядка.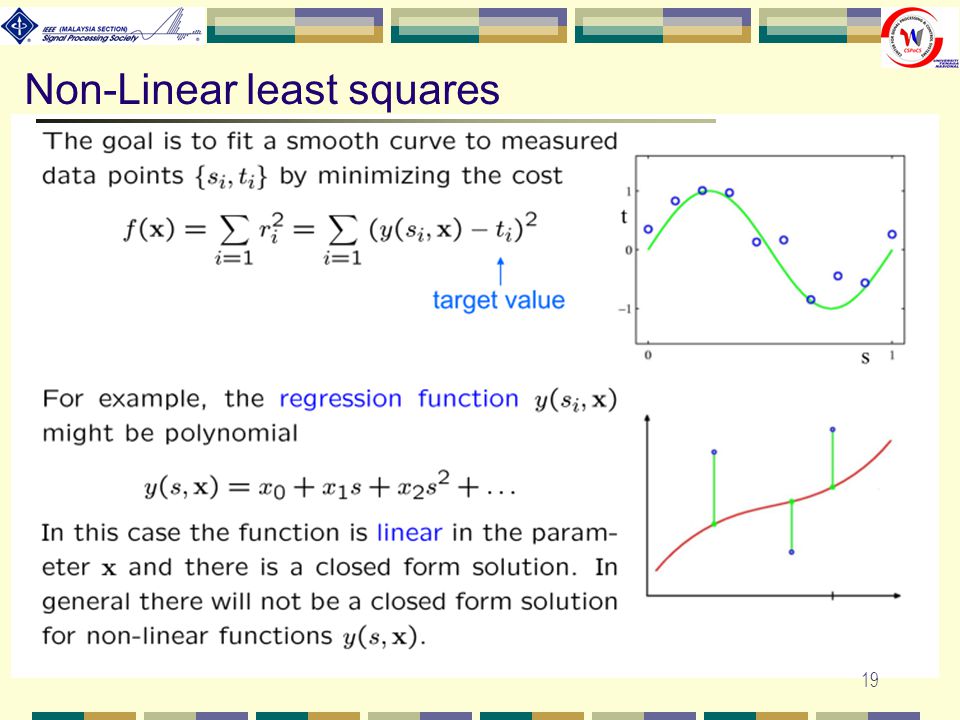 Обсуждаются элементы управления, в том числе презентация наборов инструментов для Matlab, созданных и поддерживаемых авторами, а также соответствующая документация, доступная для загрузки на центральной файловой бирже Matlab.

Индекс технологичности как показатель качества входного сигнала процесса разрушения горных пород

Процесс разрушения горных пород, механизмы механической дезинтеграции и изнашивания разъединительного инструмента изучаются более тридцати лет в связи со значительными изменениями в field…

Эффективная автоматическая экстракция средней сагиттальной плоскости при МРТ головного мозга

• H.A.U. Rehman, Sungon Lee

• Медицина

  Прикладные науки

• 2018

Был предложен полностью автоматический и эффективный в вычислительном отношении метод извлечения средней сагиттальной плоскости (MSP) в магнитно-резонансных изображениях головного мозга (МРТ), который сравнивался с современным подходом, основанным на максимизации двусторонней симметрии.

Обзор компенсации тепловой ошибки шпинделя в станках

• Yang Li, Wanhua Zhao, Shuhuai Lan, J. Ni, Wenwu Wu, B. Lu

• Материаловедение

• 2015

Обзор методов моделирования тепловых ошибок для станка -инструментов

• Yang Li, Ma Yu, Yi Bai, Zhaoyang Hou, Wenwu Wu

• Материалома представлены методы моделирования тепловых ошибок, которые были исследованы и применялись за последние десять лет, и прогнозируется направление будущих исследований моделирования тепловых ошибок.

  Оптимизация количественного анализа при функциональной визуализации мозга домашних животных

  • Yasser Alzamil

  • Биология

  • 2019

  Предлагается несколько статистических методов и методов шумоподавления для 2- и 3-мерных данных, которые применяются к смоделированным изображениям мозга 18F-FDOPA, полученным с помощью симулятора визуализации ПЭТ, для изучения возможности их использования. может уменьшить систематическую ошибку и ошибку, вызванную зашумленными изображениями, и повысить точность количественных измерений.

  Математическая модель интегрированного теплового аппарата

  • И. Коштиал, Я. Списак, Я. Микула, К. М. Пол, Ова

  • Машиностроение

  • 2011

  Разработана математическая модель интегрированного теплового аппарата. Он состоит из программных модулей, из которых можно создать индивидуальную модель печи. Для построения элементарного баланса модели…

  Функции подобия поверхностных слоев для скорости диссипации и структурных параметров температуры и влажности на основе одиннадцати полевых экспериментов

  92$$CT2, и…

  Исследование оценки параметров системы вагон-трейлер с использованием чисел состояний

  • Янгшик Ким

  • Математика

  • 2014
  900 2014

900 для системы автомобиль-трейлер, чтобы охарактеризовать производительность оценки. В этом случае мы можем выбрать лучший параметр…

Распознавание выгравированных символов колесной пары поезда на основе общего метода наименьших квадратов

В соответствии с характеристиками информации о глубине выгравированных символов и отсутствием разницы в цвете с фоном для регистрации поезда был применен линейно-структурированный датчик света…

ПОКАЗАНЫ 1–10 ИЗ 22 ССЫЛОК

Анализ полной задачи наименьших квадратов

Предлагается алгоритм решения задачи TLS, использующий разложение по сингулярным числам и обеспечивающий меру чувствительности основной задачи.

Towards optimal least square filters using the eigenfilter approach

• Cha Zhang, Tsuhan Chen

• Engineering

  2002 IEEE International Conference on Acoustics, Speech, and Signal Processing

• 2002

It is shown that the least -квадратичное решение, которое в литературе может быть получено только путем обращения матриц, может быть асимптотически достигнуто с помощью предложенного подхода с использованием собственных фильтров для проектирования фильтров наименьших квадратов ошибок.

Incremental matrix orthogonalization with an application to curve fitting

• M. Harker, P. O’Leary, P. Zsombor-Murray

• Computer Science, Mathematics

  IS&T/SPIE Electronic Imaging

• 2005

Обеспечивается наилучшая неявная полиномиальная подгонка минимального порядка, которая по существу сочетает в себе идентификацию и классификацию объектов с подгонкой объектов.

Полная задача наименьших квадратов — вычислительные аспекты и анализ

В этой статье представлен метаанализ взаимосвязей между общей оценкой методом наименьших квадратов и классической линейной регрессией в задачах мультиколлинеарности, и объясняются некоторые свойства этих взаимосвязей.

Наименьшие квадраты или наименьшие круги?

• И. Петраш, И. Подлубный

• Образование

• 2010

Студент пришел на выпускной экзамен по статистическим методам в экономике, и профессор ожидал, что студент выведет уравнение сопряженной регрессии строку и, таким образом, оценил ответ студента как неудовлетворительный.