О программных ошибках на примере MATLAB и SimInTech / Хабр
Сила — в правде. На уровне программирования она выражается в том, что одни и те же программы при одних и тех же начальных условиях обязаны выдавать истинную правду, т.е. одинаковые результаты. И даже разные программы, реализующие одну и ту же задачу, должны вести себя одинаково. Действительно, было бы странно, если бы два калькулятора выдавали отличающиеся результаты на одной и той же операции. Или, по-другому, все это своего рода «программистская аксиома».
И, вроде бы все так, да не всегда. Критично ли наличие ошибок в программах? Странный вопрос — конечно, критично. Но, тем не менее, найдутся и те, кто скажет – не беда. И даст этому свое объяснение. Здесь, правда, можно вспомнить, как фирма Intel объясняла несущественность ошибки деления с плавающей точкой в процессоре Pentium (подробнее см. [1]). Но общественность и пользователи объяснили Intel, что она не права. И, понеся большие репутационные и финансовые потери, ей пришлось с этим согласиться и исправить положение.
Далее, обсуждая конкретные программы, мы столкнемся с тем, что нужно считать ошибками. Отличие от ситуации с Intel только в том, что необходимо будет конкретизировать, кто ошибается и ошибается ли и где источник ошибок. Но то, что идет явно не по плану, подтверждают результаты нашего тестирования. Просто ситуация несколько сложнее проблемы одной операции деления FDIV.
Итак. Выберем для экспериментов три среды: две известные – это MATLAB, SimInTech и одну, известную больше по статьям вашего покорного слуги, — среду параллельного автоматного программирования ВКПа. Для первых двух можно скачать ограниченные версии. Их возможностей вполне будет достаточно для наших примеров. Ну, а в отношении третьей — придется довериться автору.
Соберем в рамках упомянутых сред простую схему, состоящую из трех блоков — генератора синусоидального сигнала, интегратора и блока отображения. На рис. 1, 2, 3 представлены как подобные решения, так и результаты их работы. И пока ни что не вызывает беспокойства.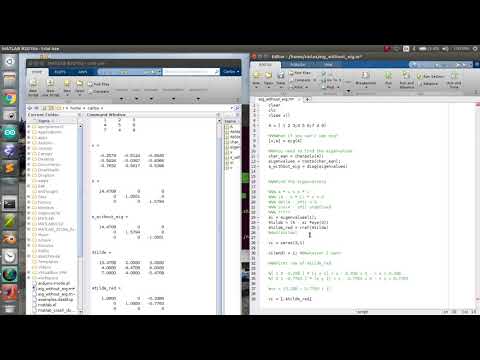
Для пущей уверенности мы собрали еще одну аналогичную схему, заменив только синусоидальный генератор на генератор импульсных сигналов. Но это в целом ситуацию не изменило. Хотя, что там греха таить, основная цель всех этих экспериментов была все же проверить «честность» блока интегрирования среды ВКПа и, если необходимо, доработать его функциональность.
Далее в рамках тестирования ВКПа на примерах все более сложных задач мы создали схемы аттракторов, описанных в статье на Хабре [2]. Это аттракторы Лоренца, Ресслера, Рикитаки и Нозе-Гувера. В статье они представлены схемами в МАТЛАБ. Аналогичные схемы мы собрали для SymInTech и ВКПа. Сравнительные результаты их тестирования оказались столь любопытны, что заслуживают того, чтобы с ними был ознакомлен и Хабр.
При этом отличия в результатах тестирования аттракторов Лоренца проявились в наибольшей степени.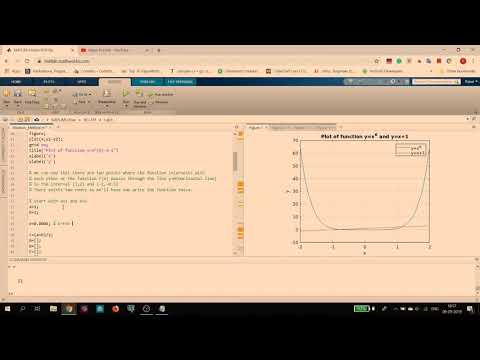
Они приведены для МАТЛАБ на рис. 4, для SymInTech — на рис. 5 и для ВКПа на рис. 6. Глядя на результаты можно лишь сказать, что они похожи и не более того. Поэтому, анализируя их, надо бы признать, что они фактически опровергают сформулированную нами ранее «программистскую аксиому». С таким положением мириться нельзя и это, безусловно, требует своего разбирательства и поиска причин случившегося.
Рис. 5. Тестирование аттрактора Лоренца в SymInTechРис. 6. Тестирование аттрактора Лоренца в ВКПа
Почему сертифицированный SimInTech выдает результаты, которые отличаются от, наверное, столь же сертифицированного пакета MATLAB? Может, можно все списать на хаос, который моделируют аттракторы? Однако, повторный перезапуск программ свидетельствует о его отсутствии.
Но автора обеспокоило совсем другое — достаточно сильное на фоне остальных программ отличие результатов, показанных ВКПа. Отметим также, что перезапуск ВКПа порождал близкие, но все же отличающиеся результаты.
Т.е. в какой-то мере они больше отвечали поставленной цели – моделированию хаоса. Но причины этого достаточно понятны. К хаосу они имеют мало отношения и это мы объясним позже.
И тут пришло время вспомнить про параллелизм. Уравнения каждого из аттракторов представляют собой систему из нескольких параллельных дифференциальных уравнений. Но только у ВКПа можно выбрать один из двух режимов работы: использовать при расчетах теневую память (это стандартный режим, обеспечивающий параллельные свойства среды [3]) или работать в обычном режиме. Напомним, что в режиме теневой памяти измененные на текущем такте данные помещаются в буфер, чтобы, когда выполнятся все действия, стать новыми значениями. В обычном режиме данные обновляются ровно в моменты их изменений.
Рис. 7. Тестирование аттрактора Лоренца в ВКПа в режиме обычной памятиПосле изменения режима расчета в ВКПа были получили графики, представленные на рис. 7. Сам режим работы при этом определяется состоянием переключателем shadow mode of variables (см.
рис. 7), т.е. код вычислительных процессов ни как не затрагивается. Как можно видеть, полученные графики в большей степени походят на результаты конкурентов, чем на свой, но полученный в теневом режиме работы среды. Из этого следует, что два других пакета, решая поставленную задачу, скорее всего, вычисления выполняют строго последовательно, искажая тем самым «правду».
С подобной проблемой параллельных расчетов автору уже приходилось сталкиваться. Тогда участником экспериментов был пакет LabVIEW и решалась проблема моделирования адаптивного ПИД-регулятора (об этом см. статью на Хабре [4]). Значения данных, рассчитанных пакетом, полностью совпадали со значениями, полученными в ВКПа, но были сдвинуты по времени. Это говорило о последовательной работе созданных моделей объекта и регулятора. Доказано это было, как и выше, путем изменения режима работы среды.
Разные же результатов у ВКПа от запуска к запуску объясняются принципом работы ядра среды. Если первые два рассчитывают работу приложения, то ВКПа ее именно моделирует.
Это происходит в дискретном времени, длительность такта которого «плавающая». Эту разницу соответственно и «ловит» блок интегрирования. Отсюда и некий «хаос» в поведении аттрактора в ВКПа. Но, еще раз, он вполне объясним и потому даже ожидаем.
Основное вывод, который следует сделать, сводится к тому, что современное программирование, как ни крути, а «антипараллельно». А потому в его рамках сложно в полной мере доверяться даже достаточно известным программным пакетам. Но самое опасное в том, что они используются огромным числом специалистов, не подозревающих о тех последствиях, которые могут произойти, если им доверяться всецело и безоглядно.
В их оправдание можно лишь сказать, что ни MATLAB ни SimInTech лишь отчасти виноваты в том, что не учитывают параллельные свойства реальных систем. Они просто следуют тенденциям и понятиям современного программирования. А те «сертификации», которые они успешно проходят, похоже, столь же «антипараллельны», как и само современное программирование.
По-хорошему теперь нужно ждать разъяснений по поводу разницы в результатах «обычных» прогонов, а также по поводу учета параллелизма, как программных, так и вполне реальных систем. Это особенно важно, т.к. в перечень решаемых пакетами задач входят те, которые весьма критичны к ошибкам. Вдруг, не дай Бог, что-то не так взлетит, не туда попадет, внезапно откажет или не вовремя утонет? Такой хаос нам не нужен!
Приложение
Схемы аттрактора Лоренца в MATLAB, SymInTech, ВКПа
Схемы остальных аттрактор аналогичны и результаты их тестирования достаточно похожи друг на друга. Даже в обоих режимах работы ВКПа.
Литература
Ошибка Pentium FDIV
Генераторы хаоса на ПЛИС
Автоматное программирование: определение, модель, реализация
Параллелизм, корутины, событийные автоматы,… живая математика
Карта сайта || Филиал КузГТУ г.Прокопьевск
|
|
Неделя 1.
Упражнение по М-скрипту (часть, вопрос 1) ЦЕЛЬ: Написать программу Matlab, которая вычисляет квадратный корень из заданного числа. ЗАДАЧИ: Вычислить квадратный корень из заданного числа. ПРОГРАММА: % Программа MATLAB для вычисления квадратного корня очистить все закрыть все clc % Шаг 1 fprintf(‘Чтобы вычислить квадратный корень из заданного значения \n \n’) % Шаг 2 :…
HTML
MATLAB
Детали проекта
Загрузка…
Оставить комментарий
Спасибо, что решили оставить комментарий. Пожалуйста, имейте в виду, что все комментарии модерируются в соответствии с нашей политикой комментариев, и ваш адрес электронной почты не будет опубликован по соображениям конфиденциальности. Пожалуйста, оставьте личный и содержательный разговор.
Пожалуйста, войдите, чтобы добавить комментарий
Другие комментарии…
Комментариев пока нет!
Оставьте первый комментарий
Подробнее Проекты Абхинава Махто (21)
Проект MATLAB на основе термодинамических данных НАСА
Цель:
ЦЕЛЬ: Написать программу MATLAB, которая помогает анализировать термодинамические данные НАСА.
ЗАДАЧИ: Написать функцию, которая извлекает 14 коэффициентов и вычисляет удельную теплоемкость, энтальпию и энтропию. Постройте Cp, энтальпию и энтропию для каждого вида. Рассчитать молекулярную массу каждого вида. ТЕОРИЯ: Разбор…
03 апр. 2022 13:57 IST
- MATLAB
Подробнее
Проект MATLAB на основе симулятора цикла Ренкина
Цель:ЦЕЛЬ: Создать программу MATLAB, которая вычисляет точки состояния цикла Ренкина. ЗАДАЧИ: Создать симулятор цикла Ренкина с помощью MATLAB. Чтобы определить его точки состояния, включая (i) чистый результат работы и (ii) коэффициент обратной работы. Постройте его диаграммы T-S и h-S по заданным данным. Объясните его работу. ТЕОРИЯ…
03 апр. 2022 13:56 IST
- MATLAB
Подробнее
Программа MATLAB на основе подбора кривой
Цель:
ЦЕЛЬ: Написать код MATLAB, чтобы подобрать линейный и кубический полином для данных cp.
ЗАДАЧИ: Написать код, соответствующий линейному и кубическому полиному для данных Cp. Постройте линейные и кубические кривые соответствия вместе с точками необработанных данных. Напишите код, показывающий метод splitwise. Объясните параметры, используемые для измерения…
03 апреля 2022 13:47 IST
- HTML
- MATLAB
Читать далее
Программа MATLAB для расчета силы сопротивления велосипедисту
Цель:
ЦЕЛЬ: Создать программу Matlab для расчета силы сопротивления велосипедиста. ЦЕЛИ: Понять поток воздуха при езде на велосипеде и рассчитать силу сопротивления, которая действует противоположно ему по скорости и коэффициенту сопротивления. График зависимости скорости от силы сопротивления и коэффициента сопротивления от сопротивления…
03 апр. 2022 13:43 IST
Подробнее
Основные команды в MATLAB
Цель:
ЦЕЛЬ: создание основных команд для строк и векторы-столбцы в Matlab.
03 апр. 2022 13:40 IST
Подробнее
Программа MATLAB для оптимизации функции сталагмита с использованием генетического алгоритма функции. ЗАДАЧИ: Оптимизировать функцию сталагмита. Чтобы понять концепцию генетического алгоритма и объяснить синтаксис слова «ga» в MATLAB. Постройте графики для исследований и для максимума F против №…
03 Apr 2022 01:39PM IST
- MATLAB
Подробнее
Программа MATLAB для решения дифференциального уравнения второго порядка для простого маятника демпфирование. ЗАДАЧИ: Написать программу, решающую ОДУ простого маятника.
03 апр. 2022 13:35 IST
- MATLAB
Подробнее
Программа MATLAB, основанная на Air Standard Cycle Это. ЗАДАЧИ: Создать PV-диаграмму. Определить тепловой КПД двигателя. ТЕОРИЯ: Цикл Отто — один из наиболее распространенных термодинамических циклов в автомобильных двигателях. Одним из ключевых параметров такого двигателя является изменение…
03 апреля 2022 13:32 IST
- MATLAB
- Python
Прочтите больше
Matlab Программа для моделирования форварда Kinematics of 2r Robotic Arm
Цель:
Цель: к созданию ATPORTAB в MATLAAB в ATPORTAAB в ATSTAAB в AT CORTE ATPORAAB в AT CORTE ATAB AT AT CORTE ATO AT AT AT AT AT AT AT AT AT AT AT AT AT TO для моделирования прямой кинематики манипулятора 2R.
ЗАДАЧИ: Решить и стимулировать поступательную кинематику 2R робота-манипулятора вместе с движением манипулятора. Создать анимацию робота-манипулятора 2R на основе его различных движений. ТЕОРИЯ: Роботизированная рука 2R — это… 92 + 10s + 20) `…
30 марта 2022 г. 11:50 IST
- MATLAB
Читать далее
Неделя 3 — Упражнение по моделированию Simulink (Часть — 03 Вопрос 1)
28 марта 2022 г. 05:55 IST
Подробнее
Неделя 4.
Упражнение по моделированию Simulink
Цель:
Que. 1 ЦЕЛЬ: Создать модель Simulink, которая выполняет простые арифметические вычисления. ЗАДАЧИ: Выполнять простые арифметические вычисления, такие как сложение, вычитание, умножение и деление. МОДЕЛЬ SIMULINK : ПОДСИСТЕМА : ИСПОЛЬЗУЕМЫЕ БЛОКИ : Подсистема констант Добавить Вычесть Разделить Отображение продукта ОБЪЯСНЕНИЕ…
27 марта 2022 г. 15:02 IST
- MATLAB
Подробнее
Неделя 3 — Упражнение по моделированию Simulink (Часть — 2)
Цель:
Que. 6 ЦЕЛЬ: Создать Simulink-модель матричного умножения 3×3 двух входных матриц. ЗАДАЧИ: Создать две входные матрицы 3×3. Чтобы выполнить умножение матриц. МОДЕЛЬ SIMULINK : ИСПОЛЬЗУЕМЫЕ БЛОКИ : Константы Отображение продукта РЕЗУЛЬТАТЫ : ЗАКЛЮЧЕНИЕ : В результате мы создали…
19 марта 2022 г.
21:17 IST
Подробнее
Неделя 2. Упражнение на М-скрипт
Цель:
Очередь. 1 ЦЕЛЬ: Создать программу MATLAB, которая увеличивает значение «a» с помощью цикла while. ЗАДАЧИ: Использовать цикл while. Увеличивать значение «а», пока оно не станет меньше «n». ПРОГРАММА : % Программа MATLAB, которую нужно выполнить, пока цикл очистить все закрыть все clc % Шаг 1: Входные переменные a = 0; п = 10; % Шаг 2…
18 марта 2022 г. 12:49 IST
- MATLAB
Подробнее
Неделя 1. Упражнение на М-скрипт (Часть 1)
Цель:
Очередь. 1 ЦЕЛЬ: Написать программу Matlab, которая вычисляет квадратный корень из заданного числа. ЗАДАЧИ: Вычислить квадратный корень из заданного числа. ПРОГРАММА: % Программа MATLAB для вычисления квадратного корня clear all close all clc % Шаг 1 fprintf(‘Чтобы вычислить квадратный корень из заданного значения \n \n’) % Шаг 2 :…
12 марта 2022 г.
14:10 IST
- HTML
- MATLAB
Подробнее
Неделя 1 — Упражнение на М-скрипт (Часть 2)
Цель:
Очередь. 1 ЦЕЛЬ: Создать программу MATLAB, которая выполняет сложение, вычитание, умножение, левое и правое деление матричных операций. ЗАДАЧИ: Выполнять сложение, вычитание, умножение, левое и правое деление. ПРОГРАММА: % Программа MATLAB для выполнения арифметических операций очистить все закрыть все clc…
11 марта 2022 г. 18:51 IST
- MATLAB
Подробнее
Моделирование вездехода на системном уровне (ATV)
Цель:
ЦЕЛЬ: Провести системное моделирование вездехода (ATV). ЗАДАЧИ: Провести моделирование квадроцикла. Подготовить технический отчет с объяснением свойств модели и комментариями по результатам.
ТЕОРИЯ: Вездеход (ATV) Вездеход (ATV), также известный как легкий грузовой автомобиль…
06 марта 2022 г. 17:14 IST
Подробнее
Неделя — 4 Stateflow модель стиральной машины Машина и переключатель передач
Задача:
Очередь. 1 ЦЕЛЬ: реализовать логику управления стиральной машиной с помощью Stateflow. ЗАДАЧИ: Создать модель стиральной машины. Чтобы выполнить заданную последовательность и показать условия ее работы. ДАННЫЕ УСЛОВИЯ: Система включена, если источник питания доступен. Остановите процедуру и подайте сигнал с помощью…
04 марта 2022 г. 10:30 IST
Подробнее
Неделя – 3. Выполнение формообразующей машины, наборов данных и масс-пружинного демпфера в Simulink и Simscape.
Цель:
Очередь. 1 ЦЕЛЬ: Определить работу, выполняемую режущим инструментом, с использованием модели Simulink.
ЗАДАЧИ: Создать модель Simulink для формовочного станка. Определить работу, совершаемую при перемещении инструмента на расстояние 100 мм. Условные условия: расстояние (мм) 0 20 50 60 80 100 100 Сила (кН) 60 72 65 53 44 50…
01 март 2022 г. 01:34 IST
- MATLAB
Прочитайте больше
-неделя -2 Модель модели модели моделиики моделиики. дверного звонка и измерение температуры обогревателя
Цель:
Очередь. 1: ЦЕЛЬ: создать Simulink-модель дверного звонка с использованием блока соленоидов. ЗАДАЧИ: Создать блок Simulink дверного звонка. Сделайте так, чтобы колокол издавал звук. Чтобы создать ситуацию, когда переключатель замкнут на 2 секунды, а затем отпущен. Для наблюдения за положением…
26 фев. 2022 17:54 IST
Читать дальше
Неделя 1.
2⋅(x−92`, используя базовые блоки Simulink, и запустите сравнение системы подвески. ЗАДАЧИ: Создать фундаментальные блоки Simulink, используя заданную функцию. Запустить пример Simulink для сравнения систем подвески. ОСНОВНОЕ УРАВНЕНИЕ : …
21 фев. 2022 11:07 IST
- MATLAB
Подробнее
Показаны 1 из 21 проектов
Nick Функция High – Samqm 90B0000000000000000
Функция MATLAB sqrtm для вычисления квадратного корня матрицы впервые появилась в 1980-е годы. Он был улучшен в MATLAB 5.3 (1999 г.) и снова в MATLAB 2015b. В этом посте я объясню, как недавние изменения привели к значительному увеличению скорости.
Вспомним, что каждая невырожденная матрица имеет квадратный корень: матрица такая, что . На самом деле, оно имеет по крайней мере два квадратных корня, а возможно, и бесконечно много. Эти две крайности возникают, когда есть один блок в форме Жордана (два квадратных корня) и когда собственное значение появляется в двух или более блоках в форме Жордана (бесконечное количество квадратных корней).
На практике обычно требуется главный квадратный корень из , т. е. тот, чьи собственные значения лежат в правой половине плоскости. Этот квадратный корень уникален, если не имеет действительных отрицательных собственных значений. Мы делаем его уникальным во всех случаях, принимая квадратный корень из отрицательного числа за тот, у которого мнимая часть неотрицательна.
Исходный sqrtm преобразован в форму Шура, а затем применен рекуррентный алгоритм Парлетта, предназначенный для общих матричных функций; на самом деле это просто называлось функцией MATLAB funm того времени. Этот подход может быть неустойчивым, если имеет почти повторяющиеся собственные значения. Я указал на нестабильность в 1999 сообщает A New Sqrtm for MATLAB и предлагает замену sqrtm, в которой используется рекуррентность, полученная специально для квадратного корня Бьорком и Хаммарлингом в 1983 г. Последняя рекуррентность совершенно стабильна. Моя функция также предоставила оценку числа обусловленности квадратного корня матрицы.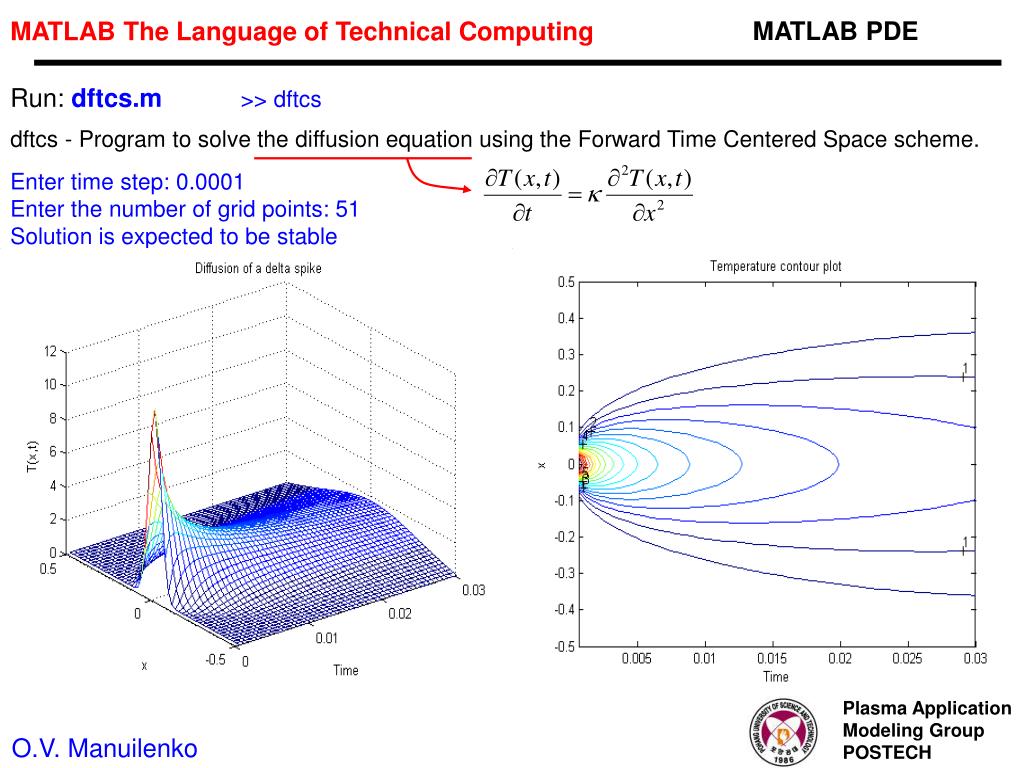
Значение sqrtm с годами возросло, потому что от него зависит logm (для матричного логарифма), как и коды для других матричных функций, для вычисления произвольных степеней матрицы и обратных тригонометрических и обратных гиперболических функций.
Для треугольной матрицы стоимость повторения вычислений такая же, как и стоимость вычислений, а именно флопс. Но в то время как обратная треугольная матрица является операцией BLAS уровня 3 и поэтому была очень эффективно реализована в библиотеках, вычисление квадратного корня не соответствует стандарту BLAS уровня 3. В результате мой sqrtm реализовал рекуррентность Бьёрка-Хаммарлинга в M-коде как тройной вложенный цикл и был довольно медленным.
Новый sqrtm, представленный в MATLAB 2015b, содержит новую реализацию повторения Бьорка–Хаммарлинга, которая, хотя и в M-коде, работает намного быстрее. Вот сравнение базовой функции sqrtm_tri (содержащейся в toolbox/matlab/matfun/private/sqrtm_tri.m ) с соответствующим фрагментом кода, извлеченным из старого файла sqrtm.
Показано время выполнения в секундах для случайных треугольных матриц на четырехъядерном процессоре Intel Core i7.
| нет | sqrtm_tri | старая квртм |
|---|---|---|
| 10 | 0,0024 | 0,0008 |
| 100 | 0,0017 | 0,014 |
| 1000 | 0,45 | 3,12 |
Для новый код работает медленнее. Но у нас уже есть ускорение в 8 раз, а для . Замедление for вызвано сочетанием двух причин: новый код является более общим, так как поддерживает настоящую форму Шура, и содержит вызовы функций, которые создают накладные расходы для малых .
Как работает sqrtm_tri? Он использует метод рекурсивного разбиения. пишет
и отмечает, что
где .
Таким образом, задача вычисления квадратного корня сводится к задачам рекурсивного вычисления квадратных корней меньших матриц и последующего решения уравнения Сильвестра для . Уравнение Сильвестра решается с использованием процедуры LAPACK для повышения эффективности. Если вы хотите взглянуть на код, введите edit private/sqrtm_tri в командной строке MATLAB. Для получения дополнительной информации об этой рекурсивной схеме вычисления квадратных корней треугольных матриц см. Блокированные алгоритмы Шура для вычисления квадратного корня матрицы (2013 г.) Дедмана, Хайэма и Ральи.
sqrtm в MATLAB 2015b включает два дополнительных усовершенствования.
- Для действительных матриц используется вещественная форма Шура, что означает, что все вычисления выполняются в вещественной арифметике, что дает преимущество в скорости и гарантирует, что результат не будет загрязнен мнимыми частями на уровне округления.
- Он оценивает номер условия 1-нормы квадратного корня матрицы вместо числа условия 2-нормы, поэтому использует функцию normest1.
