Вычислительные методы для инженеров
Вычислительные методы для инженеров
ОглавлениеПРЕДИСЛОВИЕГлава 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ С ПРИМЕНЕНИЕМ ЭВМ § 1.2. Основные этапы решения инженерной задачи с применением ЭВМ § 1.3. Вычислительный эксперимент § 1.4. Дополнительные замечания Глава 2. ВВЕДЕНИЕ В ЭЛЕМЕНТАРНУЮ ТЕОРИЮ ПОГРЕШНОСТЕЙ § 2.1. Источники и классификация погрешностей результата численного решения задачи § 2.2. Приближенные числа. Абсолютная и относительная погрешности 2. Правила записи приближенных чисел. 3. Округление. § 2.3. Погрешности арифметических операций над приближенными числами § 2.4. Погрешность функции § 2.5. Особенности машинной арифметики 2. Представление целых чисел. 3. Представление вещественных чисел. 4. Арифметические операции над числами с плавающей точкой.  5. Удвоенная точность. 6. Вычисление машинного эпсилон. § 2.6. Дополнительные замечания Глава 3. ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ. ОСНОВНЫЕ ПОНЯТИЯ § 3.2. Обусловленность вычислительной задачи 2. Примеры плохо обусловленных задач. 3. Обусловленность задачи вычисления значения функции одной переменной. 4. Обусловленность задачи вычисления интеграла … 5. Обусловленность задачи вычисления суммы ряда. § 3.3. Вычислительные методы § 3.4. Корректность вычислительных алгоритмов § 3.5. Чувствительность вычислительных алгоритмов к ошибкам округления § 3.6. Различные подходы к анализу ошибок § 3.7. Требования, предъявляемые к вычислительным алгоритмам § 3.8. Дополнительные замечания Глава 4. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ § 4.2. Обусловленность задачи вычисления корня § 4.4. Метод простой итерации § 4.5. Обусловленность метода простой итерации § 4.6. Метод Ньютона § 4.  7. Модификации метода Ньютона§ 4.8. Дополнительные замечания Глава 5. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ § 5.2. Нормы вектора и матрицы § 5.3. Типы используемых матриц § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений § 5.5 Метод Гаусса § 5.6. Метод Гаусса и решение систем уравнений с несколькими правыми частями, обращение матриц, вычисление определителей § 5.7. Метод Гаусса и разложение матрицы на множители. LU-разложение § 5.8. Метод Холецкого (метод квадратных корней) § 5.9. Метод прогонки § 5.10. QR-разложение матрицы. Методы вращений и отражений § 5.11. Итерационное уточнение § 5.12. Дополнительные замечания Глава 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ § 6.1. Метод простой итерации § 6.2. Метод Зейделя § 6.3. Метод релаксации § 6.4. Дополнительные замечания Глава 7. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ § 7.  2. Метод простой итерации§ 7.3. Метод Ньютона для решения систем нелинейных уравнений 7.4. Модификации метода Ньютона § 7.5. О некоторых подходах к решению задач локализации и отыскания решений систем нелинейных уравнений § 7.6. Дополнительные замечания Глава 8. МЕТОДЫ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 8.2. Степенной метод § 8.3. Метод обратных итераций § 8.4. QR-алгоритм § 8.5. Дополнительные замечания Глава 9. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ § 9.2. Обусловленность задачи минимизации § 9.3. Методы прямого поиска. Оптимальный пассивный поиск. Метод деления отрезка пополам. Методы Фибоначчи и золотого сечения § 9.5. Дополнительные замечания Глава 10. МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ § 10.1. Задача безусловной минимизации функции многих переменных § 10.2. Понятие о методах спуска. Покоординатный спуск § 10.3. Градиентный метод § 10.4. Метод Ньютона § 10.  5. Метод сопряженных градиентов§ 10.6. Метода минимизации без вычисления производных § 10.7. Дополнительные замечания Глава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ И СМЕЖНЫЕ ВОПРОСЫ § 11.2. Интерполяция обобщенными многочленами § 11.3. Полиномиальная интерполяция. Многочлен Лагранжа § 11.4. Погрешность интерполяции § 11.5. Интерполяция с кратными узлами § 11.6. Минимизация оценки погрешности интерполяции. Многочлены Чебышева § 11.7. Конечные разности § 11.8. Разделенные разности § 11.9. Интерполяционный многочлен Ньютона. Схема Эйткена § 11.10. Обсуждение глобальной полиномиальной интерполяции. Понятие о кусочно-полиномиальной интерполяции § 11.11. Интерполяция сплайнами § 11.12. Понятие о дискретном преобразовании Фурье и тригонометрической интерполяции § 11.13. Метод наименьших квадратов § 11.14. Равномерное приближение функций § 11.15. Дробно-рациональные аппроксимации и вычисление элементарных функций § 11.16. Дополнительные замечания Глава 12.  ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ§ 12.1. Простейшие формулы численного дифференцирования § 12.2. О выводе формул численного дифференцирования § 12.3. Обусловленность формул численного дифференцирования § 12.4. Дополнительные замечания Глава 13. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 13.2. Квадратурные формулы интерполяционного типа § 13.4. Апостериорные оценки погрешности. Понятие об адаптивных процедурах численного интегрирования § 13.5. Вычисление интегралов в нерегулярных случаях § 13.6. Дополнительные замечания Глава 14. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 14.1. Задача Коши для дифференциального уравнения первого порядка § 14.2. Численные методы решения задачи Коши. Основные понятия и определения § 14.3. Использование формулы Тейлора § 14.4. Метод Эйлера § 14.5. Модификации метода Эйлера второго порядка точности § 14.6. Методы Рунге-Кутты § 14.7. Линейные многошаговые методы. 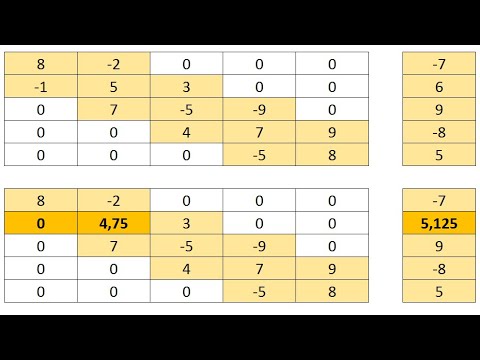 Методы Адамса§ 14.8. Устойчивость численных методов решения задачи Коши § 14.9. Неявный метод Эйлера § 14.10. Решение задачи Коши для систем обыкновенных дифференциальных уравнений и дифференциальных уравнений m-го порядка § 14.11. Жесткие задачи § 14.12. Дополнительные замечания Глава 15. РЕШЕНИЕ ДВУХТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ § 15.1. Краевые задачи для одномерного стационарного уравнения теплопроводности § 15.2. Метод конечных разностей: основные понятия § 15.3. Метод конечных разностей: аппроксимации специального вида § 15.4. Понятие о проекционных и проекционно-разностных методах. Методы Ритца и Гадеркина. Метод конечных элементов § 15.5. Метод пристрелки § 15.6. Дополнительные замечания |
Разложение Холецкого MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство.
1311 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
- MatLab
Урок 11. Матричные операции линейной алгебры
Вычисление
нормы и чисел обусловленности матрицы
Определитель
и ранг матрицы
Определение нормы вектора
Определение ортонормированного базиса матрицы
Определение угла между двумя подпространствами
Вычисление следа матрицы
Разложение Холецкого
Обращение матриц — функции inv, pinv
LU- и QR-разложения
Вычисление собственных значений и сингулярных чисел
Приведение матриц к форме Шура и Хессенберга
Что нового мы узнали?
Разложение
Холецкого — известный прием матричных вычислений.
Функция chol находит это разложение
для действительных и комплексных эрмитовых матриц.
R = chol(X) — для квадратной матрицы [ Положительно определенной называется действительная симметрическая матрица, все собственные значения которой положительны. Поскольку используется только верхний треугольник матрицы X, матрица X не обязательно должна быть симметрической. — Примеч. ред.
е. равна транспонированной матрице
(А*=А). — Примеч. ред.
];
[R.p] = chol (X) с двумя выходными аргументами никогда не генерирует сообщение об ошибке в ходе выполнения разложения Холецкого квадратной матрицы X. Если верхняя треугольная часть и диагональ X задают положительно определенную матрицу, то р=0, a R совпадает с вышеописанным случаем, иначе р. — положительное целое число, a R — верхняя треугольная матрица порядка q=p-l, такая что R’*R=X(l:q,l:q).
Пример:
» c=chol(pascal(4))
с =
1 1 1 1
0 1 2 3
0 0 1 3
0 0 0 1
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8156 0
Визуализация и графические средства MatLab
9664 0
Техническая документация по системе MatLab
6176 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Tx=y$ для Холецкого) обратной заменой. (Страница в Википедии описывает их довольно хорошо.) Как в прямой, так и в обратной подстановке ключевой момент заключается в том, что если вы выпишете уравнения для неизвестных $x_1,\ldots,x_n$ в правильном порядке (вперед для $L$ и наоборот для $U$), каждое уравнение содержит только одно новое неизвестное, чем предыдущее уравнение, которое можно легко вычислить. 9{-1}$. Существуют методы обращения треугольных матриц. В практических приложениях общепринято не вычислять обратную матрицу, если в этом нет необходимости, и обычно есть способы фактически вычислить обратную матрицу. (К сожалению, это не относится к школьным экзаменам по линейной алгебре.)
При вычислении факторизации $LU$ можно столкнуться с нулевой опорной точкой, что требует перестановки строк матрицы для получения ненулевой опорной точки. При использовании поворота фактически вычисляется разложение вида $PA = LU$, где $P$ — матрица перестановок. При выполнении факторизации $LU$ на компьютере с использованием неточной арифметики (например, арифметики с плавающей запятой) также важно выполнять перестановку, когда сводная запись просто мала, не обязательно равна нулю.
На самом деле, матрицу обычно переставляют таким образом, что мы всегда выбираем самую большую опорную точку в столбце в стратегии, известной как частичная опорная точка. При выполнении факторизации Холецкого на матрице SPD никогда не столкнется с нулевой точкой поворота, и вам не нужно делать поворот, чтобы обеспечить точность вычислений. (Кто-то может захотеть использовать перестановки по другим причинам, например, для сохранения разреженности.) 9*$ Факторизацию $LU$ можно выполнять разными способами и для прямоугольных матриц или матриц с недостаточным рангом, но квадратный случай является наиболее распространенным.
Разложение Холецкого в Python и NumPy
Следуя статье о LU-разложении в Python, мы рассмотрим реализацию на Python метода Разложение Холецкого , который используется в некоторых алгоритмах количественного финансирования.
В частности, он появляется в методах Монте-Карло, где он используется для моделирования систем с коррелированными переменными.
Разложение Холецкого применяется к корреляционной матрице, обеспечивая нижнюю треугольную матрицу L, которая при применении к вектору некоррелированных выборок u дает ковариационный вектор системы. Таким образом, это очень актуально для количественной торговли.
предполагает, что разлагаемая матрица является эрмитовой и положительно-определенной . Поскольку нас интересуют только матрицы с действительными значениями, мы можем заменить свойство эрмитовости на свойство , симметричное (т. е. матрица равна своей транспонированной). Разложение Холецкого примерно в 2 раза быстрее, чем разложение LU, где оно применяется.
Чтобы решить нижнюю треугольную матрицу, мы будем использовать 9{k-1}_{j=1} l_{ij} l_{kj} \right), i > k \end{выравнивание*}
Как и в случае с LU-декомпозицией, наиболее эффективным методом с точки зрения времени разработки и выполнения является использование библиотеки линейной алгебры NumPy/SciPy ( linalg ), которая имеет встроенный метод cholesky для декомпозиции матрицы.
Необязательный параметр нижний позволяет нам определить, создается ли нижняя или верхняя треугольная матрица:
импорт ппринт
импорт scipy
import scipy.linalg # Библиотека линейной алгебры SciPy
A = scipy.array([[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]])
L = scipy.linalg.cholesky (A, нижний = True)
U = scipy.linalg.cholesky (A, нижний = False)
напечатать "А:"
pprint.pprint(A)
напечатать "Л:"
pprint.pprint(L)
напечатать "У:"
pprint.pprint(U)
Вывод кода приведен ниже:
А:
массив([[ 6, 3, 4, 8],
[3, 6, 5, 1],
[4, 5, 10, 7],
[8, 1, 7, 25]])
Л:
массив([[ 2.44948974, 0. , 0. , 0. ],
[1.22474487, 2.12132034, 0., 0.],
[1.63299316, 1.41421356, 2.30940108, 0.],
[ 3,26598632, -1,41421356, 1,58771324, 3,13249102]])
У:
массив([[ 2.44948974, 1.22474487, 1.63299316, 3.26598632],
[ 0. , 2,12132034, 1,41421356, -1,41421356],
[0.
, 0., 2.30940108, 1.58771324],
[ 0. , 0. , 0. , 3.13249102]])
, 0., 2.30940108, 1.58771324],
[ 0. , 0. , 0. , 3.13249102]]) Как и в случае с LU-декомпозицией, маловероятно, что вам когда-либо понадобится кодировать декомпозицию Холецкого на чистом Python (т. е. без NumPy/SciPy), поскольку вы можете просто включить библиотеки и использовать гораздо более эффективные инструменты, найденные внутри. Однако для полноты картины я включил реализацию декомпозиции Холецкого на чистом Python, чтобы вы могли понять, как работает алгоритм:
из математического импорта sqrt
из pprint импортировать pprint
деф холески (A):
"""Выполняет разложение Холецкого A, которое должно
симметричная и положительно определенная матрица. Функция
возвращает нижний вариант треугольной матрицы, L."""
п = лен (А)
# Создаем нулевую матрицу для L
L = [[0.0] * n для i в xrange(n)]
# Выполнить разложение Холецкого
для я в xrange (n):
для k в xrange(i+1):
tmp_sum = sum(L[i][j] * L[k][j] для j в xrange(k))
if (i == k): # Диагональные элементы
# LaTeX: l_{kk} = \sqrt{ a_{kk} - \sum^{k-1}_{j=1} l^2_{kj}}
L[i][k] = sqrt(A[i][i] - tmp_sum)
еще:
# LaTeX: l_{ik} = \frac{1}{l_{kk}} \left( a_{ik} - \sum^{k-1}_{j=1} l_{ij} l_{kj} \ верно)
L[i][k] = (1,0 / L[k][k] * (A[i][k] - tmp_sum))
вернуть л
А = [[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]]
L = холецкий (А)
напечатать "А:"
печать(А)
напечатать "Л:"
печать(L)
Вывод чистой реализации Python приведен ниже:
А:
[[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]]
Л:
[[2,449489742783178, 0,0, 0,0, 0,0],
[1,2247448713915892, 2,1213203435596424, 0,0, 0,0],
[1,6329931618554523, 1,414213562373095, 2,309401076758503, 0,0],
[3,2659863237109046,
-1,4142135623730956,
1.