Маткад определитель матрицы: 7.3.1. Определитель квадратной матрицы MathCAD 12 руководство

Как в mathcad найти определитель матрицы

Иллюстрированный самоучитель по MathCAD 12

Вычисление определителей и обращение квадратных матриц. Определитель квадратной матрицы.

Рассмотрим еще несколько исключительно важных действий линейной алгебры, связанных с понятием определителя матрицы. Несмотря на то, что некоторые из них реализованы в Mathcad также в виде операторов, они требуют (при проведении расчетов по численным алгоритмам) несравненно больше внимания, нежели операторы упомянутые в двух предыдущих разделах.

Определитель (Determinant) матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) (листинг 7.14) или набрать на клавиатуре | (нажав клавиши SHIFT + \). В результате любого из этих действий появляется местозаполнитель, в который следует поместить матрицу. Чтобы вычислить определитель уже введенной матрицы:

1. Переместите курсор в документе таким образом, чтобы поместить матрицу между линиями ввода (напоминаем, что линии ввода – это вертикальный и горизонтальный отрезки синего цвета, образующие уголок, указывающий на текущую область редактирования).
2. Введите оператор нахождения определителя матрицы.
3. Введите знак равенства (либо символьного вывода), чтобы вычислить определитель (численно или аналитически соответственно, как это показано в листинге 7.14).

Внимание!
Не путайте операторы вычисления определителя квадратной матрицы и длины вектора. В Matncad 12 введен принудительный контроль действий пользователя при вводе этих операторов во избежание путаницы (т. к. один и тот же символ используется для этих двух операций). При попытке вычислить определитель матрицы с помощью оператора |А|, введенного с панели Calculator (Калькулятор), а не Matrix (Матрица), будет выдано сообщение об ошибке, а результат вычисления детерминанта появится только после того, как пользователь вызовет контекстное меню и подтвердит в нем, что он собирается вычислить именно определитель матрицы. То же самое касается и длины вектора, если попытаться ввести его не с панели Calculator (Калькулятор), а с панели Matrix (Матрица).

Листинг 7.14. Вычисление определителя квадратной матрицы:

MathCAD — это просто! Часть 11. Продолжаем работать с матрицами

Матрицы — вещь важная, а потому было бы просто непростительно отводить на них всего одну статью из нашего цикла о работе в среде MathCAD. Узнав о том, как можно транспонировать матрицы, вычислять определители, обратные матрицы, а также перемножать и складывать их, сегодня мы с вами продолжим издевательства над этими важными в математике объектами. Думаю, что изложенные ниже сведения будут полезны и в практических вычислениях, производимых в среде MathCAD, ведь матрицы очень часто встречаются в реальных задачах.

Еще о вспомогательных функциях

В прошлый раз мы немного поговорили о специальных MathCAD’овских функциях, позволяющих разрезать матрицы на составные части или же склеивать их. Это не единственные из вспомогательных функций, действующих над матрицами, которые могут пригодиться в практике повседневной работы. Пришло время познакомиться с некоторыми другими функциями, которые также имеют неплохой шанс оказаться весьма и весьма полезными. Особую роль в матричном исчислении играют единичные матрицы. На всякий случай напомню, что единичной называется такая матрица, у которой все недиагональные элементы равны нулю, а элементы, расположенные на главной диагонали (от верхнего левого угла к нижнему правому), равны единице. Единичные матрицы могут иметь самые разные размеры. Чтобы пользователь не тратил свое время на вбивание нулей и единиц в строки и столбцы такой матрицы, в MathCAD’е имеется специальная функция Identity, создающая единичную матрицу заданного размера. У этой функции есть единственный аргумент, задающий размерность матрицы.

Еще она по своему действию довольно близкая к Identity функция называется Diag. Она создает не матрицы, а векторы, состоящие из диагональных элементов квадратных матриц (т. е. из тех элементов, которые стоят на ее главной диагонали). Стоит при этом отметить, что размер вектора, получаемого на выходе, автоматически определяется размером входной матрицы.

Для определения размера матриц можно использовать функции Rows и Cols. Каждая из них имеет один-единственный входной параметр, которым является сама матрица, а на выходе выдают значения числа строк и столбцов соответственно. Для определения размера вектора можно использовать функцию length, которая работает аналогично указанным для матриц функциям.

Интересной также является предоставляемая MathCAD’ом функция для сортировки элементов векторов. Называется она просто и незатейливо — Sort. В качестве входного параметра этой функции нужно передать вектор, сортировкой которого мы будем заниматься, и на выходе получим почти такой же вектор, только его элементы будут упорядочены по возрастанию. Для сортировки строк и столбцов матрицы можно воспользоваться соответственно функциями Rsort и Csort, которым нужно передать в качестве параметров саму матрицу и номер того столбца или строки, которые должны быть отсортированы. Правда, работают эти функции несколько загадочно, иногда сортируя не только нужный столбец (строку), но и все остальные (см. соответствующую иллюстрацию). Чтобы изменить порядок следования чисел в векторе или порядок строк в матрице на противоположный, нужно воспользоваться функцией Reverse, в качестве аргумента для которой нужно передать изменяемые матрицу или вектор.

Ранг и норма матрицы

Два фундаментальных понятия, играющих очень важную роль в линейной алгебре — это ранг и норма матрицы. MathCAD позволяет пользователю вычислять эти характеристики матриц без лишних усилий, и сейчас я расскажу, как именно это делается.

Минором матрицы порядка k называется определитель, вычисленный для матрицы, образованной из k столбцов и k строк данной матрицы. Главным минором называется минор, для которого номера выбранных столбцов совпадают с номерами выбранных строк. Понимаю, это определение звучит несколько громоздко, но я думаю, если вы прочитаете его внимательно еще раз, то все станет просто и понятно. Рангом матрицы называется наибольший порядок среди всех ее ненулевых миноров. Ранг матрицы характеризует число линейно независимых столбцов или строк матрицы, а потому в матричной алгебре эта характеристика используется весьма широко. Для вычисления ранга матрицы в MathCAD’е используется функция Rank, которой в качестве аргумента передается та самая матрица, ранг которой нужно вычислить.

Норма матрицы — понятие более расплывчатое, чем ранг. Для полного определения нормы матрицы используется система ограничений, которым должен подчиняться строящийся по определенным правилам функционал. Вы можете найти подробное определение нормы матрицы в любом учебнике по линейной алгебре. Мы же сейчас удовлетворимся знанием того, что норма матрицы — это некоторый аналог величины, который для векторов называют длиной (норма вектора как раз и есть его длина). Впрочем, в отличие от длины вектора, где все понятно и определенно, норма матрицы может вычисляться несколькими разными способами, и в зависимости от способа вычисления ее величина может быть различной.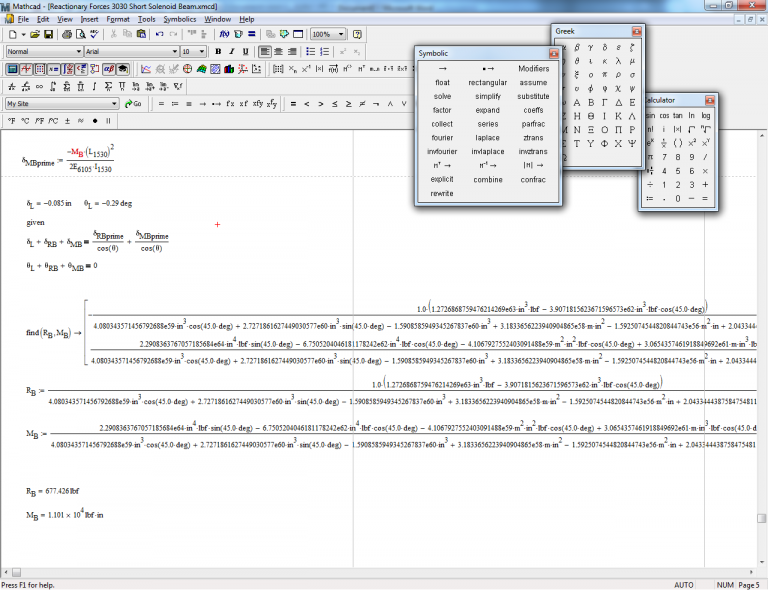 Всем функциям для вычисления нормы матрицы, о которых здесь идет речь, требуется в качестве аргумента передавать ту матрицу, для которой будет вестись вычисление нормы. Функция Norm1 определяет норму путем складывания модулей элементов для каждого из столбцов и выбором наибольшей из получившихся для столбцов сумм. Функция Normi работает аналогичным образом, только для вычисления сумм там используются не столбцы, а строки. Функция Norme вычисляет норму матрицы по тому же алгоритму, по какому вычисляется норма вектора: квадраты всех элементов матрицы суммируются, а затем из полученного числа извлекается корень.

Собственные вектора и собственные значения матриц

Собственным вектором x и собственным значением ? матрицы X называются такие вектор и число соответственно, которые удовлетворяют соотношению xX = ?x. Обычно матрица имеет несколько собственных векторов и соответствующих им собственных значений, а потому мы будем рассматривать именно этот случай. Конечно, в MathCAD’е не слишком сложно с помощью некоторых преобразований рассчитать необходимые числа и вектора самостоятельно, однако можно еще больше упростить себе жизнь, воспользовавшись встроенными в эту среду функциями.

Функция Eigenvecs принимает в качестве входного параметра некоторую матрицу, а возвращает другую, содержащую собственные вектора исходной. При интерпретации результатов работы этой функции необходимо помнить, что в MathCAD’е вектора записываются в виде столбцов, так что и в этой матрице каждый из столбцов является собственным вектором первоначальной матрицы. Другая функция, Eigenvals, также принимает на вход некоторую матрицу, однако выдает для нее уже не собственные вектора, а собственные значения. Записываются они также в виде столбика. В этом столбце они идут в том же порядке, что и столбцы в матрице, возвращаемые первой функцией. То есть i-му столбцу матрицы, получаемой на выходе функцией Eigenvecs, соответствует i-е собственное значение в векторе. Впрочем, проследить соответствие собственных векторов и собственных значений для матрицы можно и более наглядным образом. Для этого существует специальная функция Eigenvec (не путайте с Eigenvecs), которой на вход передаются матрица и одно из ее собственных значений, а она уже вычисляет соответствующий этому собственному значению собственный вектор.

Скалярное и векторное произведение векторов

Напоследок поговорим о вещах довольно простых, но очень распространенных в практике решения задач, а потому особенно важных. Сейчас мы рассмотрим, как с помощью MathCAD’а вычислять скалярное и векторное произведение векторов. Напомню, что скалярным произведением x.y называется число, равное x0y0 + x1y1 + x2y2 + … + xnyn, а вот с векторным все несколько сложнее. Оно определяется только для трехмерных векторов и вычисляется как определитель матрицы, составленной из базисных векторов (i, j и k) и элементов тех векторов, для которых вычисляется векторное произведение. Традиционно в математике векторное произведение обозначают c помощью крестика, который ставится между двумя перемножаемыми векторами.

Для вычисления скалярного и векторного произведения векторов обратимся снова к панели матричных вычислений, неоднократно выручавшей нас в наших упражнениях с MathCAD’ом. Скалярное произведение называется на ней Dot Product и обозначается как точка между двумя векторами, а векторное — Cross Product и обозначается крестиком, как я уже говорил выше. Чтобы перемножить два вектора, вы можете сначала обозначить их с помощью каких- либо символьных обозначений, а можете сразу записывать произведения между столбцами чисел.

Теперь, пожалуй, о матрицах самое основное и важное сказано. Как видите, в плане работы с векторами и матрицами MathCAD ничуть не менее мощный, чем во всем остальном. Поэтому использовать эту среду для матричных вычислений можно и нужно. Ну а как это делать, вы теперь уже знаете.

SF, spaceflyer@tut.by

Компьютерная газета. Статья была опубликована в номере 24 за 2008 год в рубрике soft

Как в mathcad найти определитель матрицы

Матрицы в Mathcad

Векторы и матрицы рассматриваются в программе Mathcad как одномерные и двумерные массивы данных.

Матрица создается с помощью диалогового окна Вставить матрицу (рис. 1.6), которое открывают командой Вставка > Матрица (Insert > Matrix) или первой кнопкой на панели «Матрица» (рис. 1.7). Вектор задается как матрица, имеющая один столбец. В диалоговом окне задается число строк и столбцов, а после вставки на рабочий лист матрица содержит вместо элементов заполнители, вместо которых следует вставить число, переменную или выражение.

Для матриц определены сложение, умножение на число, перемножение и другие операции. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы:

Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля, что задается системной переменной ORIGIN, и может быть изменено пользователем (например, блок ORIGIN:=1 устанавливает начальный индекс равным единице). Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Индекс (Subscript, x_n) на панели инструментов Mатрица (Matrix) или нажатием символа «[» после имени массива (см. приложение «Горячие клавиши»). Индексы двумерных матриц записываются через запятую.

Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки: . Для его ввода используется кнопка Столбец (Matrix Column) на панели инструментов Матрица или соответствующая «горячая» клавиша.

Для задания некоторой последовательности элементов матрицы используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через точку с запятой значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, например х:=0,0.01..1 . Если разность прогрессии равна единице (то есть, элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают.

На рис. 1.8 приведены примеры реализации некоторых операций с матрицами.

26. Матричные вычисления в MathCad

Матричные вычисления в MathCad

Маткад позволяет оперировать не только скалярными величинами но и векторами и матрицами.

Вектор – одномерный массив. Матрица – двумерный. Нумерация задается значением системной переменной ORIGIN. V₀ – первый элемент вектора V, М_0,0 – первый элемент матрицы М.

Элементами матрицы могут быть числа, константы, переменные и математические выражения. Соответственно матрицы могут быть численными и символьными.

Матрицу или вектор можно задать с помощью команды Insert–Matrix. Или жмякнув левой педалькой мыши по соответствующей кнопке на тулбаре Vector and Matrix, или просто жмякнув Ctrl+M. Появляется диалоговое окно, в котором вводится количество строк и столбцов (колонок) матрицы.

Далее появляется шаблон матрицы, в ячейки которого водятся необходимые значения.

Операции с матрицами можно набирать с клавиатуры или жмякая на соответствующие кнопки на тулбаре Vector and Matrix:

— Определение размеров матрицы;

— Вычисление определителя матрицы;

— Поэлементные операции с матрицами;

— Вычисление скалярного и векторного произведения векторов;

— Вычисление суммы компонент вектора;

— Определение столбца матрицы;

— Транспонирование матрицы.

Кроме того в система содержится ряд функций, наиболее частые:

— matrix(m, n, f) – создает и заполняет матрицу размерностью m

x n, элемент которой, расположенный в i-той строке, j-м столбце, равен значению f(i,j) функции f(x,y) $

— diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;

— indentity(n) – создает единичную матрицу порядка n;

— augment(A,B) – формирует матрицу, в первых столбцах которой содержится матрица А, а в последних – матрица В;

— stack(A, B,) – формирует матрицу, в первых строках которой матрица А, а в последних – матрица В;

— rows(A) – Вычисление числа строк в матрице А;

— cols(A) – вычисление числа столбцов в матрице А;

— max(A) – вычисление наибольшего элемента в матрице А;

— rank(A) – вычисление ранга матрицы А

Матричные вычисления в MATLAB

В системе MatLab основной единицей данных является матрица, поэтому система имеет обширный набор стандартных функций и операций по обработке матриц, который позволяет:

— формировать новые матрицы стандартного вида;

— выполнять матричные арифметические операции;

— вычислять матричные характеристики и математические функции.

Для формирования новых матриц стандартного вида применяются следующие системные функции:

rand(M,N) – формирует прямоугольную матрицу размерностью M×N, элементами которой являются случайные числа в интервале (0.0; 1.0), функция rand без параметров формирует одно случайное число в том же интервале.

ones(M,N) формирует единичную матрицу размерностью M×N.

zeros(M,N) формирует матрицу размерностью M×N, состоящую из нулей.

diag(V) создает диагональную матрицу, в которой элементы вектора V являются элементами главной диагонали.

Матричные арифметические операции представлены следующими:

A+B , A—B матричное сложение и вычитание. Оба операнда этой операции должны иметь одинаковую размерность, если они являются матрицами. поэлементное возведение матрицы в степень.

Оба операнда этих операций должны иметь одинаковую размерность, или один из них должен являться скалярной величиной.

Операция «апостраф» ′ вычисляет комплексно сопряженную транспонированную матрицу.

Операция «точка апостраф» .′ вычисляет транспонированную матрицу.

Система содержит стандартные функции, позволяющие вычислять различные характеристики матриц:

det(A) вычисляет определитель матрицы;

trace(A) вычисление следа матрицы;

rank(A) вычисление ранга матрицы;

inv(A) вычисление обратной матрицы.

Глава 99. Приложение В. Применение MathCad для решения математических задач

Решение системы линейных алгебраических уравнений методом Гаусса:

1.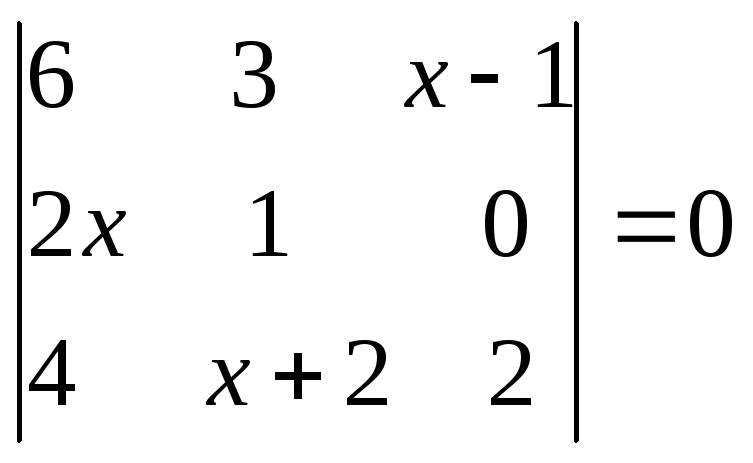 Вводите матрицу системы и матрицу-столбец правых частей.

2. Сформируйте расширенную матрицу системы.

3. Приведите расширенную матрицу системы к ступенчатому виду.

4. Сформируйте столбец решения системы.

Пример

Пусть A — матрица системы, B — матрица-столбец правых частей, Ar — расширенная матрица системы, Ag — расширенная матрица системы в ступенчатом виде, X — столбец решения системы.

Примечание

ORIGIN := 1 — установка нумерации элементов матриц с единицы.

Augment – функция объединения матриц.

Rref – функция прямого и обратного хода Гаусса.

Submatrix – функция выделения подматрицы с указанными диапазонами из большей матрицы.

Решение системы линейных алгебраических уравнений по формулам Крамера:

1. Вводите матрицу системы и матрицу-столбец правых частей.

2. Вычислите определитель матрицы системы. Если определитель отличен от нуля, то система имеет единственное решение.

3. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей.

4. Найдите решение системы по формулам Крамера.

Пример

Решение системы линейных алгебраических уравнений матричным методом:

1. Введите матрицу системы и матрицу-столбец правых частей.

2. Определите решение системы по формуле X = A-1B.

Пример

Решение неоднородной системы линейных алгебраических уравнений:

1. Введите матрицу системы и расширенную матрицу системы для правой части.

2. Вычислите ранги основной матрицы и ранги расширенной матрицы системы.

3. Приведите расширенную матрицу совместной системы к ступенчатому виду.

4. Определите базисные и свободные переменные.

5. Запишите эквивалентную систему и разрешите ее относительно базисных переменных.

6. Запишите общее решение системы.

7. Найдите частное решение системы.

Пример

Общее и частное решение системы:

Определение функций

Функция в MathCad должна иметь имя и параметры, перечисленные в скобках. Для получения значения функции в точке, вводится имя функции, указывается в скобках значение аргумента и вводится знак равенства.

Пример

Для ввода составных функций можно пользоваться кнопками панели программирования.

Пример

Построение графиков функций

Для построения графиков функции используется объект X-Y Plot. В помеченной позиции возле оси абсцисс вводится имя аргумента, а в позиции возле оси ординат – имя функции. Если нужно построить одновременно графики нескольких функций, вводятся их имена через запятую. Вместо имени функции можно ввести выражение для ее вычисления. Параметры изображения проще всего изменить, щелкнув дважды по полю графика и установив настройки в соответствующих окнах диалога.

Пример

Графики функций, заданных в параметрической форме, строятся аналогично. Отличие состоит в том, что позициях аргумента и функции вводятся выражения или имена соответствующих функций параметра.

Пример

Вычисление пределов

Три нижние кнопки панели Calculus(Вычисление) предназначены для вычисления пределов. Необходимо также пользоваться первой кнопкой со стрелкой на панели символьных операций Symbolic(Символьный).

Пример

Исследование функций

Порядок исследования:

1. Определите функцию f(x) и постройте ее график.

2. Найдите точку пересечения с осью ординат, вычислив f(0). Сравните с данными на графике.

3. Найдите точки пересечения с осью абсцисс, решив уравнение f(x) = 0. Сравните с данными на графике.

4. Проверить четность (нечетность, периодичность) функции.

5. Найдите точки разрыва функции, вычислите соответствующие односторонние пределы, запишите уравнения вертикальных асимптот. Сравните с данными на графике.

6. Вычислите пределы для определения вертикальных и наклонных асимптот. Изобразите наклонные асимптоты на графике.

7. Найдите нули производной, решив уравнение F’(x) = 0.

8. Вычислите и запишите координаты точек экстремума.

9. Постройте график второй производной.

10. Укажите тип точек экстремума (максимум/минимум).

11. Найдите нули второй производной, решив уравнение F’’(x) = 0.

12. Вычислите и запишите координаты точек перегиба.

13. Опишите интервалы выпуклости и вогнутости функции

Пример

Примечание

Функция root(F(X), X) решает уравнение F(X) = 0 относительно переменной X.

Вычисление интегралов

Для того чтобы вычислить неопределенный или определенный интеграл, необходимо воспользоваться соответствующими кнопками на панели Calculus(Исчисление).

Пример

Числовые ряды

Сходимость радов проверяется достаточно легко с помощью кнопки символьных вычислений.

Пример

< Предыдущая

Как транспонировать матрицу в маткаде

Mathcad Матрицы

Указываем размерность матрицы, rows – количество строк, columns – количество столбцов. Жмем Ок.

Последний элемент матрицы равен (нумерация первого элемента начинается с нуля)

Найдем максимальное значение матрицы max(X)

Найдем минимальное значение матрицы min(X)

Среднее значение матрицы равно

Первая матрица-столбец равна

Транспонирование матрицы в Mathcad X T

Вычисление обратной матрицы

Вычисление определителя матрицы

Умножение матрицы на матрицу

Сложение матриц — сумма элементов матрицы Mathcad

Возведение матрицы в степень

Далее, создадим две матрицы в виде векторов 3×1 и 1×3

Здесь A – матрица-столбец; B – матрица-строка

Первый элемент вектора A (нумерация начинается с нуля) равен

Количество элементов в матрице-столбце через функцию length(A) равно

Найдем значения для функции ln x, подставив значения матрицы A

Сортировка вектора sort(А)

Количество элементов в векторе rows(A), cols(A)

Векторное произведение в Mathcad

1678

Возможности и функции MATHCAD в матричных исчислениях

Матричные вычисления можно условно разделить на несколько типов. Первый тип — это простейшие действия, которые реализованы операторами и несколькими функциями, предназначенными для создания, объединения, сортировки, получения основных свойств матриц и т. п.

Второй тип — это более сложные функции, которые реализуют алгоритмы вычислительной линейной алгебры, такие как решение систем линейных уравнений, вычисление собственных векторов и собственных значений, различные матричные разложения.

Простейшие операции с матрицами

Простейшие операции матричной алгебры реализованы в MATHCAD в виде операторов. Операторы по смыслу максимально приближены к их математическому действию. Каждый оператор выражается соответствующим символом. Рассмотрим матричные и векторные операции MATHCAD. Векторы являются частным случаем матриц размерности (nx1), поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены (например, некоторые операции применимы только к квадратным матрицам (nxn)). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.

Непосредственное проведение векторных операций над строками, т. е. матрицами (1xn), невозможно; для того чтобы превратить строку в вектор, ее нужно предварительно транспонировать.

Транспонирование

Транспортированием называют операцию, переводящую матрицу размерности (nxm) в матрицу размерности (mxn), делая столбцы исходной матрицы строками, а строки — столбцами.

Рисунок 1 — Транспонирования матриц.

Ввод символа транспонирования (TRANSPOSE) осуществляется с помощью панели инструментов MATRIX или нажатием клавиш <CTRL>+<!>. He забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода.

Сложение

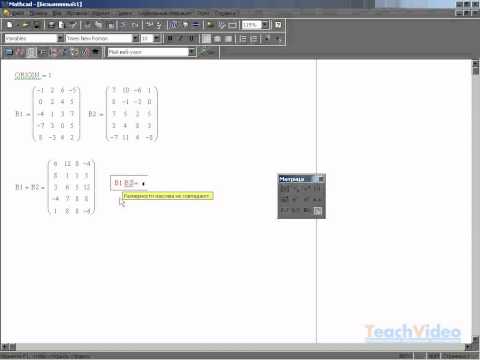
В MATHCAD можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются символы <+> или <-> соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых.

Рисунок 2 — Сложение и вычитание матриц.

Кроме сложения матриц, MATHCAD поддерживает операцию сложения матрицы со скаляром. Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.

Рисунок 3 — Сложение матрицы со скаляром.

Результат смены знака матрицы эквивалентен смене знака всех ее элементов. Для того чтобы изменить знак матрицы, достаточно ввести перед нейзнак минуса, как перед обычным числом.

MathCAD — это просто! Часть 10. Работа с векторами и матрицами

Снова здравствуйте. Мы с вами успели вполне успешно закончить со школьной алгеброй, и, значит, можем переходить к более сложным вещам — например, к тому разделу математики, который в университетах обычно называют линейной алгеброй. Конечно, раздел этот весьма и весьма обширен, и нечего даже думать о том, чтобы охватить хотя бы большую его часть. Тем не менее, нам с вами, я так думаю, кое-что из него научиться использовать практически вполне по силам — к примеру, мы можем научиться работать в MathCAD’е с векторами и матрицами. Эти два понятия — важнейшие математические абстракции, роль которых трудно переоценить в научно-техническом прогрессе. Ведь именно применение векторов и векторного анализа позволило в свое время Оливеру Хевисайду сократить количество уравнений Максвелла, описывающих электромагнитное поле, с двух десятков до всего лишь четырех. До векторного анализа, я так думаю, мы с вами в свое время еще доберемся, ну, а пока займемся более прозаическими вещами. Какими именно? Думаю, все станет ясно, если вы продолжите читать эту статью.

Немного об элементах матриц

Хотя дальше мы будем иметь дело и с векторами, и с матрицами, я краткости ради буду говорить просто «матрица», подразумевая, что под вектором мы будем иметь в виду частный случай матрицы, а именно ту ее разновидность, которая представляет собой одиночный столбец. Если же вектор будет представлять собой строку, то это будет специально оговорено. Впрочем, думаю, до этого дело вряд ли дойдет. С матрицами, вообще говоря, мы с вами работать уже немного умеем. Ну, не то чтобы прямо так вот работать — по крайней мере, вводить их в MathCAD’е мы уже вводили. Тем не менее, думаю, будет не лишним напомнить, что ввести в рабочую область матрицу можно с помощью кнопки Matrix or Vector, расположенной на панели Matrix, либо с помощью сочетания горячих клавиш Ctrl+M. Впрочем, мы с вами пока не затрагивали один небольшой, но крайне важный момент, а именно как обращаться в вычислениях не к матрице целиком, а к отдельным ее элементам. Сделать это, на самом деле, очень просто. Пусть у нас задана квадратная матрица X размером два на два элемента. Верхний левый элемент будет иметь индексы 0,0; нижний правый, соответственно, будет иметь индексы 1,1. То есть, как видите, элементы матрицы нумеруются с нуля. Это, в общем-то, довольно удобно, однако, если для вас привычнее нумеровать их с единицы, или, скажем, с 1024-х, то можно поменять значение встроенной переменной ORIGIN, введя в самом начале документа MatchCAD в строку (без кавычек). Или, соответственно, «ORIGIN := 1024». Можно поменять значение переменной и в окне опций MathCAD’а, выбрав в меню Tools пункт Worksheet options и на вкладке Built-In Variables поменяв значение переменной ORIGIN на нужное вам.

Так вот, вернемся к нашим элементам матрицы. Чтобы «вынуть» из нее первый элемент, нужно написать следующее: X0, 0. Для того, чтобы записать индексы внизу от имени переменной, которая обозначает матрицу, можно воспользоваться кнопкой Subscript со все той же панели инструментов для матричных и векторных вычислений или с клавиатуры перейти в нижний индекс клавишей «[» (русское «х»). Обратите внимание, что для разделения индексов, обозначающих строку и столбец, используется запятая. Элементы матрицы можно не только извлекать из матрицы, заданной таблично. Вы можете задать несколько элементов с соответствующими индексами по ходу вычисления, а после уже MathCAD самостоятельно сформирует из них матрицу (но только когда вы зададите уже все ее элементы — в противном случае незаданным элементам будут присвоены нулевые значения). Вы можете использовать ранжированные переменные для задания элементов матрицы. Временами это бывает не просто удобно, а очень удобно. Так, к примеру, можно задать для матрицы X следующую формулу, описывающую значения каждого ее элемента i-й строки и j-го столбца: Xi, j := i * j. Перед таким определением элементов матрицы остается только определить диапазон, в котором будут изменяться i и j. Я для примера взял значения i := 0..5 и j := 0..5, но вы, конечно же, можете установить любой другой нужный вам диапазон в зависимости от требований вашей задачи, решаемой с помощью матриц в среде MathCAD.

Операции над матрицами

Конечно, у применения матриц в реальных задачах существует множество интересных и не очень аспектов, однако все они рано или поздно упираются в необходимость проведения с матрицами простых алгебраических операций. Проводить их вручную — задача трудоемкая, и можно потратить время с гораздо большей пользой, переложив рутинную работу на MathCAD. Для начала познакомимся с теми функциями, которые собственно никаких математических операций не выполняют, но при этом являются весьма важными в действиях с матрицами. Эти функции позволяют объединять две матрицы в одну (не складывать матрицы, а просто объединять их элементы) и выделять из матрицы другую матрицу. Первая из функций — augment. Она объединяет две матрицы, имеющие одинаковое число строк, таким образом, что из них образуется одна, в которой элементы этих двух располагаются, что называется, «плечом к плечу». В качестве аргументов этой функции нужны только две объединяемые матрицы. Ее аналог для тех матриц, которые имеют одинаковое число столбцов, и должны быть объединены одна над другой, является функция stack. Ее аргументами тоже должны быть две объединяемые матрицы. Функция же, которая не объединяет, а, напротив, «разрезает» матрицы, имеет название submatrix. Для нее нужно указывать имя матрицы, из которой мы хотим выделить подматрицу, и координаты элементов новой матрицы в старой матрице. То есть для того, чтобы вырезать матрицу 4х4 из верхних левых элементов матрицы размером 5х5, нам нужно вызывать эту функцию со следующими параметрами: submatrix(Y, 0, 4, 0, 4). Здесь Y — это, конечно же, имя матрицы размером 5х5 элементов. Демонстрацию использования всех этих функций применительно к конкретным матрицам можно увидеть на соответствующей иллюстрации к статье.

Теперь, я так думаю, самое время перейти уже к арифметическим операциям над матрицами. Вы увидите, что их использование в MathCAD не потребует от вас никаких специальных знаний в области линейной алгебры — не считая, конечно, общих представлений о том, как работают матричные операции, для понимания того, что может получиться в их итоге. MathCAD хорош для пользователя тем, что позволяет ему работать с векторами и матрицами точно так же, как с обычными скалярами, сиречь переменными, содержащими исключительно и только действительные числа. Попробуйте задать две матрицы (я их назвал aa и bb), а затем применить к ним операцию сложения точно так же, как когда-то применяли ее к обыкновенным числам. Конечно, для того, чтобы матрицы можно было складывать, они должны иметь одинаковые размеры. Точно так же можете попробовать вычесть из одной матрицы другую или перемножить их. Вы увидите, что MathCAD успешно справляется с подобными задачами, не напрягая пользователя излишними вычислениями.

Транспонировать матрицы в MathCAD’е ничуть не сложнее, чем их складывать или перемножать. Вычислять обратные матрицы, впрочем, тоже. Во всех этих задачах помогут соответствующие операторы с Они обозначены на ней теми же значками, что и в учебниках по линейной алгебре, а потому пользователю, хотя бы минимально знакомому с матричным исчислением, все должно быть просто и понятно. Нужно только помнить, что нельзя вычислить обратную матрицу для той матрицы, которая является вырожденной (то есть имеет нулевые или пропорциональные друг другу строки или столбцы). Для того, чтобы не останавливаться излишне подробно на этих простых операциях, просто приведу иллюстрацию, демонстрирующую их практическое использование. Думаю, у читателей не возникнет никаких проблем ни с транспонированием, ни с вычислением обратной матрицы с помощью MathCAD.

Еще одной часто выполняемой операцией является вычисление детерминанта, или определителя матрицы. Думаю, что совсем не огорчу вас известием о том, что в MathCAD и с определителями работать так же просто, как и со всем остальным, связанным с матрицами. За его вычисление отвечает кнопка Determinant, расположенная, конечно же, на панели Matrix. Поскольку детерминант в MathCAD’е, как и вообще в линейной алгебре, обозначается с помощью символов прямых черт, ограничивающих матрицу (или имя переменной, ее обозначающей), то вполне логично, что вставить эти самые прямые черты в текст выражения можно с помощью соответствующей клавиши на клавиатуре: Shift + \. Думаю, этой несложной комбинацией будет пользоваться все же удобнее, чем искать каждый раз нужную кнопку на панели инструментов MathCAD’а.

Внешний вид матриц

Мы с вами, конечно же, далеко еще не закончили свое знакомство с матрицами в MathCAD’е, однако, думаю, на сегодня уже непосредственной математики хватит. В конце статьи я лучше расскажу о том, как можно изменить способ отображения матриц в среде MathCAD — возможно, кому-то из читателей этой статьи эта информация будет полезной и небезынтересной.

Дело в том, что MathCAD может отображать матрицы не только в привычном всем виде чисел, заключенных в скобки, но и в виде таблиц. Если вы используете этот математический пакет для каких-либо статистических расчетов и при этом работаете с большими массивами данных, то, безусловно, такое отображение матриц будет более предпочтительным для вас, чем традиционное. Для изменения способа отображения матриц дважды кликните по нужной матрице и в появившемся окне перейдите на вкладку Display Options. Далее в поле Matrix display style выберите значение Table. Матрица приобретет вид точно такой, как на соответствующей иллюстрации к этой статье.

Внешний вид таблицы можно также настроить далее, кликнув по ней правой кнопкой мыши и выбрав пункт Properties. В появившемся окне можно снять птичку с пункта Show column/row labels, чтобы убрать отображение нумерации строк и столбцов в матрице, представляемой в виде таблицы. На вкладке Data Range можно выбрать диапазон отображаемых строк и столбцов матрицы, что также полезно для матриц, содержащих большое количество элементов.

Ну что ж, на сегодня, думаю, достаточно. Это только начало работы с матрицами — в следующий раз мы поговорим о гораздо более интересных вещах, чем просто сложение, транспонирование и вычисление детерминанта.

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 23 за 2008 год в рубрике soft

3.2 Запись решения в mathcad.

_{Рис 3.1 — изображение векторов на векторной плоскостиMathcad.}

4. Расчет выражений для комплексных чисел:

Рассчитать для Z₁, Z₂, Z₃, Z₄ следующие выражения:

4. 1. Произведение расчетов вручную

1)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

2)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

3)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

4)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

5)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

6)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

7)Представим выражения в алгебраической форме:

Представим выражения в показательной форме:

4.

2. Запись решения в mathcad :

_{Рис.4.1 – расчет выражений для комплексных чисел вMathcad.}

4. Решение систем уравнений.

Решить систему уравнений, определить x и y: 1) методом Крамера; 2)при помощи специализированных функций Mathcad.

4. 1. Теоретические сведения.

Для системы n линейных уравнений с и неизвестными (над произвольным полем)

с определителем матрицы системыА, отличным от нуля, решение записывается в виде:

(j-ый столбец матрицы системы заменяется столбцом свободных членов).

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А: и п вспомогательных определителей, которые получаются из определителя заменой 1-го столбца столбцом свободных членов.

Рассмотрим систему линейных уравнений вида

Введём следующие определители:

a) Случай неоднородной системы (не все равны нулю):

— если , то система имеет единственное решение, которое определяется по формулам Крамера

— если , а хотя бы один из вспомогательных определителей не равен нулю, то система решений не имеет,

— если все четыре определителя равны нулю, то система имеет бесчисленное множество решений.

б) Случай однородной системы (все равны нулю):

— если ,то система имеет единственное (тривиальное) решение

— если, то решений у однородной системы бесчисленное множество.

Если система имеет хотя бы одно решение, то она совместна. В противном случае система уравнений несовместна.

4. 2. Решение

Введём главный и вспомогательные определители:

Вычислим главный определитель:

, значит система имеет единственное решение, которое определяется по правилу Крамера:

Далее найдём вспомогательные определители:

Найдём неизвестные:

Итак, получили решение системы уравнений:

4. 3. Запись решения в MATHCAD

Рис.5.1 – решение систем уравнений в Mathcad.

4. Построение графиков функций

   1. Условие задания

Построить на интервале 2Т графики следующих функций:

Где A=22, B=35, C=56, D=45.

4. 2. Запись решения в MATHCAD

Рис.6.1 – построение графиков функций в Mathcad.

4. Расчет средних значений для функции за период.

Рассчитать средние значения за период и средние значения по модулю за период для каждой из трёх функций задания 6, используя следующие формулы:

4. 1. Решение

Период данных функций определим по графикам в задании 6. Как видно, для всех трёх функций он имеет одно значение:

Далее рассчитаем средние значения функций

4. 2. _{Запись решения вMATHCAD.}

_{Рис. 7.1 – расчет средних значений функции за период вMathcad.}

Операции с векторами и матрицами, матричные функции в математическом пакете MathCad

 

Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.

Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).

Матричные вычисления в MathCAD можно условно разделить на три основных типа.

К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).

Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.

И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.

В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.

Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: . А для того, чтобы взять элемент матрицы В, расположенный на пересечении 3-ей строчки и 4-го столбца нужно записать: .

Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.

В системе предусмотрены различные возможности задания векторов и матриц:

1. Определение матрицы последовательным заданием каждого элемента.

2. С помощью индексированных переменных.

3. С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.

4. Задание с помощью элементов программирования.

5. Применение встроенных функций.

6. Через связь с другим приложением, например Excel.

7. Создание таблицы данных.

8. Чтение из внешнего файла.

Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.

Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.

Решение. Предоставим два варианта решения этой задачи:

1. с помощью индексированной переменной;

2. с помощью команды Insert→Matrix.

Вариант а

Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x.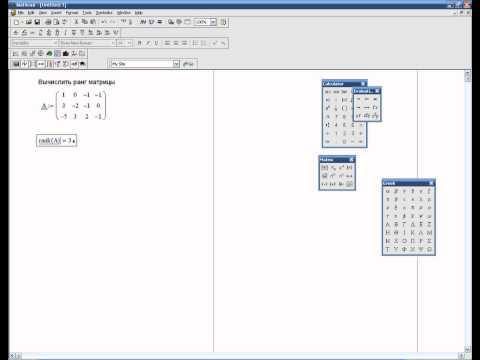 Формирование вектора представлено на рис. 3.1.

Рис. 3.1. Формирование вектора с использованием индексированной переменной

Вариант b

Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.

После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.

 

 

Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»

 

Пример 2.  В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.

Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.

Рис. 3.3. Чтение данных из файлов

 

С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: —, +, *, … .

На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.

Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x). 

 

Х-1 – получить обратную матрицу |X| – вычислить детерминант МТ – транспонировать М< > – из матрицы взять вектор-столбец v – получить сумму элементов –скалярное произведение векторов –векторное произведение векторов

 Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»

 

На рис. 3.5 представлены вычисления с использованием операций над матрицами.

 

Рис. 3.5. Примеры матричных вычислений в MathCAD

 

Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.

Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.

 

Рис. 3.6. Формирование диагональной матрицы

 

Пример 4.  Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).

Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.

 Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»

 

Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.

Решение.  Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.

 Рис. 3.8. Объединения двух матриц по правилу «друг под другом»

 

Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.

Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9. 

Рис. 3.9. Выделение подматрицы из заданной матрицы

 

Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.

Решение. Для получения векторных значений можно воспользоваться командой М^{< >} (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.

 Рис. 3.10. Выделение векторных значений из заданной матрицы

 

Пример 8.  Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.

Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.

 

Рис. 3.11. Выделение минора из заданной матрицы

 

Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.

Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.

Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.

 

Рис. 3.12. Выделение векторных значений из заданной матрицы

 

Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор — строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.

Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).

Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.

Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.

Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.

Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:

Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.

Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:

 

Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).

Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.

Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:

Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.

Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:

Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:

(3.1)

 

Введем следующие обозначения:

 

, (3. 2)

здесь:

А – матрица коэффициентов;

В – вектор свободных членов;

х – вектор неизвестных.

В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:

 

Ax=B. (3.3)

 

Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.

В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:

1. Помножим уравнение (3. 3) слева на матрицу, обратную к матрице А:

. (3.4)

2. Воспользуемся свойством, что , гдеЕ – единичная матрица. Тогда уравнение (3.4) примет вид:

. (3.5)

3. Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:

, (3.6)

где (3.6) – решение системы (3.3).

Пример 15. Требуется найти решение следующей системы линейных уравнений:

Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.

Рис. 3.13. Решение СЛАУ пакете MathCAD

12.3: Матрица, обратная, ранг и определитель

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

85048

• Кэри Смит
• Окснард Колледж

Кэри Смит

Рассмотрим эту квадратную матрицу:

В = [1 2 3;
4 5 6;
7 8 0]

Матрица, обратная B, IB, является такой матрицей, что B*IB = единичная матрица и IB*B = единичная матрица.

Не каждая квадратная матрица имеет обратную. Например, эти матрицы 3×3 не имеют инверсий:

С = [1 0 0;

0 0 0;

0 0 0]

Д = [1 0 0;

0 2 3;

1 2 3]

Матрица, не имеющая обратной, называется «сингулярной» матрицей.

Ранг матрицы — это количество независимых строк.
Когда ранг квадратной матрицы равен количеству строк, она имеет «полный ранг» и несингулярна, поэтому имеет обратную.

Ранг матрицы можно вычислить с помощью функции MATLAB rank():

B_rank = rank(B) % = 3. Поскольку B имеет 3 строки и столбца, а его ранг равен 3, B имеет полный ранг и несингулярна.

C_rank = rank(C) % = 1. C не имеет полного ранга.

D_rank = rank(D) % = 2. D не имеет полного ранга.

Другой характеристикой квадратной матрицы является ее определитель.
Если определитель не равен 0, он имеет полный ранг. Положительный или отрицательный определитель не имеет значения. Когда определитель не равен 0, матрица невырожденна и может быть инвертирована. Расчет обратного деления на определитель матрицы, поэтому он не может быть равен нулю.

Определитель матрицы можно вычислить с помощью функции MATLAB det():

B_det = det(B) = 27 => B неособое и может быть инвертировано.

C_det = det(B) = 0 => C сингулярна и не может быть инвертирована.

D_det = det(B) = 0 => C сингулярна и не может быть инвертирована.

Обратная квадратная матрица может быть вычислена с помощью функции MATLAB inv():

Вт = инв(В)

% -1,7778 0,8889 -0,1111
% 1,5556 -0,7778 0,2222
% -0,1111 0,2222 -0,1111

Проверить обратное:
IB1 = B*W
% 1 0 0
% 0 1 0
% 0 0 1

Это единичная матрица 3×3

Хотя умножение матрицы в общем случае не является кумулятивным, умножение матрицы на ее обратную является кумулятивным. Тот же результат возникает, когда порядок матрицы и ее обратной матрицы меняется на противоположный.
IB2 = W*B Вычисляет тот же результат.

Пример \(\PageIndex{1}\) Обратная матрица Пакаля 3×3

C = паскаль(3)

Вычислить ранг и определитель матрицы C.

Если матрица невырожденная, вычислите ее обратную, C_inv/

Затем проверьте, что C_inv*C является единичной матрицей.

Решение

det_C = det(C) % 1 Несингулярный
C_rank = ранг(C) % 3 Несингулярный
C_inv = inv(C)
C_inv*C

.

Пример \(\PageIndex{2}\) Сингулярные матрицы

Вычислите ранг и определитель этих сингулярных матриц:

%% Сингулярная матрица #1
% 2-я строка кратна 1-й строке,
% поэтому не независимый
S1 = [ 1 2 3
2 4 6
7 8 9]

S2 = [ 1 2 3
4 5 6
5 7 9]

S3 = [ 1 0 0 0 0
0]

Решение

Добавьте пример текста сюда.

Для получения дополнительной информации прочитайте https://en.Wikipedia.org/wiki/Invertible_matrix

Упражнение \(\PageIndex{1}\) Операции над «Гильбертовой» матрицей

Трой Симерс

Рассмотрим матрицу Гильберта 5 x 5″
H5 = [1 1/2 1/3 1/4 1/ 5;
1/2 1/3 1/4 1/5 1/6;92 и H5. /H5 и объясните свои ответы.
г. Ссылаясь на H5, создайте матрицу, состоящую из 2-й и 3-й строк H5 (не вводите данные заново).

Ответить

Добавьте сюда текст. Не удаляйте этот текст первым.

.

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Кэри Смит

   Лицензия

   CC BY-NC-SA

   Показать оглавление

   да

2. Теги

   1. от
   2. определитель
   3. Матрица, обратная
   4. ранг
   5. единственное число

Как найти определитель матрицы в Matlab?

По какой формуле находится определитель матрицы?

Определитель: |А| знак равно a (ei — fh) — b (di — fg) + c (dh — eg) . Определитель A равен «a умножить на e x i минус f x h минус b умножить на d x i минус f x g плюс c умножить на d x h минус e x g». Это может показаться сложным, но если вы внимательно наблюдаете за узором, это действительно просто!

Как вы трассируете матрицу в Matlab?

трассировка (функции MATLAB) b = trace(A) — сумма диагональных элементов матрицы A .

Как найти номер условия в Matlab?

Описание. C = cond( A ) возвращает номер условия 2-нормы для инверсии, равный отношению наибольшего сингулярного значения A к наименьшему. C = cond( A , p ) возвращает номер условия p -нормы, где p может быть 1 , 2 , Inf или ‘fro’ .

О чем говорит определитель матрицы?

Определитель квадратной матрицы — это единственное число, которое, помимо прочего, может относиться к площади или объему области. В частности, определитель матрицы отражает то, как линейное преобразование, связанное с матрицей, может масштабировать или отражать объекты .

Родственные

Как вычислить определители?

Для вычисления определителя необходимо выполнить следующие действия. Установите матрицу (должна быть квадратной). Приведите эту матрицу к форме эшелона строк, используя элементарные операции со строками, чтобы все элементы ниже диагонали были равны нулю. Умножить элементы главной диагонали матрицы — вычисляется определитель .

Родственные

Является ли Det AB )= det A det B?

Доказательство состоит в том, чтобы вычислить определитель каждой элементарной матрицы операций со строками, E, а затем использовать предыдущую теорему. det(AB) = det(A) det(B) . Доказательство: если A необратима, то AB необратима, тогда теорема верна, потому что 0 = det(AB) = det(A) det(B)=0.

Родственные

Как найти определитель матрицы 3×3 с помощью кофакторов?

Чтобы вычислить определитель матрицы 3 × 3, мы выбираем любую строку или столбец матрицы — он будет содержать три элемента. Затем мы находим трех произведений, умножая каждый элемент в выбранной нами строке или столбце на его кофактор . Наконец, мы суммируем эти три произведения, чтобы найти значение определителя.

Родственные

Что такое трассировка в Matlab?

Описание. пример. b = trace( A ) вычисляет сумму диагональных элементов матрицы A : tr ( A ) = ∑ i = 1 n a i i = a 11 + a 22 + … + a n n .

Родственные

Как написать COS 1 в Matlab?

Y = acos( X ) возвращает арккосинус (cos ^{— 1} ) элементов X в радианах. Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале [-1, 1] acos(X) возвращает значения в интервале [0, π].

Связанные

Как написать единичную матрицу в Matlab?

I = eye( n ) возвращает единичную матрицу размера n на n с единицами на главной диагонали и нулями в остальных местах. I = eye( n , m ) возвращает матрицу размером n на m с единицами на главной диагонали и нулями в других местах. I = eye( sz ) возвращает массив с единицами на главной диагонали и нулями в других местах. Вектор размера, sz , определяет size(I) .

Связанные

Как вычислить определитель матрицы?

• Чтобы вычислить определитель вам необходимо сделать следующие шаги. Установите матрицу (должна быть квадратной). Приведите эту матрицу к форме эшелона строк, используя элементарные операции со строками, чтобы все элементы ниже диагонали были равны нулю. Умножьте элементы главной диагонали матрица — определитель равен вычислено .

Связанные

Что именно означает определитель матрицы?

• Определитель матрицы — это число , специально определенное только для квадратных матриц . Детерминанты — это математические объекты, которые очень полезны при анализе и решении систем линейных уравнений. Детерминанты также имеют широкое применение в технике, науке, экономике и социальных науках.

Связанные

Как взять определитель матрицы?

• Умножьте a на определитель матрицы 2×2, которая не находится в строке или столбце .

• Аналогично для b и c

• Суммируйте их, но помните минус в перед из в b

0 Связанные

Что представляет определитель матрицы?

• Определитель матрицы — это специальное число , которое можно вычислить из квадратной матрицы . Определитель сообщает нам о матрице то, что полезно в системе линейных уравнений, помогает нам найти обратную матрицу. Это также помогает нам в определении площади, объема, а также в определении якобиана.

общий Информация СМИ Нажмите галерея иллюстрация

Поделиться этой записью:

Исследование свойств определителей с помощью численных примеров

Сандра Акельбек
Государственный университет Вебера, математика

Профиль автора

Это задание является частью коллекции Преподавание вычислений в естественных науках с использованием MATLAB Рецензируемые учебные занятия.

Скрыть

Это задание было выбрано для обучения вычислениям в науках с использованием рецензируемой учебной коллекции MATLAB

Это мероприятие получило положительные отзывы в процессе рецензирования с участием пяти категорий. Пять категорий, включенных в процесс:

• Вычислительная, количественная и научная точность.
• Согласование целей обучения, мероприятий и оценок
• Педагогическая эффективность
• Прочность (удобство использования и надежность всех компонентов)
• Полнота веб-страницы ActivitySheet

Для получения дополнительной информации о самом процессе рецензирования см. https://serc.carleton.edu/teaching_computation/materials/activity_review.html.

Эта страница впервые опубликована: 16 августа 2018 г.

Резюме

Мы используем Matlab в качестве инструмента для обогащения элементарной линейной алгебры. В этом упражнении учащиеся исследуют численно свойства определителей, создавая и используя случайные матрицы. В частности, студент исследует, является ли определитель суммы матриц суммой определителей. Является ли определитель произведения произведением определителей? Какая связь между определителем матрицы и обратным к ней? Какая связь между определителем матрицы и ее транспонированием? Учащиеся также исследуют влияние операций над строками на определители.

Использовали эту активность? Поделитесь своим опытом и изменениями

Цели обучения

Целью этого задания является исследование свойств определителей. Учащиеся используют числовые примеры, чтобы выяснить, верно ли свойство для всех матриц. Например, верно ли, что определитель суммы матриц равен сумме определителей? Кроме того, учащиеся используют числовые примеры, чтобы найти или обнаружить различные свойства определителей. Например, каково отношение между определителем матрицы и ее обратным?

Matlab поможет учащимся установить различные свойства определителей. Как только учащиеся убедятся, что данное свойство имеет место, они попытаются доказать или обосновать его, используя знания, полученные в этом курсе.

Контекст для использования

«Исследование свойств определителей с использованием числовых примеров» — это классное задание, разработанное для класса «Элементарная линейная алгебра». Поскольку учащиеся исследуют несколько свойств детерминант, работа в классе может занять около часа.

Для выполнения этого задания учащиеся должны быть знакомы с основными операциями Matlab, такими как создание матриц, использование специальных матриц, например, генерация случайной матрицы или создание случайной матрицы с целочисленными элементами. Студенты также будут использовать матричные операции, такие как: сложение, вычитание, умножение, транспонирование, возведение в степень, обратное и нахождение определителя.

Описание и учебные материалы

Определите, верны ли следующие свойства.

Если утверждение кажется верным, создайте не менее 3 примеров матриц с целочисленными элементами и не менее двух примеров матриц со случайными (без целых чисел) элементами. Исследуйте матрицы размера 2, 3, 4 и проверьте более высокие порядки, такие как размер 10 или 12.

Если утверждение кажется неверным, создайте не менее двух примеров.

1. Проверить, является ли det (A+B) = det A + det B

2. Проверить, является ли det(AB) = det A det B

3. Сравнить определитель матрицы с определителем обратной матрицы. Что вы заметили?

4. Сравните определитель матрицы с определителем ее транспонирования.

5. Проверить, если det(3A) = 3detA ? Используйте матрицы разных размеров и используйте разные скаляры. Четко сформулируйте свой вывод.

6. Исследование влияния операций со строками на определители
а) Если поменять местами две строки матрицы, определитель останется прежним?

(b) Если одну строку умножить на скаляр, останется ли определитель тем же? Используйте матрицы разных размеров. Как это свойство соотносится со свойством, которое мы проверили в 5.

(c) Если одна строка изменяется на скалярное число, кратное другой строке, определитель тот же самый?
Раздаточный материал для учащихся (Acrobat (PDF) 218kB 10 августа 18)

Учебные заметки и советы

Это упражнение можно использовать в качестве вводного занятия при обучении различным свойствам определителей.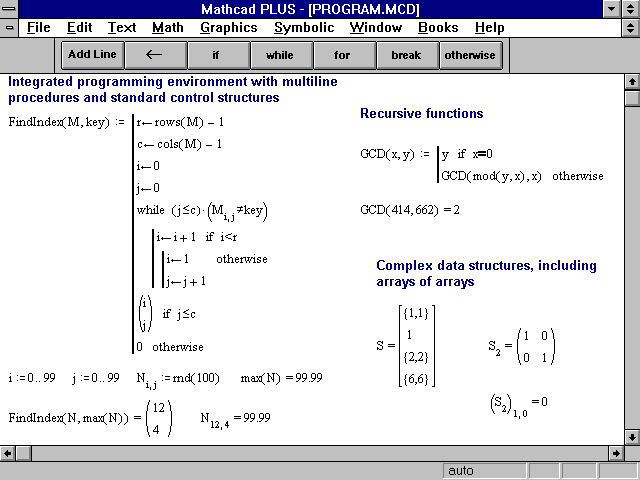 Преподаватель должен сначала объяснить, что такое определитель, и показать, как определитель можно вычислить вручную, используя определение определителей. Как только учащиеся поймут и смогут вычислить определители, они смогут исследовать различные свойства определителей.

Оценка

В конце занятия учащиеся обсуждают и доказывают все свойства, которые имеют место для определителей. Если учащийся сможет правильно определить каждое свойство, то преподаватель будет знать, что цели достигнуты.

Мы довольно часто собираем студенческие работы и оцениваем их как выполненные или неполные задания.

Ссылки и ресурсы

Подробнее Преподавательская деятельность »

Как найти определитель матрицы в Matlab?

Описание. d = det( A ) возвращает определитель квадратной матрицы A .

Посмотреть полный ответ на math.jhu.edu

Как найти определитель в MATLAB?

Перейти к функции:

d = det(X) возвращает определитель квадратной матрицы X . Если X содержит только целые числа, результат d также является целым числом.

Посмотреть полный ответ на math.jhu.edu

Как найти определитель матрицы с переменными в MATLAB?

B = det( A ) возвращает определитель квадратной матрицы символьных чисел, скалярных переменных или функций A .

Посмотреть полный ответ на mathworks.com

Как найти матрицу в MATLAB?

Описание. X = linsolve( A , B ) решает матричное уравнение AX = B, где B вектор-столбец. [ X , R ] = linsolve( A , B ) также возвращает обратную величину числа условия A, если A является квадратной матрицей. В противном случае linsolve возвращает ранг A .

Посмотреть полный ответ на mathworks.com

Что делает find() в MATLAB?

find (функции MATLAB) k = find(X) возвращает индексы массива X, которые указывают на ненулевые элементы. Если ничего не найдено, find возвращает пустую матрицу. [i,j] = find(X) возвращает индексы строк и столбцов ненулевых записей в матрице X .

См. полный ответ на ece.northwestern.edu

Matlab Раздел 30 Определитель матрицы, обратный, трассировка и ранг

Что такое матричная функция в MATLAB?

Матричная функция — это скалярная функция, которая отображает одну матрицу в другую. Предположим, что f(x) , где x — скаляр, имеет разложение в ряд Тейлора. Тогда матричная функция f(A) , где A — матрица, определяется рядом Тейлора для f(A) со сложением и умножением, выполняемым в матричном смысле.

Посмотреть полный ответ на mathworks.com

Как найти det матрицы 3×3?

Чтобы найти определитель матрицы 3×3, вы сначала берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому относится ваш первый выбранный элемент. принадлежит.

Посмотреть полный ответ на studypug.com

Как найти det матрицы 2×2?

Другими словами, чтобы найти определитель матрицы 2×2, выполните следующие действия:

1. Умножьте значения по диагонали слева вверху и справа внизу.
2. Умножьте значения по диагонали от левого нижнего угла к правому верхнему.
3. Вычесть второе произведение из первого.
4. Упростите, чтобы получить значение определителя 2 на 2.

Посмотреть полный ответ на Purplemath.com

Что такое формула определителя?

Определитель: |A| = ad − bc или определитель A равен a × d минус b × c. Это легко запомнить, когда вы думаете о кресте, где синий — положительный, идущий по диагонали слева направо, а красный — отрицательный, идущий по диагонали справа налево.

Посмотреть полный ответ на toppr.com

Что такое определитель в матрице?

Определение определителя матрицы. Определитель матрицы — это скалярное значение или число, вычисленное с использованием квадратной матрицы. Квадратная матрица может быть 2×2, 3×3, 4×4 или любого типа, например n×n, где количество столбцов и строк равно.

Посмотреть полный ответ на byjus.com

Какая из следующих команд используется для нахождения определителя матрицы?

Определитель матрицы вычисляется с помощью функции det MATLAB. Определитель матрицы A определяется как det(A).

Посмотреть полный ответ на tutorialspoint.com

Как сделать ссылку в MATLAB?

R = rref( A ) возвращает уменьшенную ступенчатую форму строки A с использованием исключения Гаусса-Жордана с частичным поворотом. R = rref( A , tol ) задает допуск поворота, который алгоритм использует для определения незначительных столбцов. [ R , p ] = rref( A ) также возвращает ненулевые опорные точки p .

Посмотреть полный ответ на mathworks.com

Как написать единичную матрицу в MATLAB?

I = eye( n ) возвращает единичную матрицу размера n на n с единицами на главной диагонали и нулями в других местах. I = eye( n , m ) возвращает матрицу размером n на m с единицами на главной диагонали и нулями в других местах. I = eye( sz ) возвращает массив с единицами на главной диагонали и нулями в других местах. Вектор размера, sz , определяет size(I) .

Посмотреть полный ответ на mathworks.com

Как найти определитель матрицы 2×3?

Невозможно найти определитель матрицы 2×3, потому что это не квадратная матрица.

Посмотреть полный ответ на byjus.com

Что такое определитель матрицы 1×1?

Определитель матрицы 1×1 — это само это число.

Посмотреть полный ответ на сайте mathinsight.org

Является ли Det A 2 Det a 2?

Условие det(A)=det(A2) эквивалентно det(A)=1, но это не означает, что A2 должно быть равно ±A или ±A−1. Например, возьмем A=(1101). так что det(A)=1=det(A2), но A2∉{A,A−1,−A,−A−1}.

Посмотреть полный ответ на math. stackexchange.com

Как ввести матрицу в MATLAB?

Чтобы ввести матрицу, используйте запятые в одной строке и точки с запятой для разделения столбцов. Мы можем определить размер вектора или матрицы с помощью команды size. На отдельные элементы матрицы можно ссылаться через индексы, заключенные в круглые скобки.

Посмотреть полный ответ на ewh.ieee.org

Что делает функция mat в MATLAB?

mat функция загрузки обрабатывает файл как данные ASCII. В зависимости от расположения вашего файла имя файла может принимать одну из этих форм. Укажите имя файла в имени файла. Если файл не находится в текущей папке или в папке на пути MATLAB, то задайте полный или относительный путь в имени файла.

Посмотреть полный ответ на mathworks.com

← Предыдущий вопрос
Зачем моему мужу секретный банковский счет?

Следующий вопрос →
Каков общий игровой идентификатор?

Функция MDETERM

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно. .. Меньше

В этой статье описаны синтаксис формулы и использование MDETERM функция в Microsoft Excel.

Описание

Возвращает определитель матрицы массива.

Синтаксис

MDETERM(массив)

Аргументы синтаксиса функции MDETERM:

Примечания

• Массив может быть задан как диапазон ячеек, например, A1:C3; как константа массива, например {1,2,3;4,5,6;7,8,9}; или как имя любого из них.

• MDETERM возвращает #VALUE! ошибка когда:

• Определитель матрицы представляет собой число, полученное из значений в массиве. Для массива из трех строк и трех столбцов A1:C3 определитель определяется как:

MDETERM(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)

• Определители матриц обычно используются для решения систем математических уравнений, включающих несколько переменных.

• MDETERM рассчитывается с точностью примерно до 16 цифр, что может привести к небольшой числовой ошибке, если расчет не завершен. Например, определитель сингулярной матрицы может отличаться от нуля на 1E-16.

Пример

Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.

Данные	Данные	Данные	Данные
1	3	8	5
1	3	6	1
1	1	1	0
7	3	10	2
Формула	Описание	Результат
=MDETERM(A2:D5)	Определитель матрицы выше	88
=MDETERM({3,6,1;1,1,0;3,10,2})	Определитель матрицы как константа массива	1
=МОПРЕДЕЛ({3,6;1,1})	Определитель матрицы в константе массива	-3
=MDETERM({1,3,8,5;1,3,6,1})	Возвращает ошибку, поскольку в массиве не равное количество строк и столбцов. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт