Основы работы в MathCAD, страница 5
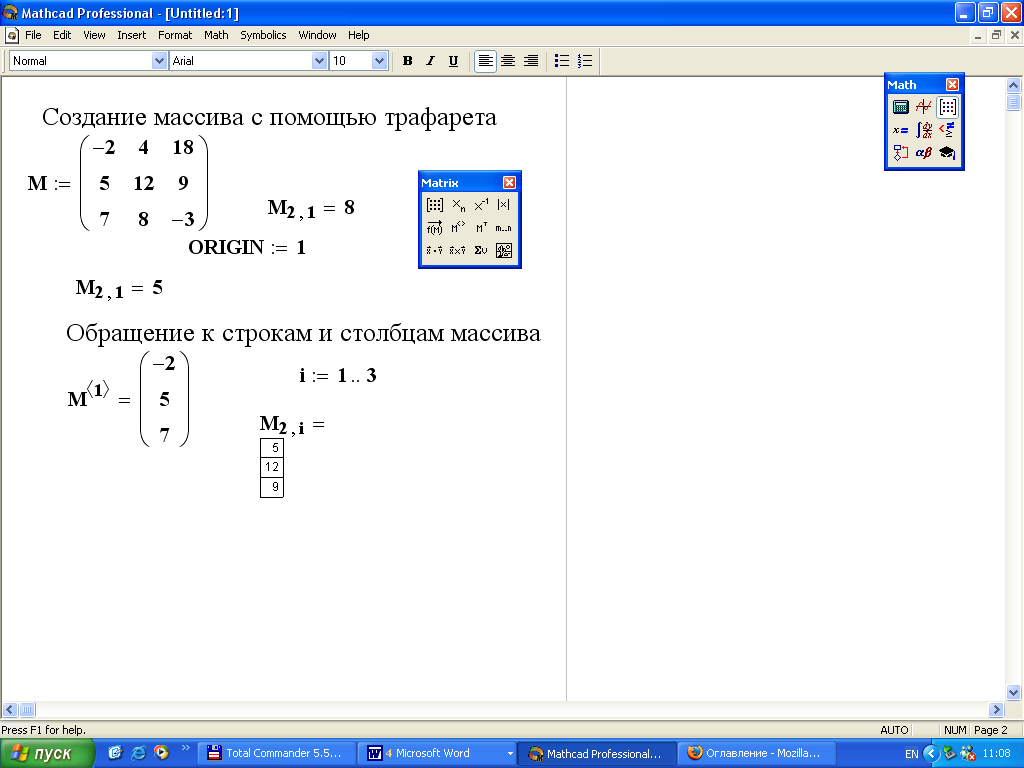
q Ввести имя переменной, например, cplM.
q Ввести знак присвоения, нажав клавиши «Shift» + «:»,
q Ввести имя матрицы, столбец которой надо присвоить переменной, например, M. ()
q Ввести верхний индекс, .
q
Варианты ввода нижнего индекса.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Ctrl» + «6» |
q ввести номер столбца, который надо считать, учитывая значение системной переменной ORIGIN, например, первый столбец ().
q Нажать клавишу «Enter» для завершения операции ().
2.2 Создание новых матриц из существующих массивов
Функции augment(A,B) и stack(A,B)
Функция augment(A,B) (где A,
B-
матрицы, имеющие одинаковое число строк) используется для создания нового
двумерного массива путем расположения матриц A и B бок о бок.
Функция stack(A,B) (где A, B- матрицы, имеющие одинаковое число столбцов) используется для создания нового двумерного массива путем расположения матрицы A над матрицей B.
На Рис. 2.4 приведен листинг с последовательностью действий при использовании функции augment(A,B) и stack(A,B).
Функция submatrix(A,ir,jr,ic,jc)
Функция submatrix(A,ir,jr,ic,jc) (где A- матрица, ir- начальный индекс строки, jr- конечный индекс строки, ic- начальный индекс колонки, jc — конечный индекс колонки) используется для создания нового двумерного массива путем копирования из массива А всех элементов, содержащихся в строках с ir по jr и столбцах с ic по jc.
На Рис. 2.5 приведен листинг с последовательностью действий при использовании функции submatrix(A,ir,jr,ic,jc).
2.3 Обработка массивов
Функции определения следа и ранга матрицы
Ранг матрицы равен порядку наибольшего отличного от нуля
минора этой матрицы. Эта величина служит для характеристики матрицы системы
линейных уравнений, а также как параметр, определяющий, базисом пространства
какой размерности может быть данное множество векторов.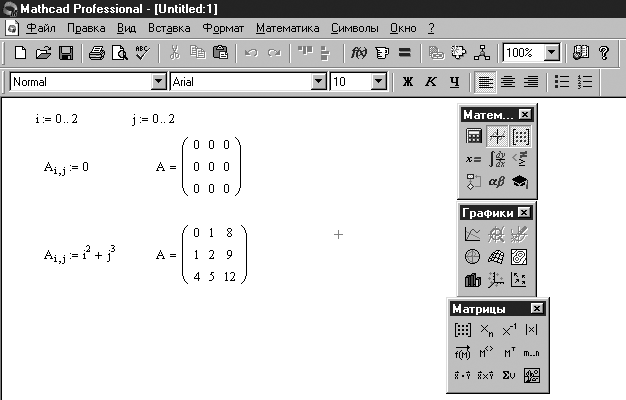
Следом называется сумма диагональных элементов матрицы.
Функция rank(M) (М- вещественная матрица) используется для определения ранга матрицы М.
Рис. 2.5. Использование функций augment(A,B) и stack(A,B)
Рис. 2.6. Использование функции submatrix(A,ir,jr,ic,jc)
Функция tr(M) (М- вещественная квадратная матрица) используется для определения следа матрицы М.
На Рис. 2.6 приведен пример использования функций rank(M) и tr(M).
Рис. 2.6. Использование функций rank(M) и tr(M)
Элементарные матричные вычисления
Арифметические операции со скалярами и матрицами
Сложение (вычитание) матрицы и скаляра.
В MathCAD к матрице может быть прибавлено (вычтено) любое число. При этом число будет прибавлено ко всем элементам (вычтено из всех элементов) исходной матрици.
Умножение (деление) матрицы и скаляра.
В MathCAD матрица
может быть умножена (поделена) на любое число. При умножении (делении) матрицы
на скаляр на него умножается каждый элемент исходной матрицы.
.
На Рис. 2.7 приведены примеры арифметических операций с матрицей и скаляром.
Рис. 2.8. Арифметические операции матрицы и скаляра
Сложение вычитание матриц
Для сложения и вычитания матриц используется функция + (или -). Матрицы должны быть одного размера. При суммировании (вычитании) двух матриц происходит их поэлементное суммирование (вычитание).
Варианты ввода функции.
Пиктограмма | ()в панели инструментов Calculator (Калькулятор) |
Клавиатура | клавиши «+» («-«) |
На Рис. 2.8 приведены примеры суммирования (вычитания) матриц.
Умножение матриц
Для умножения матриц используется функция *.
Две матрицы могут быть перемножены, если у первого множителя
количество столбцов будет равно количеству строк у второго множителя.
При
умножении матрицы размерностью MxN, на матрицу
размерностью NxK будет получена матрица размерностью MxK.
Варианты ввода функции.
Работа с векторами и матрицами в MathCad
Похожие презентации:
3D печать и 3D принтер
Системы менеджмента качества требования. Развитие стандарта ISO 9001
Операционная система. Назначение и основные функции
Adobe Photoshop
AutoCAD история и возможности
Microsoft Excel
Облачные технологии
Корпорация Microsoft и ее особенности
Веб-дизайн
Тема 2. Пакеты прикладных программ
Работа с векторами и
матрицами
в MathCad
Массивы
одномерные
(векторы)
двумерные
(матрицы)
тензоры
a «My Name»
(многоиндексные)
1
M
V2 ( 1 2 3 )
V1 2
3
Индекс – порядковый номер элемента
1 2 3
4 5 6
7 8 9
Заполнение массивов
1. С помощью шаблона:
2. Поэлементно
m0 0 0
m1 0 3
m0 1 1
m1 0 3 m1 1 4 m1 2 5
m0 2 2
0 1 2
m
m1 2 5
3 4 5
m1 1 4
1 2
3.
С использованием
и функций пользователя
0 переменных
m
00 33
i 0 1
j j
3
4T 5
0 1 2 3
T
ViV
i
0.50.5
i i 1 1 VV ( (11 1.5
MM
j j M
1.5))
i ji
j i i
1 0 1 2
4. Применение встроенных функций
5. Чтение из внешнего файла
Матричные вычисления
элементарные действия
использование
программирования
создание, сложение,
использование
умножение,
суммирование
специальных функций элементов вложенного
извлечение данных
Реализация: операторы и встроенных алгоритмов
массива
панели Math: Calculator,
матричной алгебры
Matrix, Symbolic
ранг, единичная матрица,
сортировка
Реализация: главное меню
Insert (Вставка) Function
(Функция) (или
)
раздел Vector and Matrix
(Векторы и матрицы)
Операторы и функции для работы
с векторами и матрицами
V – вектор, M – матрица,
Z – скаляр
Векторные и матричные функции
Векторные функции
Функция
length(V)
Описание
Возвращает длину вектора
last(V)
Возвращает индекс последнего элемента
max(V)
Возвращает максимальный по значению элемент
min(V)
Re(V)
Возвращает вектор действительных частей
вектора с комплексными элементами
Im(V)
Возвращает вектор мнимых частей вектора с
комплексными элементами
Векторные и матричные функции
Функции для работы с матрицами
Функция
Описание
augment(M1,M2)
Объединяет в одну матрицы М2 и М2, имеющие
одинаковое число строк (объединение «бок о бок»)
stack(M1,M2)
Объединяет в одну матрицы М1 и М2, имеющие
одинаковое число столбцов, располагая М1 над М2
Создает единичную квадратную матрицу
identity(n)
размером n×n
Возвращает субматрицу, состоящую из всех
submatrix(M,ir,jr,ic,jc) элементов, содержащихся в строках с ir по jr и
столбцов с ic по jc
diag(V)
Re(M)
Im(M)
Создает диагональную матрицу, элемент главной
диагонали которой – вектор V
Возвращает матрицу действительных, мнимых
частей матрицы M с комплексными элементами
Векторные и матричные функции
Функции для работы с матрицами
Функция
Описание
Выводит значения того элемента матрицы N, который
lookup(r,M,N) занимает в ней такое же положение, что и скаляр r в
матрице M
Ищет в векторе или матрице A заданное значение z и
match(z,M) возвращает индексы его позиций в A
Функции, возвращающие специальные
характеристики матриц
Функция
Описание
cols(M)
Возвращает число столбцов матрицы М
rows(M)
Возвращает число строк матрицы М
rank(M)
Возвращает ранг матрицы М
tr(M)
Возвращает след (сумму диагональных элементов)
квадратной матрицы М
mean(M)
Возвращает среднее значение элементов массива М
median(M)
eigenvals(M)
Возвращает медиану элементов массива М
Возвращает вектор собственных значений квадратной
матрицы M
Функции сортировки
Функция
Описание
sort(V)
Сортировка элементов вектора в порядке возрастания
их значений
reverse(V)
Перестановка элементов вектора в обратном порядке
Перестановка строк матрицы М таким образом,
чтобы отсортированным оказался n-й столбец
rsort(M,n)
Перестановка столбцов матрицы М таким образом,
чтобы отсортированной оказалась n-я строка
Примеры
1 2
m1
3 1
1 2
m2
3 2
1 2
m1
1
m10 1 2
7 2
m1 m2
6 4
m11 0 3
1 4
( m1 m2)
9 2
Примеры
2
v 3
7
length( v) 3
last ( v) 2
max( v) 7
min( v) 2
Примеры
1 2
m1
3 1
1 2
m2
3 2
1 2 1 2
augment ( m1 m2)
3 1 3 2
1
3
M stack ( m1 m2)
1
3
3 1
submatrix( M 1 2 0 1)
1 2
2
1
2
2
3
submatrix( M 1 2 0 0)
1
Примеры
1 2
m1
3 1
1 2
m2
3 2
lookup ( 3 m1 m2) ( 3 )
1
lookup ( 1 m1 m2)
2
0
0
0
match ( 1 m1 ) 0
1
match ( 1 m1)
1
1
1
1
match ( 3 m2)
0
Примеры
9
3
V
5
2
2
3
sort ( V)
5
9
2
5
reverse ( V)
3
9
9
5
reverse ( sort ( V) )
3
2
1 5 7 2
M
0
7
4
2
0 7 4 2
csort ( M 2)
1
5
7
2
7 2 1 5
rsort ( M 1)
4
2
0
7
{4,1}
{4,1}
{5,1}
{4,1}
main( D Ta i h)
{201,2}
{4,1}
{4,1}
{1,2}
0
{5,1}
main( D Ta i h) 5
{5,1}
{5,1}
0
20
main(D Ta i h)5 1 20
20
20
Формат → Результат → Параметры отображения
English Русский Правила
Как сделать матрицу из массивов?
Ибрагим МоаззамБесплатный курс собеседования по проектированию систем
Многих кандидатов отклоняют или понижают в рейтинге из-за плохой успеваемости на собеседовании по проектированию систем.
Выделитесь на собеседованиях по проектированию систем и получите работу в 2023 году благодаря этому популярному бесплатному курсу.
МатрицыМатрицы представляют собой формы множественного числа матриц, которые имеют различные применения в компьютерных науках и математике, обеспечивая быстрое приближение к сложным вычислениям.
Языки программирования используют массивы, в частности двумерные массивы , для создания матрицы. Двумерный массив — это массив, который содержит ссылки («строки» матрицы) на другие массивы («столбцы» матрицы), как показано на диаграмме ниже.
Создание двумерного массива (массив 5) из нескольких одномерных массивов (массив 1–4)
Элементы двумерного массива выше (массив 5) не являются целыми числами, а являются ссылками на одномерные массивы, Массив 1–4.
Создание матрицы
Приведенные ниже фрагменты кода показывают, как запрограммировать двумерный массив, аналогичный показанному на иллюстрации выше (массив 5).
int array1[4] = {3, 5, 1, 6};
int array2[4] = {1, 7, 2, 9};
int array3[4] = {9, 3, 7, 2};
int array4[4] = {6, 2, 4, 6};
int* exampleMatrix[4] = {массив1, массив2, массив3, массив4};
Объяснение кода
C++
Python
Печать матрицы
Чтобы напечатать матрицу (двумерный массив), мы используем вложенные для циклов, как показано в фрагментах кода ниже.
Примечание: Размеры матрицы должны быть известны перед печатью.
for (int i = 0; i < 4; i++){
for (int j = 0; j < 4; j++){
cout << exampleMatrix[i][j] << " " ;
}
cout << endl;
}
Объяснение кода
C++
Python
Индексирование двумерного массива
Двумерные массивы чаще всего индексируются с использованием скобок , as can можно увидеть ниже:
Использование квадратных скобок для индексации двумерного массива
Обозначение скобок, приведенное выше, приведет к индексированию элемента, который присутствует в строке i th и столбце j th нашей матрицы, примерМатрица .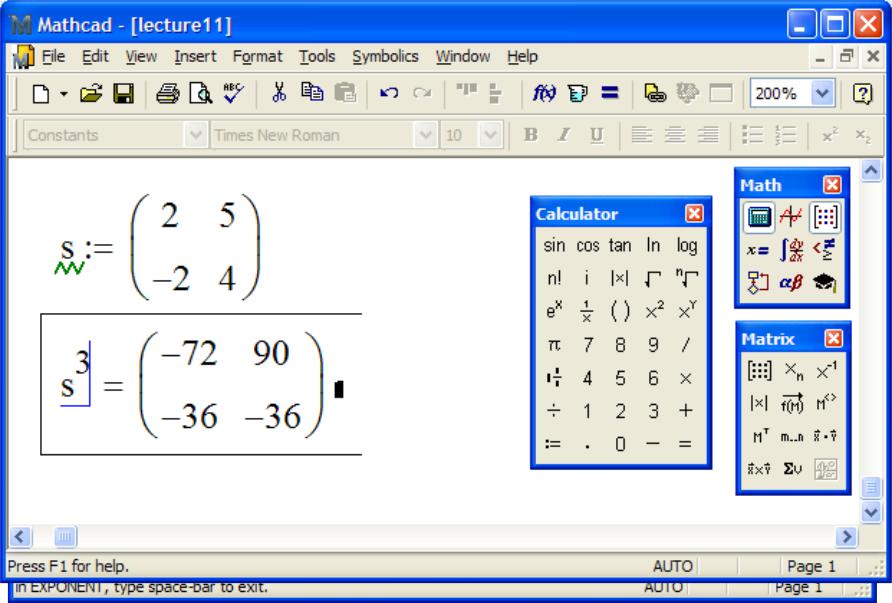
Чтобы присвоить значение этому элементу, мы используем оператор присваивания. Ниже значение 8 присвоено элементу во 2-й строке и 3-м столбце exampleMatrix .
примерMatrix[2][3] = 8;
// Печать матрицы
for (int i = 0; i < 4; i++){
for (int j = 0; j < 4; j++){
cout << exampleMatrix[i][j ] << " ";
}
cout << конец;
}
Объяснение кода
C++
Python
СВЯЗАННЫЕ ТЭГИ
массивы
c++
9 0004 pythonУЧАСТНИК
Ибрагим МоаззамCopyright © 2023 Educative, Inc. Все права защищены
Stan Справочное руководство
Это старая версия, просмотреть текущую версию.
Stan поддерживает массивы произвольной размерности. Значения в массиве
может быть любого типа, так что массивы могут содержать значения, которые являются простыми
вещественные или целые числа, векторы, матрицы или другие массивы.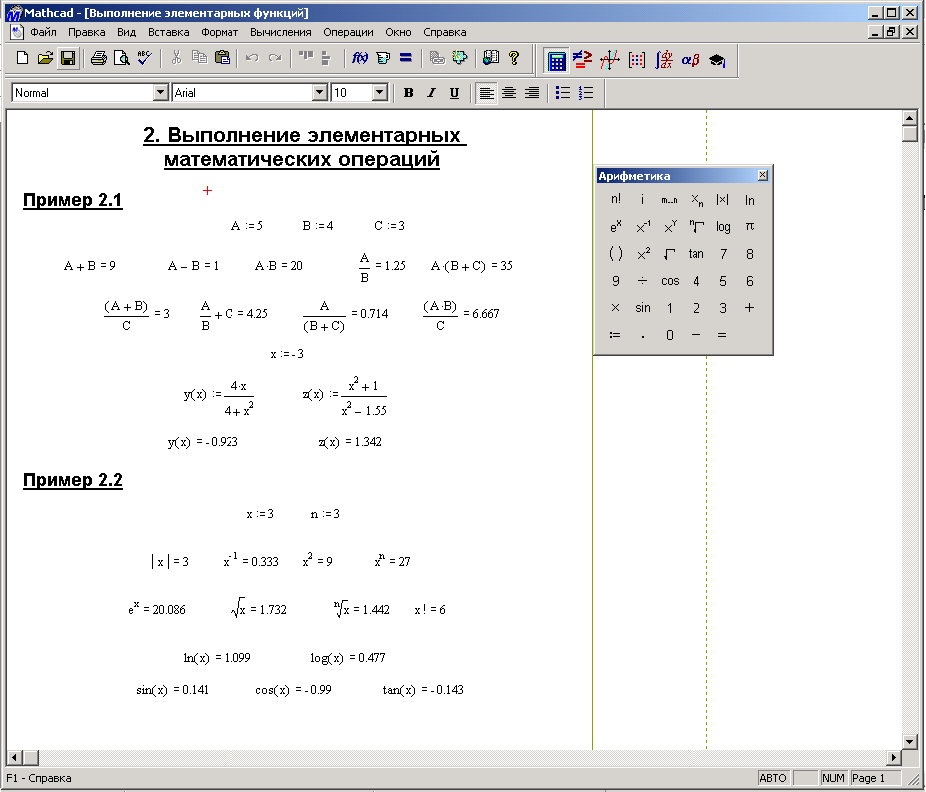
Двумерный массив — это просто массив массивов, оба концептуально
и с точки зрения текущей реализации. Когда индекс передается
массив, он возвращает значение по этому индексу. Когда более одного
index предоставляется, эта операция индексации цепочка. Например, если a — двумерный массив, тогда a[m, n] — это просто
удобное сокращение для a[m][n] .
Векторы, матрицы и массивы нельзя присваивать друг другу, даже если их размеры совпадают.
Объявление переменных массива
Массивы объявляются путем заключения размеров в квадратные скобки после имени переменной.
Переменная n объявляется как массив из пяти целых чисел следующим образом.
целое число [5];
Двумерный массив действительных значений с тремя строками и четырьмя столбцами.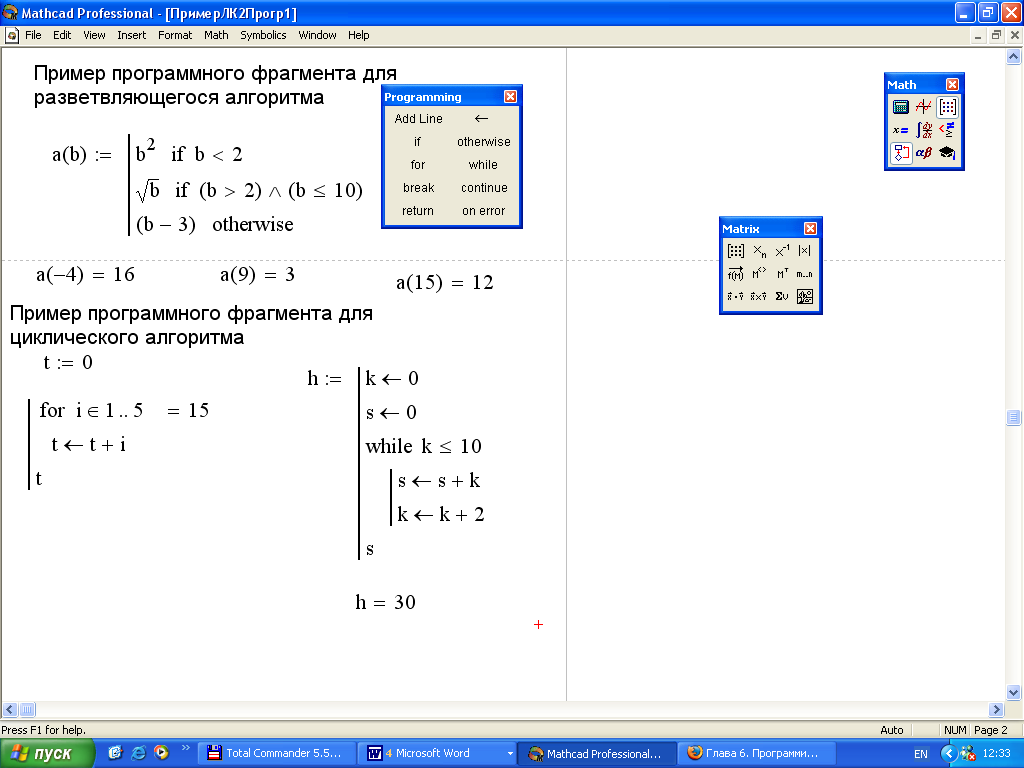
объявлено следующим.
реальный а[3, 4];
Трехмерный массив z положительных вещественных чисел с пятью строками, четырьмя
колонны и две полки можно объявить следующим образом.
реальное<нижний=0> z[5, 4, 2];
Массивы также могут быть объявлены содержащими векторы. Например,
вектор[7] мю[3];
объявляет mu массивом размера 3, содержащим векторы с 7
элементы. Массивы также могут содержать матрицы. Пример
матрица[7, 2] mu[15, 12];
объявляет массив 15 на 12 матриц \(7 \times 2\). Любой из ограниченные типы также могут использоваться в массивах, как в объявлении
cholesky_factor_cov[5, 6] mu[2, 3, 4];
массива \(2 \times 3 \times 4\) из \(5 \times 6\) коэффициентов Холецкого ковариационные матрицы.
Доступ к элементам массива и подмассивам
Если x является одномерным массивом длины 5, то x[1] является
первый элемент массива, а x[5] — последний.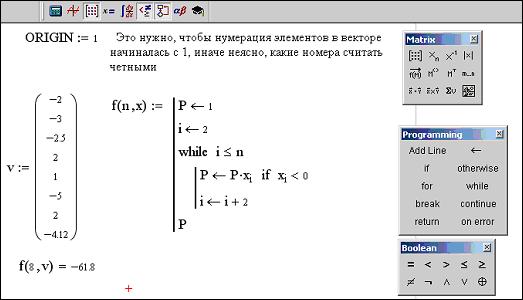
Для массива \(3 \times 4\) y из двух измерений y[1, 1] является первым
элемент и y[3, 4] последний элемент. Для трехмерного
массив z , первый элемент — z[1, 1, 1] и так далее.
Доступ к подмассивам массивов можно получить, предоставив меньше, чем полный
количество индексов. Например, предположим, что y — это двумерное число.
массив с тремя строками и четырьмя столбцами. Тогда y[3] равно
одномерный массив длины четыре. Это означает, что y[3][1] можно использовать вместо y[3, 1] для доступа к значению первого
столбец третьей строки y . Форма y[3, 1] — это
предпочтительная форма (см. примечание в этой главе).
Массивы матриц и векторов
Доступ к массивам векторов и матриц осуществляется так же, как к массивам двойников. Рассмотрим следующие векторные и скалярные объявления.
вектор[5] а[3, 4]; вектор[5] б[4]; вектор[5] с; реальный х;
С этими объявлениями допустимы следующие присвоения.
б = а[1]; // результат - массив векторов с = а[1, 3]; // результат вектор с = б[3]; // тот же результат, что и выше х = а[1, 3, 5]; // результат скалярный х = Ь[3, 5]; // тот же результат, что и выше х = с[5]; // тот же результат, что и выше
Векторы-строки и другие производные типы векторов (простые и упорядоченные) вести себя так же с точки зрения индексации.
Рассмотрим следующие объявления матрицы, вектора и скаляра.
матрица[6, 5] d[3, 4]; матрица[6, 5] e[4]; матрица[6, 5] f; строка_вектор[5] г; реальный х;
С этими объявлениями допустимы следующие определения.
е = д[1]; // результат - массив матриц е = д[1,3]; // результат - матрица е = е[3]; // тот же результат, что и выше г = д[1,3,2]; // результат - вектор-строка г = е[3,2]; // тот же результат, что и выше г = f[2]; // тот же результат, что и выше х = д[1,3,5,2]; // результат скалярный х = е[3,5,2]; // тот же результат, что и выше х = f[5,2]; // тот же результат, что и выше х = г[2]; // тот же результат, что и выше
Как показано, результат f[2] предоставления одного индекса в
матрица — индексированная строка, здесь строка 2 матрицы f .
Смешивание типов массивов, векторов и матриц
Массивы, векторы-строки, векторы-столбцы и матрицы не взаимозаменяемы в Стэне. Таким образом, переменная любого из этих фундаментальные типы не могут быть присвоены ни одному из других и не могут использоваться в качестве аргумента там, где требуется другой (использовать в качестве аргументов следует правилам присваивания).
Смешивание векторов и массивов
Например, векторы нельзя назначать массивам и наоборот.
реальный а[4]; вектор[4] б; строка_вектор с[4]; // ... а = б; // недопустимое присвоение вектора массиву б = а; // недопустимое присвоение массива вектору а = с; // недопустимое присвоение вектора-строки массиву с = а; // незаконное присвоение массива вектору-строке
Смешивание векторов-строк и векторов-столбцов
Недопустимо даже назначать векторы-строки векторам-столбцам или наоборот наоборот
вектор b[4]; строка_вектор с[4]; // ... б = с; // недопустимое присвоение вектора-строки вектору-столбцу с = б; // недопустимое присвоение вектора-столбца вектору-строке
Смешивание матриц и массивов
То же самое верно для матриц, где двумерные массивы не могут быть
присваивается матрицам или наоборот.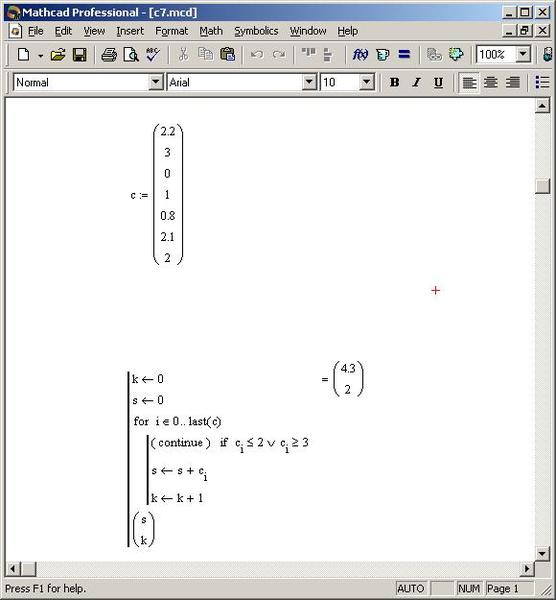
реальный а[3,4]; матрица[3,4] б; // ... а = б; // недопустимое присвоение матрицы массиву б = а; // недопустимое присвоение массива матрице
Смешивание матриц и векторов
Матрице \(1 \times N\) нельзя назначить вектор-строку или наоборот.
матрица[1,4] а; строка_вектор[4] б; // ... а = б; // недопустимое присвоение вектора-строки матрице б = а; // недопустимое присвоение матрицы вектору-строке
Аналогично, матрица \(M \times 1\) не может быть назначена вектору-столбцу.
матрица[4,1] а; вектор[4] б; // ... а = б; // недопустимое присвоение вектор-столбца матрице б = а; // недопустимое присвоение матрицы вектору-столбцу
Ограничения объявления размера
Целочисленное выражение используется для выбора размеров массивов.
применяются те же ограничения, что и для размеров векторов и матриц, а именно
размер объявляется целочисленным выражением, которое не
содержать любые параметры, преобразованные параметры или сгенерированные величины.