Дискретность и интерполяция в современных системах ЧПУ
Для работы ЧПУ необходим интерполятор – вычислительное устройство, которое передаёт информацию от PC, преобразуя в координаты. Есть два вида интерполяторов: линейные и линейно-круговые. Работают оба по принципу подачи импульса (интерполяции). Шаг, осуществляемый от одного импульса, называется дискретностью. Интерполяторы имеют важнейшее качество поддерживать заданную подачу между опорными точками неизменной.
Один из главных узлов контурных УЧПУ – это интерполятор (специальное вычислительное устройство). Интерполятор преобразует программа заданную от PC информацию непосредственно в управляющие действия на двигатели приводов подач для обеспечения требуемой траектории и скорости движения инструмента вдоль заданного контура.
Траектория перемещения инструмента относительно детали/заготовки в программе задается значениями координат отдельно взятых точек А, В, С…, так называемыми – опорными точками. Характер движения инструмента между этими опорными точками определяется естественно видом интерполяции, которую непосредственно и выполняет – интерполятор.
Сегодня в современных системах ЧПУ в основном применяются интерполяторы двух типов:
- линейные (обеспечивают перемещение инструмента между соседствующими опорными точками по прямым линиям, которые расположены под любыми углами):
- линейно-круговые (реализуют характер управления, то есть инструмент между соседствующими опорными точками способен перемещаться и по прямым линиям и по дугам окружностей).
Для осуществления кругового движения в программе помимо координат опорных точек обязательно должны быть заданы еще и координаты центров дуг окружностей. Как правило, в большинстве современных контурных системах ЧПУ, рабочие органы для перемещения получают команды дискретно, то есть в виде единичных кратковременных управляющих импульсов (управляющих воздействий).
Использование интерполятора в новейших системах ЧПУ
Интерполятор в свою очередь обеспечивает распределение поступающих импульсов между приводами подач, чтобы инструмент перемещался максимально близко к дуге окружности (в случае круговой интерполяции) или к заданной прямой (в случае линейной интерполяции) с обусловленными шагами движений. Меньше всего контролируется шаг в процессе управления в перемещении рабочего органа, который осуществляется от одного управляющего импульса и называется дискретностью отработки перемещений («разрешающая способность СЧПУ»). Между опорными точками схема движения инструмента выглядит так: А, В, С, Д, Е при линейной интерполяции (а) и опорными точками А, В, С при круговой интерполяции (б) при токарной обработке.
Меньше всего контролируется шаг в процессе управления в перемещении рабочего органа, который осуществляется от одного управляющего импульса и называется дискретностью отработки перемещений («разрешающая способность СЧПУ»). Между опорными точками схема движения инструмента выглядит так: А, В, С, Д, Е при линейной интерполяции (а) и опорными точками А, В, С при круговой интерполяции (б) при токарной обработке.
На один управляющий импульс, который выдается интерполятором, дискретность отработки перемещений формулируется в миллиметрах. В большинстве своем современные системы ЧПУ имеют дискретность отработки передвижений, равную 0,01 мм/имп. В свою очередь новые СЧПУ, осваиваемые сегодня, рассчитаны уже на дискретность в 0,001 мм/имп. Конструкция УЧПУ, двигатели подач и датчики обратной связи, обеспечивают четкое выполнение станком необходимых значений дискретности, сюда же относится передаточное отношения механизмов подач станков.
Аппроксимация контура
Во время разработки программ для станков непосредственно с линейными интерполяторами криволинейный контур, который заданный на чертеже, замещают ломаной линией. Данная замена называется «аппроксимацией контура». Во время аппроксимации, точки ломаной линии должны отклоняться от заданного контура – как можно меньше. Однако уменьшение таких отклонений приводит к неизбежному увеличению числа опорных точек, к увеличению числа кадров непосредственно в самой программе и соответственно к увеличению объема вычислений определяющих их координат.
Данная замена называется «аппроксимацией контура». Во время аппроксимации, точки ломаной линии должны отклоняться от заданного контура – как можно меньше. Однако уменьшение таких отклонений приводит к неизбежному увеличению числа опорных точек, к увеличению числа кадров непосредственно в самой программе и соответственно к увеличению объема вычислений определяющих их координат.
На практике же число опорных точек принимается минимально допустимым, чтобы максимальное их отклонение от заданного контура ни в коем случае не превышало допуска δ непосредственно на аппроксимацию контура. Этот допуск принимается равным: δ= (0,1—0,3)Δ, где Δ, то есть – на размеры заданного контура чертежный допуск.
Поскольку в кадре программы записывается лишь только координаты конечных точек дуги исключительно каждого радиуса и соответственно координаты центров этих дуг (к примеру, такие точки как, В и С и O1 и O2), то программирование для станков, имеющих линейно-круговые интерполяторы – считается более простым.
Круговая интерполяция
Однако круговая интерполяция может быть использована, причем достаточно, просто, только в том случае, когда обрабатываемый контур задан участками исключительно дуг окружностей известных ей радиусов. Но если участок дугой окружности не является, то приходится использовать, либо линейную интерполяцию с аппроксимацией контура ломаной линией, либо выполнять аппроксимацию криволинейного контура (к примеру, параболы) участками дуг окружностей.
Наибольшие преимущества при токарных обработках дает круговая интерполяция, потому как контуры осевых сечений вращения тел в большинстве своем очерчиваются дугами окружностей. Если сравнивать с токарными обработками, обычно при которых программируется траектория движения вершины резца, как правило, при фрезеровании, программируется только траектория движения центра фрезы. Траектория движения центра фрезы непосредственно с радиусом Rф при создании контура ABC, который состоит из двух дуг окружностей с радиусом R1 и R2 (А1, В1, В1′, С1 — то есть, опорные точки траектории движения самой фрезы).
Чтобы обеспечить правильное формирование обрабатываемой поверхности, данная траектория по отношению исключительно к заданному контуру основывается в виде эквидистантной кривой. Эквидистантной называется кривая, у которой все точки удалены на одно расстояние от заданного контура. При фрезеровании таким расстоянием основным, конечно же, является радиус фрезы. Размеры и форма эквидистантной кривой существенно отличаются от контура детали, именно поэтому программирование для фрезерных станков зачастую связано с достаточно резким увеличением объема вычислений.
Преимущества интерполяции
Преимуществ от использования круговой интерполяции во время фрезерования меньше, чем во время токарной обработки, потому что многие детали, которые изготавливаются на фрезерных станках, обязательно очерчиваются контурами, которые в свою очередь составлены из более сложных кривых, нежели дуги окружностей. Кроме этого, современные линейно-круговые интерполяторы четко обеспечивают относительное движение инструмента исключительно по окружностям, расположенным следующим образом: в плоскости стола, а также в плоскости перпендикулярно направлению продольной подачи стола, а также в плоскости перпендикулярно направлению поперечной подачи стола.
Именно это действие не позволяет рационально аппроксимировать достаточно сложные фасонные поверхности дугами окружностей. Посему на фрезерных станках с (числовым программным управлением) наиболее широко применяется более простая и в тоже время универсальная линейная интерполяция, соответственно при ее воздействии инструмент перемещается по прямой линии из точки М, например, в точку N. При этом траектория перемещения концевой сферической фрезы непосредственно в опорную точку N из опорной точки М при линейной интерполяции осуществляется с одновременным управлением исключительно по трем координатам.
Технологические качества интерполяции
Абсолютно все интерполяторы обладают важнейшим технологическим качеством: при линейной интерполяции они отлично поддерживают заданную системой контурную скорость движения инструмента (т. е. подачу) в промежутке между соседствующими опорными точками неизменной (т. е. стабильной). Это обеспечивается благодаря постоянству частоты выдачи управляющих импульсов, формирующиеся интерполятором в соответствии с необходимой информацией о величине подачи, которая записана в кадре управляющей программы.
Если возникает необходимость, то в автоматическом режиме эта подача может быть изменена на другую абсолютно в любой опорной точке на наиболее рациональную. Если подачу нужно изменить в промежутке между главными опорными точками, то назначают промежуточные опорные точки. Также необходимо учесть, что при круговой интерполяции заданное постоянство частоты управляющих импульсов (их выдачи) приводит подачи вдоль дуги окружности к некоторой неравномерности.
соединяем точки так, чтобы было красиво / Хабр
Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:
Немного матчасти
Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1 .
Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):
0 0 20 0 45 -47 53 335 57 26 62 387 74 104 89 0 95 100 100 0
Результат линейной интерполяции этих точек выглядит так:
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; 
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.

Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз Pi, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:
Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.
Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n
Но вот что получается:
Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.
В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (Pi), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.
Думаем и экспериментируем
Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:
В качестве прямых, на которых лежат точки Ci – 1(2), Pi и Ci(1), целесообразно взять касательные к графику интерполируемой функции в точках Pi. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).
Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:
Эвристика 1
Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C1(1) и Cn – 1(2) совпадают с точками P1 и Pn соответственно).
В этом случае получается вот такая кривая:
Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.
К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки Pi до точек Ci – 1(2) и Ci(1), но при этом сохраняем их все лежащими на одной прямой:
Эвристика для вычисления расстояний будет такой:
Эвристика 2
Расчёт l1 и l2 такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки Pi и Pi + 1 по ординате, и, если совпали, полагать l1 = l2 = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).
Результат получается такой:
В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы.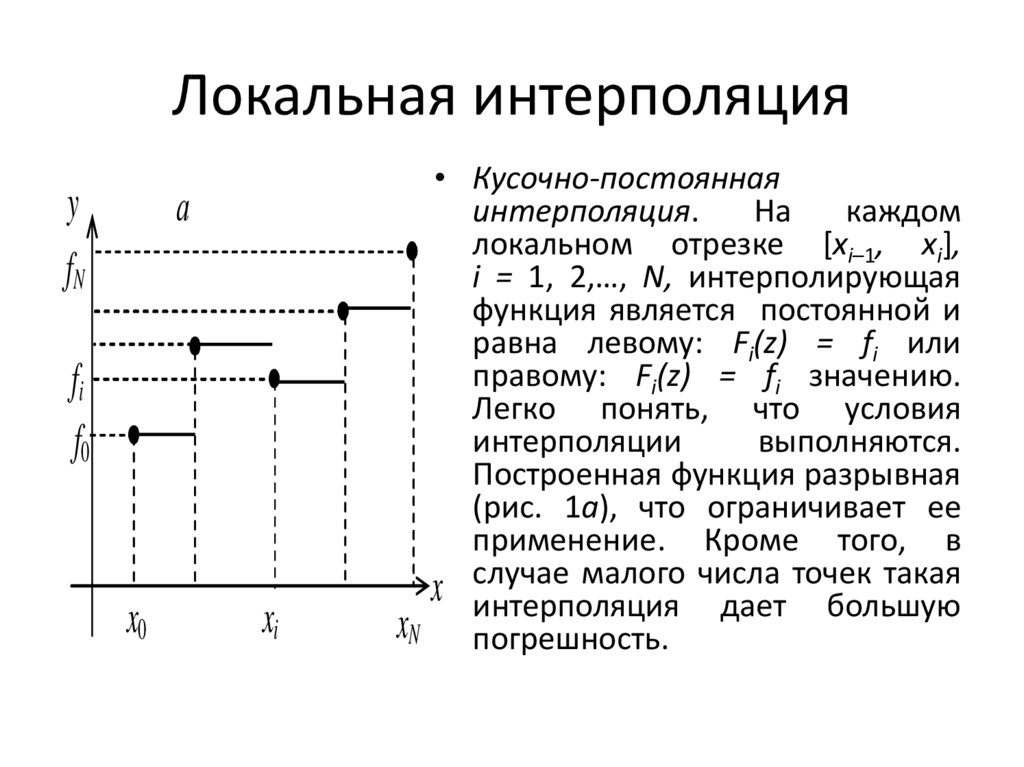 Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:
Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:
Эвристика 3
Если абсцисса точки пересечения касательных в точках Pi(xi
Результат следующий:
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.
А как люди-то делают?
Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.
MS Excel
Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.
LibreOffice Calc
В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.
Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂
Highcharts, одна из самых популярных JS-библиотек для построения диаграмм
Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).
amCharts, ещё одна популярная JS-библиотека
Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.
Coreplot, самая популярная библиотека построения графиков для iOS и OS X
Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.
aChartEngine, вроде как самая популярная библиотека построения графиков для Android
Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Вместо заключения
В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.
Как работает инструмент Интерполировать форму—ArcGIS Pro
Доступно с лицензией 3D Analyst.
Доступно с лицензией Spatial Analyst.
Инструмент Интерполировать форму конвертирует классы 2D точечных, линейных или полигональных объектов в класс 3D-объектов, используя интерполяцию z-значений входных пространственных объектов с поверхности. Входная поверхность может быть растром, TIN или набором данных terrain.
Атрибуты входных пространственных объектов копируются в выходные.
Аргумент Метод (Method) интерполяции используется для указания используемого типа интерполяции. Если входная поверхность является растром, использоваться может только билинейная интерполяция. Она вычисляет средневзвешенное расстояние между четырьмя ближайшими к интерполяционной точке центрами ячеек. Если входной поверхностью является поверхность TIN или terrain, вы можете выбрать предлагаемый по умолчанию метод линейной интерполяции, метод естественной окрестности или один из четырех вариантов слияния.
| Метод интерполяции | Описание |
|---|---|
Линейная | Используется средневзвешенное значение вершин треугольника, содержащего интерполяционную точку. |
Естественная окрестность | Использует соседние полигоны Вороного интерполяционной точки. |
Объединить мин. Z | Получение z-значения с одной из естественных окрестностей запрашиваемой точки в TIN или terrain. Будет использовано z-значение ячейки окрестности с минимальной высотой. |
Объединить макс. Z | Получение z-значения с одной из естественных окрестностей запрашиваемой точки в TIN или terrain. Будет использовано z-значение ячейки окрестности с максимальной высотой. |
Объединить ближайшие Z | Получение z-значения с одной из естественных окрестностей запрашиваемой точки в TIN или terrain. Будет использовано z-значение ячейки окрестности, расположенной в координатах x,y ближе всего к запрашиваемой точке. |
Объединить ближайшие к среднему Z | Получение z-значения с одной из естественных окрестностей запрашиваемой точки в TIN или terrain. Будет использовано z-значение ячейки окрестности, высота которой приближается к средней высоте всей окрестности. |
Расстояние разбиения – это число с плавающей точкой, используемое линиями и полигонами. Значение Расстояние разбиения используется для определения частоты интерполяции вдоль линий и границ полигонов. Расстояние между выходными вершинами не будет больше расстояния разбиения. Как правило, чем меньше расстояние разбиения, тем выше частота и тем точнее выходная геометрия повторяет поверхность.
Если входной является растровая поверхность, значение Расстояния разбиения считается по умолчанию равным размеру пиксела. Можно указать и меньшее значение, однако не рекомендуется выбирать значение, меньшее половины пиксела, поскольку выбор такого значения не приведет к получению дополнительной информации из-за ограничения, наложенного разрешением поверхности. Помните также, что меньшие расстояния разбиения приводят к большим требованиям к ресурсам компьютера. Переход от расстояния разбиения, равного одному пикселу, к расстоянию в половину пиксела может привести к удвоению количества выходных вершин и лишь к незначительному увеличению точности. Большие расстояния также могут быть выбраны, но в этом случае детальность поверхности будет передана хуже.
Помните также, что меньшие расстояния разбиения приводят к большим требованиям к ресурсам компьютера. Переход от расстояния разбиения, равного одному пикселу, к расстоянию в половину пиксела может привести к удвоению количества выходных вершин и лишь к незначительному увеличению точности. Большие расстояния также могут быть выбраны, но в этом случае детальность поверхности будет передана хуже.
Если входной поверхностью является TIN или terrain, значение по умолчанию значение Расстояния разбиения не используется. Без указания расстояния разбиения инструмент возьмет значения высот поверхности в исходных вершинах линий или границ полигонов, а также в местах пересечения объектами сторон треугольников. Присваивание высот в местах пересечения сторон треугольника используется при работе с линейной интерполяцией, поскольку в этом случае будут переданы все видимые детали поверхности, состоящей из треугольников без чрезмерной подробности.
Если входная поверхность – TIN или terrain и указано значение Расстояния разбиения, стратегия отбора высот может быть различной, в зависимости от выбранного типа интерполяции. При работе с интерполяцией естественной окрестности высоты присваиваются исходя из расстояния разбиения, а также в местах пересечения объектами резких линий перегиба. При работе с линейной интерполяцией высоты присваиваются исходя из расстояния разбиения, а также в местах пересечения объектами сторон любых треугольников. Как правило, расстояние разбиения указывается при выборе интерполяции методом естественных окрестностей и не указывается при использовании линейной интерполяции.
При работе с интерполяцией естественной окрестности высоты присваиваются исходя из расстояния разбиения, а также в местах пересечения объектами резких линий перегиба. При работе с линейной интерполяцией высоты присваиваются исходя из расстояния разбиения, а также в местах пересечения объектами сторон любых треугольников. Как правило, расстояние разбиения указывается при выборе интерполяции методом естественных окрестностей и не указывается при использовании линейной интерполяции.
Ознакомившись с приведенной ниже таблицей, вы получите представление о выборе корректного расстояния разбиения в зависимости от используемого метода интерполяции.
Выбор метода интерполяции и расстояния разбиения для входных поверхностей
| Метод интерполяции | Расстояние разбиения | Описание |
|---|---|---|
Поверхность TIN/Terrain – Линейная интерполяция | Расстояние указывается. | Интерполяция основывается на указанном расстоянии и на пересечениях объектами ребер. |
Поверхность TIN/Terrain – Линейная интерполяция | Расстояние не указано. | Интерполяция использует только пересечения объектами ребер. Для линейной интерполяции рекомендуется не вводить расстояние разбиения. |
Поверхность TIN/Terrain – Естественная окрестность | Расстояние указывается. | Интерполяция основывается на данном расстоянии разбиения и на пересечениях объектами жестких перегибов. Рекомендуется указывать расстояние разбиения при использовании интерполяции естественной окрестности. |
Поверхность TIN/Terrain – Естественная окрестность | Расстояние не указано. | Интерполяция основывается на пересечениях объектами ребер. |
Растровая поверхность – Билинейная интерполяция | Не указывается (используется значение по умолчанию). | Интерполяция основывается на размере пиксела. |
Растровая поверхность – Билинейная интерполяция | Расстояние указывается. | Интерполяция использует указанное значение расстояния. |
Для конвертации Z-единиц может использоваться дополнительный Коэффициент Z (Z factor). Выходные значения умножаются на этот коэффициент Z. Значение по умолчанию вычисляется, чтобы выразить Z-значения в тех же единицах, что и значения X,Y, если значения X,Y и Z определены в пространственной привязке входной поверхности, а координатная система не является географической (например, десятичные градусы).
Дополнительный параметр Интерполировать только вершины приведет к игнорированию инструментом расстояния разбиения и использованию им в процессе интерполяции только исходных вершин. Если все вершины объекта не попадают на поверхность, такой объект не будет записан в выходные данные. Если, однако, часть объекта на самом деле не попадает на поверхность, он, тем не менее, может быть представлен в выходных данных, если на такой части объекта, не попадающей на поверхность, нет вершин (пример: средняя часть линейного объекта).
Независимо от выбранных настроек, если объект полностью находится вне поверхности, он не добавляется к выходным данным.
Отзыв по этому разделу?
Pers.narod.ru. Обучение. Лекции по численным методам. Аппроксимация и интерполяция функций
Pers.narod.ru. Обучение. Лекции по численным методам. Аппроксимация и интерполяция функцийЭтот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
|
Pers.narod.ru. Обучение. Лекции по численным методам. Аппроксимация и интерполяция функций |
3. Аппроксимация функций
Локальная интерполяция:
Кусочно–постоянная интерполяция
Кусочно–линейная интерполяция
Кубический интерполяционный сплайн
Глобальная интерполяция:
Полином Лагранжа
Подбор эмпирических формул
Метод наименьших квадратов
Аппроксимировать
– это означает «приближённо заменять». Допустим, известны значения некоторой
функции в заданных точках. Требуется найти промежуточные значения этой функции.
Это так называемая задача о восстановлении функции. Кроме того, при
проведении расчетов сложные функции удобно заменять алгебраическими
многочленами или другими элементарными функциями, которые достаточно просто
вычисляются (задача о приближении функции).
Допустим, известны значения некоторой
функции в заданных точках. Требуется найти промежуточные значения этой функции.
Это так называемая задача о восстановлении функции. Кроме того, при
проведении расчетов сложные функции удобно заменять алгебраическими
многочленами или другими элементарными функциями, которые достаточно просто
вычисляются (задача о приближении функции).
Постановка задачи интерполяции
На интервале
[a, b] заданы точки xi,
i=0, 1,…, N; a ≤ x i ≤ b, и значения неизвестной функции в
этих точках fi, i=0, 1,…., N. Требуется найти функцию F(x), принимающую в точках xi те же значения fi. Точки называются узлами
интерполяции, а условия F(xi)=
fi. – условиями интерполяции. При этом F(x)
ищем только на отрезке [a,b]. Если необходимо найти функцию вне отрезка, то —
это задача экстраполяции. Пока мы будем рассматривать только интерполяционные задачи.
Пока мы будем рассматривать только интерполяционные задачи.
Задача имеет много решений, т.к. через заданные точки (xi, fi), i=0, 1,…, N, можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай аппроксимации функции многочленами, т.е. .
Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале [xi–1, xi] строится отдельный полином. В случае глобальной интерполяции отыскивается единый полином на всем интервале [a, b]. При этом искомый полином называется интерполяционным полиномом.
Локальная интерполяция
Кусочно–постоянная интерполяция
На каждом
отрезке интерполяционный
многочлен равен константе, а именно левому или правому значению функции.
Для левой кусочно-линейной интерполяции , т.е.
Для правой кусочно-линейной интерполяции , т.е.
Легко понять, что условия интерполяция выполняются. Построенная функция является разрывной), что ограничивает ее применение. Для левой кусочно-линейной интерполяции имеем графическое представление:
Кусочно–линейная интерполяция
На каждом интервале [xi–1, xi] функция является линейной . Значения коэффициентов находятся из выполнения условий интерполяции в концах отрезка: . Получаем систему уравнений: , откуда находим . Следовательно, функцию F(z) можно записать в виде:
, т. е.
е.
Или
F(x) = ki * (x - xi-1) + fi-1,
ki = (fi - fi-1) / (xi - xi-1), xi-1 ≤ x ≤ xi, i=1,2,...,N-1
При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение x, а затем подставить его в формулу.
Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно–постоянной интерполяции. Иллюстрация кусочно–линейной интерполяции приведена на рисунке
Пример: Заданы значений некоторой функции:
| x | 0 | 2 | 3 |
3. 5 5 |
| f | -1 | 0.2 | 0.5 | 0.8 |
Требуется найти значение функции при z=1 и z=3.2 по кусочно–постоянной и кусочно–линейной интерполяции.
Решение. Точка z=1 принадлежит первому локальному отрезку [0, 2], т.е. и, следовательно, по формулам левой кусочно–постоянной интерполяции F(1) = f0= –1, по формулам правой кусочно–постоянной интерполяции F(1)=f1=0.2. Воспользуемся формулами кусочно–линейной интерполяции:
.
Точка z=3.2 принадлежит третьему интервалу [3, 3.5], т.е. и, следовательно, по
формулам левой кусочно – постоянной интерполяции F(3. 2)==0.5, по формулам правой кусочно
– постоянной интерполяции F(3.2)= =0.8. Воспользуемся формулами кусочно–линейной
интерполяции:
2)==0.5, по формулам правой кусочно
– постоянной интерполяции F(3.2)= =0.8. Воспользуемся формулами кусочно–линейной
интерполяции:
Кубический интерполяционный сплайн
Слово сплайн (английское слово «spline») означает гибкую линейку, используемую для проведения гладких кривых через заданные точки на плоскости. Форма этого универсального лекала на каждом отрезке описывается кубической параболой. Сплайны широко используются в инженерных приложениях, в частности, в компьютерной графике. Итак, на каждом i–м отрезке [xi–1, xi], i=1, 2,…, N, решение будем искать в виде полинома третьей степени:
Si(x)=ai+bi(x–xi)+ci(x–xi)2/2+di(x–xi)3/6
Неизвестные коэффициенты ai,
bi, ci, di, i=1, 2,. .., N, находим из:
.., N, находим из:
• условий интерполяции: Si(xi)=fi, i=1, 2,…, N; S1(x0)=f0,
• непрерывности функции Si(xi–1)=Si–1(xi–1), i=2, 3,…, N,
• непрерывности первой и второй производной:
S /i(xi–1)=S /i–1(xi–1), S //i(xi–1)=S //i–1(x i–1), i=2, 3,…, N.
Учитывая, что , для определения 4N неизвестных получаем систему 4N–2 уравнений:
ai=fi, i=1, 2,. ..,
N,
..,
N,
bi hi – cihi2/2 + di hi3/6=fi – fi–1, i=1, 2,…, N,
bi – bi–1 = ci hi – di hi2/2, i=2, 3,…, N,
di hi = ci – ci–1 , i=2, 3,…, N.
где hi=xi – xi–1. Недостающие два уравнения выводятся из дополнительных условий: S //(a)=S //(b)=0. Можно показать, что при этом . Из системы можно исключить неизвестные bi , di , получив систему N+1 линейных уравнений (СЛАУ) для определения коэффициентов ci:
c0 =0, cN =0,
hici–1+2(hi+hi+1)ci+h
i+1ci+1=6, i=1, 2,…, N–1. (1)
(1)
После этого вычисляются коэффициенты bi, di:
, i=1, 2,…, N. (2)
В случае постоянной сетки hi=h эта система уравнений упрощается.
Данная CЛАУ имеет трехдиагональную матрицу и решается методом прогонки.
Коэффициенты определяются из формул:
Для вычисления значения S(x) в произвольной точке отрезка z∈[a, b] необходимо решить систему уравнений на коэффициенты ci, i=1,2,…, N–1, затем найти все коэффициенты bi, di. Далее, необходимо определить, на какой интервал [xi0, xi0–1] попадает эта точка, и, зная номер i0, вычислить значение сплайна и его производных в точке z
S(z)=ai0 +bi0(z–xi0)+ci0(z–xi0)2/2+di0(z–x i0)3/6
S /(z)=bi0+ci0(z–xi0)+di0(z–x
i0)2/2, S //(z)=ci0+di0(z–x
i0).
Пример.
|
|
x0,f0 |
x1,f1 |
x2,f2 |
x3,f3 |
x4,f4 |
|
х |
0 |
¼ |
1/2 |
3/4 |
1 |
|
f |
1 |
2 |
1 |
0 |
1 |
Требуется вычислить значения
функции в точках 0. 25 и 0.8, используя сплайн – интерполяцию.
25 и 0.8, используя сплайн – интерполяцию.
В нашем случае: hi=1/4, .
Выпишем систему уравнений для определения :
Решая эту систему линейных уравнений, получим: .
Рассмотрим точку 0.25, которая принадлежит первому отрезку, т.е. . Следовательно, получим,
Рассмотрим точку 0.8, которая принадлежит четвертому отрезку, т.е. .
Следовательно,
Глобальная интерполяция
В случае глобальной
интерполяции отыскивается единый полином на всем интервале [a, b], т.е. строится полином, который используется для
интерполяции функции f(x) на
всем интервале изменения аргумента x. Будем искать
интерполирующую функцию в виде полинома (многочлена) m–ой
степени Pm(x)=a0+a1x+a2x2+a3x3+…+amxm.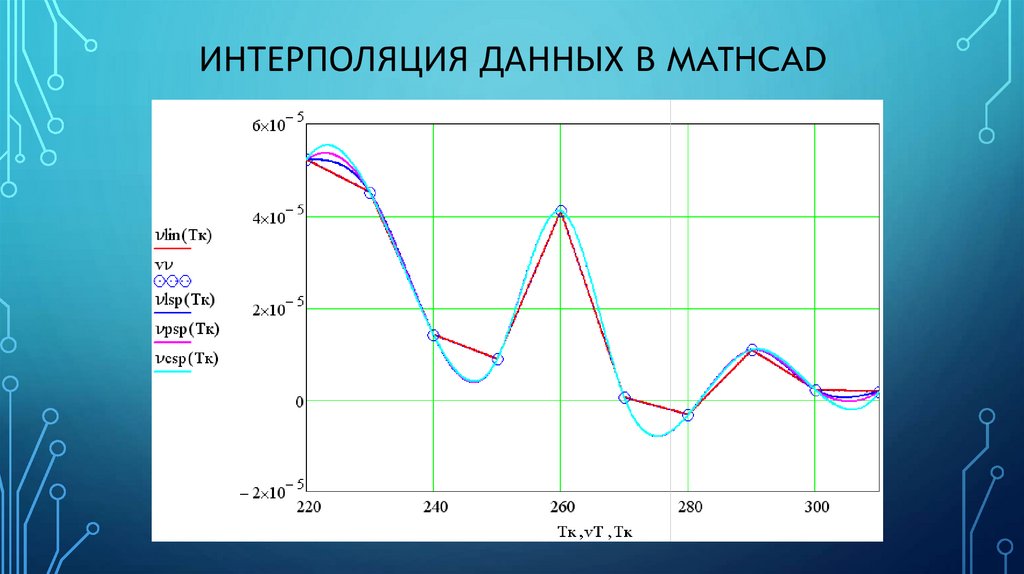 Какова
должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции?
Допустим, что заданы две точки: (x0,
f0) и (x1,
f1), т.е. N=1.
Через эти точки можно провести единственную прямую, т.е. интерполирующей
функцией будет полином первой степени P1(x)=a0+a1x. Через три
точки (N=2) можно провести параболу P2(x)=a0+a1x+a2x2 и т.д. Рассуждая таким способом, можно предположить,
что искомый полином должен иметь степень N .
Какова
должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции?
Допустим, что заданы две точки: (x0,
f0) и (x1,
f1), т.е. N=1.
Через эти точки можно провести единственную прямую, т.е. интерполирующей
функцией будет полином первой степени P1(x)=a0+a1x. Через три
точки (N=2) можно провести параболу P2(x)=a0+a1x+a2x2 и т.д. Рассуждая таким способом, можно предположить,
что искомый полином должен иметь степень N .
Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции в при каждом x=xi:
Данная система
является линейной относительно искомых коэффициентов a0, a1,
a2,…, aN.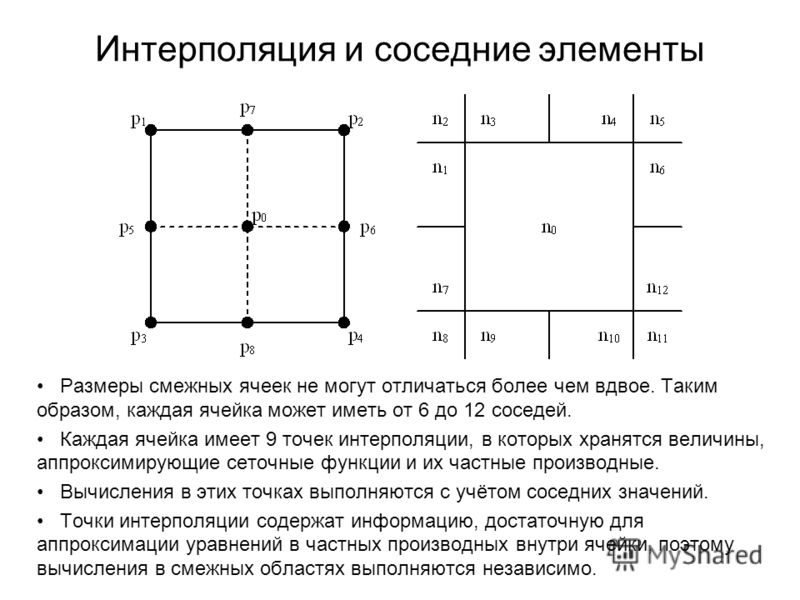 Известно, что СЛАУ имеет решение,
если ее определитель отличен от нуля. Определитель данной системы
Известно, что СЛАУ имеет решение,
если ее определитель отличен от нуля. Определитель данной системы
носит имя определителя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если xk≠ xm (т.е. все узлы интерполяции различные). Таким образом, доказано, что система имеет решение.
Мы показали,
что для нахождения коэффициентов
a0, a1,
a2,…, aN надо решить СЛАУ, что является сложной задачей.
Но есть другой способ построения полинома N–й
степени, который не требует решения такой системы.
Полином Лагранжа
Решение ищем в
виде ,
где li(z) – базисные
полиномы N–й степени, для которых выполняется
условие: . Убедимся в том, что если такие полиномы построены, то LN(x) будет удовлетворять условиям интерполяции:
Убедимся в том, что если такие полиномы построены, то LN(x) будет удовлетворять условиям интерполяции:
.
Каким образом построить базисные полиномы? Определим
, i=0, 1,…, N.
Легко понять, что
, и т.д.Функция li(z) является полиномом N–й степени от z и для нее выполняются условия «базисности»:
=0, i≠k;, т.е. k=1,…,i-1 или k=i+1,…,N.
.
Таким образом, нам удалось решить задачу о построении интерполирующего полинома N– й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы: . Погрешность этой формулы можно оценить, если исходная функция g(x) имеет производные до N+1 порядка:
.
Из этой формулы следует, что погрешность метода зависит от свойств функции g(x), а также от расположения узлов интерполяции и точки z. Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях N<20. При бόльших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом N).
Рассмотрим частные случаи. Пусть N=1, т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:
, т.е. получаем формулы кусочно–линейной интерполяции.
Пусть N=2. Тогда:
В результате мы получили формулы так называемой квадратичной или параболической интерполяции.
Пример: Заданы значений некоторой функции:
| x | 0 | 2 | 3 |
3. 5 5 |
| f | -1 | 0.2 | 0.5 | 0.8 |
Требуется найти значение функции при z=1, используя интерполяционный полином Лгранжа. Для этого случая N=3, т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при z=1:
Подбор эмпирических формул
При
интерполировании функций мы использовали условие равенства значений
интерполяционного полинома и данной функции в узлах интерполяции. Если же
исходные данные получены в результате опытных измерений, то требование точного
совпадения не нужно, так как данные не получены точно. В этих случаях можно
требовать лишь приближенного выполнения условий интерполяции . Это условие означает,
что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности, так, например, как это показано
на рис.
Это условие означает,
что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности, так, например, как это показано
на рис.
Тогда говорят о подборе эмпирических формул. Построение эмпирической формулы состоит из двух этапов6 подбора вида этой формулы , содержащей неизвестные параметры , и определение наилучших в некотором смысле этих параметров. Вид формулы иногда известен из физических соображений (для упругой среды связь между напряжением и деформацией) или выбираются из геометрических соображений: экспериментальные точки наносятся на график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками извесиных функций. Успех здесь в значительной степени определяется опытом и интуицией исследователя.
Для практики
важен случай аппроксимации функции многочленами, т. е. .
е. .
После того, как выбран вид эмпирической зависимости степень близости к эмпирическим данным определяется, используя минимум суммы квадратов отклонений вычисленных и экспериментальных данных.
Метод наименьших квадратов
Пусть для исходных данных xi, fi, i=1,…,N (нумерацию лучше начинать с единицы), выбран вид эмпирической зависимости: с неизвестными коэффициентами . Запишем сумму квадратов отклонений между вычисленными по эмпирической формуле и заданными опытными данными:
.
Параметры будем находить из условия минимума функции . В этом состоит метод наименьших квадратов (МНК).
Известно, что в точке минимума все частные производные от по равны нулю:
(1)
Рассмотрим
применение МНК для частного случая, широко используемого на практике. В
качестве эмпирической функции рассмотрим полином
В
качестве эмпирической функции рассмотрим полином
.
Формула (1) для определения суммы квадратов отклонений примет вид:
(2)
Вычислим производные:
Приравнивая эти выражения нулю и собирая коэффициенты при неизвестных , получим следующую систему линейных уравнений:
Данная система уравнений называется нормальной. Решая эту систему линейных уравнений, получаем коэффициенты .
В случае полинома первого порядка m=1, т.е. , система нормальных уравнений примет вид:
При m=2 имеем:
Как правило,
выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих
зависимостей и среди них находят наилучшую по минимальной сумме отклонений.
Пример. Заданы координаты точек:
|
x |
-5 |
-3.5 |
-2 |
1.5 |
3.25 |
5 |
|
f |
0.5 |
1. |
1.4 |
1.6 |
1.7 |
1.5 |
т.е. N=6. Требуется найти эмпирические зависимости: линейную , квадратичную , гиперболическую по методу МНК и выбрать среди них наилучшую по наименьшей сумме квадратов отклонений.
Система нормальных уравнений для линейной зависимости:
Учитывая, что N=6, , получим
Решая систему линейных уравнений, получим . Следовательно, линейная зависимость имеет вид: .
Вычислим сумму
квадратов отклонений: .
Рассмотрим квадратичную зависимость. Система нормальных уравнений имеет вид
Найдем неподсчитанные суммы:
Решая СЛАУ, получим
Следовательно, квадратичная зависимость имеет вид: .
Вычислим сумму квадратов отклонений: .
Выпишем систему нормальных уравнений для гиперболической зависимости. Согласно МНК находим сумму квадратов отклонений:
. Составляем систему нормальных уравнений:
Или
Учитывая, что , получим
Сумма квадратов отклонений:
Из трех
зависимостей выбираем наилучшую, т.е. квадратичную.
Интерполяция ключевого кадра в After Effects
Руководство пользователя Отмена
Поиск
- Руководство пользователя After Effects
- Выпуски бета-версии
- Обзор программы бета-тестирования
- Домашняя страница бета-версии After Effects
- Функции бета-версии
- Панель «Свойства» (Бета-версия)
- Выбираемые слои подложки дорожки (бета-версия)
- Встроенное кодирование H.264 (бета-версия)
- Начало работы
- Начало работы с After Effects
- Новые возможности After Effects
- Сведения о выпуске | After Effects
- Системные требования для After Effects
- Сочетания клавиш в After Effects
- Поддерживаемые форматы файлов | After Effects
- Рекомендации по аппаратному обеспечению
- After Effects для компьютеров с процессорами Apple
- Планирование и настройка
- Настройка и установка
- Рабочие среды
- Общие элементы пользовательского интерфейса
- Знакомство с интерфейсом After Effects
- Рабочие процессы
- Рабочие среды, панели управления, программы просмотра
- Проекты и композиции
- Проекты
- Основы создания композиции
- Предварительная композиция, вложение и предварительный рендеринг
- Просмотр подробных сведений о производительности с помощью инструмента «Профайлер композиций»
- Модуль рендеринга композиций CINEMA 4D
- Импорт видеоряда
- Подготовка и импорт неподвижных изображений
- Импорт из After Effects и Adobe Premiere Pro
- Импорт и интерпретация видео и аудио
- Подготовка и импорт файлов 3D-изображений
- Импорт и интерпретация элементов видеоряда
- Работа с элементами видеоряда
- Определение точек редактирования с помощью функции «Определение изменения сцен»
- Метаданные XMP
- Текст и графические элементы
- Текст
- Форматирование символов и панель символов
- Эффекты текста
- Создание и редактирование текстовых слоев
- Форматирование абзацев и панель «Абзац»
- Экструзия слоев текста и слоев-фигур
- Анимация текста
- Примеры и ресурсы для текстовой анимации
- Шаблоны динамического текста
- Анимационный дизайн
- Работа с шаблонами анимационного дизайна в After Effects
- Использование выражений для создания раскрывающихся списков в шаблонах анимационного дизайна
- Работа с основными свойствами для создания шаблонов анимационного дизайна
- Замена изображений и видео в шаблонах анимационного дизайна и основных свойствах
- Текст
- Рисование, заливка цветом и контуры
- Обзор слоев-фигур, контуров и векторных изображений
- Инструменты рисования: «Кисть», «Штамп» и «Ластик»
- Сглаживание обводки фигуры
- Атрибуты фигур, операции заливки цветом и операции с контурами для слоев-фигур
- Использование эффекта фигуры «Cмещение контура» для изменения фигур
- Создание фигур
- Создание масок
- Удаление объектов из видеоматериалов с помощью панели «Заливка с учетом содержимого»
- Инструменты «Кисть для ротоскопии» и «Уточнить подложку»
- Слои, маркеры и камера
- Выделение и упорядочивание слоев
- Режимы наложения и стили слоев
- 3D-слои
- Свойства слоя
- Создание слоев
- Управление слоями
- Маркеры слоя и маркеры композиции
- Камеры, освещение и точки обзора
- Анимация, ключевые кадры, отслеживание движения и прозрачное наложение
- Анимация
- Основы анимации
- Анимация с помощью инструментов «Марионетка»
- Управление и анимация контуров фигур и масок
- Анимация фигур Sketch и Capture с помощью After Effects
- Инструменты анимации
- Работа с анимацией на основе данных
- Ключевой кадр
- Интерполяция ключевого кадра
- Установка, выбор и удаление ключевых кадров
- Редактирование, перемещение и копирование ключевых кадров
- Отслеживание движения
- Отслеживание и стабилизация движения
- Отслеживание лиц
- Отслеживание маски
- Ссылка на маску
- Скорость
- Растягивание по времени и перераспределение времени
- Тайм-код и единицы отображения времени
- Прозрачное наложение
- Прозрачное наложение
- Эффекты прозрачного наложения
- Анимация
- Прозрачность и композиция
- Обзор композиции и прозрачности и соответствующие ресурсы
- Альфа-каналы и маски
- Корректирование цвета
- Основы работы с цветом
- Управление цветом
- Эффекты цветокоррекции
- Эффекты и стили анимации
- Обзор эффектов и стилей анимации
- Список эффектов
- Эффекты имитации
- Эффекты стилизации
- Аудиоэффекты
- Эффекты искажения
- Эффекты перспективы
- Эффекты канала
- Эффекты создания
- Эффекты перехода
- Эффект «Устранение эффекта плавающего затвора»
- Эффекты «Размытие» и «Резкость»
- Эффекты 3D-канала
- Программные эффекты
- Эффекты подложки
- Эффекты «Шум» и «Зернистость»
- Эффект «Увеличение с сохранением уровня детализации»
- Устаревшие эффекты
- Выражения и автоматизация
- Выражение
- Основы работы с выражениями
- Понимание языка выражений
- Использование элементов управления выражениями
- Различия в синтаксисе между движками выражений JavaScript и Legacy ExtendScript
- Управление выражениями
- Ошибки выражения
- Использование редактора выражений
- Использование выражений для изменения свойств текста и доступа к ним
- Справочник языка выражений
- Примеры выражений
- Автоматизация
- Автоматизация
- Сценарии
- Выражение
- Видео с погружением, VR и 3D
- Создание сред VR в After Effects
- Применение видеоэффектов с эффектом погружения
- Инструменты составления композиций для видеоизображений VR/360
- Отслеживание движений камеры в трехмерном пространстве
- Пространство для работы с трехмерными объектами
- Инструменты 3D-преобразования
- Дополнительные возможности 3D-анимации
- Предварительный просмотр изменений в 3D-дизайнах в режиме реального времени с помощью модуля режима реального времени
- Добавление гибкого дизайна в графику
- Виды и предварительный просмотр
- Предпросмотр
- Предпросмотр видео с помощью Mercury Transmit
- Изменение и использование представлений
- Рендеринг и экспорт
- Основы рендеринга и экспорта
- Экспорт проекта After Effects как проекта Adobe Premiere Pro
- Преобразование фильмов
- Многокадровый рендеринг
- Автоматический рендеринг и рендеринг по сети
- Рендеринг и экспорт неподвижных изображений и наборов неподвижных изображений
- Использование кодека GoPro CineForm в After Effects
- Работа с другими приложениями
- Dynamic Link и After Effects
- Работа с After Effects и другими приложениями
- Синхронизация настроек в After Effects
- Библиотеки Creative Cloud Libraries в After Effects
- Подключаемые модули
- CINEMA 4D и Cineware
- Совместная работа: Frame.
 io и Team Projects
io и Team Projects- Совместная работа в Premiere Pro и After Effects
- Frame.io
- Установка и активация Frame.io
- Использование Frame.io с Premiere Pro и After Effects
- Часто задаваемые вопросы
- Team Projects
- Начало работы с Team Projects
- Создание Team Project
- Совместная работа с помощью Team Projects
- Память, хранилище, производительность
- Память и хранилище
- Как After Effects справляется с проблемами нехватки памяти при предварительном просмотре
- Повышение производительности
- Установки
- Требования к графическому процессору и драйверу графического процессора для After Effects
Интерполяция — процесс заполнения неизвестных данных между двумя известными значениями. Ключевые кадры устанавливаются, чтобы определить значения свойства в определенные ключевые моменты. After Effects интерполирует значения свойства для всех моментов времени между ключевыми кадрами.
Поскольку при интерполяции генерируются значения свойств между ключевыми кадрами, ее иногда называют построением промежуточных кадров. С помощью интерполяции между ключевыми кадрами можно анимировать движение, эффекты, громкость звука, коррекцию изображений, прозрачность, изменение цвета и многие другие визуальные и звуковые элементы.
После создания ключевых кадров и пути движения для изменения значений со временем может потребоваться более точно откорректировать способ изменения значений. В After Effects доступно несколько методов интерполяции, которые влияют на способ расчета промежуточных значений.
Временная интерполяция — это интерполяция значений во времени, а пространственная интерполяция — это интерполяция значений в пространстве. Некоторые свойства, такие как «Непрозрачность», имеют только временные компоненты. Другие свойства, такие как «Положение», имеют также пространственные компоненты.
Временная интерполяция и диаграмма значений
Используя диаграммы значений в редакторе диаграмм, можно точно откорректировать ключевые кадры временного свойства, созданные для анимации. На диаграмме значений значения по оси X отображаются красным цветом, по оси Y — зеленым цветом, а по оси Z (только 3D) — синим цветом. Диаграмма значений содержит полные сведения о значениях ключевых кадров в любой момент времени в композиции, позволяя управлять ими. Кроме того, на панели «Информация» отображается метод временной интерполяции для выбранного ключевого кадра.
На диаграмме значений значения по оси X отображаются красным цветом, по оси Y — зеленым цветом, а по оси Z (только 3D) — синим цветом. Диаграмма значений содержит полные сведения о значениях ключевых кадров в любой момент времени в композиции, позволяя управлять ими. Кроме того, на панели «Информация» отображается метод временной интерполяции для выбранного ключевого кадра.
Пространственная интерполяция и путь движения
Если пространственная интерполяция применяется или изменяется для такого свойства, как «Положение», путь движения настраивается на панели «Композиция». Другие ключевые кадры на пути движения содержат сведения о типе интерполяции в любой момент времени. На панели «Информация» отображается метод пространственной интерполяции для выбранного ключевого кадра.
При внесении пространственных изменений в слое After Effects использует в качестве пространственной интерполяции по умолчанию вариант «Автоматическая по Безье».
Чтобы изменить вариант по умолчанию на линейную интерполяцию, выберите команду «Правка» > «Установки» > «Общие» (Windows) или «After Effects» > «Установки» > «Общие» (в ОС Mac OS), а затем — пункт «Использовать пространственную линейную интерполяцию». Изменение параметра не влияет на уже существующие ключевые кадры или на новые ключевые кадры в свойствах, для которых уже существуют ключевые кадры.
Изменение параметра не влияет на уже существующие ключевые кадры или на новые ключевые кадры в свойствах, для которых уже существуют ключевые кадры.
A. Линейный B. Автоматическая по Безье C. Непрерывная кривая Безье D. Кривая Безье E. Нулевого порядка
В некоторых случаях пространственная интерполяция «Автоматическая по Безье» для ключевых кадров положения может привести к нежелательному возвратно-поступательному движению (бумеранг) между ключевыми кадрами с равными значениями. В таком случае можно изменить более ранний кадр, чтобы использовать интерполяцию нулевого порядка или задать для ключевых кадров линейную интерполяцию.
Ресурсы в Интернете, посвященные интерполяции ключевого кадра
Аарон Рабинович (Aharon Rabinowitz) опубликовал на веб-сайте Creative COW два видеоурока с описанием и решением проблемы бумеранга, которая возникает из-за случайного назначения пространственной интерполяции «Автоматическая по Безье» для ключевых кадров с равными значениями:
Часть 1
Часть 2
Энтони Боланте (Antony Bolante) представил информацию и иллюстрации, касающиеся интерполяции ключевого кадра, в статье на веб-сайте Peachpit Press.
В режиме панели слоев внешний вид ключевого кадра зависит от выбранного метода интерполяции. Если половина значка имеет темно-серый цвет, темная половина означает, что на этой стороне отсутствует ключевой кадр, а его интерполяция переопределяется интерполяцией нулевого порядка, примененной к предыдущему ключевому кадру.
По умолчанию для ключевого кадра используется один метод интерполяции, но применить можно и два метода: входящий метод применяется к значению свойства, когда индикатор текущего времени доходит до ключевого кадра, а исходящий метод применяется к значению свойства, когда индикатор текущего времени покидает ключевой кадр. Если указать разные входящие и исходящие методы интерполяции, значок ключевого кадра в режиме панели слоев примет соответствующий вид. Левая его половина будет представлять входящую интерполяцию, а правая половина — исходящую интерполяцию.
Чтобы переключиться между значками и номерами ключевых кадров, выберите в меню панели «Таймлайн» команду «Использовать значки ключевого кадра» или «Использовать индексы ключевого кадра».
A. Линейный B. Линейная (входящая), нулевого порядка (исходящая) C. Автоматическая по Безье D. Непрерывная кривая Безье или кривая Безье E. Линейная (входящая), кривая Безье (исходящая)
Все используемые After Effects методы интерполяции основаны на методе интерполяции по кривой Безье, в котором доступны дескрипторы направления, чтобы можно было управлять переходами между ключевыми кадрами. Методы интерполяции, в которых не используются дескрипторы направления, представляют собой ограниченные версии интерполяции по кривой Безье, которые подходят для определенных задач.
Чтобы больше узнать о том, как разные методы интерполяции влияют на временные свойства, попробуйте установить хотя бы три ключевых кадра с различными значениями для свойства временного слоя, например «Непрозрачность», и измените методы интерполяции при просмотре диаграммы значений в режиме редактора диаграмм на панели «Таймлайн».
Чтобы больше узнать о том, как разные методы интерполяции влияют на путь движения, попробуйте установить до трех ключевых кадров для пространственного свойства, например «Положение», с различными значениями на пути движения и изменяйте методы интерполяции в ходе предпросмотра движения на панели «Композиция».
Чтобы изменить методы интерполяции, щелкните правой кнопкой мыши ключевой кадр, выберите в появившемся меню пункт «Интерполяция ключевого кадра», затем выберите нужный вариант в меню «Временная интерполяция».
Чтобы пояснить примеры в описанных ниже методах интерполяции, результат каждого метода описывается так, если бы он был применен ко всем ключевым кадрам свойства слоя. На практике можно применить любой из доступных методов интерполяции к любому ключевому кадру.
Отсутствие интерполяции
Отсутствие интерполяции — это состояние, в котором у свойства слоя нет ключевых кадров. При этом секундомер выключен, а на панели «Таймлайн» под индикатором текущего времени отображается I-образный курсор . В этом состоянии, если для свойства слоя установить значение, оно будет сохраняться на протяжении всего слоя, если только не будет переопределено выражением. По умолчанию состояние без интерполяции применяется к свойству слоя. Если для свойства слоя есть ключевые кадры, используется один из типов интерполяции.
В этом состоянии, если для свойства слоя установить значение, оно будет сохраняться на протяжении всего слоя, если только не будет переопределено выражением. По умолчанию состояние без интерполяции применяется к свойству слоя. Если для свойства слоя есть ключевые кадры, используется один из типов интерполяции.
Линейная интерполяция
Линейная интерполяция обеспечивает равномерное изменение между ключевыми кадрами, которые могут придать анимации «механический» вид. В After Effects значения интерполируются между двумя соседними ключевыми кадрами максимально прямо, то есть без учета значений других ключевых кадров.
Если применить линейную интерполяцию ко всем ключевым кадрам свойства временного слоя, изменения начинаются сразу для первого ключевого кадра и развиваются до следующего ключевого кадра с постоянной скоростью. Во втором ключевом кадре скорость изменения резко меняется на скорость вторым и третьим ключевым кадром. Если в слое достигается конечное значение ключевого кадра, изменение резко прекращается. На диаграмме значений сегмент, соединяющий два ключевых кадра с использованием линейной интерполяции, отображается как прямая линия.
На диаграмме значений сегмент, соединяющий два ключевых кадра с использованием линейной интерполяции, отображается как прямая линия.
Интерполяция по кривой Безье
Интерполяция по кривой Безье обеспечивает наиболее точное управление, потому что можно изменить форму диаграммы значений или пути движения вручную с любой стороны ключевого кадра. В отличие от автоматической интерполяции по Безье или интерполяции по непрерывной кривой Безье, два дескриптора направления ключевого кадра «Кривая Безье» действуют независимо на диаграмме значений и на пути движения.
При применении интерполяции по кривой Безье ко всем ключевым кадрам свойства слоя After Effects создает плавный переход между ключевыми кадрами. Исходное положение дескрипторов направления вычисляется на основании того же метода, который используется в автоматической интерполяции Безье. При изменении значений ключевых кадров Безье в After Effects существующие положения дескрипторов направлений сохраняются.
В отличие от других методов интерполяции интерполяция по кривой Безье позволяет создавать любые комбинации кривых и прямых линии вдоль пути движения. Так как два дескриптора направления «Кривая Безье» работают независимо друг от друга, изгибающийся путь движения может резко превратиться в острый угол в ключевом кадре кривой Безье. Пространственная интерполяция по кривой Безье идеально подходит для рисования пути движения, повторяющего сложную форму, например маршрута на карте или контура логотипа.
Так как два дескриптора направления «Кривая Безье» работают независимо друг от друга, изгибающийся путь движения может резко превратиться в острый угол в ключевом кадре кривой Безье. Пространственная интерполяция по кривой Безье идеально подходит для рисования пути движения, повторяющего сложную форму, например маршрута на карте или контура логотипа.
Существующие положения дескрипторов направлений сохраняются при перемещении ключевого кадра по пути движения. Временная интерполяция, примененная к каждому ключевому кадру, определяет скорость движения вдоль пути.
Автоматическая интерполяция по кривой Безье
Автоматическая интерполяция по кривой Безье обеспечивает плавную скорость изменения ключевого кадра. С помощью этого типа пространственной интерполяции можно создать путь автомобиля, едущего по извилистой дороге.
Если изменить значение ключевого кадра «Автоматическая по Безье» , положения дескрипторов этой кривой автоматически изменятся для создания плавного перехода между ключевыми кадрами. При автоматической коррекции изменяется форма диаграммы значений или сегменты пути движения по обе стороны ключевого кадра. Если в предыдущем и следующем ключевом кадре также используется автоматическая интерполяция по кривой Безье, форма отрезков на дальней стороне предыдущих или следующих ключевых кадров также изменяется. Чтобы вручную изменить дескриптор направления автоматической интерполяции по Безье, необходимо преобразовать его в ключевой кадр «Непрерывная кривая Безье» .
При автоматической коррекции изменяется форма диаграммы значений или сегменты пути движения по обе стороны ключевого кадра. Если в предыдущем и следующем ключевом кадре также используется автоматическая интерполяция по кривой Безье, форма отрезков на дальней стороне предыдущих или следующих ключевых кадров также изменяется. Чтобы вручную изменить дескриптор направления автоматической интерполяции по Безье, необходимо преобразовать его в ключевой кадр «Непрерывная кривая Безье» .
Автоматическая интерполяция по Безье является пространственной по умолчанию.
Интерполяция по непрерывной кривой Безье
Как и автоматическая интерполяция по кривой Безье, интерполяция по непрерывной кривой Безье обеспечивает плавную скорость изменения ключевого кадра. Однако положения дескрипторов направления «Непрерывная кривая Безье» задаются вручную. При коррекции изменяется форма диаграммы значений или сегменты пути движения по обе стороны ключевого кадра.
Если интерполяция по непрерывной кривой Безье применяется ко всем ключевым кадрам свойства, After Effects корректирует значения всех ключевых кадров для создания плавных переходов. After Effects сохраняет эти плавные переходы при перемещении ключевого кадра «Непрерывная кривая Безье» на путь движения или на диаграмму значений.
After Effects сохраняет эти плавные переходы при перемещении ключевого кадра «Непрерывная кривая Безье» на путь движения или на диаграмму значений.
Интерполяция нулевого порядка
Интерполяция нулевого порядка доступна только в качестве метода временной интерполяции. Используйте ее для изменения значения свойства слоя с течением времени, но без постепенного перехода. Этот метод временной интерполяции подходит для борьбы с эффектом стробоскопа или при внезапном появлении и исчезновении слоев.
Если применить интерполяцию нулевого порядка ко всем ключевым кадрам свойства слоя, значение первого ключевого кадра останется неизменным до следующего ключевого кадра, когда значения резко изменяются. На диаграмме значений сегмент, следующий за ключевым кадром «Нулевой порядок» , отображается как горизонтальная прямая линия.
Несмотря на то, что интерполяция нулевого порядка доступна только как метод временной интерполяции, ключевые кадры все равно отображаются на пути движения, но не связаны точками положения в слое. Например, при анимации свойства слоя «Положение» с использованием интерполяции нулевого порядка, значение положения предыдущего ключевого кадра сохраняется в слое до тех пор, пока индикатор текущего времени не достигнет следующего ключевого кадра, в котором точка слоя пропадает в предыдущем местоположения и появляется в новом положении.
Например, при анимации свойства слоя «Положение» с использованием интерполяции нулевого порядка, значение положения предыдущего ключевого кадра сохраняется в слое до тех пор, пока индикатор текущего времени не достигнет следующего ключевого кадра, в котором точка слоя пропадает в предыдущем местоположения и появляется в новом положении.
Текущий кадр можно легко зафиксировать на время продолжительности слоя с помощью команды «Зафиксировать кадр». Чтобы зафиксировать кадр, поместите в него индикатор текущего времени. Убедитесь, что слой выделен, а затем выберите команду «Слой» > «Время» > «Зафиксировать кадр». Будет включено переопределение времени, а ключевой кадр «Нулевой порядок» будет помещен в положение индикатора текущего времени, чтобы зафиксировать кадр.
Если функция переопределения времени для слоя включалась ранее, в случае применения команды «Зафиксировать кадр» все созданные ключевые кадры будут удалены.
Интерполяцию нулевого порядка можно использовать только для исходящей временной интерполяции (для кадров, следующих за ключевым кадром). Если создать ключевой кадр за кадром «Нулевой порядок», будет создан новый ключевой кадр с входящей интерполяцией нулевого порядка.
Если создать ключевой кадр за кадром «Нулевой порядок», будет создан новый ключевой кадр с входящей интерполяцией нулевого порядка.
Чтобы применить или удалить интерполяцию нулевого порядка в качестве исходящей интерполяции для ключевого кадра, выделите ключевой кадр на панели «Таймлайн», а затем выберите «Анимация» > «Переключить ключевой кадр нулевого порядка».
Метод интерполяции можно применить и изменить для любого ключевого кадра. Изменения можно вносить в диалоговом окне «Интерполяция ключевого кадра» или применять их непосредственно к ключевому кадру в режиме панели слоев, на пути движения или в редакторе диаграмм. Можно также изменить интерполяцию, используемую по умолчанию в After Effects для пространственных свойств.
Сведения об использовании элементов управления «Плавное замедление» для автоматического изменения скорости между ключевыми кадрами см. в разделе Управление скоростью между ключевыми кадрами.
Изменение метода интерполяции в диалоговом окне «Интерполяция ключевого кадра»
Диалоговое окно «Интерполяция ключевого кадра» содержит параметры для настройки временной и пространственной интерполяции и (только для пространственных свойств) параметры привязки.
В режиме панели диаграмм или в редакторе диаграмм выделите ключевые кадры, которые нужно изменить.
Выберите команду «Анимация» > «Интерполяция ключевого кадра».
Для параметра «Временная интерполяция» выберите один из следующих вариантов.
Текущие настройки
Сохраняет значения интерполяции, уже примененные к выбранным ключевым кадрам. Выберите этот вариант, если было выбрано несколько ключевых кадров или кадры были изменены вручную, и вы не хотите изменять существующие параметры.
«Линейная», «Кривая Безье», «Непрерывная кривая Безье», «Автоматическая по Безье» и «Нулевого порядка»
Примените метод временной интерполяции со значениями по умолчанию.
Если были выбраны ключевые кадры пространственного свойства слоя, выберите один из следующих вариантов для пространственной интерполяции.
Текущие настройки
Сохраняет параметры интерполяции, уже примененные к выбранным ключевым кадрам.

«Линейная», «Кривая Безье», «Непрерывная кривая Безье» и «Автоматическая по Безье»
Примените метод пространственной интерполяции со значениями по умолчанию.
Если были выбраны ключевые кадры пространственного свойства слоя, выберите в меню «Отсутствие привязки» способ определения положения ключевого кадра во времени, а затем нажмите кнопку «ОК».
Текущие настройки
Сохраняет используемый в данный момент способ определения положения выделенных ключевых кадров во времени.
Пропускать по времени
Сглаживает скорость изменения в выделенных ключевых кадрах, автоматически меняя их положение во времени на основании положений ключевых кадров непосредственно перед выделенными кадрами и после них.
Заблокировать по времени
Сохраняет выделенные ключевые кадры в их текущем положении во времени. Кадры остаются на месте, если только не переместить их вручную.
Дополнительные сведения о сглаживании скорости изменения в выделенных ключевых кадрах см. в разделе Плавное движение с использованием ключевых кадров без привязки.
Изменение метода интерполяции с помощью инструмента «Выделение» в режиме панели слоев
С помощью инструмента «Выделение» выполните одно из предложенных ниже действий.
Если для ключевого кадра используется линейная интерполяция, щелкните его, удерживая нажатой клавишу Ctrl (Windows) или Command (Mac OS), чтобы изменить интерполяцию на «Автоматическая по Безье» .
Если для ключевого кадра используется интерполяция «Кривая Безье», «Непрерывная кривая Безье» или «Автоматическая по Безье», для ее изменения на линейную интерполяцию щелкните ключевой кадр, удерживая нажатой клавишу CTRL (Windows) или COMMAND (Mac OS).
Изменение метода интерполяции в редакторе диаграмм
- Щелкните ключевой кадр с помощью инструмента «Преобразование вершины» для переключения между линейной и автоматической интерполяцией по кривой Безье.

- Выделите один или несколько ключевых кадров, а затем нажмите в нижней части экрана кнопку «Нулевого порядка», «Линейная» или «Автоматическая по Безье», чтобы изменить метод интерполяции.
A. Преобразовать выбранные ключевые кадры в тип «Остановка» B. Преобразовать выделенные ключевые кадры в тип «Линейный» C. Преобразование выбранных ключевых кадров с интерполяцией «Автоматическая по Безье»
В редакторе диаграмм к ключевым кадрам, в которых используется интерполяция по кривой Безье, привязаны дескрипторы направления. Дескрипторы направления можно вытянуть, втянуть обратно или повернуть для тонкой настройки интерполяции по кривой Безье на диаграмме значений. Дескрипторы направления можно вытянуть или втянуть обратно для тонкой настройки кривой на диаграмме скорости.
При втягивании или вытягивании дескриптора направления вместе с ним по умолчанию перемещается маркер на противоположной стороне ключевого кадра. При разделении дескриптора направления создаются два независимо работающих маркера, привязанные к ключевому кадру.
При разделении дескриптора направления создаются два независимо работающих маркера, привязанные к ключевому кадру.
- Чтобы втянуть или вытянуть дескриптор направления, потащите его к центру или от центра ключевого кадра с помощью инструмента «Выделение».
- Чтобы разделить дескриптор направления, потащите ключевой кадр, удерживая нажатой клавишу ALT (Windows) или OPTION (Mac OS) с помощью инструмента «Выделение». Можно также потащить указатель мыши, удерживая нажатой клавишу ALT (Windows) или OPTION (Mac OS), за пределами ключевого кадра, чтобы нарисовать новые маркеры независимо от того, существуют ли уже маркеры или нет.
- Чтобы одновременно изменить дескрипторы направления двух соседних ключевых кадров, потащите сегмент диаграммы значений между этими кадрами.
Справки по другим продуктам
- Управление скоростью между ключевыми кадрами
- Редактор диаграмм
- Ключевые кадры и редактор диаграмм (комбинации клавиш)
- Отображение свойств и групп на панели «Таймлайн» (комбинации клавиш)
- Сведения об анимации, ключевые кадры и выражения
- Выделение ключевых кадров
Вход в учетную запись
Войти
Управление учетной записью
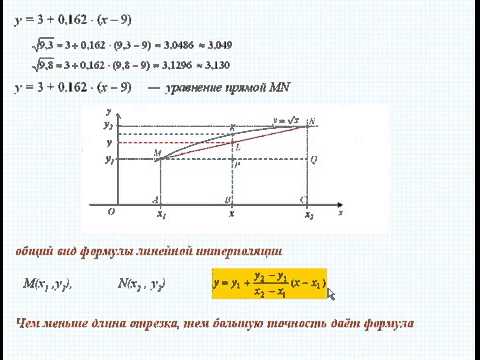
Формула линейной интерполяции — Вывод, формулы, примеры
Формула линейной интерполяции является простейшим методом, который используется для оценки значения функции между любыми двумя известными значениями. Кроме того, формула линейной интерполяции — это метод, который полезен для аппроксимации кривой с использованием линейных полиномов. В основном метод интерполяции используется для нахождения новых значений любой функции по набору значений. Неизвестные значения в таблице находятся по формуле линейной интерполяции. Давайте узнаем больше о формуле линейной интерполяции в этом разделе.
Кроме того, формула линейной интерполяции — это метод, который полезен для аппроксимации кривой с использованием линейных полиномов. В основном метод интерполяции используется для нахождения новых значений любой функции по набору значений. Неизвестные значения в таблице находятся по формуле линейной интерполяции. Давайте узнаем больше о формуле линейной интерполяции в этом разделе.
Что такое формула линейной интерполяции?
Формула линейной интерполяции используется для прогнозирования данных, прогнозирования данных, математических и научных приложений, исследований рынка и т. д. Формула линейной интерполяции может использоваться для поиска неизвестных значений в таблице. Формула для формулы линейной интерполяции имеет вид:
Линейная интерполяция(y) = \(y_{1}+ (x-x_{1})\dfrac{(y_{2}-y_{1})}{( x_{2}-x_{1})}\)
Формула линейной интерполяции
Формула для расчета линейной интерполяции:
Линейная интерполяция(y) = \(y_{1}+( x-x_{1})\dfrac{(y_{2}-y_{1})}{( x_{2}-x_{1})}\)
где,
- \(x_1\) и \(y_1\) — первые координаты
- \(x_2\) и \(y_2\) — вторые координаты
- x точка для выполнения интерполяции
- y интерполированное значение
Отличное обучение в старшей школе с использованием простых сигналов
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
Заказать бесплатный пробный урок
Примеры использования формулы линейной интерполяции
Пример 1. Найдите значение y, если x = 6 и некоторый набор значений задан как (3, 4), (6, 8)?
Решение:
х = 6 ; \(x_1\) = 3 ; \(х_2\) = 6 ; \(y_1\) = 4 ; \(y_2\) = 8 (дано)
Используя формулу линейной интерполяции,
Линейная интерполяция(y) = \(y_{1}+ (x-x_{1})\dfrac{(y_{2}-y_{1})}{(x_{2}-x_{1}) }\)
Поместите значения,
\(y= 4+(6-3)\dfrac{8-4}{6-3}\)
у = 4 + 3 (4/3)
y = 4 + 4
y = 8
Следовательно, значение y равно 8.
Пример 2. Рассчитайте примерный рост мальчика на четвертой позиции.
| позиция(х) | х | 1 | 2 | 3 | 5 |
| Высота в футах (г) | г | 3 | 4,5 | 5 | 6 |
Решение:
х = 4 ; \(х_1\) = 3 ; \(х_2\) = 5 ; \(y_1\) = 5 ;\(y_2\) = 6 (дано)
Используя формулу линейной интерполяции,
Линейная интерполяция(y) = \(y_{1}+ (x-x_{1})\dfrac {(у_{2}-у_{1})}{(х_{2}-х_{1})}\)
Поместите значения,
\(y= 5 + (4 — 3)\dfrac{(6 — 5)}{(5-3)}\)
y = 5 + 1(1/2)
у = 5 + 0,5
y = 5,5
Следовательно, рост мальчика на четвертой позиции равен 5,5 футов.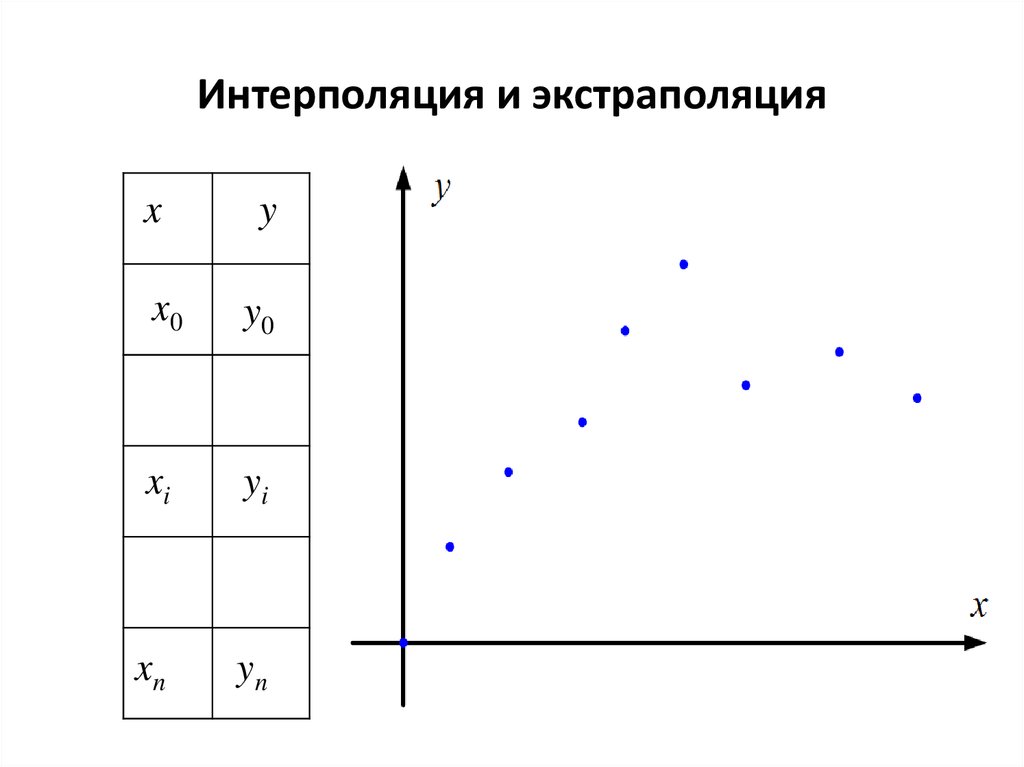
Пример 3: Найти значение y, если x = 8 и некоторый набор значений задан как (5, 3.5), (10, 6)?
Решение:
x = 8 ; \(x_1\) = 5 ; \(х_2\) = 10 ; \(у_1\) = 3,5 ; \(y_2\) = 6 (дано)
Используя формулу линейной интерполяции,
Линейная интерполяция(y) = \(y_{1}+ (x-x_{1})\dfrac{(y_{2}-y_{1})}{(x_{2}-x_{1}) }\)
Поместите значения,
\(y= 3,5 + (8- 5)\dfrac{(6 — 3,5)}{(10- 5)}\)
у = 3,5 +3(2,5/5)
y = 3,5 + 3(1/2)
y = 3,5 + 1,5
y = 5
Следовательно, значение y равно 5
Часто задаваемые вопросы о формуле линейной интерполяции
Что понимается под формулой линейной интерполяции?
Формула линейной интерполяции — это метод, полезный для аппроксимации кривой с использованием линейных полиномов. В основном метод интерполяции используется для нахождения новых значений любой функции по набору значений. Неизвестные значения в таблице находятся по формуле линейной интерполяции. Формула линейной интерполяции используется для прогнозирования данных, прогнозирования данных, математических и научных приложений, а также для исследования рынка и т. д. Формула (y) = \(y_{1}+\frac{\left(x-x_{1}) \right)\left(y_{2}-y_{1}\right)}{x_{2}-x_{1}}\)
Формула линейной интерполяции используется для прогнозирования данных, прогнозирования данных, математических и научных приложений, а также для исследования рынка и т. д. Формула (y) = \(y_{1}+\frac{\left(x-x_{1}) \right)\left(y_{2}-y_{1}\right)}{x_{2}-x_{1}}\)
Какая формула используется для расчета формулы линейной интерполяции?
Формула для расчета линейной интерполяции:
Линейная интерполяция(y) = \(y_{1}+ (x-x_{1})\dfrac{(y_{2}-y_{1})}{( x_{2}-x_{1})}\)
где,
- \(x_1\) и \(y_1\) — первые координаты
- \(x_2\) и \(y_2\) — вторые координаты
- x точка для выполнения интерполяции
- y интерполированное значение
Для чего используется формула линейной интерполяции?
Формула линейной интерполяции полезна для определения значений между любыми двумя заданными точками. Следовательно, линейная интерполяция также рассматривается как метод заполнения пробелов для любого значения в формате таблицы.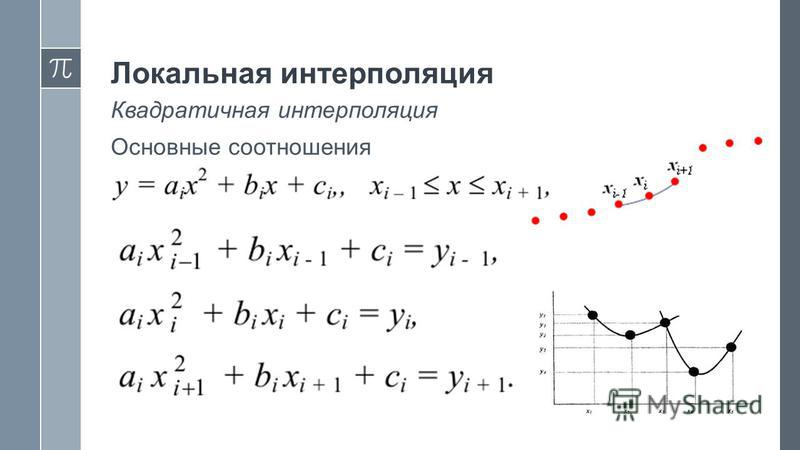 Формула помогает создать прямую линию вместе с заданными точками как с отрицательной, так и с положительной стороны.
Формула помогает создать прямую линию вместе с заданными точками как с отрицательной, так и с положительной стороны.
Используя формулу линейной интерполяции, найдите значение y при x = 8 вместе с координатами (7,5) и (10,9)
х = 8 ; \(x_1\) = 6 ; \(х_2\) = 10 ; \(y_1\) = 5 ; \(y_2\) = 9 (дано)
Используя формулу линейной интерполяции,
Линейная интерполяция(y) = \(y_{1}+ (x-x_{1})\dfrac{(y_{2}-y_ {1})}{(x_{2}-x_{1})}\)
Поместите значения,
\(y= 5+(8-6) \dfrac{9-5}{10-6 }\)
y = 5+ 2(4/4)
y = 5 + 2
y = 7
Следовательно, значение y равно 7
Линейная интерполяция — GIS Wiki
— это метод аппроксимации кривой с использованием линейных полиномов. Он широко используется в математике (особенно в численном анализе) и многочисленных приложениях, включая компьютерную графику. Это простая форма интерполяции.
Lerp — это квазиаббревиатура от линейная интерполяция , которая также может использоваться как глагол (Raymond 2003) .
Содержание
- 1 Линейная интерполяция между двумя известными точками
- 2 Интерполяция набора данных
- 3 Линейная интерполяция в качестве аппроксимации
- 4 приложения
- 5 удлинителей
- 5.1 Точность
- 5.2 Многомерный
- 6 История
- 7 Каталожные номера
- 8 См. также
- 9 Внешние ссылки
Линейная интерполяция между двумя известными точками
Учитывая две красные точки, синяя линия представляет собой линейную интерполяцию между точками и значением y при x можно найти с помощью линейной интерполяции.
Если две известные точки заданы координатами и , линейный интерполянт представляет собой прямую линию между этими точками. Для значения x на интервале значение y по прямой определяется из уравнения
, которые можно получить геометрически из рисунка справа.
Решение этого уравнения для y , неизвестного значения в x , дает
что является формулой для линейной интерполяции в интервале . Вне этого интервала формула идентична линейной экстраполяции.
Интерполяция набора данных
Линейная интерполяция набора данных (красные точки) состоит из частей линейных интерполянтов (синие линии).
Линейная интерполяция набора точек данных определяется как объединение линейных интерполяций между каждой парой точек данных. Это приводит к непрерывной кривой с прерывистой производной, таким образом, класса дифференцируемости.
Линейная интерполяция как аппроксимация
Линейная интерполяция часто используется для аппроксимации значения некоторой функции f с использованием двух известных значений этой функции в других точках. Ошибка этого приближения определяется как
где p обозначает полином линейной интерполяции, определенный выше
С помощью теоремы Ролля можно доказать, что если f имеет непрерывную вторую производную, то ошибка ограничена
Как видите, аппроксимация между двумя точками заданной функции ухудшается со второй производной аппроксимируемой функции. Интуитивно это тоже верно: чем «круче» функция, тем хуже аппроксимация, сделанная простой линейной интерполяцией.
Интуитивно это тоже верно: чем «круче» функция, тем хуже аппроксимация, сделанная простой линейной интерполяцией.
Приложения
Линейная интерполяция часто используется для заполнения пробелов в таблице. Предположим, у вас есть таблица, в которой перечислено население какой-то страны в 1970, 1919 гг.80, 1990 и 2000 гг., и что вы хотите оценить численность населения в 1994 г. Линейная интерполяция дает вам простой способ сделать это.
Основная операция линейной интерполяции между двумя значениями настолько широко используется в компьютерной графике, что на жаргоне этой области ее иногда называют lerp . Термин может использоваться как глагол или существительное для операции. например «Алгоритм Брезенхема постепенно колеблется между двумя конечными точками линии».
Операции Lerp встроены в аппаратную часть всех современных процессоров компьютерной графики. Они часто используются в качестве строительных блоков для более сложных операций: например, билинейная интерполяция может быть выполнена за два лерпа. Поскольку эта операция дешева, это также хороший способ реализовать точные таблицы поиска с быстрым поиском гладких функций без слишком большого количества записей в таблице.
Поскольку эта операция дешева, это также хороший способ реализовать точные таблицы поиска с быстрым поиском гладких функций без слишком большого количества записей в таблице.
Расширения
Точность
Если функции C 0 недостаточно, например, если известно, что процесс, создавший точки данных, является более гладким, чем C 0 , обычно заменяют линейной интерполяцией. со сплайн-интерполяцией или даже полиномиальной интерполяцией в некоторых случаях.
Многомерный
Линейная интерполяция, описанная здесь, предназначена для точек данных в одном пространственном измерении. Для двух пространственных измерений расширение линейной интерполяции называется билинейной интерполяцией, а для трех измерений — трилинейной интерполяцией. Другие расширения линейной интерполяции могут быть применены к другим типам сеток, таким как треугольные и тетраэдральные сетки.
История
Линейная интерполяция использовалась с древних времен для заполнения пробелов в таблицах, часто астрономическими данными. Считается, что его использовали вавилонские астрономы и математики в Месопотамии Селевкидов (последние три века до нашей эры) и греческий астроном и математик Гиппарх (второй век до нашей эры). Описание линейной интерполяции можно найти в Альмагесте (второй век нашей эры) Птолемея.
Считается, что его использовали вавилонские астрономы и математики в Месопотамии Селевкидов (последние три века до нашей эры) и греческий астроном и математик Гиппарх (второй век до нашей эры). Описание линейной интерполяции можно найти в Альмагесте (второй век нашей эры) Птолемея.
Каталожные номера
- Мейеринг, Эрик (2002), «Хронология интерполяции: от древней астрономии до современной обработки сигналов и изображений», Труды IEEE 90 (3): 319–342, doi: 10.1109/5.993400 .
- Рэймонд, Эрик (2003 г.), «LERP», Жаргонный файл (версия 4.4.7) .
См. также
- Билинейная интерполяция
- Алгоритм де Кастельжо
Внешние ссылки
- Уравнения прямой при разрубании узла
- Реализация линейной интерполяции в Microsoft Excel
Линейная интерполяция
Линейная интерполяция Вверх: Возврат Линейная интерполяция — это способ заполнить «дыры» в таблицах. В качестве
Например, если вы хотите найти давление насыщения воды при
температуре 40С можно посмотреть в таблице Б.1.1, (стр.674), для
40С в первой колонке. Соответствующее желаемое давление
находится в следующем столбце; в данном случае 7,384 кПа. Но что, если вы
хотите найти давление насыщения при 38C вместо
40С?
В качестве
Например, если вы хотите найти давление насыщения воды при
температуре 40С можно посмотреть в таблице Б.1.1, (стр.674), для
40С в первой колонке. Соответствующее желаемое давление
находится в следующем столбце; в данном случае 7,384 кПа. Но что, если вы
хотите найти давление насыщения при 38C вместо
40С?
Температуры 38С нет в таблице. Вы могли бы, конечно просто игнорируйте разницу между 38C и 40C, и по-прежнему считать давление насыщения равным 7,384 кПа. Но это не приемлемо в этом классе; это слишком неточно. Чтобы получить точную значение, вы должны использовать линейную интерполяцию. (Хотя беря ближайший значение, 40C, конечно, лучше, чем ничего, если вы забыл, как делать линейную интерполяцию во время экзамена.)
Введем несколько символов. Пусть г будет заданным вами значением,
38C в этом примере. Пусть г 1 и г 2 будут двумя ближайшими приближения к г в табл. Взгляд на Таблицу B. 1.1 показывает
что два ближайших значения, которые вы можете найти в таблице, равны 35C.
и 40°С, поэтому в нашем примере г 1 = 35°С и г 2 =40°С. (Желаемое значение находится между этими двумя, поэтому
«in» в «interpolation».)
1.1 показывает
что два ближайших значения, которые вы можете найти в таблице, равны 35C.
и 40°С, поэтому в нашем примере г 1 = 35°С и г 2 =40°С. (Желаемое значение находится между этими двумя, поэтому
«in» в «interpolation».)
Также пусть d будет нашим желаемым значением, в нашем примере насыщенный давление. Пусть d 1 и d 2 будут приблизительными желаемыми значениями. соответствует г 1 и г 2 . В нашем примере таблица B.1.1 дает давление насыщения при 90 208 г 90 390 1 90 391 90 209 = 35°C составляет 90 208 d 90 390 1 90 391 90 209 = 5,628 кПа и давление насыщения при г 2 =40°C, чтобы быть d 2 =7,384 кПа. Оба d 1 и d 2 являются приближениями к нашему желаемому давлению, но ни то, ни другое не является достаточно точным.
Формула линейной интерполяции:
Так, в нашем примере желаемое давление насыщения d при 38С является:
Вам нужны две переменные для считывания сжатой жидкости или
столы с перегретым паром. В следующем примере мы найдем
удельный объем пара при заданной температуре 100°С и
при давлении 20 кПа.
В следующем примере мы найдем
удельный объем пара при заданной температуре 100°С и
при давлении 20 кПа.
Пар (перегретый водяной пар) указан в таблице Б.1.3. У нас нет трудно найти заданные 100C в этой таблице, но мы не можем найти заданное давление 20 кПа. Ближайшие давления в таблице составляют 10 кПа и 50 кПа.
Итак, в формуле линейной интерполяции из предыдущего раздела
устанавливаем заданное значение г равным 20 кПа, а ближайшую таблицу ценности г 1 и г 2 до 10 кПа и 50 кПа.Требуемое количество d теперь представляет собой удельный объем при 100°С. и 20 кПа. Задаем значение d 1 удельный объем г 1 =10 кПа (и 100°С), т.е. таблицы, а d 2 к удельному объему при г 2 =50 кПа (и 100С,) так д 2 =3,41833 м 3 /кг.
Затем наша формула дает удельный объем при 20 кПа и 100°C. в качестве:
в качестве:
Вы можете спросить, что происходит с последним примером, если ни давление, ни заданная температура не указаны в таблице. Например, чтобы найти удельный объем при 20 кПа и 110С, ни 20 кПа ни 110C не указаны в таблице B.1.4. Я не думаю, что мы бы сделали это Вам во время экзамена. Но ответ будет состоять в том, чтобы сделать три линейных интерполяции: сначала интерполируйте определенный объем при 110C и 10 кПа (заполните «дыру» 110C в данных 10 кПа), затем интерполируйте конкретный объем при 110°C и 50 кПа (заполните «дыра» 110C в данных 50 кПа) и, наконец, линейная интерполируйте эти значения 110C так же, как мы делали для 100С в предыдущем разделе.
Другая проблема возникает, если вы пытаетесь интерполировать определенный объем
пара при 11 кПа и 50°С. Вы можете использовать запись B.1.3 для
50C и г 1 = 10 кПа, что дает d 1 = 14,86920 м 3 /кг. Но
к сожалению, данные 50 кПа начинаются с 81,33°C; нет 50С
пар при 50 кПа существует. Ключ, чтобы найти вторую запись в таблице, чтобы дать
you g 2 и d 2 , заключается в том, чтобы признать, что перегретый пар заканчивается на
насыщенность, которая находится в таблице Б.1.1. Вы можете найти нужную секунду
запись таблицы там; в частности, B.1.1 при 50°С дает второй
давление г 2 =12,350 и удельный объем d 2 =12,0318. Что значит
что формула
Ключ, чтобы найти вторую запись в таблице, чтобы дать
you g 2 и d 2 , заключается в том, чтобы признать, что перегретый пар заканчивается на
насыщенность, которая находится в таблице Б.1.1. Вы можете найти нужную секунду
запись таблицы там; в частности, B.1.1 при 50°С дает второй
давление г 2 =12,350 и удельный объем d 2 =12,0318. Что значит
что формула
Вверх: Возврат
Линейная интерполяция: объяснение и пример, формула
В статистике линейная интерполяция часто используется для нахождения оценочной медианы, квартилей или процентилей набора данных, особенно когда данные представлены в таблице групповых частот с интервалами классов. В этой статье мы рассмотрим, как выполнить расчет линейной интерполяции с использованием таблицы и графика, чтобы найти медиану, 1 -й -й квартиль и 3-й -й -й квартиль.
Формула линейной интерполяции
Формула линейной интерполяции — это простейший метод, используемый для оценки значения функции между любыми двумя известными точками. Эта формула также полезна для аппроксимации кривой с использованием линейных полиномов. Эта формула часто используется для прогнозирования данных, предсказания данных и других математических и научных приложений. Уравнение линейной интерполяции имеет вид:
, где:
x 1 и y 1 — первые координаты.
x 2 и y 2 — вторые координаты.
x — точка для выполнения интерполяции.
y — интерполированное значение.
Решенный пример для линейной интерполяции
Лучший способ понять линейную интерполяцию — использовать пример.
Найдите значение y, если x = 5 и некоторый заданный набор значений равен (3,2), (7,9).
Шаг 1: Сначала присвойте каждой координате правильное значение
x = 5 (обратите внимание, что это дано)
x 1 = 3 и y 1 = 2
x 2 = 7 и 0 y = 9
Шаг 2: Подставьте эти значения в уравнения, затем получите ответ для y.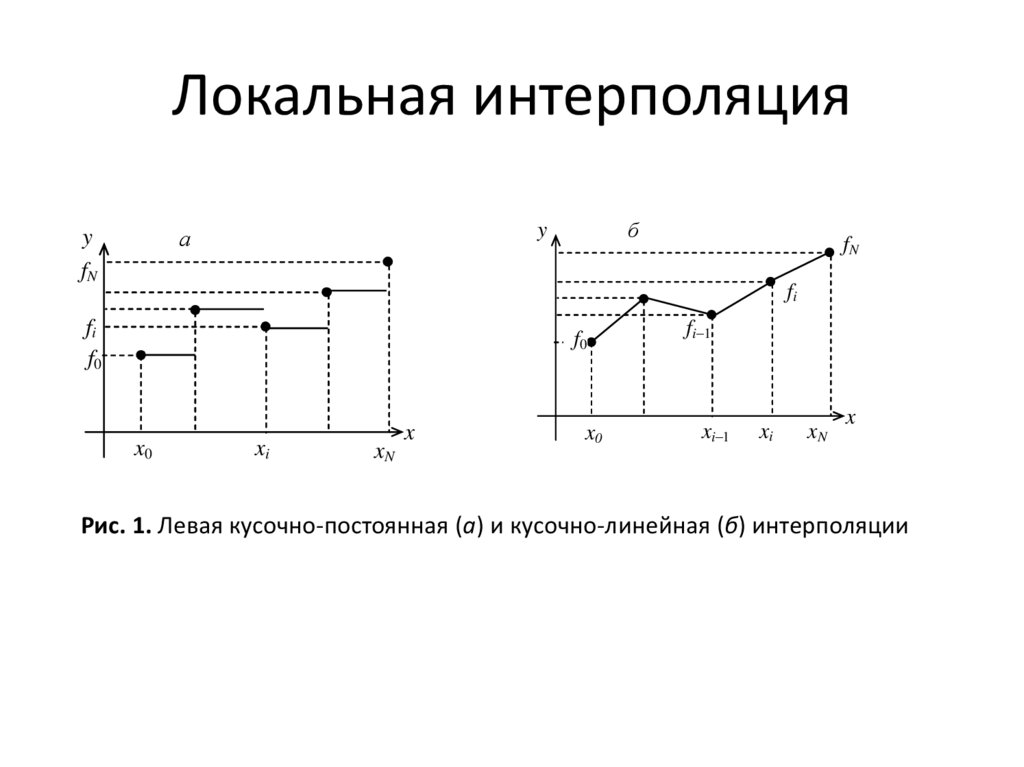
Как сделать линейную интерполяцию
Есть несколько полезных шагов, которые помогут вам вычислить желаемое значение, такое как медиана, 1 st квартиль и 3 rd квартиль. Мы пройдем каждый шаг с использованием примера, чтобы было понятно.
В этом примере мы рассмотрим сгруппированные данные с интервалами классов.
Class | Frequency |
| 0-10 | 5 |
| 11-20 | 10 |
| 21-30 | 1 |
| 31-40 | 8 |
41-50 | 18 |
51-60 | 6 |
61-70 | 20 |
Шаг 1: Учитывая класс и частоту, вы должны создать еще один столбец с именем кумулятивной частоты (также известный как CF).
Совокупная частота , таким образом, определяется как промежуточная сумма частот.
| Class | Frequency | CF |
| 0-10 | 5 | 5 |
| 11-20 | 10 | 15 |
| 21-30 | 1 | 16 |
| 31-40 | 8 | 24 |
| 41-50 | 18 | 42 |
| 51-60 | 6 | 48 |
| 61-70 | 20 | 68 |
Шаг 2: Постройте график совокупной частоты. Для этого вы наносите верхнюю границу класса на совокупную частоту.
Нахождение медианы
Медиана — это значение в середине данных.
Положение медианы равно значению, где n — общая кумулятивная частота
В этом примере n = 68
Шаг 1: Найдите положение медианы
Шаг 2: Найдите, где в данных находится позиция 34 th , используя кумулятивную частоту.
По кумулятивной частоте значение 34 th лежит в интервале 41-50 классов.
Шаг 3: Имея график, используйте линейную интерполяцию, чтобы найти конкретное медианное значение.
Мы рассматриваем сегмент графика, где лежит интервал классов, как прямую линию и используем для помощи формулу градиента.
Градиент =
Мы можем манипулировать этой формулой и подставить значение медианы (m) в качестве верхней границы и положение медианы в качестве медианы cf, которая также равна градиенту.
Градиент =
Таким образом,
Таким образом, медиана равна 46.
Нахождение первого квартиля
Квартиль 1 st также известен как нижний квартиль. Здесь лежат первые 25% данных.
Позиция квартиля 1 st является значением.
Шаги для нахождения квартиля 1 st очень похожи на шаги для нахождения медианы.
Шаг 1: определите позицию 1 st квартиля
Шаг 2: Найдите, где находится 17 th позиция в данных, используя кумулятивную частоту.
По кумулятивной частоте значение 17 th лежит в интервале 31-40 классов.
Шаг 3: Используя график, используйте линейную интерполяцию, чтобы найти конкретное значение квартиля 1 st .
Мы рассматриваем сегмент графика, где лежит интервал классов, как прямую линию и используем для помощи формулу градиента.
Градиент =
Мы можем манипулировать этой формулой и подставить значение квартиля 1 st (Q 1 ) в качестве верхней границы, а положение квартиля 1 st в качестве 1 9 st0330 квартиль ср, который также равен градиенту.
Градиент =
Из этого следует, что
Таким образом, квартиль 1 st равен 32,125.
Нахождение третьего квартиля
Квартиль 1 st также известен как нижний квартиль. Здесь лежат первые 25% данных.
Положение 3-го -го -го квартиля является значением.
Шаг 1: определите положение 3 rd quartile
Шаг 2: Найдите положение 51 st в данных, используя кумулятивную частоту.
По кумулятивной частоте значение 51 st лежит в интервале 61-70 классов.
Шаг 3: Используя график, используйте линейную интерполяцию, чтобы найти конкретное значение 3 rd квартилей.
Мы рассматриваем сегмент графика, где лежит интервал классов, как прямую линию и используем для помощи формулу градиента.
Градиент =
Мы можем манипулировать этой формулой и подставить значение 3 rd quartile (Q 3 ) в качестве верхней границы, а положение 3 rd rd в качестве 3 9 rd квартиль cf, который также равен градиенту.
Градиент =
Из этого следует, что
Таким образом, 3 -й -й квартиль равен 32,125.
Линейная интерполяция – основные выводы
- Линейная интерполяция используется для нахождения неизвестного значения функции между любыми двумя известными точками.
- Формула линейной интерполяции:
- Линейная интерполяция также может быть использована для нахождения медианы, 1 st квартиль и 3 rd квартиль
- Положение медианы
- Положение 9032 1 9032
- Положение 3-го -го -го квартиля
- График верхних границ в каждом интервале класса, построенный в зависимости от кумулятивной частоты, можно использовать для определения медианы, 1 -й -й квартиль и 3-й -й -й квартиль.
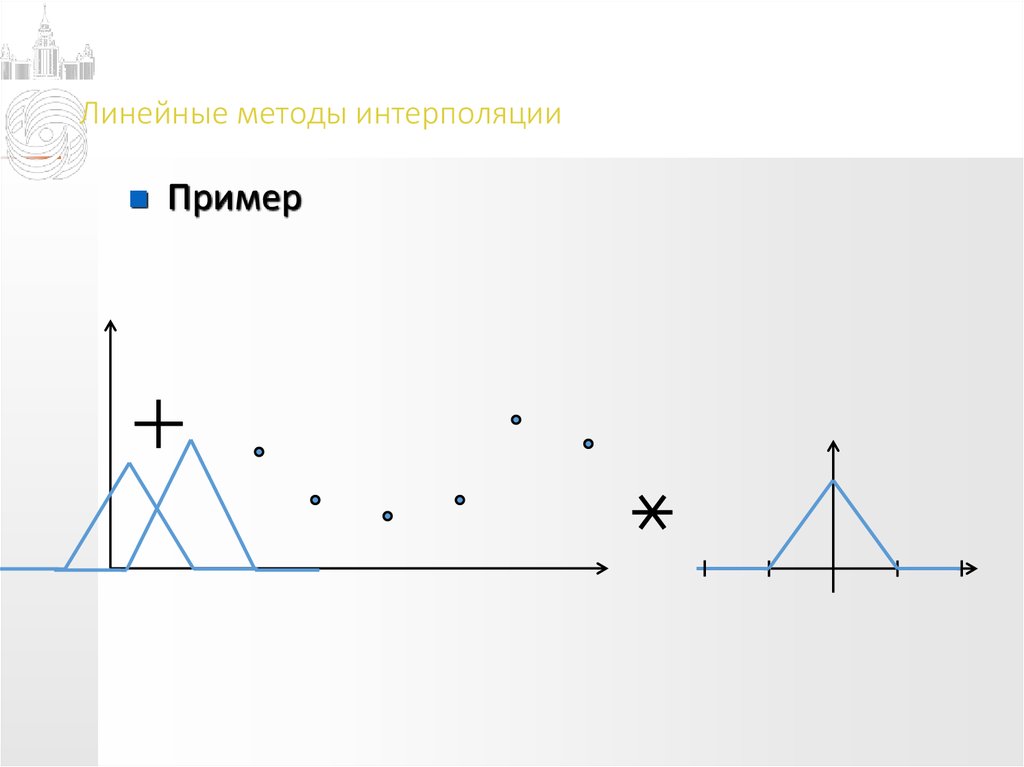
- Формулу градиента можно использовать для нахождения конкретного значения медианы, 1 st квартиль и 3 rd квартиль
Как реализовать линейную интерполяцию в Python?
Линейная интерполяция — это метод определения значений функций любых промежуточных точек, когда известны значения двух соседних точек. Линейная интерполяция — это в основном оценка неизвестного значения, которое находится в пределах двух известных значений. Линейная интерполяция используется в различных дисциплинах, таких как статистика, экономика, определение цен и т. д. Она используется для заполнения пробелов в статистических данных ради непрерывности информации.
Используя следующую формулу, мы можем линейно интерполировать данную точку данных
Здесь (x1, y1) — координаты первой точки данных. А (x2,y2 ) — координаты второй точки данных, где x — точка, по которой мы выполняем интерполяцию, а y — интерполированное значение.
Пример задачи:
Давайте рассмотрим пример для лучшего понимания. У нас есть следующие значения данных, где x обозначает число, а y — функция квадратного корня из x. Наша задача найти квадратный корень из 5,5 (х) .
x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
y ( f( x) = √x ) | 1 | 1.4142 | 1.7320 | 2 | 2.2360 | 2.4494 |
Здесь мы можем использовать метод линейной интерполяции.
1. Найдите два соседних (x1, y1) ,(x2,y2) из x. то есть (5,2.2360) и (6,2.4494).
Где x1 = 5, x2 = 6, y1 = 2,2360, y2 = 2,4494, и мы интерполируем в точке x = 5,5.
2. Используя формулу y(x) = y1 + (x – x1) \frac{(y2 – y1) }{ (x2 – x1)}
3. После подстановки значений в приведенное выше уравнение.
у = 2,3427
При x = 5,5 значение Y будет 2,3427. Таким образом, используя линейную интерполяцию, мы можем легко определить значение функции между двумя интервалами.
Подход 1:
Используя формулу
Пример: Предположим, у нас есть набор данных о населении города и год.
X(Год) | 2016 | 2017 | 2038 20180074 | 2019 | 2021 |
|---|---|---|---|---|---|
Y(Population) | 10001 | 12345 | 74851 | 12124 | 5700 |
Здесь X — год, а Y — население любого города. Наша задача найти население города в 2020 году.
Наша задача найти население города в 2020 году.
Выбираем наши (x1, y1) ,(x2,y2) как x1=2019, y1=12124, x2=2021, y2=5700, x = 2020, y = ?
Здесь (x1, y1) и (x2, y2) — две соседние точки, а x — год, для которого мы хотим предсказать значение численности населения y.
Python3
|
Выход
Популяция на год 2020 8912.0
Подход 2: 4420.INDERPLALE 9000.INDERPLALE 9000.INDERPLALE 9000.INDERPLALE 9000.INDERPLALE 9000.INDERPLALE 9000.INDERT. Точно так же мы можем добиться линейной интерполяции, используя функцию библиотеки scipy с именем interpolate.interp1d.
Синтаксис : scipy.interpolate.interp1d(x, y, kind=’linear’, axis=- 1, copy=True, bounds_error=None, fill_value=nan, accept_sorted=False)
Старший номер | Параметры | Описание | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1. | 1. | |||||||||||
1. | ||||||||||||
1. | 9007. | 1. | 9000. | 9000. | . | |||||||
2. | y | N-D массив действительных значений. | ||||||||||
3. | тип | т. е. тип интерполяции, который вы хотите, это может быть «линейная», «ближайшая», «ближайшая вверх», «ноль», «линейная», «квадратичная», «кубическая» ', 'предыдущий' или 'следующий'. «ноль», «линейный», «квадратный» и «кубический», по умолчанию это линейный . | ||||||||||
4. | ось | Определяет ось Y, вдоль которой выполняется интерполяция. | ||||||||||
5. | копия | Содержит логические значения. Если True, класс создает внутренние копии x и y . | ||||||||||
6. | bounds_error | Он содержит логические значения. |
Пример:
Допустим случайный набор данных:
X = [1,2,3,4,5], Y = [11,2.2,3.5,-88,1], и мы хотим найти значение Y в точке 2.5.
Python3
|
Выход
Значение y при x = 2,5 равно 2,85 »Забронировать сеанс! »
Поделиться
Категория: Алгебра Материалы »
Промежуточные значения
Интерполяцию можно приблизительно определить как процесс, в котором вы оцениваете неизвестные значения функции, находящиеся между известными вам значениями функции. Это обычно требуется в ситуациях с нелинейными отношениями и особенно удобно, когда вы даже не знаете фактического определения функции.
Например: у вас есть автомобиль, которому 5 лет. Вы знаете, что когда вы его купили, он стоил 10 000 долларов, а сегодня он стоит 6 500 долларов. Если вам нужно знать, сколько оно стоило 1 год назад, и у вас нет другой информации, вы можете интерполировать стоимость 4-го года между 10 000 долларов в год 0 и 6 500 долларов в год 5. Есть несколько примеров практической и необходимой интерполяции в реальных условиях. мировая математика. Вот пример из актуарной науки: вы — актуарий по страхованию жизни, работающий над проблемой, связанной с ожидаемой продолжительностью жизни в течение неполного года. Ваши таблицы жизни дают вероятности выживания в каждом возрасте, но не между ними. Например, вы можете легко рассчитать вероятность того, что случайный 40-летний человек все еще жив в возрасте 50 или 51 года, используя таблицу, но вам потребуется интерполяция, если вы рассчитываете неполную годовую вероятность, такую как вероятность того, что 40-летний до сих пор жив в возрасте 50,5 лет.
Линейная интерполяция
Линейная интерполяция является наиболее часто используемым методом, так как его легче интерпретировать и проще использовать.
Визуально линейная интерполяция означает проведение секущей линии между точками, которые вы знаете, и нахождение точки на линии, которая соответствует значению, которое вы хотите узнать. Однако нецелесообразно полагаться на наши художественные навыки для ответа, который вы хотите. можно вычислить алгебраически. В то время как визуальное представление помогает нам понять, чего мы концептуально пытаемся достичь, вы должны знать алгебру и арифметику. Вот как я предпочитаю записывать и использовать уравнение. Пусть $f(x)$ будет функцию, которую вы измеряете, и пусть $x=a$ и $x=b$ будут двумя известными вам значениями. Если вам нужно интерполировать, чтобы найти $f(c)$, где $c$ находится между $a$ и $b$, то аппроксимация для $c$ задается как $$f(c) \ приблизительно f(a) + \frac{c-a}{b-a} \cdot \big( f(b) - f(a) \big)$$Эта формула очень красиво переводится словами: чтобы получить $f(c)$, начните с $f (а) $. Затем добавьте разницу между $f(b)$ и $f(a)$, но только часть этой разницы — ту же часть того, насколько далеко $c$ отстоит от $a$ относительно $b$.
$c$ было действительно близко к $b$, тогда эта надбавка составляла бы почти 100% от $f(b)-f(a)$, и у нас было бы $$f(c) \приблизительно f(a) + (f(b)-f(a)) \ приблизительно f(b)$$Если бы $c$ было действительно близко к $a$, то дополнительная стоимость была бы почти 0% от $f(b)- f(a)$.$$f(c) \приблизительно f(a) + (0) \приблизительно f(a)$$Наконец, если интерпретация слов не помогает вам запомнить, некоторые учащиеся предпочитают запоминать форма наклона этой зависимости. $$\frac{f(c) - f(a)}{c-a} = \frac{f(b)-f(a)}{b-a)$$Это уравнение верно, потому что если приблизить $c$ с помощью линейной интерполяции, тогда мы проводим прямую линию, проходящую через все три точки, и наклон между любыми двумя точками на одной линии одинаков. Каждая часть этого уравнения представляет собой расчет наклона (изменение $y$ по сравнению с изменением $x$). Недостатком этой формы является то, что $f(c)$, то, что вы пытаетесь оценить, еще не изолировано, поэтому вы должны сделать это самостоятельно после подключения.
В более раннем примере обесценивания стоимости автомобиля мы было $$f(0) = 10000$$$$f(5) = 6500$$, и нас заинтересовало значение f(4). Воспользуемся линейной интерполяцией для получения оценки. $$f(c) \ приблизительно f(a) + \frac{c-a}{b-a} \cdot \big( f(b) - f(a) \big)$$$ $f(4) \ приблизительно f(0) + \frac{4-0}{5-0} \cdot \big( f(5) - f(0) \big)$$$$f(c) \ приблизительно 10000 + \frac{4}{5} \cdot \big( 6500 - 10000 \big)$$$$\примерно 7200$$ Мы еще раз видим, что формула интуитивно понятна. Год 4 составляет $4/5$ между годом 0 и годом 5, поэтому мы должны применить $4/5$ разницы в цене к начальной стоимости в $10,000.
Нелинейная интерполяция
Экспоненциальная интерполяцияВторым по популярности методом интерполяции является экспоненциальная интерполяция. В отличие от линейной интерполяции, которая предполагает прямолинейную интерполяцию между известными точками, экспоненциальная интерполяция предполагает гладкую вогнутую кривую между точками.
{4/5}$$$$\приблизительно 7504 $$
Другие методы
Выбор одного метода по сравнению с другим зависит как от практичности, так и от целесообразности. Как мы видели, линейная интерполяция использует только стандартные арифметические операции и, следовательно, может быть проще в некоторых случаях. Однако, если у нас есть основания полагать, что сглаженная вогнутая кривая между точками, которую мы получаем в результате экспоненциальной интерполяции, соответствует нашему ожиданию реальности, мы можем захотеть ее использовать. Существует несколько других необычных методов интерполяции: тригонометрический, полиномиальный. или даже логарифмический. Например, если вы интерполируете время восхода или захода солнца на основе годовых сезонных моделей, вы, вероятно, захотите использовать синусоидальные функции (количество дневного света в день, отображаемое на графике в течение года, имеет примерно синусоидальный характер!). Неважно, какой метод вы выберете.
или просят использовать, мы всегда должны помнить две вещи об интерполяции. Это только оценка.2. Чем меньше интервал, тем более правдоподобной будет догадка.
Это не экстраполяция
Наконец, имейте в виду: нельзя применять методы интерполяции для оценки неизвестных значений, которые находятся за пределами известных вам значений. Это называется экстраполяцией и почти никогда не подходит в качестве метода оценки. У нас просто нет оснований полагать, что паттерны будут сохраняться за пределами интервала, для которого мы знаем значения, особенно в случаях, когда мы не знаем точно, какова формула функции (которая, как мы сказали, имеет тенденцию быть типом функции, которую мы хотим интерполировать). Короче говоря, интерполяция рассматривает оценки между известными значениями, в то время как экстраполяция берет функцию или модель и проецирует ее достоверность за пределы диапазона известных данных. Держите их прямо по префиксам (inter vs extra).



 2
2

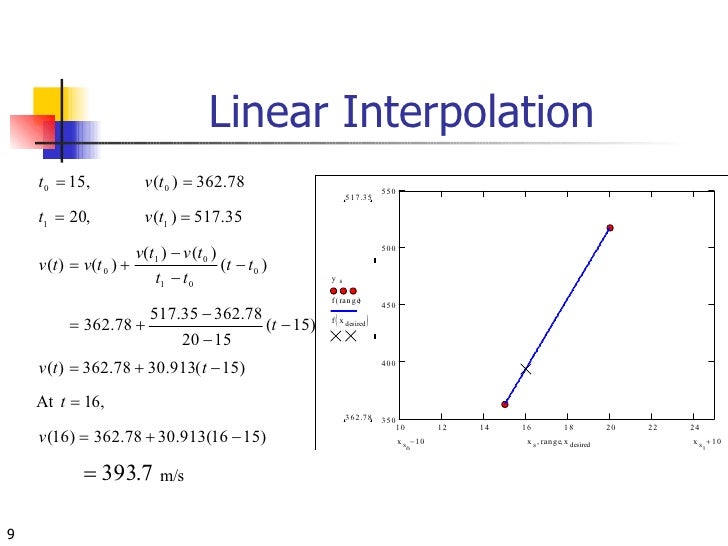

 5
5 