Критерий Краскела-Уоллиса
Определение
Пример
Пример: Дисперсионный анализ Краскела-Уоллиса и медианный тест
Определение
Критерий Краскела-Уоллиса — это непараметрическая альтернатива одномерному (межгрупповому) дисперсионному анализу. Он используется для сравнения трех или более выборок, и проверяет нулевые гипотезы, согласно которым различные выборки были взяты из одного и того же распределения, или из распределений с одинаковыми медианами.
Таким образом, интерпретация критерия Краскела-Уоллиса в основном сходна с параметрическим одномерным дисперсионным анализом, за исключением того, что этот критерий основан скорее на рангах, чем на средних. Для дополнительных деталей, см. Siegel & Castellan, 1988.
Этот непараметрический критерий — расширение двухвыборочного критерия Вилкоксона ранговых сумм. При нулевой гипотезе отсутствия различий в распределениях между группами суммы рангов в каждой из

-
Определить нулевую и альтернативную гипотезы.
: каждая группа имеет одинаковое распределение величин в популяции.
: каждая группа не имеет одинакового распределения величин в популяции.
-
Отобрать необходимые данные из двух взаимосвязанных выборок.
-
Вычислить величину статистики критерия, отвечающую ,
Проранжируйте все n значений и рассчитайте сумму рангов в каждой из групп: эти суммы — . Статистика критерия (которая должна быть модифицирована, если имеется много связанных значений) выражается формулой:
-
Сравнить значение статистики F-критерия со значением из известного распределения вероятности.
-
Интерпретировать величину р и результаты.
Интерпретируйте величину р, и если результат статистически значим, используйте двухвыборочные непараметрические критерии, корректируя их для множественного тестирования.
 Рассчитайте ДИ для медианы в каждой группе. Однофакторный ANOVA применяют тогда, когда группы соотносятся с одним фактором и независимы. Можно использовать другие виды ANOVA, если план исследования более сложен.
Рассчитайте ДИ для медианы в каждой группе. Однофакторный ANOVA применяют тогда, когда группы соотносятся с одним фактором и независимы. Можно использовать другие виды ANOVA, если план исследования более сложен.
Пример
Так, допустим, в ходе исследований изучали влияние препарата X на пациентов, разделенных по какому-то признаку Y на 3 группы равного объема (A, B, C). Результаты такого выдуманного исследования приведены в таблице:
Выбираем команду Непараметрическая статистика из меню Анализ для отображения стартовой панели модуля Непараметрическая статистика. Далее выбираем Сравнение нескольких независимых групп и нажимаем кнопку OK для отображения диалогового окна ДА Краскела-Уоллиса. Нажимаем кнопку Переменные для отображения диалогового окна Выбор переменных. Выбираем переменную Влияние как зависимую и переменную Группа как группирующую. Нажимаем кнопку Коды, отобразится диалоговое окно Выбираем коды для группирующей переменной; в этом диалоге выберите все коды (нажав кнопку Все и затем кнопку OK). Диалоговое окно ДА Краскела-Уоллиса появится на экране:
Нажимаем кнопку Коды, отобразится диалоговое окно Выбираем коды для группирующей переменной; в этом диалоге выберите все коды (нажав кнопку Все и затем кнопку OK). Диалоговое окно ДА Краскела-Уоллиса появится на экране:
Рис. 2. Диалоговое окно.
В диалоговом окне нажимаем ОК и начинаем анализ.
Рис. 3. Анализ.
Мы видим, что критерий Краскела-Уоллиса высоко значим (p = .001).Таким образом, характеристики различных экспериментальных групп значимо отличаются друг от друга. Напомним, что процедура Краскела-Уоллиса, по существу, является дисперсионным анализом, основанным на рангах. Суммы рангов (для каждой группы) показаны в правом столбце таблицы результатов. Наибольшая ранговая сумма (самое эффективное влияние препарата) относится к группе C. Наименьшая ранговая сумма (самое худшее влияние препарата) относится к группе A.
Пример: Дисперсионный анализ Краскела-Уоллиса и медианный тест
Эти тесты — альтернативны однофакторной межгрупповой ANOVA. Пример основан на (искусственных) данных, представленных в Hays (1981, стр. 592).
Пример основан на (искусственных) данных, представленных в Hays (1981, стр. 592).
Рис. 4. Пример исходных данных.
Эти данные получены в исследовании маленьких детей, которые случайным образом приписывались к одной из трех экспериментальных групп. Каждому ребенку предлагалась серия парных тестов. Задача ребенка состояла в том, чтобы сделать правильный выбор и получить вознаграждение. В первой группе тестом была форма (группа 1 — Форма — 1 — Form), во второй — цвет (группа 2 — Цвет — 2 Color), в третьей — размер 3 — Размер — 3 — Size) предмета. Зависимая переменная — число испытаний, которые требовались каждому ребенку, чтобы получить вознаграждение.
Результаты критерия Краскела-Уоллиса.
Результаты ранговой ДА Краскела-Уоллиса будут показаны в первой таблице результатов, результаты медианного теста — во второй.
Рис. 5. Результаты критерия Краскела-Уоллиса.
Вы видите, что критерий Краскела-Уоллиса высоко значим. Таким образом, характеристики различных экспериментальных групп значимо отличаются друг от друга. Напомним, что процедура Краскела-Уоллиса, по существу, является дисперсионным анализом, основанным на рангах. Суммы рангов (для каждой группы) показаны в правом столбце таблицы результатов. Наибольшая ранговая сумма (самое худшее выполнение теста) относится к Размеру — Size (это тот параметр, который надо различить, чтобы получить вознаграждение). Наименьшая ранговая сумма (лучшее выполнение) относится к Форме — Form.
Таким образом, характеристики различных экспериментальных групп значимо отличаются друг от друга. Напомним, что процедура Краскела-Уоллиса, по существу, является дисперсионным анализом, основанным на рангах. Суммы рангов (для каждой группы) показаны в правом столбце таблицы результатов. Наибольшая ранговая сумма (самое худшее выполнение теста) относится к Размеру — Size (это тот параметр, который надо различить, чтобы получить вознаграждение). Наименьшая ранговая сумма (лучшее выполнение) относится к Форме — Form.
Результаты медианного теста.
Медианный критерий также значим, однако, в меньшей степени.
Рис. 6. Результаты медианного теста.
Напомним, что медианный критерий более «грубый» и менее чувствительный, чем критерий Краскела-Уоллиса. В таблице результатов показано число наблюдений (детей) в каждой экспериментальной группе, которые лежат ниже (или равны) общей медианы и число наблюдений, лежащих выше общей медианы. Снова, наибольшее число испытуемых с числом попыток (до получения вознаграждения) выше общей медианы относятся к группе Размер — Size. Больше всего испытуемых с числом попыток ниже медианы относятся к группе Форма — Form. Таким образом, медианный тест подтверждает, что форма предмета наиболее легко различается детьми, тогда как размер различается хуже всего.
Больше всего испытуемых с числом попыток ниже медианы относятся к группе Форма — Form. Таким образом, медианный тест подтверждает, что форма предмета наиболее легко различается детьми, тогда как размер различается хуже всего.
Графическое представление результатов.
Рис. 7. График результатов медианного теста в виде диаграммы.
Снова ясно видно, выполнение теста Форма — Form было лучше любого другого; медиана числа испытаний при этом условии ниже, чем при любом другом.
Рис. 8. Категоризованная гистограмма.
Этот график снова подтверждает, что в группе Форма — Form выполнение «лучше» (распределение слегка скошено влево), чем при других условиях. Самое худшее выполнение, как отчетливо видно из графиков, для группы Размер — Size. Отсюда также можно заключить, что наиболее легко дети различают Форму — Form.
Связанные определения:
Дисперсионный анализ
Непараметрические статистические методы
Свободный от распределения критерий
Фиксированные эффекты
В начало
Содержание портала
Классические методы статистики: дисперсионный анализ по Краскелу-Уоллису
Как было отмечено ранее, важными условиями применимости классического однофакторного дисперсионного анализа являются нормальность распределения зависимой переменной и однородность (гомоскедастичность) дисперсий во всех сравниваемых группах. В случаях, когда наблюдается существенное нарушение этих условий и ситуацию не получается исправить путем трансформации исходных значений анализируемой переменной (см. Box
В случаях, когда наблюдается существенное нарушение этих условий и ситуацию не получается исправить путем трансформации исходных значений анализируемой переменной (см. Box
Немного теории
Дисперсионный анализ по Краскелу-Уоллису относится к группе непараметрических методов статистики. Это значит, что при выполнении соответствующих расчетов параметры того или иного вероятностного распределения (например, нормального) никак не задействованы. {m}n_i \) — общее число наблюдений во всех \(m\) группах, а \(R_i\) — сумма рангов наблюдений в группе \(i\). Ранг представляет собой порядковый номер конкретного наблюдения в ряду упорядоченных по возрастанию (или убыванию — не важно) наблюдений (см. также статью по критерию Уилкоксона). Чем больше значение Н-критерия, тем больше у нас оснований отклонить нулевую гипотезу об отсутствии разницы между сравниваемыми группами. Если рассчитанное по выборочным данным значение Н превышает определенное критическое значение, нулевая гипотеза отклоняется. Критическое значение определяется с учетом принятого уровня значимости и числа степеней свободы; в частности, при \(m > 5\) H-критерий сравнивается с критическими значениями критерия хи-квадрат для числа степеней свободы \(m — 1\). При меньшем числе сравниваемых групп вносятся определенные поправки (например, поправка Имана-Давенпорта).
{m}n_i \) — общее число наблюдений во всех \(m\) группах, а \(R_i\) — сумма рангов наблюдений в группе \(i\). Ранг представляет собой порядковый номер конкретного наблюдения в ряду упорядоченных по возрастанию (или убыванию — не важно) наблюдений (см. также статью по критерию Уилкоксона). Чем больше значение Н-критерия, тем больше у нас оснований отклонить нулевую гипотезу об отсутствии разницы между сравниваемыми группами. Если рассчитанное по выборочным данным значение Н превышает определенное критическое значение, нулевая гипотеза отклоняется. Критическое значение определяется с учетом принятого уровня значимости и числа степеней свободы; в частности, при \(m > 5\) H-критерий сравнивается с критическими значениями критерия хи-квадрат для числа степеней свободы \(m — 1\). При меньшем числе сравниваемых групп вносятся определенные поправки (например, поправка Имана-Давенпорта).
Интересно, что если бы мы выполнили обычный дисперсионный анализ на основе ранговых номеров исходных значений анализируемой переменной, то результат совпал бы результатом теста Краскела-Уоллиса (
 Отсюда использование «дисперсионного анализа» в названии метода Краскела-Уоллиса (см. выше). Кроме того, при наличии двух сравниваемых групп, тест Краскела-Уоллиса будет идентичен тесту Манна-Уитни.
Отсюда использование «дисперсионного анализа» в названии метода Краскела-Уоллиса (см. выше). Кроме того, при наличии двух сравниваемых групп, тест Краскела-Уоллиса будет идентичен тесту Манна-Уитни.Если бы анализируемые данные удовлетворяли условиям нормальности и однородности групповых дисперсий, то статистическая мощность теста Краскела-Уоллиса в отношении таких данных составила бы примерно 95% от обычного параметрического дисперсионного анализа. Однако при нарушении этих условий мощность тест Краскела-Уоллиса может оказаться даже выше, чем у обычного дисперсионного анализа (Zar 1999).
В теории, для расчета несмещенных оценок Н-критерия Краскела-Уоллиса значения анализируемой переменной должны иметь одинаковый разброс и форму распределения
во всех сравниваемых группах. Однако на практике нарушение этих условий мало сказывается на качестве выводов, получаемых при помощи Н-критерия, и ими обычно пренебрегают (Zar 1999).Функция kruskal. test()
test()
В R дисперсионный анализ по Краскелу-Уоллису выполняется при помощи функции kruskal.test(). В качестве примера (уже в который раз!) используем данные эксперимента по изучению эффективности 6 разных инсектицидов (таблица InsectSprays с этими данными входит в состав базовой версии R; см. также здесь, здесь и здесь). Каждым из этих средств обработали по 12 растений, после чего подсчитали количество выживших насекомых. Нулевая гипотеза, которую мы проверим при помощи теста Краскела-Уоллиса, заключается в том, что исследованные инсектициды не различаются по эффективности (т.е. наблюдаемые различия в групповых медианных значениях
kruskal.test(count ~ spray, data = InsectSprays) Kruskal-Wallis rank sum test data: count by spray Kruskal-Wallis chi-squared = 54.6913, df = 5, p-value = 1.511e-10
Как видно из полученного результата, вероятность получить столь высокое наблюдаемое значение Н-критерия при верной нулевой гипотезе крайней мала и, следовательно, мы можем смело эту гипотезу отклонить.
Следует подчеркнуть, что подобно классическому дисперсионному анализу, тест Краскела-Уоллиса позволяет сделать заключение только следующего вида: либо «сравниваемые группы статистически значимо различаются» (например, при Р < 0.05), либо «статистически значимых различий между группами нет» (например, при Р > 0.05). Ни один из этих методов сам по себе не позволяет сказать, где именно лежат различия. Чтобы выяснить это необходимо выполнить соответствующие апостериорные тесты (англ. post hoc tests). Этой теме будут посвящены следующие несколько сообщений.
Основные статистические критерии. Непараметрический критерий Краскела-Уоллеса (H-критерий Краскела — Уоллиса, односторонний дисперсионный анализ Краскела — Уоллиса, Kruskal
Порой, чтобы провести качественное исследование, получить достоверные результаты, необходимо пользоваться не только общими, всем известными приемами, но и осваивать новые инструменты. Для сравнения трех и более элементов, различных по характеру или содержанию, можно воспользоваться непараметрическим критерием Краскела-Уоллеса (критерий Н), который успешно применяют в статистических и психологических научных работах.
СОДЕРЖАНИЕ
Когда целесообразно применение методики?
Любые параметрические и непараметрические критерии, используемые в психологических исследованиях, имеют ряд ограничений и условий. Методика Краскела-Уоллеса не является исключением из данного правила.
По сути, этот инструмент является достойным и надежным аналогом однофакторной модели дисперсионного анализа. Его использование целесообразно, если исследователь намерен изучать несколько выборок, групп или элементов (3,4 и более). Эксперты рекомендуют прибегать к нему в том случае, если результаты проведенного эксперимента возможно представить в виде последовательной шкалы.
Применение критерия НКритерий Н позволяет оценить различия между объектами исследования, его элементами по конкретному признаку. Важно отметить, что применение этого непараметрического исследовательского инструмента возможно к несвязным выборкам и группам.
В основе методики Краскела-Уоллеса лежит ранжирование.
Условия применения критерия Краскела-Уоллеса
Смысл критерий Н заключается в следующем: исследователь может перейти от собранных эмпирических данных к их значениям после ранжирования.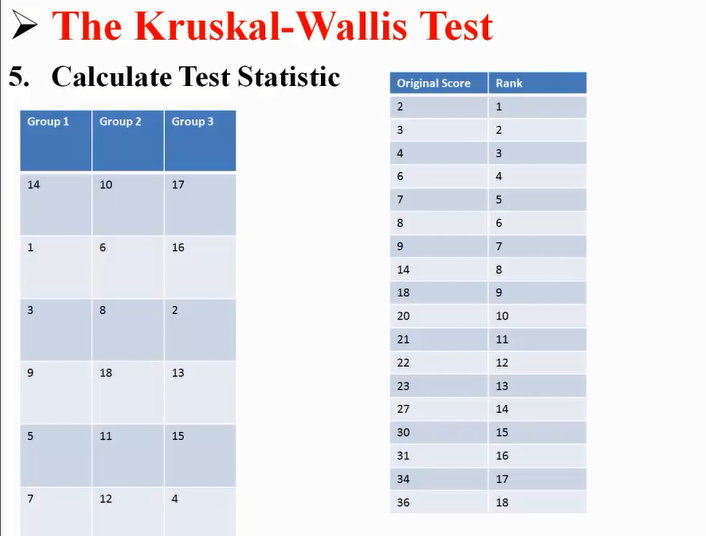
Методика применима в следующих случаях:
- Автор сумел выбрать не менее трех выборок испытуемых объектов;
- Исследователь должен провести не менее 4 наблюдений за объектами исследования первой выборки, и не менее двух наблюдений за остальными испытуемыми группами для получения достоверных эмпирических данных. Важно соблюдение соотношения 4/2/2. Количество испытуемых в каждой выборке не играет роли.
- Для оценки полученных результатов необходимо пользоваться специально разработанной таблицей критических значений.
- Если какие-либо различия становятся «стертыми», то можно выявить их посредством попарного сравнения испытуемых между собой.
Этапы применения методики Краскела-Уоллеса
Чтобы провести исследование, важно знать правильную последовательность действий, которая приведет к успеху и достоверному результату. Сейчас мы расскажем порядок «эксплуатации» критерия Н.
Как используют критерий Н?Этап №1. Замена эмпирических данных на ранги.
Для начала необходимо обработать все полученные сведения и преобразовать их в числовой (математический) вид. Лучше всего при этом ввести систему обозначений каждого элемента и признака. Допустим, все данные эксперимента были обозначены xij, а их ранги – rij. Далее необходимо проранжировать все полученные значения и сформировать «ранговую таблицу», в которой все элементы будут располагаться по возрастанию или убыванию ранга.
Этап №2. Выдвижение основной и альтернативной гипотез.
Здесь исследователь должен принять определенную позицию и выдвинуть идею, а затем сразу же предложить достойную альтернативу (на случай, если основная гипотеза не найдет своего подтверждения и буде опровергнута). Важным условием при формулировании гипотез является то, что основная гипотеза и ранжирование по ней должно отличаться от ранжирования альтернативной идеи (допускаются минимальные совпадения).
Этап №3. Определяем средние значения рангов по столбцу.
С их помощью исследователь «оптимизирует и стабилизирует» разбросанные значения. В целях анализа более точных данных, также необходимо учесть случайную величину (которая минимизирует погрешности отклонения):
Формула для расчета случайной величиныГде — характеризует общее количество числе в таблице.
Этап №4. Критическая область и результат исследования.
Далее исследователю останется лишь сравнить полученные данные с табличными (таблица критических областей). Для наглядности можно построить графическую зависимость и проследить, каким образом пересекаются выборки, есть ли сходства и различия.
Если количество испытуемых небольшое, то можно воспользоваться готовыми таблицами, но при проведении исследования над тремя и более выборками – расчеты и анализ неизбежны.
Пример применения критерия Краскела-Уоллиса
Автор исследования проводил эксперимент над молодыми людьми в возрасте 20-22 лет, которые обучались в техническом ВУЗе. Эксперимент посвящался оценке интеллектуальной настойчивости. Он предполагал оценку навыков студентов по работе с анаграммами. Всего было определено 4 анаграммы разного уровня сложности. Работа с каждым испытуемым проходила в индивидуальном порядке. Время на проведение эксперимента не ограничивалось.
Эксперимент посвящался оценке интеллектуальной настойчивости. Он предполагал оценку навыков студентов по работе с анаграммами. Всего было определено 4 анаграммы разного уровня сложности. Работа с каждым испытуемым проходила в индивидуальном порядке. Время на проведение эксперимента не ограничивалось.
Исследователь заметил, что над некоторыми неразрешимыми анаграммами студенты работали дольше, чем над остальными. Поэтому было принято решение оценить, какая анаграмма для каждого из них была неразрешимой.
Автор намерен проверить: длительность попыток решить каждую анаграмму примерно одинакова. В связи с этим он выдвинул следующие гипотезы:
На текущий момент он располагает следующими данными:
Применение методикиРассмотрим порядок дальнейших действия и расчетов.
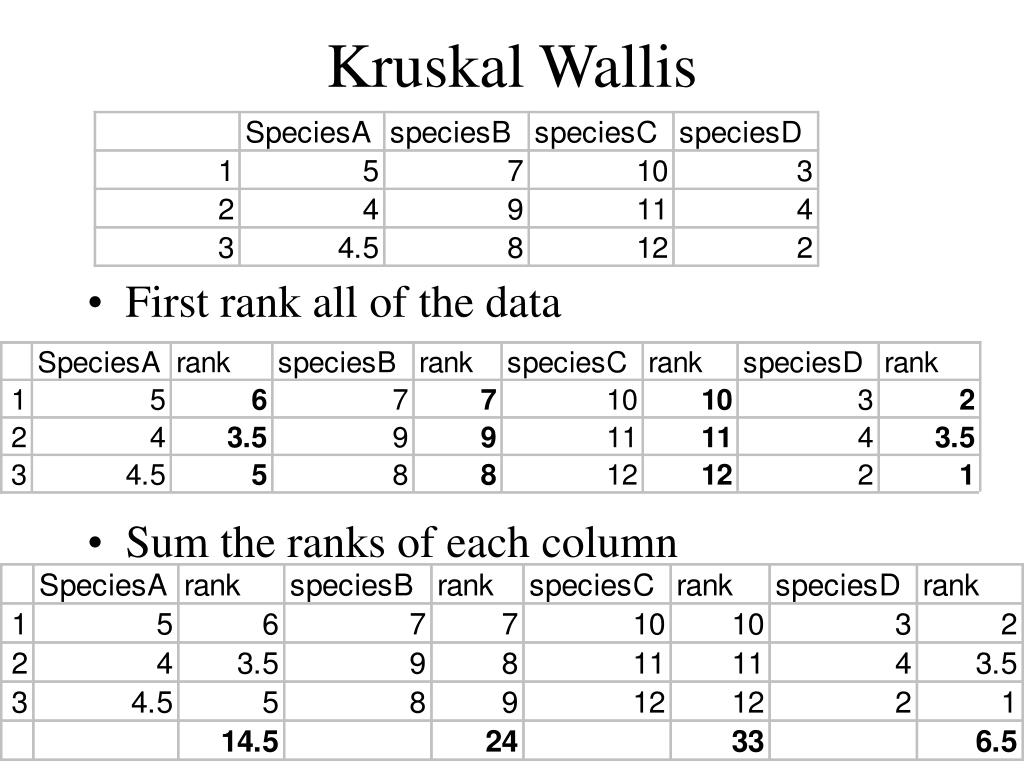
Как провести дальнейший расчет?Как подсчитать ранговые суммы?Далее необходимо сделать следующее:
Методика Краскела-УоллисаКак применяется методика на конкретном примереРанговый критерий Крускала-Уоллиса.
 Непараметрический метод для полностью рандомизированного эксперимента
Непараметрический метод для полностью рандомизированного экспериментаРанговый критерий Крускала-Уоллиса для оценки разностей между с медианами (с > 2) представляет собой обобщение рангового критерия Уилкоксона для двух независимых выборок (см. также Однофакторный дисперсионный анализ). Таким образом, критерий Крускала-Уоллиса является непараметрической альтернативой F-критерию в однофакторном дисперсионном анализе, аналогично тому, как критерий Уилкоксона представляет собой непараметрическую альтернативу t-критерию, использующему суммарную дисперсию при сравнении двух независимых выборок. Если выполняются условия, необходимые для применения F-критерия в однофакторном дисперсионном анализе, критерий Крускала-Уоллиса обладает той же мощностью. [1]
Ранговый критерий Крускала-Уоллиса применяется для проверки гипотезы, что с независимых выборок извлечены из генеральных совокупностей, имеющих одинаковые медианы. Иначе говоря, нулевая и альтернативная гипотезы формулируются следующим образом:
Н0: М1 = М2 = … =Mc
H1: не все Mj(j = 1, 2, …, с) являются одинаковыми
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Для этого необходимо знать ранги, вычисленные по всем выборкам, а с генеральных совокупностей, из которых они извлечены, должны иметь одинаковые изменчивость и вид. Для того чтобы применить критерий Крускала-Уоллиса, сначала необходимо заменить наблюдения в с выборках их объединенными рангами. При этом первый ранг соответствует наименьшему наблюдению, а ранг n — наибольшему (n = n1 + n2 + … + nc). Если некоторые значения повторяются, им присваивается среднее значение их рангов.
Для того чтобы применить критерий Крускала-Уоллиса, сначала необходимо заменить наблюдения в с выборках их объединенными рангами. При этом первый ранг соответствует наименьшему наблюдению, а ранг n — наибольшему (n = n1 + n2 + … + nc). Если некоторые значения повторяются, им присваивается среднее значение их рангов.
Критерий Крускала-Уоллиса является альтернативой F-критерию в однофакторном дисперсионном анализе. H-статистика, применяемая в критерии Крускала-Уоллиса, аналогична величине SSA— межгрупповой вариации (подробнее см. Однофакторный дисперсионный анализ), по которой вычисляется F-статистика. Вместо сравнения средних значений j всех с групп с общим средним значением , в критерии Крускала-Уоллиса средние ранги каждой из с групп сравниваются с общим рангом, вычисленным на основе всех n наблюдений. Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика Н теоретически должна быть равной нулю. Однако на практике вследствие случайных изменений статистика Н будет ненулевой, но достаточно малой.
Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика Н теоретически должна быть равной нулю. Однако на практике вследствие случайных изменений статистика Н будет ненулевой, но достаточно малой.
Критерий Крускала-Уоллиса для разностей между с медианами:
где n — общее количество наблюдений в объединенных выборках, nj — количество наблюдений в j-й выборке (j = 1, 2, … , с), Tj — сумма рангов j-й выборки.
При достаточно большом объеме выборок (больше пяти) H-статистику можно аппроксимировать χ2-распределением с с – 1 степенями свободы. Таком образом, при заданном уровне значимости α решающее правило формулируется так: гипотеза Н0 отклоняется, если H > χU2 (рис. 1), в противном случае гипотеза Н0 не отклоняется. Критические значения χ2-распределения вычисляются с помощью функции Excel =ХИ2.ОБР(вероятность;степени_свободы).
1), в противном случае гипотеза Н0 не отклоняется. Критические значения χ2-распределения вычисляются с помощью функции Excel =ХИ2.ОБР(вероятность;степени_свободы).
Рис. 1. Критическая область критерия Крускала-Уоллиса
Продемонстрируем критерий Крускала-Уоллиса на примере оценки прочности парашютов в зависимости от поставщика синтетических волокон. Если прочность парашютов не является нормально распределенной случайной величиной, для оценки различий между медианами четырех генеральных совокупностей можно применить непараметрический критерий Крускала-Уоллиса.
Нулевая гипотеза заключается в том, что прочность всех парашютов одинакова: Н0: М1 = М2 = М3 =M4. Альтернативная гипотеза утверждает, что по крайней мере один поставщик отличается от других: H1: не все Mj(j = 1, 2, 3, 4) являются одинаковыми. Результаты эксперимента, ранги и вычисления приведены на рис. 2.
2.
Рис. 2. Прочность и ранги парашютов, сшитых из синтетической ткани, приобретенной у четырех разных поставщиков
В процессе преобразования 20 показателей прочности в объединенные ранги, выясняется, что третий парашют, произведенный из синтетического волокна первого поставщика, имеет наименьшую прочность, равную 17,2. Он получает ранг 1. Четвертый парашют, произведенный из синтетического волокна первого поставщика, и второй парашют, сотканный из волокон четвертого поставщика, имеют одинаковую прочность, равную 19,9. Поскольку им соответствуют ранги 5 и 6, обоим парашютам присваивается ранг 5,5, равный среднему значению рангов 5 и 6. И, наконец, ранг 20 присваивается первому парашюту, сотканному из волокон второго поставщика, поскольку величина 26,3 является наибольшей. После присвоения рангов вычисляется их сумма в каждой группе: Т1 = 27,0; Т2 = 76,5; Т3 = 62,0; Т4 = 44,5. Для проверки рангов просуммируем эти величины:
Используя формулу (1), вычислим Н-статистику:
Статистика Н имеет приближенное χ2-распределение с с – 1 степенями свободы. При уровне значимости α, равном 0,05, определяем величину χU2 — верхнего критического значения χ2-распределения с с – 1 = 3 степенями свободы с использованием функции =ХИ2.ОБР(1 – α;с –1) = 7,815 (рис. 2). Поскольку вычисленная Н-статистика равна 7,889 и превышает критическое значение 7,815, нулевая гипотеза отклоняется. Следовательно, не все фирмы поставляют синтетическое волокно, прочность которого имеет одинаковую медиану. Аналогичный вывод можно сделать, вычислив р-значение по формуле р(Н=7,889) =1-ХИ2.РАСП(7,889;3;ИСТИНА) =0,048 (рис. 2). р-значение равно 0,048, т.е. меньше уровня значимости 0,05. Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном.
При уровне значимости α, равном 0,05, определяем величину χU2 — верхнего критического значения χ2-распределения с с – 1 = 3 степенями свободы с использованием функции =ХИ2.ОБР(1 – α;с –1) = 7,815 (рис. 2). Поскольку вычисленная Н-статистика равна 7,889 и превышает критическое значение 7,815, нулевая гипотеза отклоняется. Следовательно, не все фирмы поставляют синтетическое волокно, прочность которого имеет одинаковую медиану. Аналогичный вывод можно сделать, вычислив р-значение по формуле р(Н=7,889) =1-ХИ2.РАСП(7,889;3;ИСТИНА) =0,048 (рис. 2). р-значение равно 0,048, т.е. меньше уровня значимости 0,05. Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном.
Для применения критерия Крускала-Уоллиса должны выполняться следующие условия.
- Все с выборок случайно и независимо друг от друга извлекаются из соответствующих генеральных совокупностей.
- Анализируемая переменная является непрерывной.
- Наблюдения допускают ранжирование как внутри, так и между группами.
- Все с генеральных совокупностей имеют одинаковую изменчивость.
- Все с генеральных совокупностей имеют одинаковый вид.
Процедура Крускала-Уоллиса имеет меньше ограничений, чем F-критерий. Процедура Крускала-Уоллиса предусматривает ранжирование только по всем выборкам в совокупности. Общее распределение должно быть непрерывным, но его вид значения не имеет. Если эти условия не выполняются, критерий Крускала-Уоллиса по-прежнему можно применять для проверки гипотезы о различиях между с генеральными совокупностями. Альтернативная гипотеза утверждает, что среди с генеральных совокупностей существует хотя бы одна, которая отличается от остальных какой-нибудь характеристикой — либо средним значением, либо видом. С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
В полностью рандомизированных экспериментах, для которых выполняются условия F-критерия, следует применять именно его, а не процедуру Крускала-Уоллиса, поскольку мощность F-критерия в этой ситуации выше. С другой стороны, если эти условия не выполняются, более мощным становится критерий Крускала-Уоллиса, и следует предпочесть именно его.
Предыдущая заметка Непараметрические критерии. Ранговый критерий Уилкоксона
Следующая заметка Критерий «хи-квадрат» для дисперсий
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 748–751
Тест Крускала-Уоллиса: определение, формула и пример
Критерий Крускала-Уоллиса используется для определения наличия статистически значимой разницы между медианами трех или более независимых групп.
Этот тест является непараметрическим эквивалентом однофакторного дисперсионного анализа и обычно используется, когда нарушается предположение о нормальности.
Критерий Крускала-Уоллиса не предполагает нормальности данных и гораздо менее чувствителен к выбросам, чем однофакторный дисперсионный анализ.
Вот несколько примеров, когда вы можете провести тест Крускала-Уоллиса:
Пример 1: Сравнение методов исследования
Вы случайным образом делите класс из 90 студентов на три группы по 30 человек. Каждая группа в течение одного месяца использует разные методы обучения для подготовки к экзамену.
В конце месяца все студенты сдают один и тот же экзамен. Вы хотите знать, влияет ли техника обучения на результаты экзаменов.
Из предыдущих исследований вы знаете, что распределения экзаменационных баллов по этим трем методам обучения обычно не распределяются, поэтому вы проводите тест Крускала-Уоллиса, чтобы определить, есть ли статистически значимая разница между средними баллами трех групп.
Пример 2: Сравнение воздействия солнечного света
Вы хотите знать, влияет ли солнечный свет на рост определенного растения, поэтому вы сажаете группы семян в четырех разных местах, которые подвержены сильному солнечному свету, среднему солнечному свету, слабому солнечному свету или полному отсутствию солнечного света.
Через месяц вы измеряете высоту каждой группы растений. Известно, что распределение высот для данного конкретного растения не имеет нормального распределения и склонно к выбросам.
Чтобы определить, влияет ли солнечный свет на рост, вы проводите тест Крускала-Уоллиса, чтобы определить, есть ли статистически значимая разница между средним ростом четырех групп.
Предположения теста Крускала-УоллисаПрежде чем мы сможем провести тест Крускала-Уоллиса, нам нужно убедиться, что выполняются следующие предположения:
1. Порядковая или непрерывная переменная отклика — переменная отклика должна быть порядковой или непрерывной переменной. Примером порядковой переменной является вопрос ответа на опрос, измеряемый по шкале Лайкерта (например, 5-балльная шкала от «полностью не согласен» до «полностью согласен»), а примером непрерывной переменной является вес (например, измеряемый в фунтах).
Примером порядковой переменной является вопрос ответа на опрос, измеряемый по шкале Лайкерта (например, 5-балльная шкала от «полностью не согласен» до «полностью согласен»), а примером непрерывной переменной является вес (например, измеряемый в фунтах).
2. Независимость – наблюдения в каждой группе должны быть независимыми друг от друга. Обычно рандомизированный дизайн позаботится об этом.
3. Распределения имеют сходную форму — распределения в каждой группе должны иметь одинаковую форму.
Если эти предположения выполняются, то мы можем приступить к проведению теста Крускала-Уоллиса.
Пример теста Краскела-УоллисаИсследователь хочет знать, оказывают ли три препарата разное влияние на боль в колене, поэтому он набирает 30 человек, которые испытывают одинаковую боль в колене, и случайным образом делит их на три группы, чтобы получить либо препарат 1, либо препарат 2, либо препарат 3.
После одного месяца приема препарата исследователь просит каждого человека оценить боль в колене по шкале от 1 до 100, где 100 указывает на самую сильную боль.
Рейтинги для всех 30 человек показаны ниже:
| Препарат 1 | Препарат 2 | Препарат 3 | | — | — | — | | 78 | 71 | 57 | | 65 | 66 | 88 | | 63 | 56 | 58 | | 44 | 40 | 78 | | 50 | 55 | 65 | | 78 | 31 | 61 | | 70 | 45 | 62 | | 61 | 66 | 44 | | 50 | 47 | 48 | | 44 | 42 | 77 |
Исследователь хочет знать, по-разному ли эти три препарата влияют на боль в колене, поэтому он проводит тест Крускала-Уоллиса с уровнем значимости 0,05, чтобы определить, существует ли статистически значимая разница между средними оценками боли в колене для этих трех препаратов. группы.
Мы можем использовать следующие шаги для выполнения теста Крускала-Уоллиса:
Шаг 1. Сформулируйте гипотезы.
Нулевая гипотеза (H 0 ): средние оценки боли в колене в трех группах равны.
Альтернативная гипотеза: (Ха): по крайней мере один из медианных показателей боли в колене отличается от других.
Шаг 2. Выполните тест Крускала-Уоллиса.
Чтобы провести тест Краскела-Уоллиса, мы можем просто ввести значения, показанные выше, в Калькулятор теста Краскела-Уоллиса :
Затем нажмите кнопку «Рассчитать»:
Шаг 3. Интерпретируйте результаты.
Поскольку p-значение теста ( 0,21342 ) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
У нас нет достаточных доказательств, чтобы сказать, что существует статистически значимая разница между средними показателями боли в колене в этих трех группах.
Дополнительные ресурсыВ следующих руководствах объясняется, как выполнить тест Крускала-Уоллиса с использованием различных статистических программ:
Как выполнить тест Крускала-Уоллиса в Excel
Как выполнить тест Крускала-Уоллиса в Python
Как выполнить тест Крускала-Уоллиса в SPSS
Как выполнить тест Крускала-Уоллиса в Stata
Как выполнить тест Крускала-Уоллиса в SAS
Калькулятор теста Крускала-Уоллиса онлайн
Иллюстрированный самоучитель по SPSS > Непараметрические тесты > Н-тест по методу Крускала и Уоллиса | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| gif»/> | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Сравнение более чем двух независимых выборок Наряду Н-тестом по Крускалу и Уоллису, который установлен по умолчанию, предлагается тест медиан, не очень рекомендуемый для применения. 14.8. Н-тест по методу Крускала и Уоллиса Этот тест является модификацией U-теста Манна и Уитни на случай для более двух 1езависимых выборок. Он также базируется на общей ранговой последовательности значений всех выборок. В данном случае нам необходимо протестировать четыре возрастные категории из рассмотренного выше исследования гипертонии на предмет значимости различия исходного показателя систолического кровяного давления. Report (Сводка) jyst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходное значение)
Появится диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок) (см. Н-тест по методу Крускала и Уоллиса является установкой по умолчанию.
Рис. 14.3: Диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок)
В окне просмотра появятся следующие результаты: Ranks (Ранги)
Test Statistics (Статистика теста) а, b
a. Kruskal Wallis Test (Тест Крускала-Уолхлиса) b. Grouping Variable: Altersklassen (Групповая переменная: Возрастные категории) В результаты расчёта входят: В данном примере для которого р = 0,079 граница значимости преодолена незначительно, это означает, что всё же наблюдается тенденция к проявлению закономерности. |
H-тест Крускала-Уоллиса: определение, примеры, предположения, SPSS
Содержание:
- Определение
- Предположения
- Запустите H-тест вручную
- Как запустить Kruskal Wallis в SPSS
Посмотрите видео с обзором и примером ручной работы.
Тест Kruskal Wallis H: пример (вручную)
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
H-критерий Крускала-Уоллиса использует ранги вместо фактических данных. Критерий Крускала-Уоллиса является непараметрической альтернативой однофакторному дисперсионному анализу. Непараметрический означает, что тест не предполагает, что ваши данные поступают из определенного распределения.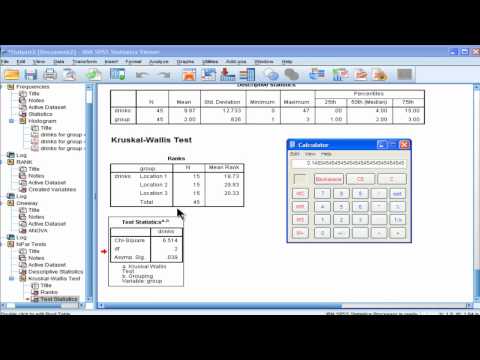 H-тест используется, когда предположения для ANOVA не выполняются (например, предположение о нормальности). Иногда его называют однофакторным дисперсионным анализом для рангов , поскольку в тесте используются ранги значений данных, а не фактические точки данных.
H-тест используется, когда предположения для ANOVA не выполняются (например, предположение о нормальности). Иногда его называют однофакторным дисперсионным анализом для рангов , поскольку в тесте используются ранги значений данных, а не фактические точки данных.
Тест определяет, различаются ли медианы двух или более групп. Как и в большинстве статистических тестов, вы вычисляете статистику теста и сравниваете ее с точкой отсечения распределения. Статистика теста, используемая в этом тесте, называется статистикой H. Гипотезы для теста:
- H 0 : медианы популяции равны.
- H 1 : медианы населения не равны.
Тест Крускала-Уоллиса покажет, есть ли существенная разница между группами. Тем не менее, он не скажет вам какие групп отличаются. Для этого вам нужно запустить тест Post Hoc.
Примеры
- Вы хотите узнать, как волнение перед экзаменом влияет на фактические результаты теста.
 Независимая переменная «тестовая тревожность» имеет три уровня: отсутствие тревожности, низкая-средняя тревожность и высокая тревожность. Зависимой переменной является экзаменационный балл, оцениваемый от 0 до 100%.
Независимая переменная «тестовая тревожность» имеет три уровня: отсутствие тревожности, низкая-средняя тревожность и высокая тревожность. Зависимой переменной является экзаменационный балл, оцениваемый от 0 до 100%. - Вы хотите узнать, как социально-экономический статус влияет на отношение к повышению налога с продаж. Ваша независимая переменная — «социально-экономический статус» с тремя уровнями: рабочий класс, средний класс и богатый. Зависимая переменная измеряется по 5-балльной шкале Лайкерта от «полностью согласен» до «полностью не согласен».
Ваши переменные должны иметь:
- Одна независимая переменная с двумя или более уровнями (независимые группы). Тест чаще используется, когда у вас есть три или более уровней. Для двух уровней лучше использовать U-тест Манна-Уитни.
- Переменные, зависящие от порядковой шкалы, шкалы отношений или шкалы интервалов.
- Ваши наблюдения должны быть независимыми. Другими словами, не должно быть никаких отношений между членами каждой группы или между группами.
 Для получения дополнительной информации по этому вопросу см.: Успение независимости.
Для получения дополнительной информации по этому вопросу см.: Успение независимости. - Все группы должны иметь одинаковое распределение формы. Большинство программ (например, SPSS, Minitab) проверяют это условие как часть теста.
Пример вопроса: Обувная компания хочет знать, имеют ли три группы рабочих разные зарплаты:
Женщины : 23 тыс., 41 тыс., 54 тыс., 66 тыс., 78 тыс.
Мужчины : 45К, 55К, 60К, 70К, 72К
Меньшинства : 20К, 30К, 34К, 40К, 44К.
Шаг 1: Сортировать данные для всех групп/выборок в порядке возрастания в одном комбинированном наборе.
- 20К
- 23К
- 30К
- 34К
- 40К
- 41К
- 44К
- 45К
- 54К
- 55К
- 60К
- 66К
- 70К
- 72К
- 90К
Шаг 2: Присвойте ранги отсортированным точкам данных. Присвоить связанным значениям средний ранг.
- 20К 1
- 23К 2
- 30К 3
- 34К 4
- 40К 5
- 41К 6
- 44К 7
- 45К 8
- 54К 9
- 55К 10
- 60К 11
- 66К 12
- 70К 13
- 72К 14
- 90К 15
Шаг 3: Суммируйте различные ранги для каждой группы/образца.
Женщины : 23К, 41К, 54К, 66К, 90К = 2 + 6 + 9 + 12 + 15 = 44.
Мужчины : 45К, 55К, 60К, 70К, 72К = 1 + 11 + 103 + 14 = 56.
Меньшинства : 20К, 30К, 34К, 40К, 44К = 1 + 3 + 4 + 5 + 7 = 20.
Шаг 4: Рассчитайте статистику H:
Где :
- n = сумма размеров выборки для всех выборок,
- с = количество образцов,
- T j = сумма рангов в выборке j th ,
- n j = размер выборки j th .
H = 6,72
Шаг 5: Найдите критическое значение хи-квадрат, с c-1 степенями свободы. Для 3–1 степени свободы и альфа-уровня 0,05 критическое значение хи-квадрат равно 5,9.915.
Для 3–1 степени свободы и альфа-уровня 0,05 критическое значение хи-квадрат равно 5,9.915.
Шаг 6: Сравните значение H из шага 4 с критическим значением хи-квадрат из шага 5. медианы равны.
Если значение хи-квадрат равно и не меньше , чем H-статистика, то недостаточно доказательств того, что медианы не равны.
В этом случае 5,9915 меньше 6,72, поэтому можно отклонить нулевую гипотезу.
Посмотрите видео с обзором теста, как его запустить и прочитать вывод в SPSS:
Как запустить тест Крускала-Уоллиса в SPSS
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Ссылки
Beyer, WH CRC Standard Mathematical Tables, 31st ed. Бока-Ратон, Флорида: CRC Press, стр. 536 и 571, 2002 г.
Агрести А. (1990) Категориальный анализ данных. Джон Уайли и сыновья, Нью-Йорк.
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
Уилан, К. (2014). Голая статистика. W. W. Norton & Company
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «H-тест Крускала-Уоллиса: определение, примеры, предположения, SPSS» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/kruskal-wallis/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
H-тест Крускала-Уоллиса в SPSS Statistics
Введение
H-критерий Крускала-Уоллиса (иногда также называемый «однофакторным ANOVA по рангам») представляет собой ранговый непараметрический критерий, который можно использовать для определения наличия статистически значимых различий между двумя или более группами независимой переменной по непрерывная или порядковая зависимая переменная. Он считается непараметрической альтернативой однофакторному дисперсионному анализу и расширением U-критерия Манна-Уитни, позволяющим сравнивать более двух независимых групп.
Он считается непараметрической альтернативой однофакторному дисперсионному анализу и расширением U-критерия Манна-Уитни, позволяющим сравнивать более двух независимых групп.
Например, вы можете использовать H-критерий Крускала-Уоллиса, чтобы понять, отличаются ли результаты экзамена, измеряемые по непрерывной шкале от 0 до 100, в зависимости от уровня тревожности (т. переменной будет «уровень тестовой тревожности», который имеет три независимые группы: студенты с «низким», «средним» и «высоким» уровнем тестовой тревожности). В качестве альтернативы вы можете использовать H-критерий Крускала-Уоллиса, чтобы понять, различается ли отношение к дискриминации в оплате труда, где отношение измеряется по порядковой шкале, в зависимости от занимаемой должности (т. е. вашей зависимой переменной будет «отношение к дискриминации в оплате труда», измеряемое по по 5-балльной шкале от «полностью согласен» до «полностью не согласен», а вашей независимой переменной будет «описание работы», которое состоит из трех независимых групп: «цех», «менеджеры среднего звена» и «зал заседаний»).
Примечание. Если вы хотите принять во внимание порядковый характер независимой переменной и иметь упорядоченную альтернативную гипотезу, вы можете запустить критерий Джонкхира-Терпстры вместо Н-критерия Крускала-Уоллиса.
Важно понимать, что H-критерий Крускала-Уоллиса является омнибусной статистикой теста и не может сказать вам, какие конкретные группы вашей независимой переменной статистически значимо отличаются друг от друга; это только говорит вам, что по крайней мере две группы были разными. Поскольку в вашем проекте исследования может быть три, четыре, пять или более групп, важно определить, какие из этих групп отличаются друг от друга. Вы можете сделать это с помощью апостериорного теста (обратите внимание, мы обсуждаем апостериорные тесты позже в этом руководстве).
В этом кратком руководстве показано, как выполнить H-критерий Крускала-Уоллиса с помощью SPSS Statistics, а также интерпретировать и представить результаты этого теста. Однако, прежде чем мы познакомим вас с этой процедурой, вам необходимо понять различные предположения, которым должны соответствовать ваши данные, чтобы H-критерий Крускала-Уоллиса дал вам достоверный результат. Далее мы обсудим эти предположения.
Однако, прежде чем мы познакомим вас с этой процедурой, вам необходимо понять различные предположения, которым должны соответствовать ваши данные, чтобы H-критерий Крускала-Уоллиса дал вам достоверный результат. Далее мы обсудим эти предположения.
Статистика SPSS
Предположения
Когда вы решите анализировать данные с помощью H-критерия Крускала-Уоллиса, часть процесса включает в себя проверку того, что данные, которые вы хотите проанализировать, действительно можно проанализировать с помощью H-критерия Крускала-Уоллиса. Вы должны сделать это, потому что использовать H-критерий Крускала-Уоллиса уместно только в том случае, если ваши данные «проходят» четыре предположения, которые требуются для того, чтобы H-критерий Крускала-Уоллиса дал вам достоверный результат. На практике проверка этих четырех допущений просто увеличивает время анализа, требуя от вас нажатия еще нескольких кнопок в SPSS Statistics при выполнении анализа, а также еще немного обдумывания ваших данных, но это не сложная задача.
Прежде чем мы познакомим вас с этими четырьмя допущениями, не удивляйтесь, если при анализе ваших собственных данных с помощью SPSS Statistics одно или несколько из этих допущений будут нарушены (т. е. не выполнены). Это не редкость при работе с реальными данными, а не с примерами из учебников, которые часто только показывают вам, как выполнять H-тест Крускала-Уоллиса, когда все идет хорошо! Однако не волнуйтесь. Даже если ваши данные не соответствуют определенным предположениям, часто есть решение, позволяющее обойти это. Во-первых, давайте взглянем на эти четыре предположения:
- Допущение №1: Ваша зависимая переменная должна измеряться на порядковом или непрерывном уровне (т. е. интервал или отношение ). Примеры порядковых переменных включают шкалу Лайкерта (например, 7-балльную шкалу от «полностью согласен» до «полностью не согласен»), а также другие способы ранжирования категорий (например, 3-балльную шкалу, объясняющую, насколько покупателю понравилось продукт в диапазоне от «Не очень много» до «Все в порядке» до «Да, много»).
 Примеры непрерывные переменные включают время пересмотра (измеряется в часах), интеллект (измеряется с помощью показателя IQ), успеваемость на экзамене (измеряется от 0 до 100), вес (измеряется в кг) и так далее. Вы можете узнать больше о порядковых и непрерывных переменных в нашей статье: Типы переменных.
Примеры непрерывные переменные включают время пересмотра (измеряется в часах), интеллект (измеряется с помощью показателя IQ), успеваемость на экзамене (измеряется от 0 до 100), вес (измеряется в кг) и так далее. Вы можете узнать больше о порядковых и непрерывных переменных в нашей статье: Типы переменных. - Допущение #2: Ваша независимая переменная должна состоять из двух или более категориальных , независимых групп . Как правило, тест Крускала-Уоллиса H используется, когда у вас трех или более категориальных независимых групп, но его можно использовать только для двух групп (т. е. U-критерий Манна-Уитни чаще используется для двух групп). Примеры независимых переменных, отвечающих этому критерию, включают этническую принадлежность (например, три группы: европеоиды, афроамериканцы и латиноамериканцы), уровень физической активности (например, четыре группы: малоподвижный образ жизни, низкий, средний и высокий), профессию (например, пять групп: хирург, врач, медсестра, стоматолог, терапевт) и так далее.

- Предположение №3: У вас должна быть независимость наблюдений , что означает отсутствие связи между наблюдениями в каждой группе или между самими группами. Например, в каждой группе должны быть разные участники, при этом ни один участник не может входить более чем в одну группу. Это скорее проблема дизайна исследования, чем то, что вы можете проверить, но это важное предположение H-теста Крускала-Уоллиса. Если ваше исследование не соответствует этому предположению, вам нужно будет использовать другой статистический тест вместо H-критерия Крускала-Уоллиса (например, критерий Фридмана). Если вы не уверены, соответствует ли ваше исследование этому допущению, вы можете воспользоваться нашим селектором статистических тестов, который является частью нашего расширенного контента.
Поскольку H-критерий Крускала-Уоллиса не предполагает нормальность данных и гораздо менее чувствителен к выбросам, его можно использовать, когда эти предположения были нарушены и использование однофакторного дисперсионного анализа нецелесообразно. Кроме того, если ваши данные порядковые, однофакторный дисперсионный анализ не подходит, а H-критерий Крускала-Уоллиса — нет. Тем не менее, H-критерий Крускала-Уоллиса включает дополнительные данные, Предположение № 4 , которое обсуждается ниже:
Кроме того, если ваши данные порядковые, однофакторный дисперсионный анализ не подходит, а H-критерий Крускала-Уоллиса — нет. Тем не менее, H-критерий Крускала-Уоллиса включает дополнительные данные, Предположение № 4 , которое обсуждается ниже:
- Предположение № 4: Чтобы знать, как интерпретировать результаты H-критерия Крускала-Уоллиса, вы должны определить, являются ли распределения в каждой группе (т. е. распределение оценок для каждой группы независимых переменная) имеют ту же форму (что также означает ту же изменчивость ). Чтобы понять, что это означает, взгляните на диаграмму ниже:
Copyright 2014. Laerd Statistics
На схеме слева вверху 9Распределение 0004 баллов для групп «кавказцев», «афроамериканцев» и «латиноамериканцев» имеет ту же форму . С другой стороны, на диаграмме справа вверху распределение баллов для каждой группы не идентично (т. е. они имеют различных форм и вариаций).
е. они имеют различных форм и вариаций).Если ваши распределения имеют одинаковую форму, вы можете использовать SPSS Statistics для проведения H-критерия Крускала-Уоллиса, чтобы сравнить медианы вашей зависимой переменной (например, «показатель вовлеченности») для различных групп независимой переменной, которую вы интересуют (например, группы европеоидов, афроамериканцев и латиноамериканцев для независимой переменной «этническая принадлежность»). Однако, если ваши дистрибутивы имеют различной формы , вы можете использовать H-критерий Крускала-Уоллиса только для сравнения средних рангов . Имея похожие распределения, вы просто можете использовать 90 004 медианы 90 005, чтобы представить сдвиг в расположении между группами (как показано на диаграмме слева выше). Таким образом, очень важно проверить это предположение, иначе вы можете неправильно интерпретировать свои результаты.
Вы можете проверить предположение №4 с помощью SPSS Statistics. Вам также следует проверить, соответствуют ли ваши данные предположениям № 1, № 2 и № 3, что можно сделать без использования SPSS Statistics. Просто помните, что если вы не проверите предположение № 4, вы не будете знать, можете ли вы сравнивать медианы или просто средние ранги, а это означает, что вы можете неправильно интерпретировать и сообщить результат H-критерия Крускала-Уоллиса. Вот почему мы посвящаем ряд разделов нашего расширенного руководства по тестированию Kruskal-Wallis H, чтобы помочь вам сделать это правильно. Вы можете узнать больше о допущении № 4 и о том, что вам нужно будет интерпретировать, в разделе 9.Раздел 0004 Предположения нашего расширенного руководства по тестированию Краскела-Уоллиса H, доступ к которому вы можете получить, подписавшись на Laerd Statistics.
Вам также следует проверить, соответствуют ли ваши данные предположениям № 1, № 2 и № 3, что можно сделать без использования SPSS Statistics. Просто помните, что если вы не проверите предположение № 4, вы не будете знать, можете ли вы сравнивать медианы или просто средние ранги, а это означает, что вы можете неправильно интерпретировать и сообщить результат H-критерия Крускала-Уоллиса. Вот почему мы посвящаем ряд разделов нашего расширенного руководства по тестированию Kruskal-Wallis H, чтобы помочь вам сделать это правильно. Вы можете узнать больше о допущении № 4 и о том, что вам нужно будет интерпретировать, в разделе 9.Раздел 0004 Предположения нашего расширенного руководства по тестированию Краскела-Уоллиса H, доступ к которому вы можете получить, подписавшись на Laerd Statistics.
В разделе «Процедура тестирования в SPSS Statistics» этого «краткого руководства» мы иллюстрируем процедуру SPSS Statistics для выполнения H-критерия Крускала-Уоллиса, предполагая, что ваши распределения не имеют одинаковой формы и что вы должны интерпретировать средние ранги, а не медианы. . Во-первых, мы приводим пример, который мы используем для объяснения процедуры H-теста Крускала-Уоллиса в SPSS Statistics.
. Во-первых, мы приводим пример, который мы используем для объяснения процедуры H-теста Крускала-Уоллиса в SPSS Statistics.
Статистика SPSS
Пример
Медицинский исследователь слышал неофициальные данные о том, что некоторые антидепрессивные препараты могут иметь положительный побочный эффект в виде уменьшения неврологической боли у людей с хронической неврологической болью в спине, если их вводить в дозах ниже тех, которые назначают при депрессии. Исследователь-медик хотел бы исследовать это неподтвержденное свидетельство с помощью исследования. Исследователь выделяет 3 хорошо известных антидепрессивных препарата, которые могут иметь этот положительный побочный эффект, и маркирует их как Препарат А, Препарат В и Препарат С. Затем исследователь набирает группу из 60 человек с одинаковым уровнем болей в спине и случайным образом относит их к одной из трех групп — группам лечения препаратом А, препаратом В или препаратом С — и прописывает соответствующий препарат на 4-недельный период. В конце 4-недельного периода исследователь просит участников оценить свою боль в спине по шкале от 1 до 10, где 10 указывает на самый сильный уровень боли. Исследователь хочет сравнить уровни боли, испытываемой различными группами в конце периода лечения наркотиками. Исследователь проводит H-критерий Крускала-Уоллиса, чтобы сравнить этот порядковый зависимый показатель (Pain_Score) между тремя лекарственными препаратами (т. е. независимая переменная, Drug_Treatment_Group, представляет собой тип препарата с более чем двумя группами).
В конце 4-недельного периода исследователь просит участников оценить свою боль в спине по шкале от 1 до 10, где 10 указывает на самый сильный уровень боли. Исследователь хочет сравнить уровни боли, испытываемой различными группами в конце периода лечения наркотиками. Исследователь проводит H-критерий Крускала-Уоллиса, чтобы сравнить этот порядковый зависимый показатель (Pain_Score) между тремя лекарственными препаратами (т. е. независимая переменная, Drug_Treatment_Group, представляет собой тип препарата с более чем двумя группами).
SPSS Statistics
Процедура тестирования в SPSS Statistics
Восемь приведенных ниже шагов показывают, как анализировать данные с помощью Н-критерия Крускала-Уоллиса в SPSS Statistics. В конце этих восьми шагов мы покажем вам, как интерпретировать результаты H-критерия Крускала-Уоллиса. Если вы хотите выяснить, в чем заключаются различия между вашими группами (т. е. H-критерий Крускала-Уоллиса только говорит вам, была ли статистически значимая разница между вашими группами), вам нужно будет продолжить H-критерий Крускала-Уоллиса с помощью апостериорный тест. Мы также покажем вам, как выполнять эти апостериорные тесты с использованием SPSS Statistics в нашем расширенном руководстве по H-тестам Краскела-Уоллиса, доступ к которому вы можете получить, подписавшись на Laerd Statistics.
Мы также покажем вам, как выполнять эти апостериорные тесты с использованием SPSS Statistics в нашем расширенном руководстве по H-тестам Краскела-Уоллиса, доступ к которому вы можете получить, подписавшись на Laerd Statistics.
Примечание 1. В SPSS Statistics есть две разные процедуры, которые можно использовать для запуска H-критерия Крускала-Уоллиса: процедура Устаревшие диалоги > K независимых выборок и процедура Непараметрические критерии > Независимые выборки . Процедура, которую мы изложили ниже, представляет собой процедуру Legacy Dialogs > K независимых выборок . Мы показываем вам эту процедуру, потому что ее можно использовать с широким спектром версий SPSS Statistics. Однако у него есть недостаток из , а не автоматически запускает апостериорные тесты. Поэтому мы покажем вам, как выполнить процедуру Непараметрические тесты > K Независимые выборки в нашем расширенном руководстве по H-тесту Крускала-Уоллиса, потому что оно имеет преимущество из автоматически запуска апостериорных тестов, что значительно ускоряет процедуру анализа. и проще.
и проще.
Примечание 2. Следующая процедура идентична для SPSS Statistics версий с 17 по 28 , а также для подписка версии SPSS Statistics, версия 28 и подписка версии являются последними версиями SPSS Statistics. Однако в версии 27 и версии подписки SPSS Statistics представила новый вид интерфейса под названием « SPSS Light », заменив предыдущий вид версий 26 и более ранних версий , который назывался « Стандарт SPSS «. Поэтому, если у вас есть SPSS Statistics версий 27 или 28 (или подписки версии SPSS Statistics), следующие изображения будут светло-серыми, а не синими. Однако процедура идентична .
- Щелкните A nalyze > N onparametric Tests > L egacy Dialogs > K Independent Samples.
 .. в верхнем меню, как показано ниже:
.. в верхнем меню, как показано ниже:Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Вам будет представлено диалоговое окно « Тесты для нескольких независимых выборок », как показано ниже:Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Примечание. Флажок K Ruskal-Wallis H в области «Тип теста» должен быть установлен по умолчанию, но если это не так, обязательно установите этот флажок. Этот параметр указывает SPSS Statistics запустить H-критерий Крускала-Уоллиса для переменных, которые вы собираетесь передать на следующем шаге этой процедуры.
- Перенесите зависимую переменную Pain_Score в поле T est Variable List: и независимую переменную Drug_Treatment_Group в поле G rouping Variable:. Вы можете передать эти переменные, либо перетащив каждую переменную в соответствующие поля, либо выделив (т. е. щелкнув) каждую переменную и нажав соответствующую кнопку.
 В итоге вы получите экран, аналогичный приведенному ниже:
В итоге вы получите экран, аналогичный приведенному ниже:Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Нажмите на кнопку. Вам будет представлено диалоговое окно « Несколько независимых выборок: определить диапазон », как показано ниже:
Примечание. Если кнопка неактивна (т. е. выглядит блеклой, как показано на рисунке ниже), убедитесь, что переменная Drug_Treatment_Group выделена желтым цветом (как показано выше на шаге 2), щелкнув ее. Это активирует кнопку.
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Введите « 1 » в поле imum Mi n и « 3 » в поле imum Ma x . Эти значения представляют собой диапазон кодов, которые вы дали группам независимой переменной Drug_Treatment_Group (т. е. от препарата А до кода С от «1» до препарата С, который был закодирован как «3»). Вы получите экран, подобный показанному ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Примечание. Если у вас есть четыре группы (например, от препарата А до препарата D) и вы хотите проанализировать только препарат В и препарат D, вы можете ввести «2» и «4» в Mi 9.0434 n imum: и Ma x imum, соответственно (при условии, что вы упорядочили группы по номерам).
- Нажмите кнопку, и вы вернетесь в диалоговое окно « Тесты для нескольких независимых выборок », но теперь с заполненным полем G Переменная группировки:, как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Нажмите на кнопку. Вам будет представлена » Несколько независимых выборок: Параметры » диалоговое окно, как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Установите флажок описательного D , если вам нужны описательные элементы, и/или флажок Q uartiles, если вам нужны медианы и квартили.
 Если вы выбрали опцию «Описания», вам будет представлен следующий экран:
Если вы выбрали опцию «Описания», вам будет представлен следующий экран:Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Нажмите на кнопку. Вы вернетесь в диалоговое окно « тестов для нескольких независимых выборок ».
- Нажмите на кнопку. Это приведет к результатам.
SPSS Statistics
SPSS Statistics Выходные данные для H-критерия Крускала-Уоллиса
Вам будут представлены следующие выходные данные (при условии, что вы не установили описательный флажок D в » Несколько независимых выборок: варианты » диалоговое окно):
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Средний рейтинг (т. е. столбец « Mean Rank » в таблице Ranks ) показателя Pain_Score для каждой группы медикаментозного лечения можно использовать для сравнения эффекта различных медикаментозных методов лечения. То, имеют ли эти группы медикаментозного лечения разные показатели боли, можно оценить с помощью таблицы Test Statistics , в которой представлены результаты H-критерия Крускала-Уоллиса. квадрат статистики (» Chi-Square «), степени свободы (строка » df «) теста и статистическая значимость теста (строка » Asymp. Sig. «).
То, имеют ли эти группы медикаментозного лечения разные показатели боли, можно оценить с помощью таблицы Test Statistics , в которой представлены результаты H-критерия Крускала-Уоллиса. квадрат статистики (» Chi-Square «), степени свободы (строка » df «) теста и статистическая значимость теста (строка » Asymp. Sig. «).
SPSS Statistics
Отчет о результатах H-теста Крускала-Уоллиса
Используя данные из двух вышеприведенных таблиц, вы можете представить результат как:
В нашем расширенном руководстве по H-тесту Краскела-Уоллиса мы покажем вам, как запустить H-критерий с использованием непараметрических тестов > K независимых выборок 9Процедура 0005 в SPSS Statistics, которая включает постфактум-тест, чтобы вы могли определить, в чем заключаются различия между вашими группами. Например, вы можете использовать апостериорный тест, чтобы определить, статистически значимо различается показатель боли между препаратом А и препаратом Б. Мы также покажем вам, как записывать свои результаты, если вам нужно сообщить о них в диссертации, задании или исследовательский отчет. Мы делаем это, используя стили Гарварда и APA. Помните, что распределение ваших данных будет определять, сможете ли вы сообщать о различиях в медианах. В нашем расширенном руководстве мы не только объясняем, как проверить это предположение, но также показываем, как интерпретировать и сообщать о результатах независимо от того, соответствуете ли вы этому предположению или нет. Вы можете узнать больше о нашем расширенном контенте в наших возможностях: Обзор стр.
Мы также покажем вам, как записывать свои результаты, если вам нужно сообщить о них в диссертации, задании или исследовательский отчет. Мы делаем это, используя стили Гарварда и APA. Помните, что распределение ваших данных будет определять, сможете ли вы сообщать о различиях в медианах. В нашем расширенном руководстве мы не только объясняем, как проверить это предположение, но также показываем, как интерпретировать и сообщать о результатах независимо от того, соответствуете ли вы этому предположению или нет. Вы можете узнать больше о нашем расширенном контенте в наших возможностях: Обзор стр.
Начало работы с тестом Краскела-Уоллиса
Что это такое?
Одним из наиболее известных статистических тестов для анализа различий между средними значениями заданных групп является тест ANOVA (дисперсионный анализ). Хотя ANOVA — отличный инструмент, он предполагает, что рассматриваемые данные подчиняются нормальному распределению. Что делать, если ваши данные не подчиняются нормальному распределению или размер выборки слишком мал для определения нормального распределения? Вот где на помощь приходит тест Крускала-Уоллиса.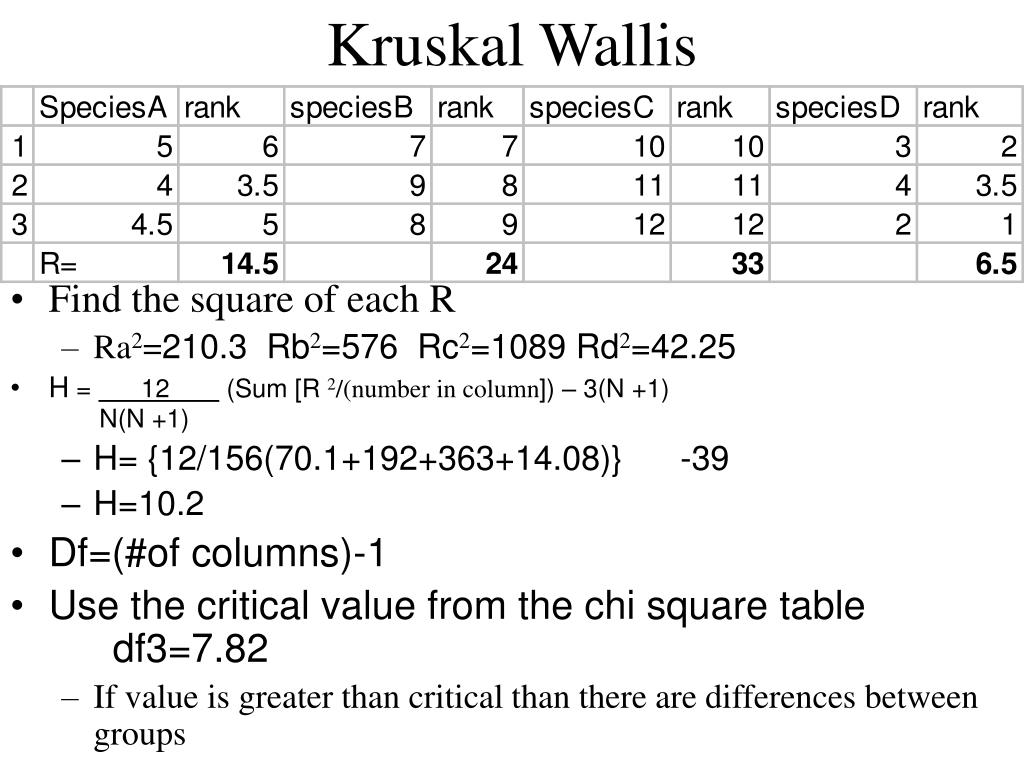
Критерий Крускала-Уоллиса можно рассматривать как непараметрический эквивалент дисперсионного анализа. Этот тест определяет, имеют ли независимые группы одинаковое среднее значение рангов; вместо использования самих значений данных каждой точке данных присваивается ранг, и эти ранги используются для определения того, происходят ли данные в каждой группе из одного и того же распределения. По сути, этот тест определяет, имеют ли группы одинаковую медиану.
Как упоминалось выше, критерий Крускала-Уоллиса — это непараметрический критерий, то есть он не делает никаких предположений о параметрах данных, таких как среднее значение, дисперсия и т. д. Поскольку он не делает никаких предположений о параметрах данных, он не может сделать предположение о распределении данных; именно так Крускал-Уоллис не предполагает нормально распределенных данных. 92}{n_i}-3(N+1)\]
, где N — общий размер выборки, k — количество групп, которые мы сравниваем, \(R_i\) — сумма рангов для группы i и \ (n_i\) — размер выборки группы i.
Затем мы сравниваем H с критической точкой отсечки, определяемой распределением хи-квадрат (используется хи-квадрат, потому что это хорошее приближение к H, особенно если размер выборки в каждой группе >= 5). Если статистика H значима (H больше, чем отсечение), мы отклоняем нулевую гипотезу. Если статистика H незначительна (H меньше порогового значения), мы не можем отвергнуть нулевую гипотезу. В этом тесте нулевая гипотеза состоит в том, что медианы каждой группы одинаковы, что означает, что все группы происходят из одного и того же распределения. Альтернативная гипотеза состоит в том, что по крайней мере одна из групп имеет другую медиану, что означает, что по крайней мере одна из них происходит из другого распределения, чем другие.
Предположения
- Порядковые переменные — рассматриваемая переменная должна быть порядковой или непрерывной, т. е. иметь некоторую иерархию для них
- Независимость – каждая группа должна быть независима от других
- Размер выборки – каждая группа должна иметь размер выборки 5 или более.
 При размере выборки в этом диапазоне распределение хи-квадрат хорошо аппроксимирует статистику H.
При размере выборки в этом диапазоне распределение хи-квадрат хорошо аппроксимирует статистику H.
Практическое руководство и пример (от руки)
Пошаговый процесс расчета статистики H выглядит следующим образом:
Шаг 1: Сформулируйте свою гипотезу – Нулевая гипотеза: медианы (средние по рангам) равны по выборкам – Альтернативная гипотеза: не менее одна медиана отличается
Шаг 2: Подготовьте и ранжируйте ваши данные – Расположите данные из всех групп вместе в один список в порядке возрастания – Присвойте ранг каждой записи данных
Шаг 3: Суммируйте ранги для каждой группы
Шаг 4: Рассчитайте статистику теста, H
Шаг 5: Сравните ее с критическим порогом, определенным критическим значением хи-квадрат
Шаг 6: Интерпретируйте результаты В качестве примера , мы будем использовать данные о выработке антител после получения вакцины. Больница вводила три разные вакцины 6 людям и измеряла наличие антител в их крови через выбранный период времени. Данные следующие:
Больница вводила три разные вакцины 6 людям и измеряла наличие антител в их крови через выбранный период времени. Данные следующие:
| А | 1232 |
| А | 751 |
| А | 339 |
| А | 848 |
| А | 447 |
| А | 542 |
| – | – |
| Б | 302 |
| Б | 57 |
| Б | 521 |
| Б | 278 |
| Б | 176 |
| Б | 201 |
| – | – |
| С | 839 |
| С | 342 |
| С | 473 |
| С | 1128 |
| С | 242 |
| С | 475 |
Мы хотим определить, как действуют три вакцины по сравнению друг с другом. Это можно определить количественно, определив, вызывает ли каждая вакцина выработку у реципиентов одинакового количества антител. По сути, мы пытаемся определить, получены ли данные об антителах для каждой вакцины из одного и того же источника. У нас относительно небольшие размеры выборки, поэтому мы не можем точно определить, нормально ли распределены данные, поэтому мы используем критерий Крускала-Уоллиса.
Это можно определить количественно, определив, вызывает ли каждая вакцина выработку у реципиентов одинакового количества антител. По сути, мы пытаемся определить, получены ли данные об антителах для каждой вакцины из одного и того же источника. У нас относительно небольшие размеры выборки, поэтому мы не можем точно определить, нормально ли распределены данные, поэтому мы используем критерий Крускала-Уоллиса.
Этап 1:
Нулевая гипотеза \(H_0 =\) вакцины вызывают выработку одинакового количества антител (все три группы происходят из одного и того же распределения и имеют одинаковую медиану)
Альтернативная гипотеза \(H_A =\) По крайней мере, одна из вакцин вызывает выработку другого количества антител (по крайней мере, одна группа происходит из другого распределения и имеет другую медиану)
Шаг 2:
Здесь мы организуем наши данные по возрастанию затем дайте каждому ранг.
| Б | 57 | 1 |
| Б | 176 | 2 |
| Б | 201 | 3 |
| С | 242 | 4 |
| Б | 278 | 5 |
| Б | 302 | 6 |
| А | 339 | 7 |
| С | 342 | 8 |
| А | 447 | 9 |
| С | 473 | 10 |
| С | 475 | 11 |
| Б | 521 | 12 |
| А | 542 | 13 |
| А | 751 | 14 |
| С | 839 | 15 |
| А | 848 | 16 |
| С | 1128 | 17 |
| А | 1232 | 18 |
Шаг 3:
Теперь мы поместим наши данные обратно в исходные группы и просуммируем ранги для каждой группы.
| А | 1232 | 18 |
| А | 751 | 14 |
| А | 339 | 7 |
| А | 848 | 16 |
| А | 447 | 9 |
| А | 542 | 13 |
| – | – | – |
| Б | 302 | 6 |
| Б | 57 | 1 |
| Б | 521 | 12 |
| Б | 278 | 5 |
| Б | 176 | 2 |
| Б | 201 | 3 |
| – | – | – |
| С | 839 | 15 |
| С | 342 | 8 |
| С | 473 | 10 |
| С | 1128 | 17 |
| С 92}{6}\right]-3(18+1)\] Вычисление дает нам тестовую статистику \[H = 7,29824\] Шаг 5: Далее мы сравниваем это H статистика критического отсечения: соответствующее значение хи-квадрат. Находим степени свободы, вычитая 1 из \(k\): \[df = k-1 \] \[ = 3-1 = 2\] Используя это значение и вероятность 0,05, мы найти 92(2)\), мы отвергаем нулевую гипотезу ; медианы не одинаковы для всех трех групп, по крайней мере, одна из них имеет другую медиану, чем другие. Это означает, что все три вакцины не действуют одинаково, по крайней мере, одна вакцина заставляет реципиентов вырабатывать другое количество антител, чем другие. Важно отметить, что Крускал-Уоллис может только сказать нам, что по крайней мере одна из групп происходит из другого распределения. не может скажите нам, какая из групп (групп) это (есть). Практическое руководство и пример (с Python) Модуль Python из статистики импорта scipy импортировать numpy как np # Сохраняем данные каждой вакцины (группы в данном примере) в отдельный массив d1 = np.массив ([1232, 751, 339, 848, 447, 542]) d2 = np.массив ([302, 57, 521, 278, 176, 201]) d3 = np.массив([839, 342, 473, 1128, 242, 475]) # Провести тест Крускала-Уоллиса H = статистика.kruskal(d1, d2, d3) печать (ч) KruskalResult (статистика = 7,298245614035082, pvalue=0,02601393801711558) Здесь мы видим, что p-значение составляет ~0,026, что меньше порогового значения 0,05, поэтому мы отвергаем нулевую гипотезу : медианы не одинаковы для всех трех групп, по крайней мере, одна из них имеет другую медиану чем другие. Еще раз подчеркнем, что тест Крускала-Уоллиса может только сказать нам, что по крайней мере одна из вакцин действует иначе, чем другие. Он не может сказать нам, какая(ие) вакцина(ы) используется(ются). Чтобы определить, какая вакцина действует по-другому, нам потребуется провести постфактум-тест. Сводка
Используйте функцию Python
отклонить нулевую гипотезу : по крайней мере одна группа имеет другую медиану, поэтому по крайней мере одна группа происходит из другого распределения не может отвергнуть нулевую гипотезу : все группы имеют одинаковую медиану, поэтому все группы происходят из одного и того же распределения Крускал-Уоллис может сказать нам только, происходят ли группы из одного и того же распределения. С вопросами или разъяснениями относительно этой статьи обращайтесь в StatLab библиотеки UVA: [email protected] Просмотрите всю коллекцию статей StatLab библиотеки UVA. Samantha LomuscioStatLab Associate University of Virginia Library 7 декабря 2021 Критерий Крускала-Уоллиса или непараметрическая версия ANOVAАнтуан Сотеви 2022-03-24 9минутное чтение
В предыдущей статье мы показали, как выполнить дисперсионный анализ в R для сравнения трех или более групп. Помните, что, как и для многих статистических тестов, однофакторный дисперсионный анализ требует выполнения некоторых допущений, чтобы можно было использовать и интерпретировать результаты. В частности, дисперсионный анализ требует, чтобы остатки приблизительно соответствовали нормальному распределению. 1 К счастью, если предположение о нормальности не выполняется, существует непараметрическая версия дисперсионного анализа: тест Крускала-Уоллиса . В оставшейся части статьи мы покажем, как выполнить тест Крускала-Уоллиса в R и как интерпретировать его результаты. Мы также кратко покажем, как проводить апостериорные тесты и как представлять все необходимые статистические результаты непосредственно на графике. Данные для настоящей статьи основаны на наборе данных # install. Исходный набор данных содержит данные о 344 пингвинах 3 разных видов (Adelie, Chinstrap и Gentoo). Он содержит 8 переменных, но в этой статье мы сосредоточимся только на длине ласт и видах, поэтому оставим только эти 2 переменные: библиотека (tidyverse) dat <- пингвины %>% select(species, flipper_length_mm) (Если вы не знакомы с оператором конвейера ( Перед выполнением теста всегда полезно провести некоторую описательную статистику для всей выборки и по группам, чтобы у нас был широкий обзор данных. # весь образец сводка(dat) ## видов flipper_length_mm ## Адели: 152 мин. :172,0 ## Подбородочный ремень: 68 1-й кв.: 190,0 ## Gentoo: 124 Медиана: 197,0 ## Среднее значение: 200,9 ## 3-й квартал: 213. # по группам библиотека (сделано) summaryBy(flipper_length_mm ~ виды, данные = дат, УДОВОЛЬСТВИЕ = медиана, na.rm = ИСТИНА ) ## # Буквы: 3 × 2 ## вид flipper_length_mm.median ## <фкт> <дбл> ## 1 Адели 190 ## 2 Подбородочный ремень 196 ## 3 Gentoo 216 # Boxplot по видам ggplot(дата) + aes(x = вид, y = длина_плавника_мм, fill = вид) + geom_boxplot() + theme(legend.position = "none") Основываясь на диаграммах и сводной статистике, мы уже видим, что в нашей выборке у пингвинов вида Адели самые маленькие ласты, а у пингвинов вида Gentoo кажется, у них самые большие ласты. Однако только надежный статистический тест покажет нам, можем ли мы сделать такой вывод для нашей популяции. Цель и гипотезы Как упоминалось ранее, тест Краскела-Уоллиса позволяет сравнивать три или более групп. Точнее, он используется для сравнения трех или более групп с точки зрения количественной переменной. В контексте нашего примера мы собираемся использовать тест Крускала-Уоллиса, чтобы ответить на следующий вопрос: «Различна ли длина ласт у 3 видов пингвинов?». Нулевая и альтернативная гипотезы теста Крускала-Уоллиса:
Обратите внимание, что, как и для ANOVA, альтернативной гипотезой является , а не , что все виды различаются по длине ласт. Противоположностью равенства всех видов (\(H_0\)) является то, что по крайней мере один вид отличается от других (\(H_1\)). В этом смысле, если нулевая гипотеза отвергается, это означает, что по крайней мере один вид отличается от двух других, но не обязательно, что все три вида отличаются друг от друга. Возможно, длина ласт у видов Gentoo отличается от длины ласт у видов Chinstrap и Adelie, но длина ласт у Chinstrap и Adelie одинакова. ПредположенияВо-первых, тест Краскела-Уоллиса сравнивает несколько групп с точки зрения количественной переменной. Таким образом, должна быть одна количественная зависимая переменная (которая соответствует измерениям, к которым относится вопрос) и одна качественная независимая переменная (по крайней мере, с двумя уровнями, которые будут определять группы для сравнения). 2 Во-вторых, помните, что критерий Крускала-Уоллиса является непараметрическим критерием, поэтому предположение о нормальности не требуется . Тем не менее, предположение о независимости все еще остается в силе . Это означает, что данные, полученные от репрезентативной и случайно выбранной части всего населения, должны быть независимыми между группами и внутри каждой группы. Допущение о независимости чаще всего проверяется на основе плана эксперимента и хорошего контроля условий эксперимента, а не с помощью формального теста. Относительно гомоскедастичности (т. е. равенства дисперсий): Пока вы используете критерий Крускала-Уоллиса для сравнения групп, гомоскедастичность не требуется. Если вы хотите сравнить медианы, критерий Крускала-Уоллиса требует гомоскедастичности. 3 В нашем примере предполагается независимость, и нам не нужно сравнивать медианы (нас интересует только сравнение групп), поэтому мы можем перейти к тому, как выполнить тест в R. В R Тест Краскела-Уоллиса в R можно выполнить с помощью kruskal.test(flipper_length_mm ~ видов, данные = дата ) ## ## Критерий суммы рангов Краскела-Уоллиса ## ## данные: flipper_length_mm по видам ## Хи-квадрат Краскела-Уоллиса = 244,89, df = 2, p-значение < 2,2e-16 Наиболее важным результатом в этом выводе является p -значение. Мы покажем, как интерпретировать его в следующем разделе. ИнтерпретацииНа основании теста Крускала-Уоллиса мы отклоняем нулевую гипотезу и делаем вывод, что по крайней мере один вид отличается по длине плавников ( p -значение < 0,001). ( Для иллюстрации , если p -значение было больше, чем уровень значимости \(\alpha = 0,05\): мы не можем отвергнуть нулевую гипотезу, поэтому мы не можем отвергнуть гипотезу о том, что 3 рассматриваемых вида пингвинов равны по длине ласт. Мы только что показали, что по крайней мере один вид отличается от других по длине ласт. Тем не менее, здесь возникают ограничения теста Крускала-Уоллиса: он не говорит, какая группа (группы) отличается (отличаются) от других. Чтобы узнать это, нам нужно использовать другие типы тестов, называемые апостериорными тестами (на латыни «после этого», то есть после получения статистически значимых результатов Крускала-Уоллиса) или тестами множественного попарного сравнения. Заинтересованному читателю более подробное объяснение апостериорных тестов можно найти здесь. Наиболее распространенными апостериорными тестами после значимого теста Крускала-Уоллиса являются:
Тест Данна является наиболее распространенным, вот как это сделать в библиотеке R. 4 Тест Данна(FSA) dunnTest(flipper_length_mm ~ виды, данные = дат, метод = "холм" ) ## Сравнение Z P. | e-54 1.497220e-53
## 3 Подбородочный ремень - Gentoo -8.931938 4.186100e-19 8.372200e-19
 Deviation (Стандартное отклонение)
Deviation (Стандартное отклонение) рис. 14.3).
рис. 14.3).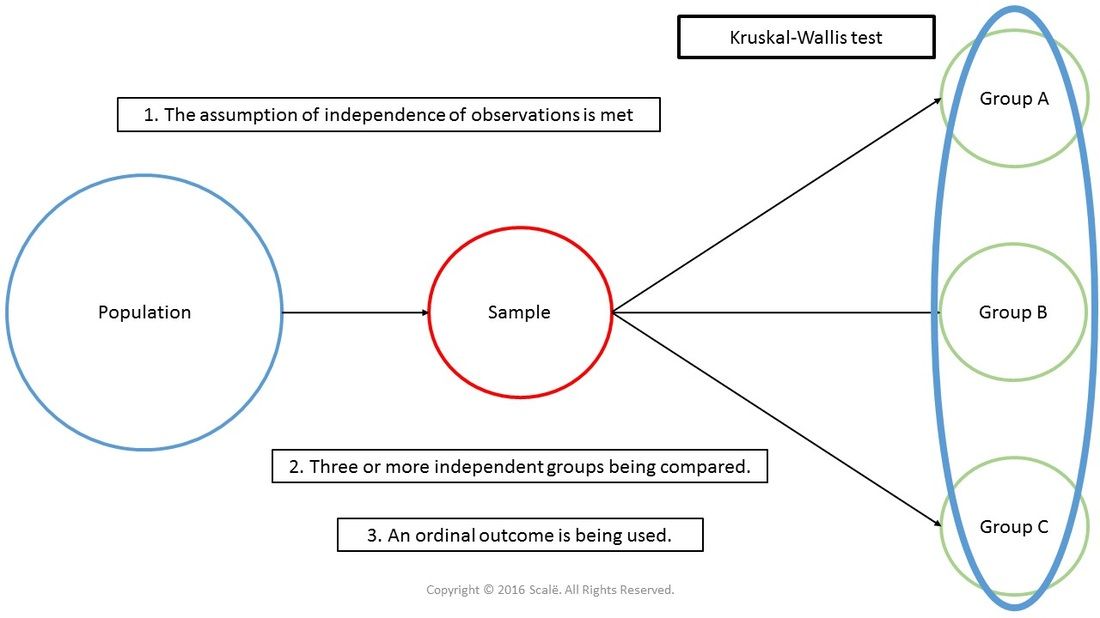 Blutdruck, Ausgangswert (Систолическое давление, исходная величина)
Blutdruck, Ausgangswert (Систолическое давление, исходная величина) Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина)
Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) В случае выявления существенной закономерности, для определения групп, которые значимо отличаются друг от друга, необходимо протестировать все группы попарно (как в тесте по методу Манна и Уитни).
В случае выявления существенной закономерности, для определения групп, которые значимо отличаются друг от друга, необходимо протестировать все группы попарно (как в тесте по методу Манна и Уитни). Мы можем определить значение хи-квадрата, обратившись к таблице вероятностей хи-квадрата.
Мы можем определить значение хи-квадрата, обратившись к таблице вероятностей хи-квадрата. Как и большинство статистических программ, функция
Как и большинство статистических программ, функция  Это означает, что вакцины не работают одинаково хорошо, потому что результирующая продукция антител неодинакова для каждой вакцины. Делаем тот же вывод, что и выше, когда сами производили расчет!
Это означает, что вакцины не работают одинаково хорошо, потому что результирующая продукция антител неодинакова для каждой вакцины. Делаем тот же вывод, что и выше, когда сами производили расчет! Если мы отвергаем нулевую гипотезу, мы можем только заключить, что одна или несколько групп имеют другую медиану (происходят из другого распределения). Тест не может сказать нам, какие группы происходят из другого распределения .
Если мы отвергаем нулевую гипотезу, мы можем только заключить, что одна или несколько групп имеют другую медиану (происходят из другого распределения). Тест не может сказать нам, какие группы происходят из другого распределения .
 packages("palmerpenguins")
library(palmerpenguins)
packages("palmerpenguins")
library(palmerpenguins)  0
## Максимум. :231.0
## NA's :2
0
## Максимум. :231.0
## NA's :2  Его можно рассматривать как расширение теста Манна-Уитни, которое позволяет сравнивать 2 группы в предположении ненормальности.
Его можно рассматривать как расширение теста Манна-Уитни, которое позволяет сравнивать 2 группы в предположении ненормальности. Другие типы тестов (известные как апостериорные тесты и описанные ниже) должны быть выполнены, чтобы проверить, различаются ли все 3 вида.
Другие типы тестов (известные как апостериорные тесты и описанные ниже) должны быть выполнены, чтобы проверить, различаются ли все 3 вида. Если вы все еще не уверены в независимости, основанной на плане эксперимента, спросите себя, связано ли одно наблюдение с другим (влияет ли одно наблюдение на другое) внутри каждой группы или между самими группами. Если нет, то, скорее всего, у вас есть независимые выборки. Если наблюдения между выборками (составляющими разные сравниваемые группы) являются зависимыми (например, если три измерения были собраны на те же лица как это часто бывает в медицинских исследованиях при измерении показателя (i) до, (ii) во время и (iii) после лечения), критерий Фридмана следует предпочесть, чтобы учесть зависимость между образцы.
Если вы все еще не уверены в независимости, основанной на плане эксперимента, спросите себя, связано ли одно наблюдение с другим (влияет ли одно наблюдение на другое) внутри каждой группы или между самими группами. Если нет, то, скорее всего, у вас есть независимые выборки. Если наблюдения между выборками (составляющими разные сравниваемые группы) являются зависимыми (например, если три измерения были собраны на те же лица как это часто бывает в медицинских исследованиях при измерении показателя (i) до, (ii) во время и (iii) после лечения), критерий Фридмана следует предпочесть, чтобы учесть зависимость между образцы. Обратите внимание, что предположение о нормальности может или может не выполняться, но для этой статьи мы предполагаем, что не удовлетворяет .
Обратите внимание, что предположение о нормальности может или может не выполняться, но для этой статьи мы предполагаем, что не удовлетворяет . )
) unadj P.adj
## 1 Адели - Подбородочный ремень -3.629336 2.841509e-04 2.841509e-04
## 2 Адели - Gentoo -15.476612 4.9
unadj P.adj
## 1 Адели - Подбородочный ремень -3.629336 2.841509e-04 2.841509e-04
## 2 Адели - Gentoo -15.476612 4.9
 ↩︎
↩︎ Цель теста состоит в том, чтобы оценить, получены ли образцы из популяций с одинаковой медианой популяции. Пожалуйста, введите образцы данных для групп, которые вы хотите сравнить, и уровень значимости \(\альфа\), и результаты теста Крускала-Уоллиса будут отображаться для вас (Сравните до 5 групп. Пожалуйста, оставьте пустыми столбцы, которые вы не будете использовать):
Цель теста состоит в том, чтобы оценить, получены ли образцы из популяций с одинаковой медианой популяции. Пожалуйста, введите образцы данных для групп, которые вы хотите сравнить, и уровень значимости \(\альфа\), и результаты теста Крускала-Уоллиса будут отображаться для вас (Сравните до 5 групп. Пожалуйста, оставьте пустыми столбцы, которые вы не будете использовать): Использование теста Крускала-Уоллиса заключается в оценке того, получены ли выборки из популяций с одинаковыми медианами. Нам нужно будет использовать тест Крускала-Уоллиса, когда измеряемая переменная (зависимая переменная) измеряется на порядковом уровне или когда предположение о нормальности не выполняется.
Использование теста Крускала-Уоллиса заключается в оценке того, получены ли выборки из популяций с одинаковыми медианами. Нам нужно будет использовать тест Крускала-Уоллиса, когда измеряемая переменная (зависимая переменная) измеряется на порядковом уровне или когда предположение о нормальности не выполняется.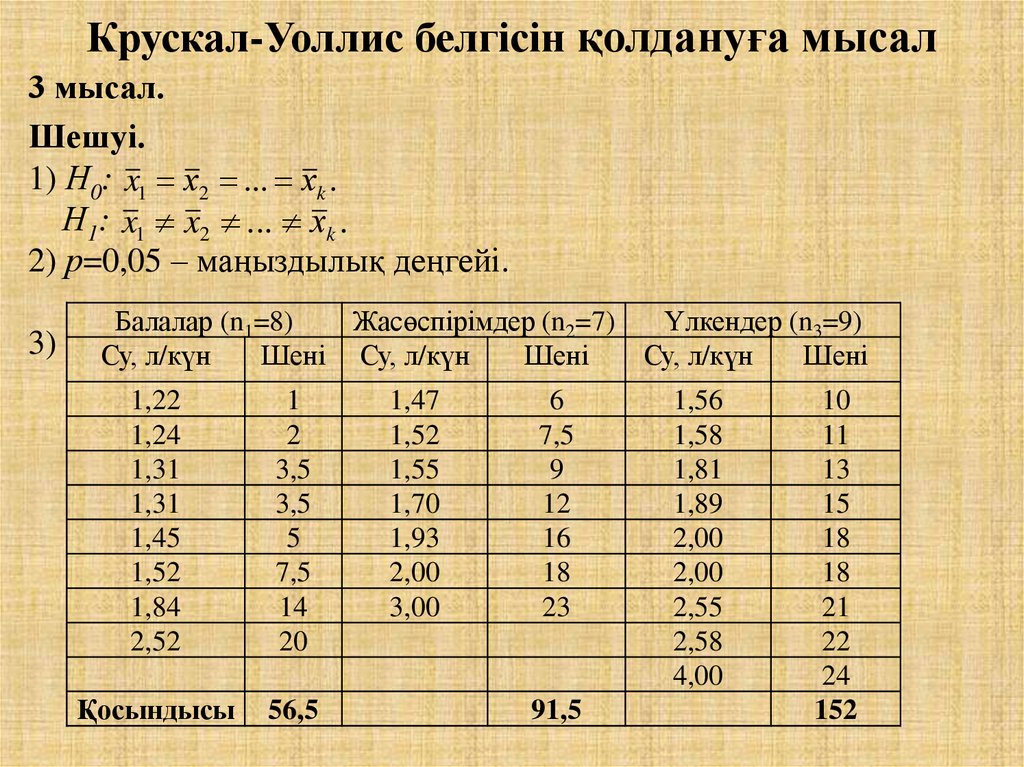

 По сути, это расширение теста суммы рангов Уилкоксона на более чем две независимые выборки.
По сути, это расширение теста суммы рангов Уилкоксона на более чем две независимые выборки.
 е. когда из каждой совокупности случайным образом выбирается один элемент, наибольший (или наименьший, или второй по величине, и т. д.) элемент с равной вероятностью будет происходить из любой из групповых совокупностей
е. когда из каждой совокупности случайным образом выбирается один элемент, наибольший (или наименьший, или второй по величине, и т. д.) элемент с равной вероятностью будет происходить из любой из групповых совокупностей Сумма ранга для группы J TH и N - общий размер выборки, то есть
Сумма ранга для группы J TH и N - общий размер выборки, то есть
 похожи (хотя значения для группы «Новые» больше, чем для двух других групп). Таким образом, мы можем использовать Крускала-Уоллиса для проверки нулевой гипотезы о том, что ни одна из групп не доминирует над другими, и, возможно, даже о том, что медианы групп равны.
похожи (хотя значения для группы «Новые» больше, чем для двух других групп). Таким образом, мы можем использовать Крускала-Уоллиса для проверки нулевой гипотезы о том, что ни одна из групп не доминирует над другими, и, возможно, даже о том, что медианы групп равны.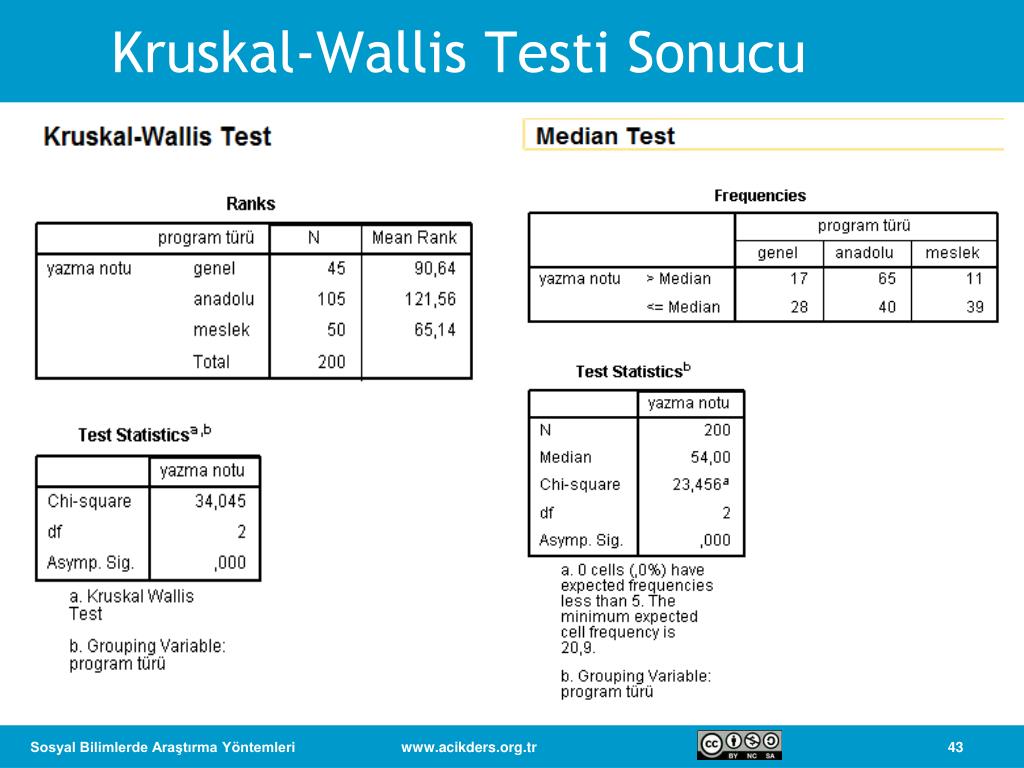 Остальные формулы на рисунке показаны в столбце L (соответствующем формулам в столбце J). Рис. 3. Критерий Крускала-Уоллиса
Остальные формулы на рисунке показаны в столбце L (соответствующем формулам в столбце J). Рис. 3. Критерий Крускала-Уоллиса
