Когда использовать критерий хи-квадрат (с примерами)
В статистике есть два разных типа тестов хи-квадрат:
1.Хи-квадрат критерия согласия — используется для определения того, следует ли категориальная переменная гипотетическому распределению.
2.Критерий независимости хи-квадрат — используется для определения наличия значимой связи между двумя категориальными переменными.
Обратите внимание, что оба эти теста подходят для использования только при работе с категориальными переменными.Это переменные, которые принимают имена или метки и могут вписываться в категории. Примеры включают:
- Цвет глаз (например, «голубой», «зеленый», «карий»)
- Пол (например, «мужской», «женский»)
- Семейное положение (например, «замужем», «холост», «разведен»)
В этом руководстве объясняется, когда использовать каждый тест, а также несколько примеров каждого из них.
Хи-квадратный тест на соответствиеВы должны использовать критерий согласия хи-квадрат всякий раз, когда хотите знать, следует ли какая-либо категориальная переменная некоторому гипотетическому распределению.
Вот несколько примеров, когда вы можете использовать этот тест:
Пример 1: подсчет клиентов
Владелец магазина хочет знать, одинаковое ли количество людей заходит в магазин каждый день недели, поэтому он подсчитывает количество людей, которые заходят каждый день в течение случайной недели.
Он может использовать критерий согласия Хи-квадрат соответствия, чтобы определить, соответствует ли распределение покупателей теоретическому распределению, согласно которому равное количество покупателей заходит в магазин каждый будний день.
Пример 2. Проверка правильности выпавшего кубика
Предположим, исследователь хотел бы знать, является ли игральная кость справедливой. Она решает бросить его 50 раз и записать, сколько раз он выпадет на каждое число.
Она может использовать критерий согласия Хи-квадрат соответствия, чтобы определить, соответствует ли распределение значений теоретическому распределению, согласно которому каждое значение встречается одинаковое количество раз.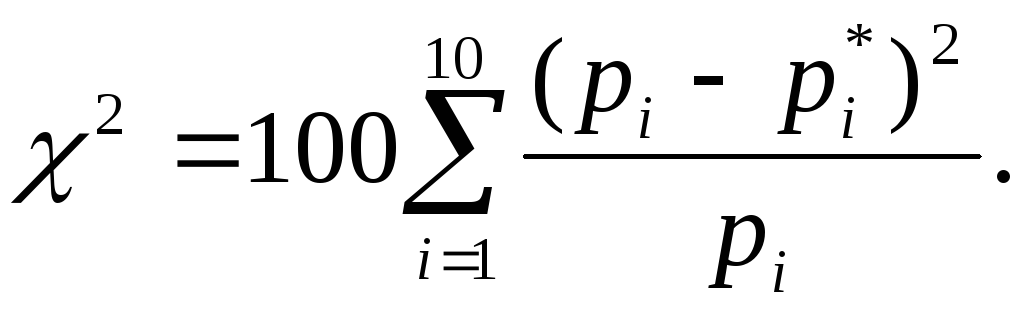
Пример 3: подсчет M&M’s
Предположим, мы хотим узнать, является ли процент M&M’s, который находится в упаковке, следующим: 20% желтых, 30% синих, 30% красных, 20% других. Чтобы проверить это, мы открываем случайный пакет M&M’s и подсчитываем, сколько выпадает каждого цвета.
Мы можем использовать критерий согласия Хи-квадрат соответствия, чтобы определить, равно ли распределение цветов заданному нами распределению.
Пошаговый пример теста на соответствие хи-квадрату см. в этом примере в Excel.
Хи-квадрат тест независимостиВы должны использовать критерий независимости хи-квадрат, когда хотите определить, существует ли значительная связь между двумя категориальными переменными.
Вот несколько примеров, когда вы можете использовать этот тест:
Пример 1: предпочтения при голосовании и пол
Исследователи хотят знать, связан ли пол с предпочтениями политических партий в определенном городе, поэтому они опрашивают 500 избирателей и записывают их пол и предпочтения политических партий.
Они могут выполнить критерий независимости хи-квадрат, чтобы определить, существует ли статистически значимая связь между предпочтениями при голосовании и полом.
Пример 2: любимый цвет и любимый вид спорта
Исследователи хотят знать, связан ли любимый цвет человека с его любимым видом спорта, поэтому они опрашивают 100 человек и спрашивают их об их предпочтениях в отношении обоих видов спорта.
Они могут выполнить тест независимости хи-квадрат, чтобы определить, существует ли статистически значимая связь между любимым цветом и любимым видом спорта.
Пример 3: Уровень образования и семейное положение
Исследователи хотят знать, связаны ли уровень образования и семейное положение, поэтому они собирают данные об этих двух переменных на простой случайной выборке из 2000 человек.
Они могут выполнить критерий независимости Хи-квадрат, чтобы определить, существует ли статистически значимая связь между уровнем образования и семейным положением.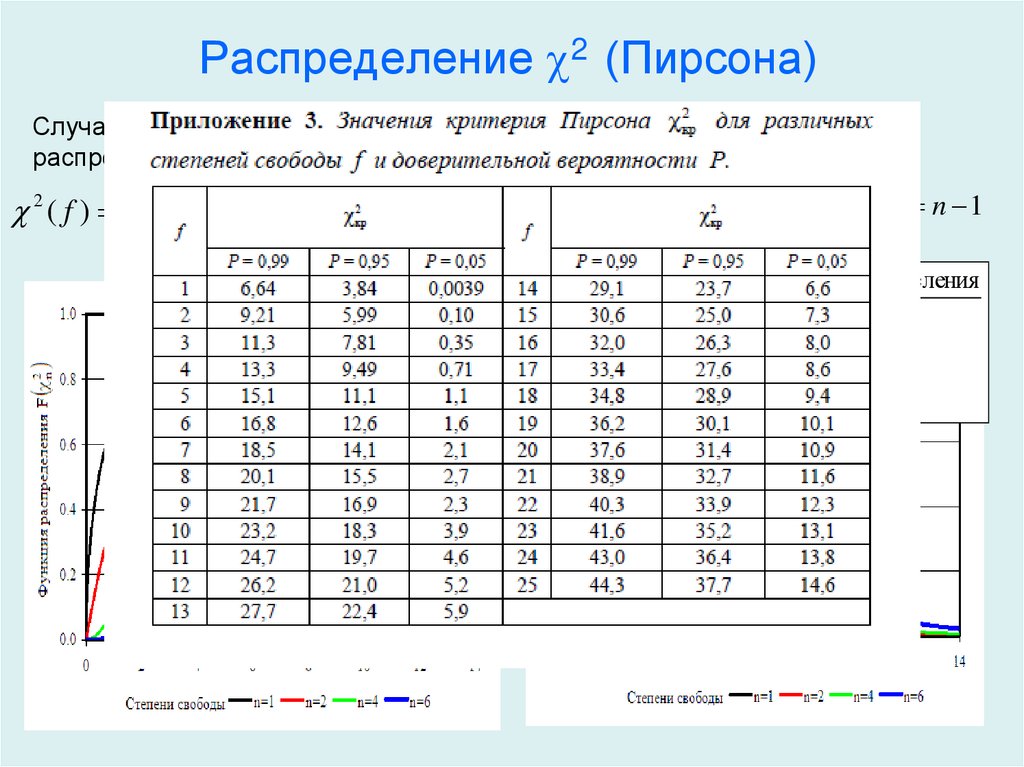
Пошаговый пример теста независимости хи-квадрат см. в этом примере в Excel.
Дополнительные ресурсыСледующие калькуляторы позволяют выполнять оба типа тестов хи-квадрат бесплатно онлайн:
Хи-квадрат Калькулятор критерия согласия
Калькулятор критерия хи-квадрат независимости
Эффект от рассылок: Как правильно оценивать улучшение
Хороший маркетинг — это доказательный маркетинг.
Но если не соблюсти несколько правил, то все насмарку: вроде бы результаты тестов положительные, конверсия растет, а выручка — нет.
Три главных правила оценки эффекта от рассылок:
- Разница в результатах должна быть значима
- Один тест — одна гипотеза
- Инвестиции в улучшения должны окупаться
1. Разница значима?
Всегда, всегда, всегда нужно помнить про статистику. Разница в результатах может быть как закономерностью, так и случайностью.
Например, на кассе вы опросили 10 покупателей, меняли ли они номер мобильного телефона за последнее время.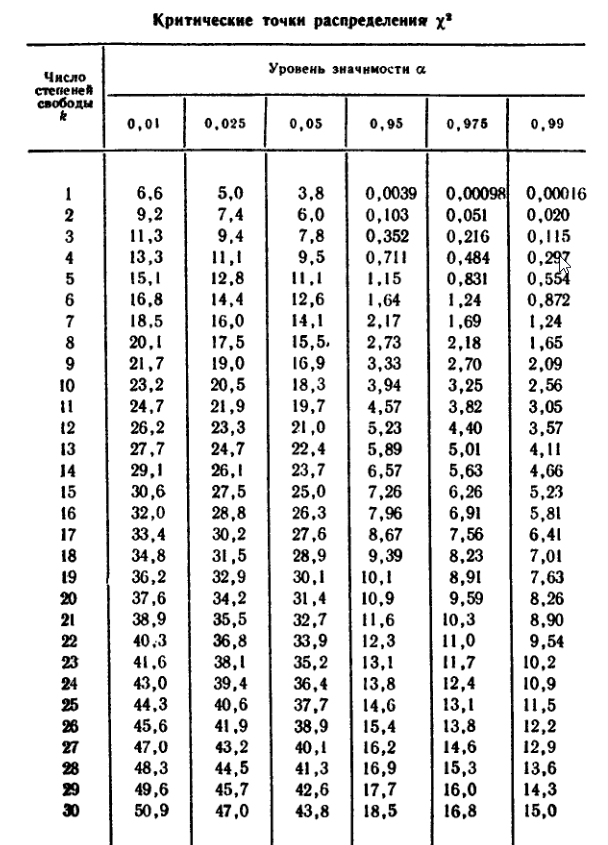
Выяснилось, что 1 человек не пользуется телефоном вообще. Сделаете ли вы вывод, что 10% ваших покупателей не пользуются телефоном? Вряд ли. Вы скажете, что это какая-то случайность. Такие люди, наверное, есть, но их точно меньше 10%. Но если вы опросили 1000 человек и 100 человек сказали, что отказались от использования мобильного телефона? Вы были бы безумно удивлены, но отмахнуться от 10% стало бы тяжелее.
Чтобы понять, когда и насколько можно доверять данным, есть разработанные методологии и готовые инструменты. Например русскоязычный калькулятор Mindbox (подробная инструкция на странице калькулятора).
Как применять это на практике?
Предположим, вы провели тест: одной группе клиентов отправили письмо с простой картинкой, а другой группе — с анимированной. Получилось, что в одном варианте конверсия 14%, а в другом — 17%. Казалось бы — ура, рост конверсии на 21,5%! Но достаточно ли наблюдений (писем или показов страницы сайта)?
Берем цифры и подставляем в калькулятор (нижний слайдер ставьте на 95%):
Для того, чтобы правильно спланировать этот тест еще до его проведения, можно рассчитать, сколько минимум нужно отправленных писем каждого варианта, чтобы сразу получить достоверную оценку результатов.
Для нашего примера калькулятор показывает, что только если в каждом варианте более 3 000 писем, можно сказать, что вариант с конверсией 17% успешнее, чем вариант с конверсией в 14%.
- Если нужно определить, какого объема должна быть выборка в каждом варианте (сколько писем, сколько показов странички сайта), вам нужно подставить две цифры в эту форму. Первая цифра — какая конверсия была до изменений или ожидается в одном из вариантов. Вторая цифры — минимум на сколько вы хотите эту конверсию увеличить.
- Если нужно понять, можно ли верить разнице конверсии в двух вариантах, нужно подставить абсолютные значения в следующую форму.
- Если надо определить, различаются ли средние чеки в двух вариантах, нужно подставить столбцы со значениями в третью форму
Если тест проводили не вы, а вам предоставляют отчет, убедитесь, что была проведена проверка на значимость или запросите данные и самостоятельно проверьте их на калькуляторе.
Если возник спорный случай или не получается разобраться, пишите нам на [email protected], мы постараемся помочь.
2. Тест точно проверяет нужную гипотезу?
Как построить эксперимент так, чтобы измерить именно то, что хочется измерить?Кажется, что все просто? Давайте разберем на примере.
Есть гипотеза: товарные рекомендации в письме увеличивают выручку.
Кажется, что АБ-тест должен быть такой: первый вариант письма — без рекомендаций, второй — с рекомендациями.
Но это не так. Давайте разберемся:
Когда мы говорим, что хотим измерить эффективность рекомендаций, мы имеем в виду измерение специального способа (алгоритма) подбора товаров. Считается, что именно качественный подбор растит конверсию. Но что мы делаем, когда добавляем рекомендации? На самом деле мы делаем две вещи:
- добавляем блок товаров в письмо
- выбираем с помощью рекомендательного алгоритма правильные товары в этот блок
Получается, что мы нарушили правило «один тест — одна гипотеза», и проверяем сразу два изменения.
В результате мы не сможем понять, что же именно изменило конверсию: само по себе наличие дополнительного блока с товарами или алгоритм их подбора?
Что делать?
Применить правило «один тест — одна гипотеза» и добавить еще один вариант: письмо с блоком товаров, подобранных случайным образом.
Сравнивая конверсии попарно, можно определить, какой вклад делает каждая составляющая.
Сколько надо писем, чтобы такая разница была значима? Немало. В первой паре 15% и 17% будут достоверно различны, если в каждом варианте будет больше 5 000 писем. Для второй же пары в 17% и 18% нужно уже больше 22 000 писем в каждом варианте.
3. Окупаются ли инвестиции?
Хорошо, допустим, мы грамотно провели тест и проверка на значимость показала, что конверсия или средний чек увеличились. Это хорошо и должно привести к увеличению выручки.
Теперь давайте разберемся, сколько нам стоил этот рост выручки, и окупились ли улучшения. В случае товарных рекомендаций, например — это затраты на разработку (или покупку) алгоритма + затраты на его обновление и поддержку.
Если эффект от рассылок дает прирост на 1%, т.е. 1 дополнительный заказ на 100 «обычных», хватает ли этого, чтобы окупить затраты?
Итог
- Проверяйте результаты на статистическую значимость
- Разбирайте тест на элементарные составляющие, 1 тест — 1 гипотеза
- Грамотно считайте деньги
Если вы делаете много тестов, выбираете выигрышные варианты, но в итоге у вас не растет выручка — это признак, что что-то вы делаете не так. АБ-тесты должны работать на ваш бизнес.
Калькулятор хи-квадрата
Как рассчитать хи-квадрат вручную
Хи-квадрат не так сложен, как некоторые статистические тесты, и иногда выполняется вручную. Вы можете использовать приведенную ниже формулу, вводя наблюдаемые (O) и ожидаемые (E) частоты для каждой группы. Суммируя рассчитанные значения для каждой из категорий, мы можем рассчитать статистику теста хи-квадрат, как показано ниже:
После того, как вы рассчитали статистику теста, вам нужно будет использовать компьютер или таблицу хи-квадрат, чтобы найти приблизительное значение P.
Хотя это можно сделать вручную, существует несколько возможностей для человеческой ошибки, поэтому мы рекомендуем этот калькулятор (или Prism для более продвинутого анализа).
Предположения хи-квадрат
Хотя хи-квадрат является одним из наиболее гибких тестов в статистике, он имеет следующие допущения:
- Анализ количества (не процентов)
- Большое количество предметов в каждой категории (обычно больше 5)
- По сравнению с теоретическим распределением
См. более подробную информацию в нашем контрольном списке анализа.
Связанные тесты и калькуляторы
Критерий хи-квадрат для таблиц непредвиденных обстоятельств
Тесты хи-квадрат также используются для анализа таблиц непредвиденных обстоятельств. Если у вас есть таблица непредвиденных обстоятельств 2×2, используйте этот калькулятор. Отличие заключается в том, что в таблицах непредвиденных обстоятельств ожидаемые значения вычисляются «за кулисами» в предположении, что переменные не связаны.
Биномиальный тест
Если у вас только две категории, используйте этот калькулятор биномиального теста. В этом случае хи-квадрат может дать слишком низкие значения P, но биномиальный тест рассчитает его точно.
Тест хи-квадрат против t-теста
Хи-квадрат проверяет, отличается ли наблюдаемое количество в каждой категории от ее ожидаемой «теоретической» совокупности, тогда как t-тесты оценивают, являются ли два выборочных средних (или одно выборочное среднее и фиксированное значение) статистически эквивалентными.
Интерпретация результатов
Значение p хи-квадрат проверяет, согласуются ли наблюдаемые значения с ожидаемыми значениями. Вы бы интерпретировали значения хи-квадрата ниже вашего порога значимости (часто 0,05) как «доказательство того, что данные не были выбраны из распределения, которое вы ожидали». Если значение P превышает ваш порог значимости, нет никаких доказательств того, что наблюдаемые значения отличались от ожидаемого теоретического распределения.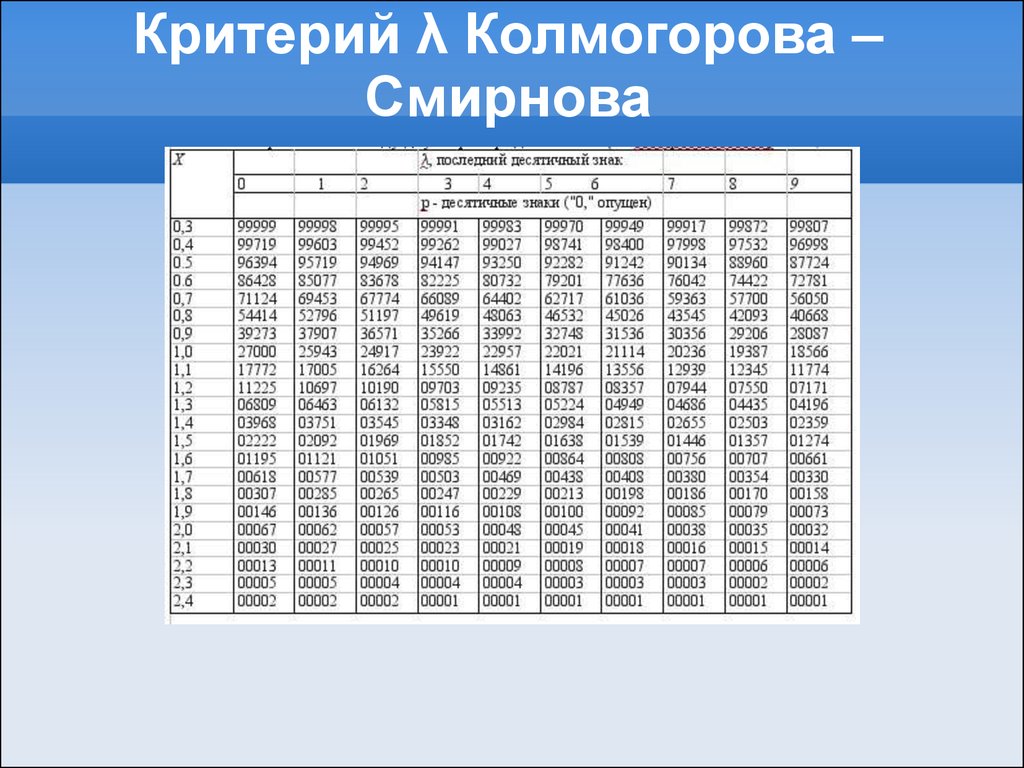
Обратите внимание, что значения P легко интерпретировать неправильно, но большие значения P не являются доказательством отсутствия различий; возможно, у вас недостаточно данных, чтобы обнаружить разницу.
Этот калькулятор выполняет двусторонний критерий хи-квадрат и предполагает, что порог значимости значения P равен 0,05.
Страница результатов также включает статистику хи-квадрат и ее степени свободы. Обратите внимание, что имена категорий вообще не участвуют в интерпретации. См. этот пример для помощи в интерпретации значения хи-квадрат P.
График результатов хи-квадрат
Этот калькулятор не создает графики результатов хи-квадрат. Сгруппированная гистограмма обычно используется для визуализации разницы между наблюдаемым и ожидаемым числом и является одним из многих настраиваемых графиков, предлагаемых Prism.
Готовы к более продвинутому анализу?
Начните 30-дневную бесплатную пробную версию Prism и получите доступ к:
- Пошаговые инструкции о том, как выполнить наиболее распространенный анализ
- Примеры данных для экономии вашего времени
- Дополнительные советы о том, как Prism может помочь в ваших исследованиях
С Prism за считанные минуты вы научитесь переходить от ввода данных к статистическому анализу и созданию высококачественных графиков.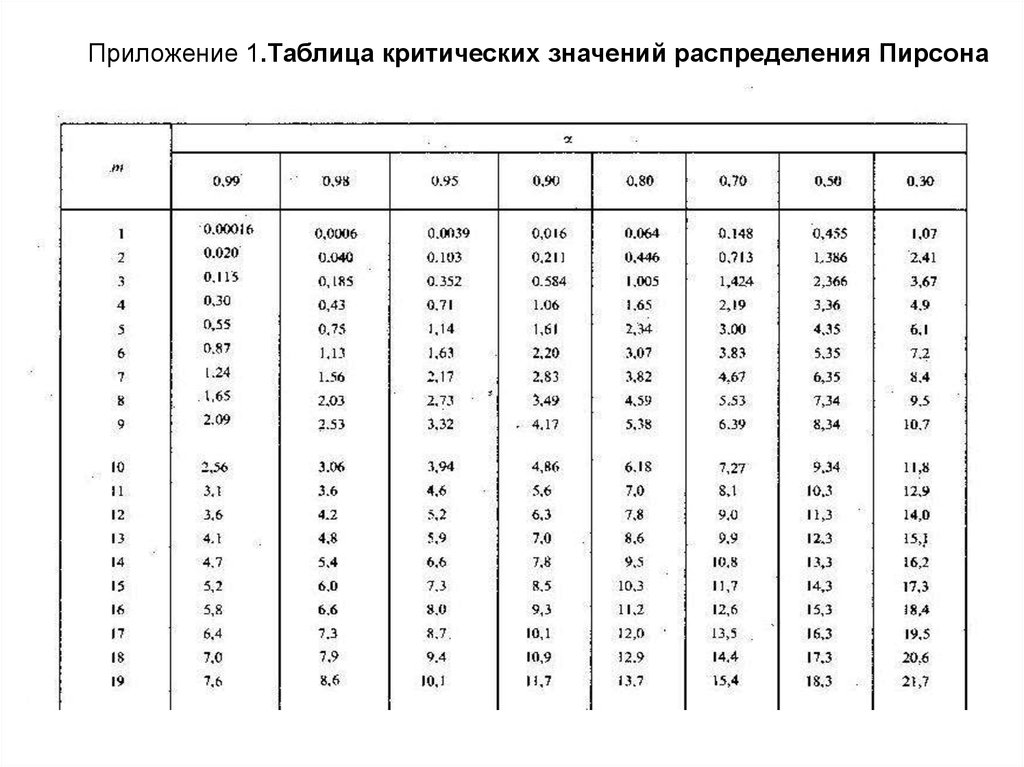
Интерактивные тесты хи-квадрат
Интерактивный инструмент для расчета критерия хи-квадрат на соответствие и независимость
Расчет для теста хи-квадрат: интерактивный инструмент для расчета критерия хи-квадрат на соответствие и независимость
Кристофер Дж. Причер ( Вандербильт University )
Как цитировать эту страницу
Эту веб-утилиту можно цитировать в стиле APA следующим образом:
Preacher, K. J. (2001, April). Расчет теста хи-квадрат: интерактивный инструмент для расчета теста хи-квадрат на соответствие и независимость [Компьютерное программное обеспечение]. Доступно на http://quantpsy.org.
Цель этой страницы
Эта веб-страница предназначена для предоставления краткого введения в тесты хи-квадрат независимости и согласия. Эти тесты используются для обнаружения групповых различий с использованием данных о частоте (количестве). Эта страница также предоставляет интерактивный инструмент, позволяющий исследователям проводить тесты хи-квадрат для своих собственных исследований.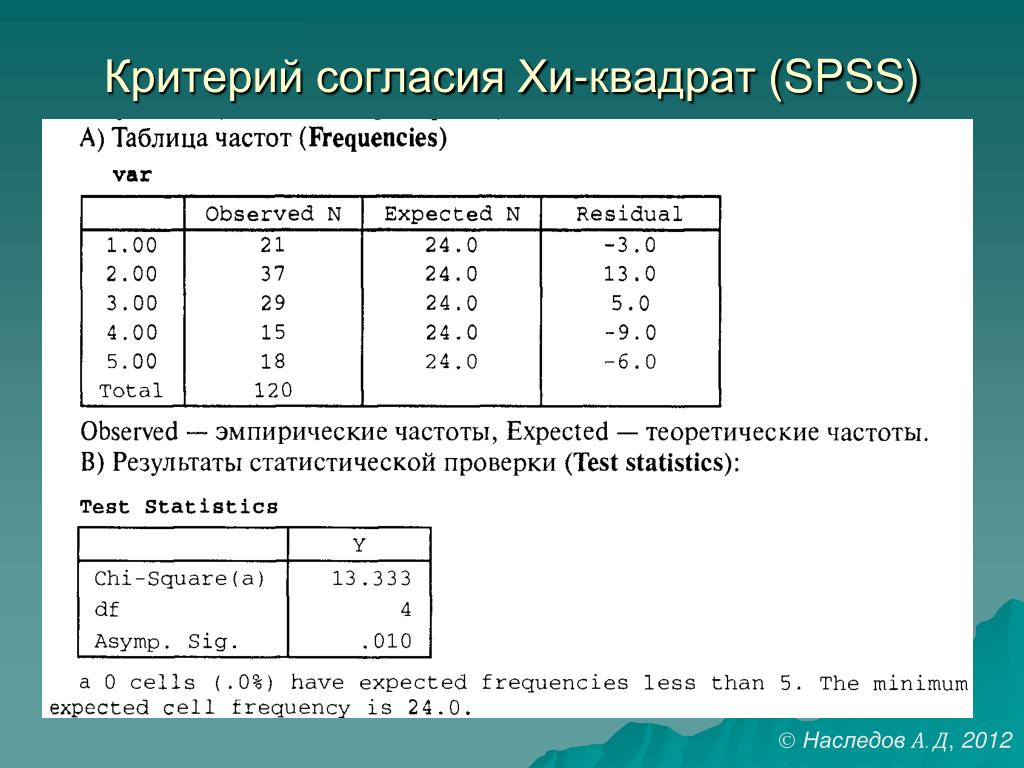
О тесте независимости хи-квадрат
Часто исследователь хочет увидеть, варьируется ли частота случаев, обладающих некоторым качеством, между уровнями данного фактора или между комбинациями уровней двух или более факторов. В таких ситуациях подходящим тестом является критерий согласия хи-квадрат согласия или критерий независимости хи-квадрат для k групп .
Как это делается
Для проведения теста хи-квадрат исследователь вводит наблюдаемые частоты, соответствующие комбинациям уровней релевантных факторов (здесь они называются «состояние» и «группа», но это обозначения для удобства). Затем вычисляются суммы элементов в строках и столбцах (назовем эти маргинальный номер ). Критерий независимости хи-квадрат используется для проверки нулевой гипотезы о том, что частота внутри ячеек соответствует ожидаемой, учитывая эти предельные значения N.
Ожидаемое значение в каждой ячейке, если истинно нулевое условие (т. е. если факторы не оказывают существенного влияния на наблюдаемые частоты в генеральной совокупности), представляет собой просто произведение суммы по строке и суммы по столбцу, деленное на общую выборку N для проверки независимости и N, деленное на количество уровней одного фактора для проверки согласия. Если O ij — наблюдаемая частота, а E ij — ожидаемая частота для ячейки, соответствующей условию i th и группе j th 901902 0:5chi-square, тогда
Если имеется только один интересующий фактор с уровнями ( k > 1), будет работать та же формула с i или j , установленными на 1. Представленный здесь тест можно использовать только для проверки 1- или 2-мерные массивы.
Возможны массивы более высокой размерности, они основаны на том же принципе и даже используют ту же формулу, хотя они включают множественные вложенные суммирования.
Как пользоваться этой страницей
Введите наблюдаемые частоты в белые ячейки. Я понимаю, что не так уж много дизайнов включают ровно 10 условий и 10 групп — если ваш дизайн меньше, то выберите некоторое подмножество строк и столбцов, в которое нужно ввести ваши данные. Например, если ваш дизайн (2 x 3), вы можете ввести свои данные в 6 ячеек в верхней левой части таблицы данных, определенных первыми двумя условиями и первыми тремя группами. Вы можете выбрать любое подмножество строк и столбцов для ваших данных. Вы также можете оставить ячейки, соответствующие наблюдаемым частотам, нулевыми. Допускаются нецелочисленные наблюдаемые частоты, хотя трудно представить, как их можно получить в реальных исследованиях.
Если вы выполняете тест на соответствие, вы можете ввести свои данные в любой отдельный столбец или строку.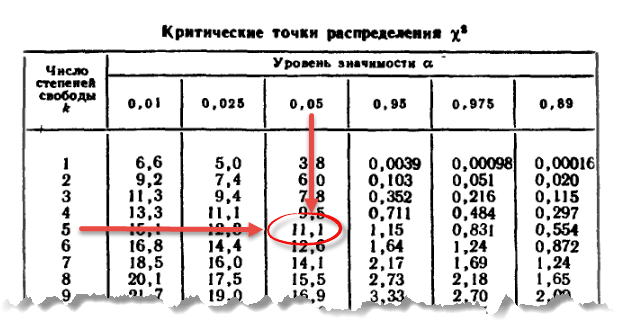
Однако наблюдаемые нулевые частоты должны быть явно включены (т. е. вам нужно фактически ввести «0» в эти ячейки, в противном случае предполагается, что эти ячейки не являются частью вашего проекта). После того, как вы ввели свои данные, нажмите кнопку Calculate и ожидайте увидеть результат в бежевых ячейках (они должны быть белыми, если вы используете старые версии Netscape). Не паникуйте, если вы видите научное обозначение для вашего p -значение — это просто означает, что p действительно мало.
Этот инструмент также дает хи-квадрат, включающий поправку Йейтса на непрерывность . Эта коррекция часто используется для повышения точности выборочного распределения хи-квадрат при нулевых условиях. Вероятно, его следует использовать только для тестов 1-df (т. е. тестов на соответствие или тестов независимости с таблицами непредвиденных обстоятельств 2×2), поэтому используйте его на свой страх и риск для тестов с df>1.
Предупреждения
Использование тестов хи-квадрат неуместно если какая-либо ожидаемая частота ниже 1 или если ожидаемая частота меньше 5 более чем в 20% ваших клеток.