Иллюстрированный самоучитель по SPSS > Непараметрические тесты > Тест Колмогорова-Смирнова (Kolmogorov-Smirnov Test) | ||||||||||||||||||
14.16. Тест Колмогорова-Смирнова для проверки формы распределения При помощи этого теста по выбору можно проверить, соответствует ли реальное распределение переменной нормальному (Гауса), равномерному, экспоненциальному распределению или распределению Пуассона. Разумеется, самым распространённым видом проверки является проверка наличия нормального распределения. Чтобы продемонстрировать работу данного теста, проверим на предмет наличия нормального распределения исходные значения холестерина, то есть переменную cho10 из файла hyper.sav.
Рис. 14.5: Диалоговое окно One Sample Kolomgorov-Smirnov Test Предварительно установленной является проверка на нормальное распределение. В окне просмотра появятся следующие результаты: One-Sample Kolmogorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
a. Test distribution is Normal. (Тестируемое распределение является нормальным распределением.) Полученные результаты включают:
Отклонение от нормального распределения считается существенным при значении р < 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты. В рассматриваемом примере (значение р = 0,616), то есть вероятность ошибки не является значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению и можно применять параметрические тесты. | ||||||||||||||||||
Deviation (Стандартное отклонение)
Домашнее задание по курсу ‘Математические и статистические методы в психологии’
#Вариант 8 ##Задание выполнили: Елисей Сажин, Даниела Чеботарь, Анна Могилевцева
library(ggplot2)
## Warning: package 'ggplot2' was built under R version 3.5.3
data <- read.csv("http://math-info.hse.ru/f/2018-19/psych-ms/Survey.csv")##Задание 1 Создаем новый датасет Section_1, в который будут включаться студенты, слушавшие 1-ую часть курса.
Section_1 <- data[data$Section == 1,]
Даем описательные статистики для всех этих студентов.
summary(Section_1$Reading)
## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1.0 54.0 100.0 170.4 200.0 2000.0
Создаем “Ящик с усами”, чтобы посмотреть, имеются ли в нашей выборке выбросы.
boxplot(Section_1$Reading)
И обнаруживаем три выброса: значения 449, 450 и 2000. Следует удалить их из выборки, поставив границу на значении 300.
Section_1 <- Section_1[Section_1$Reading <= 300,]
Проверяем “Ящик с усами”.
boxplot(Section_1$Reading)
Теперь в нем нет выбросов.
#Задание 2
Чтобы у нас не строилась отдельная гистограмма для значений NA, удалим их из выборки
Section_1 <- na.omit(Section_1)
Строим гистограммы для переменной Distance, разделяя их по группе Sex.
ggplot(data = Section_1, aes(x = Distance)) + geom_histogram(binwidth = 200, fill = 'green', color = 'black') + facet_wrap(~Sex)
#Задание 3 Строим вероятностную бумагу для переменной Distance, разделяя по группе Sex.
ggplot(data = Section_1, aes(sample = Distance)) + stat_qq(pch = 15, color = 'navy') + stat_qq_line(color = 'red') + facet_wrap(~Sex)
Визуально, для юношей есть один выброс — значение 2299, у девушек существуют два выброса: один человек проходит 5000, другой — 4500. Из-за этих выбросов распределение нельзя считать нормальным. Проверим по тестам.
#Задание 4 Для теста Колмогорова-Смирнова требуются значения mean и sd. Поскольку в задании требуется провести тесты отдельно для групп юношей и девушек, мы разделили их сразу.
Тесты Колмогорова-Смирнова и Шапиро-Уилка отличаются тем, что первый дает более достоверные результаты на небольших выборках (примерно до 60 человек), в то время как второй чаще используется на больших выборках.
f <- Section_1[Section_1$Sex == 'F',] m <- Section_1[Section_1$Sex == 'M',] f_mean <- mean(f$Distance) f_sd <- sd(f$Distance) m_mean <- mean(m$Distance) m_sd <- sd(m$Distance)
Для обоих этих тестов нулевой гипотезой является нормальное распределение.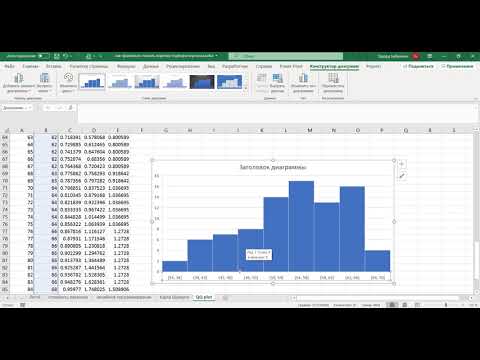
ks.test(f$Distance, 'pnorm', f_mean, f_sd)
## Warning in ks.test(f$Distance, "pnorm", f_mean, f_sd): ties should not be ## present for the Kolmogorov-Smirnov test
## ## One-sample Kolmogorov-Smirnov test ## ## data: f$Distance ## D = 0.24479, p-value = 0.1613 ## alternative hypothesis: two-sided
Значение p-value по тесту равно 0.1613, что больше 0.05, следовательно, это подтверждает нулевую гипотезу. Распределение для девушек является нормальным.
ks.test(m$Distance, 'pnorm', m_mean, m_sd)
## Warning in ks.test(m$Distance, "pnorm", m_mean, m_sd): ties should not be ## present for the Kolmogorov-Smirnov test
## ## One-sample Kolmogorov-Smirnov test ## ## data: m$Distance ## D = 0.23882, p-value = 0.07318 ## alternative hypothesis: two-sided
Значение p-value равно 0.07318, что больше 0.05, следовательно, это подтверждает нулевую гипотезу. Распределение для юношей является нормальным.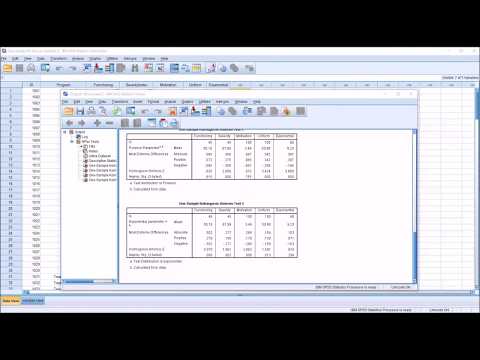
shapiro.test(f$Distance)
## ## Shapiro-Wilk normality test ## ## data: f$Distance ## W = 0.81756, p-value = 0.001233
Значение p-value очень маленькое, 0.001233, что меньше 0.05. Нулевую гипотезу следует отвергнуть, распределение ненормальное.
shapiro.test(m$Distance)
## ## Shapiro-Wilk normality test ## ## data: m$Distance ## W = 0.7738, p-value = 2.932e-05
Значение p-value также очень мало, 2.932e-05, что меньше 0.05. Мы отвергнули нулевую гипотезу, распределение нельзя считать нормальным.
Поскольку наша выборка состоит из 55 объектов, имеет смысл больше доверять результатам теста Колмогорова-Смирнова и считать распределение в обеих группах нормальным.
#Задание 5 Поскольку в обеих группах распределение мы считаем нормальным, мы будем использовать тест Student. Для теста F, который проводится до теста T, изначальная гипотеза заключается в том, что дисперсии переменных двух групп равны, или же между ними нет различий.
var.test(Section_1$Distance ~ Section_1$Sex, alternative = 'two.sided')
## ## F test to compare two variances ## ## data: Section_1$Distance by Section_1$Sex ## F = 9.5888, num df = 20, denom df = 28, p-value = 1.557e-07 ## alternative hypothesis: true ratio of variances is not equal to 1 ## 95 percent confidence interval: ## 4.295288 22.684058 ## sample estimates: ## ratio of variances ## 9.588847
Значение p-value очень маленькое, следовательно, мы отвергаем изначальную гипотезу — дисперсии не равны. В тесте T это мы и будем указывать.
t.test(Section_1$Distance ~ Section_1$Sex, var.equal = FALSE)
## ## Welch Two Sample t-test ## ## data: Section_1$Distance by Section_1$Sex ## t = 2.6462, df = 23.041, p-value = 0.01442 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## 180.835 1475.713 ## sample estimates: ## mean in group F mean in group M ## 1372.6190 544.3448
713
## sample estimates:
## mean in group F mean in group M
## 1372.6190 544.3448Значение p-value опять очень мало, значит нулевая гипотеза отвергается — дисперсии не равны. Следовательно, мы можем считать, и юноши действительно живут ближе или дальше от кампуса, чем девушки.
#Задание 6 Для построения диаграммы рассеяния мы пробовали использовать метод ‘auto’, и посчитали полученный график линейным. Потому, чтобы легче интерпретировать данные, впоследствии мы использовали метод ‘lm’.
ggplot(data = Section_1, aes(x = Texting, y = TV)) + geom_point(size = 2, shape = 23, color = 'red') + geom_smooth(method = 'lm', color = 'green')
Визуально интерпретируя график, можно сказать, что мы наблюдаем положительную среднюю линейную корреляцию.
#Задание 7 Тест коэффициента корреляции Спирмена имеет в качестве нулевой гипотезы независимость переменных (связи нет).
cor.test(Section_1$Texting, Section_1$TV, method = 'spearman')
## Warning in cor.
test.default(Section_1$Texting, Section_1$TV, method =
## "spearman"): Cannot compute exact p-value with ties## ## Spearman's rank correlation rho ## ## data: Section_1$Texting and Section_1$TV ## S = 9171.1, p-value = 2.389e-05 ## alternative hypothesis: true rho is not equal to 0 ## sample estimates: ## rho ## 0.559611
p-value очень маленький, следовательно, мы отвергаем нулевую гипотезу — признаки не независимы, связь между переменными есть.
#Задание 8 Зададим модель линейной взаимосвязи при помощи функции ‘lm’.
mod <- lm(data=Section_1, Pulse~Height)
Дадим описательные статистики для полученной модели.
summary(mod)
## ## Call: ## lm(formula = Pulse ~ Height, data = Section_1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -18.9341 -8.4435 0.4714 8.4024 30.1308 ## ## Coefficients: ## Estimate Std.
Error t value Pr(>|t|)
## (Intercept) 89.7070 21.9757 4.082 0.000168 ***
## Height -0.3405 0.3200 -1.064 0.292559
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.1 on 48 degrees of freedom
## Multiple R-squared: 0.02305, Adjusted R-squared: 0.002698
## F-statistic: 1.133 on 1 and 48 DF, p-value: 0.2926Формула вычисляется следующим способом: X = ß0 + ß1*Y, где X — зависимая переменная, Y — независимая переменная, ß0 — среднее ожидаемое значение, ß1 — изменение Х при Y.
Формула для нашей модели: 89.71 — 0.34 * Height = Pulse Поскольку Multiple R-squared равна 0.02305, соответственно, она плохо описывает
#Задание 9 Условия Гаусса-Маркова: 1. Должна существовать линейная зависимость между зависимой и независимой переменными. 2. Не должно быть закономерностей в распределении остатков модели. 3. Математическое ожидание должно быть равно 0.
4. Дисперсия остатков должна быть постоянна, не изменяться при изменении значений независимой переменной. *5. Рраспределение остатков модели должно являться нормальным.
#1 критерий Построим диаграмму рассеяния для наших переменных, чтобы увидеть, есть ли между ними линейная зависимость
ggplot(Section_1, aes(x = Pulse, y = Height)) + geom_point(size = 2, shape = 21, color = 'red') + geom_smooth(method = 'lm', color = 'green')
Можно видеть, что зависимость и правда линейная, значит первый критерий выполняется.
#2 критерий Чтобы посмотреть на наличие закономерностей в распределении остатков модели, построим для них диаграмму рассеяния, выставив прямую линию по значению 0.
Section_1$Resid <- mod$residuals #создаем отдельный столбец для остатков модели. ggplot(data = Section_1, aes(x = Height, y = Resid)) + geom_point(size = 2, shape = 21, color = 'red') + geom_hline(yintercept = 0, col = 'green')
Закономерностей в распределении остатков модели не наблюдается, значит, критерий также выполняется.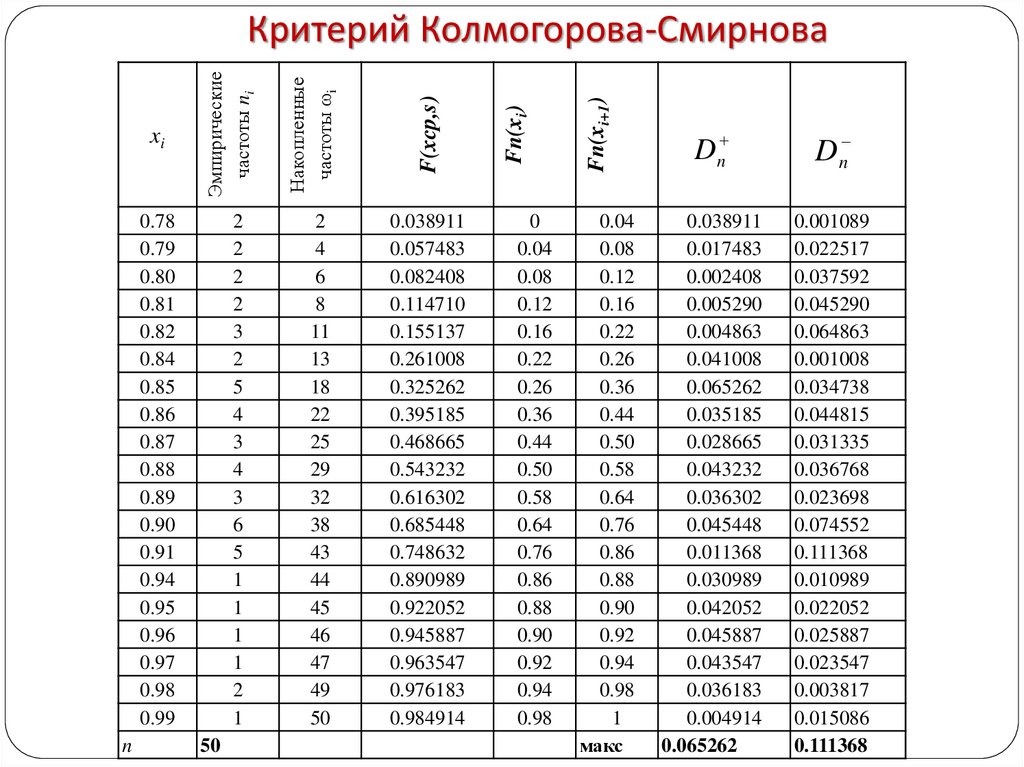
#3 критерий Проверим математическое ожидание остатков модели.
mean(Section_1$Resid)
## [1] 2.728894e-16
Математическое ожидание очень близко к нулю, поэтому мы можем считать, что этот критерий тоже выполняется.
#4 критерий Для того, чтобы определить, выполняется ли критерий №4, мы снова построим диаграмму рассеяния.
ggplot(data = Section_1, aes(x = Height, y = Resid)) + geom_point(size = 2, shape = 21, color = 'red') + geom_hline(yintercept = 0, col = 'green')
Визуально можно сказать, что разброс точек относительно 0 примерно равный, что значит, что при разных значениях независимой переменной дисперсии остатков остаются постоянными. Следовательно, четвертый критерий также выполняется.
#5 критерий Проверим распределение остатков модели на нормальность.
ggplot(data = Section_1, aes(sample = Resid)) + stat_qq(pch = 15, color = 'navy') + stat_qq_line(color = 'red')
Выбросы из модели отсутствуют, следовательно, распределение нормальное.
На всякий случай, проверим его еще и при помощи теста Колмогорова-Смирнова.
ks.test(Section_1$Resid, 'pnorm', mean(Section_1$Resid), sd(Section_1$Resid))
## Warning in ks.test(Section_1$Resid, "pnorm", mean(Section_1$Resid), ## sd(Section_1$Resid)): ties should not be present for the Kolmogorov-Smirnov ## test
## ## One-sample Kolmogorov-Smirnov test ## ## data: Section_1$Resid ## D = 0.054429, p-value = 0.9984 ## alternative hypothesis: two-sided
Значение p-value очень высоко, 0.9984, следовательно, нулевая гипотеза принимается, и распределение нормальное.
SPSS Критерий Колмогорова-Смирнова. Полное руководство
Альтернативным критерием нормальности является критерий Шапиро-Уилка.
- Что такое критерий нормальности Колмогорова-Смирнова?
- SPSS Тест Колмогорова-Смирнова от НПАРА ИСПЫТАНИЯ
- SPSS Критерий Колмогорова-Смирнова из EXAMINE VARIABLES
- Отчет о тесте Колмогорова-Смирнова
- Неверные результаты в SPSS?
Что такое критерий нормальности Колмогорова-Смирнова?
Тест Колмогорова-Смирнова проверяет, набрал ли он 9 баллов.
0019, вероятно, будут следовать некоторому распределению в некоторой популяции.
Во избежание путаницы есть 2 теста Колмогорова-Смирнова:
Средние значения и t-тесты в SPSS
Включите JavaScript
Средние значения и t-тесты в SPSS
- есть одновыборочный критерий Колмогорова-Смирнова для проверки того, следует ли переменная заданному распределению в совокупности. Это «заданное распределение» обычно — не всегда — является нормальным распределением, отсюда и «критерий нормальности Колмогорова-Смирнова».
- есть также (гораздо менее распространенный) независимых выборок тест Колмогорова-Смирнова для проверки того, имеет ли переменная идентичные распределения в 2 популяциях.
Теоретически «критерий Колмогорова-Смирнова» может относиться к любому тесту (но обычно относится к одновыборочному критерию Колмогорова-Смирнова), и его лучше избегать. Кстати, оба критерия Колмогорова-Смирнова присутствуют в SPSS.
Тест Колмогорова-Смирнова — простой пример
Допустим, у меня население 1 000 000 человек. Я думаю, что их время реакции на какую-то задачу распределено совершенно нормально. Я выбираю 233 из этих людей и измеряю время их реакции.
Теперь наблюдаемое частотное распределение для них, вероятно, будет немного отличаться, но не слишком сильно, от нормального распределения. Поэтому я строю гистограмму наблюдаемого времени реакции и накладываю нормальное распределение с тем же средним значением и стандартным отклонением. Результат показан ниже.
Частотное распределение моих баллов не полностью совпадает с моей нормальной кривой. Теперь я мог вычислить процентов случаев, которые отклоняются от нормальной кривой — процент красных областей на диаграмме. Этот процент является тестовой статистикой: он выражает одним числом, насколько мои данные отличаются от моей нулевой гипотезы. Таким образом, он указывает, в какой степени наблюдаемые оценки отклоняются от нормального распределения.
Теперь, если моя нулевая гипотеза верна, то этот процент отклонения, вероятно, должен быть довольно мал. То есть небольшое отклонение имеет высокое значение вероятности или p-значение.
И наоборот, огромный процент отклонений очень маловероятен и предполагает, что время моей реакции не соответствует нормальному распределению среди всего населения. Таким образом, большое отклонение имеет низкое p-значение . Как правило, мы
отклонить нулевую гипотезу, если p < 0,05.
Итак, если p < 0,05, мы не делаем 0052 считают, что наша переменная имеет нормальное распределение в нашей популяции.
Это самый простой способ понять, как работает критерий нормальности Колмогорова-Смирнова. Однако в вычислительном отношении он работает иначе: он сравнивает наблюдаемые и ожидаемые кумулятивные относительные частоты, как показано ниже.
Критерий Колмогорова-Смирнова использует максимальную абсолютную разницу между этими кривыми в качестве своей тестовой статистики, обозначенной D.
На этой диаграмме максимальная абсолютная разница D равна (0,48 — 0,41 =) 0,07, и она возникает при времени реакции 960 миллисекунд. Имейте в виду, что D = 0,07 , так как через минуту мы столкнемся с этим в наших выходных данных SPSS.
Тест Колмогорова-Смирнова в SPSS
Есть 2 способа запустить тест в SPSS:
- ИСПЫТАНИЯ NPAR, указанные в разделе A nalyze N о параметрических испытаниях L диалоги egacy 1 -Sample K-S… — наш метод выбора, потому что он создает хорошо детализированные выходные данные.
- ИЗУЧИТЬ ПЕРЕМЕННЫЕ из A nalyze D описательная статистика E xplore является альтернативой. Эта команда выполняет как тест Колмогорова-Смирнова, так и тест нормальности Шапиро-Уилка.
Обратите внимание, что EXAMINE VARIABLES использует исключение отсутствующих значений по списку по умолчанию. Итак, если я тестирую 5 переменных, мои 5 тестов используют только те случаи, в которых нет пропусков ни по одной из этих 5 переменных. Обычно это не то, что вам нужно, но мы покажем, как этого избежать.
Обычно это не то, что вам нужно, но мы покажем, как этого избежать.Мы продемонстрируем оба метода с помощью файла speedtasks.sav, часть которого показана ниже.
Наш главный исследовательский вопрос: какая из переменных времени реакции, вероятно, будет нормально распределена в нашей популяции? Эти данные являются хрестоматийным примером того, почему вы должны тщательно проверять свои данные, прежде чем приступить к их редактированию или анализу. Давайте сделаем именно это и запустим несколько гистограмм, используя приведенный ниже синтаксис.
* Запустите базовые гистограммы для проверки правдоподобности распределения.
частоты от r01 до r05
/формат примечательный
/гистограмма в норме.
*Обратите внимание, что некоторые дистрибутивы вообще не выглядят правдоподобными!
Результат
Обратите внимание, что некоторые дистрибутивы вообще не выглядят правдоподобными.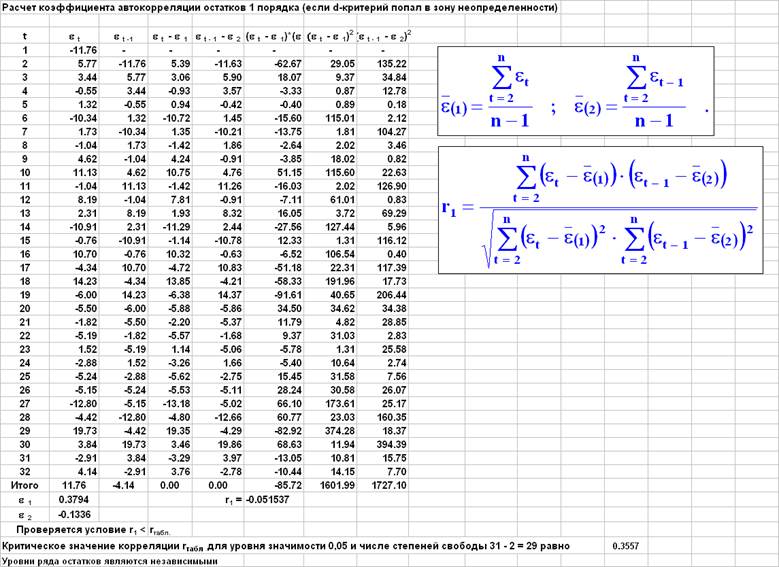
Но какие из них, вероятно, будут нормально распределены?
SPSS Тест Колмогорова-Смирнова от НПАРА ИСПЫТАНИЯ
Наш предпочтительный вариант проведения теста Колмогорова-Смирнова находится в стадии A анализ N о параметрических испытаниях L диалоги egacy 1 — Образец K-S… как показано ниже.
Далее мы просто заполняем диалоговое окно, как показано ниже.
Нажатие P приводит к приведенному ниже синтаксису. Давайте запустим его.
Синтаксис теста Колмогорова-Смирнова из непараметрических тестов
*Одновыборочный тест Колмогорова-Смирнова из анализа — непараметрические тесты — устаревшие диалоги — 1 образец ks-теста.
ИСПЫТАНИЯ NPAR
/K-S(НОРМАЛЬНЫЙ)=r01 r02 r03 r04 r05
/ОТСУТСТВУЕТ АНАЛИЗ.
*Только время реакции 4 имеет p > 0,05 и, таким образом, представляется нормально распределенным в популяции.
Результаты
Во-первых, обратите внимание, что тестовая статистика для нашей первой переменной равна 0,073 — точно так же, как мы видели на нашей кумулятивной диаграмме относительных частот чуть ранее. Диаграмма содержит точно такие же данные, на которых мы только что провели тест, поэтому эти результаты хорошо сходятся.
Относительно нашего исследовательского вопроса: кажется, что только время реакции для испытания 4 имеет нормальное распределение.
SPSS Критерий Колмогорова-Смирнова из EXAMINE VARIABLES
Альтернативный способ запуска теста Колмогорова-Смирнова начинается с A анализ D описательная статистика E исследование как показано ниже.
Синтаксис теста Колмогорова-Смирнова из непараметрических тестов
*Одновыборочный критерий Колмогорова-Смирнова из анализа — описательная статистика — исследование.
ИЗУЧИТЬ ПЕРЕМЕННЫЕ=r01 r02 r03 r04 r05
/PLOT BOXPLOT NPPLOT
/СРАВНИТЬ ГРУППЫ
/СТАТИСТИКА НЕТ
/CINTERVAL 95
/ОТСУТСТВУЕТ ПАРА /* ВАЖНО! */
/НЕ ВСЕГО.
*Короткая версия.
ПРОВЕРИТЬ ПЕРЕМЕННЫЕ r01 r02 r03 r04 r05
/PLOT NPPLOT
/отсутствует попарно /* ВАЖНО! */.
Результаты
Как правило, мы заключаем, что
переменная имеет нормальное распределение , а не , если «Sig.» < 0,05.
Таким образом, как тест Колмогорова-Смирнова, так и результаты теста Шапиро-Уилка предполагают, что только испытание времени реакции 4 следует нормальному распределению во всей популяции.
Кроме того, обратите внимание, что результаты теста Колмогорова-Смирнова идентичны результатам, полученным из NPAR TESTS.
Отчет о тесте Колмогорова-Смирнова
Для сообщения результатов наших тестов в соответствии с рекомендациями APA мы напишем что-то вроде «Тест Колмогорова-Смирнова показывает, что время реакции в испытании 1 не подчиняется нормальному распределению, D(233) = 0,07, p = 0,005». Для дополнительных переменных попробуйте сократить это, но убедитесь, что вы включили
- D (для «разности»), статистика критерия Колмогорова-Смирнова,
- df , степени свободы (что равно N) и
- p , статистическая значимость.
Неверные результаты в SPSS?
Если вы студент, который просто хочет сдать тест, вы можете прекратить чтение прямо сейчас . Просто следуйте шагам, которые мы обсуждали до сих пор, и все будет хорошо.
Хорошо, теперь давайте снова запустим точно такие же тесты в SPSS версии 18 и посмотрим на результат.
В этом выводе включены точные p-значения и, к счастью, они очень близки к асимптотическим p-значениям. Однако, к меньшему счастью,
результаты SPSS версии 18 сильно отличаются
от результатов SPSS версии 24.
мы сообщили до сих пор.
Причина, по-видимому, заключается в коррекции значимости Lilliefors, которая применяется в более новых версиях SPSS. В результате кажется, что уровни асимптотической значимости отличаются от точного значения гораздо больше, чем когда поправка не подразумевается. Это поднимает серьезные сомнения в правильности «результатов Lilliefors» — значение по умолчанию в новых версиях SPSS.
Сходящиеся доказательства этого предположения были собраны моим коллегой Алвином Стегеманом, который повторно провел все тесты в Matlab. Результаты Matlab согласуются с результатами SPSS 18 и, следовательно, не с более новыми результатами.
Критерий нормальности Колмогорова-Смирнова — Ограниченная полезность
Критерий Колмогорова-Смирнова часто используется для проверки предположения о нормальности, требуемого многими статистическими тестами, такими как ANOVA, t-критерий и многие другие. Однако почти всегда упускается из виду, что такие тесты устойчивы к нарушению этого предположения, если размеры выборки разумны, скажем, N ≥ 25. Основной причиной этого является центральная предельная теорема. Поэтому,
тесты на нормальность необходимы только для небольших размеров выборки
если цель состоит в том, чтобы удовлетворить предположение о нормальности.
К сожалению, небольшие размеры выборки приводят к низкой статистической мощности тестов нормальности. Это означает, что существенные отклонения от нормальности приведут к статистической значимости.
Тест говорит, что отклонений от нормы нет, хотя на самом деле они огромны. Короче говоря, ситуация, в которой необходимы тесты на нормальность — небольшие размеры выборки — также является ситуацией, в которой они работают плохо.
Спасибо, что прочитали.
Калькулятор теста Колмогорова-Смирнова (К-С) | ААТ Биоквест
Критерий Колмогорова-Смирнова (критерий К-С) определяет распределение выборки в популяциях без каких-либо конкретных предположений о распределении. Статистический анализ основан на D-значении, которое представляет максимальное расстояние между эмпирической функцией распределения и кумулятивным нормальным распределением. Одновременно сообщаемое p-значение используется для оценки того, значительно ли различаются результаты. Хотя тест в основном применяется в контексте непрерывных распределений, анализ может быть расширен для ответа на вопросы, касающиеся других типов распределения, включая нормальное, логарифмически нормальное, распределение Вейбулла, экспоненциальное и логистическое распределение.
Как пользоваться этим инструментом
1. Поместите экспериментальные данные в поле справа. Это можно сделать путем прямого копирования из Excel или вставки значений в форматах с разделителями-запятыми, табуляцией или пробелами. Если данные вводятся вручную, размещайте только одно значение в строке. Формат должен быть следующим:
| Набор данных 1: Выборка | Набор данных 2: Население |
| X 1 | Y 8 1 0251 |
| X 2 | Y 2 |
| X 3 | Y 3 |
| X 4 | Y 4 |
| … | … |
Пользователи могут либо ввести два набора данных для сравнения распределения между совокупностями, либо ввести один набор данных для сравнения выборочного распределения с нормальным распределением. Поместите образец в набор 1.
Чтобы добавить новый набор данных, нажмите на вкладку «+» над областью ввода данных. Если набор 2 не включен, предполагается, что набор данных имеет нормальное распределение. Наборы данных можно переименовать, дважды щелкнув вкладку. Каждый набор данных будет генерировать выходные данные с D-статистикой, p-значением, альтернативной гипотезой и графическими представлениями в виде гистограммы, нормальной кривой и эмпирической функции распределения.2. Проверьте правильность данных в появившейся таблице.
3. Нажмите кнопку «Рассчитать тест K-S», чтобы отобразить результаты.
Ввод данных
+
Данные процесса
Дополнительная информация
Тест Колмогорова-Смирнова, чаще называемый тестом К-С, представляет собой непараметрический статистический анализ без распределения, используемый для определения распределения выборки в совокупности. . В дополнение к вычислению D-статистики и p-значения для набора данных на выходе генерируется альтернативная гипотеза и несколько графических представлений в виде гистограмм, нормальных кривых и эмпирических функций распределения, которые помогают понять распределение выборки.
Критерий K-S основан на эмпирической функции распределения (ECDF) для проверки соответствия между двумя кумулятивными распределениями. Для N упорядоченных точек данных, т. е. Y1, Y2, …, YN, ECDF определяется как
EN=n(i)/N
, где n(i) — количество точек меньше Yi, а значения Yi сортируются в порядке возрастания. Уравнение генерирует возрастающую ступенчатую функцию, которая растет на 1/N в каждой упорядоченной точке данных. Тест KS работает путем сравнения эмпирической функции распределения с теоретическим распределением и вычисления максимального расстояния между двумя кривыми, которое представлено значением D. Нулевая гипотеза утверждает, что между двумя распределениями нет разницы. Получается значение p, представляющее вероятность того, что нулевая гипотеза верна, и учитывает сравнение D с критическим значением c(α), где c(α) — функция, не зависящая от размера, с α в качестве выбранного уровня значимости. для статистической значимости. При p < α нулевая гипотеза отклоняется, предполагая, что две совокупности относятся к разным распределениям.
Точно так же, если p > α, нулевая гипотеза принимается, и распределения населения считаются одинаковыми.
c(α)=sqrt(-ln(α/2)*(1/2))
Dn,m > c(α)*sqrt((n+m)/(n*m))
Следует также принимать во внимание отношение тестовой статистики (значение D) к уровню значимости (α). Для низкого значения α необходима большая разница в популяциях, чтобы отвергнуть нулевую гипотезу, что указывает на более высокое значение D. Значительно высокое значение α означает, что даже небольшие различия в распределениях увеличиваются и приводят к отклонению нулевой гипотезы независимо от малых значений D. Следовательно, нулевая гипотеза отвергается для всех наборов данных, которые не относятся к одному и тому же непрерывному распределению. Тест KS особенно полезен для понимания распределения данных и различения различных типов распределения, таких как нормальное, логарифмически-нормальное, Вейбулла, экспоненциальное и логистическое.
Обратная связь
У вас есть вопросы или пожелания по поводу этого инструмента? Не стесняйтесь обращаться к нам и дайте нам знать! Мы всегда ищем способы стать лучше!
Отправить запрос
Ссылки
Данную онлайн-инструмент можно цитировать следующим образом:
MLA | «Quest Graph™ Тест Колмогоров-Смир» AAT Bioquest, Inc. , 10 марта 2023 г., https://www.aatbio.com/tools/kolmogorov-smirnov-k-s-test-calculator. |
APA | AAT Bioquest, Inc. (10 марта 2023 г.). Quest Graph™ Калькулятор теста Колмогорова-Смирнова (К-С) . ААТ Биоквест. https://www.aatbio.com/tools/kolmogorov-smirnov-k-s-test-calculator. |
Этот онлайн-инструмент цитировался в 6 публикациях, в том числе
Отношение и восприятие потребителями использования вторичной древесины
Авторы: Craig, Mia
Journal: (2022)
Использование бесплатных веб-сайтов для выполнения статистических расчетов на курсах базовой статистики в средней школе или колледже 9 уровня0019 Авторы: Шумм, Уолтер Р. и Дуган, Меррик и Науман, Уильям и Сак, Бриана и Мальдонадо, Джулиан и Коньяк, Кайден и Паттерсон, Клэй
Журнал: (2021)
Профилактика диабета на основе способа диагностики
Авторы: Рич, Дебра Дж. Журнал
: (2021)
Структуры человеческих антител, связанных с шипом SARS-CoV-2, выявляют общие эпитопы и повторяющиеся признаки антител
Авторы: Барнс, Кристофер О и Уэст-младший, Энтони П.