Отображения. Криволинейные координаты. Преобразования. Формулы Грина
Отображения. Криволинейные координаты. Преобразования. Формулы Грина
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. ОТОБРАЖЕНИЯ. ЯКОБИАН 1. Определения. Аффинные отображения. 2. Графики. 3. Обращение. Гомеоморфизм. 4. Суперпозиция. § 2. КОЭФФИЦИЕНТ ИСКАЖЕНИЯ И ПРОИЗВОДНАЯ 6. Направление перемещения. Обратное отображение. 7. Суперпозиция. § 3. ОТОБРАЖЕНИЯ В ПЛОСКОМ СЛУЧАЕ 9. Обращение. 10. Гомеоморфизм. 11. Суперпозиция. § 4. АФФИННЫЕ ОТОБРАЖЕНИЯ 13. Равномерно распределенные точки. 14. Коэффициент искажения. 15. Направление перемещения. § 5. НЕКОТОРЫЕ ЧАСТНЫЕ АФФИННЫЕ ОТОБРАЖЕНИЯ. СВОЙСТВА ОПРЕДЕЛИТЕЛЯ 17. Сохранение площади. Движение.  18. Отображения гомотетии и подобия. 19. Свойства определителя. § 6. КОЭФФИЦИЕНТ ИСКАЖЕНИЯ (ОБЩИЙ СЛУЧАЙ) И ЯКОБИАН. РЕГУЛЯРНЫЕ ОТОБРАЖЕНИЯ 21. Обобщение. 22. Направление перемещения. 23. Регулярные отображения. § 7. СВОЙСТВА ЯКОБИАНА 25. Якобиан обратного отображения. 26. Суперпозиция. § 8. ВЫРОЖДЕНИЕ ОТОБРАЖЕНИЯ ЗАВИСИМОСТЬ ФУНКЦИИ 28. Зависимость функций. § 9. ОТОБРАЖЕНИЯ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ 30. Свойства якобиана. Зависимость функций. ГЛАВА II. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 32. Функциональная шкала § 2. ПЛОСКИЙ СЛУЧАЙ 33. Определения. Координатные линии. 34. Ортогональность системы. 35. Коэффициенты Ламе. 36. Элементы длины и площади. 37. Другой вывод. § 3. ВАЖНЕЙШИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ НА ПЛОСКОСТИ 39. Полярные координаты. 40. Обобщенные полярные координаты. § 4. ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ И ИХ ВЫРОЖДЕНИЯ 41. Общие эллиптические координаты.  42. Вырожденные эллиптические координаты. Униформизация. § 5. ДРУГИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ ОРТОГОНАЛЬНЫХ КООРДИНАТ НА ПЛОСКОСТИ 43. Параболические координаты. 44. Биполярные координаты. § 6. ПРОСТРАНСТВЕННЫЙ СЛУЧАЙ 45. Определения. Координатные поверхности и линии. 46. Ортогональность системы. 47. Коэффициенты Ламе. § 7. ЭЛЕМЕНТЫ ДЛИНЫ, ОБЪЕМА И ПЛОЩАДИ ПОВЕРХНОСТИ 49. Элемент объема. 50. Другой вывод. 51. Элемент площади поверхности. Направляющие косинусы нормали. 52. Элемент площади поверхности в криволинейных координатах в пространстве. § 8. ВАЖНЕЙШИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ В ПРОСТРАНСТВЕ 54. Цилиндрические координаты. 55. Сферические координаты. 56. Телесный угол. 57. Обобщенные сферические координаты. § 9. ЭЛЛИПСОИДАЛЬНЫЕ КООРДИНАТЫ И ИХ ВЫРОЖДЕНИЯ 59. Вырожденные эллипсоидальные координаты. Униформизация. 60. Сферические координаты. 61. Вырожденные эллипсоидальные «вытянутые» координаты. 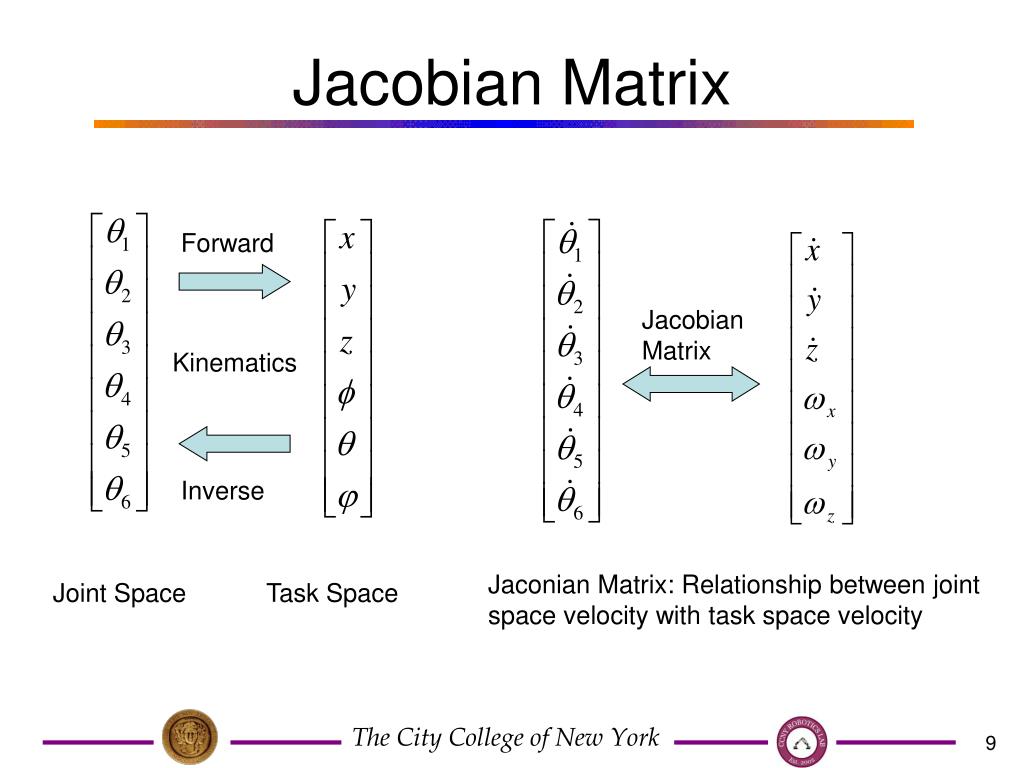 62. Вырожденные эллипсоидальные «сплюснутые» координаты. $ 10. ДРУГИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ ОРТОГОНАЛЬНЫХ КООРДИНАТ В ПРОСТРАНСТВЕ 64. Параболоидальные координаты. 65. Тороидальные координаты. 66. Биполярные координаты. 67. Цилиндрические координаты. ГЛАВА III. ПРЕОБРАЗОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ВЫРАЖЕНИЙ 69. Замена функции. 70. Замена независимой переменной и функции. § 2. СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 71. Замена независимых переменных. 72. Замена функции. 73. Замена независимых переменных и функции. 75. Параметр второго порядка (лапласиан). 76. Условия регулярности. § 4. СЛУЧАЙ ТРЕХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ. ПРЕОБРАЗОВАНИЯ «ДИФФЕРЕНЦИАЛЬНЫХ ПАРАМЕТРОВ» 78. Преобразования «дифференциальных параметров». 79. Выражения лапласиана в известных криволинейных координатах. ГЛАВА IV. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ § 1. ИНТЕГРАЛ ПО МЕРЕ ОБЛАСТИ 81.  Основные свойства.82. Вычисление интегралов. 83. Несобственные интегралы. § 2. ЗАМЕНА ПЕРЕМЕННЫХ В ИНТЕГРАЛЕ ПО МЕРЕ 85. Преобразования в декартовых координатах. 86. Преобразования в криволинейных координатах. § 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ. ПРИМЕРЫ 88. Двойной интеграл. 89. Тройной интеграл. § 4. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО КООРДИНАТЕ 91. Определение и свойства интеграла. 92. Способы вычисления. 93, Интеграл как функционал. Дополнительные замечания. § 5. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ПО КООРДИНАТАМ 95. Определение и свойства интеграла. 96. Способы вычисления. 97. Дополнительные замечания. § 6. ОСНОВНАЯ ФОРМУЛА ГРИНА И СЛЕДСТВИЯ ИЗ НЕЕ 99. Независимость интеграла от контура интегрирования. 100. Условие полного дифференциала. Формула Ньютона – Лейбница. 101. Применения. Задача термодинамики. § 7. ФОРМУЛЫ СТОКСА И ОСТРОГРАДСКОГО И СЛЕДСТВИЯ ИЗ НИХ 103. Независимость интеграла от контура интегрирования.  Условие полного дифференциала. Формула Ньютона — Лейбница.104. Формула Остроградского. 105. Независимость интеграла от поверхности интегрирования. § 8 ФОРМУЛЫ ГРИНА И ИХ ОБОБЩЕНИЯ 107. Плоский случай. 108. Пространственный случай. |
Отображения. Криволинейные координаты. Преобразования. Формулы Грина
Отображения. Криволинейные координаты. Преобразования. Формулы Грина
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. ОТОБРАЖЕНИЯ. ЯКОБИАН 1. Определения. Аффинные отображения. 2. Графики. 3. Обращение. Гомеоморфизм. 4. Суперпозиция. § 2. КОЭФФИЦИЕНТ ИСКАЖЕНИЯ И ПРОИЗВОДНАЯ 6. Направление перемещения. 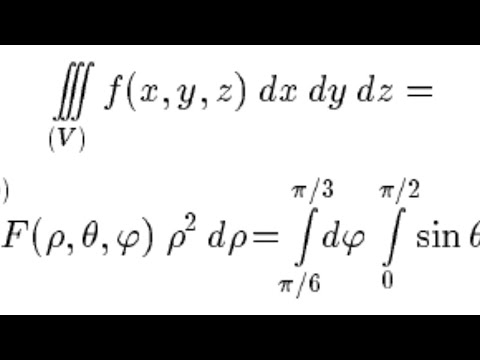 Обратное отображение.7. Суперпозиция. § 3. ОТОБРАЖЕНИЯ В ПЛОСКОМ СЛУЧАЕ 10. Гомеоморфизм. 11. Суперпозиция. § 4. АФФИННЫЕ ОТОБРАЖЕНИЯ 13. Равномерно распределенные точки. 14. Коэффициент искажения. 15. Направление перемещения. § 5. НЕКОТОРЫЕ ЧАСТНЫЕ АФФИННЫЕ ОТОБРАЖЕНИЯ. СВОЙСТВА ОПРЕДЕЛИТЕЛЯ 17. Сохранение площади. Движение. 18. Отображения гомотетии и подобия. 19. Свойства определителя. § 6. КОЭФФИЦИЕНТ ИСКАЖЕНИЯ (ОБЩИЙ СЛУЧАЙ) И ЯКОБИАН. РЕГУЛЯРНЫЕ ОТОБРАЖЕНИЯ 21. Обобщение. 22. Направление перемещения. 23. Регулярные отображения. § 7. СВОЙСТВА ЯКОБИАНА 25. Якобиан обратного отображения. 26. Суперпозиция. § 8. ВЫРОЖДЕНИЕ ОТОБРАЖЕНИЯ ЗАВИСИМОСТЬ ФУНКЦИИ 28. Зависимость функций. § 9. ОТОБРАЖЕНИЯ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ 30. Свойства якобиана. Зависимость функций. ГЛАВА II. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 32. Функциональная шкала § 2. ПЛОСКИЙ СЛУЧАЙ 33. Определения. Координатные линии.  34. Ортогональность системы. 35. Коэффициенты Ламе. 36. Элементы длины и площади. 37. Другой вывод. § 3. ВАЖНЕЙШИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ НА ПЛОСКОСТИ 38. Декартовы координаты. 39. Полярные координаты. 40. Обобщенные полярные координаты. § 4. ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ И ИХ ВЫРОЖДЕНИЯ 41. Общие эллиптические координаты. 42. Вырожденные эллиптические координаты. Униформизация. § 5. ДРУГИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ ОРТОГОНАЛЬНЫХ КООРДИНАТ НА ПЛОСКОСТИ 43. Параболические координаты. 44. Биполярные координаты. § 6. ПРОСТРАНСТВЕННЫЙ СЛУЧАЙ 45. Определения. Координатные поверхности и линии. 46. Ортогональность системы. 47. Коэффициенты Ламе. § 7. ЭЛЕМЕНТЫ ДЛИНЫ, ОБЪЕМА И ПЛОЩАДИ ПОВЕРХНОСТИ 50. Другой вывод. 51. Элемент площади поверхности. Направляющие косинусы нормали. 52. Элемент площади поверхности в криволинейных координатах в пространстве. § 8. ВАЖНЕЙШИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ В ПРОСТРАНСТВЕ 54.  Цилиндрические координаты.55. Сферические координаты. 56. Телесный угол. 57. Обобщенные сферические координаты. § 9. ЭЛЛИПСОИДАЛЬНЫЕ КООРДИНАТЫ И ИХ ВЫРОЖДЕНИЯ 59. Вырожденные эллипсоидальные координаты. Униформизация. 60. Сферические координаты. 61. Вырожденные эллипсоидальные «вытянутые» координаты. 62. Вырожденные эллипсоидальные «сплюснутые» координаты. $ 10. ДРУГИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ ОРТОГОНАЛЬНЫХ КООРДИНАТ В ПРОСТРАНСТВЕ 64. Параболоидальные координаты. 65. Тороидальные координаты. 66. Биполярные координаты. 67. Цилиндрические координаты. ГЛАВА III. ПРЕОБРАЗОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ВЫРАЖЕНИЙ 69. Замена функции. 70. Замена независимой переменной и функции. § 2. СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 71. Замена независимых переменных. 72. Замена функции. 73. Замена независимых переменных и функции. § 3. ПРЕОБРАЗОВАНИЯ «ДИФФЕРЕНЦИАЛЬНЫХ ПАРАМЕТРОВ» И «УСЛОВИЙ РЕГУЛЯРНОСТИ» 75. Параметр второго порядка (лапласиан).  76. Условия регулярности. § 4. СЛУЧАЙ ТРЕХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ. ПРЕОБРАЗОВАНИЯ «ДИФФЕРЕНЦИАЛЬНЫХ ПАРАМЕТРОВ» 78. Преобразования «дифференциальных параметров». 79. Выражения лапласиана в известных криволинейных координатах. ГЛАВА IV. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ § 1. ИНТЕГРАЛ ПО МЕРЕ ОБЛАСТИ 81. Основные свойства. 82. Вычисление интегралов. 83. Несобственные интегралы. § 2. ЗАМЕНА ПЕРЕМЕННЫХ В ИНТЕГРАЛЕ ПО МЕРЕ 85. Преобразования в декартовых координатах. 86. Преобразования в криволинейных координатах. § 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ. ПРИМЕРЫ 88. Двойной интеграл. 89. Тройной интеграл. § 4. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО КООРДИНАТЕ 91. Определение и свойства интеграла. 92. Способы вычисления. 93, Интеграл как функционал. Дополнительные замечания. § 5. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ПО КООРДИНАТАМ 95. Определение и свойства интеграла. 96. Способы вычисления. 97. Дополнительные замечания.  § 6. ОСНОВНАЯ ФОРМУЛА ГРИНА И СЛЕДСТВИЯ ИЗ НЕЕ 99. Независимость интеграла от контура интегрирования. 100. Условие полного дифференциала. Формула Ньютона – Лейбница. 101. Применения. Задача термодинамики. § 7. ФОРМУЛЫ СТОКСА И ОСТРОГРАДСКОГО И СЛЕДСТВИЯ ИЗ НИХ 103. Независимость интеграла от контура интегрирования. Условие полного дифференциала. Формула Ньютона — Лейбница. 104. Формула Остроградского. 105. Независимость интеграла от поверхности интегрирования. § 8 ФОРМУЛЫ ГРИНА И ИХ ОБОБЩЕНИЯ 107. Плоский случай. 108. Пространственный случай. |
Содержание книги в основном относится к классическому анализу, но всему изложению придается, по возможности, характер современных геометрических представлений.
многомерное исчисление — разница между градиентом и якобианом
спросил
Изменено 1 год, 3 месяца назад
Просмотрено 76 тысяч раз
$\begingroup$
Кто-нибудь может объяснить простыми словами (а может и на примере) в чем разница между градиентом и якобианом?
Градиент — это вектор с частными производными, верно?
- многомерное исчисление
- производные
- векторные поля
- якобиан
- скалярные поля
$\endgroup$
2
$\begingroup$
Это две частные формы матричного представления производной дифференцируемой функции $f,$, используемые в двух случаях: 9n$, $$\mathrm{Jac}_x(f)=\left.
m.$ 92\end{bmatrix}.$
$\endgroup$
10
$\begingroup$
Градиент — это вектор, образованный частными производными скалярной функции.
Матрица Якоби — это матрица, образованная частными производными векторной функции. Его векторы являются градиентами соответствующих компонент функции.
Например, с пропуском некоторых аргументов,
$$\nabla f(x,y)=\begin{pmatrix}f’_x\\f’_y\end{pmatrix}$$
$$J \begin{pmatrix}f(x,y), g(x,y)\end{pmatrix}=\begin{pmatrix}f’_x&&g’_x\\f’_y&&g’_y\end{pmatrix}=\begin{pmatrix}\nabla f;\nabla g\end{ pmatrix}.$$
Если хотите, якобиан — это обобщение градиента на векторные функции.
Дополнение:
Первая производная скалярной многомерной функции или градиента является вектором,
$$\nabla f(x,y)=\begin{pmatrix}f’_x\\f’ _y\end{pmatrix}.
n\to\mathbb{R}$, где $\mathbf{x}=
$$J_\mathbf{f} = \frac{\partial (f_1,\ldots,f_m)}{\partial(x_1,\ldots,x_n)} = \left[ \begin{матрица} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{матрица} \right]$$
Обратите внимание, что при $m=1$ якобиан совпадает с градиентом, потому что он является обобщением градиента. 9n$, что дает квадратную матрицу $n\times n$ для якобиана. Например,
$$\iiint_R f(x,y,z) \,dx\,dy\,dz = \iiint_S f(x(u,v,w),y(u,v,w),z( u,v,w))\left|\frac{\partial (x,y,z)}{\partial(u,v,w)}\right|\,du\,dv\,dw$ $
где якобиан $J_\mathbf{g}$ берется от функции
$$\mathbf{g}(u,v,w)=x(u,v,w)\hat{\imath}+y( u,v,w)\hat{\jmath}+z(u,v,w)\hat{k}$$
и площади $R$ и $S$ соответствуют друг другу.
$\endgroup$ 9n$ то, что обычная производная $\frac{d}{dx}$ представляет собой функцию типа $\mathbb{R} \rightarrow \mathbb{R}$, в отличие от частных производных и производных по направлениям и других подобных понятий, подобных производным. . Это «прямые» честные производные от — то, что все тексты вычислений, которые я видел, просто незаметно опускают, несмотря на то, что это невероятно важно для развития интуитивного понимания этих концепций!
Производная обычной функции в какой-то момент дает вам интуитивно следующие вещи:
- наклон линии, который аппроксимируется графиком функции при очень большом приближении к рассматриваемой точке — это герметичный интуитивный смысл касательной линии, с которой практически невозможно ошибиться (и в факт может быть непосредственно переведен в строгое определение касательной линии, для которой факт, что производная является наклоном, может быть доказан как теорема !),
- линейное отображение (т.
е. $L(x) = ax$, а не $L(x) = ax + b$, последнее является0051 аффинная карта ), что функция «выглядит» вблизи точки после учета возможного сдвига координат (это «аффинный» бит), как указано ее характеризующим числом $a$, которое совпадает с наклоном выше .
е. $L(x) = ax$, а не $L(x) = ax + b$, последнее является0051 аффинная карта ), что функция «выглядит» вблизи точки после учета возможного сдвига координат (это «аффинный» бит), как указано ее характеризующим числом $a$, которое совпадает с наклоном выше . Когда вы переходите к функции с действительным знаком $n$ переменных, производная становится чем-то другим, чем исходная карта. (*) Это можно увидеть, заметив, что если, скажем, мы рассматриваем функцию с действительным знаком двух переменных, прямым обобщением 1) выше является » наклон касательной плоскости » к поверхности, образованной функцией при отображении в виде графика поверхности в 3D, но плоскость не просто имеет крутизну, она также имеет направление, в котором она наклонена вверх или в котором она «точки» (вдоль горизонтальной плоскости) с подъемом вверх. Таким образом, чтобы задать его наклон, нам нужны и величина, и направление, то есть вектор, поэтому неудивительно, что производная нашей функции двух переменных, $\mathrm{grad}[f]$, является именно таким вектором.
Соответствующая линейная карта является линейным функционалом (линейная карта, которая выводит число), и она действует на входной вектор, действуя через скалярное произведение , Линейная карта эквивалентна 9T$, где маленькое $T$ специально выбрано так, чтобы оно совпадало с линейно-алгебраическим транспонированием, так как на самом деле равно .
Когда вы получаете функцию нескольких переменных от до нескольких переменных, теперь вы говорите об общей линейной карте между пространствами, и производная должна быть описана матрицей в каждой точке. Эта матрица является просто матрицей Якоби. Это точный эквивалент числа $a$, указанного выше, или наклона $m$ касательной, только теперь это «наклон» какой-то сверхпространственной касательной вещи к другой такой же гиперпространственной поверхностной вещи: «вещи». мы бы правильнее назвать, соответственно, 9{n+m}$) — понятия, которые мы различаем, потому что есть способ описать их в их собственных терминах без фактической необходимости ссылаться на них как на встроенные в какое-либо гиперпространственное пространство.
(*) На самом деле, технически так и обычная производная, по крайней мере, согласно второй вышеприведенной интерпретации. Линейная карта не является числом, и на самом деле, если мы хотим получить реальное придирчивое (в математике: прекратить идентификацию по изоморфизмам ), «первое» понятие производной для согласованности является 1-вектором, а не скаляром . 9{i}}{\partial\mathbf{z}_{2}}\end{bmatrix}$
Причина этого в том, что матрица Якоби применяется для решения интегралов подстановкой, где необходим определитель матрицы Якоби . Он также используется для преобразования частных производных в частные производные другой системы координат. Другим приложением является оценка метрического тензора, как упоминалось ранее.
PS: я надеюсь, что этот ответ не будет удален, потому что я разработал один лайнер, который у меня был изначально, но, вероятно, был не очень убедительным.
$\endgroup$
3
реальный анализ — Как мне доказать, что матрица Якоби является уникальным линейным преобразованием для функции многих переменных, которая является полностью дифференцируемой
Недавно я возвращался к основам и понял, что меня никогда не учили определению (сумма ) дифференцируемость для функций многих переменных.
Вместо этого мне просто вручили заявление о том, что такое полная производная, и мы убежали оттуда.
Моя цель — связать более абстрактное определение дифференцируемости с общим утверждением о полной производной, которое мы обычно встречаем на вводных курсах по многомерному исчислению.
Для начала нам нужно поработать с определением дифференцируемости.
Все сосредоточено вокруг полной производной, которая представляет собой линейное преобразование.
Учитывая это определение дифференцируемости, я был рад увидеть, как довольно хорошо получается цепное правило с несколькими переменными (через доказательство, подобное этому). До этого мне не давали формального доказательства версии с несколькими переменными, но я использовал ее всю свою жизнь.
Я также смог увидеть уникальность этого линейного преобразования.
Для меня последняя часть головоломки, которую я еще не совсем проверил, заключается в том, что якобиан обязательно является этим линейным преобразованием (в стандартных координатах), если такое линейное преобразование существует (т.
е. если функция полностью дифференцируема).
На самом деле здесь должны были начаться курсы. Они предоставили бы это как определение полной производной, вместо того, чтобы начинать с полной производной в том виде, в каком она определена, и доказывать, что она должна быть равна якобиану, если он существует. Даже эта статья в Википедии берет это за отправную точку и даже использует такие слова, как «наилучшее линейное приближение», которое на самом деле не характеризует дифференцируемость*.
*На самом деле ничего не могу сказать о характеристике. Что я знаю из собственного опыта, так это то, что слова «наилучший» и «приближенный» могут быть очень запутанными без строгих определений. Теперь я лучше понимаю эту формулировку.
Итак, как мне доказать, что если функция вполне дифференцируема, то линейное преобразование должно быть ее якобианом?
Вот моя попытка, но мне бы хотелось получить обратную связь:
- Чтобы доказать это, я думал применить аналогичную логику к этому ответу, который относится к случаю с одной переменной, но раскрывает отличную стратегию, которую мы можем использовать
- Чтобы упростить доказательство, давайте предположим, что функция f имеет однозначные выходы, потому что в противном случае мы можем просто применить логику по компонентам
- Точно так же нам действительно нужно потрудиться, чтобы доказать это только для двух переменных
- Теперь первое, что я бы сделал, это свел задачу определения уникального линейного преобразования к одной координате за раз
- Изменяя только одну переменную за раз, мы можем написать уравнения, которые позволят нам использовать инструменты одномерного исчисления. Мы получили бы уравнения, которые являются определением частных производных
- Это, естественно, вынуждает линейную карту состоять из частных производных от f, что, в свою очередь, заставляет карту быть равной якобиану
- Никакое другое преобразование не может удовлетворить этим одномерным уравнениям, поэтому оно уникально (но мы также уже знали, что отображение должно быть уникальным)
- Тогда, пожалуй, моя работа сделана! Если существует линейное отображение, удовлетворяющее определению полной дифференцируемости, то оно должно быть якобианом из-за одномерных случаев, которые также должны удовлетворяться
Мы получили бы уравнения, которые являются определением частных производныхОднако это больше похоже на несчастный случай, чем на доказательство. Я что-то пропустил?
Что меня пугает, так это то, что у нас уже нет информации (все координаты полной производной указаны), но мы проверяли только одно направление за раз! Если бы мы сделали произвольное изменение в произвольном направлении, как бы мы тогда ограничили ошибки? Проще говоря, мы не можем, просто зная только якобиан.
Я полагаю, что это задача, выходящая за рамки частных производных, и все, что мы здесь установили, это то, что если функция действительно оказывается дифференцируемой (путем другого анализа), то она должна иметь полную производную, равную якобиану.
Какими бы ни были надлежащие доказательства, у меня есть несколько заключительных мыслей. Я чувствую, что часто используемая фраза «наилучшее линейное приближение» для якобиана может довольно легко сбить студентов с толку.
Насколько мне известно, якобиан — это единственное линейное преобразование, которое может удовлетворять ограничивающим свойствам члена ошибки, требуемым определением дифференцируемости. В этом смысле он лучший.
Таким образом, значение «наилучшего» зависит от определения производной, которое было очень хорошим определением, учитывая все последующие замечательные результаты (даже до того, как мы свяжем полную производную с якобианом), такие как цепное правило. Другой подход к анализу функций может привести к другим выводам, но теперь я понимаю, насколько мощным и особенным является подход дифференцируемости.