Как в маткаде упростить выражение: Mathcad упрощение выражений

Содержание

MathCAD — это просто! Часть 15. Знакомство с символьными вычислениями

Мы с вами уже неоднократно употребляли такой термин, как символьный процессор MathCAD. Даже говорили о том, что некоторые вещи (скажем, те же определенные интегралы, которые мы с вами совсем недавно весьма и весьма подробно обсуждали) можно вычислять в MathCAD двумя принципиально отличающимися друг от друга путями: символьным и численным. Однако подробного и обстоятельного разговора о символьных вычислениях в MathCAD у нас еще до сих пор не было. Тем не менее, поскольку символьные вычисления являются очень важным аспектом использования на практике этой математической среды, то и поговорить о них мы, как бы то ни было, в любом случае рано или поздно должны. И лучше это не откладывать на потом, а заняться таким полезным делом, как символьные вычисления, прямо сейчас. Конечно, в одной статье, даже довольно большой, невозможно будет уместить рассказ не то что обо всех возможностях символьного процессора MathCAD’а, но даже хотя бы о самой существенной их части.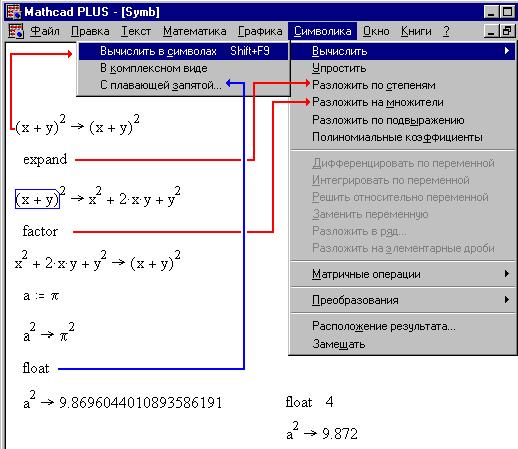

Именно поэтому эта статья и называется «Знакомство с символьными вычислениями».

Символьный процессор

Символьные вычисления выполняются встроенным в MathCAD символьным процессором, который уже упоминался неоднократно в предыдущих статьях. Стоит отметить, что символьный процессор — это та часть MathCAD’а, которая написана не самой компанией MathSoft, создавшей этот замечательный математический пакет, а фирмой Waterloo Maple Software. Об этом свидетельствует окно About, которое можно вызвать в меню Help. Waterloo Maple Software — компания, разрабатывающая другой известный математический пакет, который называется Maple. Однако это вовсе не означает, что возможности символьного вычисления в MathCAD полностью соответствуют его возможностям в Maple. Дело в том, что в MathCAD используется несколько урезанная версия символьного процессора Maple. Однако это не значит, что символьные вычисления в MathCAD реализованы хуже — вы убедитесь сами, что с помощью встроенного в MathCAD символьного процессора можно делать очень много всяческих полезных вещей.

Итак, давайте определимся: для какого рода вычислений используется символьный процессор? С этим, к счастью, все просто. Если вы хотите получить не число в результате преобразования какого-либо выражения либо решения уравнения, а аналитическую формулу, то это и называется символьными вычислениями. Именно таким родом вычислений и занимается символьный процессор. Стоит еще заметить, что, к сожалению, далеко не всегда символьный процессор способен выдавать результат именно в том виде, в каком его ожидаете увидеть вы. И даже более того: сам по себе результат в каком бы то ни было виде тоже далеко не всегда может быть найден. Дело здесь, в общем-то, не столько в каких-то внутренних дефектах или ограничениях символьного процессора MathCAD’а, сколько в том, что компьютерам, вообще говоря, не слишком свойственно креативное мышление, которое и является залогом успешного решения любой математической задачи. Очень часто компьютер может элементарно «не догадываться» о тех или иных приемах, которые представляются элементарными знакомому с математикой человеку, и глупо на него за это обижаться.

Лучше заранее быть готовым к ограниченности символьного процессора и иметь в запасе бумажку с ручкой, чтобы самостоятельно преобразовать выражение к тому виду, который уже будет понятен символьному процессору, и с которым тот уже будет в состоянии разобраться. Символьные алгоритмы, в отличие от численных, принципиально довольно сложны, а потому мы не будем рассматривать подноготную символьного процессора, как это делали с численными методами расчета определенных интегралов.

Упрощение выражений

Упрощение аналитических выражений — это, пожалуй, одна из самых частых задач, с которыми сталкивается любой человек, работающий с формулами. Чем проще выражение, тем проще вычислять какие-либо конкретные значения тех или иных величин с его использованием, и тем проще анализировать его, что немаловажно, когда перед нами стоит задача анализа не просто абстрактной математической формулы, а некой физической, экономической или иной статистической закономерности, которая скрывается за ней.

Потому нет ничего удивительного в том, что упрощение выражений является одной из самых важных способностей символьного процессора, встроенного в математическую среду MathCAD. В общем-то, поскольку сам MathCAD часто и сам выдает результаты других видов символьных преобразований в несколько, мягко говоря, неудобном для нормального человеческого восприятия виде, то упрощение выражений может использоваться в проектах MathCAD особенно часто.

Для упрощения выражений используется оператор simplify. Его можно найти на панели Symbolic, которая отличается от других рассмотренных нами панелей главного окна MathCAD тем, что на ней используются не пиктограммы (так называемые «иконки»), а полные варианты написания операторов (за исключением нескольких операторов для работы с матрицами, о которых мы с вами уже говорили, когда разбирались с матричными вычислениями в среде MathCAD).

Использовать оператор упрощения выражений в MathCAD чрезвычайно просто. Достаточно записать выражение, которое вам нужно упростить, нажать на панели символьных вычислений кнопку, отвечающую за вставку оператора символьного упрощения выражения, и, в общем-то, на этом ваша работа по упрощению выражения, если вам повезет, закончится — дальше за вас все будет делать MathCAD.

Если же не повезет, то, как я уже говорил выше, запасной вариант — это ручка, бумага и справочник с формулами.

Разложение выражений на множители

Иногда, впрочем, может быть полезен (и мало того, что полезен, но и вовсе необходим для успешного решения задачи) процесс, целиком и полностью обратный упрощению выражений. Процесс этот, конечно, называется не усложнением выражений, а их разложением. Разложение может быть разным, потому что термин этот в математике, надо сказать, весьма и весьма емкий. Можно раскладывать выражение на слагаемые (например, дробь — на сумму простых дробей), можно раскладывать функцию в ряд Фурье или Тейлора, а можно раскладывать многочлен на произведения… В общем, раскладывать нам придется много всего разного. Постараемся поговорить обо всех аспектах этого вида символьных преобразований. Для начала рассмотрим такой процесс, при котором выражение раскладывается на множители — он носит название факторизации и используется самым что ни на есть широким образом в современной криптографии.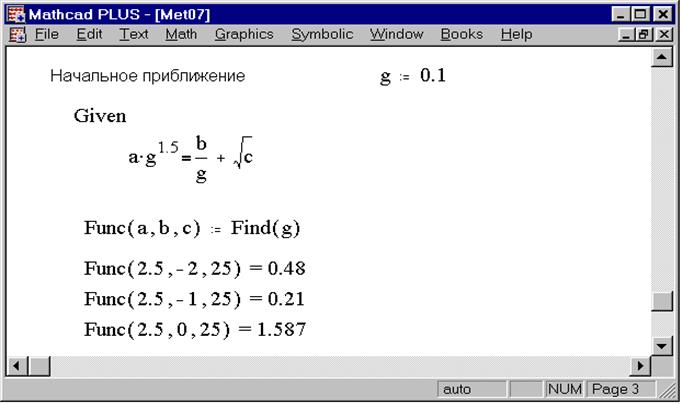 Для факторизации используется оператор factor, найти который, как вы, наверное, уже догадались, можно на панели Symbolic (там же, где и все остальные операторы символьных вычислений). В случае большинства выражений пользоваться оператором factor ничуть не сложнее, чем оператором simplify. То есть достаточно записать выражение и сам оператор, после чего MathCAD, если это вообще возможно, разложит записанное выражение на множители.

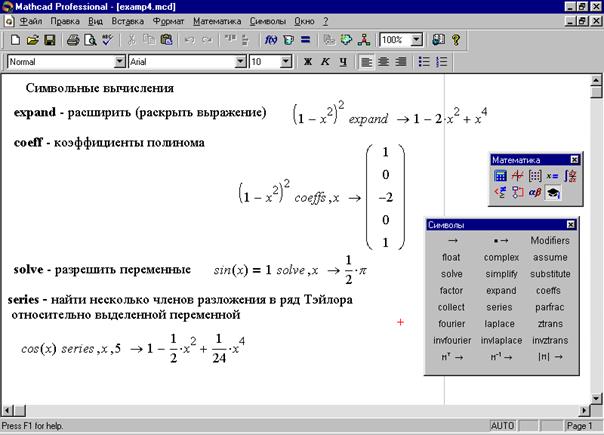Однако есть случаи, когда такой простой вид оператора factor может оказаться недостаточным. Наверное, когда вы вводили этот оператор в рабочую область MathCAD, то уже успели обратить внимание на то, что по умолчанию программа предлагает ввести после него еще один дополнительный параметр. Что это за параметр, и что именно он делает? Предложу вам сначала взглянуть на иллюстрацию, на которой оператор факторизации используется именно с этим параметром и без него, и сравнить, чем отличаются результаты. После я отдельно прокомментирую его использование, и вы сможете сравнить ваши выводы с правильным ответом.

Думаю, он вас удивит.В справочной системе MathCAD говорится, что параметр (или, говоря более точно терминами самого MathCAD’а, второй маркер ввода) требуется для разложения корней. Т.е. если мы хотим сказать MathCAD, чтобы он раскладывал все до определенной дробной степени переменных, то должны, если верить справке, указывать наши пожелания именно в этом параметре. К сожалению, в данном случае справочная система MathCAD’а несколько подмачивает свою репутацию, поскольку вводит нас в заблуждение. Дело в том, что, как вы можете увидеть из иллюстрации, при попытке указать подобные вещи алгоритму факторизации тот вообще перестает работать. Если вы попробуете перебирать различные варианты параметров или обратитесь к примерам MathCAD’а (т.н. Quicksheets), то увидите, что все, что приведено в Quicksheets, прекрасно работает и без использования второго параметра. Поэтому, если вы подумали, что он нужен для того, чтобы факторизация перестала работать, то поздравляю, ваш ответ верен — на сегодняшний день все обстоит именно так.

Поэтому, работая с оператором factor, сразу удаляйте запятую и пустое место для параметра после нее.

Ну, а если вдруг найдете какой-нибудь экзотический случай, в котором эта запятая полезна, то, пожалуйста, не поленитесь написать мне о нем. Вполне возможно, что подобная странность оператора factor связана с происхождением MathCAD’овского символьного процессора. Дополнительный параметр мог использоваться в Maple, а разработчики MathCAD’а просто механически перенесли его описание в документацию, забыв проверить, каким образом он работает в их программе. Однако, конечно, это все домыслы, и как все было на самом деле, знают только работники MathSoft. Что ж, успели мы с вами рассмотреть не так уж много, однако упрощение выражений и их факторизация играют весьма и весьма существенную роль в символьных вычислениях, а потому лучше разобраться с ними как можно полнее и внимательнее. Конечно, точно так же, как и формульные выражения, вы можете преобразовывать и числа (факторизуются, конечно, только целые числа, не являющиеся простыми).

И, несмотря на некоторые странности в своей работе, символьный процессор — действительно очень полезная часть MathCAD.

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 28 за 2008 год в рубрике soft

Символьные вычисления

Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика

”. Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=].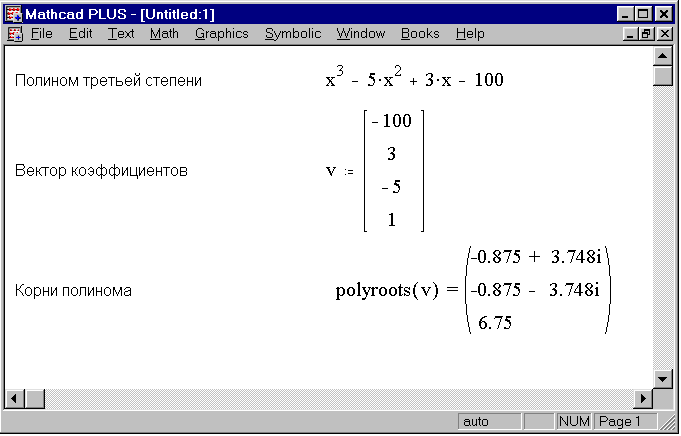 Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:

Пример использования блока given…find для решения системы уравнений:

Основные принципы работы в MathCad

1. Выполнила: студентка группы 05-ПРО Кормилицына Т.И.

Основные принципы
работы в MathCad
Выполнила:
студентка группы 05-ПРО
Кормилицына Т.И.

2. Раздел 1. Теоретические основы

3. 1.1.Начальные сведения

Среди
многообразия
существующего
сегодня
программного обеспечения для персональных ЭВМ
можно выделить класс интегрированных программных
пакетов для автоматизации математических расчетов.
К ним относятся PC-MATLAB, Derive, Mathсad,
Mathematics, MappleV и др.

Отметим преимущества
MathCad:
При наличии широких возможностей проста в
освоении и использовании;
С MathCad может работать пользователь с
любым уровнем математической подготовки;
В MathCad реализован широчайший класс
математических
методов,
что
позволяет
повысить, эффективность выполняемой работы.

5. Структура рабочего документа

Рабочий документ MathCad
представляет собой совокупность
областей. Область может
располагаться в любом месте
документа.
Для создания новой области
следует просто выполнить щелчок
мышью на свободном месте
документа.
Чтобы сделать видимыми
границы областей, следует выбрать
в меню Вид подменю Границы, в
результате чего фоновым цветом
будут отображены только
имеющиеся области

6. Средства редактирования MathCad

Визир
предназначен
для
указания позиции в рабочем
документе, в которой должна
появиться очередная область.

2 или можно после ввода 5
нажать на арифметической палитре кнопку
, а затем
ввести 2 в поле ввода.
Запомните правило: то, что заключено в
выделяющую рамку, становится операндом
следующего вводимого оператора.

9. Способы редактирования выделяющей рамки

Увеличивает выделяющую рамку. Превращает маркер
ввода в выделяющую рамку.
Уменьшает выделяющую рамку. Если выделяющая
рамка содержит имя или число, превращает ее в маркер
ввода.
Перемещает маркер ввода вправо (влево). Если
выделяющая рамка окружает операнд некоторого
выражения, переводит ее на другой операнд этого
выражения.

10. Редактирование выражений

Изменение имени или числа. Здесь редактор выражений ведет себя
аналогично текстовому редактору. Для выполнения этой операции следует
предварительно щелкнуть мышью на требуемом объекте, это поместит на
него маркер ввода.
Замена и удаление оператора. Наиболее важный шаг в этом случае —
расположить выделяющую рамку так, чтобы нужный оператор оказался в
выделенном выражении наивысшим.

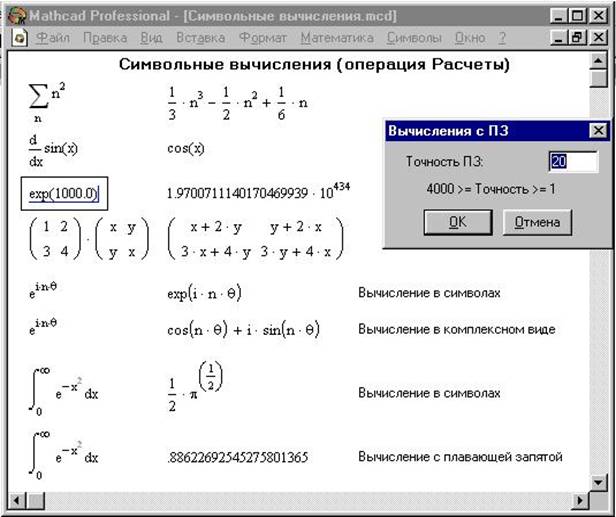Так, чтобы заменить в числителе дроби
знак минус на знак плюс, следует полностью заключить
числитель в выделяющую рамку, после чего нажать [Del] это удалит наивысший оператор (в данном случае вычитание), заменив его
пустым полем в рамке (заметим, что повторное нажатие [Del] удалило бы
числитель целиком),
и наконец нажать [+], в результате чего на месте указанного пустого поля
появится знак плюс.

11. Вставка оператора

Вставка оператора между двумя
соседними символами
выполняется
путем установки между ними маркера
ввода
и нажатия соответствующей
клавиши или кнопки на палитре
символов.
Для вставки операторов, требующих
только одного операнда необходимо
выделить все выражение, которое должно
быть в данном случае операндом, и
нажать соответствующую комбинацию
клавиш или кнопку на палитре символов.
Подобным образом выполняется вставка
скобок
–
выделив
выражение,
заключаемое в скобки, следует нажать .

12. Вычисление выражений

Для вычисления выражения
следует после его ввода нажать
[=] или выбрать, кнопку = на
арифметической палитре. В
результате значение выражения
вычисляется и отображается на
рабочем листе. Если выражение
использует переменные или
функции, то они должны быть
определены в рабочем
документе заранее.

13. 1.3. Работа с текстовой областью

Текстовые области в MathCad являются областями изменяемого размера,
при этом информация, содержащаяся в них, при выполнении вычислений
игнорируется. Как правило, текстовые области используются для
отображения комментариев к математическим выражениям и графикам.
Для создания текстовой области
необходимо
щелчком
мыши
поместить визир в позицию, с
которой предполагается начать текст,
и выбрать команду Текстовая
область меню Вставка. В результате
появляется текстовая рамка с
находящимся
внутри
маркером
ввода.

Теперь можно начинать
вводить требуемый текст.
Для редактирования вводимого текста в MathCad используются те же
принципы, что и в большинстве текстовых редакторов.

15. 1.4.Управление компоновкой рабочего документа

Выделение областей
Для этого необходимо щелкнуть на область мышью и,
удерживая кнопку нажатой, переместить мышь так, чтобы
заключить всю область в выделяющий пунктирный
прямоугольник. Можно выделить сразу несколько областей,
если все их окружить пунктирным прямоугольником.
Выделенная область легко «перетаскивается» в нужное Вам
место.

17. Копирование, вырезание, вставка и удаление областей

Эти операции
применяются к выделенным
областям, используют буфер
обмена Windows и
вызываются при помощи
меню Правка с
использованием команд
Копировать, Удалить,
Вырезать, Вставить или
щелчком правой кнопки
мыши на рабочей области и
выбираются из
выплывающего меню.

18. Выравнивание областей

Эта операция также применяется к выделенным областям и
вызывается выбором подменю Выровнять области меню
Формат или кнопками ( выровнять по верхней границе,
выровнять по нижней границе) на Панели инструментов.
Возможно выравнивание по нижней (вертикальное) и верхней
(горизонтальное) границам.
Вызов подменю
Выровнять область
Вертикальное
выравнивание
Горизонтальное
выравнивание

19. 1.5.Переменные и функции

20. Определение переменных

Следует выполнить следующие действия:
ввести
имя переменной, подлежащей
определению;
нажать
[:] или выбрать кнопку := на
арифметической палитре — результатом
будет
появление
после
имени
переменной знака определения := ;
ввести выражение, определяющее
переменную.

21. Определение функций

Определение функций
аналогично определению
переменных. Основное различие
состоит в том, что имя функции
включает список формальных
аргументов-параметров,
заключенный в скобки.

Заметим,
что эти аргументы должны быть
именами, а не более сложными
выражениями.

22. Имена переменных и функций

Имена переменных и функций могут содержать как
латинские, так и греческие буквы. Для ввода греческой буквы
следует ввести ее латинский эквивалент с учетом регистра или
воспользоваться палитрой Греческий алфавит.
Одна и та же переменная или функция может быть
определена неоднократно.
Все символы в имени должны быть введены с использованием одного и
того же шрифта с одними и теми же параметрами.
Если в определении функции используется имя переменной, которой нет
в списке аргументов, то такая переменная должна быть определена выше
определения функции.
Переменные и функции могут быть определены
глобально. Кнопка
вместо кнопки
на Панели
вычисления.

23. Встроенные переменные

24. Встроенные функции

Список всех встроенных функций с кратким
описанием каждой функции вызывается
командой Функция меню Вставка.

Двойной
щелчок мышью на выбранной функции или
нажатие кнопки «Insert» вставляет ее в
рабочий лист.

25. Определение матриц

Для определения матриц вводится
имя переменной, и нажимается
кнопка
на панели Вычисления,
затем выбирается пункт Матрицы из
меню Вставка в результате чего
открывается диалоговое окно, в
котором следует ввести необходимое
количество строк и столбцов, а затем
нажать кнопку OK. Вставить матрицу
также можно используя кнопку
на
панели Матрицы.

26. Изменение размеров матриц

Размеры можно изменять,
вставляя или удаляя строки и
столбцы. Для этого также
используется диалоговое окно
пункта Матрицы меню
Вставка, в котором задается
число строк и столбцов,
подлежащих вставке либо
удалению, а затем нажимается
одна из кнопок: Вставить или
Удалить.
Удаление
строки
Вставка
строки

27. Правила изменения размеров матриц

Если вставляются строки, MathCad создает строки пустых
полей ниже выделенного элемента; если вставляются
столбцы, MathCad создает столбцы пустых полей справа от
выделенного элемента.

Чтобы вставить строки выше верхней строки или столбцы
слева от первого столбца, следует предварительно выделить
не элемент, а всю матрицу, щелкнув внутри ее и несколько раз
нажав .
Удаление производится, начиная со строки или столбца,
содержащих выделенный элемент. Строки удаляются вниз от
этого элемента, а столбцы — направо.
Если задается количество строк (столбцов), равное нулю, то
вставлены или удалены будут только столбцы (строки).

28. Индексирование элементов матриц

Нижняя индексация. Используется для изменения
значений существующих элементов массива, для
определения новых элементов и новых массивов.
Для ввода нижнего индекса следует после ввода
имени массива нажать кнопку на панели Матрицы
,вести в появившееся поле число или пару чисел.
Верхняя индексация. Осуществляется обращение
ко всему столбцу матрицы. Для ввода верхнего
индекса следует нажать кнопку
на панели
Матрицы.
Нижняя индексация
Верхняя индексация

29.

Ограничения размеров матриц Команда Матрицы меню Вставка позволяет
оперировать с массивами, имеющими не более
100 элементов. Для создания больших массивов
можно, например, использовать функцию augment
(Вставка>Функция) , которая соединяет вместе
два массива, используемые в качестве аргументов.

30. Дискретные аргументы

Дискретный аргумент
может принимать ряд
значений, отделяемых
одинаковыми шагами.
Дискретные аргументы
позволяют организовывать
циклы повторяющихся
вычислений или
многократные вычисления,
при которых значения на
каждом шаге зависят от
значения на предыдущем
шаге.
Вид дискретных аргументов

31. Определение дискретного аргумента

Для определения дискретного аргумента следует
после ввода его имени и знака присваивания – кнопка
на панели Вычисления , задать диапазон значений:
Ввести
первое значение, принимаемое аргументом;
Через
запятую ввести второе значение в диапазоне.

Разница между первым и вторым значением является
размером шага. Этот этап может быть опущен — в
этом случае размер шага устанавливается равным 1 в
подходящем направлении;
Нажать
кнопку на панели Матрицы — в результате
отобразится знак диапазона». .» , после чего ввести
последнее значение в диапазоне.

32. Раздел 2. Применение MathCad для решения практических задач

33. 2.1. Построение графиков

34. Графики в прямоугольных координатах

Построению графика должно предшествовать определение дискретного
аргумента, принимающего значения в интервале изменения аргумента
функций.
Для создания такого графика нужно использовать
команду График>X-Y Зависимость меню Вставка или
нажать кнопку
на панели Графики. По этой команде
в документе появляется графическая область с
несколькими полями ввода.
Следующим шагом является указание тех данных,
которые должны быть представленными на графике.

В
среднем поле ввода на оси абсцисс вводится имя этой
переменной, а в среднем поле ввода на оси ординат имена функций . После нажатия Enter появляются
требуемые графики.

35. Графики в полярных координатах

Для создания графика в полярных координатах
следует
выбрать
пункт
Графики>Полярные
координаты меню Вставка или нажать кнопку
на панели Графики.
В результате появляется полярная
графическая область с полями ввода для
углового аргумента (внизу) и радиуса как
функции углового аргумента (слева). Два
поля справа предназначены для ручной
установки граничных значений радиуса.

36. Форматирование графиков

Для изменения размеров графической
области необходимо заключить ее в
выделяющий пунктирный прямоугольник а
затем, подведя мышь к нижней или к
правой стороне этого прямоугольника, так
чтобы
указатель
принял
форму
двунаправленной
стрелки,
выполнить
изменение размеров.

Если нажать
команду
Формат>График и далее
выбрать
нужный
вам
график, то появиться окно
для изменения параметров
отображения графика.

37. 2.2.Решение уравнений и систем уравнений

38. Функция ROOT

Функция находит корень уравнения f(x)=0. Перед использованием
функции root необходимо построить график левой части уравнения –
функция, затем по графику найти приближенные значения переменной x,
которые MathCad использует как начальное приближение при поиске
корня.

39. Функция POLYROOTS

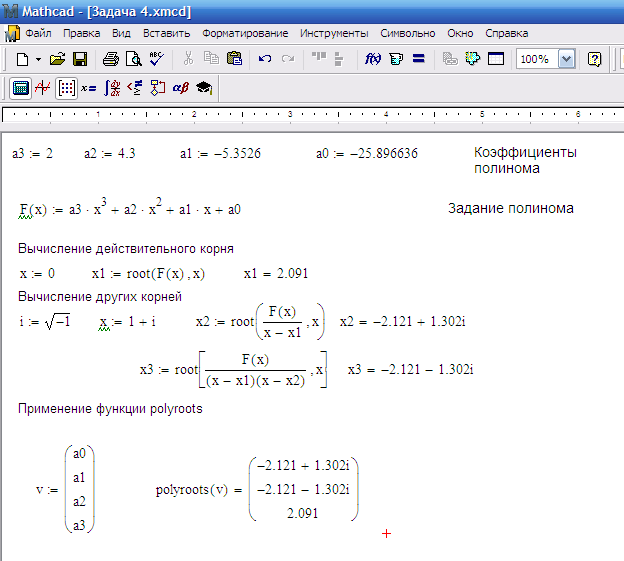
Для нахождения корней полинома степени n можно
использовать функцию polyroots(v). Коэффициенты полинома
находятся в векторе v. Если записать полином в виде
то коэффициенты должны войти в вектор v порядке a0,a1,…,an.
В отличие от функции root, функция polyroots не требует
начального приближения и возвращает сразу все корни, как
вещественные, так и комплексные.
Пример: найти корни полинома x3-10x+2
Решение при помощи функции polyroots :

40.

Решение систем уравнений Для решения системы уравнений необходимо выполнить
следующую последовательность шагов.
Задать начальные приближения для всех неизвестных,
входящих в систему.
Ввести ключевое слово Given. Оно указывает, что далее
следует система уравнений.
Ниже ключевого слова Given ввести уравнения. Знак
равенства между левыми и правыми частями вводится
нажатием кнопки на панели Булево.
Ввести любое выражение, содержащее функцию Find.
Число аргументов этой функции должно совпадать с числом
неизвестных, а имена аргументов должны соответствовать
именам неизвестных.

41. Функция MINERR

Функцию MinErr можно использовать для поиска локального,
экстремума функции на заданном отрезке, если на нем
установлены границы области значений функции. Найти
экстремум функции Z на промежутке [-1;2]:

42. 2.3.Символьные вычисления

43. Символьные вычисления

Средства символьной математики, позволяют
проводить математические выкладки в аналитической
форме.

За символьные вычисления в
MathCad отвечает меню Символы
или панель Символы.
Примечание: далее в этом подразделе, если
не будет явно указываться, из какого меню
используется команда, будет подразумеваться
именно это меню или панель.

44. Замена переменных

Эта операция представляет собой замену в
выражении
каждого
вхождения
выделенной
переменной на содержимое буфера обмена.
Для выполнения ее следует скопировать
заменяющее выражение в буфер обмена, затем
выделить переменную, которую требуется заменить, и
нажать кнопку
.

45. Упрощение выражений

Кнопка
выполняет алгебраические и
тригонометрические упрощения выражения,
заключенного в выделяющую рамку:
сокращает общие множители, упрощает
степени и корни, использует
тригонометрические тождества.

46. Разложение по степеням

Кнопка
разлагает в выражении, заключенном
в выделяющую рамку, все степени и произведения
сумм.

Синусы, косинусы, тангенсы сложного аргумента
будут разложены, насколько это возможно, в
выражения, содержащие синусы и косинусы
одиночной переменной.

47. Разложение на множители

Кнопка
разлагает выражение в
выделяющей рамке на множители.
Если выражение представляет собой целое число,
оно будет разложено в произведение степеней
простых чисел. В остальных случаях MathCad будет
пытаться
преобразовывать
выражение
в
произведение.

48. Приведение подобных

Для того, чтобы в выражении
объединить члены, содержащие
одинаковые степени выбранного
подвыражения, следует заключить это
подвыражение в выделяющую рамку и
использовать кнопку
.

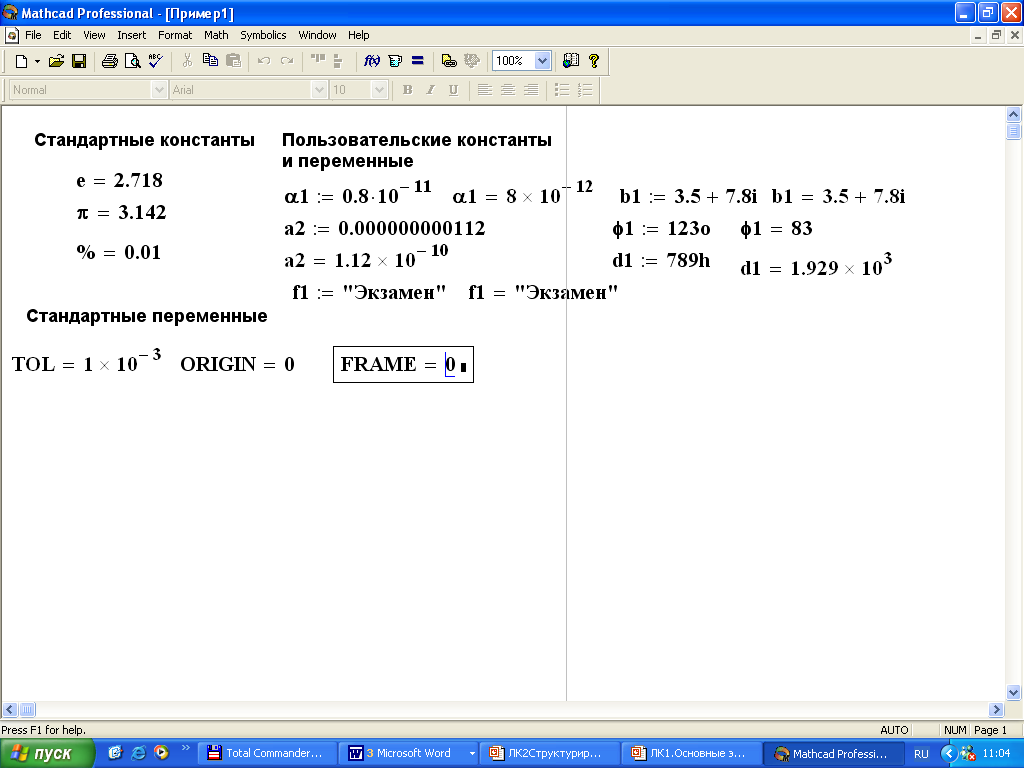
49. Разложение на элементарные дроби

При нажатии кнопки
будет произведена
попытка разложить выделенное выражение в сумму
дробей, знаменатели которых будут линейными или
квадратичными.
Эта команда может применяться только к тем
выражениям, в котором все константы являются
целыми или рациональными числами.

50. Нахождение пределов

Операторы
нахождения
пределов
в
MathСad вызываются с помощью кнопок
палитры Матанализ .
После
заполнения
полей
ввода
(перемещаться между ними можно с
помощью клавиши [Tab]) следует заключить
все выражение в выделяющую рамку и
нажать кнопку
.

51. Нахождение производных и первообразных

Для выполнения этих операций следует в
выражении, подлежащем дифференцированию или
интегрированию, заключить в выделяющую рамку
переменную, по которой необходимо выполнить эти
операции, и выбрать пункт
Переменные>Дифференциалы или
Переменные>Интеграция.

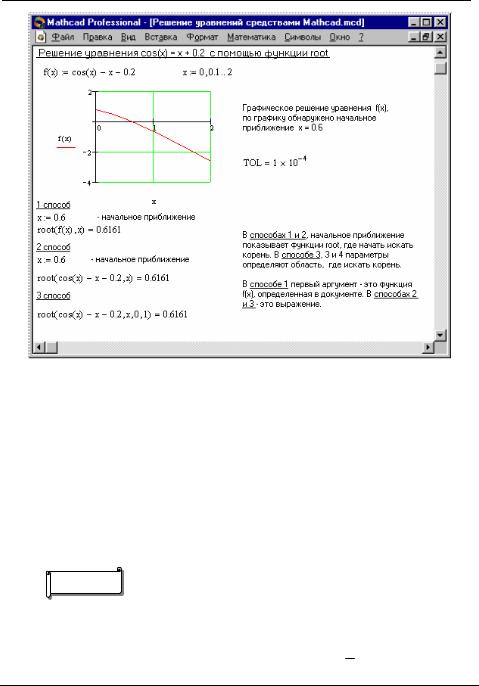
52. Разложение по формуле Тейлора

Команда
Вычисления>Разложить
на
составляющие используется для разложения
выражения по формуле Тейлора с остаточным
членом в форме Пеано по выделенной
переменной в окрестности ее нулевого
значения. При выборе этой команды вначале
запрашивается порядок остаточного члена.

Приемы работы с системой MathCad

Windows XP — для начинающих

20.08.2010/учебное пособие

Элементы рабочего стола. Общие приемы работы с окнами. Главное и контекстное меню. Создание и переименование папок. Удаление и восстановление информации. Копирование информации на съемные носители. Настройка Рабочего стола. Настройка панели задач.

Методика создания структуры базы данных на персональном компьютере

13.01.2010/лабораторная работа

Создание таблиц и просмотр содержимого базы данных. Редактирование данных и модификация структуры базы данных. Методы упорядочения записей (сортировка, индексирование). Выполнение вычислений в запросах. Приемы работы с формами, отчетами и макросами.

Технологии обслуживания файловой структуры в программе «Проводник»

13.09.2009/курсовая работа

Анализ программы «Проводник». Понятие операционной системы (ОС). Достоинства и недостатки файловых систем. Исследование методов запуска программы «Проводник», работа с файловой структурой в программе «Проводник» ОС Windows. Приемы работы с объектами.

Системы управления базами данных

16.12.2010/курс лекций

Иерархические, сетевые и реляционные модели данных. Различия между OLTP и OLAP системами. Обзор существующих систем управления базами данных. Основные приемы работы с MS Access. Система защиты базы данных, иерархия объектов. Язык программирования SQL.

Табличный процессор Excel. Формат ячеек

28.12.2010/практическая работа

Основные элементы электронных таблиц в MS Excel и приемы работы с ними. Типы переменных, способы форматирования ячеек. Создание, сохранение и переименование рабочей книги. Диапазон ячеек и их автоматический выбор. Числовой и денежный форматы ячеек.

Системы управления базами данных

16.12.2010/курс лекций

Табличный процессор Excel. Формат ячеек

28.12.2010/практическая работа

Изучение возможностей создания MDI-приложений (multiple document interface)

5.10.2010/лабораторная работа

Возможности создания MDI-приложений, их преимущества. Основные приемы работы с записью информации в файл, экспорт данных в приложения Microsoft Office с помощью использование технологии OLE, на примере MS Excel интегрированного пакета MS Office.

Сравнение упрощенного ГО при эструсе и диэструсе. Для …

Эффективной стратегией улучшения способности обнаружения QTL является выполнение межпородных валидационных исследований. Ожидается, что варианты сегрегации между породами будут иметь высокий дисбаланс по сцеплению (LD) с причинными мутациями, влияющими на экономически важные признаки. Целью этого исследования было проверить в популяции тропического композитного крупного рогатого скота (TC) ассоциации QTL, выявленные по признакам половой скороспелости в рамках полногеномного исследования ассоциаций метаанализа Неллора и Брахмана.Всего для анализа было доступно 2 816 TC, 8 001 Nellore и 2210 Brahman животных. Для этого области генома, значимо связанные с признаками полового созревания в метааналитическом исследовании, были валидированы для следующих признаков ранней половой жизни при ОК: возраст первого желтого тела (AGECL), первый послеродовой интервал анэструса (PPAI) и окружность мошонки в 18 месяцев. возраста (SC). Мы рассмотрели валидированные QTL, подкрепленные значимыми маркерами из метаанализа Неллора и Брахмана (значение P ≤ 10⁻⁴), которые также были значимы для признака TC, т.е.е. представляя значение P ≤ 10⁻³ для AGECL, PPAI или SC. Мы также считали валидированным QTL те регионы, где значимые маркеры в контрольной популяции находились на уровне ± 250 Кб от значимых маркеров в проверочной популяции. Используя этот критерий, 49 SNP были проверены для AGECL, 4 для PPAI и 14 для SC, из которых 5 были общими с AGECL, всего 62 подтвержденных SNP для этих признаков и 30 генов-кандидатов, окружающих их. Рассматривая только гены-кандидаты, наиболее близкие к верхнему SNP каждой хромосомы, для AGECL было идентифицировано 8 генов-кандидатов: COL8A1, PENK, ENSBTAG00000047425, BPNT1, ADAMTS17, CCHCR1, SUFU и ENSBTAG00000046374.Для PPAI в качестве кандидатов выступили 3 гена (PCBP3, KCNK10 и MRPS5), а для SC 8 были идентифицированы гены-кандидаты (SNORA70, TRAC, ASS1, BPNT1, LRRK1, PKHD1, PTPRM и ENSBTAG00000045690). Несколько представленных здесь регионов-кандидатов ранее были связаны с признаками полового созревания крупного рогатого скота. Большинство возникающих генов-кандидатов связаны с биологическими процессами, участвующими в репродуктивных процессах, таких как поддержание беременности, а некоторые, как известно, экспрессируются в репродуктивных тканях. Наши результаты свидетельствуют о том, что некоторые QTL, контролирующие раннее половое созревание, по-видимому, сегрегируют между породами крупного рогатого скота, адаптированными к тропическим условиям.

IJMS | Бесплатный полнотекстовый | MSX1 — потенциальный маркер для сохраняющей матку терапии карциномы эндометрия

4.1. Пациенты и коллекция тканей

Для этого исследования были использованы образцы эндометриоидных и светлоклеточных карцином эндометрия, а также эндометриоидных и светлоклеточных карцином яичников. Ретроспективно проанализировано 97 пациентов.

Образцы взяты из больничного архива отделения патологии Университета Людвига-Максимилиана. Операция проводилась с 1 января 1990 г. по 31 декабря 2001 г. в отделении гинекологии Мюнхенского университета Людвига-Максимилиана, Германия.Пациенты были распределены по стадиям и опухоли классифицированы в соответствии с критериями Международной федерации гинекологии и акушерства 1988 г. (FIGO) [38]. Все они были зафиксированы формалином и залиты парафином. Использовали ткани эндометриоидной карциномы эндометрия (n = 59), ткани светлоклеточной карциномы эндометрия (n = 6), ткани эндометриоидной карциномы яичников (n = 21) и ткани светлоклеточной карциномы яичников (n = 11).

Регистр опухолей Мюнхена предоставил данные о выживаемости пациентов. В таблицах 3 и 4 показаны характеристики пациентов.Информация о выживаемости включает дату подтвержденного гистологического диагноза после первичной операции до даты рецидива или последнего посещения.

4.2. Иммуногистохимия

Для иммуногистохимического окрашивания карциномы эндометрия и яичников использовали тканевые микроматрицы (tma). Поэтому были взяты новые образцы исходных слайдов и отобраны репрезентативные области, где предполагалась опухоль. После этого патологоанатом проверил наличие опухолевой ткани на образцах.

Парафинированные ТМА-слайды помещали в Roticlear, среду, заменяющую ксилол, на 20 минут для депарафинизации ткани. После этого их помещали в 100% этанол, а затем еще на 20 мин в 3% раствор перекиси водорода, разбавленный метанолом для ингибирования активности эндогенной пероксидазы. Для регидратации образцов использовали серию градуированных спиртов (100%, 70%, 50%) и, в конечном итоге, дистиллированную воду. С слайдов демаскировали, нагревая их до 100 ° C в скороварке, содержащей уже кипящий буферный раствор тринатрийцитрата с pH = 6.0 и готовить 5 мин.

После этого использовали блокирующий раствор (Реагент 1 из набора для обнаружения полимеров (ZytoChem Plus HRP Polymer System, Mouse Rabbit, Zytomed, Берлин, Германия)) для насыщения электростатических зарядов в ткани, и на образцы поместили первичное антитело и инкубировали 16 ч при 4 ° C. Используемое антитело представляло собой поликлональное антитело Anti-MSX1, кроличий IgG, концентрация 0,2 мг / мл (Sigma; номер заказа HPA073604. Sigma-Aldrich, Merck KGaA, Дармштадт, Германия), которое было разбавлено в соотношении 1: 200 с помощью PBS.На следующий день избыток антител был смыт и нанесен постблокирующий реагент на 20 мин. Вторичные антитела конъюгировали с пероксидазой хрена (HRP) в течение еще 30 минут и, наконец, антитело окрашивали с использованием DAB (набор субстратов хромогена, Dako North America Inc., Carpinteria, CA, USA) в течение 5 минут. Затем реакцию окрашивания останавливали дистиллированной водой, и материал контрастировали с использованием гематоксилина. Наконец, образцы были обезвожены с использованием возрастающей серии градуированных спиртов (50%, 70%, 96% и 100%) и Roticlear.На последнем этапе образцы покрывали монтажной средой и покровными стеклами.

Для оценки два независимых слепых наблюдателя смотрели на интенсивность окрашивания (0 = отсутствие окрашивания, 1 = слабая интенсивность, 2 = умеренная интенсивность, 3 = сильная интенсивность) и процент окрашенных клеток карциномы. Оценки двух наблюдателей различались в 4 случаях (n = 4,1%). Оба наблюдателя пересмотрели эти случаи вместе и пришли к одинаковым результатам. Согласованность до переоценки составила 95,9%. Также применялся IRS (иммунореактивный показатель), который является результатом процента окрашенных клеток карциномы (0 = 0%, 1 = 1–10%, 2 = 11–50%, 3 = 51–80%, 4 ≤ 81%) умножается на интенсивность закодированного окрашивания [28].В статистическом анализе все три результата рассматривались отдельно (интенсивность окрашивания, процент окрашенных клеток карциномы и IRS).

Поскольку мы пытаемся установить процедуру, которая может иметь стандартную патологию, мы сосредоточились на иммуногистохимии и не проводили метилирование промотора. анализ. Как показывают несколько исследований, метилирование промотора гена MSX1 предположительно для этого вида опухолей [21,24,25].

8dpo cervix

26 апреля, 2016 · Рак шейки матки (CC) вызван персистенцией вируса папилломы человека высокого риска из-за иммуносупрессивного микроокружения опухоли, опосредованного цитокинами.Микробиота влагалища определяет наличие определенных цитокинов локально. Мы оценили связь между разнообразием микробиоты шейки матки и гистопатологическим диагнозом каждой стадии CC, и мы оценили уровни экспрессии мРНК шейки матки …

Роды делятся на три стадии. Первый этап — это расширение шейки матки от 0 до 10 см, второй этап — рождение ребенка, третий этап — роды плаценты. Роды обычно … Беременность — преждевременные роды. Иногда младенцы рождаются рано.

Слизь из шейки матки довольно часто встречается у женщин. Когда женщины получают несколько DPO (дней после овуляции), они обычно обнаруживают эту желтую цервикальную слизь и подозревают, что это ранний симптом беременности. Желтый или беловатый густой кремообразный сантиметр — один из самых ранних признаков беременности, который обычно появляется во время пропущенного менструального цикла.

14 марта 2019 г. · Рак шейки матки вызван неконтролируемым ростом клеток шейки матки. Почти все виды рака шейки матки вызваны стойкими инфекциями, вызываемыми вирусом папилломы человека высокого риска, также называемым ВПЧ (16, 18, 31, 33, 35, 39, 45, 51, 52, 56, 58, 59, 66 и 68). .Два типа ВПЧ, 16 и 18, вызывают 80% всех случаев рака шейки матки.

3 июня 2007 г. · В дни отсутствия фертильности шейка матки закрыта, плотная и низкая. По мере приближения к фертильности шейка матки открывается, становится мягкой и высокой, и ее труднее достать. Фаза фертильности после o, однако она может проявлять некоторые фертильные характеристики даже после o из-за присутствия эстрогена.

12 DPO — это непростые временные рамки: в то время как некоторые женщины могут уже испытывать 12 симптомов беременности, связанных с DPO, другие могут вообще не иметь никаких симптомов, но все еще быть беременными.Давайте углубимся в тему, чтобы узнать, чего можно ожидать от 12 DPO, согласно науке.

25 июня 2017 г. · Повышенное содержание цервикальной жидкости Одним из симптомов ранней беременности является увеличение цервикальной слизи в организме. Это из-за вашего высокого уровня эстрогена, который, к вашему удивлению, выделяет много, как один из 7 симптомов DPO.

13 Dpo Коричневая пятнистость

Продолговатый мозг — Внутренняя структура — Сосудистая сеть

Продолговатый мозг (medulla) — одна из трех областей, составляющих ствол мозга.Он самый нижний из трех и непрерывен сверху с мостом, а снизу со спинным мозгом. В мозговом веществе находятся важные восходящие и нисходящие нервные пути, а также ядра ствола мозга.

В этой статье мы рассмотрим анатомию мозгового вещества — его внешние особенности, внутреннюю анатомию и кровоснабжение.

Внешняя анатомия продолговатого мозга

Мозговое вещество имеет коническую форму, уменьшающуюся в ширину по мере расширения вниз. Это примерно 3 см в длину и 2 см в ширину в самом большом месте.

Верхний край продолговатого мозга расположен на стыке мозгового вещества и моста, в то время как нижний край отмечен началом первой пары шейных спинномозговых нервов . Это происходит сразу после выхода мозгового вещества из черепа через большое затылочное отверстие .

Рис. 1. Три основных части ствола мозга. [/ caption]

Передняя поверхность

На передней поверхности продолговатого мозга видно несколько структур, а именно три трещины / борозды, пирамиды, оливки и пять черепных нервов.

По средней линии продолговатого мозга находится передняя срединная щель , которая проходит по всей длине спинного мозга. Однако он временно прерывается перекрестием пирамид (см. Ниже). При удалении от средней линии становятся видны две борозды — вентролатеральная борозда и заднебоковая борозда .

Пирамиды — это парные вздутия, обнаруженные между передней срединной щелью и вентролатеральной бороздой.Информацию о пирамидах можно найти здесь. Оливки — это еще одна пара вздутий, расположенных латеральнее пирамид — между вентролатеральными и заднебоковыми бороздами.

Отводящий нерв берет свое начало от соединения моста и мозгового вещества (CN VI). Из вентролатеральной борозды выходит подъязычный нерв (CN XII). В заднебоковой борозде к мозговому веществу присоединяются еще три черепных нерва (CN IX, CN X и CN XI). Дополнительная информация об этих нервах представлена здесь.

Рис. 2. Передняя поверхность продолговатого мозга. [/ caption]

Задняя поверхность

В отличие от передней поверхности продолговатого мозга, задняя поверхность в значительной степени закрыта для обзора и относительно лишена каких-либо деталей. Чтобы оценить заднюю поверхность, необходимо удалить мозжечок.

Подобно передней поверхности, задняя поверхность имеет структуру средней линии — заднюю срединную борозду , которая продолжается ниже задней срединной борозды спинного мозга.Вверху борозда заканчивается в месте развития четвертого желудочка.

Когда мы перемещаемся латерально от средней линии, мы видим fasciculus gracilis и fasciculus cuneatus , разделенные задней промежуточной бороздой .

Рис. 3. Заднебоковая поверхность ствола мозга. [/ caption]

Внутренняя анатомия продолговатого мозга

Чтобы понять структуру, необходимо рассмотреть внутренние структуры мозгового вещества в поперечном разрезе.Обычно рассматриваются три уровня мозгового вещества (нижний — верхний):

Уровень перекрестия пирамид
Уровень перекреста медиальных лемнисов
Уровень оливок

Сам мозг обычно делится на две области: открытый и закрытый мозговое вещество. Это различие основано на том, окружены ли полости, содержащие CSF, мозговым веществом (закрытым мозговым веществом) или нет (открытым мозговым веществом). Медулла открывается, когда центральный канал открывается в четвертый желудочек (см.рис.3 ).

Некоторые особенности видны во всех трех поперечных сечениях. Спереди мы видим парные образования, представляющие пирамиды , , разделенные передней срединной щелью. В центре можно увидеть центральный канал по мере того, как он поднимается, образуя четвертый желудочек на в последнем поперечном сечении.

Уровень перекрестия пирамид

Это главная точка пересечения нисходящих моторных волокон. Примерно 75% моторных волокон, размещенных в пирамидах , пересекаются по диагонали и кзади и продолжают вниз по позвоночному столбу в качестве боковых кортикоспинальных трактов.

На этом уровне центральная часть мозгового вещества содержит серого вещества, , в то время как внешние части состоят из белого вещества. Заднее белое вещество содержит fasiculus gracilis и более латеральные fasiculus cuneatus . Соответствующие части серого вещества простираются до этих областей и являются ядром gracilis и ядром cuneatus соответственно.

В отличие от спинного мозга, спиноцеребеллярных трактов (задний и передний) расположены латерально, между ними расположен латеральный спиноталамический тракт.Кзади от этих путей можно найти большое ядро тройничного нерва и его тракты. Это продолжение желатиновой субстанции спинного мозга.

Рис. 4. Поперечное сечение мозгового вещества на уровне пересечения пирамид [/ caption]

Уровень перекреста среднего лемниска

Этот уровень отмечает сенсорный перекрест медиального лемниска. ( Рис.5) . Пурпурные линии использовались для обозначения внутренних дугообразных волокон , поскольку они проходят от ядра gracilis и ядра cuneatus вокруг и кпереди от центрального серого вещества, образуя медиальный лемниск.

Латеральнее медиального лемниска, ядро тройничного нерва и спинномозговой тракт снова видны, как и спиноцеребеллярный тракт, а также латеральный спиноталамический тракт. Точно так же и задние структуры на этом уровне почти такие же.

В центре видны подъязычное ядро и медиальный продольный пучок. Двигаясь латерально, можно увидеть неоднозначное ядро. Между этой структурой и пирамидами находится нижнее оливковое ядро .

Рис. 5. Поперечный разрез продолговатого мозга на перекрестке среднего лемниска [/ caption]

Уровень маслин

По сравнению с предыдущими уровнями, этот уровень демонстрирует значительные изменения как во внешней, так и во внутренней структуре. Центральный канал теперь расширился до четвертого желудочка и, как таковой, делает эту область открытым мозговым веществом .

Большое нижнее ядро оливы отвечает за внешнее разрастание оливок. Родственные медиальное и дорсальное добавочные оливковые ядра можно увидеть медиальнее и кзади от этой структуры соответственно.

Видны большие нижние ножки мозжечка, окруженные множеством ядер. Два вестибулярных ядра (медиальное и нижнее) находятся по направлению к средней линии, в то время как два ядра улитки находятся несколько выше и ниже ножек. Теперь заметно меньшая структура, тройничный тракт и ядро, прилегающие к ножке.

Ядро неоднозначно. осталось, как было раньше, в то время как подъязычное ядро переместилось с центральным каналом назад, к нему присоединился медиальный продольный пучок. Латеральнее от подъязычного костей появляется дополнительное ядро черепа — дорсальное ядро блуждающего нерва. Двигаясь дальше в сторону, в поле зрения попадает ядро tractus solitarius.

Центрально, медиальный лемниск обнимает срединную линию кзади от пирамид, как и тектоспинальный тракт.

Между ножкой и оливковыми ядрами находится латеральный спиноталамический тракт и более латеральный передний спиноцеребеллярный тракт.

Рис. 6. Поперечный разрез продолговатого мозга на уровне маслин [/ caption]

Сосудистая сеть

Сосудистая сеть мозгового вещества сложна и зависит от просматриваемого уровня ( Рис. 7 ). Следующие попытки упростить эту сложность. Несмотря на это, читателю может быть достаточно знать, что к сосудам, снабжающим мозговой мозг, относятся: передний спинной, задний спинной, задний нижний мозжечок, передний нижний мозжечок и позвоночные артерии.

На всем протяжении продолговатого мозга передняя спинномозговая артерия снабжает область, начинающуюся у центрального канала (или переднюю границу четвертого желудочка), и расширяется, охватывая пирамиды.

Ниже уровня оливок задняя половина мозгового вещества снабжается задней спинномозговой артерией. Никакие другие регионы это судно не снабжает. Остальные части кровоснабжаются задними нижними мозжечковыми и позвоночными артериями.

В поперечном сечении оливок и задняя нижняя мозжечковая, и позвоночная артерии занимают большую территорию заднебоковой и переднебоковой стороны соответственно. Они продолжают это делать по мере подъема мозгового вещества.

В самой высокой точке мозгового вещества передняя нижняя мозжечковая артерия снабжает самые внешние части задней области.

Рис. 7: Кровоснабжение мозгового вещества на: перекрестке пирамид, перекрестке лемнисков и на уровне оливок. [/ caption]

Диаграмма доминанты — блок предохранителей и схема подключения — забавный

Схема доминантного нового один набор хромосом, клетки тела имеют две специфические хромосомы, определяющие половые хромосомы, несущие гены, гены перетасовываются, когда хромосомы обмениваются частями.class fc 2nd mar 14 2021 er диаграмма обозначает диаграмму взаимосвязи сущностей, также известную как диаграмма erd, которая отображает взаимосвязь наборов сущностей, хранящихся в базе данных, другими словами диаграммы er помогают объяснить логическую структуру баз данных. В других статьях, где обсуждается нормальный разлом, разломы с нормальным падением sp разломы возникают в результате вертикального давления, поскольку земная кора удлиняет висящую стену вниз по сравнению с подошвой.

Нормальные разломы ограничивают многие горные хребты мира и многие из них. рифтовые долины, обнаруженные по краям спрединга.фотосинтез процесс, посредством которого.

Схема доминирующего — зеленые растения и некоторые другие организмы преобразуют энергию горючего в химическую энергию во время фотосинтеза у зеленых растений энергия перехвата улавливается и используется для преобразования углекислого газа и минералов в воде в кислород и богатые энергией органические фунты. класс fc 15 ноября 2019 г. овуляция происходит в середине менструального цикла. Производство эстрогена из доминирующего фолликула приводит к резкому увеличению секреции ЛГ, в результате чего доминирующий фолликул выпускает свою яйцеклетку, яйцеклетка уносится в маточную трубу тонкими структурами на концах трубок, известных как фимбрии.Миксолидийская гамма с доминирующей шкалой бибопа 7 здесь представляет собой паритет между миксолидийской шкалой и доминирующей шкалой бибопа. Нота, добавляемая к миксолидийской шкале g, — это цифра 7, я перевернул шкалу на диаграмме, потому что именно так обычно играют шкалу бибопа. Расширенные средства управления доступом позволят вам поделиться схемой родословной.

Схема доминирующего — с другими, использующими систему и даже вносящими изменения в один и тот же документ одновременно, это очень полезно для обсуждений и встреч, чтобы получить обратную связь от коллег.

Схема подключения — это методика описания конфигурации установки электрического оборудования, например, электроустановочного оборудования на подстанции на CB, от панели к коробке CB, которая охватывает аспекты телеуправления и телесигнализации, телеметрию, все аспекты, которые требуют схемы подключения, используемой для обнаружения помех. , Новое вспомогательное оборудование и т. Д. диаграмма доминирующего элемента Эта принципиальная схема служит для обеспечения детального понимания функций и работы установки, описывая оборудование / части установки (в виде символов) и соединения. диаграмма доминантного Эта принципиальная схема показывает общее функционирование цепи.

Все его основные компоненты и соединения проиллюстрированы графическими символами, расположенными для максимально ясного описания операций, но без учета физической формы различных элементов, компонентов или соединений.

Генетика наследование характеристик доминантные рецессивные гены аллели гомозиготный гетерозиготный генотип фенотип экспрессия генов моногибридная генетическая диаграмма паннетт квадратный мендел горох растения муковисцидоз серповидноклеточная анемия igcse o уровень квадратные растения гороха Менделя кистозный фиброз серповидноклеточная анемия анемия igcse o level Обзор родословных (статья) родословные Академия хана Понимание родословных 9 класс генетика для igcse biology 3 24 pmg биология Доминирование рисунок Википедия Доминантная и рецессивная разница и сравнение diffen Файл аутосомно-доминантная родословная диаграмма svg wikipedia Commons Аутосомно-доминантное наследование группа синдрома горлина

Упростите введение ВМС с помощью стратегии KISS

Введение внутриматочной спирали (ВМС) не обязательно должно быть слепой процедурой, вызывающей беспокойство пациент или врач. Сегодня передовые медицинские технологии упрощают работу практикующего врача и сводят к минимуму осложнения, связанные с этим процессом. Конечным результатом является лучшее обслуживание пациента.

Имея в своем распоряжении эти новые технологии и инструменты, как лучше всего внедрить их в свою практику, чтобы максимально повысить их ценность для пациента? Просто будь проще, хирург! Это моя версия стратегии KISS для упрощения введения ВМС.

При наличии подходящих инструментов для получения точных и подробных изображений во время процесса введения клиницисты могут работать уверенно, а пациенты могут развеять свои заботы.Главное — использовать ультразвук в качестве ориентира.

Процесс установки ВМС

Даже самые опытные врачи сталкиваются с осложнениями при установке ВМС. Например, по данным исследования, опубликованного в Dove Medical Press, перфорация матки происходит примерно один раз на каждые 1000 вставок. К счастью, вы можете предпринять шаги, чтобы уменьшить этот и другие риски, связанные с установкой ВМС.

Начните с проведения трансвагинального УЗИ, чтобы оценить положение матки, подтвердить наличие миометрия и внутриматочной патологии, осмотреть шейку матки и исключить патологию придатков.

Затем выполните установку в соответствии с рекомендациями производителя ВМС, которые могут отличаться от поставщика к поставщику. Для повышения точности на этом этапе рекомендуется провести трансабдоминальное УЗИ.

Наконец, после того, как ВМС установлена, используйте трехмерное изображение короны дна матки, чтобы убедиться, что она правильно расположена в полости матки. После завершения процедуры прикрепите трехмерное изображение ВМС к карте пациента и сохраните его для документации.

Изображение 3D ВМС, демонстрирующее правильное размещение ВМС в матке

Ультразвук в 3D имеет значение

Визуализация 3D особенно важна на этом заключительном этапе.Хотя некоторые проблемы, связанные с ВМС, иногда могут быть обнаружены с помощью стандартного 2D-дисплея, только трехмерный коронарный вид гарантирует каждый раз изображение всей ВМС.

Такие функции, как SingleView и OmniView, улучшают визуализацию гинекологической анатомии на любой плоскости, даже если структуры асимметричны. Это избавляет от необходимости манипулировать изображениями и снижает клинические навыки, необходимые для завершения процесса. В результате рабочий процесс ускоряется, и пациент может покинуть кабинет с уверенностью, что ВМС установлена правильно.

Введение ВМС может быть таким простым, если оно будет простым. Стратегия KISS помогает врачам работать более эффективно за счет использования передовых решений визуализации для обеспечения точного размещения ВМС. Этот простой подход может помочь сократить количество неудачных попыток контрацепции ВМС и, что наиболее важно, укрепить доверие между практикующими врачами и пациентами.

Новое лечение на основе природных молекул, улучшающее функцию легких, может удерживать пациентов с COVID-19 от вентилятора — COVID-19

Новое лечение является одним из первых известных средств, снижающих тяжесть острого респираторного дистресс-синдрома (ОРДС), вызванного гриппом у животных, а также может удерживать пациентов с COVID-19 от вентилятора.

Исследования, проведенные исследователями из Университета штата Огайо (Колумбус, штат Огайо, США) на мышах, инфицированных высокими дозами гриппа, показали, что лечение может улучшить функцию легких у очень больных мышей и предотвратить прогрессирование заболевания у мышей, которых лечили превентивно. после заражения гриппом. Есть надежда, что он также может помочь людям, инфицированным гриппом и, возможно, другими причинами ОРДС, такими как инфекция SARS-CoV-2.

Специфические клетки мышей менее способны производить ключевые молекулы после того, как грипп поражает легкие, что снижает их способность производить вещество, называемое сурфактантом, которое позволяет легким расширяться и сокращаться.Нехватка сурфактанта связана с ОРДС, заболеванием настолько серьезным, что обычно требует искусственной вентиляции легких в отделении интенсивной терапии. Исследователи обошли заблокированный процесс у мышей, повторно введя недостающие молекулы по отдельности или в комбинации в виде инъекций или перорального лечения. Результат: нормализованный уровень кислорода в крови и уменьшение воспаления в легких мыши — эффекты, которые могут сделать человека достаточно здоровым для выписки из больницы.

ARDS также может быть результатом инфекций, рака, травм и многих других заболеваний.Хотя эта терапия была протестирована в контексте гриппа, ее зависимость от восстановления нарушенной функции клеток в организме хозяина, а не от уничтожения вируса, предполагает, что она может лечить практически любое повреждение легких. Экспериментальное лечение состоит из молекул, известных как липонуклеотиды, которые необходимы для образования сурфактанта в легких. Исследователи проанализировали клетки легких инфицированных гриппом мышей и определили, что путь к выработке сурфактанта был нарушен, и один из двух необходимых липонуклеотидов полностью не обнаруживался.

Команда исправила это у мышей, разработав терапию, содержащую недостающую молекулу липонуклеотида отдельно или в сочетании с одной или двумя другими. Исследователи вакцинировали мышей высокими дозами вируса гриппа h2N1, а затем лечили некоторых мышей липонуклеотидами один раз в день в течение пяти дней, а других — только один раз через пять дней после заражения. Мыши, получавшие ежедневное лечение, были защищены от серьезных заболеваний, а у очень больных мышей, получавших лечение на пятый день, у которых тяжелая потеря кислорода в крови и воспаление легких вызвали ОРДС, наблюдалось значительное улучшение.

Еще есть чему поучиться. Агенты обладают сильным противовоспалительным действием, но не восстанавливают полностью процесс производства сурфактанта, и исследователи до сих пор не уверены, почему это так. До сих пор исследования основывались на результатах исследования одного типа клеток легких, но исследователи не подтвердили, что именно эти клетки реагируют на терапию — любое количество других клеток иммунной системы, кровеносных сосудов или сердца также может играть роль. Несмотря на неизвестность, исследователи считают, что недостающие липонуклеотиды естественным образом существуют у млекопитающих, включая человека, они считаются безопасными и вряд ли вызовут побочные эффекты, даже если они не будут использоваться в организме.