|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Оснащения врачебно-сестринской бригады. Интересное: Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории. Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 10 из 13Следующая ⇒ Координаты точки принято писать в скобках рядом с обозначением точки.
Рисунок 43 – Построение точки по заданным координатам
Материал для закрепления: 1. Указать условия, при которых можно определить положение точки в пространстве. 2. Указать, сколько проекций может иметь точка в пространстве на плоскости проекций. 3. Указать названия плоскостей проекций и их обозначения. 4. Указать каким образом располагаются плоскости проекций относительно друг друга. 5. Указать названия прямых линий, по которым пересекаются плоскости проекций. 6. Показать обозначение точки пересечения плоскостей проекций. 7. Показать обозначение точек проекций на плоскостях проекций. 8. Объяснить получение эпюра или комплексного чертежа. 9. 10. Объяснить назначение координат точки. 11. Объяснить возможность переноса координат точки по оси Y. 12. Объяснить значение координат точки А (6, 10, 4).
После теоретического закрепления материала, обучающиеся выполняют индивидуальные практические задания на построение комплексного чертежа точки по заданным координатам, в соответствии с вариантом обучающегося (задание 4а). Работа выполняется на формате А4 с соблюдением линий чертежа. Название чертежа – «Графическая работа №4. Проекции точки».
Построение комплексного чертежа прямой Всякую линию, в том числе и прямую, можно рассматривать как множество последовательно расположенных точек в пространстве, а проекцию прямой АВ на плоскость Н – как множество проекций точек данной прямой (рисунок 44).
Положение прямой в пространстве определяют две её точки. Рисунок 45 – Проекции отрезка Положение отрезка прямой в пространстве определяется двумя его проекциями. Чтобы найти третью проекцию отрезка, необходимо построить третьи проекции точек, ограничивающих отрезок. На рисунке 45а,б стрелками показан ход построения профильной проекции а»б»отрезка АВ по заданным горизонтальной ав и фронтальной а’в’ проекциям.
Закрепление материала: По заданным координатам точек отрезка АВ построить комплексный чертёж в соответствии со своим вариантом (задание 13, 14, 15). Работа выполняется на формате А4, с соблюдением линий чертежа и обозначение точек на плоскостях проекций (задание 4б). Название чертежа – «Графическая работа №4. Проекции отрезка».
⇐ Предыдущая45678910111213Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ — МегаЛекции
Для однозначного определения положения точки в пространстве необходимо и достаточно иметь проекции на двух плоскостях проекций, но в инженерной практике при построении проекций различных предметов с целью полного выявления их формы часто используют больше двух плоскостей проекций.
Рис. 1 Рис. 2
Одна из плоскостей проекций расположена горизонтально и называется горизонтальной плоскостью проекций, и обозначается П1. Проекции элементов пространства на ней обозначаются с индексом 1: А1, а1, …и называются горизонтальными проекциями (точки, прямой, плоскости).
Плоскость, расположенная перед наблюдателем, перпендикулярно первой, называется фронтальной плоскостью проекций, и обозначается П2 . Проекции элементов пространства на ней обозначаются с индексом 2: А2, а 2, … и называются фронтальными проекциями(точки, прямой, плоскости).
Плоскость, расположенная справа от наблюдателя перпендикулярно одновременно горизонтальной и фронтальной плоскостям проекций, называется профильной плоскостью проекций, и обозначается П3 .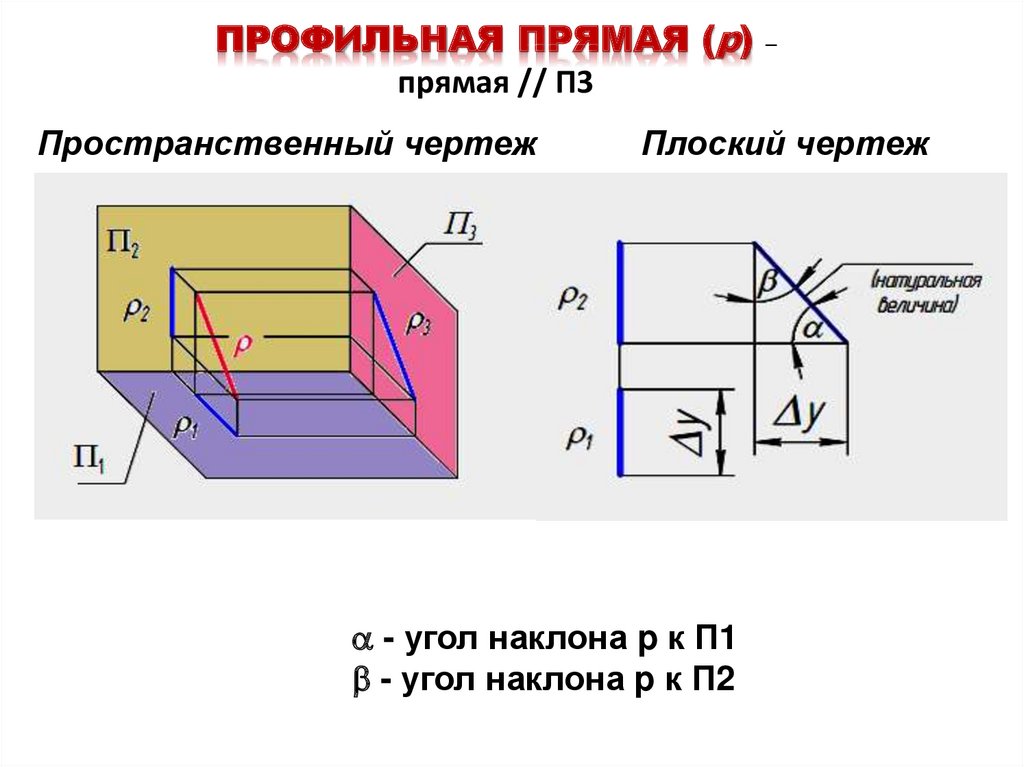 Проекции элементов пространства на ней обозначаются с индексом 3: А3, а3, … и называются профильными проекциями. Линию пересечения горизонтальной и фронтальной плоскостей проекций принимают за ось координат х.Линию пересечения горизонтальной и профильной плоскостей проекций принимают за ось координат у. Линию пересечения фронтальной и профильной плоскостей проекций принимают за
Проекции элементов пространства на ней обозначаются с индексом 3: А3, а3, … и называются профильными проекциями. Линию пересечения горизонтальной и фронтальной плоскостей проекций принимают за ось координат х.Линию пересечения горизонтальной и профильной плоскостей проекций принимают за ось координат у. Линию пересечения фронтальной и профильной плоскостей проекций принимают за
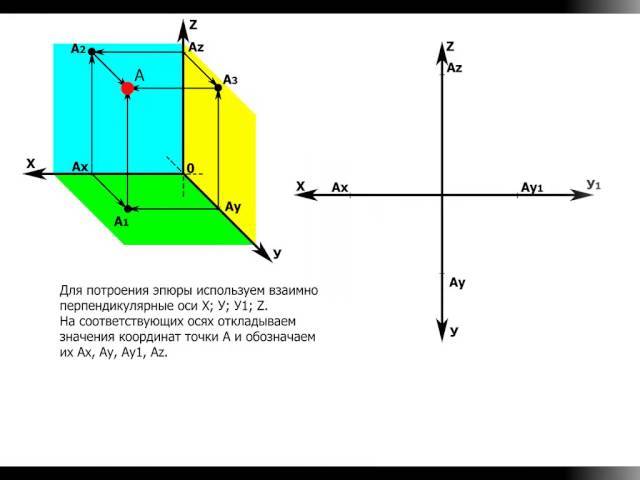
Для получения комплексного чертежа (или Эпюра Монжа — рис. 4) – за плоскость чертежа принимают фронтальную плоскость проекций П2 , горизонтальную плоскость проекций П1 совмещают с плоскостью чертежа вращением вокруг оси x, а профильную плоскость проекций П3 совмещают с плоскостью чертежа вращением вокруг оси z. Чертеж – это две (или более) проекции точки, совмещенные на одной плоскости (плоскости чертежа) и связанные линиями проекционной связи. Прямая А1-А2 , соединяющая горизонтальную и фронтальную проекцию точки, называется вертикальной линией связи; прямая А2— А3 , соединяющая фронтальную и профильную проекции точки, называется горизонтальной линией связи.
Чертеж – это две (или более) проекции точки, совмещенные на одной плоскости (плоскости чертежа) и связанные линиями проекционной связи. Прямая А1-А2 , соединяющая горизонтальную и фронтальную проекцию точки, называется вертикальной линией связи; прямая А2— А3 , соединяющая фронтальную и профильную проекции точки, называется горизонтальной линией связи.
Рассматривая чертеж точки, выделяют, что:
· две проекции точки принадлежат одной линии связи;
· линии связи перпендикулярны соответствующим осям координат;
· две проекции точки необходимо и достаточно для определения положения точки в пространстве, и две проекции точки определяют её третью проекцию.
Три основные плоскости проекций могут рассматриваться и как координатные плоскости, если точка задана координатами. Зная координаты точки можно построить её комплексный (рис. 3 а) и аксонометрический (рис. 3 б) чертеж.
Рис. 3 (а,б)
3 (а,б)
Задачи
| Задача 1 -На наглядном изображении и на чертеже построить профильную проекцию А | |||
| Обозначение | Название элементов чертежа | ||
| П1 | |||
| П2 | |||
| П3 | |||
| x, y, z | |||
| А1 | |||
| А2 | |||
| А3 | |||
Задача 2.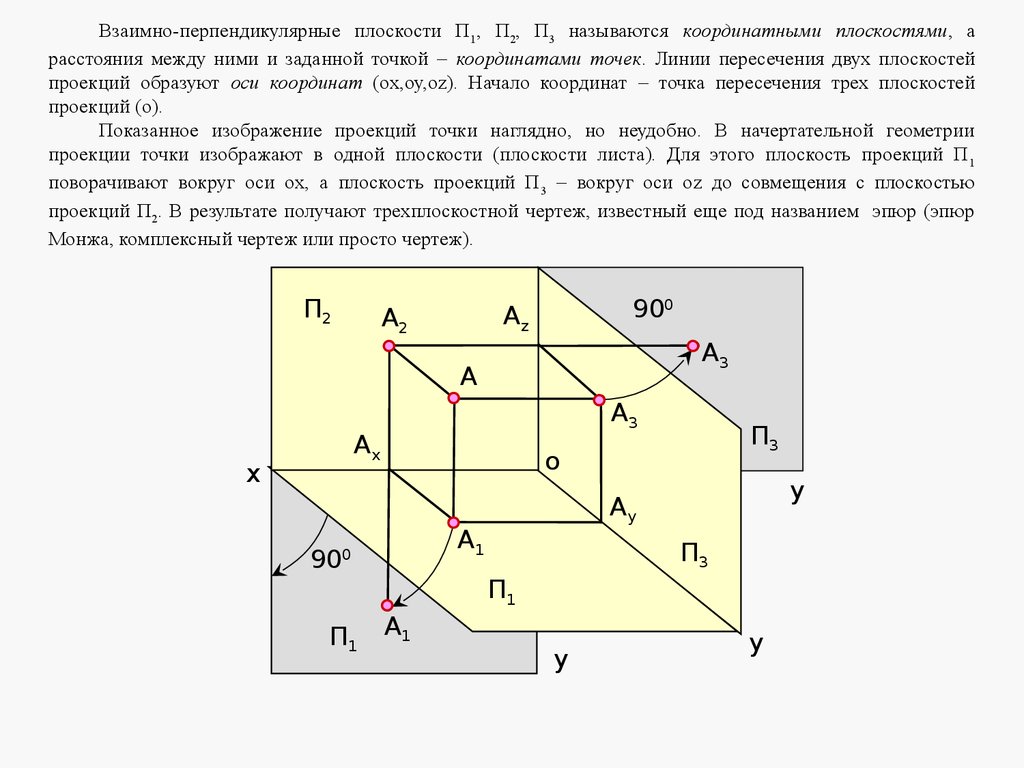 Сделайте на чертеже необходимые обозначения.
Покажите расстояния от точки В до плоскостей проекций. Сделайте на чертеже необходимые обозначения.
Покажите расстояния от точки В до плоскостей проекций.
| Задача 3.Постройте комплексный чертеж точки В. Запишите её координаты. |
Задача 4.Какие координаты надо знать, чтобы построить проекции точки?
Задача 5.По заданным координатам постройте чертежи точек. Где находятся точки?
Задача 7.По двум данным построить третью проекцию точек, заданных. Укажите положение точек относительно плоскостей проекций.
Воспользуйтесь поиском по сайту:
ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.
ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.
ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.
Комплексный чертеж точки
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства.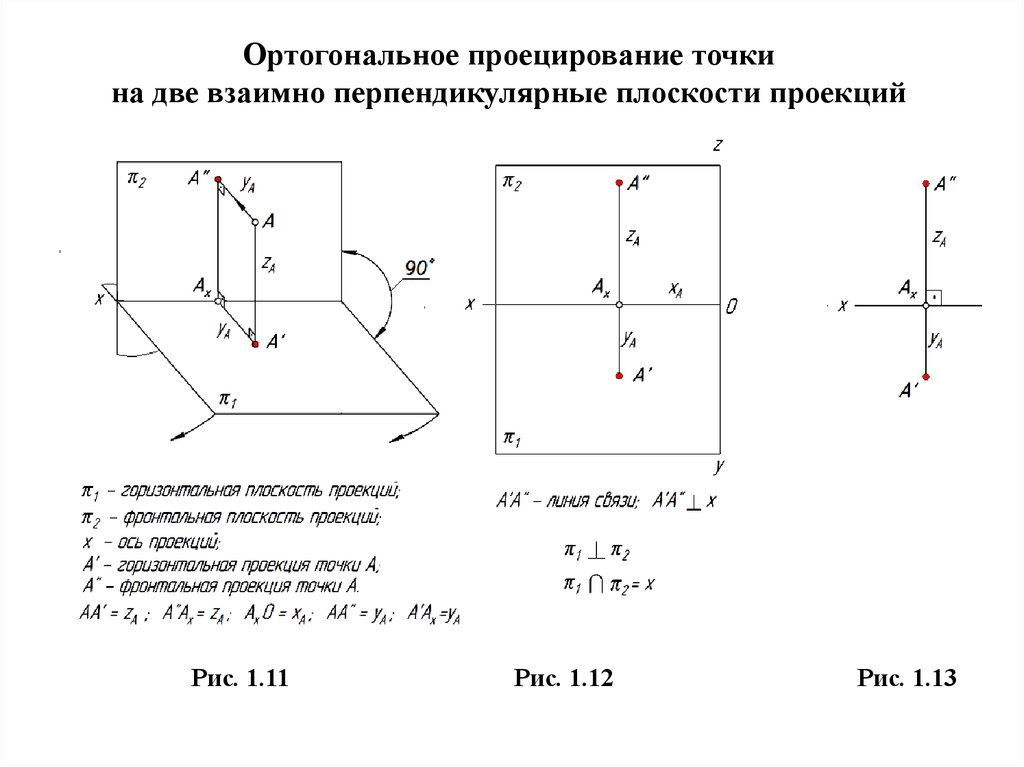 Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов
Рис. 60
Рис. 61
пространства на ней будем обозначать с индексом 1 : А1, а1, S1 .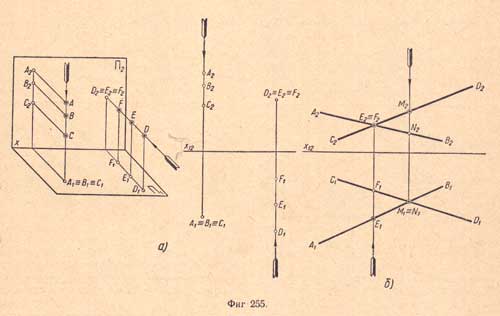 П2=A2;
П2=A2;
Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом.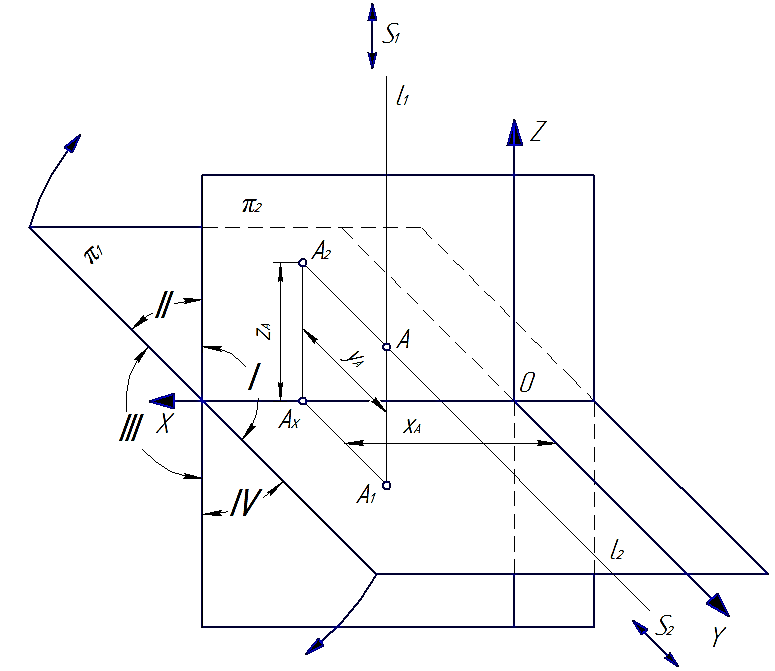 Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.
КОМПЛЕКСНЫЙ ЧЕРТЕЖ. Элементы трехпроекционного комплексного чертежа точки
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-
Рис. 62
ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.
Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1.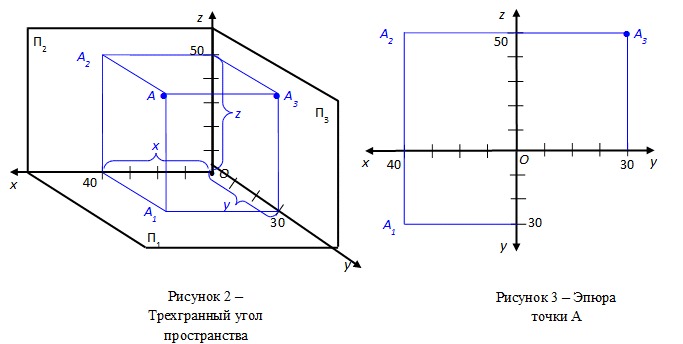 Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-
Рис. 63
ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
63, б).
Положение точки в пространстве трехмерного угла
Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:
- точка расположена в пространстве (см. рис. 62). В этом случае она имеет глубину, высоту и широту;
- точка расположена на плоскости проекций П1 — она не имеет высоты, П2 — не имеет глубины, Пз — не имеет широты;
- точка расположена на оси проекций, П2/П1 не имеет глубины и высоты, П2/П3— не имеет глубины и широты и П1/П3не имеет высоты и широты.
КОМПЛЕКСНЫЙ ЧЕРТЕЖ. Конкурирующие точки
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
Рис. 64
П2 (рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П3 [А3 == B3] (рис. 64, в), они называются профильно конкурирующими.
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.
Замена плоскостей проекций
Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.
На рис. 65, а показаны точка А и ее проекции — горизонтальная А1 и фронтальная А2. По условиям задачи необходимо произвести замену плоскостей П2. Новую плоскость проекции обозначим П4 и расположим перпендикулярно П1. На пересечении плоскостей П1 и П4 получим новую ось П1/П4. Новая проекция точки А4 будет расположена на линии связи, проходящей через точку А1 и перпендикулярно оси П1/П4.
Поскольку новая плоскость П4 заменяет фронтальную плоскость проекции П2, высота точки А изображается одинаково в натуральную величину и на плоскости П2, и на плоскости П4.
Это обстоятельство позволяет определить положение проекции A4, в системе плоскостей П1 _|_ П4 (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
Рис. 65
Рис. 66
Рис. 67
сти проекции П2, отложить ее на новой линии связи от новой оси проекций — и новая проекция точки А4 будет построена.
Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П4 _|_ П2 (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А2А4 _|_. В этом случае глубина точки одинакова и на плоскости П1, и на плоскости П4. На этом основании строят А4 (рис. 66, б) на линии связи А2А4 на таком расстоянии от новой оси П1/П4 на каком А1 находится от оси П2/П1.
Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П5. Ее располагают перпендикулярно уже введенной плоскости П4 (рис. 67, а), т. е. П5П4 и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рис. 67, б на плоскости П1) и откладывают их на новой линии связи А4А5, от новой оси проекций П5/П4. В новой системе плоскостей П4П5 получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А4 и А5, связанных линией связи
A4A5_|_П4/П5
ПРОЕКЦИИ ТОЧКИ КОМПЛЕКСНЫЙ ЧЕРТЕЖ.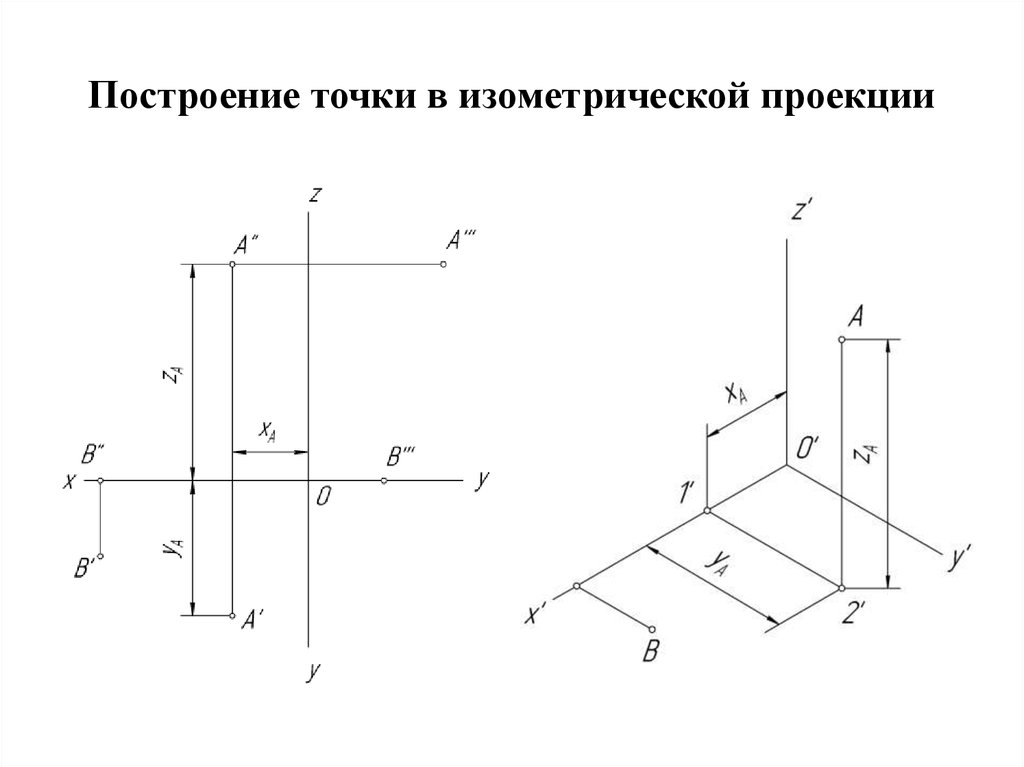 Прямоугольные координаты точек
Прямоугольные координаты точек
Три основные плоскости проекций (П1_|_П2 _|_ П3) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у,П2/П3 —осью аппликат z.
Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).
Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А1 ортогонально проецировать на ось х в точку Ах. Тогда получим пространственную координатную ломаную АА1АХО, отрезки которой параллельны осям координат и соответственно называются: ОАХ — отрезком абсциссы; АХ А1 — отрезком ординат; А1А — отрезком аппликаты.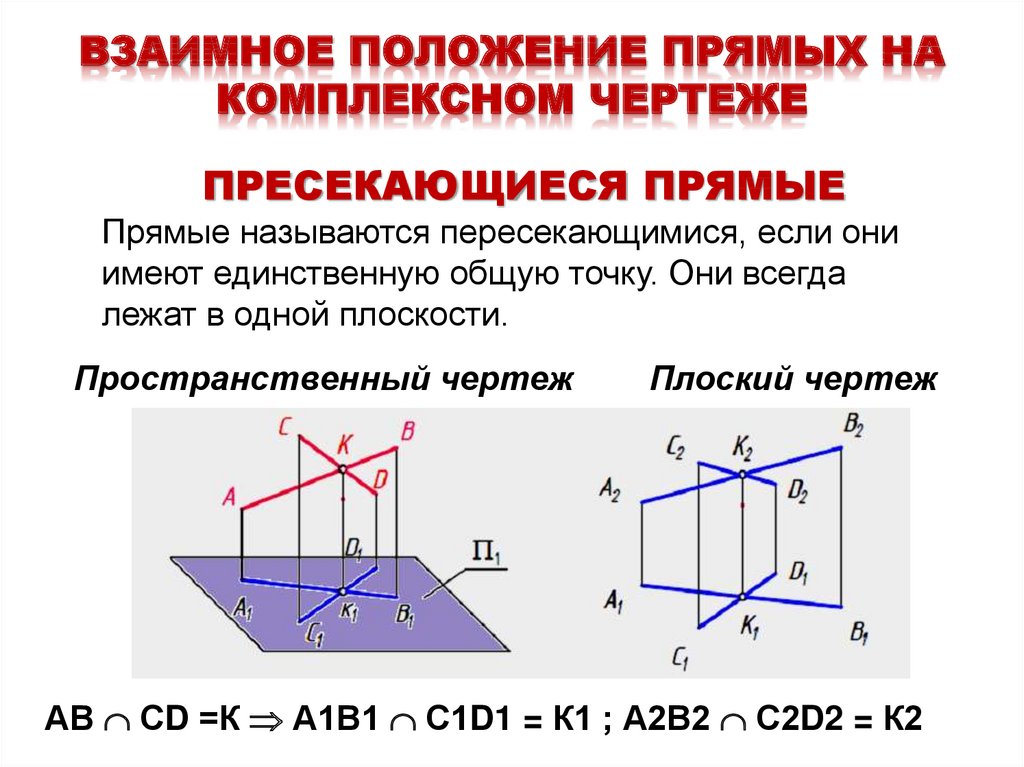
Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:
х = OAX абсцисса; у = AxA1— ордината; z = AA1 — аппликата.
Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение
Рис. 68
вертикальной линии связи (рис. 68, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная — величиной аппликаты.
изготовление чертежей, сделать чертеж
Мои услуги
Контакты для заказа чертежей
Справочная по строит. черч.
курсовая по архитектуре
объемно планировочное решение
конструкция наружных стен
перекрытие пола
план здания чертеж
разрез здания чертеж
чертеж генплана
Справочная
стандарты черчения
правила выполнения чертежей
ОФОРМЛЕНИЕ ЧЕРТЕЖЕЙ
эскиз детали
СКАЧАТЬ ЧЕРТЕЖИ
вопросы по черчению
изображение резьбы
длина болта, длина шпильки, длина винта
рабочий чертеж
сборочный чертеж
как построить тень
падающая тень
Телефон
89042493591
кроме выходных
задать вопрос, узнать о возможности, сроках и цене изготовления чертежей можно по аське:
587-149-933
Новости:
Открылся наш сайт
Цветы из шелка
Здесь вы можете заказать красивые цветы из ткани на платье и заколки.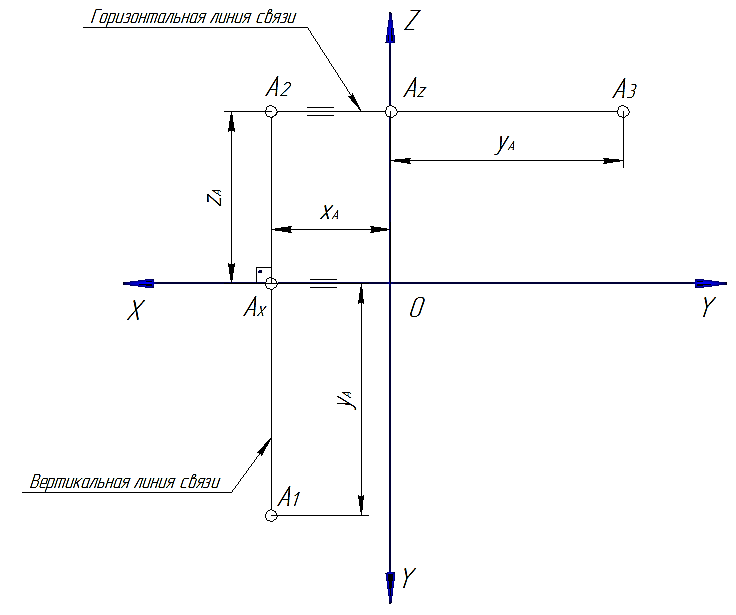
Сайт изготовлен в tehnok.ru в 2005 году
Как использовать декартовы координаты для нанесения точек на чертежи
Фотографии предоставлены Риком ЛобделломДля меня одна из самых влиятельных математических теорий называется декартовыми координатами. Прилагательное декартовский относится к французскому математику и философу Рене Декарту, который опубликовал эту идею в 1637 году. Декартовы координаты являются основой аналитической геометрии и обеспечивают поучительные геометрические интерпретации для многих других областей математики, таких как линейная алгебра, комплексный анализ, дифференциальная геометрия. , многомерное исчисление и теория групп.
Знакомый пример — понятие графика функции. Декартовы координаты также являются важным инструментом для большинства прикладных дисциплин, связанных с геометрией, включая астрономию, физику и инженерию. Это наиболее распространенная система координат, используемая в компьютерной графике, автоматизированном геометрическом проектировании и другой обработке данных, связанных с геометрией.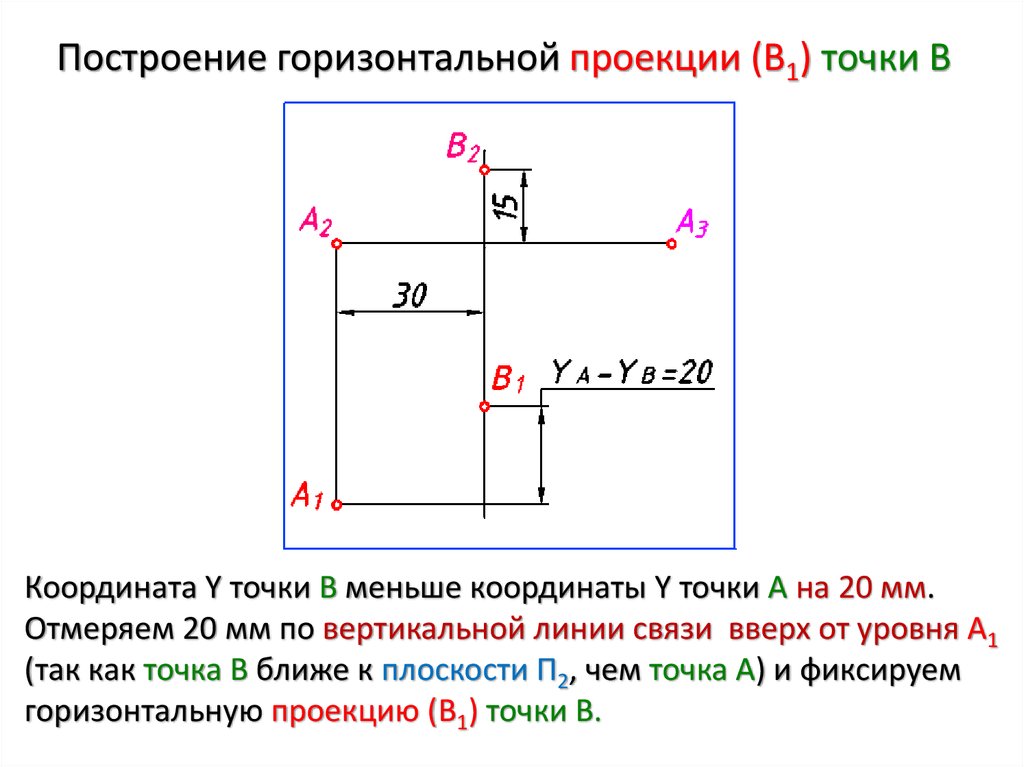
Декартова система координат в двух измерениях (также называемая прямоугольной системой координат) определяется упорядоченной парой перпендикулярных линий (осей), единой единицей длины для обеих осей и ориентацией для каждой оси. (Ранние системы допускали «наклонные» оси, то есть оси, которые не пересекались под прямым углом.)
Линии обычно называют осями x и y, где ось x горизонтальна, а ось y вертикальна. Точка, где встречаются оси, принимается за начало координат для обеих, таким образом, каждая ось превращается в числовую прямую.
Для заданной точки P через точку P проводится линия, перпендикулярная оси x, до пересечения с ней в точке X, а через точку P проводится вторая линия, перпендикулярная оси y, до точки Y. Координаты точки P равны тогда X и Y интерпретируются как числа x и y на соответствующих числовых линиях. Координаты записываются в виде упорядоченной пары (x, y).
Таким образом, до этого момента все мои статьи были посвящены основам базовой математики.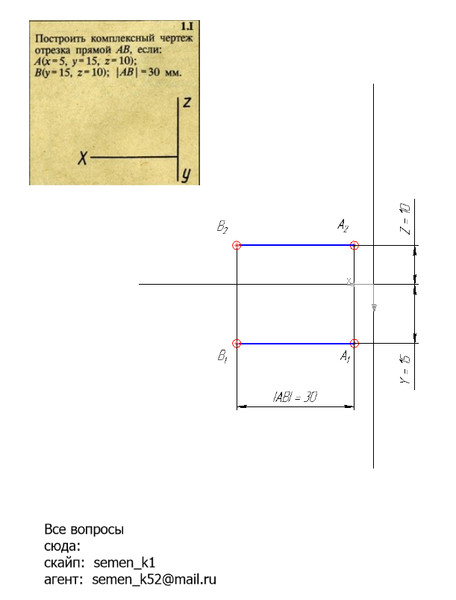 Я делал макет шаг за шагом, достраивая этот момент. Здесь начинают раскрываться мои секреты. Это больше не просто макет — это больше о точках построения.
Я делал макет шаг за шагом, достраивая этот момент. Здесь начинают раскрываться мои секреты. Это больше не просто макет — это больше о точках построения.
Практика делает совершенным
Хотя может потребоваться некоторое время, чтобы эта идея укоренилась, я могу обещать вам, что делаю это на регулярной основе, и нет предела тому, что вы можете рисовать, как только вы поймете эту теорию. По правде говоря, я не полностью придерживаюсь всех правил этой теории. Я упростил его и создал отличный способ компоновки больших медальонов с идеальной симметрией.
Давайте углубимся в то, как мы можем использовать эту теорию. Я намекнул на это в своей последней статье о геральдических лилиях. Как и в предыдущих двух статьях, начните с большого креста в середине пола. Теперь пространство разделено на четыре квадранта. Вы начнете с того, что дважды правильно нарисуете свой дизайн в одном квадранте, а затем нанесете на карту остальные три. В конце концов, вы нарисуете частичную геральдическую лилию восемь раз, по два раза в каждом квадранте.
Для этой статьи я использовал недавний дизайн, в котором я взял теорию геральдической лилии и добавил к ней поворот. Я начал с того, что решил, какого размера мне нужен медальон. В этом случае длина диагонали составила 8 футов. Я отмерил 4 фута от центра моего X. Затем я выбрал первую линию, чтобы начать рисовать, и нарисовал начало геральдической лилии. Я не могу научить вас рисовать идеальную кривую. Требуется много практики, стирания и перерисовки, пока вы не научитесь правильно.
График утолщается
Создав одну сторону изображения, вы можете нанести на нее важные точки. Чем больше точек вы начертите, тем легче нарисовать остальные квадранты. Обычно я наношу точки на основе внешних краев изображения.
Точно так же, как и в компьютере, фактические декартовы координаты требуют точек. Но мне не нужно наносить столько точек, сколько компьютеру. Мне просто нужно достаточно, чтобы иметь возможность дублировать исходное изображение.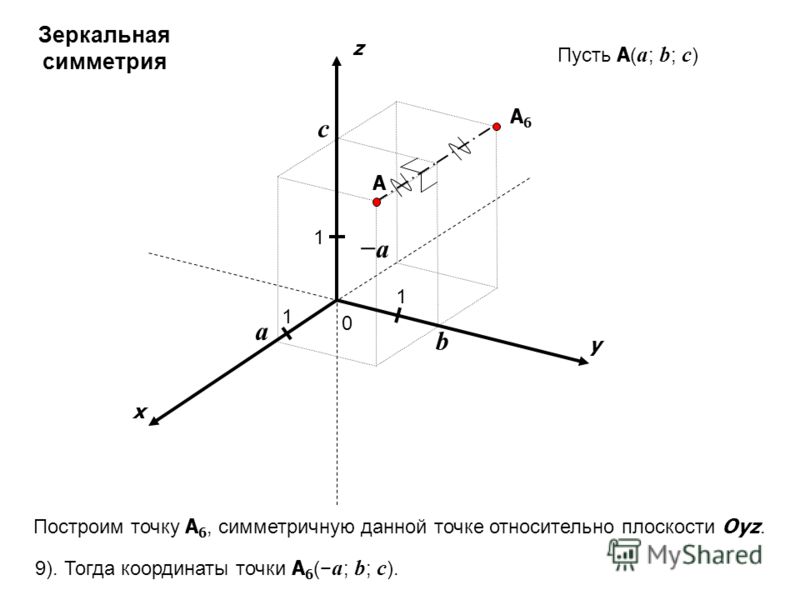 Для этого дизайна я нанес восемь точек (но я предлагаю вам нанести больше 10-15, чтобы упростить задачу). Те же самые восемь точек наносятся на каждый квадрант дважды.
Для этого дизайна я нанес восемь точек (но я предлагаю вам нанести больше 10-15, чтобы упростить задачу). Те же самые восемь точек наносятся на каждый квадрант дважды.
Представьте точки в дюймах. Первый измеряет, насколько далеко точка находится от горизонтальной линии, а второй измеряет вертикальную точку. Для этого проекта все точки графика, использующие оси x, y в качестве координат:
0,48 – 3,38 – 10,41 – 18,34,5 – 12,31 – 9,33 – 1,5,24 – 12,12
В точку
Я потерял тебя? Позвольте мне объяснить эти цифры. На втором фото внизу справа вы видите кучу маленьких отметин. Каждая метка является точкой сюжета исходного изображения. Первый — 0,48 — означает, что я начал с вертикальной линии в 48 дюймах от центра. Второй 3,38. Я измерил 3 дюйма от горизонтального центра, а затем 38 дюймов вверх по вертикальной линии. С 10,41 я измерил 10 дюймов до горизонтальной линии, а затем 41 дюйм по вертикали. И так далее.
Чтобы не запутаться, по мере продвижения делайте одно и то же измерение в каждом квадранте. Например, для второй отметки начертите 3,38 семь раз, прежде чем перейти к отметке 10,41. Это не только упростит процедуру построения графика, но и ускорит процесс.
Например, для второй отметки начертите 3,38 семь раз, прежде чем перейти к отметке 10,41. Это не только упростит процедуру построения графика, но и ускорит процесс.
На моих снимках вы видите только шесть различных меток вместо восьми, о которых я упоминал. Одна из меток, которую трудно увидеть, находится на вертикальной линии на кончике рисунка. Другой находится ближе к центру рисунка, где встречаются противоположные стороны квадранта.
Последние штрихи
Чтобы закончить этот дизайн, мне нужно было нарисовать кривую, которая объединяет каждую секцию геральдической лилии. После того, как я закончил рисовать основные области дизайна, я вернулся, чтобы добавить границу в центр. Я сделал это, измерив ширину, которую хотел, и нанес несколько маленьких точек, которым я следовал, чтобы я мог точно нарисовать изогнутую линию. Это не то, что вам нужно делать, но мне нравится, чтобы все было одинаковой ширины. Чтобы добавить изюминки, я доработал некоторые изгибы, чтобы придать изюминку моему дизайну.
В видео к этой статье я не ходил по квадрантам в идеальном порядке, как должен был. Я сделал это специально, чтобы показать вам, что это не имеет значения. Если точки совпадают, дизайн соберется, когда вы закончите.
Видеоруководство
Есть еще вопросы по вашему проекту?
- Вопрос*
- У вас есть фотография проекта, которой вы хотели бы поделиться с нами?
Перетащите файлы сюда или
Допустимые типы файлов: jpeg, jpg, gif, png, pdf, макс. размер файла: 50 МБ.
Разрешенные форматы: JPEG, JPG, GIF, PNG, PDF
- Имя
- Последняя название
- Ваша роль*
.
 будут опубликованы анонимно с их ответами в конце этой истории, чтобы поделиться с другими читателями.
будут опубликованы анонимно с их ответами в конце этой истории, чтобы поделиться с другими читателями.
Комплексные числа и полярные координаты
Давным-давно математики погрузились в свое воображение и изобрели совершенно новый набор чисел. Им нужны были эти числа, чтобы решить некоторые математические задачи — задачи, в которых встречается квадратный корень из отрицательного числа.Такие области, как инженерия, электричество и квантовая физика, используют мнимые числа в своих повседневных приложениях. воображаемое число — это квадратный корень из отрицательного числа. Воображаемая единица , , обозначаемая как i, , является решением уравнения i 2 = –1.
Комплексное число может быть представлено в виде a + bi, , где a и b — действительные числа, а i обозначает мнимую единицу. В комплексном числе а + bi а называется действительной частью, а b называется мнимой частью. Действительные числа можно рассматривать как подмножество комплексных чисел, имеющих форму a + 0 i. Когда a равно нулю, тогда 0 + bi записывается просто как bi и называется чисто мнимым числом.
В комплексном числе а + bi а называется действительной частью, а b называется мнимой частью. Действительные числа можно рассматривать как подмножество комплексных чисел, имеющих форму a + 0 i. Когда a равно нулю, тогда 0 + bi записывается просто как bi и называется чисто мнимым числом.
Как выполнять операции с комплексными числами и строить графики
Комплексные числа в виде a + bi можно изобразить на комплексной координатной плоскости . Каждому комплексному числу соответствует точка ( а, б ) в комплексной плоскости. Действительная ось – это прямая на комплексной плоскости, состоящая из чисел, имеющих нулевую мнимую часть: a + 0 i. Каждое действительное число соответствует уникальной точке на действительной оси. Мнимая ось — это прямая на комплексной плоскости, состоящая из чисел, имеющих нулевую действительную часть: 0 + bi.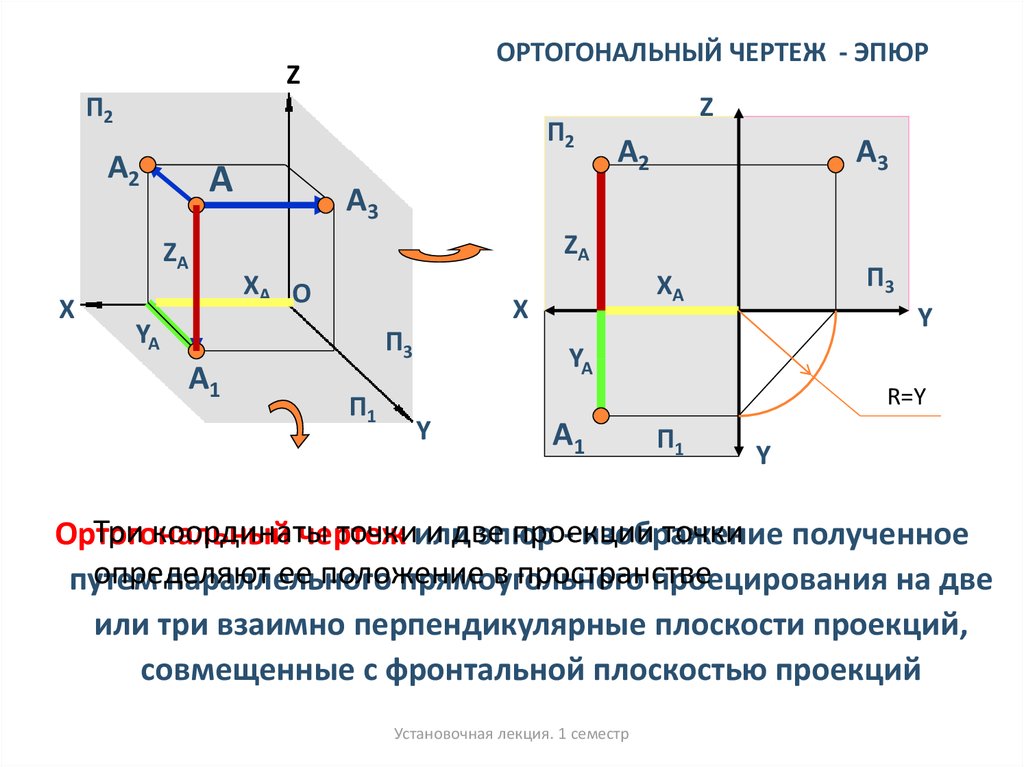 На рисунке показано несколько примеров точек на комплексной плоскости.
На рисунке показано несколько примеров точек на комплексной плоскости.График комплексных чисел.
Сложение и вычитание комплексных чисел — это еще один пример сбора подобных терминов: вы можете складывать или вычитать только действительные числа, а складывать или вычитать — только мнимые числа.
При умножении комплексных чисел вы СЛОМАЕТЕ два двучлена. Все, что вам нужно сделать, это помнить, что воображаемая единица определяется так, что i 2 = –1, поэтому каждый раз, когда вы видите i 2 в выражении, замените его на –1. Имея дело с другими степенями i, обратите внимание на следующую закономерность:
. Так продолжается вечно, повторяя в цикле каждую четвертую силу. Чтобы найти большую степень i, , а не считать бесконечно, поймите, что схема повторяется. Например, чтобы найти i 243 , разделите 4 на 243, и вы получите 60 с остатком 3. Шаблон повторится 60 раз, и тогда у вас останется 3, поэтому i 243 = i 240 × i 3 = 1 × i 3 , то есть – i .
Сопряжение комплексного числа a + bi равно a – bi и наоборот. Когда вы умножаете два комплексных числа, сопряженных друг с другом, вы получаете чистое действительное число: 9.0003
( a + bi )( a – bi ) = a 2 – abi + abi – b 2 i 2
Combining like terms and replacing i 2 with –1: = a 2 – b 2 (–1) = a 2 + b 2
Remember что столбцы абсолютного значения, окружающие действительное число, представляют расстояние. В случае комплексного числа | а + би| представляет собой расстояние от точки до начала координат. Это расстояние всегда равно длине гипотенузы прямоугольного треугольника, проведенного при соединении точки с осями х и у .
При делении комплексных чисел числитель и знаменатель умножаются на сопряженное. Если задействован квадратный корень числа, то вы будете рационализировать знаменатель.
В общем случае задача на деление комплексных чисел выглядит так:
Вокруг столба: как построить график полярных координат
До сих пор ваш опыт построения графиков мог быть ограничен прямоугольной системой координат . Прямоугольная система координат получила такое название, потому что она основана на двух числовых линиях, перпендикулярных друг другу. Пришло время развить эту концепцию и ввести полярных координат. В полярных координатах каждая точка располагается вокруг центральной точки, называемой полюсом , и называемой ( r ,n θ ). r — это радиус, а θ — это угол, образованный между полярной осью (представьте, что использовал как положительную ось x ) и отрезком, соединяющим точку с полюсом (что использовал в качестве источника).
В полярных координатах углы обозначаются либо в градусах, либо в радианах (или в обоих). На рисунке показана полярная координатная плоскость.
Круговое построение графиков в плоскости полярных координат.
Обратите внимание, что точка на плоскости полярных координат может иметь более одного имени. Поскольку вы движетесь по кругу, вы всегда можете прибавить или вычесть 2π к любому углу и оказаться в одной и той же точке. Это важная концепция при графическом отображении уравнений в полярных формах, поэтому в этом обсуждении она будет хорошо освещена.
Если и радиус, и угол положительны, угол движется против часовой стрелки. Если радиус положительный, а угол отрицательный, точка движется по часовой стрелке. Если радиус отрицательный, а угол положительный, сначала найдите точку, в которой оба значения положительны, а затем отразите эту точку на полюсе. Если и радиус, и угол отрицательные, найдите точку, в которой радиус положительный, а угол отрицательный, а затем отразите ее на полюсе.
Переключение на полярную и обратно
Вы можете использовать как полярные, так и прямоугольные координаты для обозначения одной и той же точки на координатной плоскости. Иногда проще написать уравнение в одной форме, чем в другой, поэтому это должно познакомить вас с вариантами выбора и с тем, как переключаться с одной формы на другую. На этом рисунке показано, как определить взаимосвязь между этими двумя не такими уж разными методами.Прямоугольный треугольник показывает взаимосвязь между прямоугольными и полярными координатами.
Немного тригонометрии прямоугольного треугольника и теорема Пифагора:
x 2 + y 2 = r 2
Графические полярные уравнения
Когда вам дадут уравнение в полярном формате и попросят построить его график, вы всегда можете воспользоваться методом «подключи и пыхни»: выберите значения для θ из единичного круга, который вы так хорошо знаете, и найдите соответствующее значение r . У полярных уравнений есть различные типы графиков, и их легче изобразить, если у вас есть общее представление о том, как они выглядят.
У полярных уравнений есть различные типы графиков, и их легче изобразить, если у вас есть общее представление о том, как они выглядят.Спираль Архимеда
r = aθ дает график, образующий спираль. a — это константа, умножающая угол. Если и положительны, спираль движется против часовой стрелки, как и положительные углы. Если и отрицательные, спираль движется по часовой стрелке.Кардиоидная
Вы можете узнать слово кардиоида , если вы когда-либо тренировались и делали кардио. Это слово относится к сердцу, и когда вы рисуете кардиоидную диаграмму, она действительно выглядит как сердце. Кардиоиды записываются в форме ИЛИ.Уравнения косинуса — это сердечки, которые указывают влево или вправо, а уравнения синусов открываются вверх или вниз.
Роза
Роза под любым другим названием — это… полярное уравнение. Если r = a sin bθ или r = a cos bθ , то графики выглядят как цветы с лепестками.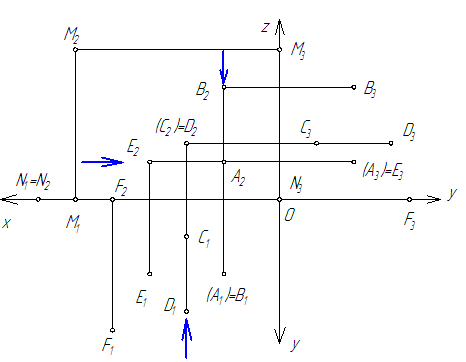 Количество лепестков определяется b . Если b нечетное, то b (одинаковое количество) лепестков. Если b четно, то 2 б лепестки.
Количество лепестков определяется b . Если b нечетное, то b (одинаковое количество) лепестков. Если b четно, то 2 б лепестки.Круг
Когда r = a sin θ или r = a cos θ , вы получите круг диаметром a. Окружности с косинусом в них центрированы на оси x , а окружности с синусом в них центрированы на оси y . Это особые типы окружностей, проходящих через начало координат.Лемниската
Лемниската образует восьмерку; это лучший способ запомнить это. образует восьмерку между осями и образует восьмерку, которая лежит на одной из осей как линия симметрии.Лимасон
Кардиоида — это действительно особый тип лимасона, поэтому они выглядят похожими друг на друга, когда вы их изображаете. Знакомые формы limaçons: ORPoint at Coordinate — Ekins Solutions, LLC
Point at Coordinate
Возможно, но не очень просто, создать точку построения в определенной координате XYZ в Fusion 360.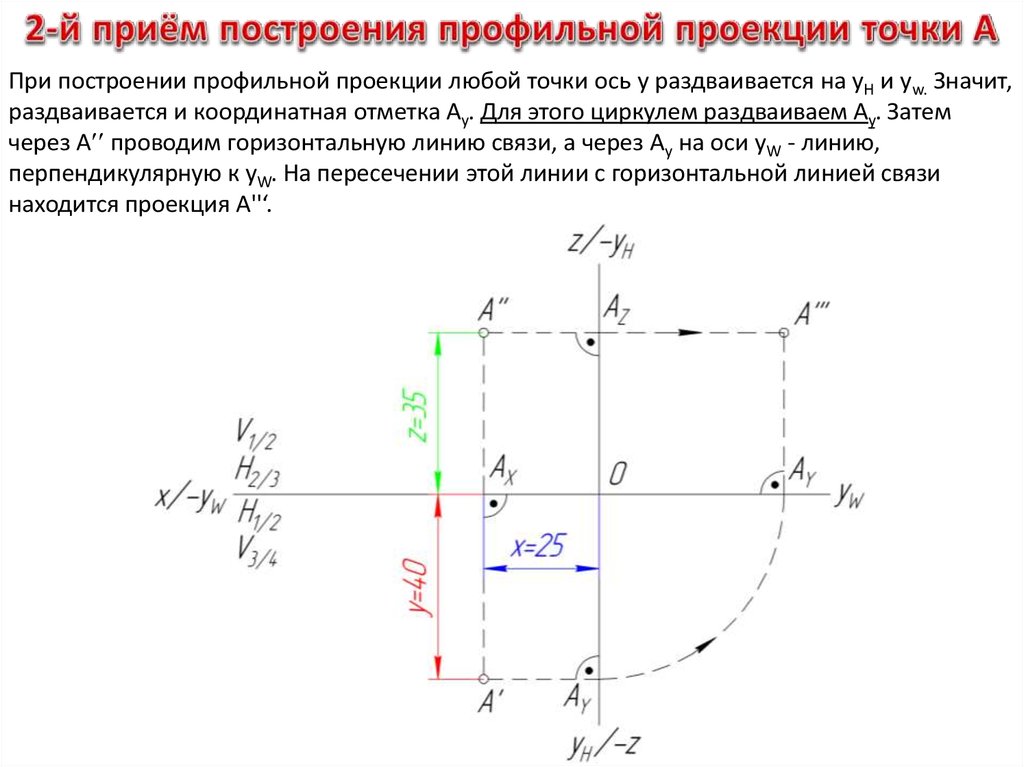 Процесс также немного отличается в зависимости от того, работаете ли вы с параметрической моделью или нет. Во-первых, давайте посмотрим на процесс работы с моделью прямого редактирования. Вы определяете, находитесь ли вы в параметрическом режиме или нет, используя переключатель «Захват истории проекта», как показано ниже.
Процесс также немного отличается в зависимости от того, работаете ли вы с параметрической моделью или нет. Во-первых, давайте посмотрим на процесс работы с моделью прямого редактирования. Вы определяете, находитесь ли вы в параметрическом режиме или нет, используя переключатель «Захват истории проекта», как показано ниже.
Если история проектирования не фиксируется, точка построения может существовать где угодно в пространстве и не зависит ни от какой другой геометрии. Однако Fusion 360 не поддерживает команду, позволяющую указать местоположение. Вместо этого вы должны сначала создать точку относительно какой-либо существующей геометрии, удобна базовая исходная точка. Затем вы можете использовать команду Move/Copy для перемещения точки в нужное место, так как команда Move/Copy поддерживает ввод координат. Это работает, но очень утомительно.
Создать точку построения в любом месте параметрической модели сложнее. При работе с параметрической моделью все точки построения зависят от другой геометрии и не могут существовать где-либо в пространстве, поэтому невозможно разместить точку в произвольном месте X, Y, Z. В параметрической модели вы ограничены методами создания, которые предоставляет Fusion 360. Однако есть способ обойти это, используя так называемую «базовую функцию». Базовый элемент позволяет вам создать «остров» данных прямого редактирования в параметрическом проекте, поэтому в конечном итоге он представляет собой тот же рабочий процесс, что и в проекте прямого моделирования, за исключением того, что вам также необходимо сначала создать базовый элемент, как показано ниже.
В параметрической модели вы ограничены методами создания, которые предоставляет Fusion 360. Однако есть способ обойти это, используя так называемую «базовую функцию». Базовый элемент позволяет вам создать «остров» данных прямого редактирования в параметрическом проекте, поэтому в конечном итоге он представляет собой тот же рабочий процесс, что и в проекте прямого моделирования, за исключением того, что вам также необходимо сначала создать базовый элемент, как показано ниже.
После создания базового элемента рабочий процесс аналогичен модели прямого редактирования, описанной выше.
Но создание точки построения в нужном месте по осям XYZ требует много работы, особенно если нужно создать несколько точек. Вот причина для этого маленького приложения. После установки он добавляет новую кнопку в меню CONSTRUCT для команды Point at Coordinate , как показано ниже.
При запуске команды в проекте прямого моделирования отображается диалоговое окно слева, а в параметрическом проекте отображается диалоговое окно справа.
Поля «Положение X», «Положение Y» и «Положение Z» представляют собой значения X, Y и Z, где будет создана точка построения. Вы можете использовать любое допустимое выражение при указании этих значений, включая использование имен параметров. Например, если у вас есть параметр с именем «Длина», вы можете использовать «Длина/2». Единицы измерения по умолчанию — это текущие проектные единицы. Но вы также можете переопределить это, указав единицы измерения. Например, «3 дюйма» будет интерпретироваться как 3 дюйма. Что бы вы ни использовали в качестве входных данных, важно понимать, что точка не запоминает эту взаимосвязь, поэтому, если вы используете имя параметра, а затем измените значение параметра, точка не будет двигаться.
Когда команда запускается в параметрическом проекте, в верхней части диалогового окна отображается раскрывающийся список «Базовый элемент», поскольку при работе в параметрическом проекте необходимо создать точки в произвольном месте внутри базового элемента.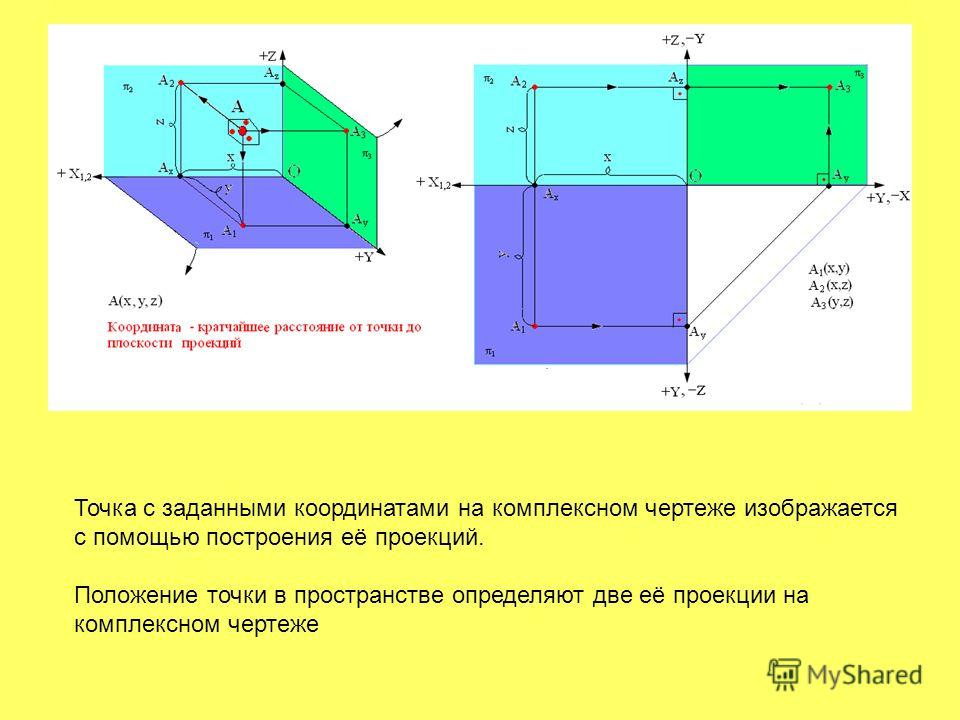 укажите, в каком базовом объекте они будут созданы. Если существующего базового объекта нет, будет создан новый, который будет базовым объектом по умолчанию при повторном запуске команды, хотя у вас есть возможность выбрать любой существующая базовая функция.b
укажите, в каком базовом объекте они будут созданы. Если существующего базового объекта нет, будет создан новый, который будет базовым объектом по умолчанию при повторном запуске команды, хотя у вас есть возможность выбрать любой существующая базовая функция.b
С помощью поля «Имя» вы можете указать, какое имя будет у новой точки построения. По умолчанию используется «Точка XYZ», но иногда, в зависимости от того, как вы собираетесь использовать точку, может быть полезно дать ей имя, чтобы вы могли легко определить, какая из них какая, глядя в браузер. Как только имя и позиции определены, вы можете нажать кнопку OK, чтобы создать и завершить команду. Однако вы также можете нажать кнопку «Создать», чтобы указать точку, но остаться в команде, чтобы продолжить создание дополнительных точек. Точки, созданные при нажатии кнопки «Создать», являются временными точками, пока вы не нажмете кнопку «ОК». Нажатие «Отмена» прервет все действия с момента запуска команды.
Чтобы использовать надстройку, просто распакуйте загруженный zip-файл в любое место на вашем компьютере.

 Например: запись В(3, 2, 3) означает, что координаты точки В следующие: Х=3; Y=2; Z=3. На рисунке 43 показаны построения на аксонометрическом изображении и на эпюре точки В по заданным координатам.
Например: запись В(3, 2, 3) означает, что координаты точки В следующие: Х=3; Y=2; Z=3. На рисунке 43 показаны построения на аксонометрическом изображении и на эпюре точки В по заданным координатам.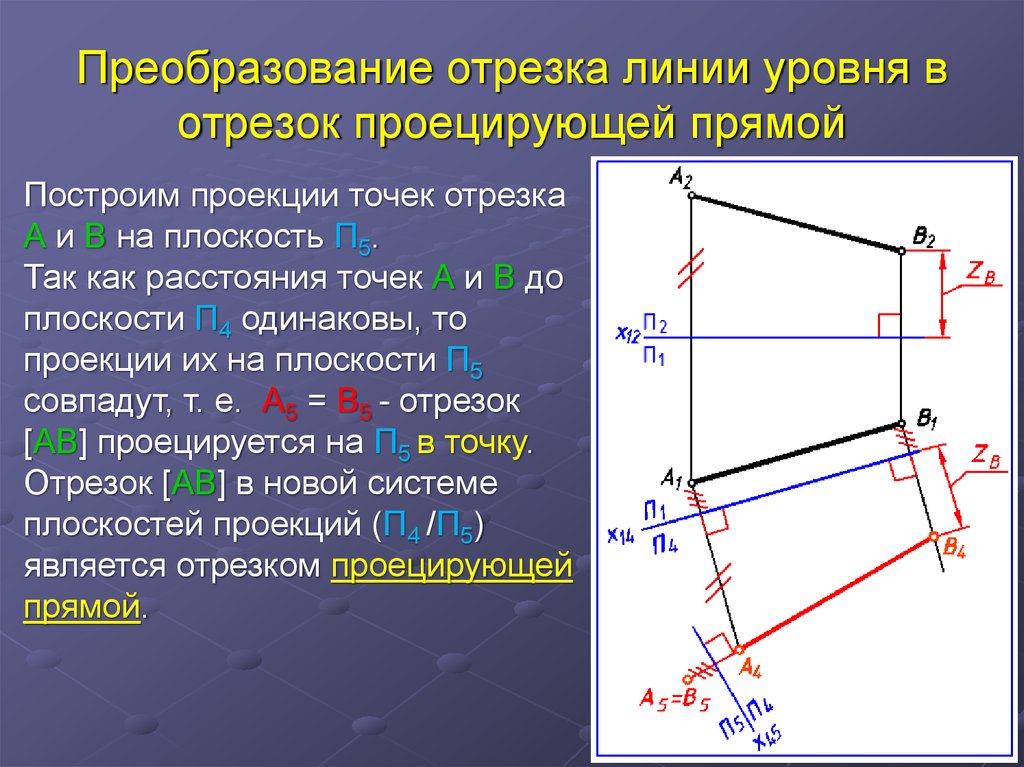 Объяснить назначение эпюра.
Объяснить назначение эпюра.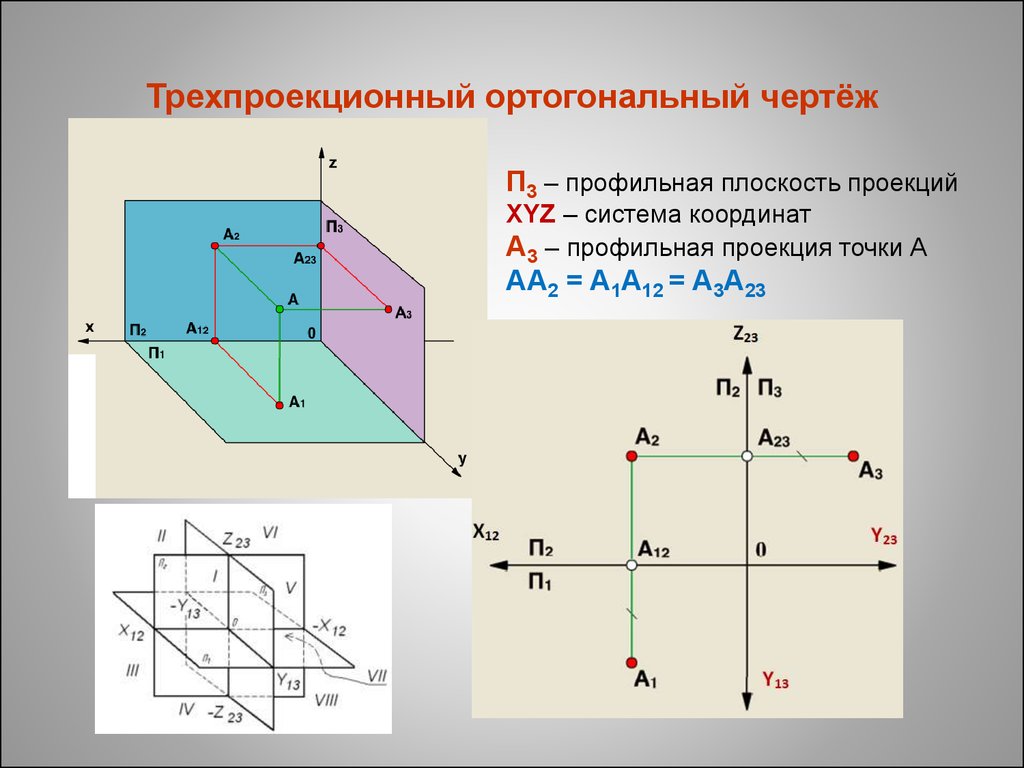 Часть прямой, ограниченная двумя точками, называется отрезком. Чтобы построить проекции отрезка АВ, достаточно построить проекции его крайних точек. Соединив прямыми одноименные проекции этих точек, получим проекции отрезка (рисунок 45).
Часть прямой, ограниченная двумя точками, называется отрезком. Чтобы построить проекции отрезка АВ, достаточно построить проекции его крайних точек. Соединив прямыми одноименные проекции этих точек, получим проекции отрезка (рисунок 45).