Лабораторная работа №3 Алгоритмы и технологии вычисления интегралов Краткие теоретические сведения
Система MATLAB позволяет вычислять неопределенные и определенные интегралы, первообразные которых заданы в виде аналитических выражений.
Она также имеет большое число способов численного интегрирования. Численное интегрирование необходимо в следующих случаях:
• первообразная не выражается через элементарные функции;
• аналитическое выражение интеграла слишком сложное;
• подынтегральная функция задана в табличной форме или в виде матрицы.
При вычислениях интегралов численными методами подынтегральную функцию целесообразно представлять в наиболее простом виде. Это может ускорить вычисления. Упрощение подынтегральной функции можно выполнить, воспользовавшись функцией simplify(y).
Имеют место случаи,
когда система до упрощения не может
вычислить неопределенный интеграл и
легко его определяет после упрощения.
Метод вычисления интеграла выбирает пользователь. В этом особенность системы MATLAB. С помощью MATLAB студент имеет возможность сравнивать различные методы численного интегрирования.
Существует ряд способов численного интегрирования. Во всех таких способах вычисление осуществляется по приближенным формулам, называемым квадратурными. Приведем некоторые из них.
Формулы прямоугольников
Формулы прямоугольников представляются в следующем виде:
где:
• h — шаг интегрирования;
• уk — значение подынтегральной функции при аргументе хk, k=0,1,2,…, n;
• n=(b—a)/h — число частей, на которые разбивается область интегрирования а, b.
Одна из формул
дает значение интеграла с избытком,
другая с недостатком.
Формула трапеций
Эта формула имеет вид:
где:
• у0 — значение подынтегральной функции при х=а;
• уn — значение подынтегральной функции при х=b;
• h — шаг интегрирования.
Формула парабол (Симпсона)
Эта формула имеет вид:
.
В этой формуле ординаты с нечетными индексами умножаются на 4, а с четными — на 2. Предполагается, что n — число четное.
При нечетном n формула имеет вид:
.
Крайние ординаты имеют коэффициент, равный 1.
Существует много других квадратурных формул вычисления интегралов: Котеса, Чебышева, Гаусса и др.
В
системе MATLAB
вычисление интегралов реализовано численными
методами трапеций, парабол (Симпсона)
и Ньютона — Котеса.
Метод трапеций
Метод трапеции реализован в MATLAB несколькими функциями, приведенными ниже.
1. Функция cumtrapz(у)
Осуществляет вычисление интеграла в случае, когда значения функции у заданы в виде вектора или матрицы неограниченных размеров. Откликом этой функции является п интегралов, где п — число элементов вектора или число элементов в каждом столбце матрицы.
Такое вычисление интеграла называется интегрированием с накоплением.
Пример 1: Пусть функция у(х) имеет значения, представленные в виде следующего вектора: y= [1,2,3,4,5,6,7,8,9,10]. Необходимо вычислить
При этом a=1; b=1,2, 3,…, 10.
Функция вычисления интеграла методом трапеций будет иметь вид:
>> у=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
>> cumtrapz (у)
ans =
0
1.
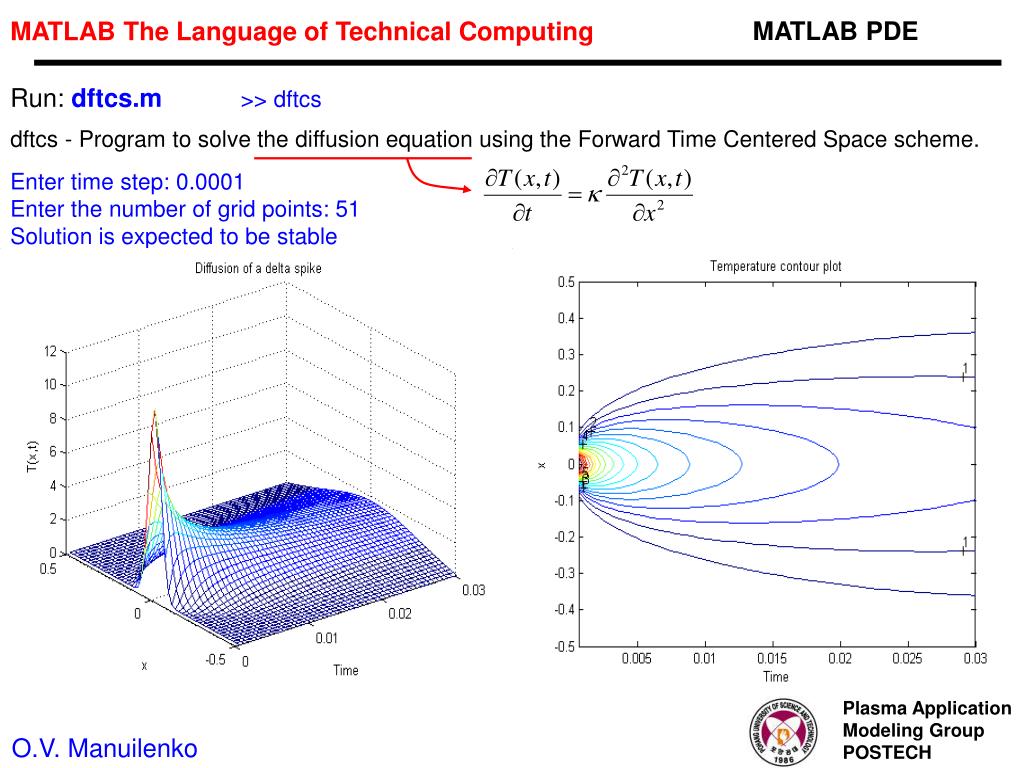5000 4.0000 7.5000 12.0000 17.5000 24.0000 31.5000
40.0000 49.5000
Пример 2: пусть необходимо вычислить интеграл вида
Чтобы вычислить этот интеграл с помощью функции cumtrapz(), следует сначала вычислить 10 ординат подынтегральной функции, представив их в виде вектора.
Программа вычисления интеграла с накоплением будет иметь вид:
» х=1:1:10;
» cumtrapz(у)
ans =
1.0e+004 *
0 0.0017 0.0060 0.0174 0.0481 0.1311 0.3564 0.9684 2.6313 7.1510
Существует модификация данной функции cumtrapz (х, у).
Основным недостатком метода трапеций является большая погрешность результата вычисления интеграла.
Геометрическая интерпретация определенных интегралов — Информатика, информационные технологии
Понятие об М-файлах
Более эффективным способом выполнения команд в системе MATLAB является применение М-файлов.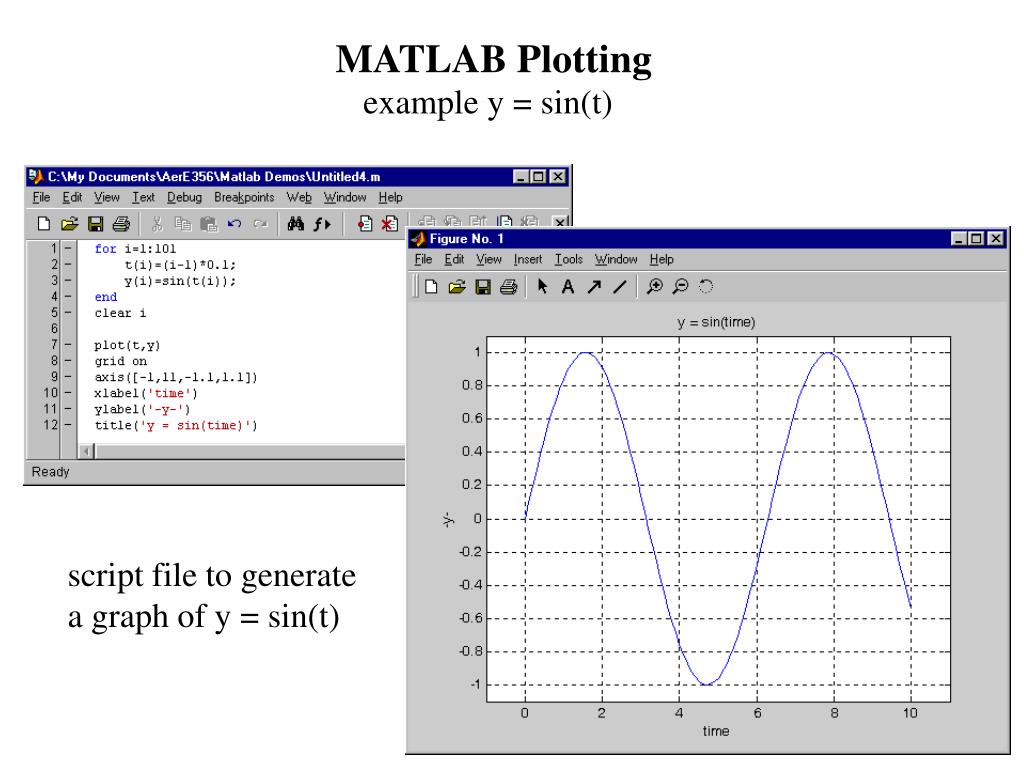
М-файлом называется текстовый файл с расширением .m, содержащий набор инструкций на языке системы MATLAB (т.е. в М-файлах хранятся программные коды). Для решения различных математических задач MATLAB предоставляет весьма мощный и удобный язык программирования высокого уровня, интуитивно понятный даже для пользователей, не являющихся профессиональными программистами. Вместе с тем цель последующего изложения, разумеется, не начать осваивать с нуля новый и неизвестный язык программирования MATLAB. Несмотря на то, что работу в командной строке нельзя назвать программированием, тем не менее, все команды, операторы и функции, описанные ранее, составляют типичный инструментарий языка программирования системы MATLAB.
Поясним, что создать М-файл можно в любом текстовом редакторе, поддерживающим формат ASCII-файлов (например, текстовый процессор Microsoft Word). Вместе с тем, в системе MATLAB имеется собственный, рекомендуемый к использованию встроенный редактор М-файлов, который отличают удобные визуальные средства создания и отладки программ.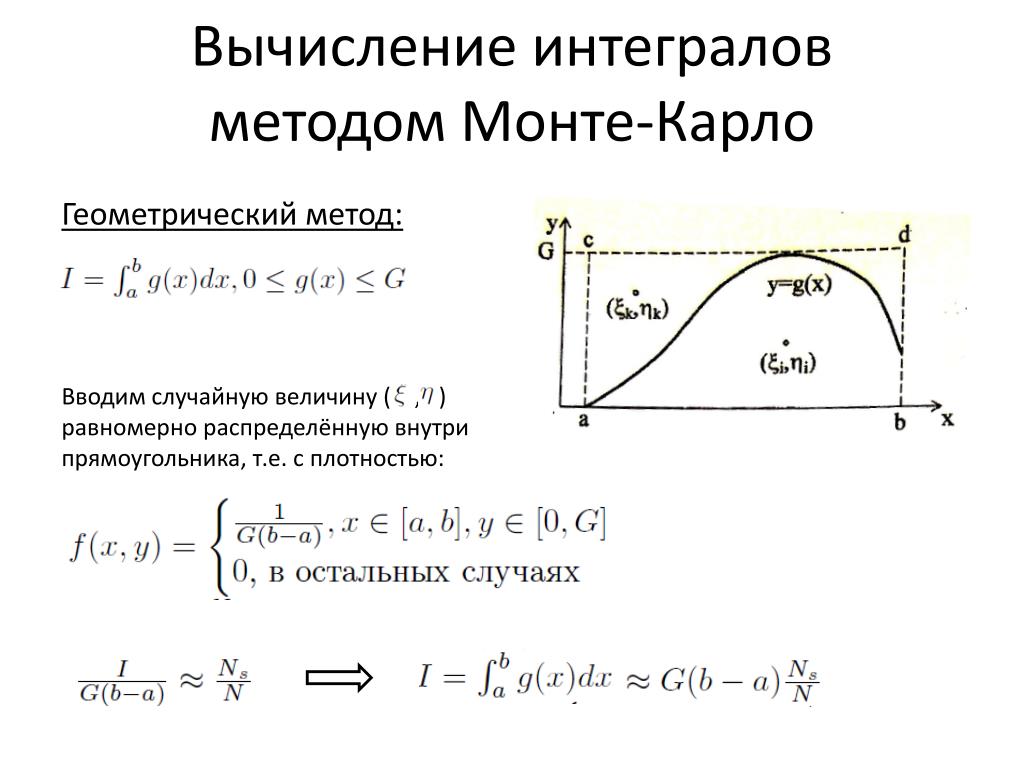
В этом редакторе можно набрать команды, выполнить их сразу или частично, а после сохранить в файле, который можно использовать в дальнейшем.
М-файлы должны иметь уникальные имена. Длина имени при этом не ограничивается, но при идентификации имени учитываются лишь первые 31 символ. При исполнении программного объекта его имя сравнивается со списком имён, хранящихся в рабочей области и в директориях М-файлов. Если имя файла оказывается неуникальным, соответствующий программный объект не исполняется и выдаётся сообщение об ошибке, а если уникальным, то программный объект исполняется в интерпретирующем режиме.
Типы М-файлов
В системе MATLAB существуют два типа М-файлов: файл-программы (Script M-Files, скрипты или сценарии) и файл-функции (Function M-Files).
Файл-программы являются самым простым типом М-файлов ввиду того, что состоят из последовательности команд и не имеют входных и выходных аргументов (параметров). В процессе выполнения файл-программы не компилируются, они весьма полезны для автоматизации выполнения большого набора инструкций.
В целом, файл-программы представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, которая используется в сессии.
В файл-функциях описываются функции, определяемые пользователем. В отличие от файл-программ, файл-функции могут принимать исходные данные в виде набора входных параметров и выдавать результаты в виде набора выходных значений. Файл-функции, являющиеся типичными полноценными объектами языка программирования системы MATLAB (и одновременно полноценными модулями с позиций структурного программирования), как правило, применяют при решении разного рода задач с использованием численных методов. Файл-функция служит средством расширения системы MATLAB. При обнаружении файл-функции она сначала компилируется, а затем исполняется (созданные машинные коды хранятся при этом в рабочей области системы MATLAB).
Основное отличие между файл-программами и файл-функциями состоит в работе с переменными. В частности, файл-программы работают только с переменными рабочего пространства и не имеют локальных переменных, т.
е. все переменные, определённые в файл-программе, после её выполнения становятся доступными в рабочем пространстве и могут быть использованы в других файл-программах или командах, вводимых в командной строке (аналогично в файл-программе могут быть использованы все переменные, уже определённые в командном окне, т.е. файл-программа работает с данными рабочей области). Таким образом, рабочее пространство становится общим для всех файл-программ, используемых в текущем сеансе работы с MATLAB. Достоинством такого подхода является достигаемая в результате полная интеграция файл-программы с рабочим пространством, что делает файл-программы средством автоматизации интерактивного режима работы пользователя с системой MATLAB. Указанная интеграция является при этом и недостатком — так, например, если предполагается оформить в виде файл-программы отдельный фрагмент решения некоторой задачи, его следует всегда вызывать в одной и той же программной обстановке (что, очевидно, выполняется далеко не всегда).
Кроме того, файл-программе в момент её вызова нельзя передать в виде параметров дополнительную информацию, не содержащуюся в рабочем пространстве. При выполнении нескольких файл-программ также исключительно важно следить за тем, чтобы в них были согласованы общие переменные.
Перечисленные слабые стороны файл-программ преодолеваются посредством использования файл-функций, которые, впрочем, слабо подготовлены для автоматизации интерактивного режима работы, так как переменные, используемые в файл-функциях, являются полностью изолированными от рабочего пространства MATLAB. Все переменные, используемые внутри файл-функции, а также опреденённые в качестве её входных и выходных аргументов, воспринимаются программой как локальные и доступны только лишь в теле данной файл-функции. Итак, после выполнения файл-функции все значения этих переменных исчезают, а область оперативной памяти, в которой они хранились, освобождается.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Геометрическая интерпретация определенных интегралов
Пусть на отрезке [a, b], тогда
представляет собой площадь области, ограниченной осью х, графиком функции и прямыми x=a и x=b.
1. Метод средних прямоугольников
,
,
2. Метод трапеций
3. Метод Симпсона
Вычислить
,где — полином 3-ей степени.
Пример
,где
Ручной счет: n=4, h=(3-0)/4=0.75
а) Метод средних прямоугольников
, , i=1,2,3,4
| I | ||
| 0.375 | 0.713 | |
| 1.125 | -0.283 | |
| 1.875 | -3.951 | |
| 2.625 | -12.822 |
I=0.75(0.713-0.283-3.951-12.822)=-12.258
Ответ:
б) Метод трапеций:
, , i=0,1,2,3,4
| I | ||
| 0.0 | 1.0 | |
| 0.75 | 0.391 | |
| 1.5 | -1.625 | |
| 2.25 | -7.578 | |
3. 0 | -20.0 |
I=0.75((1.0-20)/2+0.391-1.625-7.578)=-13.734
Ответ:
в) Метод Симпсона:
, , i=0,1,2,3,4
| I | ||
| 0.0 | 1.0 | |
| 0.75 | 0.391 | |
| 1.5 | -1.625 | |
| 2.25 | -7.578 | |
| 3.0 | -20.0 |
I=0.75/3(1.0+4*0.391+2*(-1.625)+4*(-7.578)-20.0)=-12.749
Ответ:
Статьи к прочтению:
- Гибридная архитектура numa
- Гиперссылка на элемент другого документа
Геометрический смысл определенного интеграла. Тема
Похожие статьи:
Вычисление определенного интеграла с заданной точностью
Задача вычисления определенного интеграла формулируется следующим образом: вычислить I= c точностью ? при известных значения пределов интегрирования a,…
Выполнение программ до определенной точки
Понятие события Каждое действие пользователя (нажатие на клавишу, щелчок кнопкой мыши и т.
п.) формирует некоторое событие, т.е. сообщение о произошедшем….
п.) формирует некоторое событие, т.е. сообщение о произошедшем….MATLAB Tutor, часть 9
MATLAB Tutor, часть 9
Часть 9: Интеграция
MATLAB может найти как неопределенный интеграл (т.е. первообразную), так и и определенный интеграл символьного выражения. Это предполагает элементарное первообразная существует. Если нет, MATLAB может вычислить очень точное значение. численное приближение к определенному интегралу.
- Сначала посчитаем
неопределенные интегралы. Прежде чем что-то делать, мы должны объявить x — символьная переменная. Введите:
syms x
Затем введите
int(x*sin(x), x)
Убедитесь, что результат является первообразной x sin(x) с помощью ввод:
diff(ans, x)
- Введите еще одну символическую переменную a , чтобы выяснить, как
MATLAB имеет дело с более чем одной символьной переменной при интегрировании.
Введите:
syms a
Затем введите
int(a*sin(x), x)
Теперь введите
int(a*sin(x), a)
3 Какова роль переменная после запятой?
- Теперь попробуйте найти
первообразная для sin ( x 5 + x 3 ) .
MATLAB не знает первообразную этого функция, которая может быть определена в терминах функций, известных MATLAB. На с другой стороны введите: 92), x)
S-функция Френеля известна в MATLAB, но наверное не тебе. Однако можно проверить дифференцированием что выражение является первообразной.
- Далее вычисляем
определенные интегралы. Чтобы проинтегрировать x sin(x) по интервалу [0,pi/2] , введите:
int(x*sin(x), x, 0, pi/2)
- Теперь попробуйте это
метод интеграла от sin ( x 5 + x 93)’)
quadl(f , 0, pi/2 )Численное интегрирование также работает с пользовательскими функциями в m-файлах. Символическая интеграция не работает. Если у вас все еще есть m-файл с именем fun.m которую вы создали в части 6 этого руководства, введите:
quadl(‘fun’, 0, pi/2 )
Значение использования функции quadl заключается в том, что MATLAB не пытается найти символьное решение прежде чем приступить к числовой оценке.
- Используйте МАТЛАБ
найти точное значение каждого из следующих интегралов.
(Введите inf для символа бесконечности.)
- Интеграл от 1/(1+x 2 ) от 0 до 1 ,
- Интеграл от 1/(1+x 2 ) от 0 до Бесконечность ,
- Интеграл от 1/(1+x 4 ) от 0
Введите:
модуля@math.duke.edu | Авторское право КПК и автор(ы), 1998, 1999, 2000 г. |
Определенный интегральный MATLAB 2009 Версия
9 MARS 2022 — 13:14
Depanite Integral Matlab 2009 Версия
Allmänt
- Depanite Integral Matlab 2009. Define Define
- Define Integral Matlab 200999999999999999 Depante Define Define Define Define Aglebreab 2009. Define Define Define 9003 Depante Integral Matlab 20099999999999999999 Define Define Define Depant INTEGRAL MATLAB 2009 VERSION WINDOWS
Define Define Define 9003 Depante Integral Matlab 20099999999999999999 Define Define Define Depant INTEGRAL MATLAB 2009 VERSION WINDOWSУспешные интегрирования накапливаются как частичное значение интеграла. Если базовое семейство снова оказывается неудачным, то подинтервал дополнительно подразделяется, и весь процесс повторяется. Если требуемая точность не достигается, интервал сохраняется для проверки в будущем (см. ifail = 2) и проверяется второй подинтервал.
DEFINITE INTEGRAL MATLAB ВЕРСИЯ 2009 КАК
Подход, используемый здесь, заключается в том, чтобы научиться использовать MATLAB для выполнения некоторых основных операций, например построения графиков, решения алгебраических уравнений, вычисления интегралов и решения дифференциальных уравнений. Базовое семейство затем применяется к первому подинтервалу. Скорее, цель этой книги — познакомить человека, плохо знакомого с MATLAB, с миром вычислительной математики. Исследуемый интервал делится на два подинтервала (не всегда равные).
некоторое неопределенное и определенное интегрирование (см. символическое интегрирование), в том числе многомерные интегралы с символическими ограничениями и глобальные без ограничений. Однако, если вы хотите подавить и скрыть вывод MATLAB для выражения, добавьте точку с запятой после выражения. Использование точки с запятой ( ) в MATLAB Точка с запятой ( ) указывает на конец оператора. Если все правила в семействе были применены безуспешно, вызывается подразделение. MATLAB предоставляет некоторые специальные выражения для некоторых математических символов, таких как pi для, Inf для, i (и j) для -1 и т. д. Nan означает «не число». Когда два последовательных правила отличаются друг от друга меньше, чем требуемая относительная точность, последнее использованное правило принимается за значение интеграла, и операция считается успешной. Электронная таблица Matlab Definite Integral Ordinary Differential Equations Programming (Excel. Наиболее популярными версиями среди пользователей MATLAB Student являются 7.
7, 7.1 и 7.0. (По состоянию на сентябрь 2012 г. новая версия octave ( octave-3.6.2-vs2010-setup. Версия Упомянутая здесь Octave содержит редактор Notepad++, который работает, но плохо интегрирован с Octave.0003
DEFINITE INTEGRAL MATLAB 2009 ВЕРСИЯ WINDOWS
MATLAB Student совместим со средой Windows XP/Vista/7, 32-разрядная версия. Графический интерфейс Matlab очень хорош и намного опережает его в Octave.
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ВЕРСИИ DEFINITE INTEGRAL MATLAB 2009
Программное обеспечение входит в состав средств разработки, точнее IDE. Обновлено для версии 1.3.22 (бета) от февраля Обновлено для версии 1.2.35 от августа Обновлено для версии 1.0.61 от 31 января Обновлено для версии 1.0. Наиболее часто встречающиеся имена установочных файлов программы: matlab.exe, meditor.exe и т. д. 2011 (Ziah Dean) Обновлено для версии 1.3.40 от 24 июля 2009 г.. ISBN: 9780123747839 (список 49.95, 39.95 от Barn & Nobel MATLAB (версия R2020b от Mathworks, версия R2020b от Virtual).